Дифференциальные операции второго порядка
Контрольная работа
тема: "Дифференциальные операции
второго порядка"
Москва 2014
Содержание
Введение
1. Оператор Лапласа
2. Градиент дивергенции
3. Дивергенция градиента и ротора
4. Ротор градиента и ротора
5. Формулы Грина
Список использованной литературы и источников
Введение
Вычисление градиента, дивергенции и ротора связано с
однократным дифференцированием некоторых функций, поэтому эти операции называют
дифференциальными операциями первого порядка.
Для скалярного поля  был введен один оператор первого порядка
был введен один оператор первого порядка
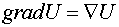 .
.
Для векторного поля введены два оператора первого порядка
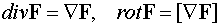 .
.
Повторное применение оператора "набла" приводит к
необходимости вычисления вторых производных. Т.о. мы приходим к
дифференциальным операторам второго порядка.
Имеет смысл рассматривать пять дифференциальных операций второго
порядка:
) 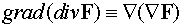 ;
;
) 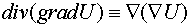 ;
;
) 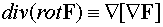 ;
;
) 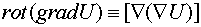 ;
;
) 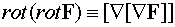 .
.
Будем считать, что необходимые условия дифференцируемости,
непрерывности и пр. выполнены. Более детально эти вопросы обсуждаются в расширенных
курсах высшей математики.
1. Оператор
Лапласа
Рассмотрим скалярное поле 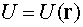 . Существует единственный дифференциальный оператор, действующий
на это поле
. Существует единственный дифференциальный оператор, действующий
на это поле
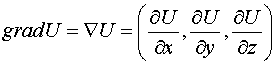 .
.
Полученный вектор указывает величину и направление максимального
возрастания функции 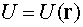 .
.
Вычислим в явном виде 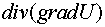 . Используя оператор "набла", имеем
. Используя оператор "набла", имеем
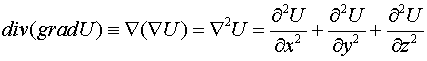 .
.
Убедимся в справедливости этого выражения путем непосредственного
дифференцирования:
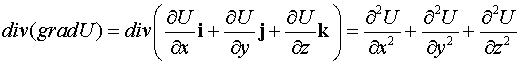 .
.
Выражение, естественно, получилось таким же.
Такое выражение часто встречается в различных задачах
математической физики и для его записи введен специальный дифференциальный
оператор второго порядка:
дифференциальная операция градиент дивергенция
 .
.
Этот оператор называют оператором Лапласа или лапласианом.
Формально можно записать
 .
.
Итак, дивергенция градиента скалярной функции равна лапласиану
этой функции. Оператор Лапласа широко применяется в различных задачах. Так,
например, расчет температурного поля сводится к решению уравнения Лапласа

с соответствующими граничными условиями.
. Градиент
дивергенции
Рассмотрим операцию 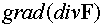 . В прямоугольной декартовой системе координат имеем
. В прямоугольной декартовой системе координат имеем

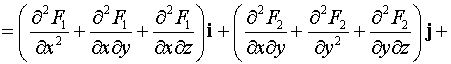
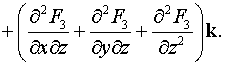
Полученное выражение является вектором, компонентами которого
являются комбинации частных производных второго порядка.
Отметим, что некорректное использование оператора
"набла" может привести к неверным результатам:
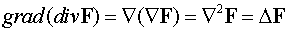 .
.
В этой формуле, которая отличается от полученной в начале
параграфа, допущена ошибка в преобразовании
 .
.
Три вектора, которые здесь используются, не образуют смешанное
произведение векторов (в смешанном произведении 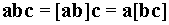 ). Заменять действие двух операторов "набла" одним
оператором Δ недопустимо,
т.к. их последовательные действия в отношении вектора F различаются.
). Заменять действие двух операторов "набла" одним
оператором Δ недопустимо,
т.к. их последовательные действия в отношении вектора F различаются.
Следует иметь в виду, что операции с оператором 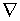 требуют внимания и аккуратности, поэтому
соответствующие преобразования следует сопровождать непосредственными
вычислениями, выполняя дифференцирование по координатам.
требуют внимания и аккуратности, поэтому
соответствующие преобразования следует сопровождать непосредственными
вычислениями, выполняя дифференцирование по координатам.
3.
Дивергенция градиента и ротора
Дивергенцию градиента 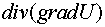 мы определили в §1
мы определили в §1
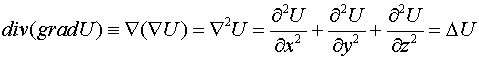 ,
,
где был введен оператор Лапласа
 .
.
Найдем дивергенцию ротора с помощью оператора "набла":
 .
.
Нетрудно убедиться в справедливости этого равенства и
непосредственным дифференцированием. Предлагается сделать это самостоятельно.
В выражении 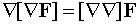 рассматривается смешанное произведение
трех векторов
рассматривается смешанное произведение
трех векторов 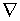 ,
, 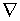 и
и 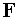 . Отметим отличие этого случая от
выражения
. Отметим отличие этого случая от
выражения
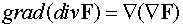 ,
,
которое не является смешанным произведением (выражение 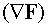 является скалярным произведением, а не
векторным).
является скалярным произведением, а не
векторным).
4. Ротор
градиента и ротора
Для операции  можно также использовать оператор
"набла":
можно также использовать оператор
"набла":
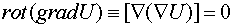 ,
,
Здесь учтено, что векторное произведение коллинеарных операторов
равно нулю. Предлагается получить этот же результат путем непосредственного
дифференцирования.
Из полученного результата можно получить важное следствие.
Рассмотрим некоторую замкнутую кривую L и натянем на нее произвольную поверхность S.
Используя теорему Стокса, можем записать
 .
.
Полученный результат сформулируем в виде теоремы:
Теорема 1. Циркуляция векторного поля 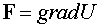 по любому замкнутому контуру равна нулю.
по любому замкнутому контуру равна нулю.
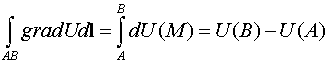 .
.
Доказательство. Сделаем рисунок.
Выполним простейшие преобразования
 ,
,
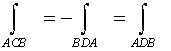
Следовательно
 . Имеем
. Имеем
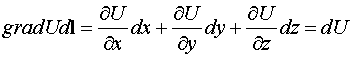 .
.
Это означает, что подынтегральное выражение является полным
дифференциалом. Следовательно, величина интеграла зависит только от выбора
точек А и В:
 .
.
Вычислим операцию 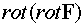 . Для этого используем известную из векторной алгебры формулу для
двойного векторного произведения
. Для этого используем известную из векторной алгебры формулу для
двойного векторного произведения
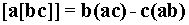 .
.
Перепишем эту формулу в более удобном для нас виде
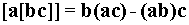 .
.
Преобразование сделано так, чтобы в дальнейших формулах оператор
"набла" не стоял на последней позиции. В терминах оператора
"набла" получим
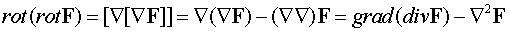 .
.
(Что было бы, если использовать обычную формулу для двойного
векторного произведения?)
Используя обозначение оператора Лапласа, можно записать
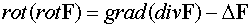 .
.
Имеем систему трех дифференциальных соотношений, записанных для
компонент вектора F.
Мы рассмотрели основные дифференциальные операции второго порядка.
В дальнейшем будем их использовать при решении различных задач.
5. Формулы
Грина
Получим еще несколько формул общего характера, которые
связывают свойства различных функций и широко используются в приложениях.
Запишем формулу Гаусса-Остроградского
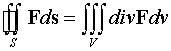 .
.
Пусть  и
и 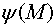 - две произвольные скалярные функции. Положим
- две произвольные скалярные функции. Положим
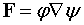 .
.
Тогда теорема Гаусса-Остроградского принимает вид
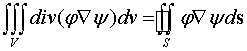 .
.
Можно записать
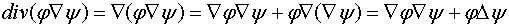 ,
,
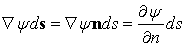 .
.
Здесь введено обозначение

для производной функции 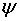 по направлению
по направлению 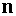
После подстановки этих выражений в видоизмененную формулу
Гаусса-Остроградского получим
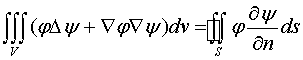 .
.
Эта формула называется первой формулой Грина.
Аналогично, если положить
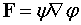 ,
,
то первая формула Грина примет вид
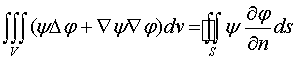 .
.
Вычитая соответствующие формулы, получим
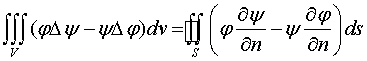 .
.
Эта формула называется второй формулой Грина.
Используя формулы Грина, можно получить связи между значениями
функции во внутренних точках выделенного объема и на границах.
Теорема 1. Значение функции 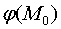 во внутренней точке
во внутренней точке  области Т, ограниченной поверхностью S, определяется формулой
области Т, ограниченной поверхностью S, определяется формулой
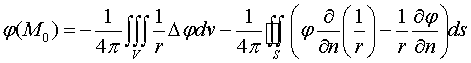 , где
, где
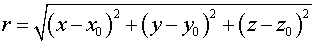 -
-
расстояние между точками  и
и  . Доказательство. Рассмотрим точку
. Доказательство. Рассмотрим точку  и окружим ее маленькой сферической
поверхностью
и окружим ее маленькой сферической
поверхностью 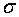 радиуса
радиуса 
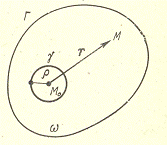
Введем функцию
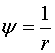 , где
, где
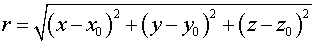 .
.
Нетрудно вычислить оператор Лапласа от функции 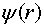 (сделать самостоятельно)
(сделать самостоятельно)
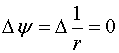 .
.
Из второй формулы Грина
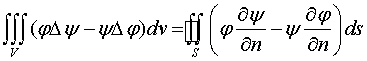 ,
,
записанной для области, ограниченной поверхностями S и 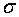 , получим
, получим
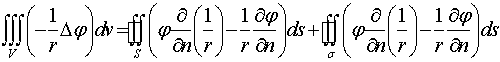
Рассмотрим интеграл по поверхности сферы
Учитывая условие  , получим
, получим
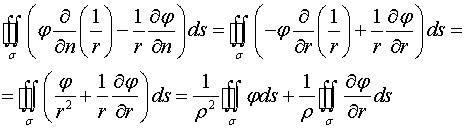
Пусть 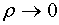 . Теорема о среднем для поверхностного
интеграла имеет вид
. Теорема о среднем для поверхностного
интеграла имеет вид
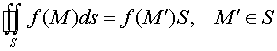 .
.
Применим к нашему интегралу теорему о среднем
 .
.
В пределе  получим
получим
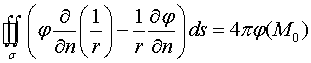 .
.
Возвращаемся к первоначальной формуле Грина
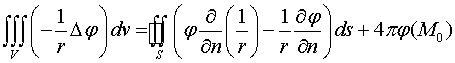 . тсюда
. тсюда
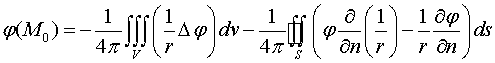 .
.
. Вопросы и задачи
. Вычислить оператор Лапласа для функций:
а) 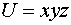 ,
,
б) 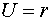 , где
, где 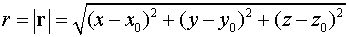 ,
,
в) 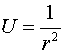 ,
,
г) 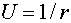 ,
,
д) 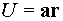 , где
, где 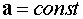 .
.
Список
использованной литературы и источников
1.
Тихонов А.Н., Самарский А.А. Уравнения математической физики, М.: МГУ, 1999,
798 с.
.
Кальницкий Л.А., Добротин Д.А., Жевержев В.Ф. Специальный курс высшей
математики для втузов, М.: "Высшая школа", 1976, 390 с.
.
Берман Г.Н. Сборник задач по курсу математического анализа, М.: Наука, 1985,
384 с.
.
Все решения к "Сборнику задач по общему курсу физики" В.С.
Волькенштейн, М.: Аст, 1999, книга 1, 430 с., книга 2, 588 с.
.
Красильников О.М. Физика. Методическое руководство по обработке результатов
наблюдений. М.: МИСиС, 2002, 29 с.
.
Супрун И.Т., Абрамова С.С. Физика. Методические указания по выполнению
лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.