Построение математической модели привода двигателя

Построение математической модели привода двигателя

Введение

Цель курсовой работы - получить навыки в построении математических моделей приводов.

В соответствии с заданием необходимо разработать следящую систему, удовлетворяющую определенным техническим условиям и смоделировать работу двигателя в различных режимах работы с учетом нелинейности.

1. Техническое задание

Построить математическую модель привода.

Моделировать работу двигателя в различных режимах работы с учетом нелинейности.

Технические требования:

Максимальная скорость слежения………..Щ_m = 40⁰/c

Максимальное ускорение слежения………е_m = 50⁰/c²

Статическая ошибка………………………..д_ст = 8`

Динамическая ошибка………………………д_дин = 20`

Показатель колебательности……………….М = 1,3

Момент инерции нагрузки……………………J_н = 400 кг∙м²

Возмущающий момент……………………..M_в = 5 кг∙м

Статический момент………………………..M_ст = 10 кг∙м

КПД редуктора………………………….…з = 0,75

2. Обобщенная функциональная схема привода

привод передаточный двигатель

ИУ - измерительное устройство

ПУ - предварительный усилитель

ЭМУ - электромашинный усилитель

Д - двигатель

Р - редуктор

Также в двигателе присутствует нелинейность типа

3. Энергетический расчет, выбор двигателя

Целью расчета является выбор исполнительного двигателя и ЭМУ

Определяем среднеквадратический момент нагрузки.

Находим ориентировочную мощность двигателя.

 - коэффициент запаса по скорости.

Из справочника выбираем двигатели постоянного тока, с мощностью близкой к расчетной.

Для выбранного двигателя вычисляем эквивалентный момент.

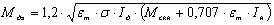
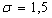 - коэффициент, учитывающий момент инерции редуктора.

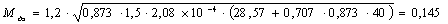 кгм;

Проверяем выполнение условия нагрева: М_дэ ≤ М_ном

,45 < 16,1 - условие выполняется;

Вычисляем передаточное число редуктора.

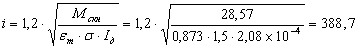
Проверяем выполнение условия обеспечения максимальной скорости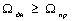

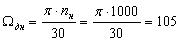 ^рад/_с.

< 208,8 - условие не выполняется.

Корректируем передаточное число редуктора

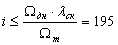; i = 190.

Проверяем двигатель на перегрузку.

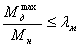
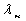 = 2,5 - коэффициент перегрузки.

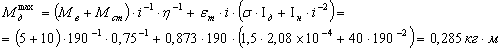
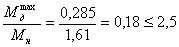 - перегрузка отсутствует.

Двигатель ДК1 - 2,3 подходит по всем параметрам.

Определим необходимые параметры двигателя:

- механическая постоянная:

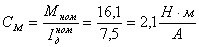
электрическая постоянная:

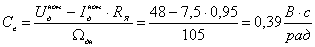
сопротивление якоря:

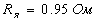
индуктивность якоря:

р = 2 - число пар полюсов; в = 0,3 - коэффициент, учитывающий конструктивное исполнение двигателя.

Выберем ЭМУ:

Для двигателя ДК1 - 2,3 подберем ЭМУ 5А с параметрами

Номинальная мощность: 0,5 кВт;

Номинальное напряжение: 60 В;

Номинальный ток: 8,3 А;

Коэффициент усиления по напряжению: (10ч12);

Коэффициент усиления по мощности: ≤ 2500;

Постоянная времени обмотки управления; 0,05 с;

Постоянная времени короткозамкнутой цепи: 0,04 с.

4. Расчет параметров передаточных функций элементов

Передаточная функция электромашинного усилителя:

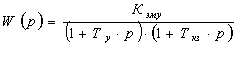
К_эму = 11; Т_у = 0,05 с; Т_кз = 0,04 с.

.

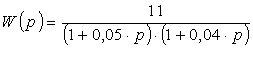Передаточная функция двигателя:

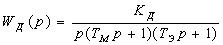
электромеханическая постоянная времени

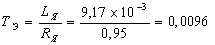с.;

- коэффициент передачи двигателя

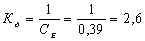
электромагнитная постоянная времени

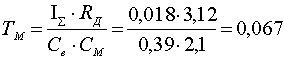с.

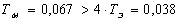 - следовательно, Т_Э пренебрегаем.

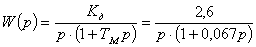
Коэффициент редукции:

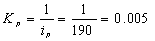
Коэффициент предварительного усилителя

Выбираю эмпирически.

5. Моделирование работы системы

Математическая модель системы без нелинейности:

При этом график переходного процесса угловой скорости на выходе имеет вид:

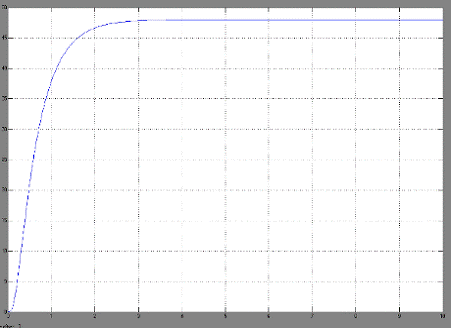
Видно, что отсутствует перерегулирование, быстродействие равно 3 с.

Математическая модель с учетом существенной нелинейности:

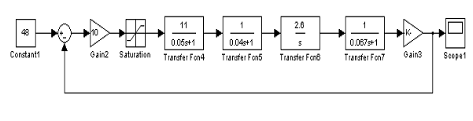
При этом график переходного процесса угловой скорости на выходе имеет вид:

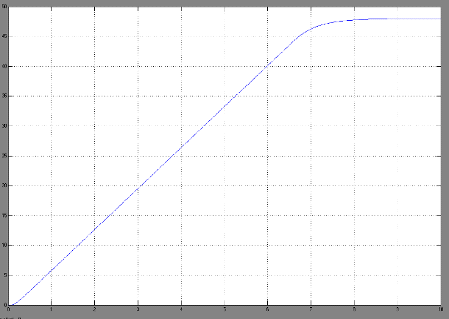
Введение нелинейности уменьшило быстродействие системы(8с).

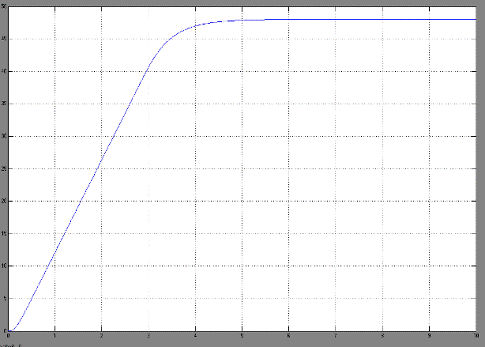
При увеличении пределов нелинейности быстродействие системы увеличивается (5с).

Математическая модель с раскрытым двигателем. Воздействие момента сопротивления равно 0 Нм.

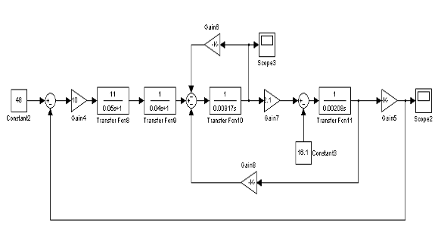
График переходного процесса тока якоря двигателя имеет вид:

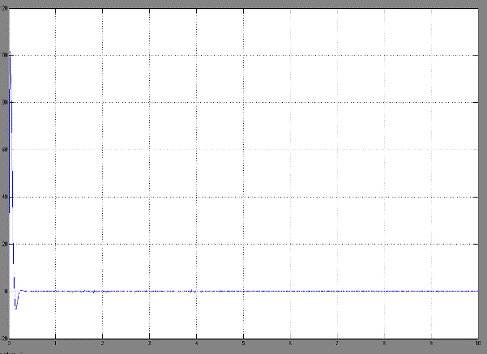
Для преодоления момента сопротивления, момент, развиваемый двигателем, должен быть много выше номинального. Этим обьясняется скачёк тока в начале переходного процесса.

При этом график переходного процесса угловой скорости на выходе имеет вид:

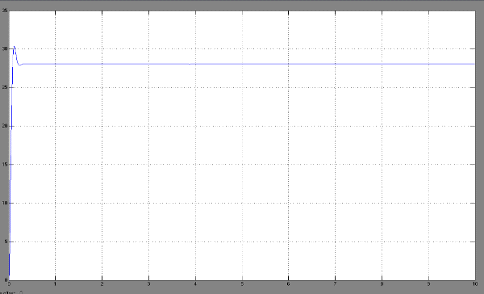
Увеличим момент сопротивления до значения равному половине номинальному моменту двигателя (8.05Нм).

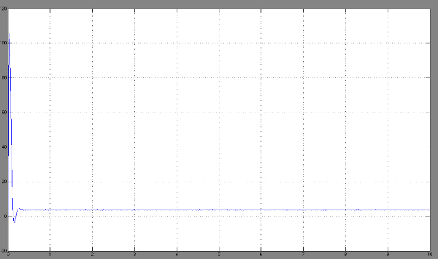
При увеличении момента нагрузки - растет ток якоря.

При этом график переходного процесса угловой скорости на выходе имеет вид:

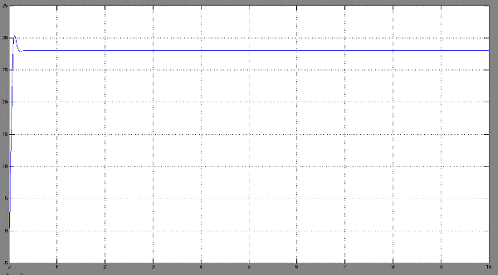
Значение угловой скорости практически не меняется.

Увеличим момент сопротивления до значения равному номинальному моменту двигателя (16,1Нм).

График переходного процесса тока якоря двигателя имеет вид:

Увеличилось как скачкообразное, так и установившееся значение тока. Что свидетельствует об увеличении нагрузки.

При этом график переходного процесса угловой скорости на выходе имеет вид:

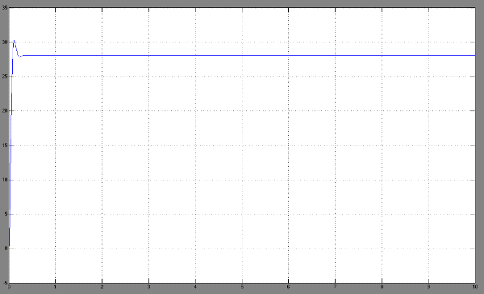
При увеличении нагрузки, скорость не изменилась.

Математическая модель с нелинейностью и раскрытым двигателем. Воздействие момента сопротивления - шаговое. Воздействие момента сопротивления равно 0 Нм.

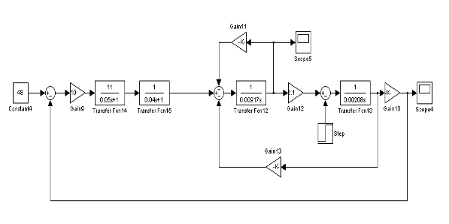
График переходного процесса тока якоря двигателя имеет вид:

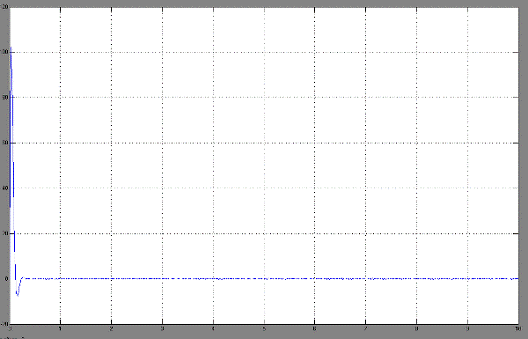
При этом график переходного процесса угловой скорости на выходе имеет вид:

Увеличим момент сопротивления до значения равному половине номинальному моменту двигателя (8.05Нм).

График переходного процесса тока якоря двигателя имеет вид:

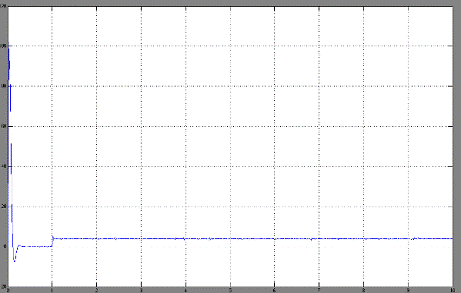
Значение тока якоря увеличилось, скачкообразно.

При этом график переходного процесса угловой скорости на выходе имеет вид:

Увеличим момент сопротивления до значения равному номинальному моменту двигателя (16,1Нм).

График переходного процесса тока якоря двигателя имеет вид:

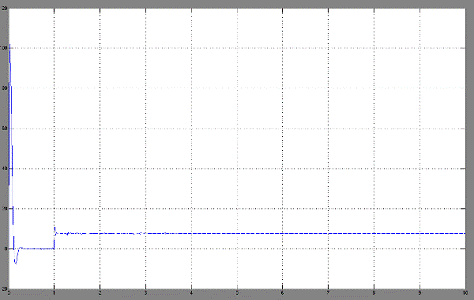
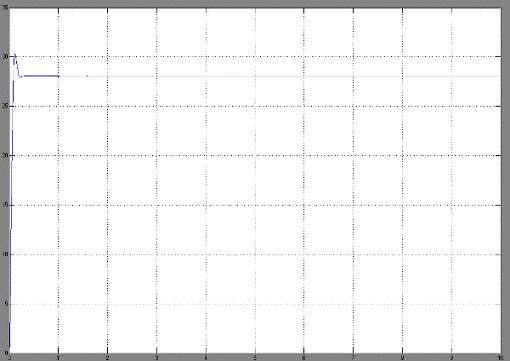
При этом график переходного процесса угловой скорости на выходе имеет вид:

Вывод

В ходе курсовой работы мною была построена математическая модель привода, и промоделирована работа двигателя в различных режимах работы с учетом нелинейности. Также была построена обобщенная функциональная схема привода, произведен энергетический расчет двигателя постоянного тока, расчет параметров передаточных функций.

Список использованной литературы

1. Хрущёв В.В. Электрические машины систем автоматики. - Л.: Энергоатомиздат, 1985.

. Коровин В.В. Электрические машины - М.: Машиностроение. 1984.

. Лекции по дисциплине «Приводы роботов».

. Лекции по дисциплине «Моделирование роботов и РТС».