|
Значения
коэффициентов дифференциального уравнения объекта
|
|
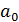
|
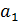
|
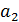
|
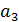
|
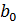
|

|

|
|
-4
|
2
|
3
|
1
|
5
|
6
|
12
|
0
|
Объект описан дифференциальным уравнением:
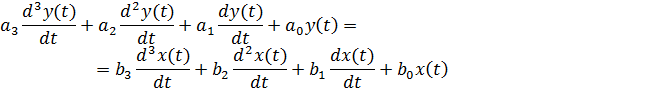
Постановка задачи:
. Записать модель объекта в форме передаточной
функции.
. Записать модель объекта в пространстве
состояний.
. Определить нули и полюса передаточной функции.
. Определить коэффициент усиления системы в
установившемся режиме и полосу пропускания системы.
. Построить карту расположения нулей и полюсов,
импульсную и переходную характеристики, частотные характеристики.
. Построить процесс на выходе системы при
произвольном входном сигнале.
. Использовать модуль LTI-Viewer для построения
различных характеристик.
Для описания линейных систем могут применяться
несколько способов:
− дифференциальные уравнения;
− модели в пространстве состояний;
− передаточные функции;
− модели вида «нули-полюса».
Первые два способа называются временными,
поскольку описывают поведение системы во временной области и отражают
внутренние связи между сигналами. Передаточные функции и модели вида
«нули-полюса» относятся к частотным способам описания, т.к. непосредственно
связаны с частотными характеристиками системы и отражают свойства объекта
«вход-выход».
Модель объекта в форме передаточной функции:

Текст программы
all;;
% Ввод передаточной функции %
num=[0 12 6 5]=[1 3 2
-4]=tf(num,den)
% Построение модели объекта в пространстве
состояний %_ss=ss(w)
% Нахождение нулей и полюсов передаточной
функции %
z=zero(w)=pole(w)
% Нахождение коэффициента усиления системы %
% в установившемся режиме %=dcgain(w)
% Определение полосы пропускания системы %=bandwidth(w)
% Построение модели системы в форме
"нули-полюса" %_zpk=zpk(w)
% Расположение нулей и полюсов системы на
графике %
pzmap(w);grid;-dmeta;
% Построение переходной функции
%(w);grid;-dmeta;
% Построение импульсной переходной функции %
impulse(w);grid;-dmeta;
% Создание массива частот для построения %
% амплитудно-частотной характеристики
%=logspace(-4,4,500);
r=freqresp(w,freq);=r(:);(freq,abs(r));grid;
print -dmeta;
% Создание массива частот для построения %
% фазо-частотной характеристики %=logspace(-4,4,500);
r=freqresp(w,freq);=r(:);=angle(r)*180/pi;(freq,phi);grid;-dmeta;
% Диаграмма
Боде
%(w);grid;
print -dmeta;
% Частотный годограф Найквиста %
nyquist(w);grid;-dmeta;
% Сигнал, имитирующий прямоугольные импульсы %
% единичной амплитуды %
% (период - 4 секунды, количество - 5 импульсов)
%
[u,t]=gensig('square',4);
lsim(w,u,t);grid;
print -dmeta;
Результаты работы программы
= 0 12 6 5= 1 3 2 -4=
12 s^2 + 6 s + 5
--------------------^3 + 3 s^2 + 2 s
- 4time transfer function._ss = = x2 x3-3 -1 22 0 00 1 0= 400= x2 x33 0.75
0.625= 0time state-space model.=
.2500 + 0.5951i
.2500 - 0.5951i=
.8982 + 1.1917i
.8982 - 1.1917i
.7963 + 0.0000i=
.2500=
.3819_zpk =
(s^2 + 0.5s + 0.4167)
(s-0.7963) (s^2 + 3.796s +
5.023)time zero/pole/gain model.
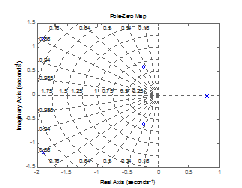
Рис.
2.1. Расположение нулей и полюсов системы на графике
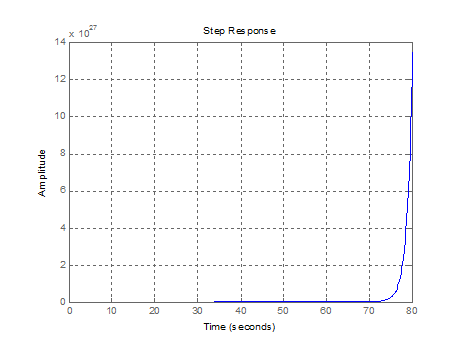
Рис.
2.2. Переходная функция
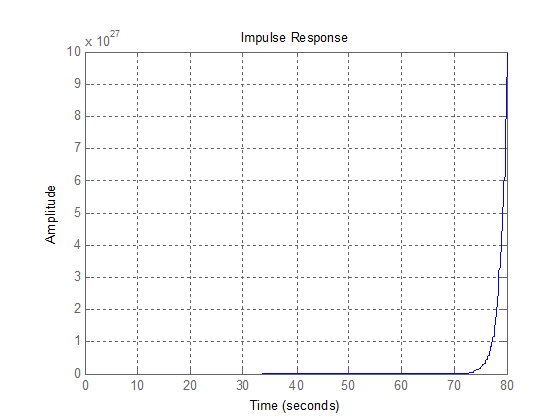
Рис.
2.3. Импульсная переходная функция
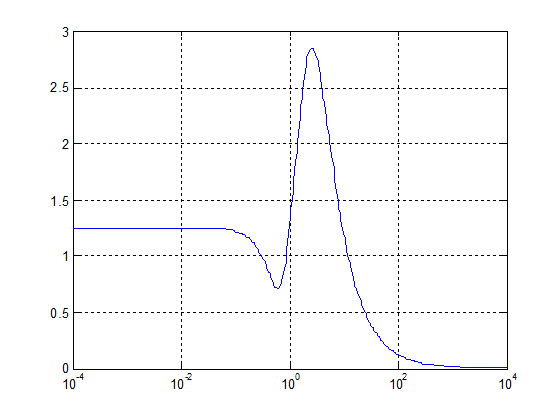
Рис.
2.4. Амплитудно-частотная характеристика

Рис.
2.5. Фазо-частотная характеристика

Рис.
2.6. Диаграмма Боде

Рис.
2.7. Частотный годограф Найквиста
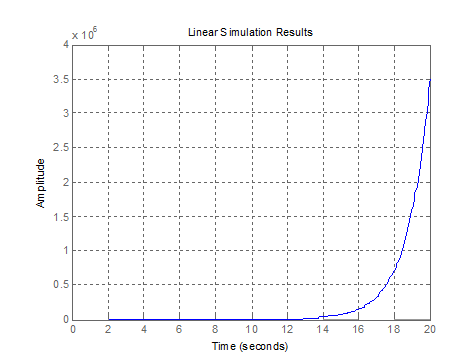
Рис.
2.8. Сигнал, имитирующий прямоугольные импульсы единичной амплитуды (период −
4 секунды, количество − 5 импульсов)
3.
Построение модели с распределенными параметрами
.1
Исходные данные
Рассмотрим
стержень из теплопроводящего материала с коэффициентом теплопроводности k.
Предположим, что температура на концах стержня задана, а боковая поверхность
стержня теплоизолирована. Пусть ось x направлена
вдоль оси стержня, а его концы расположены в точках x=0 и x=L.
.2
Общие теоретические сведения
Задача
сводится к определению зависимости от времени t температуры
u в точках стержня, то есть функции двух переменных u(x,t). Функция u(x,t)
должна удовлетворять уравнению теплопроводности
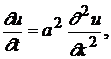 (0<x<L),(3.1)
(0<x<L),(3.1)
начальному условию
u(x,0)=f(x),
(0<x<L),(3.2)
и условиям на концах стержня
u(0,t)=j1(t), u(L,t)=j2(t), (tV0).(3.3)
Значения u(0,0) и u(L,0), полученные
из (2) и (3), должны совпадать. Это будет если jj1(0)=f(0), jj2(0)=f(L).
Следует отметить, что путем замены
переменных t^ў=a2t уравнение (1) можно преобразовать к виду:
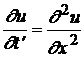 (3.4)
(3.4)
Это означает, что решение задачи (3.1÷3.3)
путем замены переменных сводится к решению задачи (3.4). Далее будем полагать
а=1.
Построим на плоскости (x,t) сетку с
шагом h по переменной x (xi=(i-1)h; i=1, …, n+1; h=L/n) и с шагом
tt по переменной t (tj=(j-1)tt). Обозначим uij=u(xi,tj).
Производные в уравнении (1) аппроксимируем следующим образом:
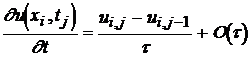 (3.5)
(3.5)
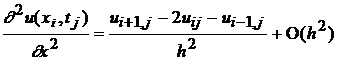 (3.6)
(3.6)
Подставляя (3.5) и (3.6) в (3.1) при a=1,
получим разностное уравнение:
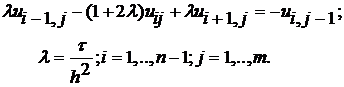 (3.7)
(3.7)
В соответствии с (3.2) и (3.3) значения
ui0=f(xi), u0j=j1(tj), unj=j2(tj)(3.8)
являются известными. Тогда,
подставляя в (3.7) j=0, получим систему n-1 линейных уравнений, решив которую
можно определить ui1 (i=1, …, n-1). При этом, поскольку u01=jj1(t1),
…, un1=jj2(t1), известными оказываются все
значения временного слоя j=1, (t=t1). Затем, подставляя в (3.7) j=2,
решаем систему уравнений относительно ui2 и т.д. для всех j=2, …, m.
Из (3.7) следует, что в каждое i-тое
уравнение (i=1, …, n-1) с ненулевыми коэффициентами входят только три
неизвестных (ui-1,j, uij, ui+1,j). Величина ui,j-1
к этому моменту является известной и потому отнесена в правую часть уравнения.
Таким образом, матрица системы уравнений является трехдиагональной и эту
систему можно решить методом прогонки. Для этого представим ее в стандартном
виде:
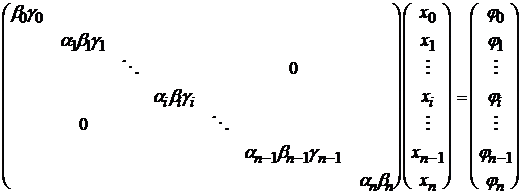 (3.9)
(3.9)
Для данной задачи
xi=uij, ai=l, gi=l, bi=1-2l,
b0=1, g0=0, j0=u0j=j1(tj),
jn=unj=j2(tj), ji=-ui,j-1
(i=1, …, n-1).
Пусть на j-том шаге заданными
являются параметры ui,j-1 (i=1, …, n-1), u0j, unj,
ll. Все неизвестные значения uij можно разместить в массиве xi
(xi=uij; i=0, …, n). Ищем связь xi-1 с xi
в виде рекуррентного соотношения:
xi-1=ci-1xi+ni-1, i=1, …, n.(3.10)
Подставляя (3.10) в (3.7), получаем:
lci-1xi-(1+2l)xi+lxi+1
= -ui,j-1-lni-1.(3.11)
Отсюда
 (3.12)
(3.12)
Сравнивая (3.12) с (3.10), находим рекуррентные
соотношения:
 ,
,
 (3.13)
(3.13)
cc0=0, nn0=u0j.
Таким образом, алгоритм определения
значений uij по известным ui,j-1 состоит из двух этапов:
прямого хода прогонки по формулам (3.13) при (i=1, …, n-1) и обратного хода
прогонки по формуле (3.10) при (i=n, …, 2).
а) 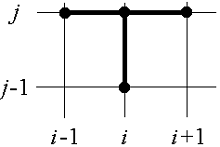 б)
б)
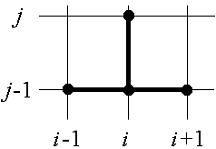
Рис. 3.1. Шаблоны неявной (а) и явной (б)
разностных схем
Необходимо отметить, что разностное уравнение
(7) связывает одно известное значение Ui,j-1
(из предыдущего j-1 временного слоя) и три неизвестных (Ui,j,
Ui-1,j,
Ui+1,j).
Поэтому найти значения Ui,j
(i=1, …, n-1) можно только все сразу путем решения системы уравнений. Такая
схема связи переменных в разностном уравнении называется неявной. Шаблон
неявной разностной схемы представлен на рис. 3.1 (а).
Наряду с неявной возможна организация явной
разностной схемы. Для этого вместо выражения (5) для первой разностной
производной по времени используют формулу:
 (3.14)
(3.14)
Тогда разностное уравнение запишется в виде:
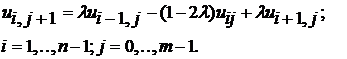 (3.15)
(3.15)
В этом случае связываются три неизвестные
значения, относящиеся к предыдущему временному слою (здесь j-тому) и только
одно неизвестное Ui,j+1.
Шаблон явной разностной схемы представлен на рис. 3.1 (б).
При использовании этой схемы неизвестные
параметры определяются путем последовательного применения формулы (2.14) при
i=1, …, n-1. Поскольку при этом не надо решать системы уравнений, то процесс
определения параметров одного временного слоя требует меньших затрат времени,
чем в случае неявной схемы.
Однако, неявная схема устойчива (ошибка не
возрастает от шага к шагу) при любых значениях λ=τ/h2.
Явная схема является устойчивой только при λ
<1/2. В противном случае развивается экспоненциальный рост погрешности так,
что обычно происходит аварийная остановка ЭВМ по переполнению порядка. Поэтому
при использовании явной схемы вычисления приходится вести с очень малым шагом
по времени.
В случае применения неявной схемы затраты
машинного времени для расчета одного временного слоя больше, но возможность
выбора значительно большего шага по времени t может обеспечить общее ускорение
процесса расчета по сравнению с явной схемой.
При выполнении данной работы будем предполагать,
что температура на концах стержня поддерживается постоянной
j1(t)Tf(0), j2(t)Tf(L).
.3 Решение задачи для исходных
данных
Решить смешанную задачу для
уравнения теплопроводности с начальными u(x,0)=f(x) и граничными условиями
u(0,t)=f(0), u(1,t)=b, L=1.
Табл. 3.1. Вариант задания
|
№
|
b
|
c
|
d
|
f(x)
|
|
1
|
1,1
|
3
|
0,05
|
|

|
Текст программы
//---------------------------------------------------------------------------
#include
<vcl.h>
#pragma hdrstop
#include "Unit1.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource
"*.dfm"*Form1;
//---------------------------------------------------------------------------
__fastcall
TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
#define a 14
#define b 16
#define c 0.25
#define d 0.5
#define N 20
#define L 1
#define tau 60
#define ro 7800
#define lam 46
#define c_f 460
#define t_max
3000T[N+1],alpha[N+1],beta[N+1],time1=0,h;A[N+1],C[N+1],B[N+1],F[N+1];h_iav,tau_iav,a_iav,T_iav[N+1],TT_iav[N+1],time_iav=0;funkf(float
x)
{m;(x>=0)
{(x<c)
{=a-(x/c)*a;
}(x<d)
{=0;
}
else
if(x<=1)
m=((1-x)*b)/(1-d);
}(m);
}start_heat_field(float h)
{(int
i=1;i<=N;i++)[i]=funkf(h*(i-1));
}neiavnii_metod_start(){=(float)L/(float)(N);_heat_field(h);(int
i=1;i<=N;i++)->Series1->AddXY(h*i,T[i]);
}neiavnii_metod_calc(){=time1+tau;[1]=0;[1]=funkf(0);(int
i=2;i<=N-1;i++){[i]=C[i]=lam/(h*h);[i]=(2*lam)/(h*h)+(ro*c_f)/tau
;[i]=-((ro*c_f)/tau)*T[i];[i]=A[i]/(B[i]-C[i]*alpha[i-1])
;[i]=(C[i]*beta[i-1]-F[i])/(B[i]-C[i]*alpha[i-1]);
}[N]=funkf(L-0.0000001);(int
i=N-1;i>=2;i--){[i]=(A[i]/(B[i]-C[i]*alpha[i]))*T[i+1]+(C[i]*beta[i-1]-F[i])/(B[i]-C[i]*alpha[i-1]);->Series1->Clear();[0]=funkf(0.0000001);(int
i=1;i<=N;i++)->Series1->AddXY(h*i,T[i]);
}
}iavnii_metod_start(){_iav=lam/(ro*c);_iav=(h*h)/(4*a_iav);(int
i=1;i<=N;i++)_iav[i]=funkf(h*(i-1));(int
i=1;i<=N;i++)->Series2->AddXY(h*i,T_iav[i]);_iav[1]=funkf(0.0000001);_iav[N]=funkf(L-0.0000001);
}iavnii_metod_calc(){_iav=time_iav+tau_iav;(int
i=1;i<=N+1;i++)_iav[i]=T_iav[i];(int
i=2;i<=N-1;i++)_iav[i]=TT_iav[i]+((lam*tau_iav)/(ro*c))*((TT_iav[i+1]-2*TT_iav[i]+TT_iav[i-1])/(h*h));->Series2->Clear();(int
i=1;i<=N;i++)->Series2->AddXY(h*i,T_iav[i]);
}__fastcall
TForm1::FormCreate(TObject *Sender)
{_metod_start();_metod_start();
}
//---------------------------------------------------------------------------__fastcall
TForm1::Button1Click(TObject *Sender)
{=0;_metod_start();_metod_start();(time1<t_max){_metod_calc();_metod_calc();
}->Caption="Time=
"+FloatToStr(time1);
}
//---------------------------------------------------------------------------__fastcall
TForm1::Button2Click(TObject *Sender)
{=0;_metod_start();_metod_start();(time1<TrackBar1->Position*tau){_metod_calc();_metod_calc();
}->Caption="Time=
"+FloatToStr(time1);
}
//---------------------------------------------------------------------------
Результаты работы программы
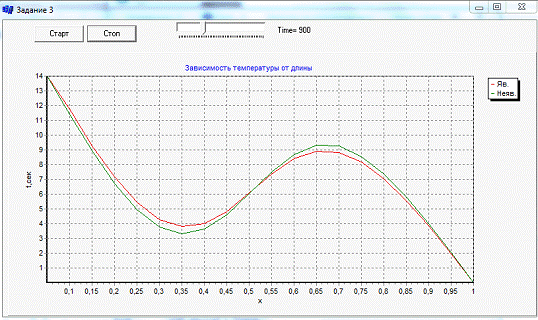
Вывод:
В процессе разработки программы были изучены
явный и неявный методы конечных разностей. По уравнению теплопроводности
программа моделирует процесс нагрева стержня.
корреляция модель итерационный
функция
4. Численные процедуры оценивания параметров
нелинейных регрессионных моделей
Метод Ньютона, алгоритм Ньютона (также известный
как метод касательных) − это итерационный численный метод нахождения
корня (нуля) заданной функции. Поиск решения осуществляется путем построения последовательных
приближений и основан на принципах простой итерации. Метод обладает
квадратичной сходимостью. Улучшением метода является метод хорд и касательных.
Также метод Ньютона может быть использован для решения задач оптимизации, в
которых требуется определить нуль первой производной либо градиента в случае
многомерного пространства.
Основная идея метода заключается в следующем:
задается начальное приближение вблизи предположительного корня, после чего
строится касательная к исследуемой функции в точке приближения, для которой
находится пересечение с осью абсцисс. Эта точка и берется в качестве следующего
приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть 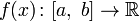 − определена на отрезке
− определена на отрезке 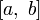 и
дифференцируемая
<#"723183.files/image093.gif">
и
дифференцируемая
<#"723183.files/image093.gif">
где  − угол наклона касательной в
точке
− угол наклона касательной в
точке  .
.
Следовательно, искомое выражение для
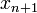 имеет вид:
имеет вид:

Итерационный процесс начинается с
некоего начального приближения 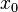 (чем ближе к корню, тем лучше, но
если предположения о его нахождении отсутствуют, методом проб и ошибок можно
сузить область возможных значений, применив теорему о промежуточных значениях
<#"723183.files/image098.gif">.
(чем ближе к корню, тем лучше, но
если предположения о его нахождении отсутствуют, методом проб и ошибок можно
сузить область возможных значений, применив теорему о промежуточных значениях
<#"723183.files/image098.gif">.
. Пока не выполнено условие
остановки, в качестве которого можно взять 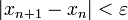 или
или 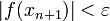 (т.е. погрешность в нужных
пределах), вычисляют новое приближение:
(т.е. погрешность в нужных
пределах), вычисляют новое приближение: 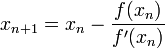 .
.
Недостатки:
. Если начальное приближение
недостаточно близко к решению, то метод может не сойтись.
. Если производная
<#"723183.files/image102.gif">
Вывод:
Освоен метод оптимизации Ньютона на примере
регрессионного уравнения, посредством которого достигнута более высокая
точность его коэффициентов.
Заключение
В ходе выполнения курсовой работы были получены
практические навыки в построении математических моделей технических объектов,
написании программ для решения задач моделирования с использованием
математического пакета MATLAB,
изучены теоретические основы и особенности выполнения параметрической
идентификации различных моделей, реализации алгоритмов линейного и нелинейного
регрессионного анализа, планирования эксперимента.
Перечень ссылок
1. Автоматизированные системы
управления технологическими процессами. Идентификация и оптимальное управление
/ Под ред. Салнги В.И. − Харьков: «Вища
школа», 1976 г. −
180 с.
. Брикман М.С., Кристинков Д.С.
Аналитическая идентификация управляемых систем. − Рига: «Зинатне», 1974
г. − 206 с.
. Гельфандбейн Я.А. Методы
кибернетической диагностики динамических систем. Идентификация функционирующих
систем математическими моделями. − Рига: «Зинатне», 1967 г. − 542
с.
. Дрейпер Н., Смит Г. Прикладной
регрессионный анализ. − М.: «Статистика»,
1973 г. − 391 с.
. Демиденко Е.З. Линейная и
нелинейная регрессии. - М.: «Финансы
и статистика», 1981 г.