Математическая модель оптимизации плана производства промышленного предприятия

Математическая модель оптимизации плана производства промышленного предприятия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

СТЕРЛИТАМАКСКИЙ ФИЛИАЛ

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Кафедра экономической теории и анализа

КУРСОВАЯ РАБОТА

по дисциплине «Экономико-математическое моделирование»

на тему «Математическая модель оптимизации плана производства промышленного предприятия»

Выполнил:

Сурашева Кристина Аликовна

Проверил:

Нафикова Альбина Ринатовна

Стерлитамак 2013

Содержание

Введение

Глава 1. Теоретические основы задач оптимизации

.1 Математическое программирование

.2 Линейное программирование

.3 Дифференциальные и разностные уравнения в экономико-математических моделях

Глава 2. Решение социально-экономических задач в математическом пакете Maple

.1 Задачи, подчиняющиеся закону естественного роста

.2 Задачи роста в социально-экономической сфере с учетом насыщения

.3 Задачи на применение экономико-математического моделирования

Заключение

Список литературы

Введение

Характерной чертой современности является стремительный научно-технический прогресс, что требует от менеджеров и бизнесменов значительного повышения ответственности за качество принятия решений. Это основная причина, которая обусловливает необходимость научного принятия управленческих решений. Одним из направлений научно-технического прогресса стало математическое программирование <#"722518.files/image001.gif">-мерного векторного пространства <#"722518.files/image002.gif"> 

Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП).

,

.

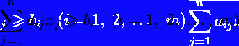Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства:

,

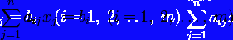Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств.

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты  с обратным знаком.

Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод <#"722518.files/image007.gif"> при выполнении условий

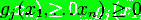
где  - параметры, 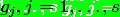 - ограничения,

 - количество параметров,  - количество ограничений.

В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе области, определенной ограничениями.

Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений, является метод неопределенных множителей <#"722518.files/image013.gif"> является линейной <#"722518.files/image014.gif">

После интегрирования обеих частей находим

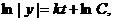
Откуда следует, что общим решением уравнения (1) является показательная функция

.

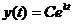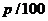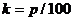Поскольку ежегодный прирост величины y(t) составляет p%, то скорость изменения величины составляет  от и коэффициент . Кроме того, по условию задачи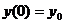. Поэтому сумма, которую заимодавец должен уплатить кредитору от занятых 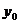 денежных единиц за t лет, составит

От каждой единицы занятой суммы заимодавец обязан уплатить 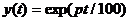. А за год эта сумма составит  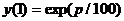денежных единиц.

Уравнение (9) с 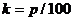 может быть применено не только при изучении кредитования. Оно применяется всякий раз, когда скорость изменения некоторой величины y(t) прямо пропорциональна ее значению в данный момент времени t, а ежегодный прирост равен p%.

Приведем листинг решения дифференциальной задачи в Maple.

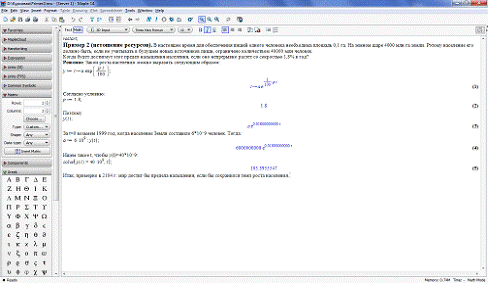
2. Задача истощения ресурсов. В настоящее время для обеспечения пищей одного человека необходима площадь 0,1 га. На земном шаре 4000 млн га земли. Поэтому население его должно быть, если не учитывать в будущем новых источников пищи, ограничено количеством 40000 млн человек.

Когда будет достигнут этот предел насыщения населения, если оно непрерывно растет со скоростью 1,8% в год?

Решение. Согласно формуле (19), закон роста населения можно выразить следующим образом:

.

За t = 0 возьмем 1999 год, когда население Земли составило 6 • 10⁹ человек. Тогда

.

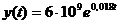Ищем такое t, чтобы

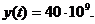
Тогда

,

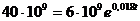откуда

.

Логарифмируя последнее равенство, имеем

,

откуда 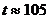лет.

Итак, примерно в 2104 г. мир достиг бы предела насыщения, если бы сохранился темп роста населения.

Приведем листинг решения дифференциальной задачи в Maple.

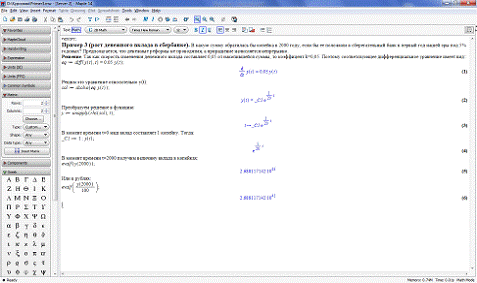
. Задача роста денежного вклада в сбербанке. В какую сумму обратилась бы копейка в 2000 году, если бы ее положили в сберегательный банк в первый год нашей эры под 5% годовых? Предполагается, что денежные реформы не проводятся, а приращение начисляется непрерывно.

.

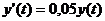Решением является функция .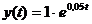

При t=2000 получим  коп. или 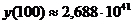 руб.

Приведем листинг решения дифференциальной задачи в Maple.

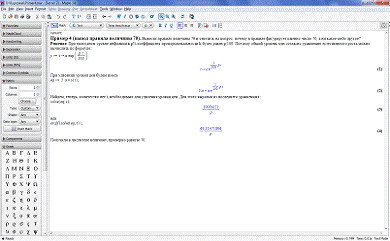
. Задача вывода правила величины 70. Вывести правило величины 70 и ответить на вопрос: почему в правиле фигурирует именно число 70, а ни какое-либо другое?

Решение. При ежегодном уровне инфляции в p% коэффициент пропорциональности k будет равен p/100. Поэтому общий уровень цен согласно уравнению естественного роста можно вычислить по формуле:

.

При удвоении уровня цен будем иметь:

,

.

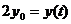Найдем, теперь, количество лет t, необходимых для удвоения уровня цен. Для этого выразим из последней формулы t. В результате получим

.

Поскольку 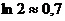, можно принять, что .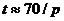

Формула получена. В числителе этой формулы стоит 70, так как 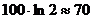. Если речь шла об утроении цен, то в числителе соответствующей формулы стояло бы не 70, а 110, так как в этом случае имели бы

,

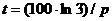a .

Приведем листинг решения дифференциальной задачи в Maple.

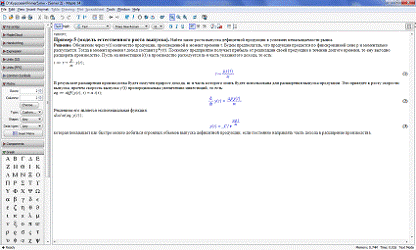
5. Задача модели естественного роста выпуска. Найти закон роста выпуска дефицитной продукции в условиях ненасыщаемости рынка.

Решение. Обозначим через y(t) количество продукции, произведенной в момент времени t. Будем предполагать, что продукция продается по фиксированной цене p и моментально раскупается. Тогда в момент времени t доход составит 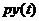. Поскольку предприятие получает прибыль от реализации своей продукции в течении долгого времени, то ему выгодно расширять производство. Пусть на инвестиции i(t) в производство расходуется m-я часть указанного дохода, то есть:

.

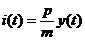В результате расширения производства будет получен прирост дохода, m-я часть которого опять будет использована для расширения выпуска продукции. Это приведет к росту скорости выпуска, причем скорость выпуска y'(t) пропорциональна увеличению инвестиций, то есть:

.

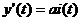Подставив (21) в (20), получим дифференциальное уравнение естественного роста

 .

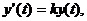
Решением его является экспоненциальная функция , которая показывает как быстро можно добиться огромных объемов выпуска дефицитной продукции, если постоянно направлять часть дохода в расширение производства.

Приведем листинг решения дифференциальной задачи в Maple.

2.2 Задачи роста в социально-экономической сфере с учетом насыщения

. Задача роста населения Земли. Определить как будет меняться рост населения Земли y(t) в условиях насыщения.

Решение. Согласно Ферхюльсту величина y(t) в условиях насыщения удовлетворяет дифференциальному уравнению:

,

.

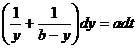Проинтегрировав это соотношение, имеем

,

то есть

.

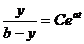Отсюда получим, что

.

Таким образом, рост в условиях насыщения описывается функцией (22). Приведем листинг решения дифференциальной задачи в Maple.

. Задача роста производства с учетом инвестиций. Государство решает перечислить в течении двух лет в только созданное предприятие и расширение его производства денежную сумму 20 тыс. условных единиц. При этом оно должно выбрать одну из непрерывных схем финансирования, изображенных на рис. 2:

Первая схема. Перечислять каждый год по 10 тыс. у.е.

Вторая схема. Перечислить в первый год все 20 тыс. у.е., и во второй год не перечислять ничего.

(По оси ординат единице соответствует 10 тыс. у.е.)

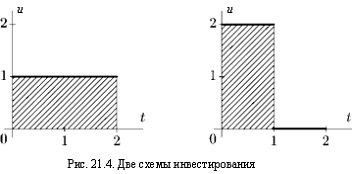
Рис. 2. Две схемы инвестирования.

Какую из двух схем инвестирования должно выбрать государство, чтобы предприятие выпустило больший объем продукции?

Решение. Предприятие начинает с нуля и еще не в состоянии делать инвестиции. Поэтому считаем, что у(0)=0. Государство вкладывает в каждый момент времени t сумму в u(t) денежных единиц. Поскольку в нашей упрощенной модели предполагается, что с момента создания первые же денежные инвестиции позволяют выпускать предприятию свою продукцию, то количество выпущенной продукции y(t) в денежном эквиваленте выражается уравнением

, .

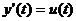. Для первой схемы инвестирования имеем

, при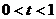

т.е. ,,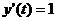

откуда 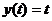, при .

Объем Y₁, выпущенной продукции за два года равен площади фигуры под графиком функции y(t). Площадь этой фигуры, представляющей собой треугольник (рис. 3), равна 2:

 (20 тыс. у.е.).

. Для второй схемы инвестирования имеем:

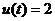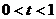, при ,

, при ,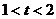

т. е.

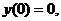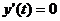  при

 при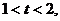

откуда

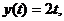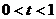 при ,

 при

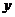
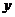
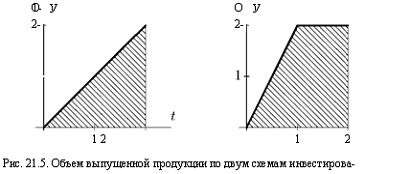
Рис. 3. Объем выпущенной продукции по двум схемам инвестирования.

Объем Y₂ продукции, выпущенной за два года по второй схеме инвестирования, равен площади трапеции (рис.3). Стало быть, Y₂ = 3 (30 тыс. у.е.).

Приведем листинг решения дифференциальной задачи в Maple.

.3 Задачи на применение экономико-математического моделирования

. Решение уравнения Хикса. Предположим, что a=1,25, m=0,95, n=0,1. Тогда уравнение Хикса примет вид

.

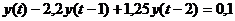Найдем частное решение. Положив 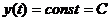 и подставив в (24), получим

, .

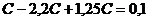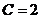Частное решение . Найдем общее решение соответствующего однородного уравнения.

Корни характеристического уравнения

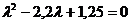
равны 1,1±0,2i.

Этим корням соответствуют линейно независимые решения вида

,

где 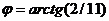. После округления получим

.

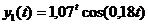
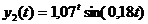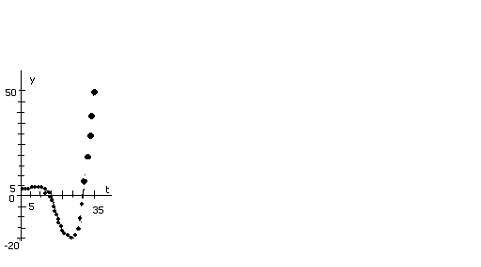
Рис. 4. Модель Самуэльсона-Хикса

Таким образом, общим решением однородного уравнения является функция

,

где С₁ и С₂ - Произвольные константы. Следовательно, общим решением уравнения (24) будет функция

.

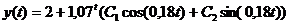График этой функции при С₁=С₂=1 и 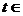N изображен на рис. 4.

Приведем листинг решения дифференциальной задачи в Maple.

Заключение

Во время написания данной работы нами были изучены примеры применения дифференциальных и разностных уравнений в социально-экономической сфере и приведены примеры их решения в математическом пакете Maple.

Необходимо отметить, что при использовании моделей естественного роста в социальных науках надо иметь в виду, что темпы роста, описываемые первоначально экспоненциальной функцией, в дальнейшем замедляются, наступает период насыщения. Экстраполяция этих показателей при условиях естественного роста часто приводит к заведомому абсурду. Например, рост числа научных работников в индустриально развитых странах в недавнем прошлом описывался экспоненциальной функцией. Экстраполяция привела бы к тому, что уже в ближайшие десятилетия численность научных работников должна была бы превзойти население страны.

Харрод и Домар считали, что можно добиться устойчивого роста не только объемов выпуска дефицитной продукции предприятия, но и также всей мировой рыночной экономики. Харрод считал, что устойчивый темп роста производства обеспечивается естественным ростом населения и естественным ростом производительности труда. Третьим фактором роста Харрод считал размеры накопления капитала, норма накопления которого должна быть постоянной.

Модель Самуэльсона - Хикса предполагает, что рост потребления c(t) (consumption) запаздывает от роста национального дохода у, т.е. что

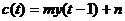
где m (marginal) - предельная склонность к потреблению (показывает на сколько увеличится потребление при увеличении текущего дохода на единицу (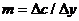)), a n - автономное потребление.

Предполагается также, что предприниматели осуществляют инвестиции i(t) (investments) после того, как убедятся в том, что приращение национального дохода устойчиво.

Модель Саймона является формализацией некоторых постулатов теории малых групп Д. Хоманса. Эти постулаты согласно Д. Хомансу таковы:

. Если деятельность изменяется, то взаимодействие, вообще говоря, также изменяется, и обратно.

. Лица, которые часто взаимодействуют друг с другом, стремятся любить друг друга.

. Если взаимодействие между членами группы часто осуществляется во внешней системе, чувство любви между членами растет, и это чувство, в свою очередь, способствует проявлению взаимодействия во внешней системе.

. Лица, которые имеют чувство любви друг к другу, будут выражать это чувство сверх деятельности внешней системы, и эта деятельность в дальнейшем будет усиливать чувство любви.

. Чем более часто люди взаимодействуют друг с другом, тем более в некотором отношении они становятся похожими как в своей деятельности, так и в чувствах.

Литература

1. Варламов А.С. Совершенствование управления ассортиментом на современных производственных предприятиях. - Ч.: Изд-во Челябинского. ун-та, 2009. - 74 с.

. Ахтямов А.М. Математика для социологов и экономистов: Учеб. пособие. - М.: ФИЗМАТЛИТ, 2009. - 464с.

. Котлер Ф. Армстонг Г. Сондерс Д. Вонг В.Основы маркетинга: Пер. с англ. 2-е европ.изд.: Учеб. пособие. - М.: Изд.дом «Вильямс», 2000. - 208 с.

. Замков О.О., Толстопятенко А.В., Черемных Ю.П. Математические методы в экономике: Учебник. Изд. 2-е. - М.: Дело и сервис, 2010. - 368 с.

. Коршунова П. П., Плясунов В. С. Математика в экономике: Учеб. пособие. - М.: Вита-Пресс, 2009. - 368 с.

. Красе М.С. Математика для экономических специальностей: Учебник. - М.: ИНФРА-М, 2010 - 464 с. (Серия «Высшее образование»).

. Кремер П. Путко Б.А., Тришин И.М., Фридман М.П. Высшая математика для экономистов: Учеб. пособие для вузов. - М.: Банки и биржи, ЮНИТИ, 2009. - 439 с.

. Солодовников А.С, Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике: Учебник в 2-х ч. 4.2. - М.: Финансы и статистика, 1011. - 376 с.

. Большой экономический словарь: Под ред. А.Н. Арилияна. Изд. 5-е дополненное и переработанное. - М.: Институт новой экономики, 2012. - 1280с.

. Ассэль Г. Маркетинг: принципы и стратегия: Учебник для вузов.

М.:ИНФРА-М, 2001. - 607с.

.Афоничкина А.Н. Разработка бизнес-приложений в экономике на базе MS EXCEL. - М.: Диалог-МИФИ, 2003. - 216с.