Измерительные сигналы

Измерительные сигналы

Министерство Образования и Науки РФ

Федеральное агентство по образованию

ГОУ ВПО: «Магнитогорский государственный технический университет им. Г.И. Носова»

Кафедра физики

Реферат:

«Измерительные сигналы»

Проверил:

профессор каф. Физики Бахматов Ю.Ф.

Выполнил:

ст. гр. ТС-03-2  Антипова Е.Ю.

Магнитогорск

Чем измерительный сигнал отличается от сигнала? Приведите примеры измерительных сигналов, используемых в различных разделах науки и техники

Измерительный сигнал - это материальный носитель информации, содержащий количественную информацию об измеряемой физической величине и представляющий собой некоторый физический процесс, один из параметров которого функционально связан с измеряемой физической величиной. Такой параметр называют информативным. А сигнал несет количественную информацию только об информативном параметре, а не об измеряемой физической величине.

Примерами измерительных сигналов могут быть

выходные сигналы различных генераторов (магнитогидродинамического, лазеров, мазеров и др.), трансформаторов (дифференциального, тока, напряжения)

различные электромагнитные волны (радиоволны, оптическое излучение и др.)

Перечислите признаки, по которым классифицируются измерительные сигналы

По характеру измерения информативного и временного параметров измерительные сигналы делятся на аналоговые, дискретные и цифровые. По характеру изменения во времени сигналы делятся на постоянные и переменные. По степени наличия априорной информации переменные измерительные сигналы делятся на детерминированные, квазидетерминированные и случайные.

Чем аналоговый, дискретный и цифровой сигналы отличаются друг от друга?

Аналоговый сигнал - это сигнал, описываемый непрерывной или кусочно-непрерывной функцией Y_a(t), причем как сама эта функция, так и ее аргумент t могут принимать любые значения на заданных интервалах (Y_min; Y_max) и (t _min; t _max).

Дискретный сигнал - это сигнал, изменяющийся дискретно во времени или по уровню. В первом случае он может принимать в дискретные моменты времени nТ, где Т = const - интервал (период) дискретизации, n = 0; 1; 2; ... - целое, любые значения в интервале (Y_min; Y_max)называемые выборками, или отсчетами. Такие сигналы описываются решетчатыми функциями. Во втором случае значения сигнала Yд(t) существуют в любой момент времени t в интервале (t _min; t _max) однако они могут принимать ограниченный ряд значений h_j = nq, кратных кванту q.

Цифровые сигналы - квантованные по уровню и дискретные по времени сигналы Y_ц (nТ), которые описываются квантованными решетчатыми функциями (квантованными последовательностями), принимающими в дискретные моменты времени nТ лишь конечный ряд дискретных значений - уровней квантования h₁ h₂, ... , h_n.

Расскажите о характеристиках и параметрах случайных сигналов

Случайный сигнал - это изменяющаяся во времени физическая величина, мгновенное значение которой является случайной величиной.

 Семейство реализаций случайного процесса является основным экспериментальным материалом, на основе которого можно получить его характеристики и параметры.

Каждая реализация является неслучайной функцией времени. Семейство реализаций при каком-либо фиксированном значении времени t_o представляет собой случайную величину, называемую сечением случайной функции, соответствующим моменту времени t_o. Следовательно, случайная функция совмещает в себе характерные признаки случайной величины и детерминированной функции. При фиксированном значении аргумента она превращается в случайную величину, а в результате каждого отдельного опыта становится детерминированной функцией.

Наиболее полно случайные процессы описываются законами распределения: одномерным, двумерным и Т.д. Однако оперировать с такими, в общем случае многомерными функциями очень сложно, поэтому в инженерных приложениях, каковым является метрология, стараются обойтись характеристиками и параметрами этих законов, которые описывают случайные процессы не полностью, а частично. Характеристики случайных процессов, в отличие от характеристик случайных величин, которые подробно рассмотрены в гл. 6, являются не числами, а функциями. К важнейшим из них относятся математическое ожидание и дисперсия.

Математическим ожиданием случайной функции X(t) называется неслучайная функция

(t) = M[X(t)] = хр(х, t)dx,

которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения. Здесь р(х, t) - одномерная плотность распределения случайной величины х в соответствующем сечении случайного процесса X(t). Таким образом, математическое ожидание в данном случае является средней функцией, вокруг которой группируются конкретные реализации.

Дисперсией случайной функции X(t) называется неслучайная функция

Dx(t) = D[X(t)] = [x - m_x(t)]²p(x, t)dx,

значение которой для каждого момента времени равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно m_x(t).

Математическое ожидание случайного процесса и его дисперсия являются весьма важными, но не исчерпывающими характеристиками, так как определяются только одномерным законом распределения. Они не могут характеризовать взаимосвязь между различными сечениями случайного процесса при различных значениях времени t и t'. Для этого используется корреляционная функция - неслучайная функция R(t, t') двух аргументов t и t', которая при каждой паре значений аргументов равна ковариации соответствующих сечений случайного процесса:

Корреляционная функция, называемая иногда автокорреляционной, описывает статистическую связь между мгновенными значениями случайной функции, разделенными заданным значением времени τ = t'-t. При равенстве аргументов корреляционная функция равна дисперсии случайного процесса. Она всегда неотрицательна.

На практике часто используется нормированная корреляционная функция

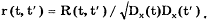
Она обладает следующими свойствами: 1) при равенстве аргументов t и t' r(t, t') = 1; 2) симметрична относительно своих аргументов: r(t,t') = r(t',t); 3) ее возможные значения лежат в диапазоне [-1;1], т.е. |r(t,t')| ≤ 1. Нормированная корреляционная функция по смыслу аналогична коэффициенту корреляции между случайными величинами, но зависит от двух аргументов и не является постоянной величиной.

Случайные процессы, протекающие во времени однородно, частные реализации которых с постоянной амплитудой колеблются вокруг средней функции, называются стационарными. :Количественно свойства стационарных процессов характеризуются следующими условиями.

• Математическое ожидание стационарного процесса постоянно, Т.е. m_х(t) = m_х = const. Однако это требование не является существенным, поскольку от случайной функции X(t) всегда можно перейти к центрированной функции, для которой математическое ожидание равно нулю. Отсюда вытекает, что если случайный процесс нестационарен только за счет переменного во времени (по сечениям) математического ожидания, то операцией центрирования его всегда можно свести к стационарному.

• Для стационарного случайного процесса дисперсия по сечениям является постоянной величиной, Т.е. Dx(t) = Dx = const.

• :Корреляционная функция стационарного процесса зависит не от значения аргументов t и t', а только от промежутка τ = t'-t, т.е. R(t,t') = R(τ). Предыдущее условие является частным случаем данного условия, Т.е. Dx(t) = R(t, t) = R(τ = О) = const. Таким образом, зависимость автокорреляционной функции только от интервала 't является единственным существенным условием стационарности случайного процесса.

Важной характеристикой стационарного случайного процесса является его спектральная плотность S(ω), которая описывает частотный состав случайного процесса при ω≥0 и выражает среднюю мощность случайного процесса, приходящуюся на единицу полосы частот:

Спектральная плотность стационарного случайного процесса является неотрицательной функцией частоты S(ω)≥0. Площадь, заключенная под кривой S(ω), пропорциональна дисперсии процесса. Корреляционная функция может быть выражена через спектральную плотность

(τ) = S(ω)cosωτdω .

Стационарные случайные процессы могут обладать или не обладать свойством эргодичности. Стационарный случайный процесс называется эргодическим если любая его реализация достаточной продолжительности является как бы "полномочным представителем" всей совокупности реализаций процесса. В таких процессах любая реализация рано или поздно пройдет через любое состояние независимо от того, в каком состоянии находился этот процесс в начальный момент времени.

Для описания погрешностей используются теория вероятностей и математическая статистика. Однако прежде необходимо сделать ряд существенных оговорок:

• применение методов математической статистики к обработке результатов измерений правомочно лишь в предположении о независимости между собой отдельных получаемых отсчетов;

• большинство используемых в метрологии форму л теории вероятностей правомерны только для непрерывных распределений, в то время как распределения погрешностей вследствие неизбежного квантования отсчетов, строго говоря, всегда дискретны, Т.е. погрешность может принимать лишь счетное множество значений.

Таким образом, условия непрерывности и независимости для результатов измерений и их погрешностей соблюдаются приближенно, а иногда и не соблюдаются. В математике под термином "непрерывная случайная величина" понимается существенно более узкое, ограниченное рядом условий понятие, чем "случайная погрешность" в метрологии.

С учетом этих ограничений процесс появления случайных погрешностей результатов измерений за вычетом систематических и прогрессирующих погрешностей обычно может рассматриваться как центрированный стационарный случайный процесс. Его описание возможно на основе теории статистически независимых случайных величин и стационарных случайных процессов.

При выполнении измерений требуется количественно оценить погрешность. Для такой оценки необходимо знать определенные характеристики и параметры модели погрешности. Их номенклатура зависит от вида модели и требований к оцениваемой погрешности. В метрологии принято различать три группы характеристик и параметров погрешностей. Первая группа - задаваемые в качестве требуемых или допускаемых нормы характеристик погрешности измерений (нормы погрешностей). Вторая группа характеристик - погрешности, приписываемые совокупности выполняемых по определенной методике измерений. Характеристики этих двух групп применяются в основном при массовых технических измерениях и представляют собой вероятностные характеристики погрешности измерений. Третья группа характеристик - статистические оценки погрешностей измерений отражают близость отдельного, экспериментально полученного результата измерения к истинному значению измеряемой величины. Они используются в случае измерений, проводимых при научных исследованиях и метрологических работах.

В качестве характеристик случайной погрешности используют СКО случайной составляющей погрешности измерений и, если необходимо, ее нормализованную автокорреляционную функцию.

Систематическая составляющая погрешности измерений характеризуется:

• СКО неисключенной систематической составляющей погрешности измерений;

• границами, в которых неисключенная систематическая составляющая погрешности измерений находится с заданной вероятностью (в частности, и с вероятностью, равной единице).

Требования к характеристикам погрешности и рекомендации по их выбору приведены в нормативном документе МИ 1317-86 "ГСИ. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров".

Что такое помехи, как они классифицируются? Приведите примеры помех

Помеха - сигнал, однородный с измерительным и действующий одновременно с ним. Его присутствие приводит к появлению погрешности измерения.

По месту возникновения помехи делятся на внешние и внутренние. Причиной возникновения внешних помех являются природные процессы и работа различных технических устройств. Последние создают так называемые индустриальные помехи.

Внутренние помехи обусловлены процессами, происходящими при работе самого средства измерений.

В зависимости от вида включения источников помехи и измерительного сигнала в эквивалентных схемах средств измерений различают помехи общего вида (синфазные) и помехи нормального (последовательные) вида. Источник помехи общего вида включен между общими точками (корпусами) схем объекта измерений и СИ. Источник помехи нормального вида включен последовательно во входную цепь СИ.

По виду частотного спектра помехи делятся на белый и розовый шумы. Спектральные составляющие белого шума равномерно распределены по всему частотному диапазону. У розового шума спектральная мощность, приходящаяся на декаду частоты, постоянна.

По основным свойствам помехи можно разделить на три вида: флуктуационные, сосредоточенные и импульсные.

Флуктуационные помехи представляют собой хаотическое, беспорядочное изменение во времени сигнала, однородного с измеряемым, в каком-либо месте средства измерений. Такие помехи часто называют шумом Различают следующие виды шумов:

• тепловой (шум Джонсона), по своим свойствам близкий к белому шуму. Тепловой шум генерируется любым резистором, находящимся в измерительной цепи. Значение его состоит в том, что он устанавливает нижнюю границу напряжения шумов любого измерительного преобразователя, имеющего выходное сопротивление;

• фликкер-шум. К данному виду относят шумы, у которых спектральная мощность на декаду частоты примерно постоянна, т.е. розовые шумы

Сосредоточенными называют помехи, основная часть мощности которых сосредоточена на отдельных участках диапазона частот, меньших полосы пропускания СИ. Помехи, наводимые в измерительных цепях СИ от промышленной силовой сети частотой 50 Гц, являются сосредоточенными. Эффективность их подавления в значительной мере определяется достоверностью априорных данных о частотном спектре.

Импульсными помехами называется регулярная или хаотическая последовательность импульсных сигналов, однородных с измерительным сигналом. Источниками таких помех являются цифровые и коммутирующие элементы СИ или работающего рядом с ними устройства. Характерный пример импульсных помех - помехи от устройств зажигания двигателей внутреннего сгорания. Импульсные и сосредоточенные помехи часто называют наводками.

Поскольку основным следствием действия помехи является появление погрешности измерения, то стараются устранить или, по крайней мере, ослабить их действие на средства измерений. Для устранения влияния помех целесообразно, если это возможно, исключить причины их возникновения. Способы борьбы с помехами в значительной мере зависят от их спектрального состава, вида измерительного сигнала и помехи.

Многие из электрических помех можно устранить путем экранирования, заземления средства измерений, применения специальных фильтров. Тепловые шумы могут быть заметно уменьшены при охлаждении их источника. Однако в целом борьба с помехами чрезвычайно сложна и является скорее искусством, нежели наукой. В отдельных случаях приходится применять особенно изощренные меры, как то: использование монолитных каменных столов для исключения посторонней вибрации, размещение средств измерений или их частей в термостатах, проведение электрической и электромагнитной экранировки помещений для устранения электромагнитных наводок.

Примером розового шума является шум постоянного резистора, пропорциональный протекающему через него току, шум тока базы транзистора и др. Пример флуктуационных помех - внутренние шумы измерительных электронных усилителей.

Какие типы математических моделей измерительных сигналов используются в метрологии?

В метрологии измерительные сигналы описываются математическими моделями вида Y= f(X, А, В, С,. .. ), где Y - основной информативный пара метр сигнала; Х - независимый аргумент сигнала; А, В, С - параметры сигнала. В зависимости от рода независимого сигналы описываются временными (Х = t) и частотными (Х = ω) математическими моделями. Вид модели выбирается в зависимости от конкретных условий решаемой задачи.

Во временной области применяют известные математические функции f(t, А, В, С, ... ), наиболее точно описывающие изменение сигнала, в которых один из параметров А, В, С и т.д. зависит от измеряемой величины. Временная форма представления сигнала позволяет легко определить такие важные характеристики, как энергия, мощность и длительность сигнала.

Наряду с временным описанием сигналов широко используется их спектральное (частотное) представление. В процессе передачи и обработки сигналов оно играет особую роль, поскольку определяет параметры используемой аппаратуры.

Частотное представление основывается на преобразовании Фурье сигнала Y(t):

,

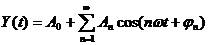где A₀ - постоянная составляющая; A_n, φ_n - амплитуда и фаза n-й гармоники. Множество значений A_n(ω) и φ_n(ω) образуют соответственно амплитудный и фазовый спектры, которые характеризуют свойства сигнала Y(t) в частотной области. Такой спектр называют линейчатым, или дискретным.

При постепенном увеличении периода сигнала (в пределе до бесконечности) разности соседних частотных составляющих спектра становятся ничтожно малыми и дискретный спектр превращается в непрерывный.

Для описания непрерывного спектра непериодического сигнала Y(t) используют спектральную функцию S(ω), модуль спектральной функции |S(ω)| , часто называемый спектром, и аргумент спектральной функции агgS(ω).

Спектральную функцию можно определить с помощью интеграла Фурье.

Сколько и каких параметров нужно знать для описания каждого из элементарных измерительных сигналов?

К элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями, а также дельта-функцией.

Постоянный сигнал - самый простой из элементарных сигналов, описываемый математической моделью вида Y = А, где А (время или частота) - единственный параметр сигнала.

Единичная функция, называемая иногда функцией Хевисайда, описывается уравнением

1(t-t_o) =                   0  при t < t_o;

                                1  при t ≥ t_o.

Она имеет один параметр - момент времени t_o.

Дельта-фуnкция описывается уравнением

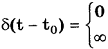
при t ≠t_o;

при t = t_o.

Она также имеет один параметр - момент времени t_o.

Гармонический сигнал описывается уравнением

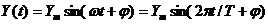
Параметрами такого сигнала являются: амплитуда, период (или частота или круговая частота) и начальная фаза.

Что такое амплитудная, частотная и фазовая модуляции?

Модулированные сигналы. Модулированным - называется сигнал, являющийся результатом взаимодействия двух или более сигналов, т.е. модуляции.

Модуляция - это воздействие измерительного сигнала X(t) на какой-либо параметр стационарного сигнала Y(t), обладающего такими физической природой и характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала, именуемого несущим, обычно выбирают синусоидальное (гармоническое) колебание или последовательность импульсов.

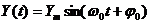
Физический процесс, обратный модуляции, называется демодуляцией, или детектированием, и заключается в получении из модулированного сигнала другого сигнала, пропорционального модулирующему. Задача демодуляции - по возможности полное восстановление информации, содержащейся в модулирующем сигнале X(t).

Вид модуляции и способ детектирования зависят от требований, предъявляемых к точности передачи информации. Наиболее простым модулированным гармоническим сигналом является амплитудно-модулированный сигнал, в котором измерительная информация содержится в амплитуде несущего синусоидального сигнала.

Амплитудно-модулированные сигналы описываются формулой

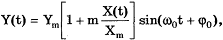
где m - глубина амплитудной модуляции (всегда меньше единицы).

При частотной модуляции измерительная информация содержится в частоте модулированного сигнала, т.е.

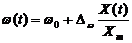
где 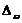 - наибольшее изменение частоты модулированного сигнала, т.е. девиация частоты, пропорциональная амплитуде модулирующего сигнала.

При фазовой .модуляции модулирующий сигнал X(t) воздействует на фазу несущего колебания:

где m_ф - коэффициент фазовой модуляции.

Для того чтобы при детектировании можно было восстановить модулирующий сигнал, необходимо иметь сигнал вида, называемый опорным. Относительно него наблюдают, как меняется фаза модулированного сигнала.

Что такое амплитудно-импульсная, частотно-импульсная и широтно-импульсная модуляции?

измерительный сигнал измерение помеха

Если модулируемым сигналом является периодическая последовательность прямоугольных импульсов, то возможны три вида модуляции:

-   амплитудно-импульсная (АИМ);

-   частотно-импульсная (ЧИМ);

-   широтно-импульсная (ШИМ).

При этом параметром, несущим измерительную информацию, соответственно являются амплитуда, частота и длительность импульсов.

Дайте определение операции квантования. Где и каким образом она используется в метрологии? Что такое погрешность квантования?

Квантование - измерительное преобразование непрерывно изменяющейся величины .в ступенчато изменяющуюся с заданным размером ступени q -квантом. В результате проведения этой операции непрерывное множество значений сигнала Y(t) в диапазоне от Уmin до Уmах преобразуется в дискретное множество значений У_KB(t). Квантование широко применяется в измерительной технике. Различают равномерное (q - постоянная величина) и неравномерное (q - переменная величина) квантование. Неравномерное квантование применяется достаточно редко, в специфических случаях, например при большом динамическом диапазоне квантуемой величины.

Процесс квантования описывается уравнением

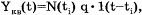
где У_KВ(t) - квантованный сигнал; N(t_i) - число квантов; 1(t-t_i) -единичная функция.

Любой процесс измерения по сути своей есть процесс квантования. Например, при измерении длины тела линейкой с миллиметровыми делениями определяется целое число миллиметров, наиболее близкое к истинному размеру тела. В данном случае в роли кванта выступает миллиметр. При использовании микрометра квантом является величина, равная 10^-6 м.

Разность между истинным значением длины тела и измеренным линейкой есть погрешность квантования. Погрешность квантования ∆ - методическая погрешность отражения непрерывной величины ограниченным по числу разрядов числом. Она равна разности между значением непрерывной функции и значением, полученным в результате квантования.

Дайте определение дискретизации. Расскажите о том, как проводится дискретизация измерительных сигналов. Что утверждает теорема Котельникова?

Дискретизация - измерительное. преобразование непрерывного во времени сигнала Y(t) в последовательность мгновенных значений этого сигнала У_k =Y(k∆t), соответствующих моментам времени k∆t, где k =1; 2; ... Интервал времени ∆t называется шагом дискретизации, а обратная ему величина f_д =1/∆t - частотой дискретизации.

Математически процесс дискретизации описывается с помощью дельта-функции δ(t-k∆t), которая, как известно, обладает стробирующим действием. Идеальный дискретизированный сигнал Уд является последовательностью импульсов нулевой длительности и аналитически может быть представлен в виде

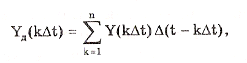
где Y(k∆t) - значение непрерывного сигнала в k-й точке дискретизации.

Процесс дискретизации проходит следующим образом: исходный непрерывный сигнал разбивается на последовательность мгновенных значений этого сигнала в соответствующих моментах времени. Затем восстанавливается с помощью палиндрома Лагранжа нулевой степени в непрерывный во времени сигнал. В дискретизированном сигнале отсутствуют промежуточные значения, которые содержались в исходном непрерывном сигнале. Однако часто принципиально необходим непрерывный сигнал. Поэтому во многих случаях дискретизированный сигнал требуется преобразовать в непрерывный, Т.е. восстановить его промежуточные значения.

Восстановление сигнала в данном случае регулируется теоремой Котельникова, которая формулируется следующим образом: если функция Y(t), удовлетворяющая условиям Дирихле - ограничена, кусочно-непрерывна, имеет конечное число экстремумов - и обладающая спектром с граничной частотой f_c, дискретизирована циклически с периодом ∆t, меньшим или равным 1/(2f_c), т.е. f_д ≥ 2f_c, то она может быть восстановлена по всей этой совокупности ее мгновенных значений без погрешности.

Если теорема Котельникова выполняется, то непрерывный сигнал Y(t) может быть восстановлен как сумма базисных функций, называемых рядом Котельникова:

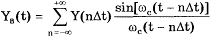
где ω=2πf_c - круговая граничная частота спектра непрерывного сигнала Y(t); ∆t - период дискретизации; F _oт(t) - функция отсчетов.

Ряд Котельникова является одним из примеров обобщенного ряда Фурье и замечателен тем, что его коэффициенты равны мгновенным дискретизированным значениям сигнала Y(t) и, следовательно, определяются наиболее простым способом.

Какие интегральные параметры используются для описания переменных сигналов?

Переменный периодический сигнал Y(t) кроме совокупности мгновенных значений часто описывается несколькими общепринятыми обобщающими параметрами, называемыми uнтегральнымu и характеризующими в целом период сигнала. Каждому закону изменения сигнала соответствуют определенные интегральные значения: амплитудное, среднее, средневыпрямленное и среднеквадратическое.

Амnлuтудное (nиковое) значение Уm равно максимальному на периоде значению сигнала Y(t). По сути своей амплитудное значение является мгновенным, а не интегральным. Однако оно используется при расчете коэффициентов формы, амплитуды и усреднения и поэтому рассматривается в этом разделе.

Среднее значение  описывает постоянную составляющую сигнала. Так, для синусоидального сигнала среднее значение равно нулю, следовательно, он не содержит постоянной составляющей.

Средневыnрямленное значение  используется для симметричных относительно оси времени сигналов, т.е. не содержащих постоянной составляющей.

Среднеквадратическое значение

где Y_k - среднеквадратическое значение k-й гармоники сигнала Y(t). Его иногда называют действующим или эффективным, хотя эти термины ГОСТ 16465-70 считает устаревшими. Среднеквадратическое значение сигнала является единственной истинной мерой его мощности. Эти значения широко используются в практике электрических измерений. Подавляющее большинство вольтметров проградуировано в среднеквадратических значениях напряжения.

Связь между перечисленными параметрами устанавливается с помощью следующих коэффициентов: формы 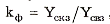 амплитуды 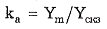 и усреднения .