Модель Леонтьева
1. Статистические модели
экономики
1.1 Модель Леонтьева
Рассмотрим статическую линейную модель
многоотраслевой экономики. В основе модели лежат следующие предположения:
в экономической системе производятся,
продаются, покупаются, потребляются и инвестируются n продуктов;
каждая отрасль является «чистой», т.е.
производит только один продукт, совместное производство различных продуктов
исключается. Различные отрасли выпускают разные продукты;
под производственным процессом в каждой
отрасли понимается преобразование некоторых (возможно, всех) типов продуктов в
определенный продукт. При этом соотношение затраченного продукта и выпускаемого
предполагается постоянным. Таким образом, если для производства единицы j-го продукта надо
затратить аij единиц i-го продукта, то выпуск λ единиц j-го продукта потребует λ аij единиц i-го продукта.
Итак, независимо от масштаба производства
удельный выпуск и соотношение затрат предполагаются постоянными.
Валовой выпуск i-го продукта за год хi распадается на две
части: на производственное потребление во всех отраслях и на конечное
(непроизводственное) потребление.
В предположениях 1-3 производственное потребление i-го продукта всеми отраслями равно  , поэтому чистый выпуск j-го продукта составит
, поэтому чистый выпуск j-го продукта составит
xj -  , i = 1, …, n, (1.1)
, i = 1, …, n, (1.1)
Если приравнять чистый выпуск каждого i-го продукта и конечный спрос на него yi, то образуется система уравнений:
xj -  = yi, i = 1, …, n, (1.2)
= yi, i = 1, …, n, (1.2)
которая и составляет модель Леонтьева.
Конечный спрос и состоит из конечного потребления, экспорта и
инвестиций. Однако в самой модели величины уi мыслятся как экзогенно заданные. Поэтому при заданных уi, i = 1,…, n, n линейных уравнений модели Леонтьева позволяют определить n отраслевых выпусков хi, i = 1,…, n.
Таким образом, сущность метода Леонтьева состоит в определении
валового выпуска отраслей по заданному экзогенно конечному спросу на основе
данных о технологических возможностях, воплощенных в расходных коэффициентах аij. Разумеется, по этим же уравнениям может быть решена и обратная
задача: по заданным валовым выпускам определяются объемы конечного спроса yi на каждый продукт.
Величины хi, уi: могут быть представлены в натуральных
или стоимостных единицах измерения, в соответствии с этим различают натуральный
или стоимостный межотраслевые балансы.
Система (1.2) - это система п линейных уравнений с п неизвестными
хi, i = 1,…, п, которая является хорошо изученным объектом линейной
алгебры. Однако система описывает отраслевую структуру экономики и поэтому
обладает следующими свойствами: коэффициенты прямых затрат аij, объемы конечного спроса уi, и валовые выпуски xi - неотрицательны. Система (1.2)
называется работоспособной или продуктивной если она разрешима в неотрицательных
хi, т, е. 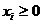 , i = 1,…, n. Двойственной
к системе (1.2) называется следующая система линейных уравнений для цен
продуктов рj:
, i = 1,…, n. Двойственной
к системе (1.2) называется следующая система линейных уравнений для цен
продуктов рj:
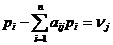 , j=1,…, n, (1.3)
, j=1,…, n, (1.3)
где 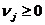 - добавленная стоимость на единицу
выпускаемой j-й отрасли.
- добавленная стоимость на единицу
выпускаемой j-й отрасли.
Поскольку 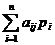 - сумма издержек на единицу выпуска j-й отрасли, то в левой части каждого из уравнений (1.3)
стоит чистый доход от единичного выпуска j-й отрасли, который и приравнивается, к добавленной стоимости
- сумма издержек на единицу выпуска j-й отрасли, то в левой части каждого из уравнений (1.3)
стоит чистый доход от единичного выпуска j-й отрасли, который и приравнивается, к добавленной стоимости 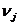 .
.
Система (1.3) называется прибыльной, если она разрешима в
неотрицательных  , j = 1, …, n. Можно доказать,
что продуктивность (1.2) и прибыльность (1.3) эквивалентны: из продуктивности
(1.2) следует прибыльность (1.3), и наоборот.
, j = 1, …, n. Можно доказать,
что продуктивность (1.2) и прибыльность (1.3) эквивалентны: из продуктивности
(1.2) следует прибыльность (1.3), и наоборот.
Квадратная матрица D называется
неотрицательно обратимой, если D невырождена и
ее обратная матрица неотрицательна.
Система (1.2) может быть записана в матричной форме:
(1-А) х = у, (1.4)
где I = In - единичная матрица с размерами
n x n, x = (xi, …, xn)¢, y=(yi,…, yn)¢
Из (1.4) видно, что условие продуктивности (1.2) эквивалентно
неотрицательной обратимости матрицы (I - A). Если
одно из этих условий выполнено, то
 , (1.5)
, (1.5)
причем 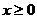 , т.е. задача определения вектора
неотрицательного конечного спроса у решена.
, т.е. задача определения вектора
неотрицательного конечного спроса у решена.
Обозначим через N множество номеров отраслей= {1, 2,…, n}. Подмножество отраслей S изолировано, если аij=
0
для
 ,
, 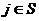 . Это означает, что отрасли S не нуждаются в товарах, производимых другими отраслями
. Это означает, что отрасли S не нуждаются в товарах, производимых другими отраслями  , хотя, быть может, передают им свои
товары. Если перенумеровать отрасли так, чтобы первыми располагались k отраслей S, то матрица А
примет следующий вид:
, хотя, быть может, передают им свои
товары. Если перенумеровать отрасли так, чтобы первыми располагались k отраслей S, то матрица А
примет следующий вид:
 , (1.6)
, (1.6)
где А1 - квадратная матрица с размерами k х k, отвечающая
отраслям S;
А3 - квадратная матрица с размерами (n-k) x (n-k), соответствующая; отраслям  .
.
Технологическая матрица называется неразложимой, если ее нельзя
путем перестановок строк и столбцов привести к виду (1.6). Неразложимость А
означает, что каждая отрасль хотя бы косвенно использует продукцию всех
отраслей.
Для неразложимой матрицы имеет место теорема Фробениуса - Перрона:
. Неразложимая матрица А имеет положительное собственное число lA>0, которое превосходит модули всех
остальных собственных чисел.
. Собственному числу lA
отвечает единственный собственный вектор хA (с точностью до скалярного множителя), все координаты которого
ненулевые и имеют один знак (т.е. его всегда можно выбрать положительным за
счет скалярного множителя).
Опираясь на теорему Фробениуса - Перрона можно доказать следующую
важную для приложений теорему: модель Леонтьева продуктивна тогда и только
тогда, когда lA < 1.
Достаточность. Поскольку
AxA =lA xA, xA>0, 0 < lA < 1, то АkxA=Аk-1(AxA)= lA(Аk-1xA) =
= 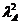 (Аk-2xA)=…=
(Аk-2xA)=…=
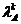 xA,
xA,
поэтому  . Но хА >0, Аk ³ 0, следовательно
. Но хА >0, Аk ³ 0, следовательно 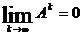 .
.
Рассмотрим математическое равенство,
которое легко проверить, если раскрыть скобки в левой части:
(I-A) (I+A+A2+
… +Ak-1) = I - Ak, (1.7)
Поскольку предел правой части при k ®¥ равен I, то существует и предел левой части.
Таким образом,  , т.е. обратная матрица
, т.е. обратная матрица 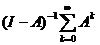 существует и для нее имеет место
разложение, аналогичное сумме бесконечной геометрической прогрессии. Кроме
того, так как все Ak ³ 0, то (I-А)-1³ 0, поэтому для любого вектора конечного спроса у ³ 0 существует неотрицательное решение
системы уравнений:
существует и для нее имеет место
разложение, аналогичное сумме бесконечной геометрической прогрессии. Кроме
того, так как все Ak ³ 0, то (I-А)-1³ 0, поэтому для любого вектора конечного спроса у ³ 0 существует неотрицательное решение
системы уравнений:
х = (I-А)-1 y (1.8)
т.е. модель Леонтьева продуктивна.
1.2 Модели определения оптимального плана
предприятия, относящегося к задачам целочисленного программирования
Более целесообразно целочисленное
программирование было бы назвать дискретным программированием. Это есть часть
математического программирования, занимающаяся исследованием экстремальных
задач на целочисленных решетках и конечных множествах. В терминах дискретного
программирования формализуются многие важные задачи экономики, управления,
планирования, проектирования, а так же ряд других задач, например: размещение и
специализация предприятий; оптимизация комплекса технических средств доставки
грузов; важные сельскохозяйственные задачи и т.д.
Рассмотрим задачу математического
программирования, в которой требуется, чтобы все переменные принимали целые
неотрицательные значения.
Максимизировать линейную функцию
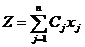 , (1.9)
, (1.9)
при условиях
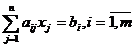 , (1.10)
, (1.10)
xj = 0, или 1, или 2, или 3, …; 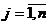 , (1.11)
, (1.11)
причем 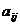 , bi. предполагаются целыми числами.
, bi. предполагаются целыми числами.
Симплекс-метод приводит непосредственно к целочисленному решению
лишь для немногих задач. В общем же случае требуются специальные методы,
заключающиеся в подборе дополнительных линейных ограничений к системе
ограничений (1.10), обеспечивающих целочисленность решения.
Один из таких методов, приводящий к
целочисленному решению за конечное число шагов, предложен Р.Е. Гомори.
Предположим, что задача линейного
программирования имеет многоугольник (многогранник) допустимых решений.

Рис. 1.1. Многоугольник (многогранник) допустимых решений
Если наложить требование целочисленности,
то допустимое множество решений вырождается в систему точек и уже в общем
случае не является выпуклым. Если добавить новые ограничения, связывающие
внешние целочисленные точки, а затем в качестве многоугольника (многогранника)
решений использовать все выпуклое множество, то получим новую задачу линейного
программирования со следующими свойствами:
новый многоугольник решений содержит все
целые точки, заключавшиеся в первоначальном многоугольнике (многограннике)
решений; любая угловая его точка является целой;
- так как линейная функция достигает оптимума в угловой точке
многоугольника (многогранника) решений, то построением такого многоугольника и
обеспечивается целочисленность оптимального решения.
Решение поставленной задачи ведем
симплексным методом без учета требования целочисленности. Если оптимальный план
целочисленный, то вычисления заканчивают; если же в оптимальном решении такой
задачи хотя бы одна компонента не будет целым числом, то вводятся
дополнительные ограничения и процесс решения продолжается.
Предположим, что, максимизируя (1.9) при
условиях (1.10) и (1.11) без учета требования целочисленности переменных мы
пришли к оптимальному решению с предпочитаемым эквивалентом системы ограничений
(1.10) вида:
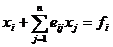 ,
,  , (1.12)
, (1.12)
Пусть правые части fi
некоторых уравнений оказалиcm дробными.
Выберем одну из них, например f1. Каждый коэффициент е1j при неизвестной в соответствующем
уравнении системы и свободный член f1 представим в виде суммы целой части и
правильной неотрицательной дроби
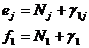 ,
, 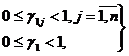 (1.13)
(1.13)
помня, что целой частью любого числа называется наибольшее целое
число, не превосходящее данного числа. Тогда соответствующее уравнение системы
можно записать:
 ,
,
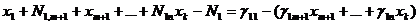 , (1.14)
, (1.14)
где k = n + m.
Левая часть этого равенства должна быть числом целым, так как мы
требуем, чтобы все переменные принимали целые неотрицательные значения. Поэтому
и правая часть должна быть целым числом и, очевидно, это число не больше, чем  . Но
. Но  есть правильная неотрицательная дробь и, следовательно, правая
часть не может превышать нуля:
есть правильная неотрицательная дробь и, следовательно, правая
часть не может превышать нуля:
 , (1.15)
, (1.15)
откуда
 (1.16)
(1.16)
Вычитая из левой части новую неотрицательную неизвестную хn+1, заменим неравенство (d) уравнением:
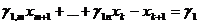 , или
, или
 ,
, (1.17)
(1.17)
где 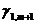 ,
, 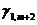 ,… коэффициенты, стоящие в первой строке оптимальной, но
нецелочисленной таблицы, и под неизвестными хm + 1,
хm + 2,….
,… коэффициенты, стоящие в первой строке оптимальной, но
нецелочисленной таблицы, и под неизвестными хm + 1,
хm + 2,….
Это и есть дополнительное ограничение, которое следует ввести.
Новая задача с (m + 1) уравнениями (1.10) и (1.17) является задачей дискретного
программирования, так как 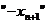 совпадает с правой частью равенства
(1.14). На данном этапе значение хn + 1 равно
совпадает с правой частью равенства
(1.14). На данном этапе значение хn + 1 равно 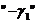 , т.е. отрицательно и дробно. Мы добавляем
к последней симплексной таблице еще одну строку, соответствующую уравнению
(1.17). При этом относительные оценочные коэффициенты не изменяются, т.е.
условие оптимальности сохраняется.
, т.е. отрицательно и дробно. Мы добавляем
к последней симплексной таблице еще одну строку, соответствующую уравнению
(1.17). При этом относительные оценочные коэффициенты не изменяются, т.е.
условие оптимальности сохраняется.
Возобновляя процесс преобразования симплексных таблиц, применим
двойственный метод и переведем неизвестную хn+1
из базисных в свободную. Возможно, что после этого получится базисное
неотрицательное решение с целочисленными компонентами и задача решена. Если
нет, то составляем следующее дополнительное ограничение, учитывающее
целочисленность. Процесс присоединения дополнительных ограничений повторяют до
тех пор, пока либо будет найден целочисленный оптимальный план, либо будет
доказано, что задача не имеет целочисленных планов. Если имеются несколько
дробных fi, то дополнительное ограничение (1.17)
составляют для mах  . Это ускоряет процесс получения оптимального целочисленного
решения.
. Это ускоряет процесс получения оптимального целочисленного
решения.
1.3 Предпочтения потребителя и его функция полезности
Одним из важных понятий экономической
теории является домашнее хозяйство (потребитель). Главная проблема при изучении
поведения потребителя заключается в том, чтобы установить, в каких объемах он
приобретет наличные товары и услуги при заданных ценах и доходе.
Конкретное решение потребителя о покупке
определенного набора товаров математически можно представить как выбор
конкретной точки в пространстве товаров. Пусть п - конечное число
рассматриваемых товаров; х = (х1,…, х2)' - вектор-столбец
объемов товаров, приобретенных потребителем за определенный срок (например, за
год) при заданных ценах и доходе за тот же срок. Пространство товаров - это
множество всевозможных наборов товаров х с неотрицательными координатами: С
={х: x ³ 0}.
В теории потребительского выбора предполагается, что каждый
Потребитель изначально имеет свои предпочтения на некотором подмножестве
пространства товаров 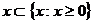 , Это означает, что для каждой пары
, Это означает, что для каждой пары 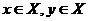 имеет место одно из трех отношений:
имеет место одно из трех отношений:
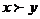 - набор х предпочтительнее у;
- набор х предпочтительнее у;
 - набор x менее
предпочтителен, чем;
- набор x менее
предпочтителен, чем;
x~y - для потребителя оба
набора обладают одинаковой степенью предпочтения.
Отношения предпочтения обладают, по
крайней мере следующими свойствами:
1) если 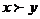 ,
, 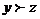 , то
, то 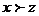 (транзитивность);
(транзитивность);
) если х > у, то 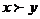 (ненасыщаемостъ; больший набор всегда предпочтительнее меньшего).
(ненасыщаемостъ; больший набор всегда предпочтительнее меньшего).
Отношения предпочтения каждого потребителя при определенных слабых
предположениях, касающихся предпочтений, можно (и удобно!) представить в форме
индикатора предпочтений, т.е. такой функции полезности и(х), что из 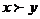 следует и(х) > и(у) и из x~y следует и(х) = и(у). Для каждого потребителя такое
представление многовариантно. Например, если и(х) - функция полезности, Сu(х), ln[u(x)] - это также индикаторы, предпочтений.
следует и(х) > и(у) и из x~y следует и(х) = и(у). Для каждого потребителя такое
представление многовариантно. Например, если и(х) - функция полезности, Сu(х), ln[u(x)] - это также индикаторы, предпочтений.
Введение функции полезности позволяет
заменить отношения предпочтения привычными отношениями между числами: больше,
меньше, равно.
В теории потребления предполагается, что
функция полезности обладает следующими свойствами:
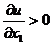 1) - с ростом потребления блага полезность растет;
1) - с ростом потребления блага полезность растет;
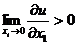 2) - небольшой прирост блага при его первоначальном
отсутствии резко увеличивает полезность;
2) - небольшой прирост блага при его первоначальном
отсутствии резко увеличивает полезность;
 3) - с ростом потребления блага скорость та полезности
замедляется;
3) - с ростом потребления блага скорость та полезности
замедляется;
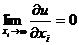 4) - при очень большом объеме блага его дальнейшее
увеличение не приводит к увеличению полезности.
4) - при очень большом объеме блага его дальнейшее
увеличение не приводит к увеличению полезности.
Условие 3 обычно используется в более
расширительной трактовке: матрица вторых производных (матрица Гессе)
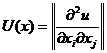
отрицательно определена.
Предельной, полезностью товара называется предел отношения
приращения полезности к вызвавшему этот прирост приращению товара:
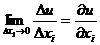
таким образом, предельная полезность показывает, насколько
возрастает полезность, если товар возрастет на малую единицу.
Поверхностью безразличия называется гиперповерхность размера (n-1), на которой полезность постоянна:
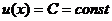 ,
,
или в дифференциальной форме:
 , (1.18)
, (1.18)
Условие (1.18) означает, что касательная к
поверхности безразличия перпендикулярна градиенту полезности.
С точки зрения потребителя наличие множества
наборов товаров, обладающих одинаковой полезностью (т.е. одинаковой степенью
предпочтения), означает возможность замены одного набора другим равноценным
набором, в том числе возможность замены одного товара другим.
Пусть в соотношении (1.18) dxi = 0 для i = 3,…, n, тогда это соотношение
примет вид
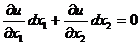 ,
,
откуда
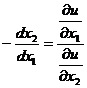 (1.19)
(1.19)
т.е. предельная норма замены первого товара вторым равна
отношению предельных полезностей первого и второго товаров. Норма замены
показывает, сколько требуется единиц второго товара, чтобы заменить выбывшую
малую единицу первого товара.
Бюджетным множеством называется множество
тех наборов товаров, которые может приобрести потребитель, имея доход М:
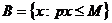 ,
,
где p = (p1,…, pn) - вектор-строка цен.
Модель поведения потребителя
В теории потребления предполагается, что
потребитель стремится максимизировать свою полезность и единственное, что его
сдерживает, - это ограниченность дохода:
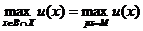 (1.20)
(1.20)
В задаче (1.20) предполагается, что точка максимума  . Эта задача на условный экстремум
сводится к нахождению безусловного экстремума функции Лагранжа:
. Эта задача на условный экстремум
сводится к нахождению безусловного экстремума функции Лагранжа:
 .
.
Необходимые условия локального экстремума:
 , (1.21)
, (1.21)
 ,
, 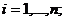 (1.22)
(1.22)
эти условия действительно определяют точку максимума, поскольку
матрица U отрицательно определена.
Из (1.22) видно, что потребитель при фиксированном доходе так
выбирает набор x*, что в этой точке отношения предельных
полезностей равны отношениям цен:
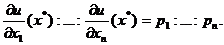
Если разрешить (1.21), (1.22) относительно
х*, получим функцию спроса потребителя:
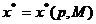 . (1.23)
. (1.23)
Уравнение Слуцкого
Рассмотрим, как изменится спрос
потребителя, определяемый моделью (1.20), если изменится цена одного из
товаров.
Пусть цена n-го товара возросла на dрn, тогда
согласно (1.23) спрос на каждый товар изменится следующим образом:
 , i = 1, 2,…, n,
, i = 1, 2,…, n,
но поскольку (1.23) - это, другая запись соотношений (1.21),
(1.22), то уравнение для 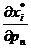 получим путем дифференцирования по рп
этих соотношений:
получим путем дифференцирования по рп
этих соотношений:
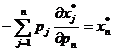 , (1.24)
, (1.24)
 ,
,
Система из (n + 1) линейного
уравнения (1.24) относительно (п + 1) неизвестного 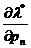 ,
, 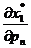 , …,
, …,  в матричной форме запишется следующим
образом (штрих означает транспортирование; р - вектор-строка цен; U - матрица Гессе; х* - вектор-столбец спроса на
товары):
в матричной форме запишется следующим
образом (штрих означает транспортирование; р - вектор-строка цен; U - матрица Гессе; х* - вектор-столбец спроса на
товары):
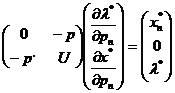 . (1.25)
. (1.25)
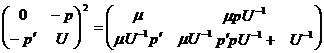 ,
,
 где
где 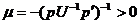 .
.
Поэтому решение уравнений (1.25) в
матричной форме выглядит так:
 .
.
2. Динамические модели экономики
2.1 Модель Солоу
Модель Солоу является односекторной моделью экономического
роста. В этой модели экономическая система рассматривается как единое целое,
производит один универсальный продукт, который может как потребляться, так и
инвестироваться. Модель достаточно адекватно отражает важнейшие
макроэкономические аспекты процесса воспроизводства. Экспорт - импорт в явном
виде не учитывается.
Состояние экономики в модели Солоу задается следующими пятью
эндогенными переменными:
X - валовой внутренний продукт (ВВП);
С - фонд непроизводственного потребления;
I - инвестиции;
L - число занятых;
К - фонды.
Кроме того, в модели используются следующие экзогенные
(заданные вне системы) показатели:
v - годовой темп прироста числа занятых;
μ - доля выбывших за год
основных производственных фондов;
ρ - норма накопления (доля
валовых инвестиций в валовом внутреннем продукте).
Экзогенные параметры находятся в следующих границах: 
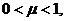

Предполагается, что эндогенные переменные изменяются во времени
(аргумент t опущен, но присутствует по умолчанию).
Экзогенные показатели считаются постоянными во времени, причем норма накопления
является управляющим параметром, то есть в начальный момент времени может
устанавливаться управляющим органом системы на любом уровне из области
допустимых значений.
Время t считается непрерывным и измеряется в
годах. Для мгновенных показателей L = L(t), K = K(t) это представляется совершенно естественным, поскольку, в
принципе, в любой день можно установить число занятых и путем инвентаризации -
объем основных производственных фондов. Значения показателей типа потока Х = X(t), I = I(t), C = C(t) в момент t =[t] + {t} определяются в виде накопленных за год, начинающихся на {t} дней позже 1 января года [t].
Предполагается, что годовой выпуск в каждый момент времени
определяется линейно-однородной неклассической прозведенной функцией
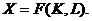 (2.1)
(2.1)
Рассмотрим, как меняются ресурсные показатели за небольшой
промежуток времени 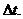 Согласно определению темпа прироста
Согласно определению темпа прироста
 t, или
t, или 
поэтому

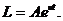
Используя начальное условие L(0) = L0, получаем L = L0evt.
Износ и инвестиции в расчете на год равны µК∆t, I∆t, поэтому прирост фондов за это время
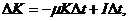
откуда получаем дифференциальное уравнение


Инвестиции и фонд потребления следующим образом выражаются через
ВВП:


Итак, получаем следующую запись модели Солоу в абсолютных
показателях:
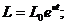
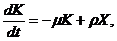
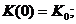 (2.2)
(2.2)



Схема функционирования экономики согласно модели Солоу приведенная
на рис. 2.1. видно, что входом в систему служит число занятых L, выходом - фонд потребления С, поэтому эта система
односвязная. В структуре системы имеется контур обратной связи, который
образуется из нелинейного статического элемента X = F (K, L), распределительного линейного
статического звена X = I + C и инерционного звена
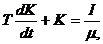
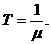
Поскольку в системе имеется нелинейный элемент X = F (K, L), то система -
нелинейная.
Поскольку
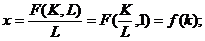
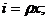
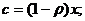
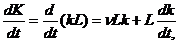
то запись модели Солоу приобретает форму в удельных показателях:


 (2.3)
(2.3)

Рис. 2.1. Структурная схема модели Солоу
Таким образом, каждый абсолютный или относительный показатель
изменяется во времени, то есть можно говорить о траектории системы в абсолютных
или относительных показателях.
Траектория называется стационарной, если показатели не
изменяются во времени:
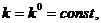
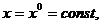

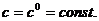
Как видно из формул (2.3), установленные фондовооруженности на
постоянном уровне kE приводит к выводу на стационарную
траекторию. На стационарной траектории  поэтому
поэтому
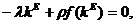 (2.4)
(2.4)
Поскольку функция F (K, L) -
неоклассическая, то 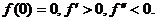 Если еще задано условие
Если еще задано условие  то уравнение (2.4) будет иметь
единственное ненулевое решение
то уравнение (2.4) будет иметь
единственное ненулевое решение 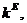
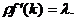
2.2 Модель Эванса
В модели рассматривается рынок одного товара. Время t считается непрерывным. Обозначим через 
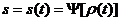 совокупный спрос и предложение в момент t, а через
совокупный спрос и предложение в момент t, а через  цену товара в этот момент.
цену товара в этот момент.
В модели постулируется, что спрос и предложение является линейными
функциями цены:


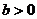 (спрос с ростом цены убывает);
(спрос с ростом цены убывает);
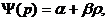
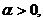
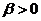 (предложение с ростом цены растет).
(предложение с ростом цены растет).
Кроме того, естественно считать 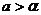 (при нулевой цене спрос превышает предложение!).
(при нулевой цене спрос превышает предложение!).
Основное предположение модели состоит в том, что изменение
цены пропорционально превышению спроса над предложением:
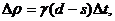
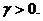 (2.5)
(2.5)
Согласно предложению (2.5) взаимодействие потребителей и
производителей происходит таким образом, что отражающая это взаимодействие цена
непрерывно приспосабливается к ситуации на рынке: в случае превышения спроса
над предложением - возрастает, в противоположном случае - падает.
Используя сделанные предположения, проходит к следующему
дифференциальному уравнению относительно цены:
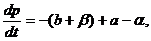
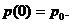 (2.6)
(2.6)
Это уравнение имеет стационарную (равновесную) точку
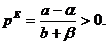 (2.7)
(2.7)
Из (2.2.) видно, что при 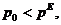
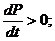 при
при 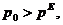
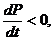 поэтому
поэтому 

 (в первом случае цена достигает равновесного значения,
возрастая, а во втором случае - убывая, при этом равновесная цена
(в первом случае цена достигает равновесного значения,
возрастая, а во втором случае - убывая, при этом равновесная цена  совершенно не зависит от начальной
совершенно не зависит от начальной 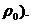 Равновесная цена
Равновесная цена  - абсцисса точки пересечения прямых спроса
и предложения, то есть при такой цене спрос равен предложению.
- абсцисса точки пересечения прямых спроса
и предложения, то есть при такой цене спрос равен предложению.
Эти выводы получены без непосредственного решения уравнения (2.6).
Разумеется, они будут точно такими же, если напрямую использовать решение этого
уравнения
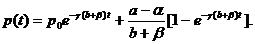
2.3 Динамическое
программирование. Принцип Белмана
Введем некоторые обозначения и сделаем
необходимые для дальнейшего предположения.
Будем считать, что состояние рассматриваемой системы S на k-ом шаге (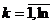 ) определяется совокупностью чисел x = (
) определяется совокупностью чисел x = ( ,…,
,…,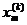 ), которые получены в результате реализации управления uk, обеспечивающего переход системы S из состояния х(k-1)
в состояние х(k)
), которые получены в результате реализации управления uk, обеспечивающего переход системы S из состояния х(k-1)
в состояние х(k)
Далее, будем считать, что если в результате реализации k-го шага обеспечен определенный доход, также зависящий от
исходного состояния системы x(k-1) и выбранного управления Uk, равный Wk(х(k-1); uk), то общий доход за n шагов составляет

где u = (u1, u2,…,
uп).
Таким образом, сформированы два условия,
которым должна удовлетворять рассматриваемая задача динамического
программирования. Первое условие обычно называют условием отсутствия
последействия, а второе - условием аддитивности целевой функции задачи.
Задача состоит в нахождении оптимальной стратегии управления, т.е.
такой совокупности управлений u* = (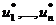 ), в результате реализации которых система S за n шагов переходит из начального состояния х(0) в
конечное х(n) и при этом функция дохода W(u) принимает
наибольшее значение.
), в результате реализации которых система S за n шагов переходит из начального состояния х(0) в
конечное х(n) и при этом функция дохода W(u) принимает
наибольшее значение.
Принцип оптимальности Беллмана. Каково бы
ни было состояние системы перед очередным шагом, надо выбрать управление на
этом шаге так, чтобы доход на данном шаге плюс оптимальный доход на всех
последующих шагах был максимальный.
Из принципа оптимальности следует, что оптимальную стратегию
управления можно получить, если сначала найти оптимальную стратегию управления
на n-м шаге, затем двух последних шагах, затем
на трех последних шагах и т.д., вплоть до первого шага. Таким образом, решение
рассматриваемой задачи динамического программирования целесообразно начинать с
определения оптимального решения на последнем, n-м шаге. Для того чтобы найти это решение, очевидно, нужно сделать
различные предположения о том, как окончиться предпоследний шаг, и с учетом
этого выбрать управление 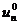 , обеспечивающее максимальное значение
функции дохода
, обеспечивающее максимальное значение
функции дохода  . Такое управление, выбранное при
определенных предположениях о том, как окончился предыдущий шаг, называется
условно оптимальным управлением. Следовательно, принцип оптимальности требует
находить на каждом шаге условно оптимальное управление любого из возможных
исходов предшествующего шага.
. Такое управление, выбранное при
определенных предположениях о том, как окончился предыдущий шаг, называется
условно оптимальным управлением. Следовательно, принцип оптимальности требует
находить на каждом шаге условно оптимальное управление любого из возможных
исходов предшествующего шага.
Чтобы построить алгоритм решения задач, дадим математическую
формулировку принципа оптимальности. Для этого введем некоторые дополнительные
обозначения. Обозначим через F0(х(о)) максимальный доход,
получаемый за n шагов при переходе системы S из начального состояния х(о) в конечное
состояние х(n) при реализации оптимальной стратегии
управления u* = (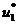 ,…,
,…, 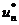 ), а через Fk(х(k)) - максимальный доход, получаемый при переходе из любого
состояния х(n) в конечное состояние х(n) при оптимальной стратегии управления на оставшихся (n-k) шагах. Тогда
), а через Fk(х(k)) - максимальный доход, получаемый при переходе из любого
состояния х(n) в конечное состояние х(n) при оптимальной стратегии управления на оставшихся (n-k) шагах. Тогда
 , (2.8)
, (2.8)
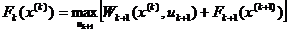 , (2.9)
, (2.9)
при 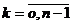 .
.
Выражение (2.9) представляет собой
математическую запись принципа оптимальности Беллмана и носит название
основного функционального уравнения Беллмана. Используя уравнение (2.9)
находится решение рассматриваемой задачи динамического программирования.
Рассмотрим этот процесс более подробно. Полагая k = n - 1 в уравнении
Беллмана (2.9), получим следующее функциональное уравнение:
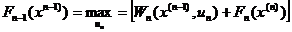 (2.10)
(2.10)
В уравнении (2.10) Fп(х(n)) можно считать известным. Используя теперь уравнение (2.10) и
рассматривая всевозможные допустимые состояния системы S на (n-1) - ом шаге 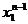 ,
,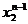 ,…,
,…,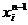 ,… находим условные оптимальные решения
,… находим условные оптимальные решения
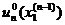 ,
, 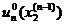 , …,
, …, 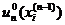 ,…
,…
и соответствующие значения функции (2.10)
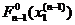 ,
, 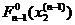 ,…,
,…, 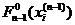 ,…
,…
Таким образом, на n-ом шаге
находим условно оптимальное управление при любом допустимом состоянии системы S после (n-1) - го шага,
т.е. в каком бы состоянии система оказалась после (п-1) - го шага, нам уже
известно, какое следует принять решение на n-м шаге.
Перейдем теперь к рассмотрению функционального уравнения при k= n-2:
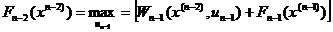 . (2.11)
. (2.11)
Решая функциональное уравнение (2.11) при различных состояниях на
(n-2) - ом шаге, получим условно оптимальные
управления 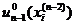 , i =1,2,… Каждое из этих управлений совместно с уже выбранным
управлением на последнем обеспечивает максимальное значение дохода на двух
последних шагах.
, i =1,2,… Каждое из этих управлений совместно с уже выбранным
управлением на последнем обеспечивает максимальное значение дохода на двух
последних шагах.
Последовательно осуществляя описанный выше
итерационный процесс, дойдем, наконец, до первого шага. На этом шаге известно,
в каком состоянии может находиться система. Поэтому уже не требуется делать
предположений о допустимых состояниях системы, а остается лишь только выбрать
управление, которое является наилучшим с учетом условно оптимальных управлений,
уже принятых на всех последующих шагах.
Чтобы найти оптимальную стратегию управления, определить искомое
решение задачи, нужно теперь пройти всю последовательность шагов, только на
этот раз от начала к концу. А именно: на первом шаге в качестве оптимального
управления 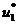 возьмем найденное условно оптимальное
управление
возьмем найденное условно оптимальное
управление 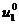 . На втором шаге найдем состояние
. На втором шаге найдем состояние 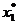 , в которое переводит систему управление
, в которое переводит систему управление 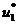 . Это состояние определяет найденное
условно оптимальное управление
. Это состояние определяет найденное
условно оптимальное управление 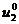 , и которое теперь будем считать оптимальным. Зная
, и которое теперь будем считать оптимальным. Зная 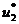 , находим
, находим 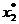 , а значит, определяем
, а значит, определяем 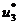 и т.д. В результате этого находим решение задачи, т.е.
максимально возможный доход и оптимальную стратегию управления, включающую
оптимальные управления на отдельных шагах.
и т.д. В результате этого находим решение задачи, т.е.
максимально возможный доход и оптимальную стратегию управления, включающую
оптимальные управления на отдельных шагах.
Из изложенного видно, что этот процесс
является довольно громоздким. Однако использование ЭВМ позволяет находить на
основе метода динамического программирования решение и более сложных
практических задач.
Список литературы
модель уравнение солоу полезность
1. Андрейчиков А.В., Андрейчикова О.Н. «Анализ. Синтез.
Планирование решений в экономике» - М.: Финансы и статистика, 2002.
. Бережная Е.В., Бережной В.И. «Математические методы
моделирования экономических систем» М.: Финансы и статистика, 2001.
3. Большаков А.С. «Моделирование в менеджменте» - М.:
Филинь, 2000.
4. Жданов С.А. «Экономические модели и методы в
управление» - М.: Дело и сервис, 1998.
5.
Канторович Л.В., Горстко А.Б. «Оптимальные решения в экономике» - М., Наука,
1998.
6. Колемаев
В.А. Математическая экономика: Учебник для вузов. - 2-е издание, - М.: ЮНИТИ,
2003.
7. Конюховский
П. «Математические методы исследования операций в экономике: Учебное пособие» -
Спб: Питер, 2000.
. Моисеев
Н.Н. «Человек, среда, общество. Проблемы формализованного описания» - М.:
Наука, 1998.
. Лабскер
Л.Г. и др. «Игровые методы в управлении экономикой и бизнесом: Учебное пособие»
- М.: Дело, 2001.
. «Математические
методы принятия решений в экономике». Под ред. Колемаева В.А.М.: ЗАО
«Финстатинформ», 1999.