Операции сетевого планирования

Операции сетевого планирования

Введение

С переходом Республики Беларусь к рыночной модели развития одной из приоритетных задач стало повышение качества продукции, выпускаемой предприятиями промышленной и непромышленной сферы, снижение затрат на производство продукции, в том числе уменьшение затрат времени.

Речь здесь идет о многих параметрах, влияющих на затраты, которые, в свою очередь, формируют себестоимость продукции. Однако важную роль играет время завершения производства продукции, а значит, и календарное планирование. Разумные ответы для решения задач календарного планирования технологических комплексов с единичным и мелкосерийным характером производства может дать только класс операционно-сетевых моделей. Поэтому тема "Задачи сетевого планирования и управления", раскрытая ниже, достаточно актуальна.

Особо стоит подчеркнуть, что для производственных задач методы сетевого планирования в так называемом "чистом виде" оказываются малоприемлемыми ввиду ограниченности ресурсов, располагаемых предприятием или его отдельными звеньями при выполнении поставленного задания. Но методы систем сетевого планирования и управления (СПУ) становятся эффективными в качестве составного элемента более общей теории расписаний. Данная тема достаточно разработана в литературе. Ей посвящены многие книги.

Курсовая работа состоит из двух глав, введения и заключения. В первой главе, теоретической, рассматриваются основные понятия теории графов, необходимые для дальнейшего рассмотрения темы, также показано построение сети (графа) исследовательского, опытно-конструкторского или производственного проекта, определено время завершения всего комплекса работ, резервы событий и операций в случае, когда длительности операций являются вполне определенными детерминированными величинами. Во второй главе, практической, приведена практическая часть курсовой работы, где необходимо четыре задачи решить с помощью симплекс-метода, в двух задачах нужно составить математические модели в общем и развернутом видах, также необходимо самостоятельно составить и решить транспортную задачу. В заключении работы отражены основные выводы.

Цель работы заключается в следующем: раскрыть основные понятия теории графов, научиться проводить исследования порядка выполнения операций, определять время завершения всего комплекса работ, находить критический путь и резервы событий, а также освоении навыков решения задач.

Глава 1. Задачи сетевого планирования и управления

Определим понятие графа. Для этого рассмотрим множество, состоящее из конечного числа элементов, которые обозначим буквами Х_1, Х₂, ..., Х_п, а само множество - буквой X; запишем это символически:

 = {X₁, X₂,...,X_n}.(1)

Каждому элементу X_i , принадлежащему X, поставим в соответствие нуль, один или несколько элементов из X; мы построим тогда, пользуясь терминологией теории множеств некоторый "граф". Обозначив через Г закон, представляющий данное соответствие, запишем граф символически: G = (X, Г).

Возьмем пример для иллюстрации этого определения. Пусть мы имеем множество из 6 элементов: X = {A, B, C, D, E, F}, и рассмотрим следующее соответствие, определенное с помощью символа Г:

ГА = {B,C,D}, ГВ = {A,B,C}, ГС = {B,D,E,F}, ГD = {C,D,E}, ГЕ = {C,E}, ГF = Ø,

где символ Ø означает, пользуясь терминологией теории множеств, пустое множество и аналогичен нулю при числовой нумерации.

Граф может быть представлен с помощью чертежа, как это сделано на рис. 1. Это называется "представлением графа с помощью направленных дуг". Граф может быть представлен так же, как это показано на рис. 2, или, наконец, с помощью таблицы с двумя входами или матрицей (таблица 1).

В теории множеств "графом" называют всякое отображение множества в себя. Символ Г представляет это отображение.

Элемент множества, образующего граф, называется "вершиной". На рис. 1 элементы А, В, С, D, Е и F представляют собой вершины графа. Некоторыми авторами вершина называется также "точкой".

Ориентированная пара (X_i X_j) вершин X_t и X_j называется "дугой". Так, на рис. 1, (А, В), (В, А), (А, С), (Е, Е),(С, F) представляют собой дуги.

Таблица 1. Матрица графа

Обозначим через U множество дуг, тогда в нашем примере:

 = {(А, В), (А, С), (А, D), (В, А), (В, В), (В, С), (С, В), (С, D),

(С, Е), (С, F), (D, С), (D, D), (D, Е), (Е, С), (Е, Е)}.

Контур - это путь, начальная вершина которого совпадает с конечной: (А, С, В, А), (А, D, Е, С, В, А), (А, С, В, А, С, В, А),(А, В, А), (В, В) являются контурами, см. рис. 1.

Петля - это дуга, начало и конец которой совпадают: (В, В), (D, D) и (Е, Е) представляют собой петли, см. рис. 1.

Длина пути или контура - это число дуг пути или контура. Так, длина (А, В, С, F) равна 3, длина (А, D, Е, С, В, А) равна 5.

Если две вершины графа соединены дугой, начинающейся в любой из них, то говорят, что между этими вершинами есть ребро. Поэтому понятие ребра эквивалентно понятию "неориентированного" графа.

Например, на рис. 1. между А и D есть ребро. Нет ребра между В и D. Ребро обозначается (А, D) или ( А, В); множество ребер обозначим U. Так, в нашем примере, см. рис. 1:

U = {(A,B), (A,C), (A,D),(B,C), (C,D), (C,E), (C,F), (D,E)}

Цепь - это последовательность сцепленных ребер, т. е. последовательность дуг, сцепленных без учета их ориентации. Так, на рис. 1 (В, С, A, D, Е) не есть путь (из-за дуги АС), но это цепь. Всякий путь является, очевидно, цепью, но, как видно, цепь не всегда является путем.

Граф называется "связным", если между всякой парой его вершин существует хотя бы одна цепь. Граф на рис. 1 связен. Граф "сильно связен", если между всякой парой его вершин существует хотя бы один путь. Граф на рис. 1 не является сильно связным, т.к. не существует путей от F к другим вершинам. Антисимметричный" граф. Рассмотрим множество U дуг графа. Если для всякой дуги (X_i X_j), принадлежащей U, дуга (X_j, X_i), т. е. противоположная ей, не принадлежит U, то говорят, что граф "антисимметричен". В силу этого определения антисимметрический граф не может содержать петель. Например, граф на рис. 3 "антисимметричен".

Рассмотрим граф без контуров. На рис. 3 мы видим граф, не содержащий ни одного контура. Очевидно, что всякий граф без контура антисимметричен, но обратное утверждение неверно.

Представляет интерес представление проектов (комплексов операций) с помощью сетей. Сеть - это граф, описывающий комплекс операций (проект). Проект (комплекс операций) - совокупность операций, необходимых для достижения некоторой цели, длительность (детерминированная или случайная) каждой из которых нам известна и которые связаны отношением порядка (обязательным предшествованием).

Проект может быть представлен сетью, называемой "сетевой моделью проекта" или логической диаграммой, дуги которой представляют операции. Времена выполнения операций или длительности операций предполагаются известными и приписываются дугам как неотрицательные величины. Вершины сети, называемые событиями и обозначаемые E_i могут интерпретироваться как результаты выполнения отдельных частных задач (например, окончания монтажа блока). Если разбиение произведено слишком детально (при этом операции все более и более упрощаются, а их длительности уменьшаются), то в этом случае практическое значение рассматриваемых событий значительно снижается, за исключением тех из них, которые фиксируют основные этапы проекта. Длительность операции Р_ij, участвующей в реализации события E_j, будет обозначаться t_ij. На приведенном ниже рис. 4 представлен некоторый проект.

Рис. 4

При построении сети необходимо знать операции, непосредственно предшествующие данной операции. Сеть выражает, таким образом, соотношения порядка, существующие во множестве операций. Заметим, что одни и те же порядковые соотношения или одна и та же сеть могут соответствовать нескольким различным проектам, если длительности операций будут различными. Отметим, что отсутствие контуров в сети равносильно тому, что ни одна операция не следует после себя самой.

Первое, что необходимо сделать, имея в виду применение метода критического пути, это составить перечень операций, который может быть детализирован в большей или меньшей степени в зависимости от точности, которую желательно получить. Операции надо стараться выбирать настолько простыми, насколько это возможно, и такими, чтобы времена операций были сравнимы по величине. Затем для каждой операции определяют предшествующие ей операции. Эта часть анализа работ является наиболее важной и часто занимает много времени. Она требует тесного сотрудничества всего персонала (инженеров, мастеров, рабочих), заинтересованного в выполнении проекта, и, несомненно, является полезной даже сама по себе.

Для конкретизации мы возьмем пример строительства дачи. Чтобы построить дачу, необходимо выполнить определенное число операций; перечислим их в некотором порядке:

1        разработка проекта

2        получение разрешения на строительство

3        подписание контракта

          подвоз материалов к стройке (бетон, плиты, кирпич)

          подвод электричества и воды к стройке

          фундамент

7        кирпичная кладка

          плотницкие работы

          покрытие

          грунтовка

          перегородки (из пустотелого кирпича)

          трубы (вода, центральное отопление, газ)

          внутренняя электропроводка

          установка рам и окон

          обработка стен и перегородок (цемент)

          установка двух дымовых труб

          плиточная облицовка - санитарное оборудование - кухонный настил

          штукатурка

          установка штепселей и электрических выключателей

          установка дверей и окон

          покраска и оклейка обоев

          установка котла центрального отопления и радиаторов

          подвоз земли для сада

          установка счетчиков и подвод радио, телевидения, телефона, воды

          уборка строительной площадки

          предварительный прием.

Рассмотрим построение сети, изображенной на рис. 5. Обозначим через Е₁ начальное событие (т. е. начало выполнения работ), а через Е₂ - событие: контракт может быть подписан. Между Е₁ и Е₂ находятся две операции: составление плана и получение разрешения на строительство. Если административный порядок предполагает, что разрешение на строительство не может быть выдано без представления проекта (что обычно имеет место), поместим между Е₁ и Е₂ событие Е₃: разработка проекта закончена. После события Е₂ можно приступить одновременно к операциям е и с с длительностями операций t₂₄ и t₂₅. Действительно, подвод электричества и воды не есть, вообще говоря, дело подрядчика. Событие Е₅ означает подписание контракта. После этого можно приступить к операции d с временем операции t₅₄. Операция f с временем t₄₆ помещается после события Е₄, так как она может начаться только после окончания операций d и e. И так далее по операциям.

Представление проекта с помощью сети может быть сделано и другим образом. Будем изображать вершинами не события, а операции. Дуги же используем для представления порядка, в котором операции O_ij и O_jk должны следовать так, чтобы можно было задавать сроки между началом O_ij и началом O_jk .В этом представлении принято называть "работами" то, что раньше мы назвали операциями, и "связями" - дуги, которым приписаны сроки. На рис. 6 приведена сеть, соответствующая рис. 5 после такой замены.

Чтобы до конца разъяснить переход от одного представления к другому, возьмем другой пример - переход от рис. 7 к рис. 9. Как видно на рис. 8 и 9, принято добавлять две работы D и F, представляющие начало (debut) и конец (fin) проекта.

Рис. 7

На рис. 9, видно, что работа g помещается после работ b и d. Между g b существует связь: g может начаться только тогда, когда пройдет 6 единиц времени после начала b. Между g и d существует связь: g может начаться только тогда, когда пройдет 4 единицы времени после начала d. В свою очередь работы d, f и е могут начаться только после того, как пройдет 3 единицы времени после начала а. Оба представления обладают и преимуществами и недостатками. Обычно выбирают то или другое представление в зависимости от существа той задачи, для которой составляется проект. Заметим, однако, что представление "работы-связи" позволяет вводить в проект новые связи или изменять отношения порядка между работами простым добавлением дуг без перестройки сети в целом.

В сетевом планировании существую различные виды операций:

) составные операции. Рассмотрим операцию а, состоящую из трех элементарных операций: а₁ , а₂ и а₃, см. рис. 10, и пусть операция с следует за а_и d следует за а₂ и b следует за а₃. Рис. 11 представляет эту ситуацию в терминах, "работы-связи". Рис. 12 показывает, что это представление можно упростить; исчисление новых связей не представляет трудностей.

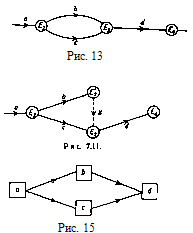
2) параллельные операции. Предположим, что между двумя событиями E_i и E_j находятся две различные операции b и с, следующие за операцией а. Введем тогда фиктивное событие Е_j` и дополнительную фиктивную операцию х между E<sub>j</sub>` и E_j. В случае, когда имеется три, четыре и т. д. параллельные операции, поступают так же, вводя для каждой из них фиктивное событие и дополнительную фиктивную операцию. На рис. 15, введение фиктивных событий и операций нецелесообразно.

3) операции зависимые и независимые. Рассмотрим на рис. 16 операции c и d, следующие за а и b. Предположим теперь, что с следует за. а и b, но d следует только за b и не обязано следовать за а. В этом случае уже нельзя пользоваться данной сетью и необходимо ввести событие Ез` и фиктивную операцию х, см. рис. 17.

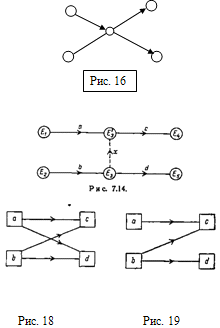
В представлении "работы-связи" нет необходимости вводить фиктивные события и операции. Рис.18 соответствует рис.16, а рис. 19 -рис. 17.

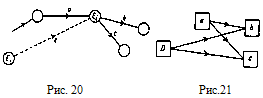
Имеют значение также особые ограничения и условия на сроки начала выполнения операций. Предположим, что некоторая операция может быть начата только по наступлении какого-то момента, т. е. по прошествии некоторого срока после события Е₁ , принимаемого за начальное. Такое ограничение выражается введением фиктивной операции между E₁ и событием Е_i , где начинается рассматриваемая операция, см. рис. 20. В другом представлении вводится связь между D и b, см. рис. 21.

Во многих задачах встречаются некоторые "условия отсрочки начала выполнения операции". Ими могут быть, например, сроки поставки материалов, климатические условия и т.п. Эти особые условия легко могут быть введены в сеть.

Стоит отметить также и другой тип встречающихся ограничений: для того, чтобы некоторая работа j могла быть начата, необходимо, чтобы время, прошедшее с момента начала другой работы i, было бы не больше данного срока t_ij. С помощью этих ограничений можно избежать нежелательных осложнений и обеспечить преемственность работ или их одновременное выполнение. Для того чтобы иметь возможность учесть такие ограничения и ввести их в сеть, сформулируем их по-другому: для того чтобы некоторая работа i могла быть начата, необходимо, чтобы время, прошедшее с момента начала другой работы j, было не меньше данного (-t_ij). Это приводит к обычным связям, но с отрицательной длительностью (длина соответствующей дуги будет отрицательна).

Когда сеть проекта построена, перед руководителем встает следующий вопрос: каково время завершения всего комплекса операций, т. е. какова продолжительность реализации проекта. Это время не может быть меньше суммы длительностей операций, взятой вдоль "самого неблагоприятного пути" из Е₁ в Е_п, т. е. вдоль такого пути между этими двумя точками, который дает максимальную сумму длительностей операций. Такой путь (их может оказаться несколько) называется "критическим путем".

Это можно понять с помощью простейшей сети, изображенной на рис. 2.2. Событие Е₃ означает выполнение трех операций Р₁₃, Р₁₂ ,и Р₂₃. Для того чтобы все эти операции могли быть реализованы, необходимо 8 единиц времени.

Беря в качестве продолжительности выполнения комплекса работ сумму длительностей операции вдоль наименее благоприятного пути из E_i в Е_п,, мы тем самым обеспечиваем возможность действительного выполнения всех намеченных операций с учетом их длительностей.

Рис. 22

Вычисление момента реализации Е_п сводится, таким образом, к отысканию в сети самого длинного или критического" пути (пути максимальной величины). Рассмотрим пример.

Рассмотрим рис. 23. В Е₂ входит только одна дуга (1,2). Поскольку для Е₁ имеем 0, то для Е₂ получим 0 + 8 = 8. В Е₃ входят две дуги (2,3) и (1,3): сравнивая 8 + 4=12 с 0+13=13, приписываем Е₃ значение 13, это означает, что наступление события Ез нельзя ожидать раньше 13. В Е₄ входят две дуги (3,4) и (1,4): сравнивая 13 + 7 = 20 с 0 + 9 = 9, приписываем Е₄ значение 20. Е₅ приписываем значение 17. В Е₆ входят две дуги (2,6) и (3,6): сравнивая 8 + 6=14 с 13+10 = 23, приписываем Е₆ значение 23. В Е₈ входят три дуги (6,8), (3,8) и (4,8): сравнивая 23 + 3 = 26, 13 + 6=19 и 20 + 9 = 29, приписываем Е₈ значение 29. Так продолжаем вплоть до события Е₁₂, которому приписываем окончательно значение 61.

Это число представляет собой время выполнения проекта, начинающегося с нулевого момента. Путь, соответствующий этому времени в 61 единицу, легко получить, возвращаясь шаг за шагом обратно из Е₁₂ в Е₁ это и будет критический путь. На рис. 23 он отмечен жирной линией.

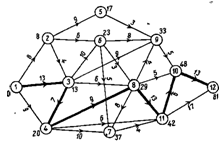
Рис. 23

Если проект (комплекс операций) будет разворачиваться без неожиданных нарушений, его продолжительность должна будет составить 61 неделю и соответствующие события произойдут в моменты, указанные на рис. 23.

Операции Р₁₃, Р₃₄, Р₄₈, Р_8,11, Р_11,10, Р_10,12 называются "критическими операциями". С них нужно начинать работу после наступления начальных событий соответствующих дуг. Так, к примеру, операция Р₄₈ должна начаться в первую очередь после реализации события Е₄, т. е. в момент 20. Если критическая операция будет задержана, это вызовет запаздывание выполнения всего проекта. Например, если операция Р₄₈ начнется только, в момент 22, проект будет завершен не раньше, чем к моменту 63.

Таким образом, критические операции представляют собой те операции проекта, на ход выполнения которых руководитель должен направить все свое внимание, так как от их своевременного выполнения зависит общий срок завершения всего проекта (всего комплекса работ).

Приходим к выводу, что для каждого некритического события E_i важно знать предельный срок его наступления, т. е. срок, превышение которого приведет к задержке выполнения всего проекта. Для этого рассмотрим событие Е_i. Минимальное время, необходимое для наступления всех событий, расположенных между событиями E_i и Е_п, получается определением в сети "самого длинного" пути от E_i до Е_п. Эта процедура обеспечивает нам уверенность в возможности действительного выполнения операций, следующих за Ei, с учетом соответствующих им длительностей. Искомый предельный срок t_i* получается вычитанием этого минимального времени из времени t_n наступления конечного события Е_п.

Таким образом, для каждого некритического события мы получаем два граничных срока:

·   время t_i , ожидаемое время наступления события E_i ,

·   время t_i *, предельное время наступления события E_i ,превышение которого приведет к изменению общего времени завершения всего комплекса операций.

Ожидаемое время t_i иногда называют "наиболее ранний срок", а пре- дельное время t_i* - "наиболее поздний срок". Для критических событий предельный срок t_i* совпадает с ожидаемым временем t_i. Эти события не допускают никакого запаздывания в сроках их наступления, или (что означает то же самое) критические операции не допускают никакой задержки в их выполнении.

Интервал [t_i , t_i*] называется интервалом свободы события (резервным интервалом). Резервный интервал - это интервал времени, в течение которого может наступить событие Е_i без изменения общего времени завершения всех работ. Длина интервала свободы события (резервного интервала), т. е. величина t_i* - t_i , называется резервом времени события E_i.

Обратимся опять к примеру постройки дачи и вычислим граничные сроки t_i*, используя тот же метод, как и при вычислении t_i,, но отправляясь на этот раз от конечного события Е₁₂. Рассмотрим сначала, см. рис. 24, событие Е_1, отделенное от события Е₁₁ операцией длительностью 4, так что операция P_7,11 может начаться за четыре недели до события Е₁₁ и, следовательно, событие Е₇ должно произойти в интервале [37, 38]. Событие E₉ отделено от события Е₁₀ операцией длительностью 5, так что операция Р_9,10 может начаться за пять недель до события Е₁₀ и поэтому событие E₉ должно произойти в интервале [33,43]. Событие Е₆ отделяет от события E₉ операция в 8 недель, от события Е₈ - 3 недели, от события Е₇ - 5 недель; из сравнения 43-8 = 35, 29-3 = 26 и 38-5 = 33 видно, что событие Е₆ должно произойти не позднее момента 26 (наименьшее из трех), чтобы не вызвать нарушений, которые отразились бы на завершающей дате. Числа, которые при этом получаются, выписаны на рис. 2.21 и заключены в скобки, чтобы не путать их с теми числами, которые были получены при нахождении критического пути. Событию Е₅ припишем 40; событию Е₂ после сравнения 40-9 = 31, 26-6 = 20, 13-4 = 9 припишем 9.

Рис. 24

Подводя итоги, можно сказать, что моменты наступления событий Ei могут находиться в приведенных ниже интервалах (от-до), причем на критическом пути эти интервалы сводятся к точным датам:

Для каждой операции P_ij также важно знать, какая задержка может быть допущена при ее выполнении без того, чтобы это привело к нарушению срока наступления события E_j. Эта возможная отсрочка начала выполнения операции P_ij - есть "свободный резерв времени" операции Р_ij, обозначаемый в дальнейшем через М_ij.

Если t_i и t_j - ожидаемые сроки наступлений событий E_i и Ej, между которыми имеется операция Р_ij длительностью t_ij, то ее свободный резерв времени равен:

М_ij =t_j - t_i - t_ij. (2)

Свободный резерв времени критических операций равен нулю, так как в отношении этих операций не может быть допущена никакая отсрочка в начале их выполнения.

Таким же образом определяются для каждой операции "полный резерв времени" и "независимый резерв времени".

По определению полный резерв времени операции Р_ij равен:

_j^* - t_i - t_ij , (3)

а ее независимый резерв времени равен:

_j - t_i ^* - t_ij (4)

Резервы событий и операций характеризуют эластичность проекта. Чем более они уменьшаются, тем жестче сеть проекта. Сеть проекта "полной жесткости" такова, что все ее пути являются критическими. В ней нет ни резервов событий, ни свободных резервов операций. При таком положении недопустимы никакие задержки ни по какой из операций.

Существенное различие между резервом события E_i и свободным или полным резервом операции Р_ij состоит в том, что резерв события представляет собой запаздывание, которое может быть допущено в наступлении события E_i, без изменения фиксированных сроков наступления критических событий, и в частности конечного события, соответствующего выполнению проекта, в то время как свободный резерв операции М_ij представляет собой отсрочку начала выполнения операции Р_ij, без изменения ожидаемого срока наступления события E_j, а полный резерв представляет собой максимальную допустимую отсрочку начала выполнения этой операции.

Другой аспект понятия свободный резерв может быть выявлен в случае, когда продолжительность некритических операций может быть удлинена. В этом случае свободный резерв М_ij соответствует возможному удлинению длительности операции P_ij,, оставляющему неизменными сроки t_i и t_j наступления событий E_i и E_j,, определяющих эту операцию.

Эта разница между резервом события и свободным резервом, или полным резервом операции, лучше всего видна в сети, изображенной на рис. 24 и воспроизведенной на рис. 25.

Здесь интервал свободы события Е₆ есть [23, 26]. Свободный резерв операции Р₆₉ равен:

М₆₉ = 33 - 23 - 8 = 2.

Следовательно, операция Р₆₉ может начаться в момент 23+2 = 25 без изменения времени t₉ - срока наступления события E₉, который остается равным 33. Свободные резервы операций указаны на рис. 25 в скобках.

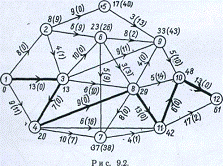
Рис. 25

Полный резерв операции Р₆₉ равен 43-23-8 =12. Таким образом, операция Р₆э может начаться в момент 23+12=35, не вызывая задержку выполнения всего комплекса работ.

Важное значение понятий граничных сроков событий и свободных резервов операций особенно дает себя знать в процессе выполнения проекта. Если все события наступают в пределах граничных сроков, то проект осуществляется нормально и конечный срок t_n будет выдержан. Если, напротив, по каким-либо причинам случится, что момент наступления некоторого события превысит предельный срок t_i, то руководители проекта должны произвести, если это возможно, перераспределение сил, чтобы ускорить работы в этой части выполнения проекта. Если такой возможности нет, то можно утверждать, что срок выполнения всего комплекса операций будет задержан, и эту задержку можно вычислить.

Граничные сроки событий представляют собой, таким образом, "пределы безопасности" и являются для руководителя "сигналом тревоги", предупреждающим о срыве срока выполнения проекта.

Стоит отметить, что сам по себе метод критического пути не является методом упорядочения. Он применим только тогда, когда сеть проекта уже составлена, т. е. когда операции уже упорядочены. Его роль состоит фактически в том, чтобы расшифровать сеть с временной точки зрения, т. е. дать все необходимые указания относительно сроков, в которые должны наступить различные события проекта.

Очевидно, что наиболее важным длительным и сложным делом является составление сети проекта, т. е. та часть исследования, при выполнении которой приходится обращаться к исследованию упорядочения. В самом деле, порядковые отношения операций не всегда являются достаточно строгими или вполне определенными; некоторые операции могут быть начаты прежде, чем закончится какая-нибудь предыдущая (составные операции). На практике существует много различных способов разработки проектов (комплексов операций) и их сетей.

Итак, попробуем проиллюстрировать эти методы упорядочения на примере и показать, как метод критического пути позволяет сопоставлять различные сети проектов, относящиеся к одному и тому же комплексу операций. Этот пример относится к строительству промышленного здания, состоящего из пяти пролетов. На рис. 26 приведен план одного пролета.

В таблице 2 пунктирные стрелки указывают порядковые отношения различных операций. Проект начинается с операций А, В и Е.

Исходя из этого, мы можем начертить сеть проекта, см. рис. 27. При этом потребовалось ввести две дополнительные фиктивные операции, показанные на рисунке пунктирной линией. Числа, проставленные в вершинах сети, представляют собой ожидаемые сроки наступления соответствующих событий. Конечной вершине приписан срок 250. Следовательно, проект дол- жен быть закончен в течение 250 дней. Критический путь показан жирной линией.

Рис. 27

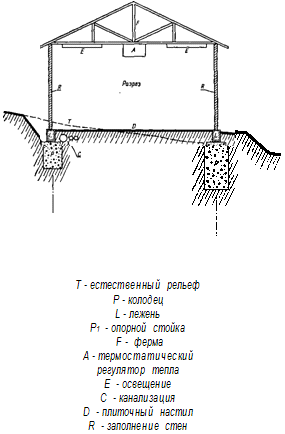
Рис. 26

Таблица 2. Виды работ и операции

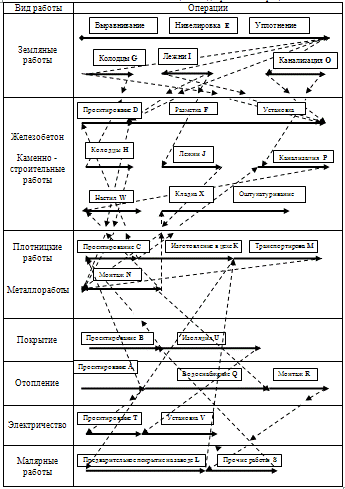
Таблица 3 Длительности операций (в днях)

Стоит заметить, что некоторые операции могут быть разложены, их можно было бы начинать до полного окончания предшествующих им операций. Это может иметь место в том случае, если сооружение здания будет производиться пролет за пролетом. При этом могут быть составлены различные сети, каждая из которых будет соответствовать определенной организации строительства.

·        Сеть, соответствующая организации строительства с приоритетом первого пролета.

Обозначим детализированные операции - это операции-Л, С, К, L, M, N, R, S, U, V. Обозначения операций и их длительности указаны в таблице 4. Теперь можно вычертить сеть проекта и вычислить ожидаемые сроки наступления различных событий, см. рис. 28

Видно, что теперь дата наступления конечного события - 210. Таким образом, разбив некоторые операции, мы выиграли 40 дней.

Как и ранее, пунктирными линиями показаны дополнительные фиктивные операции, необходимость в ведении которых бесспорна.

Рис. 28

Таблица 4. Длительности операций

Сеть, соответствующая строительству с приоритетом двух пролетов.

Новые длительности операций характеризуются следующими данными:

Таблица 5. Длительности операций (в днях)

Длительности других операций остаются прежними. В результате получаем сеть, приведенную на рис. 29. Дата наступления конечного события -177. Таким образом, мы добились нового сокращения продолжительности всего проекта.

Рис. 29

·        Сеть, соответствующая строительству с приоритетом трех пролетов

Новые длительности операций характеризуются следующими данными:

Таблица 6. Длительности операций (в днях)

Длительности других операций остаются прежними. В результате получаем сеть, приведенную на рис. 30. Дата наступления конечного события -165. Критические операции отмечены жирными линиями.

Рис. 30

Таким образом, выше представлены три сети, соответствующие трем возможным планам организации строительства. В данном примере руководитель проекта выберет план № 3, так как он дает общий, минимальный в данном случае, срок строительства в 165 дней.

Глава 2. Практическая часть

Задача 1.

 Z = 3X₁ + 2X₂ + X₃

3X₁ + 4X₂ + 5X₃ ≤ 5

X₁ + 4X₂ + 8X₃ ≤ 8

X₁ + 6X₂ + 4X₃ ≤ 4

X₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0.

Решение:

Приведем данную модель к каноническому (стандартному) виду. Для этого в каждое ограничение вводим дополнительную переменную, дополняющую неравенство до равенства. Эти дополнительные переменные возьмем за базисные. В целевую функцию дополнительные переменные вводятся с нулевыми коэффициентами.

= 3X₁ + 2X₂ + X₃ + 0X₄ + 0X₅ + 0X₆ → max

X₁ + 4X₂ + 5X₃ + X₄ = 5

X₁ + 4X₂ + 8X₃ + X₅ = 8

X₁ + 6X₂ + 4X₃ + X₆ = 4₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0.

На основе канонической модели строим так называемую симплексную таблицу.

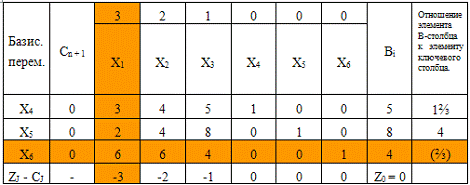
По значениям Z-строки мы видим, что решение не оптимально. (Так как задача на максимум, а полученные значения отрицательны). Следующим шагом выбираем максимальное значение по абсолютной величине Z-строки из отрицательных значений, поскольку задача на максимум. Это значение -3. Получаем ключевой столбец. Затем находим минимум отношения элемента В-столбца к соответствующему элементу ключевого столбца. Получаем ключевую строку. На пересечении ключевой строки и ключевого столбца получаем ключевой элемент. Соответствующая переменная столбца вводится в состав базисной и строится новая симплексная таблица.

В данной таблице значения Z-строки - положительные числа, следовательно, данное решение оптимально.

Вывод:

₀ = 2; X₄ = 3, X₅ = 6⅔ , X₁ = ⅔, X₂ = X₃ = X₆ = 0.

Задача 2

 Z = 5X₁ + 3X₂ + 4X₃ + X₄₁ + 3X₂ + 8X₃ + 7X₄ ≥ 24

X₁ + 2X₂ + X₃ + 4X₄ ≥ 12

4X₁ + 3X₂ + 5X₃ + X₄ ≥ 24

X₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0; X₄ ≥ 0.

Решение:

Данную задачу целесообразно решать двойственным симплекс-методом.

Для превращения неравенств в равенства введем дополнительные переменные:

Z = 5X₁ + 3X₂ + 4X₃ + X₄ - 0X₅ - 0X₆ - 0X₇ → min₁ + 3X₂ + 8X₃ + 7X₄ - X₅ = 24

X₁ + 2X₂ + X₃ + 4X₄ - X₆ = 12

4X₁ + 3X₂ + 5X₃ + X₄ - X₇ = 24

X₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0; X₄ ≥ 0.

Поскольку в двойственном симплекс-методе мы исходим из недопустимости планов, то базис можно получить умножением системы ограничений на - 1. Тогда получим:

Z = 5X₁ + 3X₂ + 4X₃ + X₄ - 0X₅ - 0X₆ - 0X₇ → min

X₁ - 3X₂ - 8X₃ - 7X₄ + X₅ = -24

X₁ - 2X₂ - X₃ - 4X₄ + X₆ = -12

-4X₁ - 3X₂ - 5X₃ - X₄ + X₇ = -24₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0; X₄ ≥ 0.

Теперь составляем первоначальную симплексную таблицу по правилам прямого алгоритма симплекс-метода.

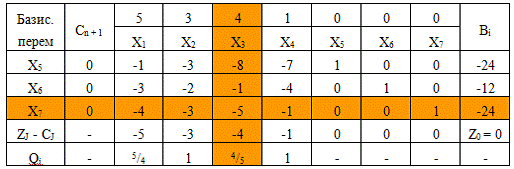
Видим, что все значения Z-строки положительны, т.е. решение оптимально. Но оно, в то же время, является недопустимым, так как свободные члены (B_i) отрицательны. Это базисное решение называется псевдопланом.

Преобразование симплексных таблиц в двойственном симплекс-методе осуществляется так же, как и в прямом алгоритме. Единственное различие осуществляется в правилах определения ключевого элемента. Здесь он находится следующим образом: вначале выбирается ключевая строка, соответствующая базисной переменной, для которой B_i является наименьшей величиной среди всех отрицательных B_i.Затем определяется вектор, вводимый в базис (ключевой столбец), для чего рассчитывается величина Q_j = Z_J - C_J/ а_ij , причем а_ij должны быть отрицательны и принадлежать ключевой строке. Ключевой столбец соответствует переменной, для которой │ Q_j │ → min. Ключевой элемент находится на пересечении ключевой строки и ключевого столбца.

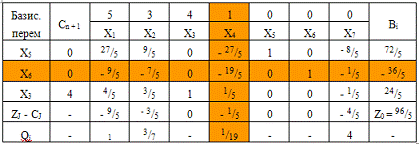
Значения Z-строки положительны, а задача на минимум, то по правилам двойственного симплекс-метода строим новую симплексную таблицу.

Задача на минимум, и значения Z-строки отрицательны, следовательно, найдено оптимальное решение.

Вывод:

₀ = ³⁷²/₁₉; X₃ = ⁸⁴/₁₉, X₄ = ³⁶/₁₉, X₅ = ⁴⁶⁸/₁₉, X₁ = X₂ = X₆ = X₇ =0.

Задача 3

Max Z = X₁ + 2X₂ + 3X₃

4X₁ + 3X₂ + 2X₃ + X₄ ≤ 20

X₁ + 3X₂ + 2X₃ ≤ 27

X₁ + 2X₂ + X₃ + X₄ ≥ 18

X₁ + X₂ + X₃ ≤ 20

X₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0.

Решение:

Поскольку в данной задаче присутствуют знаки ≤ и ≥, поэтому решать ее целесообразнее прямым симплекс-методом с искусственными переменными. Преобразуем неравенства в равенства. Для этого введем дополнительные переменные в неравенства со знаком ≤ и дополнительную и искусственную - в неравенство со знаком ≥. Так как задача на максимум, то в целевую функцию искусственная переменная, образующая базис, вводится со знаком "-":

Z = X₁ + 2X₂ + 3X₃ + X₄ + 0X₅ + 0X₆ - 0X₇ - МX₈ + 0X₉

4X₁ + 3X₂ + 2X₃ + X₆ = 27

X₁ + 2X₂ + X₃ + X₄ - X₇ - X₈ = 18

2X₁ + X₂ + X₃ + X₉ =20

X₁ ≥ 0; X₂ ≥ 0; X₃ ≥ 0.

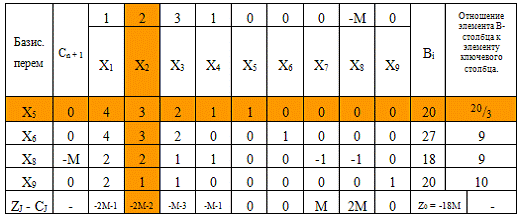
Некоторые значения Z-строки отрицательны, а задача на максимум, следовательно, решение не оптимально. Строим новую симплексную таблицу.

После данного преобразования не все значения Z-строки положительны, а задача на максимум, следовательно, решение не оптимально. Строим новую симплексную таблицу.

Среди значений Z-строки есть отрицательные значения, а задача на максимум, следовательно, решение не оптимально. Строим новую симплексную таблицу.

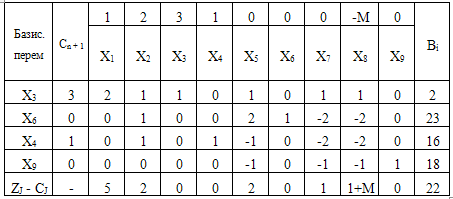
Итак, значения Z-строки положительны, а задача на максимум, следовательно, решение оптимально.

Вывод:

₀ = 22; X₃ =2; X₄ =16; X₆= 23; X₉ = 18; X₁ = X₂ = X₅ = X₇ = X₈ =0.

Задача 4

 Z = Х₁ + 2Х₂

Х₁ + 4Х₂ ≤ 30

Х₁ + 5Х₂ ≤ 30

Х₁ ≤ 12

Х₁ + 4Х₂ ≥ 24

Х₁ + 7Х₂ ≥ 30

Х₁ + 8Х₂ ≥ 30

Решение:

Поскольку в данной задаче присутствуют знаки ≤ и ≥, поэтому решать ее целесообразнее прямым симплекс-методом с искусственными переменными. Преобразуем неравенства в равенства. Для этого введем дополнительные переменные в неравенства со знаком ≤ и дополнительные и искусственные - в неравенства со знаком ≥. Так как задача на минимум, то в целевую функцию искусственная переменная, образующая базис, вводится со знаком "+":

 = Х₁ + 2Х₂ + 0Х₃ + 0Х₄ +0 Х₅ - 0 Х₆ + МХ₇ - 0Х₈ + МХ₉ - 0 Х₁₀ + МХ₁₁→ min;

Х₁ + 4Х₂ + Х₃ =30

Х₁ + 5Х₂ + Х₄ =30

Х₁ + Х₅ =12

Х₁ + 4Х₂ - Х₆ + Х₇ =24

Х₁ + 7Х₂ - Х₈ + Х₉ =30

Х₁ + 8Х₂ - Х₁₀ + Х₁₁ = 30

Строим первоначальную симплексную таблицу.

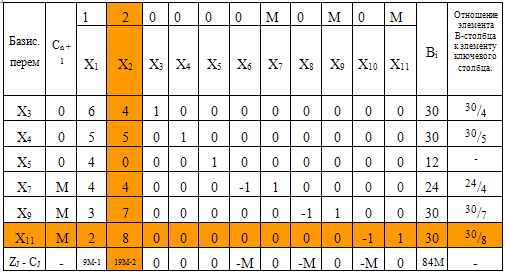
сетевой планирование операция симплекс

Некоторые значения Z-строки - положительные значения, а задача на минимум, то строим новую симплексную таблицу.

Среди значений Z-строки снова есть положительные числа, строим новую симплексную таблицу.

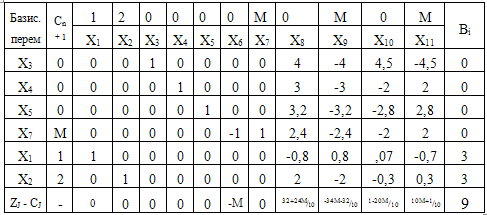
По значениям Z-строки мы видим, что решение не оптимально. Можно продолжить преобразование, однако, по значениям В-столбца видно, что дальнейшее преобразование не имеет смысла.

Вывод: данная задача не имеет решения.

Задача 5

В данной задаче необходимо составить математические модели в общем и развернутом видах, дать определения всем используемым переменным и константам.

Условие: предприятие выпускает машины трех различных моделей: модель А, модель В и модель С. Каждая машина указанных моделей приносит предприятию доход в размере 8, 15 и 25 рублей, соответственно. Необходимо, чтобы предприятие выпускало за неделю не менее 100 машин модели А, 150 машин модели В и 75 машин модели С. Каждая модель характеризуется определенным временем на изготовление комплектующих, на сборку и упаковку. Так, на 10 машин модели А требуется 10 часов на изготовление комплектующих, 4 часа на сборку и 1 час на упаковку. Соответствующие показатели в расчете на 10 машин модели В равняются 4, 5 и 1,5 часам, а на 10 машин модели С - 5, 3 и 3 часа. В течение ближайшей недели предприятие может израсходовать на производство комплектующих 150 часов, на сборку 200 часов и на упаковку 60 часов. Определить недельный выпуск машин каждой модели, максимизирующий доход предприятия.

Решение:

Пусть i -модели машин, i = 1, m =1,3. А j -индекс вида работ, j = 1,n = 1,3.

Тогда M_ij - время каждого j-го вида работ, необходимого для производства каждой i-той модели машин;

В_j - фонд времени на каждый j-тый вид работ;

С_i - доход предприятия от каждой i-той машины;

Х_i - какое количество машин i-го вида необходимо произвести, чтобы максимизировать прибыль предприятия.

Построим математическую модель в общем виде:

 = ∑Y_i X_i → max

∑ M_ij X_i ≤ В_j j = 1, n_i ≥ 0.

ЭММ в развернутом виде будет иметь вид:

С₁ Х₁ + С₂ Х₂ + С₃ Х₃ → max

M₁₁ Х₁ + M₁₂ Х₂ + M₁₃ Х₃ ≤ 150

M₂₁ Х₁ + M₂₂ Х₂ + M₂₃ Х₃ ≤ 200

M₃₁ Х₁ + M₃₂ Х₂ + M₃₃ Х₃ ≤ 60

Х₁ ≥ 100; Х₂ ≥ 150; Х₃ ≥ 75.

Задача 6

Распределить работу между тремя рабочими таким образом, чтобы максимизировать валовой выпуск деталей трех видов. Трудоемкость изготовления деталей рабочими, их цена, а также фонд времени каждого рабочего приведены в таблице.

Решение:

Пусть i - индекс № рабочего, i = 1, m =1,3,

j - индекс (А,Б,В) детали, j = 1,n = 1,3.

Тогда А_ij - трудоемкость изготовления каждой i-той детали на каждом j-том станке,

В_i - фонд времени каждого i-того рабочего,

С_j - цена одной детали j-того,

Х_j - какое количество деталей каждого j-того вида выпустить, чтобы максимизировать валовой выпуск деталей.

ЭММ в общем виде:

Z = ∑ C_j X_j → max

∑ А_ij Х_j ≤ В_i i = 1, m =1,3

Х_j ≥ 0.

ЭММ в развернутом виде:

 = С₁ Х₁ + С₂ Х₂ + С₃ Х₃ → max

А₁₁ Х₁ + А₁₂ Х₂ + А₁₃ Х₃ ≤ В₁

А₂₁ Х₁ + А₂₂ Х₂ + А₂₃ Х₃ ≤ В₂

А₃₁ Х₁ + А₃₂ Х₂ + А₃₃ Х₃ ≤ В₃

Х_1,2,3 ≥ 0.

Задача 7

Составить и решить транспортную задачу методом потенциалов. Допустимый план получить методом северо-западного угла. По условию видно, что здесь представлена закрытая транспортная задача (возможности всех поставщиков равны потребностям всех потребителей). Распределение поставок начинаем с верхней левой (северо-западной) клетки таблицы. Возможности первого поставщика исчерпаны, начинаем распределение поставок от второго поставщика тем потребителям, потребности которых удовлетворены частично или не удовлетворены совсем. В итоге сумма поставок в каждой строчке таблицы должна быть равна наличию продукта у соответствующего поставщика, а сумма поставок по столбцам - потребности соответствующих потребителей.

Для решения задачи необходимо рассчитать потенциалы:

β_j= α_i+c_ij ; α_i= β_j-c_ij

α_i принимается равным 0.

Расчет потенциалов ведется только по базисным ячейкам. Базисная ячейка- ячейка, в которой есть поставки, в том числе фиктивные (нулевые).

Рассчитываются также общие затраты на перевозку:

 = 90 3 + 30 6 + 50 3 +30 7 + 40 8 = 1130.

Теперь необходимо провести проверку плана распределения на оптимальность. Проверка плана ведется по свободным ячейкам, в которых должно выполняться следующее условие: α_i+c_ij ≥ β_j

Проведя проверку плана, видим, что он не оптимален. Значит, есть необходимость перераспределения поставок. Для этого выбирается свободная клетка, в которой данное неравенство не соблюдается больше всего(в данном случае она одна) и в ней ставим знак "+". Это означает, что в данную клетку целесообразно произвести поставку. Ходом шахматной ладьи производится обход базисных клеток таблицы таким образом, чтобы последним ходом вернуться в исходную клетку. Базисные клетки, через которые осуществляется обход, попеременно помечаются "-" и "+", в каждой строке или столбце не должно быть более двух таких отметок. Путь может проходить как по всем базисным клеткам, так и по части из них. Далее просматриваем базисные клетки, отмеченные знаком "-", и среди них находится клетка с наименьшей поставкой. Затем величина этой поставки прибавляется в клетки, отмеченные знаком "+", и вычитается из клеток, помеченных знаком "-". При этом клетка, из которой поставка убирается, объявляется свободной, а клетка, куда поставка записывается, - базисной.

После проведения вышеперечисленных операций таблица перевозок будет выглядеть следующим образом.

Снова рассчитаем общие затраты на перевозку:

 = 90 3 + 0 7 + 80 3 + 30 2 + 40 8 = 890

Видим, что затраты на перевозку уменьшаются, значит ход решения верен. Полученное решение снова проверяем на оптимальность. Затем проверяется выполнение неравенств: α_i+c_ij ≥ β_j. Неравенство не выполняется в одной из клеток, поэтому продолжим, решение описанным образом, решение. Построим новую таблицу перевозок.

Рассчитаем опять общие затраты на перевозку:

 = 50 3 + 40 4 + 80 3 + 70 2 + 0 7 = 690.

Видим, что затраты на перевозку снизились до минимума, решение задачи оптимально: неравенства α_i+c_ij ≥ β_j выполняются для всех свободных клеток таблицы.

Заключение

Выше было изложено, как строится сеть проекта (комплекса операций), исходя из отношений порядка, существующих между различными операциями, после чего метод критического пути дает возможность определить на основе этого время завершения всего комплекса операций, а также резервы событий и операций.

Критические операции представляют собой те операции проекта, на ход выполнения которых руководитель должен направить все свое внимание, так как от их своевременного выполнения зависит общий срок завершения всего проекта (всего комплекса работ). Критический путь - ход вдоль такого пути между двумя точками (начальной и конечной), который дает максимальную сумму длительностей операций.

В заключение, стоит сказать, что нахождение критического пути (путей) позволяет выявить ключевые операции, определяющие ход выполнения проекта, в частности среднюю продолжительность его реализации. Вычисление резервов времени событий и свободных резервов времени операций дает представление об эластичности некритических событий и операций и о той степени свободы, которой можно будет располагать при их выполнении. Возможность располагать такими сведениями в фазе "контроль проекта в процессе его выполнения" имеет большое значение. При осуществлении проекта могут возникнуть новые критические операции, не предусмотренные в первоначальном плане реализации проекта и требующие внимания со стороны руководства. В этих случаях руководство будет располагать информацией, необходимой для определения того, куда именно должны быть направлены усилия, чтобы уложиться в намеченные сроки.

Стоит отметить, что сам по себе метод критического пути не является методом упорядочения. Он применим только тогда, когда сеть проекта уже составлена, т. е. когда операции уже упорядочены. Его роль состоит фактически в том, чтобы расшифровать сеть с временной точки зрения, т. е. дать все необходимые указания относительно сроков, в которые должны наступить различные события проекта.

Литература

1. А. Кофман. Г. Дебазей. Сетевые методы планирования. М, 1968. - 293 с.

. Математические модели в управлении производством. А.А. Первозванский. М: Главная редакция физико-математической литературы "Наука", 1975. - 616 с.

. М/ук 3056. Экономико-математические методы и модели: практ. руководство к курсовой работе по одноим. курсу для студентов эконом. специальностей днев. и заоч. отд-ний / Авт.-сост.: Е.А. Кожевников, А.Н. Шутова. - Гомель: ГГТУ им. П.О. Сухого, 2005. - 22 с.

. М/ук 1719. Г. А. Нарышев. Исследование операций. Учебное пособие по одноименному курсу. ГПИ, 1993. - 46 с.

. М/ук 2660. Экономико-математические методы и модели: практическое пособие по одноименному курсу для студентов экономических специальностей/ Автор-составитель: Г.А. Нарышев.- Гомель ГГТУ им. П.О. Сухого, 2002. - 52 с.