Корреляционно-регрессионный анализ. Анализ сезонности потребления электроэнергии
Содержание
Задание 1
Задание 2
Список литературы
Задание 1
1.Постройте поле корреляции.
.Рассчитайте параметры линейного, степенного,
экспоненциального(показательного), параболического, гиперболического трендов с
помощью пакета Excel.
.Оцените тесноту связи с помощью показателей
корреляции и детерминации.
.Оцените адекватность линейной модели, проверив:
v Случайность колебаний уровней по критерию пиков;
v Соответствие распределения случайной компоненты
нормальному закону с помощью RS-критерия;
v Равенство нулю среднего значения случайной
компоненты на основе l-критерия
Стьюдента;
v Независимость значений уровней случайной
компоненты по критерию Дарбина-Уотсона.
С помощью средней ошибки аппроксимации оцените
точность уравнения.
. Оцените с помощью F-критерия
Фишера статистическую надёжность нелинейных моделей. Для этого рассчитайте
индексы корреляции для каждой модели;
v Вычислите относительную ошибку аппроксимации;
v Проверьте ряд остатков на гомоскедастичность
графическим методом.
.Выберите лучшее уравнение тренда и дайте его
обоснование. По выбранному уравнению регрессии рассчитайте прогнозное значение
результата, если прогнозное значение фактора увеличится на 10% от его среднего
уровня. Определите доверительный интервал прогноза для уровня значимости a=0,05.
7. оцените полученные результаты, выводы
оформите.
|
Район
|
Средний
размер назначенных ежемесячных пенсий, тыс.руб. у
|
Прожиточный
минимум в среднем на одного пенсионера в месяц, тыс.руб. х
|
|
Брянской
обл.
|
240
|
228
|
|
Владимир.обл.
|
226
|
202
|
|
Ивановск.обл.
|
221
|
197
|
|
Калужск.обл.
|
226
|
201
|
|
Костромск.обл.
|
220
|
189
|
|
г.Москва
|
250
|
302
|
|
Московск.олб.
|
237
|
215
|
|
Орловск.обл.
|
232
|
196
|
|
Рязанск.обл.
|
215
|
199
|
|
Смоленск.обл.
|
220
|
180
|
|
Тверская
обл.
|
222
|
181
|
|
Тульская
обл.
|
231
|
186
|
|
Ярославк.обл.
|
229
|
216
|
Решение:
.Построим поле корреляции:
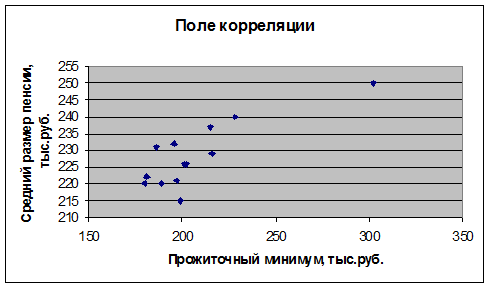
. С помощью офисного пакета Microsoft
Excel построим различные
виды трендов:
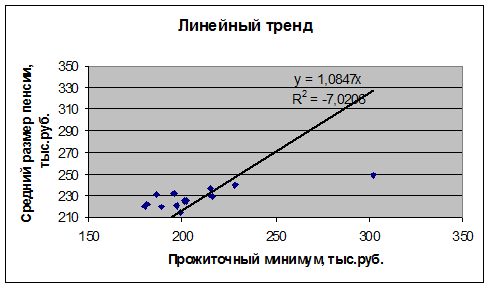
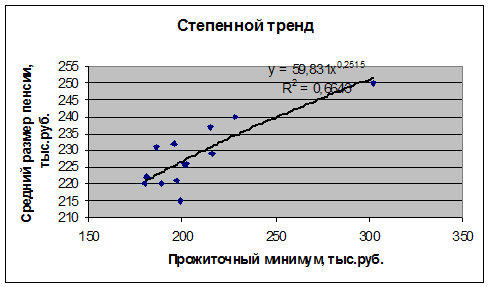
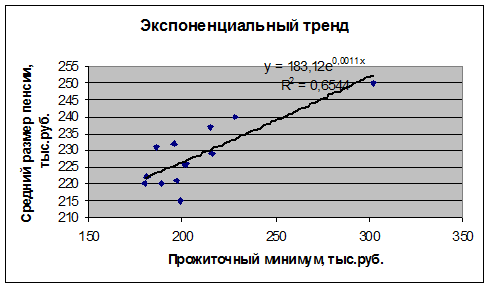

Оценим тесноту связи с помощью показателей
корреляции и детерминации.
|
№
|
х
|
y
|
Y-Yср
|
X-Xср
|
(Х-Хср)(Y-Yср)
|
(Y-Yср)^2
|
(X-Xср)^2
|
|
1
|
228
|
240
|
11,62
|
20,92
|
243,03
|
134,92
|
437,78
|
|
2
|
202
|
226
|
-2,38
|
-5,08
|
12,11
|
5,69
|
25,78
|
|
3
|
197
|
221
|
-7,38
|
-10,08
|
74,41
|
54,53
|
101,54
|
|
4
|
201
|
226
|
-2,38
|
-6,08
|
14,49
|
5,69
|
36,93
|
|
5
|
189
|
220
|
-8,38
|
-18,08
|
151,57
|
70,30
|
326,78
|
|
6
|
302
|
250
|
21,62
|
94,92
|
2051,80
|
467,22
|
9010,39
|
|
7
|
215
|
237
|
8,62
|
7,92
|
68,26
|
74,22
|
62,78
|
|
8
|
196
|
232
|
3,62
|
-11,08
|
-40,05
|
13,07
|
122,70
|
|
9
|
199
|
215
|
-13,38
|
-8,08
|
108,11
|
179,15
|
65,24
|
|
10
|
180
|
220
|
-8,38
|
-27,08
|
227,03
|
70,30
|
733,16
|
|
11
|
181
|
222
|
-6,38
|
-26,08
|
166,49
|
40,76
|
680,01
|
|
12
|
186
|
231
|
2,62
|
-21,08
|
-55,12
|
6,84
|
444,24
|
|
13
|
216
|
229
|
0,62
|
8,92
|
5,49
|
0,38
|
79,62
|
|
сумма
|
2692
|
2969
|
Х
|
Х
|
3027,62
|
1123,08
|
12126,92
|
|
среднее
|
207,0769
|
228,3846
|
Х
|
Х
|
Х
|
Х
|
Х
|
Показатель корреляции:
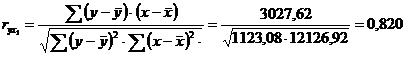
Связь между результатом и фактором
прямая и достаточно сильная.
Для определения качества построения
модели вычислим коэффициент детерминации:
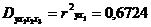 .
.
Следовательно, в данной модели
учтено 67,24% фактора, оказывающего влияние на результат, а оставшиеся 32,76%
составляют факторы, влияющие на результат, но в данную модель не включенные.
Оценим адекватность линейной модели y=1,0847*x
А) Проверим гипотезу о случайности значений
остаточной компоненты методом поворотных точек (методом пиков).
Критическое число поворотных точек
рассчитывается по формуле:
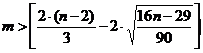
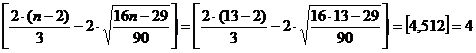
Количество поворотных точек данной
модели равно 4.
|
t
|
Yt
|
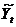 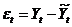 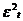
|
|
|
|
1
|
240
|
247,312
|
-7,3116
|
53,4595
|
|
2
|
226
|
219,109
|
6,8906
|
47,4804
|
|
3
|
221
|
213,686
|
7,3141
|
53,4961
|
|
4
|
226
|
218,025
|
7,9753
|
63,6054
|
|
5
|
220
|
205,008
|
14,9917
|
224,751
|
|
6
|
250
|
327,579
|
-77,5794
|
6018,56
|
|
7
|
237
|
233,211
|
3,7895
|
14,3603
|
|
8
|
232
|
212,601
|
19,3988
|
376,313
|
|
9
|
215
|
215,855
|
-0,8553
|
0,73154
|
|
10
|
220
|
195,246
|
24,754
|
612,761
|
|
11
|
222
|
196,331
|
25,6693
|
658,913
|
|
12
|
231
|
201,754
|
29,2458
|
855,317
|
|
13
|
229
|
234,295
|
-5,2952
|
28,0391
|

Т.к. количество поворотных точек на графике
остаточной компоненты равно необходимому (4=4), то вывода о выполнении гипотезы
о случайности значений остаточной компоненты сделать нельзя.
Соответствие ряда остатков нормальному закону
распределения определим при помощи R/S-критерия.
Вычислим вариационный размах  =
=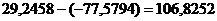 и
среднеквадратическое отклонение остаточной компоненты:
и
среднеквадратическое отклонение остаточной компоненты:
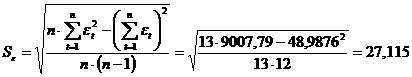 .
.
Рассчитаем критерий R/S:

Вычисленное значение критерия R/S
попадает в заданный интервал, следовательно, можно сделать вывод об
адекватности модели наблюдаемому процессу по данному критерию.
Проверим гипотезу о независимости значений
остаточной компоненты
Для проверки данной гипотезы рассчитаем критерий
Дарбина-Уотсона (в качестве критических принимаем уровни d1=1,08
и d2=1,36).
|
t
|
Y(t)
|
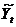 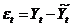 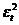 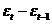 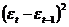
|
|
|
|
|
|
1
|
240
|
247,312
|
-7,3116
|
53,4595
|
Х
|
Х
|
|
2
|
226
|
219,109
|
6,8906
|
47,4804
|
14,2022
|
201,702
|
|
3
|
221
|
213,686
|
7,3141
|
53,4961
|
0,4235
|
0,17935
|
|
4
|
226
|
218,025
|
7,9753
|
63,6054
|
0,6612
|
0,43719
|
|
5
|
220
|
205,008
|
14,9917
|
224,751
|
7,0164
|
49,2299
|
|
6
|
250
|
327,579
|
-77,579
|
6018,56
|
-92,571
|
8569,41
|
|
7
|
237
|
233,211
|
3,7895
|
14,3603
|
81,3689
|
6620,9
|
|
8
|
232
|
212,601
|
19,3988
|
376,313
|
15,6093
|
243,65
|
|
9
|
215
|
215,855
|
0,73154
|
-20,254
|
410,229
|
|
10
|
220
|
195,246
|
24,754
|
612,761
|
25,6093
|
655,836
|
|
11
|
222
|
196,331
|
25,6693
|
658,913
|
0,9153
|
0,83777
|
|
12
|
231
|
201,754
|
29,2458
|
855,317
|
3,5765
|
12,7914
|
|
13
|
229
|
234,295
|
-5,2952
|
28,0391
|
-34,541
|
1193,08
|
|
Сумма
|
|
|
48,9876
|
9007,79
|
|
17958,3
|
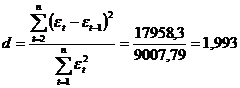
Вычисленное значение d попадает в
интервал между d2=1,36 и 2.
Таким образом, ряд остатков
некоррелирован. Свойство взаимной независимости уровней остаточной компоненты
подтверждается. Модель адекватна по этому критерию.
Вычислим среднюю ошибку аппроксимации:
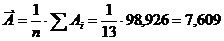
|
t
|
Y
|
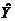 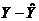 
|
|
|
|
1
|
240
|
247,312
|
-7,312
|
3,047
|
|
2
|
226
|
219,109
|
6,891
|
3,049
|
|
3
|
221
|
213,686
|
7,314
|
3,310
|
|
4
|
226
|
218,025
|
7,975
|
3,529
|
|
5
|
220
|
205,008
|
14,992
|
6,814
|
|
6
|
250
|
327,579
|
-77,579
|
31,032
|
|
7
|
237
|
233,211
|
3,790
|
1,599
|
|
8
|
232
|
212,601
|
19,399
|
8,362
|
|
9
|
215
|
215,855
|
-0,855
|
0,398
|
|
10
|
220
|
195,246
|
24,754
|
11,252
|
|
11
|
222
|
196,331
|
25,669
|
11,563
|
|
12
|
231
|
201,754
|
29,246
|
12,661
|
|
13
|
229
|
234,295
|
-5,295
|
2,312
|
|
Сумма
|
|
|
|
98,926
|
Следовательно, модель является точной.
Вычислим для каждой модели индекс корреляции:
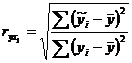
Степенная функция:
|
t
|
X
|
Y
|
Yрасч
|
(Y-Yср)^2
|
(Yрасч-Yср)^2
|
|
1
|
228
|
240
|
234,39
|
134,92
|
36,12
|
|
2
|
202
|
226
|
227,36
|
5,69
|
1,04
|
|
3
|
197
|
221
|
225,94
|
54,53
|
6,00
|
|
4
|
201
|
226
|
227,08
|
5,69
|
1,70
|
|
5
|
189
|
220
|
223,59
|
70,30
|
22,97
|
|
6
|
302
|
250
|
251,56
|
467,22
|
537,27
|
|
7
|
215
|
237
|
230,96
|
74,22
|
6,63
|
|
8
|
196
|
232
|
225,65
|
13,07
|
7,50
|
|
9
|
199
|
215
|
226,51
|
179,15
|
3,51
|
|
10
|
180
|
220
|
220,87
|
70,30
|
56,54
|
|
11
|
181
|
222
|
221,17
|
40,76
|
52,01
|
|
12
|
186
|
231
|
222,69
|
6,84
|
32,38
|
|
13
|
216
|
229
|
231,23
|
0,38
|
8,09
|
|
Сумма
|
2692
|
2969
|
Х
|
1123,08
|
771,75
|
|
Среднее
|
207,077
|
228,385
|
Х
|
Х
|
Х
|
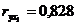
Экспоненциальная функция:
|
t
|
X
|
Y
|
Yрасч
|
(Y-Yср)^2
|
(Yрасч-Yср)^2
|
|
1
|
228
|
240
|
235,32
|
134,92
|
48,08
|
|
2
|
202
|
226
|
228,68
|
5,69
|
0,09
|
|
3
|
197
|
221
|
227,43
|
54,53
|
0,91
|
|
4
|
201
|
226
|
228,43
|
5,69
|
0,00
|
|
5
|
189
|
220
|
225,44
|
70,30
|
8,69
|
|
6
|
302
|
250
|
255,28
|
467,22
|
723,10
|
|
7
|
215
|
237
|
231,98
|
74,22
|
12,91
|
|
8
|
196
|
232
|
227,18
|
13,07
|
1,45
|
|
9
|
199
|
215
|
227,93
|
179,15
|
0,21
|
|
10
|
180
|
220
|
223,22
|
70,30
|
26,71
|
|
11
|
181
|
222
|
223,46
|
40,76
|
24,23
|
|
12
|
186
|
231
|
224,69
|
6,84
|
13,62
|
|
13
|
216
|
229
|
232,23
|
0,38
|
14,81
|
|
Сумма
|
2692
|
2969
|
Х
|
1123,08
|
874,81
|
|
Среднее
|
207,077
|
228,385
|
Х
|
Х
|
Х
|
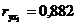
Параболическая функция:
|
t
|
X
|
Y
|
Yрасч
|
(Y-Yср)^2
|
(Yрасч-Yср)^2
|
|
1
|
228
|
240
|
240,88
|
134,92
|
156,18
|
|
2
|
202
|
226
|
229,69
|
5,69
|
1,72
|
|
3
|
197
|
221
|
227,06
|
54,53
|
1,75
|
|
4
|
201
|
226
|
229,18
|
5,69
|
0,63
|
|
5
|
189
|
220
|
222,53
|
34,29
|
|
6
|
302
|
250
|
249,78
|
467,22
|
457,94
|
|
7
|
215
|
237
|
235,81
|
74,22
|
55,17
|
|
8
|
196
|
232
|
226,52
|
13,07
|
3,49
|
|
9
|
199
|
215
|
228,13
|
179,15
|
0,06
|
|
10
|
180
|
220
|
216,95
|
70,30
|
130,66
|
|
11
|
181
|
222
|
217,60
|
40,76
|
116,35
|
|
12
|
186
|
231
|
220,73
|
6,84
|
58,65
|
|
13
|
216
|
229
|
236,24
|
0,38
|
61,69
|
|
Сумма
|
2692
|
2969
|
Х
|
1123,08
|
1078,58
|
|
Среднее
|
207,077
|
228,385
|
Х
|
Х
|
Х
|
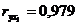
Коэффициент детерминации максимален
у степенной модели. Поэтому лучшим уравнением тренда является:
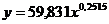
Рассчитаем прогнозное значение
результата, если прогнозное значение фактора увеличится на 10% от его среднего
уровня.
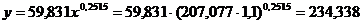
Задание 2
Исследовать сезонность потребления
электроэнергии. Построить модель сезонных колебаний, рассчитать прогнозное
значение на 4 шага вперёд. Построить график сезонной волны.
корреляция линейный модель
сезонность
|
Годы
и кварталы
|
данные
|
|
1986,
1
|
159
|
|
2
|
50
|
|
3
|
293
|
|
4
|
350
|
|
1987,
1
|
133
|
|
2
|
75
|
|
3
|
348
|
|
4
|
339
|
|
1988,
1
|
171
|
|
2
|
95
|
|
3
|
304
|
|
4
|
563
|
|
1989,
1
|
161
|
|
2
|
112
|
|
3
|
314
|
|
4
|
211
|
|
1990,
1
|
163
|
|
2
|
132
|
|
3
|
207
|
|
4
|
193
|
|
1991,
1
|
137
|
|
2
|
130
|
|
3
|
178
|
|
4
|
175
|
|
1992,
1
|
166
|
|
2
|
125
|
|
3
|
190
|
|
4
|
217
|
|
1993,
1
|
200
|
|
2
|
168
|
|
3
|
217
|
|
4
|
141
|
|
1994,
1
|
166
|
|
2
|
140
|
|
3
|
189
|
|
4
|
214
|
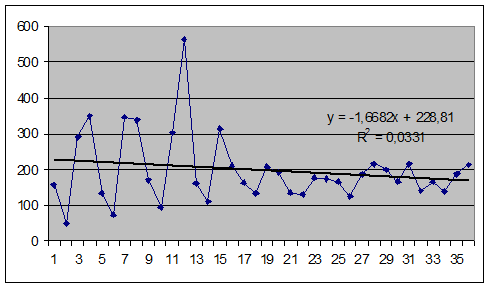
Решение:
Изобразим графически данные таблицы:

Для каждого месяца рассчитаем среднюю величину
уровня 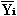 , затем вычислим
среднеквартальный уровень для всего ряда Y.
После чего определим показатель сезонной волны - индекс сезонности Is
как
процентное отношение средних величин для каждого квартала к общему среднему
уровню ряда, %:
, затем вычислим
среднеквартальный уровень для всего ряда Y.
После чего определим показатель сезонной волны - индекс сезонности Is
как
процентное отношение средних величин для каждого квартала к общему среднему
уровню ряда, %:
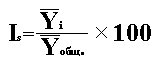
Применяя формулу простой средней арифметической
определим среднеквартальные уровни:
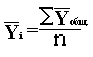
Сезонная волна определяется процентным
отношением уровней поквартальных средних к средней квартальной.
|
|
1
квартал
|
2
квартал
|
3
квартал
|
4
квартал
|
Потребление
за год
|
Среднее
|
|
1986
|
159
|
50
|
293
|
350
|
852
|
213
|
|
1987
|
133
|
75
|
348
|
339
|
895
|
223,75
|
|
1988
|
171
|
95
|
304
|
563
|
1133
|
283,25
|
|
1989
|
161
|
112
|
314
|
211
|
798
|
199,5
|
|
1990
|
163
|
132
|
207
|
193
|
695
|
173,75
|
|
1991
|
137
|
130
|
178
|
175
|
620
|
155
|
|
1992
|
166
|
125
|
190
|
217
|
698
|
174,5
|
|
1993
|
200
|
168
|
217
|
141
|
726
|
181,5
|
|
1994
|
166
|
140
|
189
|
214
|
709
|
177,25
|
|
Среднее
|
161,78
|
114,11
|
248,89
|
267,00
|
791,78
|
197,94
|
|
Индексы
сезонности
|
81,73
|
57,65
|
125,74
|
134,89
|
Х
|
Х
|
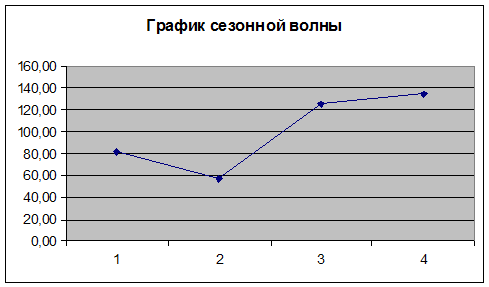
Для прогнозирования будущих значений составим
модель как сумму линейного тренда и сезонной составляющей.
Используя Microsoft
Excel, находим уравнение
линейного тренда:
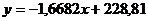
|
Наблюдение
|
Потребление
электроэнергии
|
Тренд
|
Сезонная
составляющая
|
|
1
|
159
|
227,1418
|
-68,1418
|
|
2
|
50
|
225,4736
|
-175,474
|
|
3
|
293
|
223,8054
|
69,1946
|
|
4
|
350
|
222,1372
|
127,8628
|
|
5
|
133
|
220,469
|
-87,469
|
|
6
|
75
|
218,8008
|
-143,801
|
|
7
|
348
|
217,1326
|
130,8674
|
|
8
|
339
|
215,4644
|
123,5356
|
|
9
|
171
|
213,7962
|
-42,7962
|
|
10
|
95
|
212,128
|
-117,128
|
|
11
|
304
|
210,4598
|
93,5402
|
|
12
|
563
|
208,7916
|
354,2084
|
|
13
|
161
|
207,1234
|
-46,1234
|
|
14
|
112
|
205,4552
|
-93,4552
|
|
15
|
314
|
203,787
|
110,213
|
|
16
|
211
|
202,1188
|
8,8812
|
|
17
|
163
|
200,4506
|
-37,4506
|
|
18
|
132
|
198,7824
|
-66,7824
|
|
19
|
207
|
197,1142
|
9,8858
|
|
20
|
193
|
195,446
|
-2,446
|
|
21
|
137
|
193,7778
|
-56,7778
|
|
22
|
130
|
192,1096
|
-62,1096
|
|
23
|
178
|
190,4414
|
-12,4414
|
|
24
|
175
|
188,7732
|
-13,7732
|
|
25
|
166
|
187,105
|
-21,105
|
|
26
|
125
|
185,4368
|
-60,4368
|
|
27
|
190
|
6,2314
|
|
28
|
217
|
182,1004
|
34,8996
|
|
29
|
200
|
180,4322
|
19,5678
|
|
30
|
168
|
178,764
|
-10,764
|
|
31
|
217
|
177,0958
|
39,9042
|
|
32
|
141
|
175,4276
|
-34,4276
|
|
33
|
166
|
173,7594
|
-7,7594
|
|
34
|
140
|
172,0912
|
-32,0912
|
|
35
|
189
|
170,423
|
18,577
|
|
36
|
214
|
168,7548
|
45,2452
|
|
37
|
Х
|
167,0866
|
Х
|
|
38
|
Х
|
165,4184
|
Х
|
|
39
|
Х
|
163,7502
|
Х
|
|
40
|
Х
|
162,082
|
Х
|
Список литературы
1. Кремер Н.Ш., Путко Б.А.
Эконометрика: Учебник для вузов // Под ред. проф. Н.Ш. Кремера. - М.:
«ЮНИТИ-ДАНА», 2002.
2. Кулинич Е.И. Эконометрия. -
М.: «Финансы и статистика», 2001.
. Луговская Л.В. Эконометрика
в вопросах и ответах: учебное пособие. - М.: «Проспеки», 2005.
. Магнус Я.Р., Катышев П.К.,
Пересецкий А.А. Эконометрика. Начальный курс: Учебник. - М.: «Дело», 2001.
5. Орлов
<http://orlovs.pp.ru/> А.И. Эконометрика <http://www.aup.ru/books/m153/>
- М.: «Экзамен», 2002.
. Практикум
по эконометрике: Учебн. пособие // Под ред. И.И. Елисеевой. - М.: «Финансы и
статистика», 2003.
. Эконометрика:
Учебник // Под ред. И.И. Елисеевой. - М.: «Финансы и статистика», 2002.