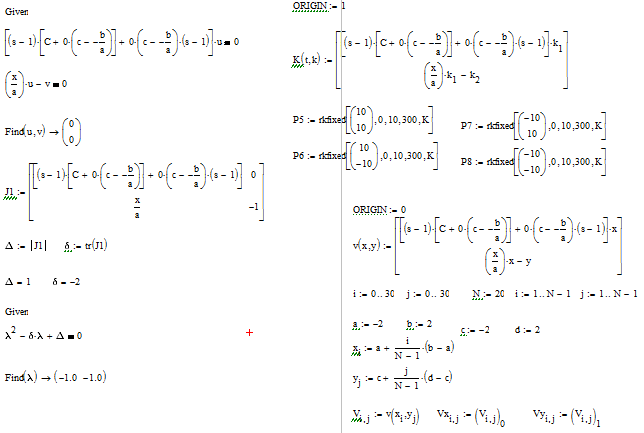Аналіз поведінки системи, що описана моделлю динаміки ринкового середовища за різних співвідношень вхідних параметрів
ПЛАН
ВСТУП
. АНАЛІТИЧНЕ ДОСЛІДЖЕННЯ МОДЕЛІ ДИНАМІКИ РИНКОВОГО СЕРЕДОВИЩА
.1 Постановка задачі дослідження моделі динаміки ринкового середовища.
.2 Особливі точки системи, що описана моделлю динаміки ринкового
середовища
.3 Дослідження моделі динаміки ринкового середовища за допомогою
біфуркаційної діаграми
.4 Дослідження моделі динаміки ринкового середовища за допомогою коренів
характеристичного рівняння.
.5 Умови стійкості та точки біфуркації
. ЧИСЛОВЕ ДОСЛІДЖЕННЯ МОДЕЛІ ДИНАМІКИ РИНКОВОГО СЕРЕДОВИЩА
.1 Числове дослідження першої точки рівноваги
.2 Числове дослідження другої точки рівноваги
.3 Числове дослідження третьої точки рівноваги
.4 Економічна інтерпретація отриманих результатів
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Об’єктом дослідження виступає модель динаміки ринкового
середовища. Воно описує економічну систему з точки зору зміни її характеристик
і властивостей.
Предметом аналізу є поведінка системи, що описана моделлю
динаміки ринкового середовища за різних співвідношень вхідних параметрів.
Метою виконання курсової роботи є дослідження поведінки
системи що описана моделлю динаміки ринкового середовища за різних
співвідношень вхідних параметрів засобами економічної динаміки.
Згідно з поставленою метою можна сформулювати такі завдання
до роботи:
- знайти особливі точки системи;
- визначити їх тип та стійкість на
основі біфуркаційної діаграми;
- визначити їх тип та стійкість за
допомогою коренів характеристичного рівняння;
- сформулювати умови стійкості системи;
- визначити точки біфуркації (якщо вони
є);
- перевірити правильність результатів
дослідження числовим моделюванням (побудова фазових портретів, динамічних
графіків, векторних полів);
- прокоментувати результати аналізу з
точки зору реальної економічної системи.
1. АНАЛІТИЧНЕ ДОСЛІДЖЕННЯ МОДЕЛІ ДИНАМІКИ РИНКОВОГО
СЕРЕДОВИЩА
1.1 Постановка задачі дослідження моделі динаміки
ринкового середовища
Виробничо-економічна система може використовувати свій
прибуток для потреб розвитку виробництва і для невиробничого накопичення:
P = І + S, (1.1)
де Р прибуток;
І - інвестиції;накопичення.
Накопичення здійснюється з метою подальшого використання
грошових коштів для формування резервного фонду, матеріального заохочення
працівників, проведення наукових досліджень і розробок, проведення маркетингових
досліджень та ін. Таким чином, накопичення відноситься до зміни структури
самого виробництва.
Крива ринкового попиту задається функцією попиту. Припустимо,
що функція попиту визначається лінійною залежністю від ціни товару, який
продається:
D = ap + b, (1.2)
де D попит;
р ціна товару.
У загальному випадку для функції попиту характерно, що
a<0, b>0.
Припустимо, що весь обсяг продукції, що був вироблений у
визначений період, повинен бути реалізований на ринку, тобто ніякі запаси не
утворюються. У цьому випадку для управління ціною використовується регулювання
за відхиленням із коефіцієнтом x, 0 < x < 1:
' = x((q - b)/a - p). (1.3)
Прибуток від реалізації продукції визначається так:
= (p - c)q - C, (1.4)
де c - умовно змінні витрати, C - умовно постійні витрати.
Динаміка накопичення визначається динамікою прибутку:
= sP, (1.5)
модель динаміка ринковий біфуркація
де 0 < s < 1 - так званий мультиплікатор накопичення.
З першого і останнього рівнянь отримуємо:
І = (1 - s) P. (1.6)
Збільшення обсягів виробництва здійснюється за рахунок частки
прибутку:
' = q(1 - s)[(p - c)q - C], (1.7)
де q - граничні витрати на збільшення випуску.
Таким чином, модель динаміки ринкового середовища
представлена рівняннями:
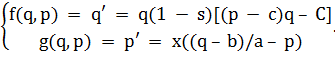
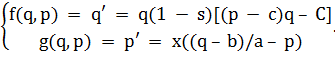 (1.8)
(1.8)
1.2 Особливі точки системи, що описана моделлю
динаміки ринкового середовища
Оскільки змінна c - умовно змінні витрати, а змінна C -
умовно постійні витрати сформуємо для них обмеження > 0.
Складемо матрицю обмежень для змінних моделі:
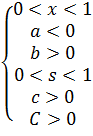
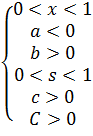 .
(1.9)
.
(1.9)
Знайдемо координати особливих точок системи. Для цього прирівняємо її
рівняння до нуля та відобразимо у символьному вигляді:

 (1.10)
(1.10)
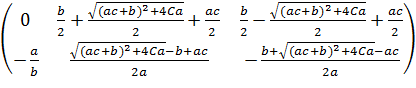
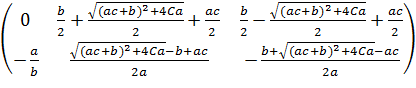 . (1.11)
. (1.11)
Як бачимо система має 3 особливі точки:



 .
.
Для того, щоб точка мала економічний зміст, кожна її координата має
бути невід’ємною. Проаналізуємо необхідні значення змінних враховуючи систему
обмежень 1.9.
Перевіримо чи має перша точка економічний зміст.
Перша її координата дорівнює 0, що задовольняє умові.
Друга її координата дорівнює 
 ,
оскільки змінна a менше нуля, то вираз буде більше 0, що також задовольняє
умові.
,
оскільки змінна a менше нуля, то вираз буде більше 0, що також задовольняє
умові.
Отже, перша особлива точка має економічний зміст при будь-яких
допустимих значеннях параметрів.
Перевіримо чи має друга особлива точка економічний зміст.
Перша її координата дорівнює 
 .
Підкореневий вираз
.
Підкореневий вираз 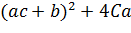
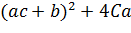 має
бути додатнім. Отже, необхідно, щоб виконувалась умова
має
бути додатнім. Отже, необхідно, щоб виконувалась умова 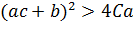
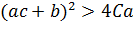 .
Точка має бути невід’ємною
.
Точка має бути невід’ємною 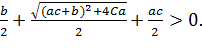
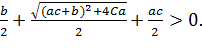
Друга її координата дорівнює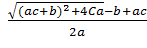
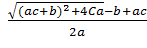 .
Підкореневий вираз
.
Підкореневий вираз 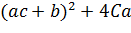
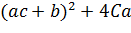 має
бути додатнім. Отже, необхідно, щоб виконувалась умова
має
бути додатнім. Отже, необхідно, щоб виконувалась умова 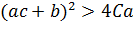
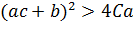 .
Точка має бути додатною
.
Точка має бути додатною 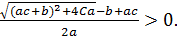
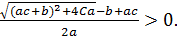
Отже друга особлива точка має економічний зміст за умов: 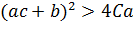
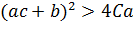 ,
,
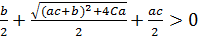
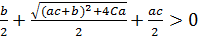 ,
,
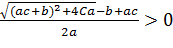
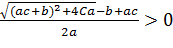 .
.
Перевіримо чи має третя особлива точка економічний зміст.
Перша її координата дорівнює 
 .
Підкореневий вираз
.
Підкореневий вираз 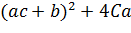
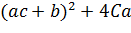 має
бути додатнім. Отже, необхідно, щоб виконувалась умова
має
бути додатнім. Отже, необхідно, щоб виконувалась умова 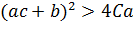
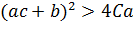 .
Точка має бути додатною
.
Точка має бути додатною 

Друга її координата дорівнює 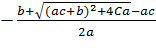
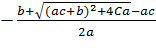 .
Підкореневий вираз
.
Підкореневий вираз 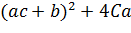
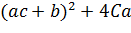 має
бути додатнім. Отже, необхідно, щоб виконувалась умова
має
бути додатнім. Отже, необхідно, щоб виконувалась умова 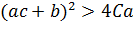
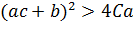 .
Точка має бути додатною
.
Точка має бути додатною 

Отже, третя особлива точка має економічний зміст за умов: 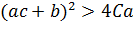
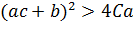 ,
,

 ,
,
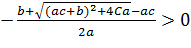
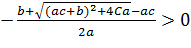 .
.
1.3 Дослідження моделі динаміки ринкового
середовища за допомогою біфуркаційної діаграми
Початкова система є нелінійною, тому для її розв’язання необхідно
виконати лінеаризацію.
Виконаємо лінеаризацію на основі Якобіана. Для цього складемо матрицю
Якобі:
= 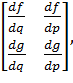
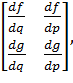 (1.12)=
(1.12)=
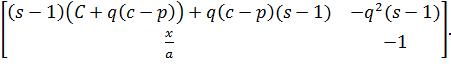
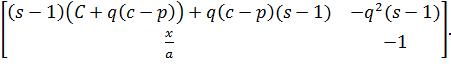 (1.13)
(1.13)
Побудувавши матрицю Якобі підставимо в неї замість значень q та p
координати особливих точок і отримаємо матриці J1, J2, J3:
J1 = 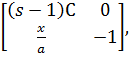
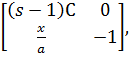 (1.14)=
(1.14)=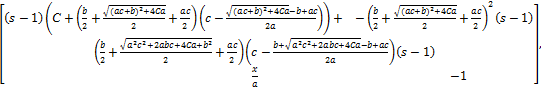
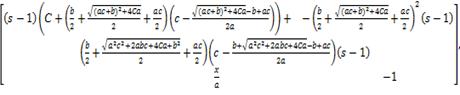 (1.15)=
(1.15)=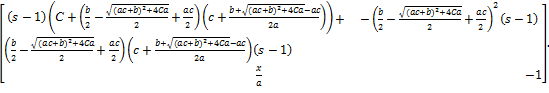
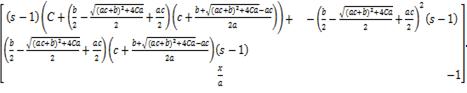 (1.16)
(1.16)
Знайдемо значення ∆ та δ для матриці J1 у символьному вигляді.
∆ = C - Cs, δ = C(s - 1) - 1.
Маючи ∆ та δ визначимо необхідні значення змінних для знаходження
точок біфуркації.
Визначимо можливі точки біфуркації.
Оскільки, відповідно до системи 1.9, змінні C та s завжди додатні, а s
< 1 то у виразі ∆ = C - Cs перший доданок завжди більший другого тому
вираз завжди більше 0. У виразі δ = C(s - 1) - 1 другий множник завжди від’ємний тому δ завжди менше нуля. Розглянемо можливі точки
біфуркації при цих умовах:
) ∆ = 
 , δ < 0. Фазовий портрет - “Стійкий вироджений вузол”.
, δ < 0. Фазовий портрет - “Стійкий вироджений вузол”.
Необхідна умова: C - Cs = 
 :
:
C(1 - s) =


 +
4C(s - 1) = 0
+
4C(s - 1) = 0

 -
2C(s - 1) + 1 + 4C(s - 1) = 0
-
2C(s - 1) + 1 + 4C(s - 1) = 0

 +
2C(s - 1) + 1 = 0
+
2C(s - 1) + 1 = 0
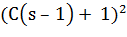
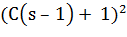 =
0=
=
0= 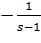
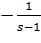 ;
;
) 0 < ∆ < 
 ,
δ
< 0. Фазовий портрет -
“Стійкий вузол”.
,
δ
< 0. Фазовий портрет -
“Стійкий вузол”.
Необхідна умова: C - Cs < 
 :
:
4C(1 - s) <


 +
4C(s - 1) > 0
+
4C(s - 1) > 0

 -
2C(s - 1) + 1 + 4C(s - 1) > 0
-
2C(s - 1) + 1 + 4C(s - 1) > 0

 +
2C(s - 1) + 1 > 0
+
2C(s - 1) + 1 > 0
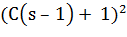
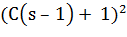 >
0
>
0
Для цієї умови підходять будь-які значення змінних крім
попередньої - C = 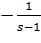
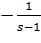 ,
тому подальших змін точки біфуркації не буде.
,
тому подальших змін точки біфуркації не буде.
Таблиця 1.1 - Тип
особливої точки в залежності від значень tr і det
|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Стійкий вироджений вузол
|
C = 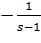 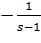
|
|
Стійкий вузол
|
C > 0, 0 < s < 1, C ≠ 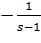 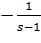
|
Знайдемо значення ∆ та δ
для матриці J2 у
символьному вигляді:
∆ = 
 +
+
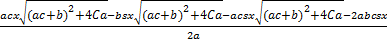
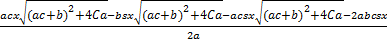 ,
,
δ=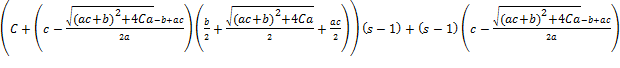
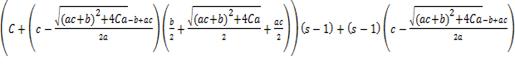
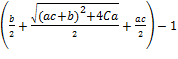
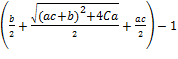 .
.
Маючи ∆ та δ визначимо необхідні значення змінних для знаходження
точок біфуркації.
Визначимо можливі точки біфуркації.
Керуючись системою обмежень 1.9 та враховуючи необхідні умови
економічної сутності задамо значення деяких змінних: a=-2, b=300, С = 10,
c=100, а значення коефіцієнта регулювання за відхиленням x та мултиплікатор
накопичення s будемо визначати залежно від умов точки біфуркації.
Підставимо значення змінних:
∆ = -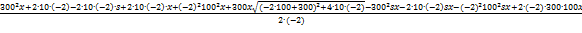
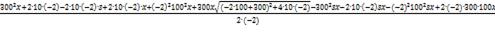 +
+

δ = 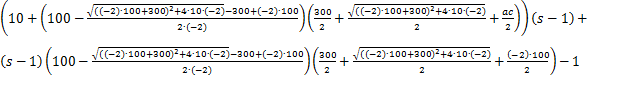
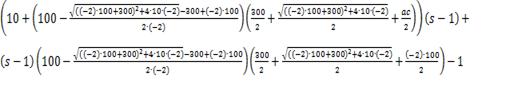 .
.
∆ = (1 - s)(4980x - 10),
δ = 9 - 10s.
1) ∆ < 0. Фазовий портрет - “Сідло”.
Необхідна умова:
(1 - s)(4980x - 10) < 0. Оскільки 0 < s < 1 то
перший множник завжди більше нуля. Оскільки 0 < х < 1 то другий множник
менше нуля при x < 0.002. При цих умовах вираз буде від’ємний.
) ∆ > 0, δ = 0. Фазовий портрет - “Центр”.
Перша умова:
(1 - s)(4980x - 10) > 0. Оскільки 0 < s < 1 то
перший множник завжди більше нуля. Оскільки 0 < х < 1 то другий множник
більше нуля при x > 0.002. При цих умовах вираз буде додатний.
Друга умова:
- 10s = 0
s = 0.9.
) ∆ = 0, δ ≠ 0.
Фазовий портрет
- “Пряма на фазовій площині”.
Перша умова:
(1 - s)(4980x - 10) < 0. Оскільки 0 < s < 1 то
перший множник завжди більше нуля. Оскільки 0 < х < 1 то другий множник
дорівнює нулю при x = 0.002. При цих умовах вираз дорівнює нулю.
Друга умова:
- 10s ≠ 0
s ≠
0.9.
4) ∆ = 
 ,
δ
< 0. Фазовий портрет -
“Стійкий вироджений вузол”.
,
δ
< 0. Фазовий портрет -
“Стійкий вироджений вузол”.
Перша умова:
(1 - s)(4980x - 10) = 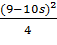
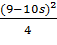
(1 - s)(4980x - 10) - 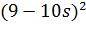
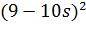 =
0
=
0
x - 40 - 11920sx + 40s - 81 +180s -100
 = 0(19920 - 19920s) = 100
= 0(19920 - 19920s) = 100
 - 220s + 121
- 220s + 121
= 

Друга умова:
- 10s < 0
s > 0.9.
) ∆ = 
 ,
δ
> 0. Фазовий портрет - “
Нестійкий вироджений вузол”.
,
δ
> 0. Фазовий портрет - “
Нестійкий вироджений вузол”.
Перша умова:
(1 - s)(4980x - 10) = 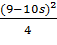
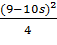
(1 - s)(4980x - 10) - 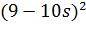
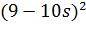 =
0
=
0
x - 40 - 11920sx + 40s - 81 +180s -100
 = 0(19920 - 19920s) = 100
= 0(19920 - 19920s) = 100
 - 220s + 121=
- 220s + 121= 

Друга умова:
- 10s > 0
s < 0.9.
) 0 < ∆ < 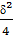
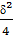 ,
δ
< 0. Фазовий портрет -
“Стійкий вузол”.
,
δ
< 0. Фазовий портрет -
“Стійкий вузол”.
Перша умова:
(1 - s)(4980x - 10) > 0. Оскільки 0 < s < 1 то
перший множник завжди більше нуля. Оскільки 0 < х < 1 то другий множник
більше нуля при x > 0.002. При цих умовах вираз буде додатний.
Друга умова:
(1 - s)(4980x - 10) < 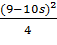
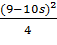
(1 - s)(4980x - 10) - 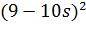
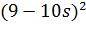 <
0
<
0
x - 40 - 11920sx + 40s - 81 +180s -100
 < 0(19920 - 19920s) < 100
< 0(19920 - 19920s) < 100
 - 220s + 121<
- 220s + 121< 

Третя умова:
- 10s < 0
s > 0.9.
) 0 < ∆ < 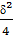
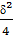 ,
δ
> 0. Фазовий портрет -
“Нестійкий вузол”.
,
δ
> 0. Фазовий портрет -
“Нестійкий вузол”.
Перша умова:
(1 - s)(4980x - 10) > 0. Оскільки 0 < s < 1 то
перший множник завжди більше нуля. Оскільки 0 < х < 1 то другий множник
більше нуля при x > 0.002. При цих умовах вираз буде додатний.
Друга умова:
(1 - s)(4980x - 10) < 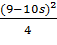
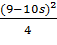
(1 - s)(4980x - 10) - 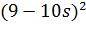
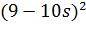 <
0
<
0
x - 40 - 11920sx + 40s - 81 +180s -100
 < 0(19920 - 19920s) < 100
< 0(19920 - 19920s) < 100
 - 220s + 121<
- 220s + 121< 

Третя умова:
- 10s > 0
s < 0.9.
) ∆ > 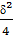
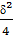 ,
δ
< 0. Фазовий портрет - “
Стійкий фокус”.
,
δ
< 0. Фазовий портрет - “
Стійкий фокус”.
Перша умова:
(1 - s)(4980x - 10) > 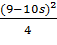
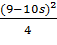
(1 - s)(4980x - 10) - 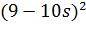
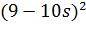 >
0
>
0
x - 40 - 11920sx + 40s - 81 +180s -100
 > 0(19920 - 19920s) > 100
> 0(19920 - 19920s) > 100
 - 220s + 121>
- 220s + 121> 

Друга умова:
- 10s < 0
s > 0.9.
) ∆ > 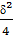
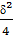 ,
δ
> 0. Фазовий портрет - “
Нестійкий фокус”.
,
δ
> 0. Фазовий портрет - “
Нестійкий фокус”.
Перша умова:
(1 - s)(4980x - 10) > 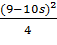
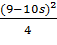
(1 - s)(4980x - 10) - 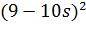
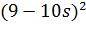 >
0
>
0
x - 40 - 11920sx + 40s - 81 +180s -100
 > 0(19920 - 19920s) > 100
> 0(19920 - 19920s) > 100
 - 220s + 121>
- 220s + 121> 

Друга умова:
- 10s > 0
s <
0.9.
Таблиця 1.2 - Тип особливої точки залежності від значень tr і
det
|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Сідло
|
x < 0.002
|
|
Центр
|
x > 0.002, s = 0.9
|
|
Пряма на фазовій
площині
|
x = 0.002, s ≠
0.9
|
Стійкий вузол x < 
 ,
,
Нестійкий вузол x < 
 ,
,
Стійкий вироджений вузол x = 
 ,
,
Нестійкий вироджений вузол x = 
 ,
,
Стійкий фокус x > 

Нестійкий фокус x > 

Знайдемо значення ∆ та δ
для матриці J3 у
символьному вигляді.
∆ = 
 +
+
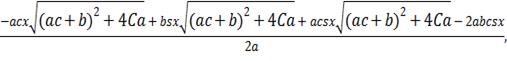
δ=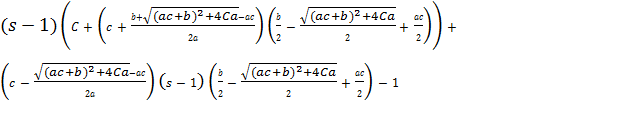
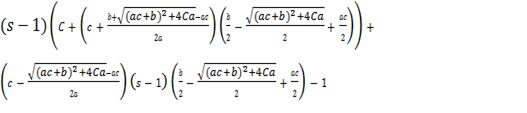 .
.
Маючи ∆ та δ визначимо необхідні значення змінних для знаходження
точок біфуркації.
Визначимо можливі точки біфуркації.
Керуючись системою обмежень 1.9 та враховуючи необхідні умови економічної
сутності задамо значення деяких змінних: a=-2, b=300, С = 10, c=100, а значення
коефіцієнта регулювання за відхиленням x та мултиплікатор накопичення s будемо
визначати залежно від умов точки біфуркації.
Підставимо значення змінних:
∆ = -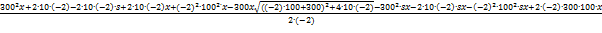
 +
+
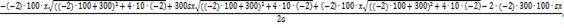
δ=
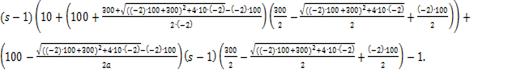
∆ =10s - 10,
δ = 9 - 10s.
1) ∆ < 0. Фазовий портрет - “Сідло”.
Необхідна умова:
s - 10 < 0. Оскільки 0 < s < 1 то перший доданок
завжди менший за другий. Отже при будь-яких допустимих значеннях s та x вираз
буде від’ємний, тому подальших змін точки біфуркації не буде.
Таблиця 1.3 - Тип особливої точки в залежності від значень tr
і det
|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Сідло
|
0 < s < 1, 0
< x < 1
|
1.4 Дослідження моделі динаміки ринкового середовища
за допомогою коренів характеристичного рівняння
модель динаміка ринковий біфуркація
Складемо характеристичне рівняння для матриці J1:

 δλ + ∆ = 0.
(1.17)
δλ + ∆ = 0.
(1.17)
Підставимо знайдені значення δ та ∆ у символьному вигляді:

 (C(s - 1) -
1)λ + C - Cs = 0.
(1.18)
(C(s - 1) -
1)λ + C - Cs = 0.
(1.18)
Підрахуємо корені характеристичного рівняння:
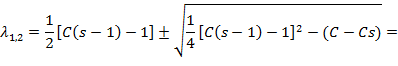
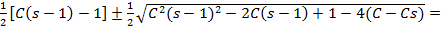
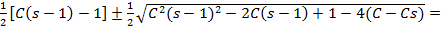

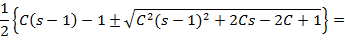
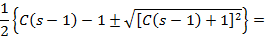
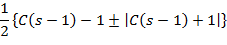

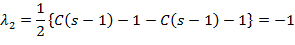
Корені характеристичного рівняння: 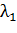
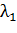 =
-1,
=
-1, 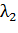
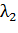 =
Cs - C.
=
Cs - C.
Маючи 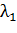
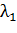 та
та
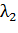
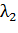 визначимо
необхідні значення змінних для знаходження точок біфуркації.
визначимо
необхідні значення змінних для знаходження точок біфуркації.
Розглянемо можливі точки біфуркації при цих умовах:
) 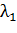
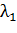 та
та 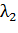
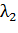 дійсні,
співпадаючі, від’ємні. Фазовий портрет - “Стійкий вироджений вузол”.
дійсні,
співпадаючі, від’ємні. Фазовий портрет - “Стійкий вироджений вузол”.
Перша умова:
C(s - 1) < 0. Оскільки С > 0, 0 < s < 1, тому перший
доданок завжди менший за другий. Отже при будь-яких допустимих значень s корінь
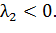
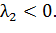
Друга умова:
(s - 1) = -1
C = 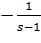
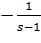
) 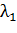
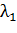 та
та 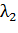
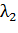 дійсні,
різні, від’ємні. Фазовий портрет - “Стійкий вузол”.
дійсні,
різні, від’ємні. Фазовий портрет - “Стійкий вузол”.
Перша умова:
C(s - 1) < 0. Оскільки С > 0, 0 < s < 1, тому перший
доданок завжди менший за другий. Отже при будь-яких допустимих значень s корінь
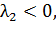
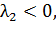 тому
подальших змін точки біфуркації не буде.
тому
подальших змін точки біфуркації не буде.
Друга умова:
(s - 1) ≠ -1
C ≠ 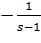
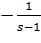
Таблиця 1.4 - Тип особливої точки в залежності від значень 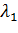
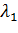 та
та


|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Стійкий вироджений вузол
|
C = 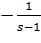 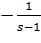
|
|
Стійкий вузол
|
C > 0, 0 < s < 1, C ≠ 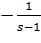 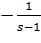
|
Складемо характеристичне рівняння для матриці J2:

 δλ + ∆ = 0.
(1.19)
δλ + ∆ = 0.
(1.19)
Підставимо знайдені значення δ та ∆ та визначемо 
 та
та

 у
символьному вигляді:
у
символьному вигляді:

 (
(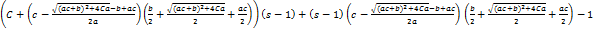
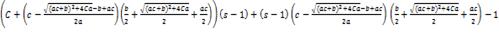 )λ -
)λ - 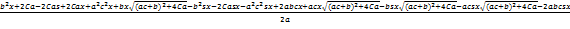
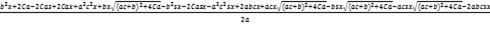 =
0. (1.20)
=
0. (1.20)
Оскільки дане рівняння є досить складним підрахунок його коренів
проводився у математичному пакеті Mathcad, а результати наведено в
додатках.
Корені характеристичного рівняння:


Керуючись системою обмежень 1.9 та враховуючи необхідні умови
економічної сутності задамо значення деяких змінних: a=-2, b=300, С = 10,
c=100, а значення коефіцієнта регулювання за відхиленням x та мултиплікатор
накопичення s будемо визначати залежно від умов точки біфуркації.
Підставимо значення змінних:


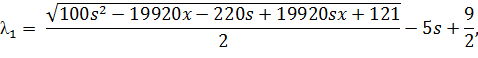

Маючи 
 та
та

 визначимо
необхідні значення змінних для знаходження точок біфуркації.
визначимо
необхідні значення змінних для знаходження точок біфуркації.
Розглянемо можливі точки біфуркації при цих умовах:
) 
 < 0,
< 0, 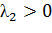
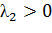 .
Фазовий портрет - “Сідло”.
.
Фазовий портрет - “Сідло”.
Перша
умова:
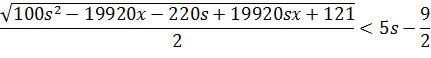
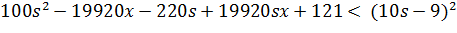
19920sx - 19920x - 40s + 40
< 0
x < 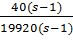
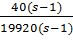
x < 0.002
Друга
умова
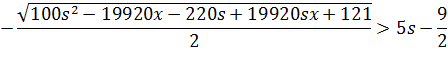
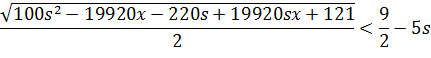
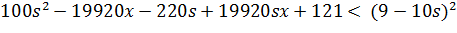
sx - 19920x - 40s + 40 < 0< 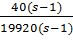
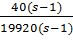 <
0.002
<
0.002
) 
 та
та 
 комплексні
чисто уявні. Фазовий портрет - “Центр”.
комплексні
чисто уявні. Фазовий портрет - “Центр”.
Перша
умова:
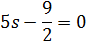
s = 0.9
Друга умова:
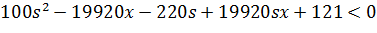
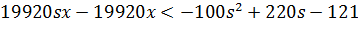
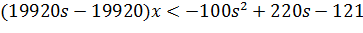

Оскільки перша умова s = 0.9 то підставимо необхідне значення s:
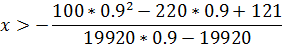
 > 0.002
> 0.002
3) 
 та
та 
 дійсні
від’ємні різні. Фазовий портрет - “Стійкий вузол”.
дійсні
від’ємні різні. Фазовий портрет - “Стійкий вузол”.
Перша
умова:
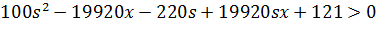
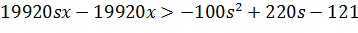

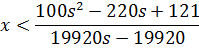
Друга
умова:
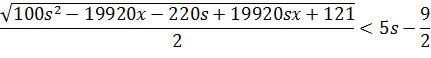
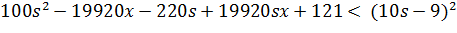
19920sx - 19920x - 40s + 40
< 0
x < 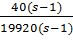
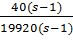
x < 0.002
Третя умова:
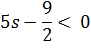 >
0.9
>
0.9
4) 
 та
та 
 дійсні
додатні різні. Фазовий портрет - “Нестійкий вузол”.
дійсні
додатні різні. Фазовий портрет - “Нестійкий вузол”.
Перша
умова:
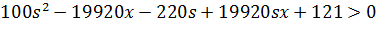
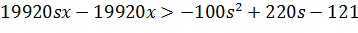

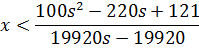
Друга
умова:
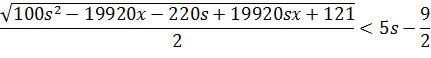
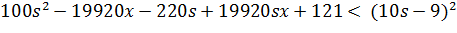
19920sx - 19920x - 40s + 40
< 0
x < 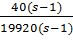
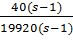
x < 0.002
Третя умова:
 < 0.9
< 0.9
5) 
 та
та 
 дійсні
співпадаючі від’ємні. Фазовий портрет - “Стійкий
дійсні
співпадаючі від’ємні. Фазовий портрет - “Стійкий
вироджений вузол”.
Перша
умова:
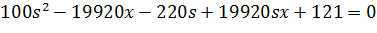
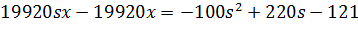
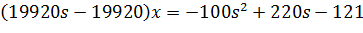
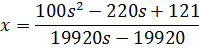
Друга
умова:
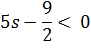 > 0.9
> 0.9
6) 
 та
та 
 дійсні
співпадаючі додатні. Фазовий портрет - “ Нестійкий вироджений вузол”.
дійсні
співпадаючі додатні. Фазовий портрет - “ Нестійкий вироджений вузол”.
Перша
умова:
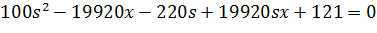
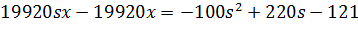
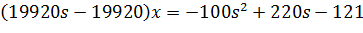
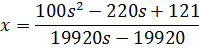
Друга
умова:
 < 0.9
< 0.9
)

 та
та

 комплексні
з додатною дійсною частиною. Фазовий
комплексні
з додатною дійсною частиною. Фазовий
портрет - “ Стійкий фокус”.
Перша
умова:
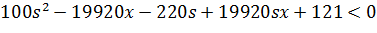

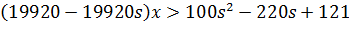
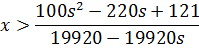
Друга умова:
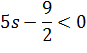 > 0.9
> 0.9
8) 
 та
та 
 комплексні з від’ємною дійсною
частиною Фазовий
комплексні з від’ємною дійсною
частиною Фазовий
портрет - “ Нестійкий фокус”.
Перша
умова:

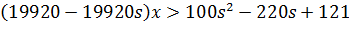
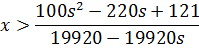
Друга умова:
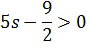 < 0.9
< 0.9
Таблиця 1.5 - Тип особливої точки в залежності від значень 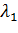
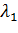 та
та


|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Сідло
|
x < 0.002
|
|
Центр
|
x > 0.002, s = 0.9
|
|
Пряма на фазовій
площині
|
x = 0.002, s ≠
0.9
|
Стійкий вузол x < 
 ,
,
Нестійкий вузол x < 
 ,
,
Стійкий вироджений вузол x = 
 ,
,
Нестійкий вироджений вузол x = 
 ,
,
Стійкий фокус x > 

Нестійкий фокус x > 

Складемо характеристичне рівняння для матриці J3:

 δλ + ∆ = 0.
(1.19)
δλ + ∆ = 0.
(1.19)
Підставимо знайдені значення δ та ∆ та визначемо 
 та
та

 у
символьному вигляді:
у
символьному вигляді:

 (
(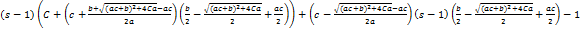
 )λ -
)λ - 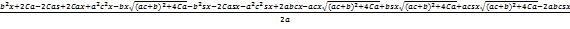
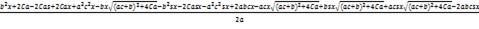 =
0. (1.20)
=
0. (1.20)
Оскільки дане рівняння є досить складним підрахунок його коренів
проводився у математичному пакеті Mathcad, а результати наведено в
додатках.
Корені характеристичного рівняння:


Керуючись системою обмежень 1.9 та враховуючи необхідні умови
економічної сутності задамо значення деяких змінних: a=-2, b=300, С = 10,
c=100, а значення коефіцієнта регулювання за відхиленням x та мултиплікатор
накопичення s будемо визначати залежно від умов точки біфуркації.
Підставимо значення змінних:


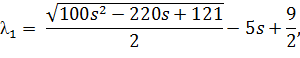
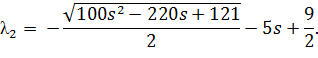
Маючи 
 та
та

 визначимо
необхідні значення змінних для знаходження точок біфуркації.
визначимо
необхідні значення змінних для знаходження точок біфуркації.
Розглянемо можливі точки біфуркації при цих умовах:
) 
 > 0,
> 0, 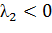
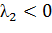 .
Фазовий портрет - “Сідло”.
.
Фазовий портрет - “Сідло”.
Необхідна умова:
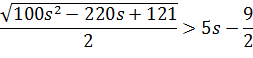
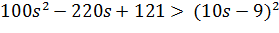
-40s + 40 > 0
s <
1
Оскільки 0 < s < 1 то дана умова завжди виконується.
Отже при будь-яких допустимих значеннях s та x вираз буде від’ємний, тому
подальших змін точки біфуркації не буде.
Таблиця 1.6 - Тип особливої точки в залежності від значень 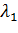
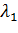 та
та


|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Сідло
|
0 < s < 1, 0
< x < 1
|
1.5 Умови стійкості та точки біфуркації
Відобразимо точки біфуркації системи, що описана моделлю динаміки
ринкового середовища для першої особливої точки 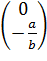
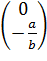 у
таблиці 1.6, для другої особливої точки
у
таблиці 1.6, для другої особливої точки 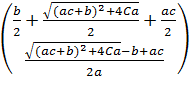
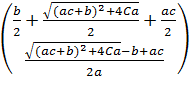 у
таблиці 1.7, для третьої особливої точки
у
таблиці 1.7, для третьої особливої точки 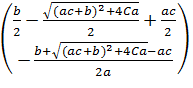
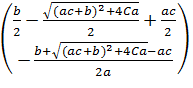 у
таблиці 1.8.
у
таблиці 1.8.
Таблиця 1.7 - Точки біфуркації для першої особливої
|
Тип особливої точкиСпіввідношення параметрів
|
|
|
Стійкий вироджений вузол
|
C = 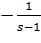 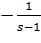
|
|
Стійкий вузол
|
C > 0, 0 < s < 1, C ≠ 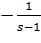 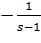
|
Таблиця 1.8 - Точки біфуркації для другої особливої
|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Сідло
|
x < 0.002
|
|
Центр
|
x > 0.002, s = 0.9
|
|
Пряма на фазовій
площині
|
x = 0.002, s ≠
0.9
|
Стійкий вузол x < 
 ,
,
Нестійкий вузол x < 
 ,
,
Стійкий вироджений вузол x = 
 ,
,
Нестійкий вироджений вузол x = 
 ,
,
Стійкий фокус x > 

Нестійкий фокус x > 

Таблиця 1.9 - Точки біфуркації для третьої особливої
|
Тип особливої точки
|
Співвідношення
параметрів
|
|
Сідло
|
0 < s < 1, 0
< x < 1
|
Отже, умовою стійкості для першої особливої точки є будь-яке
допустиме значення параметрів, оскільки для неї можливі лише стійкі точки
біфуркації.
Для другої особливої точки умова стійкості виконується при
таких значеннях параметрів (таблиця 1.9):
Таблиця 1.10 - Співвідношення параметрів для забезпечення
стійкості другої особливої точки
|
Співвідношення
параметрів
|
|
x > 0.002, s = 0.9
|
|
x = 0.002, s ≠
0.9
|
x < 
 ,
,
x = 
 ,
,
x > 

Для третьої особливої точки умова стійкості ніколи не
виконується тому, що не існує стійких точок біфуркації.
2. ЧИСЛОВЕ ДОСЛІДЖЕННЯ МОДЕЛІ ДИНАМІКИ РИНКОВОГО СЕРЕДОВИЩА
2.1 Числове дослідження першої точки рівноваги
Маючи матрицю 1.14 підставимо значення змінних: a=-2, b=300,
С = 10, c=100, а значення коефіцієнта регулювання за відхиленням x та
мултиплікатор накопичення s будемо підставляти залежно від умов точки
біфуркації:
) Фазовий портрет - “Стійкий вироджений вузол”.
Необхідна умова: C = 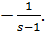
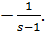
Підставимо значення s = 0.5 та C = 2
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:

Рисунок 2.1 - Біфуркаційна діаграма “Стійкий вироджений вузол”
Побудуємо фазовий портрет:
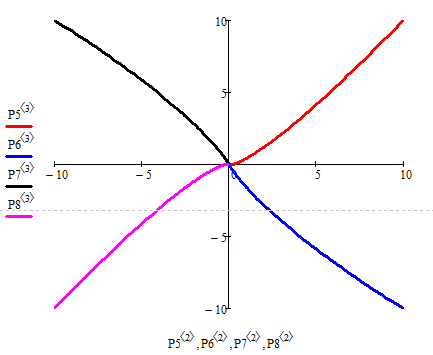
Рисунок 2.2 - Фазовий портрет “Стійкий вироджений вузол”
Побудуємо векторне поле:
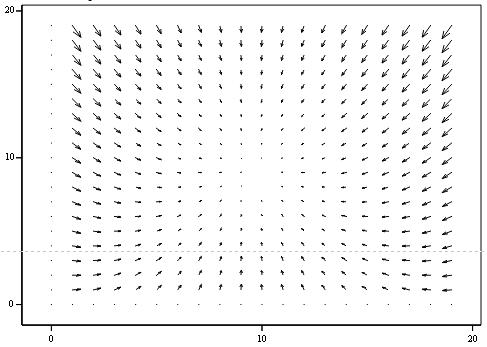
Рисунок 2.3 - Векторне поле “Стійкий вироджений вузол”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають вироджений вузол, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують до точки, що говорить
про її стійкість і також підтверджує правильність розрахунків.
2) Фазовий портрет - “Стійкий вузол”.
Необхідна умова: C ≠ 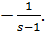
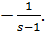
Підставимо значення s = 0.5 та C = 10
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
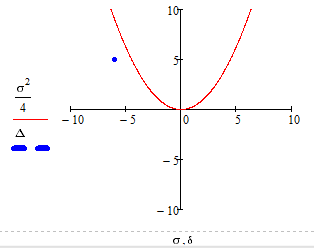
Рисунок 2.4 - Біфуркаційна діаграма “Стійкий вузол”
Побудуємо фазовий портрет:

Рисунок 2.5 - Фазовий портрет “Стійкий вузол”
Побудуємо векторне поле:
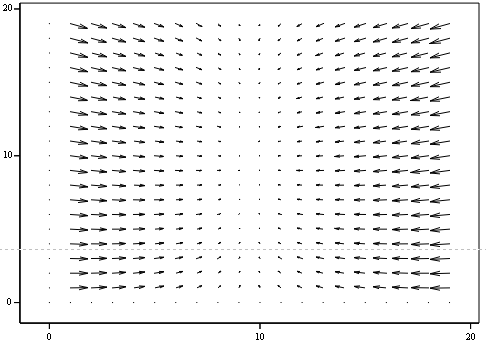
Рисунок 2.6 - Векторне поле “Стійкий вузол”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають вузол, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують до точки, що говорить
про її стійкість і також підтверджує правильність розрахунків.
2.2 Числове дослідження другої точки рівноваги
Маючи матрицю 1.15 підставимо значення змінних: a=-2, b=300,
С = 10, c=100, а значення коефіцієнта регулювання за відхиленням x та
мултиплікатор накопичення s будемо підставляти залежно від умов точки
біфуркації:
) Фазовий портрет - “Сідло ”.
Необхідна умова: x < 0.002
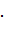
Підставимо значення s = 0.9999 та x = 0.001
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
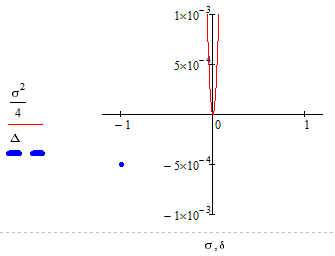
Рисунок 2.7 - Біфуркаційна діаграма “Сідло”
Побудуємо фазовий портрет:
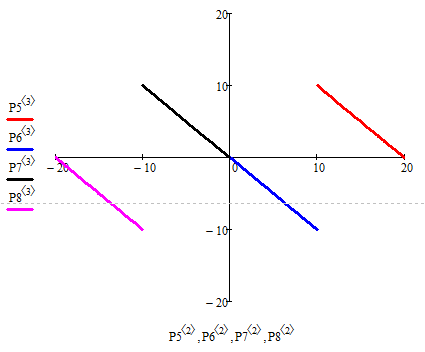
Рисунок 2.8 - Фазовий портрет “Сідло”
Побудуємо векторне поле:
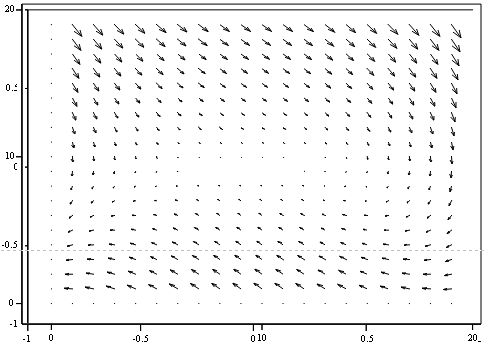
Рисунок 2.9 - Векторне поле “Сідло”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають сідло, що підтверджує правильність розрахунків.
2) Фазовий портрет - “Центр”.
Необхідна умова: x > 0.002, s = 0.9
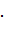
Підставимо значення s = 0.8 та х = 0.011
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
Рисунок 2.10 - Біфуркаційна діаграма “Центр”
Побудуємо фазовий портрет:

Рисунок 2.11 - Фазовий портрет “Центр”
Побудуємо векторне поле:
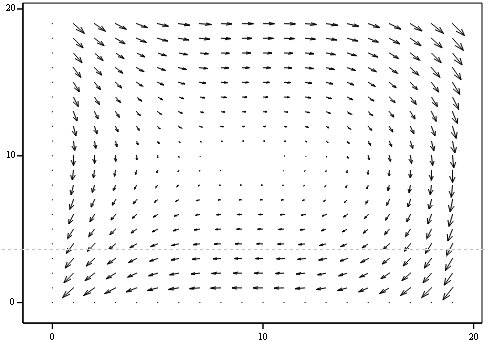
Рисунок 2.12 - Векторне поле “Центр”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають центр, що підтверджує правильність розрахунків.
3) Фазовий портрет - “ Пряма на фазовій площині ”.
Необхідна умова: x = 0.002, s ≠ 0.9
Підставимо значення s = 0.5 та х = 0.002
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
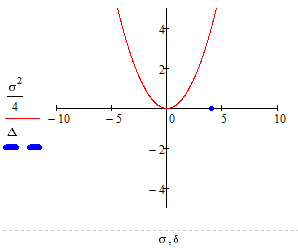
Рисунок 2.13 - Біфуркаційна діаграма “ Пряма на фазовій площині ”
Побудуємо фазовий портрет:

Рисунок 2.14 - Фазовий портрет “ Пряма на фазовій площині ”
Побудуємо векторне поле:

Рисунок 2.15 - Векторне поле “ Пряма на фазовій площині ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають пряму, що підтверджує правильність розрахунків.
4) Фазовий портрет - “ Стійкий вузол ”.
Необхідна умова: x < 
 ,
x > 0.002, s > 0.9
,
x > 0.002, s > 0.9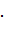
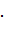
Підставимо значення s = 0.9999 та х = 0.3
Корені системи рівнянь: (0;0).
Побудуємо
біфуркаційну діаграму:
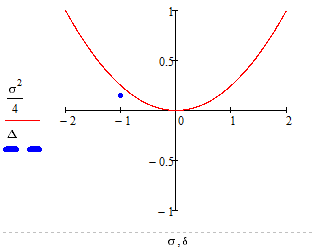
Рисунок 2.16 - Біфуркаційна діаграма “ Стійкий вузол ”
Побудуємо фазовий портрет:

Рисунок 2.17 - Фазовий портрет “ Стійкий вузол ”
Побудуємо векторне поле:
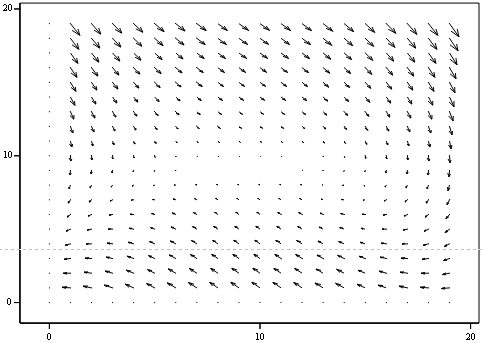
Рисунок 2.18 - Векторне поле “ Стійкий вузол ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають вузол, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують до точки,
що говорить про її стійкість і також підтверджує правильність розрахунків.
) Фазовий портрет - “ Нестійкий вузол ”.
Необхідна умова: x < 
 ,
x > 0.002, s < 0.9.
,
x > 0.002, s < 0.9.
Підставимо значення s = 0.89999 та х = 0.002007.
Корені системи рівнянь: (0;0).
Побудуємо
біфуркаційну діаграму:
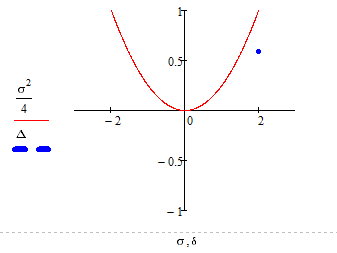
Рисунок 2.19 - Біфуркаційна діаграма “ Нестійкий вузол ”
Побудуємо фазовий портрет:
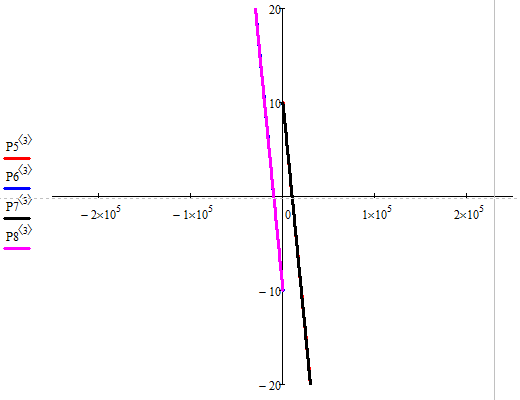
Рисунок 2.20 - Фазовий портрет “ Нестійкий вузол ”
Побудуємо векторне поле:
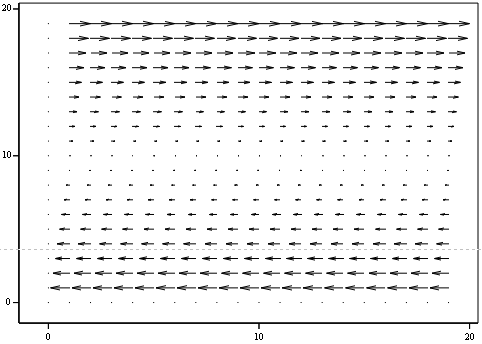
Рисунок 2.21 - Векторне поле “ Нестійкий вузол ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають вузол, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують від точки,
що говорить про її нестійкість і також підтверджує правильність розрахунків.
) Фазовий портрет - “ Стійкий вироджений вузол ”.
Необхідна умова: x = 
 ,
s > 0.9
,
s > 0.9
Підставимо значення s = 0.9999 та х = 0.05
Корені системи рівнянь: (0;0).
Побудуємо
біфуркаційну діаграму:
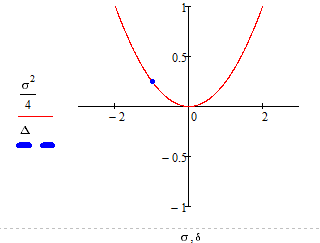
Рисунок 2.22 - Біфуркаційна діаграма “ Стійкий вироджений
вузол ”
Побудуємо фазовий портрет:
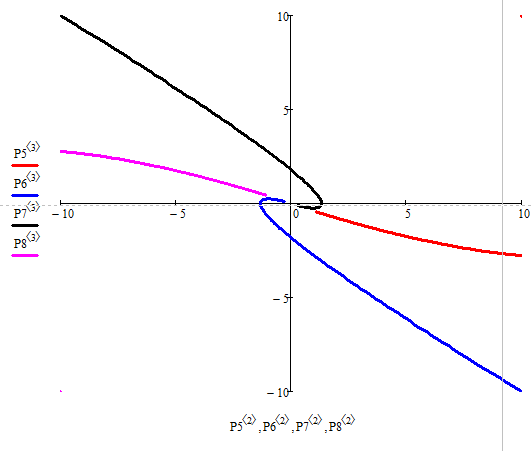
Рисунок 2.23 - Фазовий портрет “ Стійкий вироджений вузол ”
Побудуємо векторне поле:

Рисунок 2.24 - Векторне поле “ Стійкий вироджений вузол ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають вироджений вузол, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують до точки,
що говорить про її стійкість і також підтверджує правильність розрахунків.
) Фазовий портрет - “ Неcтійкий вироджений вузол ”.
Необхідна умова: x = 
 ,
s < 0.9
,
s < 0.9
Підставимо значення s = 0.9999 та х = 0.5
Корені системи рівнянь: (0;0).
Побудуємо
біфуркаційну діаграму:
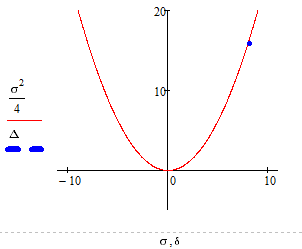
Рисунок 2.25 -
Біфуркаційна діаграма “ Неcтійкий вироджений вузол ”
Побудуємо фазовий портрет:
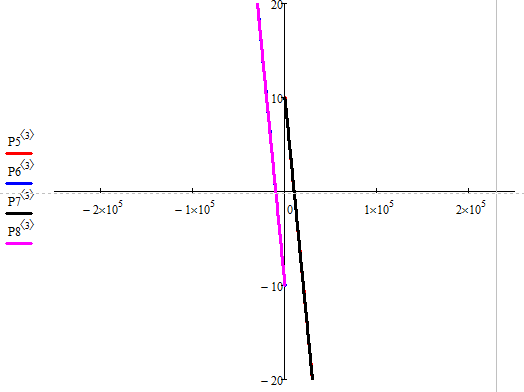
Рисунок 2.26 - Фазовий портрет “ Неcтійкий вироджений вузол ”
Побудуємо векторне поле:

Рисунок 2.27 - Векторне поле “ Неcтійкий вироджений вузол ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають вироджений вузол, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують від точки,
що говорить про її нестійкість і також підтверджує правильність розрахунків.
) Фазовий портрет - “ Стійкий фокус ”.
Необхідна умова: x > 
 s > 0.9
s > 0.9
Підставимо значення s = 0.9999 та х = 0.9999
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
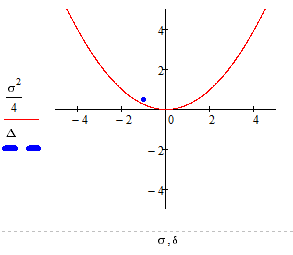
Рисунок 2.28 - Біфуркаційна діаграма “ Стійкий фокус ”
Побудуємо фазовий портрет:
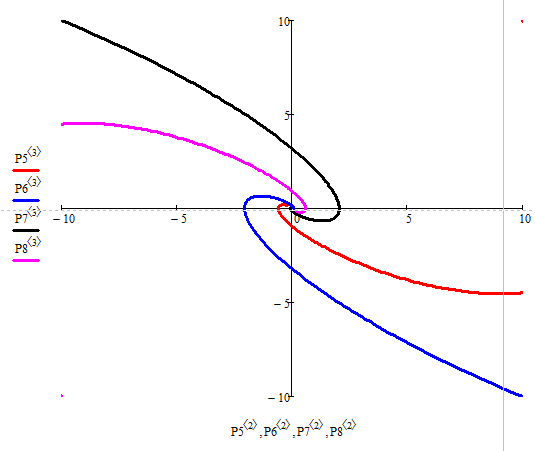
Рисунок 2.29 - Фазовий портрет “ Стійкий фокус ”
Побудуємо векторне поле:
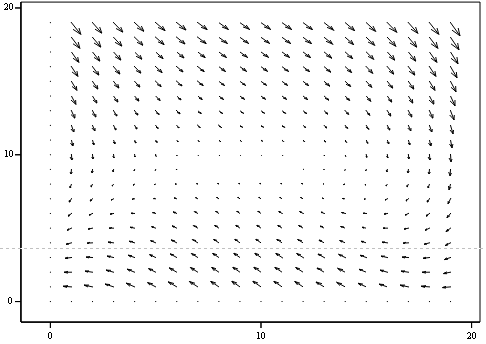
Рисунок 2.30 - Векторне поле “ Стійкий фокус ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають фокус, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують до точки, що говорить
про її стійкість і також підтверджує правильність розрахунків.
9) Фазовий портрет - “ Нестійкий фокус ”.
Необхідна умова: x > 
 s < 0.9
s < 0.9
Підставимо значення s = 0.79999 та х = 0.89999
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
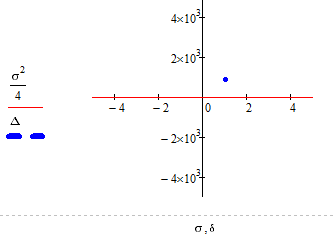
Рисунок 2.31 - Біфуркаційна діаграма “ Нестійкий фокус ”
Побудуємо фазовий портрет:

Рисунок 2.32 - Фазовий портрет “ Нестійкий фокус ”
Побудуємо векторне поле:
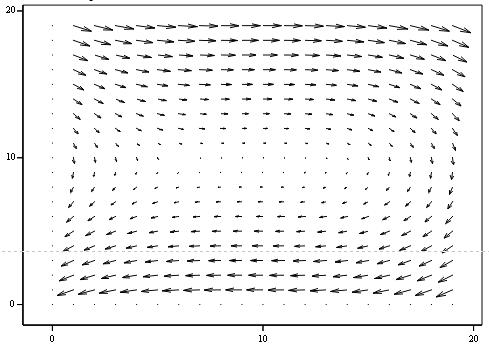
Рисунок 2.33 - Векторне поле “ Нестійкий фокус ”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають фокус, що підтверджує правильність розрахунків.
На векторному полі ми бачимо, що стрілки прямують від точки, що говорить
про її нестійкість і також підтверджує правильність розрахунків.
2.3 Числове дослідження третьої точки
рівноваги
Маючи матрицю 1.16 підставимо значення змінних: a=-2, b=300,
С = 10, c=100, а значення коефіцієнта регулювання за відхиленням x та мултиплікатор
накопичення s будемо підставляти залежно від умов точки біфуркації:
) Фазовий портрет - “Сідло ”.
Необхідна умова: 0 < s < 1, 0 < x < 1
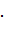
Підставимо значення s = 0.8 та x = 0.9
Корені системи рівнянь: (0;0).
Побудуємо біфуркаційну діаграму:
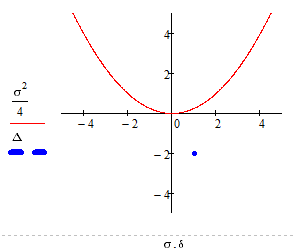
Рисунок 2.31 - Біфуркаційна діаграма “Сідло”
Побудуємо фазовий портрет:

Рисунок 2.32 - Фазовий портрет “Сідло”
Побудуємо векторне поле:
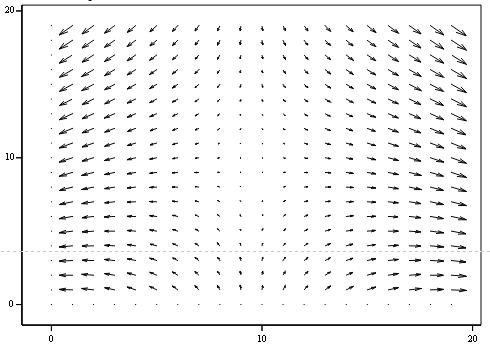
Рисунок 2.33 - Векторне поле “Сідло”
Положення точки на біфуркаційній діаграмі та фазовий портрет
відображають сідло, що підтверджує правильність розрахунків.
2.4 Економічна інтерпретація
отриманих результатів
Для першої особливої точки усі можливі допустимі значення
параметрів утворюють стійкий стан, що свідчить про задовільний та
передбачуваний стан ринкової динаміки. Будь-які зрушення та зміни як в
зовнішньоекономічному плані так і в локальному для підприємця є прогнозовані та
прямо пов’язані.
Для другої особливої точки існує декілька випадків стійкого
стану. Ці випадки найчастіше мають умову при якій коефіцієнт регулювання за
відхиленням х має бути більшим за 0.002, а мультиплікатор накопичення s має бути більшим 0.9. Не дотримання
цих умов може спричинити втрату стійкості, що приведе до непередбачуваних
наслідків у економічній динаміці.
Третя особлива точка не має стійких станів, що говорить про
непередбачуваність динаміки ринкового середовища та малу ймовірність отримання
бажаних результатів при певних діях.
ВИСНОВКИ
У результаті виконання курсової роботи було досліджено модель
динаміки ринкового середовищ за допомогою інструментів і принципів економічної
динаміки. Шляхом аналітичних розрахунків і за допомогою числового моделювання
виявлено три особливі точки системи. Далі проводилося дослідження на умови
стійкості моделі.
Перша особлива точка показала абсолютну стійкість при
будь-якій зміні параметрів на відміну від третьої особливої точки, що має
постійний нестійкий стан.
Друга ж точка має як стійкі так і не стійкі стани, що
залежить від зміни значень коефіцієнту регулювання за відхиленням х, який має
бути більшим за 0.002 та мультиплікатор накопичення s, який має бути більшим 0.9.
Отже, для гарного функціонування ринкового середовища та
забезпечення економічної стабільності або росту необхідно дотримуватись
вказаних умов стійкості.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Моделювання
економіки : методичні рекомендації щодо виконання курсової роботи. / [укл.
Перхун Л.П., Братушка С.М., Вахнюк С.В., Кузьменко О.В.]; Державний вищий
навчальний заклад «Українська академія банківської справи Національного банку
України». - Суми : ДВНЗ «Українська академія банківської справи Національного
банку України», 2013. - 34 с.
2. Наконечний,
С. І. Економетрiя [Текст]: Навчальний посібник. / С. І. Наконечний, Т. О.
Терещенко, Т. П. Романюк - К. : КНЕУ, 1997. - 352 с.
. Поттосина,
С. А. Экономико-математические методы и модели [Текст] : Учеб. пособие для
студ. экон. спец. БГУИР всех форм обуч. / С. А. Поттосина, В. А. Журавлев. -
Мн. : БГУИР, 2003. - 94 с.
. Томашевський,
В. М. Моделювання систем. [Текст] /
В. М. Томашевський - К. : Видавнича група BHV, 2005. - 352 с.
. Філонич
О.М. Економіко-математична модель інвестиційної привабливості регіонального
ринку рекреаційних послуг України / О.М. Філонич // Вісник Хмельницького
національного університету - 2010. - № 4, T. 4. - С. 170 - 174.
Додаток А - Аналітичне дослідження моделі динаміки ринкового
середовища
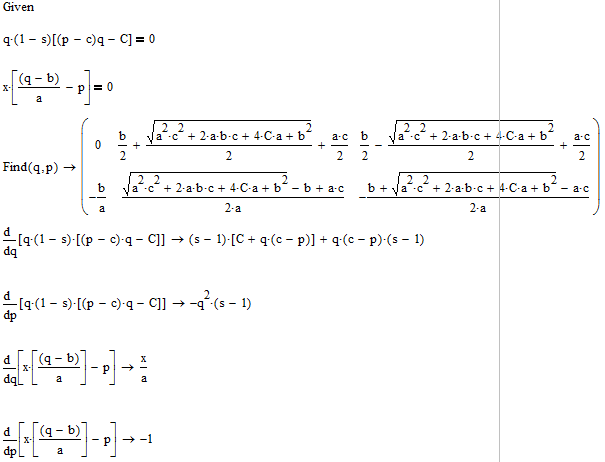



Додаток Б - Дослідження моделі за
допомогою біфуркаційної діаграми для другої особливої точки
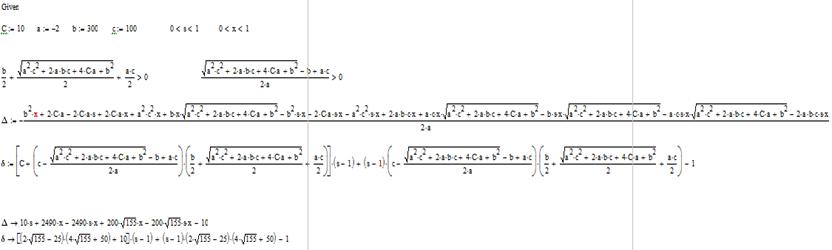
Додаток В - Дослідження моделі за
допомогою біфуркаційної діаграми для третьої особливої точки
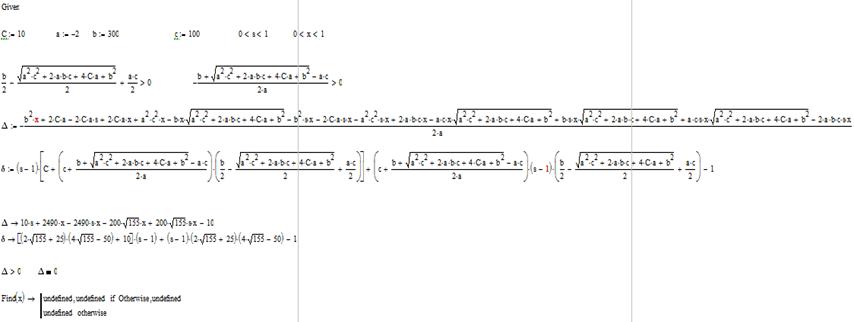
Додаток Г - Дослідження моделі за
допомогою коренів характеристичного рівняння для другої особливої точки

Додаток Д - Дослідження моделі за
допомогою коренів характеристичного рівняння для третьої особливої точки

Додаток Д - Побудова біфуркаційної
діаграми, фазового портрета та векторного поля