|
Рабочие
|
Средние
затраты времени на одну деталь, мин. (х)
|
Всего
затрачено времени, час. (хm)
|
Количество
изготовленных деталей за день, шт. (m)
|
|
1
|
4
|
8,2
|
123
|
|
2
|
7
|
8,1
|
69,4
|
|
3
|
8
|
8,2
|
61,5
|
|
4
|
10
|
7,6
|
45,6
|
|
5
|
12
|
7,2
|
36
|
|
Всего
|
|
39,3
|
335,5
|
Из табл.2 следует, что всего было изготовлено
335,5 деталей. При этом суммарные затраты времени для пяти рабочих составили
39,3 часа.
Анализ приведенных данных показывает, что
приведенные средние затраты времени на одну деталь относятся к качественно
однородной совокупности примерно одного порядка и к ним можно применить
методику расчета средней арифметической по заданному вариационному ряду.
Следует отметить, что средние величины в статистике выражаются в тех же
единицах, в которых заданы данные по исходной совокупности (мин.).
В заданном примере необходимо найти среднюю
арифметическую взвешенную, поскольку присутствует повторяемость значений
единиц совокупности.
Средняя арифметическая взвешенная рассчитывается
по формуле
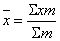 ,
,
где х - средние затраты времени на 1
деталь одним из рабочих; - количество изготовленных деталей одним из рабочих
(частота, повторяемость значения).
Следовательно, на изготовление одной
детали в среднем потребовалось
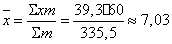 мин.
мин.
Задача 13. По приведенным ниже
данным:
a) построить дискретный или интервальный
вариационный ряд (число групп равно 10, интервалы равные);
b) для полученного интервального ряда
вычислить с точностью до 0,1
1) среднюю арифметическую;
2) медиану;
) коэффициент вариации;
) среднее квадратическое отклонение;
c) построить графики ряда (полигон и
гистограмму);
d) определить, насколько фактическое
распределение согласуется с нормальным;) изложить письменно основное
содержание выполненной работы, указав на значение и принципы вычисления
показателей (средней арифметической, среднего квадратического отклонения,
медианы и коэффициента вариации), а также выводы, которые можно сделать на
основе вычисленных показателей.
Имеются следующие данные о пробеге 100 шин
нового типа (в тыс.км) (табл.3).
Таблица 3
|
40,1
|
42,1
|
44,2
|
48,9
|
40,6
|
43,9
|
43,2
|
43,7
|
49,4
|
43,7
|
|
47,5
|
42,6
|
41,3
|
42,3
|
46,9
|
46,7
|
38
|
46,2
|
44,8
|
46,1
|
|
46,9
|
41,9
|
48,2
|
44,4
|
46,4
|
44,7
|
44,8
|
43,2
|
51,2
|
40
|
|
45,8
|
43,9
|
49,8
|
47,7
|
44,5
|
43,6
|
44,5
|
46,1
|
44,5
|
46,1
|
|
47,2
|
46,7
|
47,9
|
47,7
|
43,4
|
46,3
|
44,5
|
46,1
|
47,9
|
43,7
|
|
45,2
|
50,2
|
42,6
|
45,5
|
40,4
|
43,1
|
43,2
|
43,7
|
40,3
|
44,5
|
|
44,1
|
43,6
|
49,1
|
42,8
|
43,7
|
41,8
|
46,6
|
44,8
|
43,2
|
46,6
|
|
42,9
|
48,8
|
46,1
|
39,1
|
41,5
|
45,5
|
47,9
|
47,3
|
47,4
|
40,3
|
|
47
|
45
|
50,8
|
39,4
|
43,3
|
48,8
|
40
|
44,35
|
44,8
|
49,9
|
|
52
|
46
|
51,2
|
40,7
|
43,9
|
44,8
|
43,7
|
49,4
|
43,7
|
44,8
|
Решение
Ряды цифровых статистических данных получаются в
результате обработки и систематизации первичных статистических данных, заданных
в примере в виде табл.3.
Для решения задачи и проверки заданного
распределения по критериям согласия вначале построим интервальный вариационный
ряд.
Для построения интервального вариационного ряда
расположим приведенные в табл.3 данные в порядке возрастания приведенных
значений и поместим их в табл.4.
№ Заданное значение Интервалы,
тыс.км Кол-во значений в интервале  Накопленные частоты значений
Накопленные частоты значений
|
тыс.км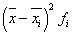
|
|
|
|
|
|
38
|
38
-39,4
|
3
|
3
|
38,8
|
81,1
|
|
39,1
|
|
|
|
|
|
|
39,4
|
|
|
|
|
|
|
40
|
св.39,4
- 40,8
|
8
|
11
|
40,3
|
109,5
|
|
40
|
|
|
|
|
|
|
40,1
|
|
|
|
|
|
|
40,3
|
|
|
|
|
|
|
40,3
|
|
|
|
|
|
|
40,4
|
|
|
|
|
|
|
40,6
|
|
|
|
|
|
|
40,7
|
|
|
|
|
|
|
41,3
|
св.40,8
- 42,2
|
5
|
16
|
41,7
|
25,45
|
|
41,5
|
|
|
|
|
|
|
41,8
|
|
|
|
|
|
|
41,9
|
|
|
|
|
|
|
42,1
|
|
|
|
|
|
|
42,3
|
св.42,2
-43,6
|
14
|
30
|
43.1
|
11,3
|
|
42,6
|
|
|
|
|
|
|
42,6
|
|
|
|
|
|
|
42,8
|
|
|
|
|
|
|
42,9
|
|
|
|
|
|
|
43,1
|
|
|
|
|
|
|
43,2
|
|
|
|
|
|
|
43,2
|
|
|
|
|
|
|
43,2
|
|
|
|
|
|
|
43,2
|
|
|
|
|
|
|
43,3
|
|
|
|
|
|
|
43,4
|
|
|
|
|
|
|
43,6
|
|
|
|
|
|
|
43,6
|
|
|
|
|
|
|
43,7
|
св.43,6
- 45
|
27
|
57
|
44,3
|
2,4
|
|
43,7
|
|
|
|
|
|
|
43,7
|
|
|
|
|
|
|
43,7
|
|
|
|
|
|
|
43,7
|
|
|
|
|
|
|
43,7
|
|
|
|
|
|
|
43,7
|
|
|
|
|
|
|
43,9
|
|
|
|
|
|
|
43,9
|
|
|
|
|
|
|
43,9
|
|
|
|
|
|
|
44,1
|
|
|
|
|
|
|
44,2
|
|
|
|
|
|
|
44,35
|
|
|
|
|
|
|
44,4
|
|
|
|
|
|
|
44,5
|
|
|
|
|
|
|
44,5
|
|
|
|
|
|
|
44,5
|
|
|
|
|
|
|
44,5
|
|
|
|
|
|
|
44,5
|
|
|
|
|
|
|
44,7
|
|
|
|
|
|
|
44,8
|
|
|
|
|
|
|
44,8
|
|
|
|
|
|
|
44,8
|
|
|
|
|
|
|
44,8
|
|
|
|
|
|
|
44,8
|
|
|
|
|
|
|
44,8
|
|
|
|
|
|
|
45
|
|
|
|
|
|
|
45,2
|
св.45
- 46,4
|
13
|
70
|
45,9
|
46,9
|
|
45,5
|
|
|
|
|
|
|
45,5
|
|
|
|
|
|
|
45,8
|
|
|
|
|
|
|
46
|
|
|
|
|
|
|
46,1
|
|
|
|
|
|
|
46,1
|
|
|
|
|
|
|
46,1
|
|
|
|
|
|
|
46,1
|
|
|
|
|
|
|
46,1
|
|
|
|
|
|
|
46,2
|
|
|
|
|
|
|
46,3
|
|
|
|
|
|
|
46,4
|
|
|
|
|
|
|
46,6
|
св.46,4
- 47,8
|
13
|
83
|
47,1
|
124,9
|
|
46,6
|
|
|
|
|
|
|
46,7
|
|
|
|
|
|
|
46,7
|
|
|
|
|
|
|
46,9
|
|
|
|
|
|
|
46,9
|
|
|
|
|
|
|
47
|
|
|
|
|
|
|
47,2
|
|
|
|
|
|
|
47,3
|
|
|
|
|
|
|
47,4
|
|
|
|
|
|
|
47,5
|
|
|
|
|
|
|
47,7
|
|
|
|
|
|
|
47,7
|
|
|
|
|
|
|
47,9
|
св.47,8
- 49,2
|
8
|
91
|
48,4
|
154,9
|
|
47,9
|
|
|
|
|
|
|
47,9
|
|
|
|
|
|
|
48,2
|
|
|
|
|
|
|
48,8
|
|
|
|
|
|
|
48,8
|
|
|
|
|
|
|
48,9
|
|
|
|
|
|
|
49,1
|
|
|
|
|
|
|
49,4
|
св.49,2
- 50,6
|
5
|
96
|
49,7
|
162,45
|
|
49,4
|
|
|
|
|
|
|
49,8
|
|
|
|
|
|
|
49,9
|
|
|
|
|
|
|
50,2
|
|
|
|
|
|
|
50,8
|
св.50,6
- 52
|
4
|
100
|
51,5
|
225
|
|
51,2
|
|
|
|
|
|
|
51,2
|
|
|
|
|
|
|
52
|
|
|
|
|
|
|
Сумма
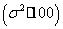 942,9 942,9
|
|
Из табл.4 видно, что наименьшее значение равно
38 тыс.км, а наибольшее - 52 тыс.км. Следовательно, все значения находятся на
интервале от 38 до 52, а сам интервал равен 52-38=14.
Если максимальное значение признака превышает не
более чем в 10 раз минимальное значение, применяют равные интервалы [2].
В нашем случае
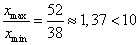 ,
,
поэтому принимаем равные интервалы.
Поскольку число групп равно 10,
длина каждой интервальной группы будет равна 14/10=1,4.
Подставим в табл.4 интервальные
значения каждой из 10 групп, подсчитаем количество шин попавших в каждую
интервальную группу и частоту попаданий (f) заданных значений в заданные
интервалы, при этом, если какое то значение попадает на границу предыдущего и
последующего интервалов, то это значение приписываем к предыдущему интервалу.
Найдем среднюю арифметическую для
каждого интервального ряда и подставим найденные значения в табл.4. Тогда
средняя арифметическая для всей совокупности значений определится по формуле
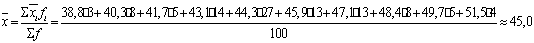
Найдем медиану Ме для полученного
интервального ряда по формуле [1]:
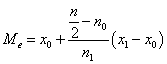
где х0 х1 - соответственно нижняя и
верхняя граница медианного интервала; n - сумма частот ряда; n0 - сумма
накопленных частот до начала медианного интервала; n1 - частота медианного
интервала:
§ найдем медианный интервал на который приходится
50% накопленных частот. Из табл.5 следует, что таким интервалом является 5-й,
находящийся в пределах св.43,6 - 45;
§ найдем медиану
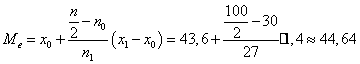 тыс.км.
тыс.км.
Найденное значение медианы показывает, что
половина (50%) всех шин (50 шт.) имеют пробег более 44,65 тыс.км. У остальные
50 шин пробег менее 44,64 тыс.км.
Найдем среднее квадратичное отклонение и
коэффициент вариации для полученного интервального ряда.
Среднее квадратичное отклонение и коэффициент
вариации относят к показателям вариации, которые, наряду со средней величиной,
характеризующей уровень варьирующего признака, также рассматривают показатели
вариации, позволяющие количественно измерить величину (размах) этой вариации.
Среднее квадратичное отклонение является
наиболее точным показателем вариации. Для его определения применяется формула
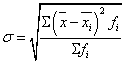
Найдем значения величин  и подставим
полученные значения в табл.4, а затем найдем
и подставим
полученные значения в табл.4, а затем найдем 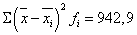 . Следовательно
. Следовательно
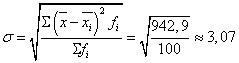
Если распределение подчиняется
нормальному закону, считается что разброс от средней величины  влево и
вправо равно
влево и
вправо равно  .
.
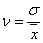 или
или 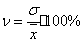 .
.
Коэффициент вариации показывает, на
сколько процентов в среднем отклоняются значения признака ряда от средней
величины. Изменчивость признака считается незначительной, если коэффициент
вариации не превышает 10%. Для заданного ряда
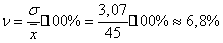
поэтому имеем незначительную
изменчивость признака.
Интервальные вариационные ряды
изображают в виде полигонов распределении или в виде гистограмм. В случае
построения полигонов диаграмма состоит из ломаной линии. По оси абсцисс
откладываются средние интервальные значения заданного распределения, а по оси
ординат - частоты этих значений. Полученные точки соединяются отрезками прямых.
Полигон распределения, построенный по данным табл.4 приведен на рис.1.
При построении гистограмм, диаграмма
состоит из прямоугольников. По оси абсцисс откладываются заданные (полученные)
интервалы заданного распределения (основания прямоугольников), а по оси ординат
откладываются средние интервальные значения распределения (высоты
прямоугольников). Гистограмма распределения, построенная по данным табл.4,
приведена на рис.2.

38,8 40,3 41,7 43,1 44,3 45,9 47,1 48,4 49,7
51,5
Рис.1. Полигон распределения

38 39,4 40,8 42,2 43,6 45 46,4 47,8
49,2 50,6 52
Рис.2. Гистограмма распределения
Чтобы определить, насколько заданный
вариационный ряд согласуется с нормальным распределением, применяем критерий
согласия Колмогорова. Он основан на сравнении кумулятивных частот в
вариационном ряду, согласно формулы
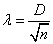 ,
,
где D - максимальное отклонение
суммы фактических частот от суммы теоретических частот; n - число уровней ряда.
Как установил Колмогоров, когда n
неограниченно возрастает, вероятность того, что D будет меньше величины 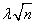 приближается
к значениям функции
приближается
к значениям функции
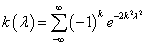 .
.
λ находят по таблицам
вероятностей 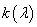 .
.
Расчет по критерию Колмогорова:
§ определяется отклонение от средней величины по
каждому интервалу 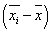 ;
;
§ рассчитывается среднее квадратичное отклонение σ. В нашем
случае σ
= 3,07;
§ определяется нормированное отклонение по формуле
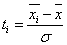
Полученные значения заносятся в
табл. 5;
§ по таблице значений функции нормального
распределения находим 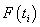 и заносим в
табл.5;
и заносим в
табл.5;
§ рассчитываем теоретические значения отклонений 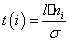 , где l -
длина интервала; ni -номер интервала.
, где l -
длина интервала; ni -номер интервала.
§ по таблице значений функции нормального
распределения находим теоретические значения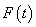 и заносим в табл.5.
и заносим в табл.5.
§ рассчитываем разницу 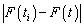 и находим
среди них максимальную, которая равна D = 0,17;
и находим
среди них максимальную, которая равна D = 0,17;
§ рассчитываем критерий Колмогорова для
определения соответствия эмпирического распределения нормальному. Для этого
зададим уровень значимости a
= 5%. Для этого уровня значимости по таблице Приложения Б [2] находим
соответствующее значение 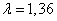 . Поскольку
количество уровней ряда равно 10, получаем
. Поскольку
количество уровней ряда равно 10, получаем 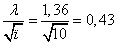 > D. Из этого следует, что с
вероятностью Р = 1 - 0,05 = 0,95, можно утверждать, что рассматриваемое
распределение следует нормальному распределению.
> D. Из этого следует, что с
вероятностью Р = 1 - 0,05 = 0,95, можно утверждать, что рассматриваемое
распределение следует нормальному распределению.
Таблица 5
№ интерв. (i) 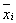
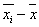
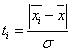
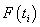
табл.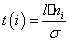 теор.
теор.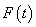
|
теор.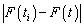
|
|
|
|
|
|
|
|
|
38,8
|
-
6,2
|
2,02
|
0,957
|
2,28
|
0,977
|
0,02
|
|
40,3
|
-
4,7
|
1,53
|
0,874
|
1,82
|
0,931
|
0,06
|
|
41,7
|
-
3,3
|
1,07
|
0,715
|
1,37
|
0,829
|
0,11
|
|
43.1
|
-
1,9
|
0,62
|
0,465
|
0,91
|
0,637
|
0,17
|
|
44,3
|
-
0,7
|
0,23
|
0,182
|
0,46
|
0,354
|
0,17
|
|
45,9
|
0,9
|
0,29
|
0,228
|
0,46
|
0,354
|
0,13
|
|
47,1
|
2,1
|
0,68
|
0,504
|
0,91
|
0,637
|
0,13
|
|
48,4
|
3,4
|
1,11
|
0,733
|
1,37
|
0,829
|
0,10
|
|
49,7
|
4,7
|
1,53
|
0,874
|
1,82
|
0,931
|
0,06
|
|
51,5
|
6,5
|
2,12
|
0,966
|
2,28
|
0,977
|
0,01
|
Выводы
1) Найденный коэффициент вариации
показывает, на сколько процентов в среднем отклоняются значения признака ряда
от средней величины. Изменчивость признака считается незначительной, если
коэффициент вариации не превышает 10%. В нашем случае он равен 6,8%, поэтому
изменчивость признака является незначительной.
2) Для определения соответствия
эмпирического распределения нормальному использовался критерий Колмогорова. Как
следует из полученного расчета, с вероятностью Р = 1 - 0,05 = 0,95, можно
утверждать, что рассматриваемое распределение следует нормальному
распределению.
Задача 2
Задано производство цемента в табл.6.
Таблица 6
|
Периоды
|
Цемент,
млн.т
|
|
45,5
|
|
50,9
|
|
57,8
|
|
61
|
|
64,9
|
|
72,4
|
|
80
|
|
84,8
|
|
87,5
|
|
89,8
|
Вычислить следующие показатели динамики;
a) абсолютные значения одного процента по
годам;
b) среднегодовые
скорость роста и темп прироста;) нанести на линейный график эмпирические
значения динамического ряда;) произвести сглаживание динамического ряда на
основе аналитического выравнивания;) нанести полученные сглаженные (теоретические)
уровни ряда динамики на график с исходными уровнями;) определить устойчивость
динамического ряда;) сделать прогноз по полученной модели на период
равный трем;) сделать выводы.
Решение
Одним из требований предъявляемых к
использованию абсолютных и относительных величин, заключается в том, что их
нужно брать вне отрыва друг от друга, поэтому вычисление одного процента
прироста имеет важное значение. Для вычисления абсолютного значения одного
процента по годам (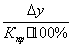 ), найдем
коэффициенты прироста по цепной схеме
), найдем
коэффициенты прироста по цепной схеме 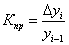 и все вычисления сведем в табл.7.
и все вычисления сведем в табл.7.
Таблица 7
|
Периоды
|
Цемент,
млн.т
|
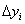 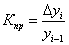 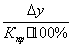
|
|
|
|
45,5
|
|
|
|
|
50,9
|
5,4
|
0,119
|
0,455
|
|
57,8
|
6,9
|
0,136
|
0,507
|
|
61
|
3,2
|
0,055
|
0,582
|
|
64,9
|
3,9
|
0,064
|
0,609
|
|
72,4
|
7,5
|
0,116
|
0,647
|
|
80
|
7,6
|
0,105
|
0,724
|
|
84,8
|
4,8
|
0,060
|
0,800
|
|
87,5
|
2,7
|
0,032
|
0,844
|
|
89,8
|
2,3
|
0,026
|
0,885
|
Среднегодовые скорость роста и темп прироста.
Средний темп роста представляет
собой средний коэффициент роста выраженный в процентах 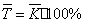 , где
, где 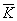 - средний
коэффициент роста (прироста), определяемый по формуле
- средний
коэффициент роста (прироста), определяемый по формуле
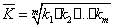
Здесь 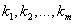 - коэффициенты роста по цепной схеме,
- число коэффициентов роста.
- коэффициенты роста по цепной схеме,
- число коэффициентов роста.
Поскольку 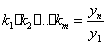 , то средний
коэффициент роста можно вычислить по формуле:
, то средний
коэффициент роста можно вычислить по формуле: 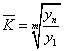 , где
, где 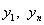 - первый и последний уровни
временного ряда.
- первый и последний уровни
временного ряда.
Следовательно
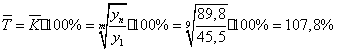 .
.
Темп прироста определяется по
формуле 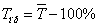 и в нашем
случае он равен 7,8%.
и в нашем
случае он равен 7,8%.
Нанесение на линейный график
эмпирических значений динамического ряда.
Первоначальные уровни динамики ряда
приведены на рис.3.
Сглаживание динамического ряда на
основе аналитического выравнивания.
Аналитическое выравнивание
динамического ряда основано на допущении, что изменения в рядах динамики могут
быть выражены определенным математическим законом.
Данный метод сводится к следующему:
1) на основе экономического анализа
выявляется характер динамического ряда;
2) исходя из характера явления, выбирается
подходящее математическое уравнение;
) определяются параметры уравнения;
) рассчитываются выровненные значения
ряда, которые наносятся на график эмпирических значений;
) определяется устойчивость динамического
ряда;
) на основе полученной модели
аппроксимации прогнозируются уровни динамического ряда на будущий период

1
2 3 4 5 6 7 8 9 10
Рис.3. Динамика производства цемента, млн.т.
первоначальные
уровни динамики ряда
выровненные
во времени динамики ряда
Аналитическое выравнивание динамического ряда
производится с помощью метода наименьших квадратов, при этом вычисляется линия
теоретических уровней, которая должна проходить в максимальной близости к
фактическим уровням ряда. Для осуществления метода аналитического выравнивания
построим вспомогательную таблицу (табл.8).
Таблица 8
|
Периоды
n
|
Цемент,
млн.т (у)
|
t
|
t2
|
tу
|
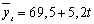
|
|
45,5
|
-4,5
|
20,25
|
-204,75
|
46,1
|
|
50,9
|
-3,5
|
12,25
|
-178,15
|
51,3
|
|
57,8
|
-2,5
|
6,25
|
-144,5
|
56,5
|
|
61
|
-1,5
|
2,25
|
-91,5
|
61,7
|
|
64,9
|
-0,5
|
0,25
|
-32,45
|
66,9
|
|
72,4
|
0,5
|
0,25
|
36,2
|
72,1
|
|
80
|
1,5
|
2,25
|
120
|
77,3
|
|
84,8
|
2,5
|
6,25
|
212
|
82,5
|
|
87,5
|
3,5
|
12,25
|
306,25
|
87,7
|
|
89,8
|
4,5
|
20,25
|
404,1
|
92,9
|
|
Итого
|
694,6
|
0
|
82,5
|
427,2
|
695
|
Исходя из характера графика
первоначальных уровней динамики принимаем аналитическое выравнивание
динамического ряда с помощью прямой, имеющей вид 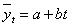 . Для нахождения параметров
. Для нахождения параметров 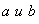 используем
систему уравнений и донные из табл.8.
используем
систему уравнений и донные из табл.8.
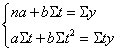 .
.
Поскольку 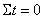 , получаем
, получаем
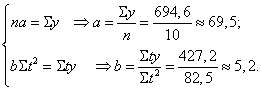
Следовательно, уравнение прямой
примет вид 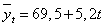 и будет в
данном случае искомым, т.к.
и будет в
данном случае искомым, т.к.  практически равны.
практически равны.
Определение устойчивости
динамического ряда.
Для определения устойчивости
динамического ряда воспользуемся коэффициентом корреляции рангов Спирмена:
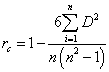 ,
,
где n - число уровней; D - разность
рангов уровней и номеров периодов времени.
Для вычисления этого коэффициента
составим вспомогательную таблицу (табл.9).
Таблица 9
|
Периоды
n
|
у
|
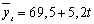 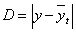 D2 D2
|
|
|
|
45,5
|
46,1
|
0,6
|
|
|
50,9
|
51,3
|
0,4
|
|
|
57,8
|
56,5
|
1,3
|
|
|
61
|
61,7
|
0,7
|
|
|
64,9
|
66,9
|
2,0
|
|
|
72,4
|
72,1
|
0,3
|
|
|
80
|
77,3
|
2,7
|
|
|
84,8
|
82,5
|
2,3
|
|
|
87,5
|
87,7
|
0,2
|
|
|
89,8
|
92,9
|
0,1
|
|
|
Итого
|
694,6
|
695
|
|
19,42
|
Используя данные табл.9 находим коэффициентом
корреляции рангов Спирмэна:
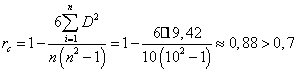 .
.
Следовательно, данный динамический
ряд устойчив, т.к. считается, что если коэффициент больше 0,7 можно говорить об
устойчивости направленного изменения уровней динамического ряда.
Прогноз по полученной модели на
период равный трем.
Для прогнозирования выпуска цемента
в будущие периоды подставляем в полученную модель 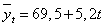 перспективные
значения t. Для t = 7,5 получим
перспективные
значения t. Для t = 7,5 получим 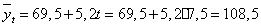 млн.т.
млн.т.
Выводы
1) Среднегодовые скорость роста и темп
прироста соответственно равны 107,8% и 7,8%.
2) Полученный с помощью аналитического
выравнивания динамический ряд является устойчивым, т.к. коэффициентом
корреляции рангов Спирмэна для выровненного ряда равен 0,88. Считается, что
если коэффициент больше 0,7 можно говорить об устойчивости направленного
изменения уровней динамического ряда.
Задача 3
Данные о продукции машиностроительного завода
представлены в табл.10. На основе приведенных данных вычислить базисные
агрегатные индексы себестоимости продукции за май и июнь (база - январь).
Таблица 10
|
Месяцы
n
|
Себестоимость
(у)
|
|
1.Январь
|
221
|
|
2.Февраль
|
235
|
|
3.Март
|
272
|
|
4.Апрель
|
285
|
|
5.Май
|
304
|
|
6.Июнь
|
320
|
|
7.Июль
|
360
|
|
8.Август
|
371
|
|
9.Сентябрь
|
395
|
|
Итого
|
2763
|
Решение. При базисном способе расчета за базу
принимается индексируемая величина одного (базисного) периода. В нашем случае
это январь. Существуют цепные и базисные индивидуальные индексы. В цепных
индексах, каждый последующий период сравнивается с предыдущим. Обозначим
себестоимость в базисном периоде Р0, а себестоимости в каком то отдельном
месяце через Рi. Тогда себестоимость мая будет Р5 и т.д.
При определения цепного индекса применяется
формула
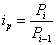 ,
,
при этом в числителе стоит
себестоимость текущего месяца, а в знаменателе - себестоимость предыдущего
месяца.
Перемножение цепных индексов дает в
итоге сравнение месяцев разделенных во времени и таким способом определяются
базисные индексы.
Базисный агрегатный индекс
себестоимости продукции за май месяц будет равен
 .
.
Базисный агрегатный индекс
себестоимости продукции за июнь месяц будет равен
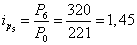 .
.
Задача 4
Себестоимость продукции
машиностроительного завода представлена в табл.11. На основе приведенных данных
вычислить цепные агрегатные индексы себестоимости продукции за февраль и март.
Таблица 11
|
Месяцы
n
|
чугун
|
цемент
|
окон.
стекло
|
авто-
мобили
|
|
1.Январь
|
46,8
|
65,3
|
45,5
|
147,2
|
138,8
|
|
2.Февраль
|
50,9
|
70,8
|
50,9
|
153,1
|
148,9
|
|
3.Март
|
55,3
|
76,3
|
57,8
|
165,6
|
169
|
Решение
Найдем цепные агрегатные индексы физического
объема продукции за февраль и март по формуле
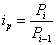 :
:
1) по выпуску чугуна: за февраль
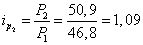 ;
;
за март
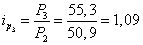 ;
;
2) по выпуску стали: за февраль
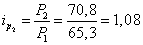 ;
;
за март
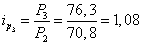 ;
;
3) по выпуску цемента: за февраль
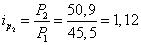 ;
;
за март
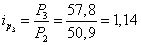 ;
;
4) по выпуску стекла: за февраль
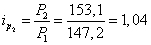 ;
;
за март
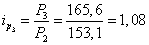 ;
;
5)
по выпуску авто: за февраль
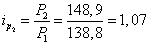 ;
;
за март
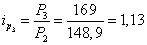 .
.
Задача 5
По данным табл.12:
1) построить групповую таблицу,
показывающую зависимость между указанными признаками;
2) дать графическое изображение
зависимости;
) найти линейное уравнение связи;
) оценить существенность параметров уравнения;
5) вычислить по найденному
уравнению связи среднюю величину 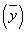 для каждой группы в групповой
таблице, сравнить вычисленные средние с эмпирическими (нанести на график).
для каждой группы в групповой
таблице, сравнить вычисленные средние с эмпирическими (нанести на график).
Таблица 12
|
№
пескомойки
|
Ширина
ковшей, мм
|
Средняя
часовая производительность, м3
|
|
300
|
5,5
|
|
3600
|
7
|
|
510
|
14
|
|
390
|
6
|
|
380
|
5,4
|
|
440
|
9
|
|
610
|
15,6
|
|
390
|
9
|
|
380
|
8
|
|
480
|
11,5
|
|
300
|
5
|
|
540
|
15
|
|
510
|
13,5
|
|
610
|
17
|
|
460
|
10,5
|
|
480
|
12
|
Решение
При изучении связи между экономическими
явлениями выделяют факторные и результативные признаки. Факторным признаком
является то, который обуславливает изменение результативного признака [1].
Экономические явления бывают двух типов:
функциональные и корреляционные.
При функциональных связях каждому значению
факторного признака соответствует вполне определенное значение результативного
признака. Например, объем выпуска продукции функционально связан с двумя
факторами сомножителями: средней выработки продукции на одного рабочего и
средней списочной численности рабочих. При функциональных связях. применяется
индексный метод анализа.
При корреляционных связях, отдельным значениям
факторного признака может соответствовать может соответствовать несколько
значений результативного признака. Корреляционная связь проявляется при большом
количестве наблюдений в виде определенной зависимости между средними значениями
результативного и факторного признаков. Например, в корреляционной зависимости
находится объем выпуска продукции от следующих факторов: уровня
механовооруженности, коэффициента сменности, квалификации рабочих и др. При
корреляционных связях применяется корреляционный метод анализа. Число
наблюдений для построения однофакторной регрессионной модели должно быть более
10 -12.
Произведем корреляционный анализ для приведенных
в табл.12 данных.
1) Построим вспомогательную групповую
таблицу в ранжированном порядке по возрастанию ширины ковшей, показывающую
зависимость между указанными признаками (табл.13).
Таблица 13
|
№
|
Ширина
ковшей, (х)
|
Сред.
часовая производ. (у)
|
ху
|
х2
|
у2
|
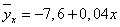
|
|
300
|
5,5
|
1650
|
90000
|
30,25
|
4,4
|
|
300
|
5
|
1500
|
90000
|
25
|
4,4
|
|
360
|
7
|
2520
|
129600
|
49
|
6,8
|
|
380
|
5,4
|
2052
|
144400
|
29,16
|
7,6
|
|
380
|
8
|
3040
|
144400
|
64
|
7,6
|
|
390
|
6
|
2340
|
152100
|
36
|
8
|
|
390
|
9
|
3510
|
152100
|
81
|
8
|
|
440
|
9
|
3960
|
193600
|
81
|
10
|
|
460
|
10,5
|
4830
|
211600
|
110,25
|
10,8
|
|
480
|
11,5
|
5520
|
230400
|
132,25
|
11,6
|
|
480
|
12
|
5760
|
230400
|
144
|
11,6
|
|
510
|
14
|
7140
|
260100
|
196
|
12,8
|
|
510
|
13,5
|
6885
|
260100
|
182,25
|
12,8
|
|
540
|
15
|
8100
|
291600
|
225
|
14
|
|
610
|
15,6
|
9516
|
372100
|
243,36
|
16,8
|
|
610
|
17
|
10370
|
372100
|
289
|
16,8
|
|
Итого
|
7140
|
164
|
78693
|
3324600
|
1917,52
|
164
|
2) Построим графическое изображение
зависимости между заданными признаками (рис.4)

200 300
400 500 600
Рис.4.
эмпирическая
линия регрессии
теоретическая
линия регрессии
3) Найдем линейное уравнение связи
Исходя из построенного графика (рис.4), зависимость
между заданными признаками прямолинейная.
Для аналитического выражения прямолинейной
регрессии используется уравнение прямой линии:
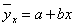 ,
,
где 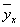 - выровненное значение
результативного признака;
- выровненное значение
результативного признака;
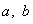 - параметры.
- параметры.
Параметры уравнения определяются по
методу наименьших квадратов путем решения следующей системы уравнений:
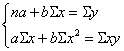 .
.
Для решения системы, промежуточные
расчеты сводятся в табл.13.
Используя итоговые значения из
табл.13 получим:
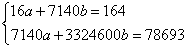 .
.
Решая систему получим: 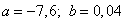 .
.
Следовательно, найденное уравнение
связи имеет вид 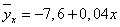 . Подставим
соответствующие значения х в уравнение, найдем новые значения
. Подставим
соответствующие значения х в уравнение, найдем новые значения 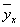 и подставим
в табл.13.
и подставим
в табл.13.
4) Оценка существенности параметров
уравнения.
Для установления тесноты связи между факторным и
результативным признаками в случае линейной зависимости, применяется линейный
коэффициент корреляции.
Рассчитаем величину линейного коэффициента
корреляции:
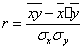 .
.
Здесь:
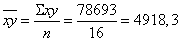 ;
;
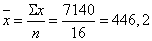 ;
;
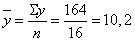 ;
;
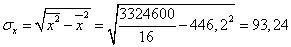 ;
;
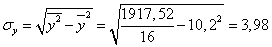 .
.
Тогда получим
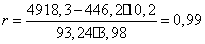 .
.
Следовательно, связь между шириной
ковшей пескомоек, их средней производительностью достаточно велика, т.к.
линейный коэффициент корреляции близок к единице.
) Вычислить по найденному
уравнению связи среднюю величину 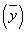 для каждой группы в групповой
таблице, сравнить вычисленные средние с эмпирическими (нанести на график).
для каждой группы в групповой
таблице, сравнить вычисленные средние с эмпирическими (нанести на график).
По найденным значениям 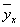 (табл.13)
построим теоретическую линию регрессии, которая, как видно из графика (рис.4),
с некоторыми отклонениями, воспроизводит эмпирическую линию регрессии.
(табл.13)
построим теоретическую линию регрессии, которая, как видно из графика (рис.4),
с некоторыми отклонениями, воспроизводит эмпирическую линию регрессии.
Так как 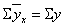 , то можно
считать, что построенное парное уравнение корреляции является искомым. Из
графика следует: с увеличением ширины ковшей пескомоек, их средняя
производительность также растет. Рост производительности составляет 0,4 м3 на
каждые 10 мм увеличения ширины ковшей.
, то можно
считать, что построенное парное уравнение корреляции является искомым. Из
графика следует: с увеличением ширины ковшей пескомоек, их средняя
производительность также растет. Рост производительности составляет 0,4 м3 на
каждые 10 мм увеличения ширины ковшей.
Задача 6
В результате десяти процентного
выборочного обследования возраста деревянных строений в районе А получены
следующие данные (табл.14.):
Таблица 14
|
Возраст
строений
|
Число
выборочно обследован. строений в районе А
|
|
20
|
15
|
|
25
|
37
|
|
30
|
31
|
|
35
|
44
|
|
40
|
23
|
|
Итого
|
150
|
Вычислить средний возраст строений по данным
выборки и определить величину возможной максимальной ошибки этой средней с
вероятностью, равной 0,954; обследование проводилось на основе бесповторной
случайной выборки.
Решение. Наиболее распространенным методом
статистического исследования является выборочный метод, при котором применяется
не сплошное наблюдение.
Под выборочным понимается метод статистического
исследования, при котором обобщающие показатели совокупности устанавливаются по
некоторой ее части на основе отбора. При этом обследованию подвергается
небольшая часть совокупности (5-10%) [2].
Всю массу единиц изучаемого объекта называют
генеральной совокупностью. Совокупность единиц, отобранных для выборочного
наблюдения, называют выборочной совокупностью.
Обозначим:- число единиц, входящих в генеральную
совокупность;- число единиц, входящих в выборочную совокупность;
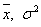 - соответственно средняя величина и
дисперсия в выборочной совокупности;
- соответственно средняя величина и
дисперсия в выборочной совокупности;
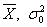 - соответственно средняя величина и
дисперсия в генеральной совокупности;
- соответственно средняя величина и
дисперсия в генеральной совокупности;
р - доля признака в генеральной
совокупности генеральная доля);- доля единиц, не обладающих определенным
признаком (р + q = 1);- отношение числа единиц, обладающих определенным
признаком в выборочной совокупности к общей численности выборочной совокупности
(выборочная доля).
Определим по исходным данным
выборочной совокупности средний возраст строений по формуле:
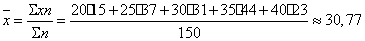 .
.
Найдем дисперсию по формуле
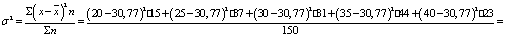
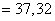 .
.
Определим среднюю ошибку выборки по
формуле
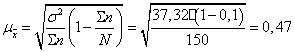 .
.
Поскольку признак варьирует, следует
определить предельную ошибку выборки. Она определяется по формуле 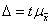 ,
,
где t - коэффициент доверия, который
берется по таблице (приложение Б [2]). Из таблицы для вероятности Р= 0,954 t =
0,51. Следовательно 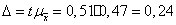 .
.
Следовательно, с вероятностью 0,954
можно утверждать, что средний возраст строений 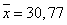 находится в пределах:
находится в пределах: 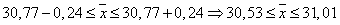 .
.
Литература
вариационный ряд агрегатный индекс
1. Горемыкина Т.К. Статистика.
Часть 1. Общая теория статистики: Учебное пособие. - М.: ГИНФО, 2002.
2. Контрольные задания и
методические указания по статистике для студентов заочной формы обучения
специальностей 060800, 061100, 311000 / Сост.: Л.И. Бернасовская и др., НовГУ
им. Ярослава Мудрого. - Новгород, 1999.
. Теория вероятностей и
математическая статистика: Учебное пособие для студентов дистанционной формы
обучения. А.И. Мартыненко, О.Е. Шишанин. - М.: ГИНФО, 2002.