Условно-стандартная задача линейного программирования
Условно-стандартная задача линейного программирования
двойственный линейный
программирование гомори
Необходимо выполнить в указанном
порядке следующие задания.
. Найти оптимальный план прямой
задачи:
а) графическим методом;
б) симплекс-методом (для построения
исходного опорного плана рекомендуется использовать метод искусственного
базиса).
. Построить двойственную задачу.
. Найти оптимальный план
двойственной задачи из графического решения прямой, используя условия
дополняющей нежесткости.
. Найти оптимальный план
двойственной задачи по первой теореме двойственности, используя окончательную
симплекс-таблицу, полученную при решении прямой задачи (см. п. 1б). Проверить
утверждение «значения целевых функций пары двойственных задач на своих оптимальных
решениях совпадают».
. Двойственную задачу решить
симплекс-методом, затем, используя окончательную симплекс-таблицу двойственной
задачи найти оптимальный план прямой задачи по первой теореме двойственности.
Сравнить результат с результатом, который был получен графическим методом (см.
п. 1а).
. Найти оптимальное целочисленное
решение:
а) графическим методом;
б) Методом Гомори.
Сравнить значения функций
целочисленного и нецелочисленного решений.
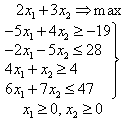
1. а) Найдем оптимальный
план прямой задачи графическим методом
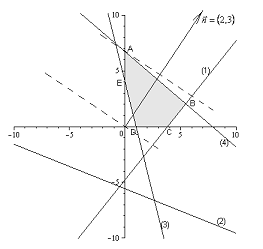
Решение: Изобразим на
плоскости систему координат Ох1х2 и
построим граничные прямые области допустимых решений (номера прямых
соответствуют их порядковому номеру в системе):

Область допустимых
решений определяется множеством АВСDЕ.
Для линий уровня 2х1
+ 3х2 = h
(h - const) строим
нормальный вектор 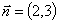 .
Перпендикулярно нормальному вектору построим одну из линий уровня (на рисунке
она проходит через начало координат) Так как задача на максимум, то перемещаем
линию уровня в направлении вектора
.
Перпендикулярно нормальному вектору построим одну из линий уровня (на рисунке
она проходит через начало координат) Так как задача на максимум, то перемещаем
линию уровня в направлении вектора  до опорной прямой. В
данном случае опорной прямой является прямая, проходящая через точку
пересечения граничных прямых L6
и L4, т.е. через точку
до опорной прямой. В
данном случае опорной прямой является прямая, проходящая через точку
пересечения граничных прямых L6
и L4, т.е. через точку 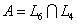 . Для определения
координат точки А решаем систему уравнений:
. Для определения
координат точки А решаем систему уравнений:
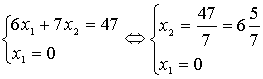
Это и будет оптимальным
решением данной задачи, которому соответствует максимальное значение целевой
функции Zmax:
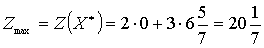 .
.
. б) Найдем оптимальный
план прямой задачи симплекс-методом.
Приводим задачу к
каноническому виду. Умножим первое ограничение на -1:
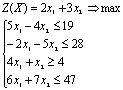
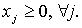
Для этого в левую часть
ограничений-неравенств типа «£» вводим по дополнительной
переменной с коэффициентом (+1). В целевую функцию эти переменные входят с
коэффициентом (0). Получаем

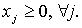
В 3-м ограничении
отсутствует базисная переменная. Формулируем задачу искусственного базиса.
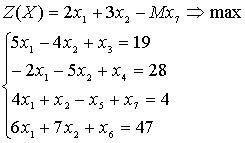
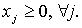
Полученную задачу будем
решать модифицированным симплексным методом [1].
Сформулируем
вспомогательную задачу, которая позволит исключить искусственные переменные из
базиса и построить начальное опорное решение исходной канонической задачи.

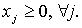
Находим начальное
опорное решение. Для этого свободные переменные приравниваем к нулю х1
= х2 = 0. Получаем опорное решение Х1 =
(0,0,19,28,0,47,19) с единичным базисом
Б1 = (А3,
А4, А7, А6).
Вычисляем оценки
разложений векторов условий по базису опорного решения,
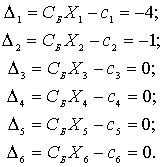
Оценки векторов,
входящих в базис, всегда равны нулю. Опорное решение, коэффициенты разложений и
оценки разложений векторов условий по базису опорного решения записываем в
симплексную таблицу
|
Сб
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
|
|
|
|
xb
|
b
|
x1
|
¯x2
|
x3
|
x4
|
x5
|
x6
|
х7
|
b/x1
|
b/x2
|
|
|
0
|
x3
|
19
|
5
|
-4
|
1
|
0
|
0
|
0
|
0
|
3 4/5
|
-
|
|
|
0
|
x4
|
28
|
-2
|
-5
|
0
|
1
|
0
|
0
|
0
|
-
|
-
|
|
|
-1
|
¬x7
|
4
|
4
|
1
|
0
|
0
|
-1
|
0
|
1
|
1
|
4
|
Min
|
|
0
|
x6
|
47
|
6
|
7
|
0
|
0
|
0
|
1
|
0
|
7 5/6
|
6 5/7
|
|
|
Dk
|
-4
|
-4
|
-1
|
0
|
0
|
1
|
0
|
0
|
4
|
4
|
|
Начальное опорное решение не является
оптимальным, так как оценки D1 = -4, D2 = -1 для векторов А1 и А2 противоречат признаку
оптимальности. Для оптимальности опорного решения в задаче на максимум
требуется неотрицательность оценок для всех векторов условий.
Определим, введение,
какого из двух векторов приведёт к большему приращению целевой функции.
Приращения целевой функции найдём по формуле 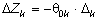 . Вычислим значения
параметра q01
для первого и третьего столбцов по правилу Креко, получим q01
= 1 при l = 2 и q02 =4 при l
=2. Находим приращение целевой функции при введении в базис первого вектора
. Вычислим значения
параметра q01
для первого и третьего столбцов по правилу Креко, получим q01
= 1 при l = 2 и q02 =4 при l
=2. Находим приращение целевой функции при введении в базис первого вектора  и
второго вектора
и
второго вектора  .
Следовательно, для наиболее быстрого нахождении оптимального решения необходимо
ввести в базис опорного решения вектор А2 вместо вектора базиса А7.
.
Следовательно, для наиболее быстрого нахождении оптимального решения необходимо
ввести в базис опорного решения вектор А2 вместо вектора базиса А7.
Далее выполним
преобразование Жордана-Гаусса с элементом х22 = 1, получим
второе опорное решение Х2:
|
Сб
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
|
xb
|
b
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
х7
|
|
0
|
x3
|
35
|
21
|
0
|
1
|
0
|
-4
|
0
|
4
|
|
0
|
x4
|
48
|
18
|
0
|
0
|
1
|
-5
|
0
|
5
|
|
0
|
x2
|
4
|
4
|
1
|
0
|
0
|
-1
|
0
|
1
|
|
0
|
x6
|
19
|
-22
|
0
|
0
|
0
|
7
|
1
|
-7
|
|
Dk
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
Так как оценки неотрицательны,
построенный план оптимален.
Искусственные переменные выведены из
базиса.
Оптимальное решение вспомогательной
задачи - это х7=х8=0, max G=0.
Попутно построен опорный план
исходной канонической задачи:
Вернемся к ней. Используем последнюю
симплекс-таблицу, из которой исключим переменную х7 и изменим цены базисных
переменных, взяв их из заданной целевой функции. Получим
|
Сб
|
|
|
2
|
3
|
0
|
0
|
0
|
0
|
|
|
|
xb
|
b
|
x1
|
x2
|
x3
|
x4
|
¯x5
|
x6
|
b/x5
|
|
|
0
|
x3
|
35
|
21
|
0
|
1
|
0
|
-4
|
0
|
-
|
|
|
0
|
x4
|
48
|
18
|
0
|
0
|
1
|
-5
|
0
|
-
|
|
|
3
|
x2
|
4
|
4
|
1
|
0
|
0
|
-1
|
0
|
-
|
|
|
0
|
¬x6
|
19
|
-22
|
0
|
0
|
0
|
7
|
1
|
2 5/7
|
Min
|
|
Dk
|
12
|
10
|
0
|
0
|
0
|
-3
|
0
|
|
|
План необходимо улучшить. Вводим в
базис х5, выводим х6
|
Сб
|
|
|
2
|
3
|
0
|
0
|
0
|
0
|
|
xb
|
b
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
|
0
|
x3
|
45 6/7
|
8 3/7
|
0
|
1
|
0
|
0
|
4/7
|
|
0
|
x4
|
61 4/7
|
2 2/7
|
0
|
0
|
1
|
0
|
5/7
|
|
3
|
x2
|
6 5/7
|
6/7
|
1
|
0
|
0
|
0
|
1/7
|
|
0
|
x5
|
2 5/7
|
-3 1/7
|
0
|
0
|
0
|
1
|
1/7
|
|
Dk
|
20 1/7
|
4/7
|
0
|
0
|
0
|
0
|
3/7
|
Проверим план на оптимальность.
Оценки неотрицательны, план оптимален.
Ответ: max Z(X) = 20 1/7 при Х*=
(0; 6 5/7; 45 6/7; 61 4/7; 2 5/7; 0).
2. Построим двойственную задачу к
исходной. Так как исходная задача на максимизацию, то приведём все неравенства
системы ограничений к виду «£», для
чего обе части 1-го и 3-го неравенств умножим на (-1). Получим
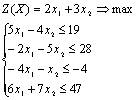
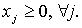
Составим расширенную
матрицу системы
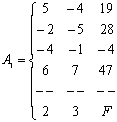 .
.
Найдём матрицу 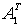 ,
транспонированную к А
,
транспонированную к А
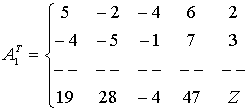 .
.
Сформулируем
двойственную задачу:
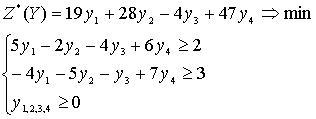
. Найдем оптимальный
план двойственной задачи из графического решения прямой, используя условия
дополняющей нежесткости.
Чтобы допустимые решения
х, у пары двойственных задач были оптимальны, необходимо и достаточно, чтобы
выполнялись соотношения, т.е. условия дополняющей нежесткости:
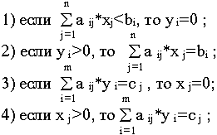
Так как прямая задача
разрешима, то двойственная тоже имеет решение, и, в силу первой теоремы
двойственности,  .
Найдем значения переменных.
.
Найдем значения переменных.
Подставим найденное
оптимальное решение Х*= (0; 6 5/7) в систему ограничений исходной
задачи:
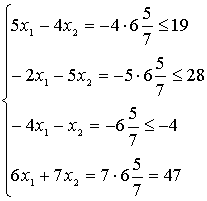
В силу условия 1
дополняющей нежесткости получаем: 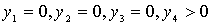 .
.
Получаем систему
уравнений для нахождения оставшихся неизвестных:
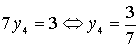
Ответ: оптимальное
решение двойственной задачи
. Найдем оптимальный
план двойственной задачи по первой теореме двойственности, используя
окончательную симплекс-таблицу, полученную при решении прямой задачи. Решению
двойственной задачи соответствуют оценки переменных х3 - х6.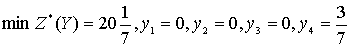 .
.
Проверим утверждение
«значения целевых функций пары двойственных задач на своих оптимальных решениях
совпадают», то есть 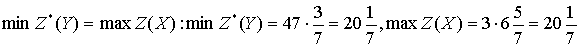 то
есть равенство
то
есть равенство 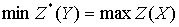 выполняется.
выполняется.
. Двойственную задачу
решим симплекс-методом.
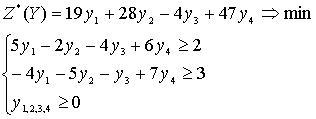
Запишем задачу в
каноническом виде.
Перейдем к канонической
задаче. Из левой части второго неравенства вычтем дополнительную переменную, к
левой части первого неравенства прибавим, перейдем к задаче на максимум.
Получим
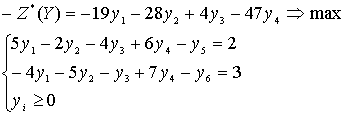
Сформулируем задачу
искусственного базиса
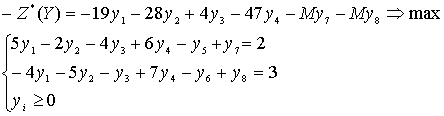
Сформулируем
вспомогательную задачу искусственного базиса. Ее решение даст нам опорный план
исходной канонической задачи (см. [1])

Решаем вспомогательную
задачу симплекс-методом:
|
Сб
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
-1
|
|
|
|
|
xb
|
b
|
y1
|
y2
|
y3
|
¯y4
|
y5
|
y6
|
y7
|
y8
|
b/y1
|
b/y4
|
|
|
-1
|
¬y7
|
2
|
5
|
-2
|
-4
|
6
|
-1
|
0
|
1
|
0
|
2/5
|
1/3
|
Min
|
|
-1
|
y8
|
3
|
-4
|
-5
|
-1
|
7
|
0
|
-1
|
0
|
1
|
-
|
3/7
|
|
|
Dk
|
-5
|
-1
|
7
|
5
|
-13
|
1
|
1
|
0
|
0
|
2/5
|
4 1/3
|
|
|
Сб
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
-1
|
|
|
|
xb
|
b
|
y1
|
y2
|
y3
|
y4
|
¯y5
|
y6
|
y7
|
y8
|
b/y3
|
b/y5
|
|
0
|
y4
|
1/3
|
5/6
|
- 1/3
|
- 2/3
|
1
|
- 1/6
|
0
|
1/6
|
0
|
-
|
-
|
|
-1
|
¬y8
|
2/3
|
-9 5/6
|
-2 2/3
|
3 2/3
|
0
|
1 1/6
|
-1
|
-1 1/6
|
1
|
2/11
|
4/7
|
|
Dk
|
- 2/3
|
9 5/6
|
2 2/3
|
-3 2/3
|
0
|
-1 1/6
|
1
|
2 1/6
|
0
|
2/3
|
2/3
|
|
Сб
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
-1
|
|
xb
|
b
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
y8
|
|
0
|
y4
|
3/7
|
- 4/7
|
- 5/7
|
- 1/7
|
1
|
0
|
- 1/7
|
0
|
1/7
|
|
0
|
y5
|
4/7
|
-8 3/7
|
-2 2/7
|
3 1/7
|
0
|
1
|
- 6/7
|
-1
|
6/7
|
|
Dk
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
Оценки неотрицательны,
следовательно, решение задачи искусственного базиса, т.е. 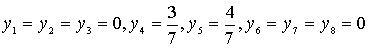 ,
max (-G(y))=0. Параллельно построен начальный опорный план исходной
канонической задачи:
,
max (-G(y))=0. Параллельно построен начальный опорный план исходной
канонической задачи: 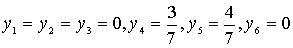 .
.
Исключим из рассмотрения
искусственные переменные, перепишем последнюю таблицу, заменив в ней нулевые
цены на цены переменных из исходной задачи.
Пересчитаем оценки.
|
Сб
|
|
|
-19
|
-28
|
4
|
-47
|
0
|
0
|
|
xb
|
b
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
|
-47
|
y4
|
3/7
|
- 4/7
|
- 5/7
|
- 1/7
|
1
|
0
|
- 1/7
|
|
0
|
y5
|
4/7
|
-8 3/7
|
-2 2/7
|
3 1/7
|
0
|
1
|
- 6/7
|
|
Dk
|
-20 1/7
|
45 6/7
|
61 4/7
|
2 5/7
|
0
|
0
|
6 5/7
|
Так как оценки неотрицательны,
построенный план не требует дальнейшего улучшения.
Решение двойственной задачи:
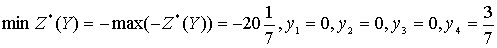 .
.
Используя окончательную
симплекс-таблицу двойственной задачи, найдем оптимальный план прямой задачи по
первой теореме двойственности.
Решение исходной задачи
(т.е. двойственной к двойственной) будет равно оценкам дополнительных
переменных  и
и
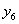 ,
а максимум функции исходной задачи будет равен минимуму функции двойственной
задачи:
,
а максимум функции исходной задачи будет равен минимуму функции двойственной
задачи:
 .
.
Сравним результат с
результатом, который был получен графическим методом (см. п. 1а).
Очевидно, что результаты
совпадают.
. а) Найдем оптимальное
целочисленное решение графическим методом.
Для этого используем
рисунок п. 1. а), дополнив его построением прямых линий х=с и у=с. Проведем
линии уровня (пунктир) через точки пересечения этих прямых линий, расположенные
в области допустимых решений и отстоящие как можно дальше в направлении
градиента целевой функции.
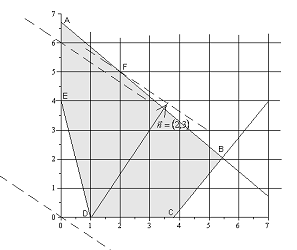
Точка максимума с
целочисленными координатами - это, очевидно, F
(2; 5). Максимальное значение функции в этом случае равно Z=2*2+3*5= 19.
. б) Найдем оптимальное
целочисленное решение методом Гомори.
Для этого используем
последнюю таблицу п. 1 б)
|
Сб
|
|
|
-19
|
-28
|
4
|
-47
|
0
|
0
|
|
xb
|
b
|
y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
|
-47
|
y4
|
3/7
|
- 4/7
|
- 5/7
|
- 1/7
|
1
|
0
|
- 1/7
|
|
0
|
y5
|
4/7
|
-8 3/7
|
-2 2/7
|
3 1/7
|
0
|
1
|
- 6/7
|
|
Dk
|
-20 1/7
|
45 6/7
|
61 4/7
|
2 5/7
|
0
|
0
|
6 5/7
|
Построим отсечение дробной части
решения. Для этого построим дополнительное ограничение и запишем его
коэффициенты в последнюю (перед Dk) строку.
Построим отсечение дробной части по
переменной х4.
В новую строку запишем дробную часть
соответствующего элемента строки х4, взятую с противоположным
знаком.
|
Сб
|
|
0
|
2
|
3
|
0
|
0
|
0
|
0
|
0
|
|
|
|
xb
|
b
|
x1
|
x2
|
x3
|
x4
|
x5
|
¯x6
|
х7
|
b/x1
|
b/x6
|
|
0
|
x3
|
45 6/7
|
8 3/7
|
0
|
1
|
0
|
0
|
4/7
|
0
|
5 26/59
|
80 1/4
|
|
0
|
x4
|
61 4/7
|
2 2/7
|
0
|
0
|
1
|
0
|
5/7
|
0
|
26 15/16
|
86 1/5
|
|
3
|
x2
|
6 5/7
|
6/7
|
1
|
0
|
0
|
0
|
1/7
|
0
|
7 5/6
|
47
|
|
0
|
x5
|
2 5/7
|
-3 1/7
|
0
|
0
|
0
|
1
|
1/7
|
0
|
19
|
|
0
|
¬x7
|
- 4/7
|
- 2/7
|
0
|
0
|
0
|
0
|
- 5/7
|
1
|
2
|
4/5
|
|
|
20 1/7
|
4/7
|
0
|
0
|
0
|
0
|
3/7
|
0
|
|
|
Оценки переменных остались
неизменными. Но в столбце свободных членов появился отрицательный элемент.
Следовательно, выводим из базиса х7. Наименьшее отношение
дает 4/5, поэтому вводим в базис х6.
|
Сб
|
|
0
|
2
|
3
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
xb
|
b
|
¯x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
х7
|
х8
|
b/x1
|
b/x7
|
|
|
0
|
x3
|
45 2/5
|
8 1/5
|
0
|
1
|
0
|
0
|
0
|
4/5
|
0
|
5 22/41
|
56 3/4
|
|
|
0
|
x4
|
61
|
2
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
30 1/2
|
61
|
|
|
3
|
x2
|
6 3/5
|
4/5
|
1
|
0
|
0
|
0
|
0
|
1/5
|
0
|
8 1/4
|
33
|
|
|
0
|
x5
|
2 3/5
|
-3 1/5
|
0
|
0
|
0
|
1
|
0
|
1/5
|
0
|
- 13/16
|
13
|
|
|
0
|
x6
|
4/5
|
2/5
|
0
|
0
|
0
|
0
|
1
|
-1 2/5
|
0
|
2
|
- 4/7
|
|
|
0
|
¬x8
|
- 3/5
|
- 4/5
|
0
|
0
|
0
|
0
|
0
|
- 1/5
|
1
|
3/4
|
3
|
min
|
|
Dk
|
19 4/5
|
2/5
|
0
|
0
|
0
|
0
|
0
|
3/5
|
0
|
|
|
|
Получено оптимальное, но
нецелочисленное решение. Выполним отсечение дробной части по переменной х2.
Дробные части чисел строки х2 запишем в строку х8
с отрицательными знаками. Введем в базис х1, выведем х8.
Получим следующую таблицу:
|
Сб
|
|
0
|
2
|
3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
xb
|
b
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
х7
|
¯х8
|
х9
|
b/x7
|
b/x8
|
|
0
|
x3
|
39 1/4
|
0
|
0
|
1
|
0
|
0
|
0
|
-1 1/4
|
10 1/4
|
0
|
-
|
3 34/41
|
|
0
|
x4
|
59 1/2
|
0
|
0
|
0
|
1
|
0
|
0
|
1/2
|
2 1/2
|
0
|
119
|
23 4/5
|
|
3
|
x2
|
6
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
-
|
6
|
|
0
|
x5
|
5
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
-4
|
0
|
5
|
-
|
|
0
|
x6
|
1/2
|
0
|
0
|
0
|
0
|
0
|
1
|
-1 1/2
|
1/2
|
0
|
-
|
1
|
|
2
|
х1
|
3/4
|
1
|
0
|
0
|
0
|
0
|
0
|
1/4
|
-1 1/4
|
0
|
3
|
-
|
|
0
|
¬х9
|
- 1/2
|
-0
|
0
|
0
|
0
|
0
|
0
|
- 1/2
|
- 1/2
|
1
|
1
|
1
|
|
Dk
|
19 1/2
|
0
|
0
|
0
|
0
|
0
|
0
|
1/2
|
1/2
|
0
|
|
|
|
|
0
|
x1
|
x2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
xb
|
b
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
х7
|
х8
|
х9
|
|
0
|
x3
|
29
|
-0
|
0
|
1
|
0
|
0
|
0
|
-11 1/2
|
0
|
20 1/2
|
|
0
|
x4
|
57
|
-0
|
0
|
0
|
1
|
0
|
0
|
-2
|
0
|
5
|
|
3
|
x2
|
5
|
-0
|
1
|
0
|
0
|
0
|
0
|
-1
|
0
|
2
|
|
0
|
x5
|
9
|
0
|
0
|
0
|
0
|
1
|
0
|
5
|
0
|
-8
|
|
0
|
x6
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
-2
|
0
|
1
|
|
2
|
х1
|
1
|
0
|
0
|
0
|
0
|
0
|
1 1/2
|
0
|
-2 1/2
|
|
0
|
х9
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
-2
|
|
|
19
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
Так как оценки Dk неотрицательны, а числа
в столбце «b» целые, получено оптимальное целочисленное решение задачи: х1=2,
х2=5, max Z= 19.
Сравним значения функций
целочисленного и нецелочисленного решений: значение функции, полученное без
условия целочисленности, больше: 20 1/7 > 19.