Рівняння Пфаффа

КУРСОВА РОБОТА

на тему: «Рівняння Пфаффа»

ЗМІСТ

Вступ

. Рівняння Пфаффа

. Цілком інтегровані рівняння Пфаффа

. Інтегральні криві рівняння Пфаффа

. Цілком інтегровані рівняння Пфаффа в R3

Висновки

Додаток

Список літератури

Вступ

Сучасна теорія диференціальних рівнянь посідає чільне місце серед інших математичних дисциплін. Гармонійне поєднання суто математичного й прикладного аспектів робить її однаково привабливою як для теоретиків, так і для тих, хто займається застосуванням математики в різноманітних галузях знань. Механіка, фізика, радіоелектроніка, машинобудування, хімія, біологія, економіка - це далеко не повний перелік наук, в яких широко використовуються диференціальні рівняння.

Мета даної роботи - ознайомити з основними, базовими поняттями, фактами, методами та найпростішими застосуваннями теми, підготувати до самостійної роботи та виконання завдань щодо розв’язання рівнянь Пфаффа.

Центральним об'єктом вивчення є звісно поняття рівняння Пфаффа (як диференціальне рівняння з кількома незалежними змінними) - аналітичний запис задачі про відшукання інтегральних поверхонь максимально можливої вимірності, яке пов’язує між собою значення шуканої функції, її похідних та аргументу. Однак в курсовій роботі диференціальне рівняння Пфаффа розглядається не лише як аналітичний об 'єкт. Значна увага приділяється геометричним поняттям і образам, які дають змогу глибше зрозуміти природу цього об'єкта, пояснити відповідні теоретичні побудови.

рівняння пфафф інтегральний

1. Рівняння Пфаффа

Нехай в області D с R³ задано диференціальну форму

ω := а(х)dх := а₁(x) dx₁ + ... + а_n(x) dx_n

з неперервно диференційовними коефіцієнтами а_і : D → R , i =1, …, n. Усюди надалі ми розглядатимемо лише невироджений випадок, для якого виконується умова || а(х) || ≠ 0 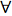 х є D.

Рівняння вигляду

ω = 0 (1)

називається рівнянням Пфаффа.

При n = 2 це рівняння знайоме нам. Тепер ми зробимо це в загальному випадку. Ставлячи кожній точці х₀  D у відповідність гіперплощину

Р(х₀) : а₁(х₀)(х₁ - х₀₁) + ... + а_n(х₀) (х_n - х_0n) = 0, (2)

ортогональну до вектора а_n(х₀), рівняння (1) задає в області D поле гіперплощин Р. Природно сформулювати задачу про відшукання k-вимірної (k ≤ n - 1) інтегральної поверхні поля Р, тобто такої поверхні, яка в кожній своїй точці х₀ дотикається відповідної гіперплощини Р(х₀). Про таку поверхню можна також сказати, що вона ортогональна до векторного поля а(х). Для k -вимірної поверхні, заданої параметричними рівняннями

х = х(s), х(s)  С¹ (D → D),

де D - область у R^k, умова інтегральності виражається тотожністю a(x(s))dx(s) ≡ 0.

Основою для рівняння Пфаффа є задача відшукання інтегральних поверхонь максимально можливої вимірності k = n - 1.

Виникає завдання про знаходження сімейства поверхонь U (x, y, z) = c, ортогональних до векторних ліній. Рівняння таких поверхонь має вигляд (F• t) = 0. Де t - віктор, що лежить в дотичній площині до шуканих поверхонь:

t = i dx + j dy + k dz,

бо в розгорнутому вигляді

Р (х, у, z) dx + Q (x, у, z) dy + R (x, у, z) dz = 0. (3)

Рівняння вигляду (3) називаються рівняннями Пфаффа.

Якщо поле F = Pi+Qj+Rk потенційне:

F = grad U, тобто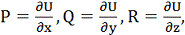

то шуканими поверхнями є поверхні рівня U (x, y, z) = c з потенційною функції U. В цьому випадку знаходження шуканих поверхонь не становить труднощів, оскільки

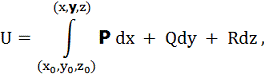
де криволінійний інтеграл береться на будь-якому шляху між обраною фіксованою точкою (x₀, y₀, z₀) і точкою зі змінними координатами (х, у, z), наприклад, по ламаній, що складається з прямолінійних відрізків, паралельних осям координат.

Якщо ж поле F не потенційне, то в деяких випадках можна підібрати скалярний множник µ(х, у, z), після множення на який вектора F поле стає потенційним.

Якщо такий множник існує, то µ F = grad U або

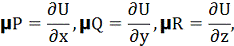
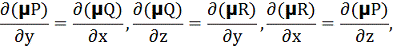
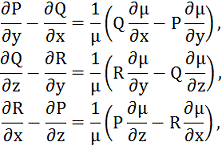
Примножуючи перше з цих тотожностей на R, друге на P, третє на Q і складаючи почленно всі три тотожності, отримаємо необхідну умову існування інтегруючого множника µ:

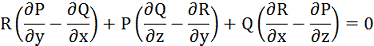
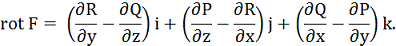
Якщо ця умова, яка називається умовою повної інтегровності рівняння (3), не виконується, то не існує сімейства поверхностей U (x, y, z) = c, ортогональних векторним лініям поля F (x, у, z).

Дійсно, якщо б таке сімейство U (x, y, z) = c існувало, то ліва частина рівняння (3) могла б відрізнятися від

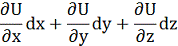
лише деяким множником µ(x, у, z), який і був би інтегровним множником рівняння (3).

Отже, для існування сімейства поверхонь U (x, y, z) = c, ортогональних векторним лініям векторного поля F, необхідно, щоб вектори F і rot F були б ортогональні, тобто (F• rot F) = 0.

ЗАУВАЖЕННЯ

Умова (F• rot F) = 0 називається також умовою інтегровності рівняння Пфаффа Р dx + Q dy + R dz = 0 одним співвідношенням U (x, y, z) = c.

Іноді потрібно визначити не поверхні, ортогональні векторним лініям поля F, а лінії, що володіють тією ж властивістю, іншими словами, треба проінтегрувати рівняння Пфаффа не одним, а двома співвідношеннями:

U₁ (x, y, z) = 0 та U₂ (x, y, z) = 0. (4)

Для знаходження таких ліній можна одне з рівнянь (4) задати довільно, наприклад

U₁ (x, y, z) = 0, (5)

і, виключивши з рівняння (3) за допомогою рівняння (5) одну з змінних, наприклад z, отримаємо диференціальне рівнянняння виду

М (х, y) dx + N (x, y) dy = 0,

інтегруючи яке, знайдемо шукані лінії на довільно обраній поверхні U₁ (x, y, z) = 0.

Покажемо, що умова (F • rot F) = 0 є не тільки необхідним, але і достатнім для існування сімейства поверхностей, ортогональних векторним лініям.

Зауважимо, що на шуканих поверхнях U (x, y, z) = c повинно обертатися в тотожність рівняння

Р dx + Q dy + R dz = 0

або, що те ж саме, на цих поверхнях криволінійний інтеграл

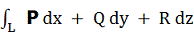 (6)

має дорівнювати нулю по будь-якому шляху (в тому числі і по незамкнутим шляхам).

Розглянемо всілякі вихрові поверхні, тобто векторні поверхні поля rot F. Очевидно, що в силу теореми Стокса

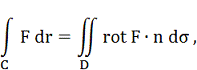
де dr = i dx + j dy + k dz, і інтеграл (6) по будь-якому замкнутому шляху на вихровий поверхні дорівнює нулю (так як скалярний добуток одиничного вектора нормалі до поверхні n і вектора rot F дорівнює нулю). Виберемо тепер серед вихрових поверхонь ті, на яких всі інтеграли

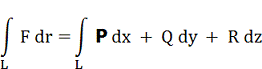
Р dx + Q dy + R dz = 0 , (3)

до якого додано рівняння довільної поверхні z=f (x, у), що проходить через точку М (найчастіше рівняння цієї поповерхні беруть у вигляді z = f₁ (x) або z = f₂ (y) або навіть у вигляді z = a, де а - константа). Підставляючи z = f (x, у) в (3), отримаємо звичайне рівняння виду

М (х, y) dx + N (x, y) dy = 0,

інтегруючи яке і враховуючи початкову умову у (х₀) = у₀, отримаємо шукану криву l, що проходить через точку М (x₀, y₀, z₀) і ортогональну векторним лініям (рис. 1).

Якщо ця лінія не є лінією вихору, то, проводячи через кажну точку лінії l лінію вихору, отримаємо шукану поверхню S, ортогональну векторним лініям поля F.

Дійсно, взявши будь-яку незамкнену криву l на поверхні S (рис. 1) і провівши через її граничні точки вихрові лінії до перетину з кривою l в точках р₁ і р₂, отримаємо замкнутий контур, що складається з відрізка лінії l між точками р₁ і р₂, кривої l і двох вихрових ліній.

Криволінійний 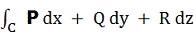інтеграл . Взятий з цього замкнутого контуру С, дорівнює нулю, так як контур лежить на вихровій поверхні, причому той же інтеграл, узятий на відрізку дуги l, і по відрізках вихрових ліній дорівнює нулю, так як дуга l і вихрові лінії ортогональні векторним лініях поля F (вихрові лінії ортогональні векторним лініях поля F в силу умови (F • rot F) = 0). Отже, інтеграл 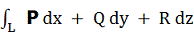 по довільно обраному нами незамкнутому шляху l дорівнює нулю, тобто поверхня S є інтегральною поверхнею рівняння (3), що проходить через задану точку М.

Цей метод доказу достатності умови (F • rot F) = 0 для існування сімейства поверхонь, ортогональних векторним лініям поля F, одночасно вказує шлях, правда не найкоротший, для знаходження цих поверхонь.

ПРИКЛАД 1

z dx + (x - y) dy + zy dz = 0.

Умова (F • rot F) = 0, де F = zi + (x -y)j + yzk, не виконується, отже, дане рівняння не інтегрується одним співвідношенням.

ПРИКЛАД 2

(6x + yz) dx + (xz - 2у) dy + (ху + 2z) dz = 0.F ≡ 0, де F = (6x + yz) i + (xz - 2y) j + (xy + 2z) k, то F = grad U, де

.

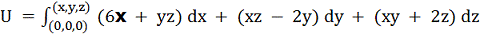В якості шляху інтегрування вибираємо ламану, ланки якої паралельні осям координат. Інтегруючи, отримуємо U = 3x² - y² + z² + xyz, і отже, шуканим інтегралом є 3x² - y² + z² + xyz = с.

2. Цілком інтегровані рівняння Пфаффа

ОЗНАЧЕННЯ 1

Рівняння (1) називають цілком інтегрованим, якщо через кожну точку області D проходить інтегральна гіперповерхня (тобто (п - 1)-вимірна інтегральна поверхня) поля Р.

Як нам уже відомо, при n = 2 кожне рівняння Пфаффа є цілком інтегрованим. Цього, однак, уже не можна стверджувати при n ≥ 3.

Найпростішим прикладом цілком інтегрованого рівняння Пфаффа є рівняння в повних диференціалах, яке характеризується тим, що форма ω є точною, тобто існує функція U(х)  С² (D → R) така, що

ω = dU (7)

[Зрозуміло, що точній формі ω відповідає потенціальне векторне поле а(х) = gгad U(х).] У цьому випадку область D розшаровується інтегральними гіперповерхнями

M_c :={x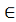 D : U(x) = с} (8)

- поверхнями рівня функції U(х) (стала с пробігає область значень функції U(х).

Навпаки, припустимо, що для довільної точки х₀  D у деякому її околі В(х₀) існує функція U(х)  C²(D → R) з ненульовим градієнтом, поверхні рівня якої є інтегральними для поля Р, а отже, ортогональними до векторного поля а. Легко бачити, що тоді вектори grad U(x) та а(х) будуть колінеарними кожному х  D. А це, своєю чергою, означає, що в околі точки х₀ для форми ω існує інтегрувальний множник, тобто функція µ : D → R \ {0}, яка має властивість

µω = dU. (9)

Із невиродженості форми ω випливає, що функція µ неперервно дифе-ренційовна.

Зрозуміло, що рівняння Пфаффа, для якого існує інтегрувальний множник, цілком інтегроване, причому, знаючи інтегрувальний множник, ми зможемо виписати й рівняння інтегральних поверхонь (принаймні локально).

Далі, якщо для форми

µω := b(х) dx ≡ b₁(х) dx₁ + ... + b_n(x) dx_n

виконується рівність (9), то з урахуванням рівностей ,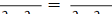

i, j = 1, …, n дістаємо умови на коефіцієнти b_i :

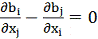, i, j = 1, ..., n. (10)

ОЗНАЧЕННЯ 2

Форму b(x) dx, для якої умови (10) виконуються в кожній точці х 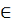 D, називають замкненою формою в області D.

Відомо, що в разі виконання умов (10) криволінійний інтеграл 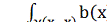, принаймні в околі точки х₀, не залежить від конкретного вибору шляху γ(х₀, х), який сполучає х₀ з х і цілком лежить в околі точки х₀. Даний інтеграл і визначає функцію U(х), яка рівностями (8) задає інтегральні поверхні рівняння (1). Таку функцію назвемо інтегралом рівняння Пфаффа.

Знайдемо необхідні умови існування інтегрувального множника. При b_і = µа_i як наслідок (13) маємо

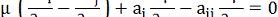
За допомогою визначників цю рівність можна подати у вигляді

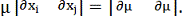 (11)

Оскільки всі мінори третього порядку матриці

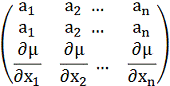
дорівнюють нулю, то з огляду на рівності (11) таку саму властивість має й символічна матриця

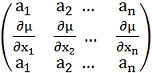 (12)

Щоб переконатися в цьому, достатньо розкласти будь-які два відповідних мінори таких матриць за їх першими рядками.

Виявляється, знайдена умова є не лише необхідною, а й достатньою.

ТЕОРЕМА (ФРОБЕНІУСА)

Для того щоб рівняння (1) було цілком інтегрованим, необхідно й достатньо, щоб усі мінори третього порядку матриці (12) перетворювалися в нуль в області D.

Доведення цієї теореми для n = 3 буде наведено в п. 4. У цьому випадку умова теореми Фробеніуса набирає вигляду

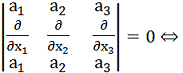a(x) rot a(x) = 0 (13)

і означає, що векторне поле а(х) ортогональне до свого ротора.

. Інтегральні криві рівняння Пфаффа

Для рівняння (1) завжди можна побудувати одновимірні «інтегральні поверхні», тобто інтегральні криві. При n = З це можна зробити таким чином. Візьмемо довільну точку х₀  D. У деякому її околі B(х₀) завжди можна визначити двічі неперервно диференційовну функцію F: В(х₀) → R, для якої grad F(x) був би неколінеарний вектору а(х). Тоді система

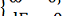 (14)

визначає поле напрямів у B(х₀). Це поле напрямів можна задати деякою системою в симетричній формі

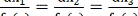 , (15)

якій відповідає автономна система

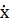 = f(х). (16)

Векторне поле f = (f₁, f₂, f₃) з точністю до множника визначається умовою: вектор f(x) ортогональний до векторів а(x) та grad F(x). Наприклад, можна покласти

f(x) := | а(x), grad F(х) |, (17)

де | ∙, ∙ | - операція векторного добутку в R³.

Інтегральні криві системи (15) [фазові криві системи (16)] будуть інтегральними кривими системи (14), а отже, рівняння (1).

Зауважимо, що система (14) має очевидний перший інтеграл F. Тому її вимірність можна знизити на одиницю.

Припустимо, наприклад, що а₃(х₀) ≠ 0. Нехай F = F (х₁, х₂) - довільна двічі неперервно диференційовна в околі точки (х₀₁, х₀₂) функція, яка в цьому околі задовольняє умову невиродженості 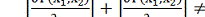 і F(х₀₁,х₀₂)=0. На площині х₁Ох₂ рівняння

F (х₁, х₂) = 0. (18)

визначає криву γ, яка проходить через точку (х₀₁, х₀₂). У просторі R³ воно визначає циліндричну поверхню S із напрямною γ і твірними, паралельними осі Ох₃. Зрозуміло, що вектори а(х) та gгad F(х) 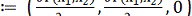 неколінеарні в деякому околі точки х₀. Тоді існує єдина інтегральна крива

Г : х = ξ(s), s 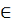 I (19)

системи (17), яка лежить на поверхні S і проходить через точку х₀.

Для відшукання цієї кривої потрібно рівняння (18) розв'язати відносно однієї зі змінних і результат підставити в рівняння (1). Дістанемо рівняння Пфаффа на площині. Якщо, наприклад, із (18) можна виразити змінну х₂ через х₁, так що х₂ = φ(х₁) (х₀₂ = φ (х₀₁)), то рівняння на площині х₁Ох₃ матиме вигляд

.

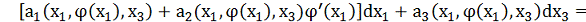Звичайно, функцію F слід намагатися вибирати так, щоб це рівняння легко розв'язувалося. Знайшовши його інтегральну криву х₁ = ξ₁(s), х₃ = ξ₃(s), яка проходить через точку (х₀₁, х₀₂), дістанемо рівняння кривої (19), в якому ξ(s)= (ξ₁(s),φ(ξ₁(s)), ξ₁(s)). Вона водночас є фазовою кривою автономної системи (19), де f(x) визначено формулою (17).

ПРИКЛАД 3

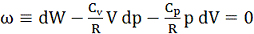 , (20)

де R - газова стала, С_ѵ - теплоємність газу при сталому об'ємі, С_р = С_ѵ+АR - теплоємність газу при сталому тиску, А - стала (термічний еквівалент роботи).

Для даного випадку умова теореми Фробеніуса не виконується:

.

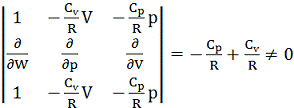Тому рівняння (20) не є цілком інтегрованим. Із фізичного погляду не означає, що теплова енергія газу не є функцією його стану, який визначається значеннями V, р. Тепло, котре поглинається (виділяється) під час деякого процесу - переходу зі стану (V₀, р₀) у стан (V, р), залежить від кривої γ, що сполучає точки x₀ та x, і зображується криволінійним інтегралом

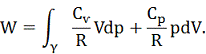
Наприклад, крива, вздовж якої виконується рівність

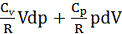, (21)

забезпечує адіабатичний процес (W = const). Із рівняння (21) після відокремлення змінних дістаємо формулу Пуассона для адіабати: 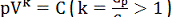, де С - довільна стала.

Якщо скористатися формулою Клапейрона рV = RТ, де Т - абсолютна температура газу, й домножити обидві частини рівняння (20) на 1/T, то побачимо, що

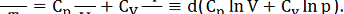
Тому криволінійний інтеграл 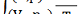 не залежить від шляху інтегрування, який сполучає точку (V₀, р₀) зі змінною точкою (V, р). Цей інтеграл визначає ентропію - фізичну величину, яка вже є функцією стану газу.

4. Цілком інтегровані рівняння Пфаффа в R³

Нехай n = З, а форма ω задовольняє умову (13). Покажемо, що через кожну точку х₀ = (х₀₁, х₀₂, х₀₃)  D можна провести інтегральну поверхню рівняння (1), і притому лише одну. Спосіб побудови цієї поверхні нагадує конструкцію розв'язку задачі Коші для рівняння з частинними похідними й передбачає такі кроки.

•        Знаходимо інтегральну криву Г : х = ξ(s), s  I рівняння Пфаффа, яка проходить через точку х₀.

•        Задаємо в D векторне поле g(x)  С¹ (D → R³ ) так, щоб воно було ортогональне до векторного поля а(х), тобто задовольняло умову

a(x)g(x) = 0, (22)

і не дотикалося кривої Г у жодній її точці. Зокрема, якщо для кожного s 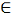 I вектори ξ'(s) і rot a(ξ(s)) неколінеарні, то можна покласти

g(x) = rot a(x).

Поле g(х) бажано вибирати так, щоб система

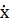 = g(х) (23)

була інтегровною.

•        З кожної точки кривої Г випускаємо фазову криву системи (23) і таким чином утворюємо поверхню M_Г, яка проходить через цю криву (рис. 2, а).

Виявляється, м_г і є шуканою інтегральною поверхнею рівняння Пфаффа. Точніше, якщо позначити через χ(t, s) розв'язок системи (23), який задовольняє початкову умову χ(0, s) = ξ(s), то для деякого δ > 0 рівняння

x = χ (t, s), t ∈ (-δ, δ), s ∈ (s₀ - δ, s₀ + δ) (24)

визначають (локальну) інтегральну поверхню рівняння Пфаффа (1), яка проходить через точку х₀.

Множина (24) справді є поверхнею. Цей факт випливає з міркувань, наведених у доведенні теореми існування розв'язку задачі Коші для квазілінійного рівняння з частинними похідними першого порядку. Отже, для обґрунтування сформульованого алгоритму залишається переконатися в тому, що

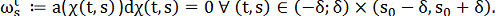
Для цього виведемо диференціальні рівняння, які описують зміну в часі t коефіцієнтів при ds і dt форми . Маємо

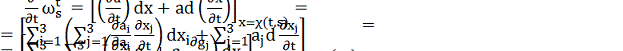(25)

З (22) знаходимо

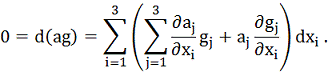
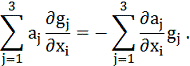
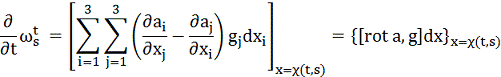
Оскільки виконуються умови (13) та (22), то векторне поле 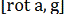 колінеарне векторному полю а. Тому знайдеться така функція ρ(х), що

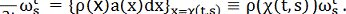
Це й є шукане рівняння для . Розв'язавши його, дістанемо

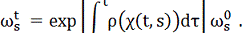
Оскільки Г є інтегральною кривою рівняння Пфаффа, то

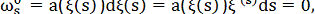
а тому й 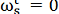. Таким чином, рівняння (24) справді визначають інтегральну поверхню рівняння (1).

Доведемо її єдиність. Нехай, навпаки, існують дві інтегральні поверхні S₁, та S₂ рівняння (1), які проходять через точку х₀ і не збігаються в будь-якому о колі цієї точки. Вони мають спільну дотичну площину П, Ортогональну до вектора а(х₀). Уведемо в R³ нову декартову прямокутну систему координат (х, у, z) із початком О у точці х₀ так, щоб площина хОу збігалася з П, а вісь Оz була спрямована вздовж вектора a(x₀). Тоді кожна поверхня S₁ (i= 1, 2) в околі точки О буде графіком деякої неперервно диференційовної функції z = f_i (х, у). Згідно з припущенням для як завгодно малого е > 0 існує точка (х_е, у_е) така, що |х_е| + |у_е| < е і f₁(х_е, у_е) ≠ f₂(х_е, у_е). Покладемо f= у_еx - х_еy. Рівняння f= 0 визначає площину, яка проходить через точки (х_е, у_е, f₁(х_е, у_е)) і перетинає поверхні S₁ та S₂ по двох різних кривих Г₁ та Г₂.

Повернемося до старих координат. Кожна з кривих Г₁ та Г₂ проходить через точку x₀ і є інтегральною кривою системи (14). Для останньої існує лише одна інтегральна крива, яка проходить через точку x₀. Ця суперечність доводить єдиність інтегральної поверхні, яка проходить через задану точку.

ПРИКЛАД 4

Розглянемо рівняння

(2yz + Зх) dx + xz dy + ху dz = 0. (26)

Уданому випадку а(х, у, z) = (2yz + 3х, xz, ху). Оскільки rot а(х, у, z) = (0, у, -z), то умова (16) виконується.

Знайдемо інтегральні криві рівняння (29), які лежать у площині

F  y=1.

На ній рівняння (29) набирає вигляду

(2z + 3х) dх + х dz = 0.

Це лінійне відносно z рівняння легко інтегрується, і ми дістаємо сім'ю інтегральних кривих рівняння (29), які лежать у площині y=1:

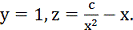 (27)

Тепер побудуємо векторне поле g так, щоб воно не лежало в площині у = 1, задовольняло умову аg = 0 і систему  = g(х) можна було легко зінтегрувати. Зручно покласти g(x, у, z)  rot а(х, у, z) = (0, у, -z). Відповідна система в симетричній формі має вигляд

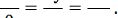
Її загальний інтеграл

yz = c₁, х = с₂. (28)

Тепер для того щоб утворити поверхню з інтегральних кривих сім'ї (28), які для фіксованого с виходять із точок кривої (27), робимо так само, як і під час розв'язування задачі Коші для рівняння з частинними похідними: підставляємо (27) у (28), виключаємо змінну х, в одержаному співвідношенні 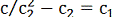, заміняємо с₁, с₂ лівими частинами рівностей (28). Остаточно дістаємо рівняння сім'ї інтегральних поверхонь рівняння (26):

х²уz + x³ = с.

Звідси, зокрема, випливає, що інтегрувальним множником форми (2yz + Зх) dx + xz dy + ху dz є функція µ = х.

Висновки

Розбудова теорії звичайних диференціальних рівнянь триває вже понад три століття. Сьогодні ця математична дисципліна являє собою багаторівневу систему знань із розгалуженою внутрішньою структурою, різноманітними зв'язками з іншими розділами математики, розвинутим понятійним апаратом, потужним арсеналом аналітичних, геометричних та чисельних методів.

Коло проблем, які досліджує теорія диференціальних рівнянь, невпинно розширюється. Зараз у ній можна виділити близько двадцяти великих розділів. Згідно з класифікаційною системою провідних реферативних математичних журналів загальне число тематичних напрямів (рубрик), які безпосередньо стосуються теорії звичайних диференціальних рівнянь, перевищує півтори сотні й продовжує зростати. Можна також налічити кілька десятків рубрик, які відображають зв'язки цієї теорії з іншими математичними дисциплінами. І тому навіть лаконічні огляди її здобутків за останні десятиліття нерідко виливаються в багатотомні видання.

Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів.

Основою для рівняння Пфаффа є задача відшукання інтегральних поверхонь максимально можливої вимірності k = n - 1.

Виникає завдання про знаходження сімейства поверхонь U (x, y, z) = c, ортогональних до векторних ліній.

ДОДАТОК

ЗАДАЧА 1

Знайти поверхню, що задовольняє рівняння Пфаффа:

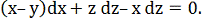
Розв’язок:

Оскільки (F• rot F) = z - 2x + y і функція z = 2x - y не є розв’язком даного рівняння, то воно не може бути про інтегровано одним співвідношенням. Про інтегруємо його двома співвідношеннями, беручи, наприклад, z = x + y. Тоді отримаємо рівняння

dx - dy = 0,

Таким чином, одно параметричне сімейство прямих

x = t, y = t + C₁, z = 2t + C₁

задовольняє дане рівняння.

ЗАДАЧА 2

Знайти поверхню, що задовольняє рівняння Пфаффа:

Розв’язок:

F = (3yz, 2xz, xy).

Так як

rot F = -ix + 2jk - kz та (F• rot F) = 0,

то дане рівняння інтегрується одним співвідношенням. Таким чином, існує множник µ = µ(x, y, z) такий, що rot µF = 0, тобто поле µF потенційне. Звідси, для множника µ маємо рівняння:

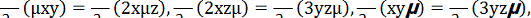
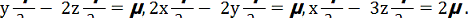
Інтегруючи перше рівняння, отримуємо загальний розв’язок:

µ = yφ(x,ξ), ξ = yz².

Підставляючи отримане значення µ у друге рівняння, маємо:

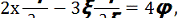
звідки знаходимо

φ = x²ψ(x³y²z⁴).

µ = yx²ψ(η), η = x³y²z⁴.

Залишається знайти ψ. Для цього скористаємося третім рівнянням. Маємо

-9x⁵y³z⁴ ψ'(η) = 0,

звідси

ψ(η) = C.

Таким чином

µ= yx²

(нехай С рівне одиниці). Помноживши почленно дане рівняння на yx², отримуємо рівняння

x²y²zdx + 2x³yzdy + x³y²dz = 0,

ліва частина якого є повний диференціал функції 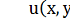, яку ми знайдемо вичисливши криволінійний інтеграл

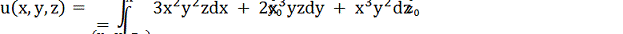
Таким чином,

x³y²z = C

є шуканий інтеграл даного рівняння.

ЗАДАЧА 3

Знайти поверхню, що задовольняє рівняння Пфаффа:

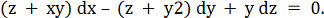
Розв’язок:

Так як (F• rot F) = z + x - y² ≠ 0, то дане рівняння не може бути проінтегроване одним співвідношенням. Значить, залишається перевірити, чи буде функція z = y² - xy розв’язком цього рівняння. Вичисливши dz = 2ydy - xdy - ydx й підставивши значення z і dz в рівняння, отримаємо тотожність. Отже, поверхня

z = y² - xy

є єдиною, яка ортогональна полю F = (z + xy, -z, -z - y², y).

Список літератури

1.   А. К. Боярчук, Г.П.Головач - дифференциальные уравнения в примерах и задачах. Справочное пособие по высшей математике. Т. 5 М.: Эдиториал УРСС, 2010. - 384 с.

2.       Вестник самгу - Естественнонаучная серия. 2010. № 2(76)

3.       Диригивцев А. Я. Математичний аналіз: У 2 ч. - К.: Либідь, 1994. -Ч. І. - 320 с.

4.       Диференціальні рівняння / І. 1. Ляшко, О. К. Боярчук, Я. Г. Гай та ін. - К.: Виша шк. Головне вид-во, 1981. - 504 с.

5.   Диференціальні рівняння: Підручник / А. М. Самойленко, М. О. Перестюк, І. О. Парасюк. - 2-ге вид., перероб. І дон. - К.: Либідь, 2007. - 600с.

6.   Лаерешок С. //. Курс диференціальних рівнянь. - Львів: Вид-во паук.-техн. л-ри. 2009. - 216 с.

7.       Филиппов А. Ф. - Сборник задач по дифференциальным уравнениям. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000, 176 с.

8.   Эльсгольц Л.Э. - Дифференциальные уравнения и вариационное исчисление - М.: Наука , 1969. - 425с.