Практическое применение теоремы Пойа и перечисления графов
Введение
граф теорема пойа
Графы - это замечательные математические
объекты, с помощью, которых можно решать математические, экономические и
логические задачи. Также можно решать различные головоломки и упрощать условия
задач по физике, химии, электронике, автоматике. Сама теория графов является
частью как топологии, так и комбинаторики.
Решение многих задач перечисления графов
сводится к подсчету числа классов эквивалентностей. Эффективный метод решения
таких задач базируется на известной теореме Пойа.
Цель исследования: изучить основные свойства
групп подстановок и метод решения комбинаторных задач с помощью теоремы Пойа.
Задачи исследования:
. Изучить такие основополагающие понятия
теории графов и теории групп, как граф, группа подстановок и её цикловой
индекс.
. Рассмотреть определение
эквивалентности, порождаемое группой подстановок, и доказать лемму Бернсайда о
числе классов такой эквивалентности.
. Разобрать определение перечня
конфигурации и доказать теорему Пойа.
. Рассмотреть задачу о перечислении
графов и метод её решения с помощью теоремы Пойа.
Объектом исследования: теория графов.
Предмет исследования: группы подстановок и
методы решения комбинаторных задач с помощью теоремы Пойа. Работа состоит из
двух разделов - теоретической и практической части. В ходe работы нами
использовались слeдующиe мeтоды исслeдования: изучeниe научной, учeбной и
мeтодичeской литeратуры, Интeрнeт-источников, анализ, обобщeниe и
систематизация.
1. Теорема Пойа и перечисление графов
.1 Понятия теории графов и теории групп
В математической теории графов и информатике
граф - это совокупность непустого множества вершин и множества пар вершин
(связей между вершинами). Объекты представляются как вершины, или узлы графа, а
связи - как дуги, или рёбра. Для разных областей применения виды графов могут
различаться направленностью, ограничениями на количество связей и
дополнительными данными о вершинах или рёбрах [2].
Граф, или неориентированный граф 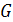
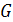 - это упорядоченная пара
- это упорядоченная пара 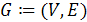
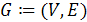 , для которой выполнены следующие
условия:
, для которой выполнены следующие
условия:
- 
 это непустое множество вершин или
узлов,
это непустое множество вершин или
узлов,
- 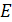
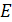 это множество пар (в случае
неориентированного графа - неупорядоченных) вершин, называемых рёбрами.
это множество пар (в случае
неориентированного графа - неупорядоченных) вершин, называемых рёбрами.

 (а значит и,
(а значит и,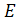
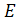 , иначе оно было бы
мультимножеством) обычно считаются конечными множествами. Многие хорошие
результаты, полученные для конечных графов, неверны (или каким-либо образом
отличаются) для бесконечных графов. Это происходит потому, что ряд соображений
становится ложным в случае бесконечных множеств.
, иначе оно было бы
мультимножеством) обычно считаются конечными множествами. Многие хорошие
результаты, полученные для конечных графов, неверны (или каким-либо образом
отличаются) для бесконечных графов. Это происходит потому, что ряд соображений
становится ложным в случае бесконечных множеств.
Вершины и рёбра графа называются
также элементами графа, число вершин в графе - 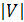
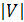 порядком, число рёбер
порядком, число рёбер 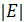
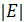 - размером графа.
- размером графа.
Вершины 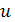
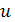 и
и 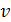
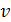 называются концевыми вершинами (или
просто концами) ребра
называются концевыми вершинами (или
просто концами) ребра 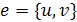
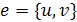 . Ребро, в свою очередь, соединяет
эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра
называются кратными, если множества их концевых вершин совпадают. Ребро
называется петлёй, если его концы совпадают, то есть
. Ребро, в свою очередь, соединяет
эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра
называются кратными, если множества их концевых вершин совпадают. Ребро
называется петлёй, если его концы совпадают, то есть 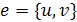
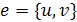 . Степенью
. Степенью 
 вершины
вершины 
 называют количество инцидентных ей
рёбер (при этом петли считают дважды). Вершина называется изолированной, если
она не является концом ни для одного ребра; висячей (или листом), если она
является концом ровно одного ребра.
называют количество инцидентных ей
рёбер (при этом петли считают дважды). Вершина называется изолированной, если
она не является концом ни для одного ребра; висячей (или листом), если она
является концом ровно одного ребра.
Ориентированный граф.
Ориентированный граф (сокращённо
орграф) 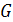
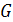 - это упорядоченная пара
- это упорядоченная пара 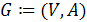
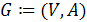 , для которой выполнены следующие
условия:
, для которой выполнены следующие
условия:
- 
 это непустое множество вершин или
узлов,
это непустое множество вершин или
узлов,

 это множество (упорядоченных) пар
различных вершин, называемых дугами или ориентированными рёбрами.
это множество (упорядоченных) пар
различных вершин, называемых дугами или ориентированными рёбрами.
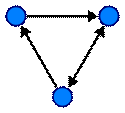
Рисунок 1.1 - Ориентированный граф
Дуга - это упорядоченная пара вершин

 , где вершину
, где вершину 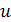
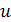 называют началом, а
называют началом, а 
 - концом дуги. Можно сказать, что
дуга
- концом дуги. Можно сказать, что
дуга 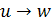
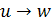 ведёт от вершины
ведёт от вершины 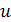
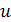 к вершине
к вершине 
 .
.
Смешанный граф
Смешанный граф 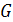
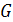 - это граф, в котором некоторые
рёбра могут быть ориентированными, а некоторые - неориентированными.
Записывается упорядоченной тройкой
- это граф, в котором некоторые
рёбра могут быть ориентированными, а некоторые - неориентированными.
Записывается упорядоченной тройкой 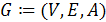
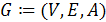 , где ,
, где , 
 и
и 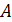
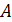 определены так же, как выше.
определены так же, как выше.
Ориентированный и неориентированный
графы являются частными случаями смешанного.
Изоморфные графы
Граф 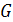
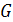 называется изоморфным графу
называется изоморфным графу 
 , если существует биекция
, если существует биекция 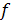
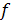 из множества вершин графа
из множества вершин графа 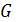
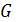 в множество вершин графа
в множество вершин графа 
 , обладающая следующим свойством:
если в графе
, обладающая следующим свойством:
если в графе 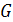
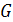 есть ребро из вершины
есть ребро из вершины 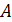
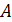 в вершину
в вершину 
 , то в графе
, то в графе 
 должно быть ребро из вершины
должно быть ребро из вершины 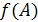
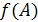 в вершину
в вершину 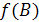
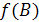 и наоборот - если в графе
и наоборот - если в графе 
 есть ребро из вершины
есть ребро из вершины 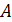
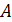 в вершину
в вершину 
 , то в графе
, то в графе 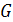
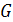 должно быть ребро из вершины
должно быть ребро из вершины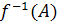
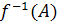 в вершину
в вершину 
 . В случае ориентированного графа
эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа
биекция также должна сохранять вес ребра.
. В случае ориентированного графа
эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа
биекция также должна сохранять вес ребра.
Прочие связанные определения
Путём (или цепью) в графе называют конечную
последовательность вершин, в которой каждая вершина (кроме последней) соединена
со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе
называют конечную последовательность вершин 
 , для которой все пары
, для которой все пары 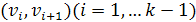
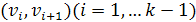 являются (ориентированными)
рёбрами.
являются (ориентированными)
рёбрами.
Циклом называют путь, в котором
первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют
число составляющих его рёбер. Заметим, что если вершины 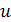
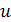 и
и 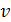
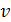 являются концами некоторого ребра,
то согласно данному определению, последовательность
являются концами некоторого ребра,
то согласно данному определению, последовательность 
 является циклом. Чтобы избежать
таких «вырожденных» случаев, вводят следующие понятия.
является циклом. Чтобы избежать
таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым,
если ребра в нём не повторяются; элементарным, если он простой и вершины в нём
не повторяются. Несложно видеть, что:
· всякий путь, соединяющий две
вершины, содержит элементарный путь, соединяющий те же две вершины.
· всякий простой неэлементарный путь
содержит элементарный цикл.
· всякий простой цикл, проходящий через
некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий
через ту же вершину (или ребро).
· петля - элементарный цикл.
Бинарное отношение на множестве
вершин графа, заданное как «существует путь из 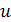
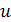 в
в 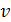
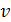 », является отношением
эквивалентности и, следовательно, разбивает это множество на классы
эквивалентности, называемые компонентами связности графа. Если у графа ровно
одна компонента связности, то граф связный. На компоненте связности можно
ввести понятие расстояния между вершинами как минимальную длину пути,
соединяющего эти вершины.
», является отношением
эквивалентности и, следовательно, разбивает это множество на классы
эквивалентности, называемые компонентами связности графа. Если у графа ровно
одна компонента связности, то граф связный. На компоненте связности можно
ввести понятие расстояния между вершинами как минимальную длину пути,
соединяющего эти вершины.
Всякий максимальный связный подграф
графа G называется связной компонентой (или просто компонентой) графа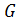
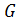 . Слово «максимальный» означает
максимальный относительно включения, то есть не содержащийся в связном подграфе
с большим числом элементов
. Слово «максимальный» означает
максимальный относительно включения, то есть не содержащийся в связном подграфе
с большим числом элементов
Ребро графа называется мостом, если
его удаление увеличивает число компонент.
Группы подстановок и их цикловой индекс.
Для решения задач перечисления нам необходимо
вспомнить некоторый материал из теории групп.
Множество Г называется группой, если на нем
задана бинарная операция (·), не выводящая за пределы множества и
удовлетворяющая следующим трем условиям:
. Для любых x, y и z из Г справедливо
(x·y)·z = x·(y·z);
. В Г существует единичный элемент e,
такой что для любого x из Г e·x = x·e = x;
3. Для любого элемента x из Г
существует обратный элемент 
 также из множества Г, такой что
также из множества Г, такой что 
 .
.
Непустое подмножество A множества Г называют
подгруппой группы Г, если оно удовлетворяет следующим двум условиям:
. Бинарная операция не выводит за пределы
подмножества A;
2. Для любого элемента x из A
обратный к нему элемент 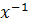
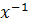 также лежит в A.
также лежит в A.
Пусть A - некоторая подгруппа группы
Г. Правым классом смежности группы Г по подгруппе A называется множество вида
Ax 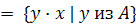
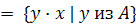 , где x - произвольный элемент из Г
(аналогично определяются левые классы смежности). Известно также утверждение о
том, что если A - подгруппа группы Г, то группу Г можно разложить в объединение
правых (левых) классов смежности по подгруппе A.
, где x - произвольный элемент из Г
(аналогично определяются левые классы смежности). Известно также утверждение о
том, что если A - подгруппа группы Г, то группу Г можно разложить в объединение
правых (левых) классов смежности по подгруппе A.
Рассмотрим теперь множество 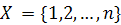
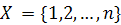 . Подстановкой называется взаимно
однозначное отображение
. Подстановкой называется взаимно
однозначное отображение 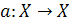
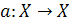 . Умножением подстановок будем
называть их композицию. Пусть A - некоторая совокупность подстановок множества
X, замкнутая относительно операции умножения. Тогда A является группой
подстановок на множестве объектов X. Порядок группы A, обозначаемый |A|, есть
число подстановок A, а степень группы - это число n элементов в множестве
объектов X.
. Умножением подстановок будем
называть их композицию. Пусть A - некоторая совокупность подстановок множества
X, замкнутая относительно операции умножения. Тогда A является группой
подстановок на множестве объектов X. Порядок группы A, обозначаемый |A|, есть
число подстановок A, а степень группы - это число n элементов в множестве
объектов X.
Наиболее важными для нас примерами
группы подстановок являются симметрическая группа Sn - группа всех подстановок
на множестве из n объектов, изнакопеременная группа An - группа всех четных
подстановок. Чтобы определить понятие четной подстановки введем понятие
транспозиции.
Транспозицией называется
подстановка, меняющая два элемента местами друг с другом и оставляющая
остальные элементы на своих местах. Можно показать, что любая подстановка
раскладывается в произведение транспозиций. Подстановка называется четной, если
число транспозиций, в которые раскладывается подстановка, четно.
Пусть A - группа подстановок с
множеством объектов 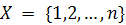
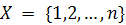 . Циклом длины k называется
подстановка, обозначаемая
. Циклом длины k называется
подстановка, обозначаемая 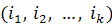
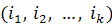 , которая переводит
, которая переводит 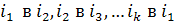
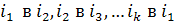 Известно, что каждая подстановка a
может быть представлена в виде произведения непересекающихся циклов.
Известно, что каждая подстановка a
может быть представлена в виде произведения непересекающихся циклов.
Например,
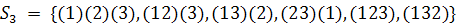
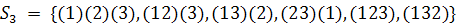 или
или
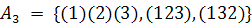
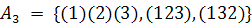 .
.
Существует естественная связь между
группами подстановок и графами.
Рассмотрим два графа 
 . Взаимно однозначное отбражение a
множества вершин графа
. Взаимно однозначное отбражение a
множества вершин графа 
 на множество вершин графа
на множество вершин графа 
 , сохраняющее смежность,
называютизоморфизмом. Если
, сохраняющее смежность,
называютизоморфизмом. Если 
 , то a называется автоморфизмом
графа. Совокупность всех автоморфизмов графа G, обозначаемая Г(G), образует
группу, называемуюгруппой графа G, или группой автоморфизмов графа G. Таким
образом, элементы группы Г(G) являются подстановками, действующими на множестве
вершин графа.
, то a называется автоморфизмом
графа. Совокупность всех автоморфизмов графа G, обозначаемая Г(G), образует
группу, называемуюгруппой графа G, или группой автоморфизмов графа G. Таким
образом, элементы группы Г(G) являются подстановками, действующими на множестве
вершин графа.
Рассмотрим граф G, изображенный на
рисунке.
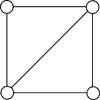
Рисунок 1.2 - граф G
Его четыре вершины составляют
множество X целых чисел 1, 2, 3, 4. Заметим, что следующий список подстановок
· 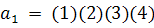
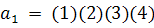
· 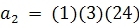
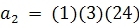
· 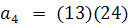
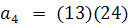
включает все подстановки множества X,
сохраняющие отношение смежности в графе G. К примеру, вершины 1 и 4 смежны в G.
Подстановка (13)(2)(4) преобразует вершины 1 и 4 в вершины 3 и 4, и эти образы
3 и 4, также являются смежными. Таким образом, подстановка (13)(2)(4) сохраняет
смежность вершин 1 и 4. Так как совокупность подстановок в этом списке замкнута
относительно операции умножения, то она образует группу.
Теперь можем переходить к определению такого
понятия, как цикловой индекс группы подстановок.
Пусть A - группа подстановок с
множеством объектов 
 и
и 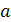
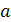 - некоторая подстановка из этой
группы. Для каждого
- некоторая подстановка из этой
группы. Для каждого 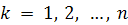
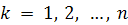 через
через 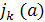
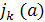 обозначим число циклов длины
обозначим число циклов длины 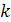
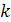 в разложении подстановки
в разложении подстановки 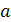
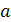 в произведение непересекающихся
циклов.
в произведение непересекающихся
циклов.
Тогда цикловой индекс группы 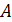
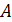 , обозначаемый
, обозначаемый 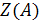
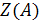 или
или 
 , представляет собой многочлен от
переменных
, представляет собой многочлен от
переменных 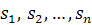
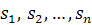 , определяемый формулой:
, определяемый формулой:
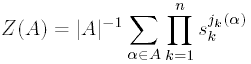

Рассмотрим для примера
симметрическую группу 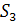
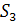 . Заметим, что тождественная подстановка
(1)(2)(3) имеет три единичных цикла дающих слагаемое
. Заметим, что тождественная подстановка
(1)(2)(3) имеет три единичных цикла дающих слагаемое 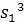
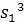 . Три подстановки (1)(23), (2)(13) и
(3)(12) имеют каждая по единичному циклу и по одному циклу длины 2, так что
получается одно слагаемое
. Три подстановки (1)(23), (2)(13) и
(3)(12) имеют каждая по единичному циклу и по одному циклу длины 2, так что
получается одно слагаемое 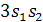
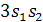 . Наконец, подстановки (123) и (132)
вносят
. Наконец, подстановки (123) и (132)
вносят 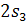
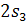 . Таким образом, имеем
. Таким образом, имеем 

Для вычисления циклового индекса
симметрической группы 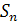
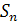 введем понятие разбиения числа и
рассмотрим несколько утверждений.
введем понятие разбиения числа и
рассмотрим несколько утверждений.
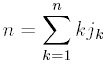
Назовем разбиением натурального
числа n его представление в виде суммы некоторых натуральных чисел. Заметим,
что каждая подстановка a на n объектах может быть связана с определенным
разбиением числа n, имеющим для каждого 
 точно
точно 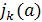
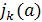 частей, равных числу k. Будем
задавать разбиение числа n посредством вектора
частей, равных числу k. Будем
задавать разбиение числа n посредством вектора 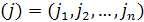
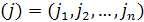 , где
, где 
 - число частей разбиения, равных k.
Итак,
- число частей разбиения, равных k.
Итак,
Пример
4 = 1 + 1 + 1 + 1 (4,
0, 0, 0)
= 1 + 1 + 2 (2,
1, 0, 0)
= 2 + 2 (0,
2, 0, 0)
= 1 + 3 (1,
0, 1, 0)
= 4 (0,
0, 0, 1)
Пусть h(j) - число подстановок в
группе 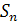
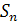 , разложение которых на
непересекающиеся циклы соответствует разбиению (j), в том смысле, что для
каждого k выполняется
, разложение которых на
непересекающиеся циклы соответствует разбиению (j), в том смысле, что для
каждого k выполняется 
 . Тогда имеет место следующая лемма.
. Тогда имеет место следующая лемма.
Лемма
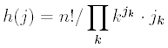

Таким образом, после приведения
подобных членов в выражении (1.1), цикловой индекс 
 примет следующий вид.
примет следующий вид.
Теорема
Цикловой индекс симметрической
группы дается формулой


где сумма берется по всем разбиениям (j) числа
n, а h(j) задается выражением

 (1.2).
(1.2).
Пример
3 = 1 + 1 + 1 (3,
0, 0) h = 3! / 3! = 1
= 1 + 2 (1,
1, 0) h = 3! / 1·1!·2·1! = 3
= 3 (0,
0, 1) h = 3! / 3·1!
Иногда удобно расматривать производящую функцию
цикловых индексов и пользоваться следующим свойством.
Теорема
где 
 по определению.
по определению.
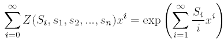

Часто бывает удобным выразить 
 через
через 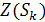
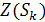 , где
, где 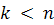
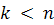 . Рекуррентная формула, следующая из
(1.4), может быть представлена следующим образом.
. Рекуррентная формула, следующая из
(1.4), может быть представлена следующим образом.
Теорема Цикловой индекс
симметрической группы удовлетворяет рекуррентному соотношению
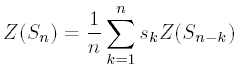
Пример




1.2 Эквивалентность, порождаемая группой
подстановок
Отношение эквивалентности
Отношение эквивалентности 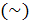
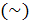 на множестве
на множестве 
 - это бинарное отношение, для
которого выполнены следующие условия:
- это бинарное отношение, для
которого выполнены следующие условия:
· Рефлексивность: 
 для любого
для любого 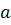
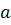 в
в 
 ,
,
· Симметричность: если 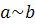
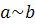 , то
, то 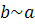
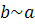 ,
,
· Транзитивность: если 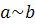
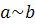 и
и 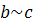
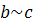 , то
, то 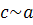
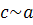 .
.
Запись вида «
 » читается как « a эквивалентно
b».
» читается как « a эквивалентно
b».
Пусть A - группа подстановок с
множеством объектов 
 . Элементы x и y из X называются
A-эквивалентными, если существует подстановка a из A, такая, что
. Элементы x и y из X называются
A-эквивалентными, если существует подстановка a из A, такая, что 
 . Нетрудно показать, что введенное
нами отношение есть отношение эквивалентности. Множество X разбивается на
классы эквивалентности. Эти классы называются орбитами.
. Нетрудно показать, что введенное
нами отношение есть отношение эквивалентности. Множество X разбивается на
классы эквивалентности. Эти классы называются орбитами.
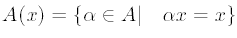
Для каждого x из X положим
Так определенное множество A(x)
называется стабилизатором элемента x. Нетрудно видеть, что стабилизатор
является подгруппой группы A. Заметим, что всякий раз, когда элементы x и y
принадлежат одной и той же орбите, множества A(x) и A(y) являются сопряженными
подгруппами группы A (то есть существует такая подстановка a из A, что 
 и, следовательно, |A(x)| = |A(y)|.
и, следовательно, |A(x)| = |A(y)|.
Теорема
Для любого элемента y из орбиты Y
группы A выполнятся следующее соотношение
|A| = |A(y)| · |Y|
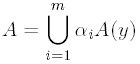
Доказательство. Разложим группу A в
объединение правых классов смежности по подгруппе A(y):
Теперь остается только указать
естественноe взаимно однозначное соответствие между этими классами смежности и
элементами орбиты Y. Для каждого 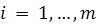
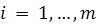 сопоставляем классу смежности
сопоставляем классу смежности 
 элемент
элемент 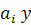
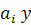 из Y. Если i не равно j, то
из Y. Если i не равно j, то 
 y не равно
y не равно 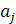
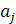 y, так как иначе бы подстановка
y, так как иначе бы подстановка 
 принадлежала подгруппе A(y) и,
следовательно, подстановка
принадлежала подгруппе A(y) и,
следовательно, подстановка 
 являлась бы элементом множества
являлась бы элементом множества 
 A(y), что противоречит соотношению
A(y), что противоречит соотношению 
 A(y) ∩
A(y) ∩ 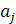
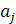 A(y) = Ø. Значит,
указанное соответствие является взаимно однозначным. Для всякого объекта y′
из Y при некоторой подстановке a из A выполняется равенство ay = y′. Из
разложения группы A на классы смежности следует, что
A(y) = Ø. Значит,
указанное соответствие является взаимно однозначным. Для всякого объекта y′
из Y при некоторой подстановке a из A выполняется равенство ay = y′. Из
разложения группы A на классы смежности следует, что 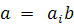
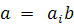 , если b принадлежит A(y).
Следовательно,
, если b принадлежит A(y).
Следовательно, 
 и, таким образом, каждый элемент
орбиты Y соответствует некоторому классу смежности. Значит, m есть число
элементов в орбите Y и формула (1.7) доказана.
и, таким образом, каждый элемент
орбиты Y соответствует некоторому классу смежности. Значит, m есть число
элементов в орбите Y и формула (1.7) доказана.
Теперь мы подготовлены к
доказательству леммы, в которой дается формула, выражающая число N(A) орбит
группы A как среднее арифметическое числа неподвижных точек всех подстановок
группы A.
Лемма Бернсайда
Число N(A) орбит группы A дается
формулой

Доказательство. Пусть 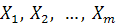
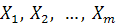 - орбиты группы A, и для каждого
- орбиты группы A, и для каждого 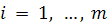
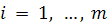 пусть
пусть 
 - элемент i-й орбиты
- элемент i-й орбиты 
 . Тогда из формулы (1.7) имеем
. Тогда из формулы (1.7) имеем

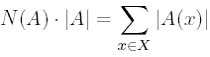
Мы видели, что если x и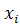
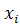 принадлежат одной и той же орбите,
то
принадлежат одной и той же орбите,
то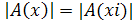
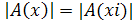 . Следовательно, соотношение (1.9)
можно записать так:
. Следовательно, соотношение (1.9)
можно записать так:


или, в других обозначениях,
Теперь, меняя порядок суммирования в правой
части формулы (1.9) и изменяя соответствующим образом индексы суммирования,
имеем

Также нам нужно будет ограничивать
действие группы A на некоторое подмножество Y множества X, где Y объединение
каких-либо орбит группы A. Поэтому обозначим через A|Y множество подстановок,
действующих на Y и получающихся с помощью ограничения на подмножество Y
соответствующих подстановок группыA. Для каждой подстановки a из группы A число
элементов в Y, неподвижных относительно подстановки a, обозначим через 
 . Теперь можно сформулировать
следствие леммы Бернсайда.
. Теперь можно сформулировать
следствие леммы Бернсайда.
Ограниченная форма леммы Бернсайда
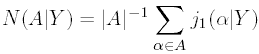
1.3 Теорема Пойа
Пусть A - группа подстановок с
множеством объектов 
 и пусть B - конечная группа
подстановок со счетным множеством объектов Y, содержащим не менее двух
элементов. Тогда степенная группа, обозначаемая
и пусть B - конечная группа
подстановок со счетным множеством объектов Y, содержащим не менее двух
элементов. Тогда степенная группа, обозначаемая 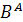
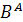 , имеет в качестве множества
объектов совокупность
, имеет в качестве множества
объектов совокупность 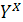
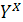 всех функций, действующих из X в Y.
Подстановками группы
всех функций, действующих из X в Y.
Подстановками группы 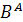
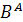 являются все упорядоченные пары
подстановок a из A и b из B, записываемые в виде (a, b). Образ произвольной
функции f из
являются все упорядоченные пары
подстановок a из A и b из B, записываемые в виде (a, b). Образ произвольной
функции f из 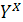
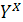 при действии на нее подстановки (a,
b) дается формулой
при действии на нее подстановки (a,
b) дается формулой
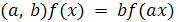
при всех x из X.
Для того, чтобы привести
классическую формулу перечисления Пойа, мы возьмем B = E - единичной группе на
множестве Y. Рассмотрим теперь степенную группу 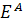
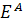 , действующую на множестве
, действующую на множестве 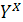
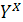 . Пусть
. Пусть 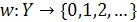
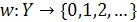 - функция, область значений которой
является множеством неотрицательных целых чисел и для которой
- функция, область значений которой
является множеством неотрицательных целых чисел и для которой 
 при всех k. В терминах теории
перечисления
при всех k. В терминах теории
перечисления 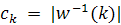
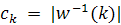 для каждого
для каждого 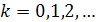
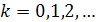 называют числом «фигур» веса k.
называют числом «фигур» веса k.
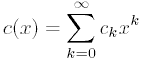
Об элементе y из Y, для которого 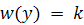
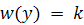 , говорят, что он имеет вес k, а
функцию w называют весовой функцией. Далее, ряд
, говорят, что он имеет вес k, а
функцию w называют весовой функцией. Далее, ряд
относительно переменной x, который
перечисляет элементы множества Y в соответствии с их весами, называют
«перечисляющим рядом для фигур».
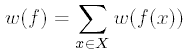
Вес функции f из YX определяется
формулой
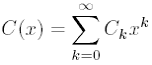
и тогда нетрудно показать, что
функции, принадлежащие одной и той же орбите степенной группы 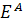
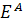 , имеют одинаковые веса. Весом w(F)
орбиты F группы
, имеют одинаковые веса. Весом w(F)
орбиты F группы 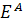
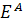 назовем вес любой функции f из
орбиты F. Так как
назовем вес любой функции f из
орбиты F. Так как 
 для всякого k = 0, 1, 2, …, то
существует только конечное число орбит каждого веса. Обозначим через
для всякого k = 0, 1, 2, …, то
существует только конечное число орбит каждого веса. Обозначим через 
 число орбит веса k. Ряд
относительно переменной x назовем «перечисляющим рядом для функций» или
«перечисляющим рядом для конфигураций».
число орбит веса k. Ряд
относительно переменной x назовем «перечисляющим рядом для функций» или
«перечисляющим рядом для конфигураций».
Теперь мы можем сформулировать
основную теорему, выражающую ряд C(x) в терминах циклового индекса Z(A) и ряда
c(x). В приводимой ниже формуле Z(A, c(x)) является сокращением для Z(A, c(x),
c(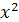
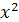 ), c(
), c(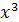
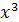 ), …).
), …).
Теорема (теорема перечисления Пойа,
1927)
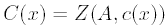
Ряд C(x), перечисляющий функции,
получается с помощью подстановки в цикловой индекс Z(A) на место каждой
переменной 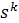
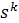 ряда
ряда 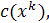
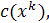 перечисляющего фигуры.
Символически:
перечисляющего фигуры.
Символически:

Доказательство. Пусть e -
тождественная подстановка на Y. Для всякой подстановки a из A и любого k = 0,
1, 2, … обозначим через ц(a, k) число функций веса k, неподвижных относительно
подстановки (a; e). Ограничивая для каждого k действие степенной группы 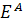
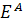 на множество функций веса k и
применяя ограниченную форму леммы Бернсайда (1.13), имеем
на множество функций веса k и
применяя ограниченную форму леммы Бернсайда (1.13), имеем
Следовательно,
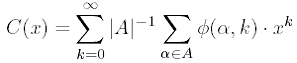
и, меняя порядок суммирования,
получаем

Ряд 
 перечисляет все функции,
неподвижные относительно подстановки (a; e), и мы постараемся найти другую
форму для этого ряда.
перечисляет все функции,
неподвижные относительно подстановки (a; e), и мы постараемся найти другую
форму для этого ряда.
Предположим, что функция f из 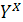
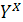 непожвижна относительно подстановки
(a; e). Тогда
непожвижна относительно подстановки
(a; e). Тогда 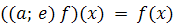
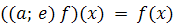 для всех x из X и в силу формулы
(1.14), имеем
для всех x из X и в силу формулы
(1.14), имеем 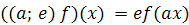
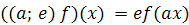 . Таким образом, для всех x должно
выполняться равенство
. Таким образом, для всех x должно
выполняться равенство 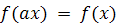
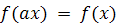 , то есть функция f должна быть
постоянной на непересекающихся циклах подстановки a. Обратно, все функции,
постоянные на циклах подстановки a, неподвижны относительно подстановки (a; e).
, то есть функция f должна быть
постоянной на непересекающихся циклах подстановки a. Обратно, все функции,
постоянные на циклах подстановки a, неподвижны относительно подстановки (a; e).
Пусть 
 - цикл длины r в подстановке a.
Если функция f отображает элементы цикла
- цикл длины r в подстановке a.
Если функция f отображает элементы цикла 
 в один из
в один из 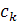
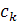 элементов множества Y, имеющих вес
k, то цикл
элементов множества Y, имеющих вес
k, то цикл 
 вносит в вес функции f значение
r·k. Тогда легко видеть, что для каждого k коэффициент при
вносит в вес функции f значение
r·k. Тогда легко видеть, что для каждого k коэффициент при 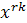
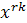 в ряду
в ряду

равен числу способов, которыми можно
определить функцию f на элементах цикла 
 так, чтобы она была неподвижна
относительно подстановки (a; e) и чтобы вклад в вес w(f) составлял r·k. Отсюда
следует, что ряд
так, чтобы она была неподвижна
относительно подстановки (a; e) и чтобы вклад в вес w(f) составлял r·k. Отсюда
следует, что ряд 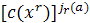
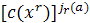 перечисляет в соответствии с их
весами различные способы определения функций, постоянных на всех циклах длины r
подстановки a.
перечисляет в соответствии с их
весами различные способы определения функций, постоянных на всех циклах длины r
подстановки a.
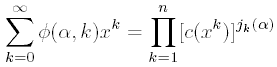
Рассматривая все циклы подстановки
a, мы можем выразить ряд для функций, постоянных на циклах, в виде произведения
Теперь утверждение теоремы Пойа (18)
следует из (1.21), (1.23) и определения циклового индекса Z(A).
2. Практическое применение Теоремы Пойа и
перечисления графов
.1 Решение задач о перечислении графов с
помощью теоремы Пойа
Мы будем перечислять графы с n
вершинами. Мы считаем, что задана некая нумерация множества вершин V, т.е. 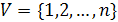
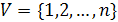 . Множество X, с которым мы будем
работать, это множество функций, область определения которых - это множество
пар вершин (т.е. пар чисел)
. Множество X, с которым мы будем
работать, это множество функций, область определения которых - это множество
пар вершин (т.е. пар чисел)
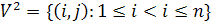
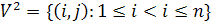 ,
,
а область значений это множество из
двух элементов {0,1}. Такая функция полностью описывает граф: если 
 i-я и j-я вершины не соединены
ребром а если
i-я и j-я вершины не соединены
ребром а если 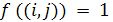
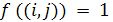 - то соединены. Иначе это можно
описать так: рассмотрим полный граф
- то соединены. Иначе это можно
описать так: рассмотрим полный граф 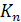
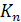 , т.е. граф с n вершинами, где
каждая пара вершин соединена ребром. Раскрасим множество ребер графа
, т.е. граф с n вершинами, где
каждая пара вершин соединена ребром. Раскрасим множество ребер графа 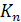
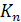 в два цвета - черный и белый.
Теперь удалим белые ребра.
в два цвета - черный и белый.
Теперь удалим белые ребра.
Группа перестановок действует на
множестве V (перенумерация вершин). Но она действует и на множестве 
 следующим образом. Перестановку s мы
рассматриваем как отображение множества {1, 2, . . . , n} в себя. Так
перестановка s = 2, 4, 1, 3 - это отображение s : {1, 2, 3, 4} → {1, 2,
3, 4}: s(1) = 2, s(2) = 4, s(3) = 1, s(4) = 3. Перестановка s действует на
множестве
следующим образом. Перестановку s мы
рассматриваем как отображение множества {1, 2, . . . , n} в себя. Так
перестановка s = 2, 4, 1, 3 - это отображение s : {1, 2, 3, 4} → {1, 2,
3, 4}: s(1) = 2, s(2) = 4, s(3) = 1, s(4) = 3. Перестановка s действует на
множестве 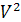
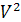 так: s переводит пару (i, j) в пару
(s(i), s(j)), если s(i) < s(j), и в пару (s(j), s(i)) в противном случае. В
терминах теоремы Пойя множество
так: s переводит пару (i, j) в пару
(s(i), s(j)), если s(i) < s(j), и в пару (s(j), s(i)) в противном случае. В
терминах теоремы Пойя множество 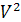
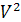 - это множество M , а множество X -
это множество раскрасок элементов
- это множество M , а множество X -
это множество раскрасок элементов 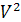
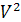 в два цвета - черный и белый. Выбор
раскраски задает граф, а перенумерация вершин дает другую раскраску
в два цвета - черный и белый. Выбор
раскраски задает граф, а перенумерация вершин дает другую раскраску 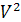
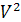 , но изоморфный граф.
, но изоморфный граф.
Пример. Пусть n = 4. Перестановка s
= 2, 4, 1, 3 действует на 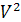
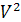 так:
так:
s((1,2))=(2,4),s((1,3))=(1,2),s((1,4))=(2,3),s((2,3))=(1,4)s((2,4))=(3,4)),s((3,4))=
(1, 3).
Если ((1, 2)) =
0, f ((1, 3)) = 1, f ((1, 4)) = 0, f ((2, 3)) = 0, f ((2, 4)) = 1, f ((3, 4)) =
1, то
((1, 2)) = 1, g((1, 3)) = 1, g((1, 4)) = 0, g((2, 3)) = 0, g((2, 4)) = 0, g((3,
4)) = 1,
где g
= s(f
).
Функции f и g задают следующие графы

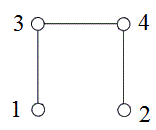
Рисунок 2.1 - граф f.
Рисунок 2.2 - граф g.
Разумеется эти графы изоморфны.
Число графов - это число орбит
действия группы Sn на множестве раскраскок множества 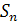
 в два цвета. Чтобы найти число орбит
нам нужно вычислить цикловый индекс действия
в два цвета. Чтобы найти число орбит
нам нужно вычислить цикловый индекс действия 
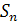 на
на 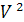
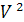 .
.
Пример. n = 3. Рассмотрим действие
группы 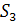
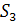 на
на 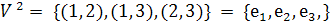
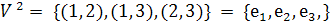 . Имеем
. Имеем
· s = e. Действие s: (
 )(
)(
 ))(
))(
 ).
).
· s = (1,
2)(3). Действие s: (
 )(
)(
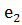 ,
, 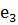
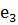 ).
).
· s = (1,
3)(2). Действие s: (
 ,
, 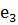
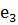 )
)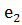
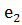 ).
).
· s = (1)(2,
3). Действие s: (
 ,
, 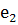
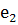 )(
)(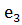
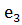 ).
).
· s = (1, 2,
3). Действие s: (
 ).
).
· s = (1, 3, 2). Действие s: (
 ).
).
Таким образом, 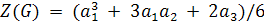
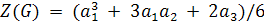 . Пусть переменная x отвечает белому
цвету, а y - черному.
. Пусть переменная x отвечает белому
цвету, а y - черному.
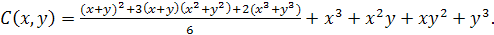
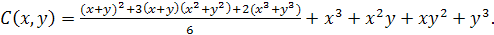 (2.1)
(2.1)
Это означает, что у нас есть четыре
графа с тремя вершинами: один граф без ребер, один с одним ребром, один с двумя
ребрами и один с тремя ребрами.
Пример. n = 4. Рассмотрим действие
группы 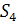
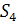 на
на 
 . одночлен -
. одночлен - 
 .
.
· 2-цикл, например (1, 2)(3)(4), действует так:
(1, 2) и (3, 4) неподвижны; (1, 3) → (2, 3) → (1, 3); (1, 4) →(2,
4) → (1, 4). Соответствующий одночлен -
 . Так как в
. Так как в 
 шесть 2-циклов, то они дают в
цикловый индекс вклад
шесть 2-циклов, то они дают в
цикловый индекс вклад 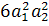
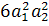
· 3-цикл, например (1, 2, 3)(4), действует так:
(1, 2) → (2, 3) → (1, 3) → (1, 2); (1, 4) → (2, 4) →
(3, 4) →(1, 4). Соответствующий одночлен - 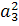
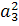 . Так как в
. Так как в 
 восемь 2-циклов, то они дают в
цикловый индекс вклад 8
восемь 2-циклов, то они дают в
цикловый индекс вклад 8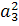
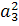 .
.
· 4-цикл, например (1, 2, 3, 4), действует так:
(1, 2) → (2, 3) → (3, 4) → (1, 4) → (1, 2); (1, 3) →
(2, 4) →(1, 3). Соответствующий одночлен -
 . Так как в
. Так как в 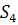
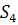 шесть 4-циклов, то они дают в
цикловый индекс вклад
шесть 4-циклов, то они дают в
цикловый индекс вклад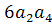
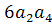 .
.
· 2,2-цикл, например (1, 2)(3, 4), действует так:
(1, 2) и (3, 4) неподвижны; (1, 3) → (2, 4) → (1, 3); (1, 4) →2,
3) → (1, 4). Соответствующий одночлен - 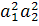
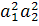 . Так как в S4 три 2,2-цикла, то они
дают в цикловый индекс вклад
. Так как в S4 три 2,2-цикла, то они
дают в цикловый индекс вклад 
 .
.
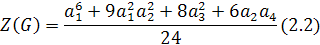
Пример. Пусть n = 4. Мы знаем, что 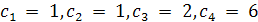
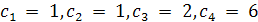 . Имеется 5 разбиений числа 4: 4, 3
+ 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.
. Имеется 5 разбиений числа 4: 4, 3
+ 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.
· Первое разбиение отвечает случаю
связного графа - таких графов 6.
· Второе разбиение отвечает случаю
двух компонент связности - с тремя вершинами и с одной вершиной. Таких графов
2.
· Третье разбиение отвечает случаю
двух компонент связности - с двумя вершинами каждая. Такой граф один.
· Четвертое разбиение отвечает случаю
трех компонент связности - одна с двумя вершинами и две с одной вершиной. Такой
графов один.
Следовательно, 
 = 11.
= 11.
На языке производящих рядов эту
конструкцию можно описать так. Количество графов с n вершинами равно
коэффициенту при tn в произведении рядов
(1+ 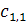
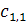 t +
t + 
 +
+ 
 +. . .) × (1+
+. . .) × (1+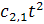
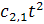 +
+ 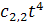
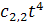 +. . .)×(1+
+. . .)×(1+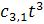
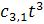 +
+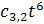
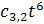 +. . .)×. . .
+. . .)×. . .
Здесь коэффициент 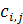
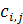 равен числу графов, состоящих из j
связных компонент, причем каждая компонента имеет i вершин. Тоесть
равен числу графов, состоящих из j
связных компонент, причем каждая компонента имеет i вершин. Тоесть 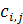
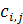 - это количество способов выбрать j
связных графов из
- это количество способов выбрать j
связных графов из 
 , причем в выборке могут быть и
одинаковые графы.
, причем в выборке могут быть и
одинаковые графы.
Таким образом,
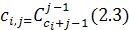
и i-й сомножитель в произведении есть

Следовательно
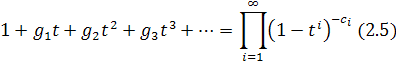
Перейдем к логарифмам

Разложим каждый логарифм в ряд и
приведем подобные. Легко видеть, что в разложении 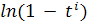
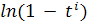 в степенной ряд слагаемое
появляется лишь в том случае, когда i - делитель n. Тогда соответствующий
коэффициент равен
в степенной ряд слагаемое
появляется лишь в том случае, когда i - делитель n. Тогда соответствующий
коэффициент равен 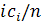
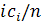 . Следовательно,
. Следовательно,

Где
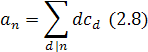
Здесь сумма берется по всем делителям числа n.
Таким образом,
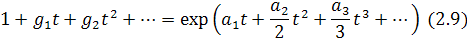
Правило перехода от 
 достаточно простое. Действительно,
продифференцируем это равенство. Имеем (2.10)
достаточно простое. Действительно,
продифференцируем это равенство. Имеем (2.10)
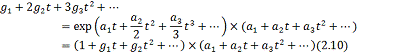
Теперь сравниваем коэффициенты при 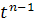
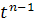 :
:

Так как 
 , то мы получили рекуррентную
формулу для вычисления чисел
, то мы получили рекуррентную
формулу для вычисления чисел
Пример. Найти количество ожерелий,
составленных из n бусинок двух цветов. Ожерелья, совпадающие при повороте,
считаются одинаковыми.
Пусть множество 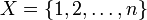 соответствует номерам бусинок в ожерелье, а
соответствует номерам бусинок в ожерелье, а 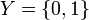 - множество возможных цветов. Весовую функцию положим равной
- множество возможных цветов. Весовую функцию положим равной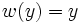 для всех
для всех 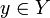 . Во
множестве
. Во
множестве 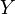 имеется
один элемент веса 0 и один - веса 1, то есть
имеется
один элемент веса 0 и один - веса 1, то есть  и
и  .
Откуда
.
Откуда 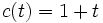 .
.
Пусть  - множество всех функций из
- множество всех функций из  в
в 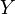 . Любая
функция
. Любая
функция 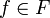 задает некоторое ожерелье и, наоборот, каждое ожерелье задаётся
некоторой функцией из
задает некоторое ожерелье и, наоборот, каждое ожерелье задаётся
некоторой функцией из  . При
этом вес функции равен количеству бусинок цвета 1 в соответствующем ожерелье.
. При
этом вес функции равен количеству бусинок цвета 1 в соответствующем ожерелье.
На множестве  действует группа поворотов
действует группа поворотов  , порожденная циклической перестановкой
, порожденная циклической перестановкой  , которая определяет отношение эквивалентности на
, которая определяет отношение эквивалентности на  . Тогда ожерелья совпадающие при повороте будут в точности
соответствовать эквивалентным функциям, и задача сводится к подсчёту числа
орбит.
. Тогда ожерелья совпадающие при повороте будут в точности
соответствовать эквивалентным функциям, и задача сводится к подсчёту числа
орбит.
Цикловой индекс группы  равен
равен
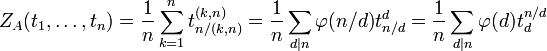 ,
,
где 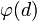 - функция Эйлера,
- функция Эйлера, 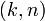 -
наибольший общий делитель чисел
-
наибольший общий делитель чисел  и
и 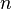 .
.
По теореме Редфилда-Пойа
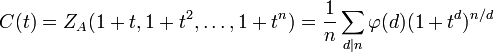
Число орбит веса  (то есть различных ожерельев с
(то есть различных ожерельев с  бусинками цвета 1) равно
бусинками цвета 1) равно  , коэффициенту при
, коэффициенту при 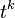 в
в  :
:
 .
.
Общее число различных орбит (или
ожерелий) равно

Заключение
Сейчас почти в любой отрасли науки и техники
встречается применение графов. В физике - при построении электрических схем, в
химии и биологии- при изучении молекул и их цепочек, в географии - при
составлении карт, в истории - при составлении родословной, в геометрии - в
чертежах многоугольников, многогранников, пространственных фигур, в экономике -
при решении задач о выборе оптимального пути для потоков грузового транспорта
(схем авиалиний, метро, железных дорог).
Графами являются блок-схемы программ для ЭВМ,
сетевые графики строительства. С помощью графов решается задача о назначении на
должности.
Изучая теорию перечисления графов приходится
решать проблемы изоморфизмов для многих классов графов. Теорема перечисления
Пойа, когда она впервые стала широко цениться в начале 1960-х, служила основным
инструментом для решения проблем изоморфизмов.
В данной курсовая работе я изучила описание
этого инструмента. Для осознания проблемы я рассмотрела перечисление помеченных
графов, это наиболее простая задача из теории перечисления. Затем рассмотрела
основные виды графов, понятие теории графов и теории групп, понятие
эквивалентности, лемму Бернсайда (William Burnside) и, наконец, доказала
теорему Пойа.
Итак, практический смысл теории перечисления
графов состоит в том, чтобы подсчитать число графов определённого класса и
оценить трудоёмкость задач, связанных с перечислением выявленного множества
объектов. Теорема Пойа даёт нам механизм для проведения подобной оценки.
Список используемых источников
1. Burnside, William
Theory of groups of finite order. - Cambridge University Press, 1897.
. Diestel R. Graph
Theory, Electronic Edition. - NY: Springer-Verlag, 2005.
3. Балашова Н.А., Кукин Г.П.
Комбинаторика. Омск, 1992.
. Басакер Р., Саати Т.
Конечные графы и сети М., Наука, 1974
. Белов В.В., Воробьев Е.М.,
Шаталов В.Е. Теория графов. М.: ВШ, 1976.
. Березина Л.Ю. Графы и их
применения: Пособие для учителей. - М., 1979
. Берж К. Теория графов и ее
приложения. М.: ИЛ, 1962.
. Емеличев В.А. Лекции по
теории графов. - М.: Наука, 1990.
. Зелянин Р.В. Некоторые
задачи перечисления графов - Сыктывкарский ГУ (сайт).
. Зыков А. А. Основы теории графов.
- М.: «Вузовская книга», 2004.
. Калужнин Л.А.,
СущанскийВ.И. Преобразования и перестановки - М.: Наука,1985
12. Камерон П., ван Линт Дж.
Теория графов. Теория кодирования и блок-схемы. М.: Наука,
1980.
. Комбинаторная прикладная
математика / Под ред. Э.Беккенбаха. - М.: Мир, 1968.
. Комбинаторный анализ.
Задачи и упражнения. - М.: Наука 1982
. Кофман А., Фор Р. Займемся
исследованием операций. М.: Мир, 1966
. Кристофидес Н.Теория
графов. Алгоритмический подход. М.: Мир, 1978.
. Липский В. Комбинаторика
для программистов: Пер. с польск. - М.: Мир, 1988.
. Оре О. Графы и их
применение. М., Мир, 1965.
. Оре О. Теория графов. - М.:
Наука, 1968.
. Перечислительные задачи
комбинаторного анализа / Сборник переводов под редакцией Г.П. Гаврилова. - М.:
Мир, 1979.
. Салий В.Н. Богомолов А. М.
Алгебраические основы теории дискретных систем. - М.: Физико-математическая
литература, 1997.
. Татт У. Теория графов. Пер.
с англ. М.: Мир, 1988.
. Уилсон Р. Введение в теорию
графов М.: Мир, 1977.
. Харари Ф. Теория графов. -
М.: Мир, 1973.
. Харари Ф., Палмер Э.
Перечисление графов: Пер. с. англ. - М.: Мир, 1977.
. Яковенко Д.И. Задача об
ожерельях // Вестник Омского университета. - 1998. - В. 2. - С. 21-24.