Приблизительное решение нелинейного уравнения (метод касательных)

Приблизительное решение нелинейного уравнения (метод касательных)

Кафедра інформаційних систем та технологій

КУРСОВА РОБОТА

на тему

Наближене розв’язання нелінійного рівняння (метод дотичних)

з дисципліни Основи програмування та алгоритмічні мови

Виконав: студентка 2 курсу, 206 група

факультету ІСТ Безнощенко Т.С.

Керівник: к.т.н. Стешенко В.І.

Донецьк - 2005 р.

Содержание

1. Титульный лист

. Содержание

. Введение

. Постановка задачи

.1 Обзор существующих методов

.2 Анализ метода касательных (метода секущих Ньютона)

.3 Решение нелинейного уравнения аналитически

. Описание алгоритма решения задачи

.1 Описание пользовательских идентификаторов

.2 Блок-схема программы

.3 Описание блок-схем

. Тестирование программы на контрольном примере

. Сравнительный анализ данных ручного просчета и машинных экспериментов

. Описание программного обеспечения

.1 Описание ОС

.2 Описание среды программирования

.3 Описание программных модулей

Вывод

Список литературы

Приложение

3. Введение

В данной курсовой работе рассмотрена тема приблизительного решения нелинейного уравнения методом касательных, который также называется методом секущих Ньютона.

При решении задач математической физики (при исследовании колебаний стержней, пластин и оболочек, при изучении тепловых полей и т.д.) с использованием метода Фурье, возникает необходимость решения трансцендентных уравнений. Большинство задач инерции движения твердых тел сводятся к решению алгебраических уравнений n-ой степени.

Решение некоторых задач непосредственно сводятся к нахождению корней трансцендентных уравнений. Например, простейшая цепь (рис.1) состоит из источника έ, нелинейного элемента (диод, транзистор и т.д.) RH и резистора нагрузки с сопротивлением R. Необходимо найти ток в цепи IA и напряжение на нелинейном элементе UА.

 0

Рис.1

Напряжение и ток резистора рассчитывается согласно закону Ома для замкнутой цепи с помощью уравнения U=E-IR. Нелинейный элемент определяется вольтамперной характеристикой U=U(I). В результате для определения параметров IA и UA получаем нелинейное уравнение относительно I: U(I)=E-IR.

Чтобы решить нелинейное уравнение f(x)=0, где f(x) - алгебраическая или трансцендентная функция, определенная и непрерывная на конечном или бесконечном интервале a<x<b, необходимо пройти 2 этапа:

-й этап: выделение корней, то есть нахождение промежутков, в которых содержится только один корень уравнения;

-й этап: уточнение приближенных корней, то есть получение значений корня с заданной точностью.

4. Постановка задачи

.1 Обзор существующих методов

Для решения нелинейных уравнений пользуются следующими методами: метод хорд, метод итераций, метод половинного деления, комбинированный метод, метод касательных, метод перебора, метод хорд-касательных. Рассмотрим первые три метода.

. Метод хорд. Заменим на отрезке [a,b] кривую y=f(x) хордой, которая соединяет точки А и В (рис.1.). За приближенное значение корня выберем точку пересечения хорды с осью ох. Значение функции f(x1) сравниваем со значениями f(a) и f(b). В дальнейшем рассматриваем отрезок [a1,b1]=[a1,x1], если f(a)f(x1)<0, и отрезок [a1,b1]=[x1,b] в противном случае. Для нахождения приближенного значения корня имеем формулу:

+1=xn+c-xn/1-f(c)/f(xn)

где xn+c-xn - числитель,

-f(c)/f(xn) - знаменатель,

С - неподвижный конец отрезка [a,b].

За неподвижный конец следует выбирать точку с=а, если f(a)f”(a)>0, и точку с=b, если f(b)f”(b)>0.

В случае, когда имеет место неравенство

М≤2m1,

где=min|f’(x)|, M1=max|f’(x)|

[a,b]  [a,b]

для оценки неточности можно пользоваться формулой

|x*-x|<|xn+1-xn|<ε

(Рис.1)

Недостаток этого метода в неточности вычислений.

. Метод итераций. При решении нелинейного уравнения методом итераций пользуются записью уравнения в виде x=f(x). (Уравнение f(x)=0 заменили равнозначным). Задаются начальное значение аргумента x0 и точность ε. Первое приближение решения x1 находим из выражения x1=f(x0), второе - x2=f(x1) и т.д. В общем случае i+1 приближение найдем по формуле xi+1 =f(xi). Указанную процедуру повторяем пока |f(xi)|>ε. Условие сходимости метода итераций |f'(x)|<1.

Недостатки данного метода в том, что необходимо вводить вспомогательную функцию и в неудобстве вычисления. Но в то же время, простая итерационная формула и не нужны дополнительные исследования функций.

. Метод половинного деления. При решении нелинейного уравнения методом половинного деления задаются интервал [a,b], на котором существует только одно решение, и желаемая точность ε. Затем определяется середина интервала с=(а+b)/2 и проверяется условие F(a)∙F(c)<0. Если указанное условие выполняется, то правую границу интервала b переносим в среднюю точку с (b=c). Если условие не выполняется, то в среднюю точку переносим левую границу(a=c). Деление отрезка пополам продолжается пока |b-a|>ε.

Эти методы используются лишь для непрерывных функций и ищут только действительные корни. (Исключением является метод Лобачевского, который позволяет находить и комплексные корни).

.2 Анализ метода касательных (метод секущих Ньютона)

В основу метода касательных лежит идея линеаризации. Но в этом случае, кривая y=f(x) последовательно замещается касательными, для которых находится точка пересечения с осью ox (рис.2) (в случае действительных корней). Формула для последовательных приближений к корню:

+1=xn-f(xn)/f’(xn)

Причем, x0=a, если f(a)f”(a)>0, и x0=b, если f(b)f”(b)>0.

Метод Ньютона наиболее эффективен при решении тех уравнений, у которых значение модуля производной |f’(x)| приближения корня достаточно велик, то есть график функции f(x) вокруг данного корня имеет быструю сходимость.

Для контроля сходимости можно использовать условие:

|xn+1-xn|<√2m1ε/M2, где M2=max|f”(x)|

[a,b]

(Рис.2)

.3 Решение нелинейного уравнения аналитически

Метод Ньютона рассмотрен на нижеприведенном уравнении:

¹-x³-2x²+3x-3=0

-й этап: нахождение промежутков, в которых находится корень уравнения.

(x)= x¹-x³-2x²+3x-3

Область допустимых значений функции f(x) вся числовая ось: є]-∞,∞[.

Найдем f’(x): f’(x)=4x³-3x²-4x+3

Найдем корни производной: 4x³-3x²-4x+3=0

x(x²-1)-3(x²-1)=0

(x²-1)(4x-3)=0=-1; =1; =3/4.

Составим таблицу значений функции f(x):

То есть, уравнение имеет 2 действительных корня, которые находятся на промежутках: x1є]-∞,-1[ и x2є]1,∞[.

Уменьшим промежутки, которые имеют корни таким образом, чтоб их длина была не больше единицы:

Отсюда видно, что x1є]-2,-1[; x2є]1,2[.

-й этап: уточнение корней при помощи метода Ньютона.

Рассмотрим промежуток [-2;-1], где находится первый корень x1.

’=4x³-3x²-4x+3”=12x²-6x-4(a)*F2(a)=392 >0

Заметка: под f1(a) подразумевается 1-я производная, а под F2(a) подразумевается 2-я производная.

’=4x³-3x²-4x+3=min|y’(x)|

[-2;-1]

x²-6x-4=0

x²-3x-2=0=b²-4ac=9+48=57,2=-b±√D/2a,2=3±√57/12=0,87 - не принадлежит отрезку [-2;-1]=-0,38

|f’(-2)|=|-33| ’(-0,38)=3,87’(-1)=0 m1(min)=0”’=24x-6 ”(-2)=56”(-1)=14 M2(max)=56

Ниже данные сгруппированы в таблицу:

Расчеты и график функции, сделанные в Excel:

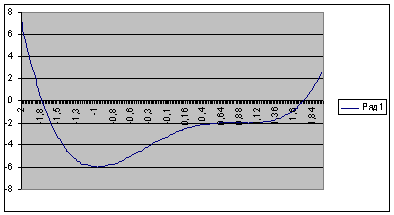
Как видно из расчетов таблицы, первый корень рамен: -1,73205.

Рассмотрим промежуток [1;2], где находится второй корень x2.

’=4x³-3x²-4x+3”=12x²-6x-4

(f’и f”такие же как и для первого корня)

Теперь ищем m1 и M2:

|f’(1)|=|0|

|f’(2)|=|15| m1(min)=0

|f”(1)|=|2|

|f”(2)|=|32| M2(max)=32

Ниже данные сгруппированы в таблицу:

Расчеты и график функции, сделанные в Excel:

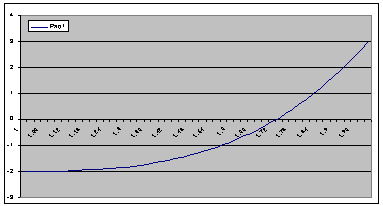
Как видно из расчетов таблицы, второй корень равен: -1,732051.

5. Описание алгоритма решения задачи

.1 Описание пользовательских идентификаторов

- константа, типа real (вещественный тип), размер: 8 байт, в 1 случае равная -2, во 2 случае 1; обозначает край промежутка, на котором находится корень уравнения.- константа, типа real (вещественный тип), размер: 8 байт, в 1 случае равная -1, во 2 случае 2; обозначает край промежутка, на котором находится корень уравнения.- константа, равная 0,0000000001, типа real (вещественный тип), размер 8 байт; обозначает погрешность.- константа, типа integer (целого типа), размер 4 байта, в 1 случае равная 0 и во 2 случае также равна 0. Обозначает минимальное значение (по модулю) производной значения точки (-1) в первом случае и точки (1) во втором случае.- константа, типа integer (целого типа), размер 4 байта, в 1 случае равная 56,во 2 случае равна 32. Обозначает максимальное значение (по модулю) производной значения точки (-2) в первом случае и точки (2) во втором случае.- переменная, вещественный тип, размер 8 байт, участвует в формулах по вычислению производной и функции.- переменная, вещественный тип, размер 8 байт, участвует в формулах по присвоению и вычислению значений.- переменная, вещественный тип, размер 8 байт, участвует в формулах по присвоению и вычислению значений.- локальная переменная, вещественного типа, размер 8 байт, это функция,которая вычисляется по формуле.- (также как и f) но явл.производной функции.- (также как f1) но в отличии от f1 является второй прозводной.

.2 Блок-схема программы

Основная блок-схема

Вспомогательные блок-схемы

Для f

Для f1-для нахождения приближений

Для f2-для нахождения края, с которого начинаются итерации

.3 Описание блок-схем программы

нелинейное уравнение программный алгоритм

Блок-схема №1

. Блок начала программы.

. Блок объявления констант.

. Блок объявления переменных.

. Проверка условия.

. Присвоение переменной значения в случае выполнения условия.

. Присвоение переменной значения в случае не выполнения условия.

. Расчет начального приближенного значения.

. Проверка следующего условия (начало цикла). В случае не выполнения, переходим к блоку 8. В случае выполнения, в цикл не заходим и сразу осуществляем переход к 10 блоку.

. Расчет приближенного значения.

. Вывод промежуточных результатов.

. Вывод окончательных результатов.

. Блок окончания программы.

. Блок начала программы.

. Ввод аргумента

. Расчет функции по формуле.

. Вывод результата f(x)

. Блок окончания программы.

Блок-схема №3

. Блок начала программы.

. Ввод аргумента

. Расчет функции по формуле.

. Вывод результата f1(x)

. Блок окончания программы.

Блок-схема №4

. Блок начала программы.

. Ввод аргумента

. Расчет функции по формуле.

. Вывод результата f2(x)

. Блок окончания программы.

6. Тестирование программы на контрольном примере

Программа была тестирована на следующем примере: x¹-x³-2x²+3x-3=0.

Результаты выполнения расчетов программой, написанной на языке программирования Turbo Pascal приведены ниже.

Правильность метода была проанализирована ручным расчетом.

A=-2.0000 do B=-1.0000E 0.0000000001= -1.7878787879 xn+1= -1.7351386122 f(xn+1)= 0.0615150328= -1.7351386122 xn+1= -1.7320609420 f(xn+1)= 0.0002012359= -1.7320609420 xn+1= -1.7320508077 f(xn+1)= 0.0000000022= -1.7320508077 xn+1= -1.7320508076 f(xn+1)= 0.0000000000= -1.7320508076 xn+1= -1.7320508076 f(xn+1)= 0.0000000000.znach= -1.7320508076f(xn1)= 0.0000000000korenA= 1.0000 do B= 2.0000E 0.0000000001= 1.8000000000 xn+1= 1.7377551020 f(xn+1)= 0.0451679035= 1.7377551020 xn+1= 1.7320951358 f(xn+1)= 0.0003482818= 1.7320951358 xn+1= 1.7320508103 f(xn+1)= 0.0000000212= 1.7320508103 xn+1= 1.7320508076 f(xn+1)= 0.0000000000= 1.7320508076 xn+1= 1.7320508076 f(xn+1)= 0.0000000000.znach= 1.7320508076f(xn1)= 0.0000000000

7. Сравнительный анализ данных ручного просчета и машинных экспериментов

Нижняя выделенная строка содержит окончательный ответ xn. Как видно из таблицы, численные значения приближений совпадают. Это говорит о правильности расчетов программы.

8. Описание программного обеспечения

.1 Описание ОС Windows

- популярная графическая операционная система. Она очень проста и удобна в эксплуатации. С каждой новой версией этих программных продуктов расширяется диапазон задач, которые ПК могут решать в различных сферах информационно-вычислительной деятельности.обеспечивает вытесняющую многозадачность и многопоточность. Пользовательские программы могут выполнятся с разделением во времени в различных окнах. Каждая программа может содержать несколько информационных потоков, которые одновременно решают самостоятельные задачи.

Совместимость между интерфейсами различных прикладных программ достигается в Windows благодаря 32-разрядному интерфейсу API (Application Program Interface - интерфейс прикладных программ), предоставляющему программистам полный набор функций и ресурсов для создания средств интерфейса, с помощью которого приложения могут управлять файлами или отображением информации на экране дисплея.

Одной из важнейших возможностей Windows является поддержка технологии самонастраивающихся устройств Plug and Play. Их назначение - распознавание операционной системой любых периферийных устройств и управление ими.располагает встроенными возможностями для организации одноранговой локальной сети. Операционная система поддерживает все основные протоколы и стандарты, автоматически анализирует параметры локальной сети.

Архитектура Windows построена на системе представлений об управлении виртуальной машиной в защищенном режиме работы процессора. Черты Windows:

Мультизадачный режим работы.

Оптимальное управление ресурсами компьютера.

Графический пользовательский интерфейс.

Наличие техники связывания и встраивания объектов других программ.

Возможность работы в сетевой среде.

Интерфейс мультимедиа.

.2 Описание среды программирования

Алгоритмический язык Паскаль разработан профессором Цюрихского технологического института Никлаусом Виртом в 1969-71 гг для обучения студентов структурному программированию. Идеи, заложенные в основу создания языка, позволили фирме Borland International значительно расширить алгоритмические средства языка, а удобное меню команд и высокая скорость компиляции сделали язык Турбо Паскаль одним из самых распространенных среди начинающих программистов.

Процесс программирования начинается, как правило, с составления алгоритма - последовательности операций, описывающих процесс решения задачи. Программирование заключается в записи алгоритма на языке программирования и отладки программы. Текст программы записывается в текстовом редакторе, затем программа компилируется - переводится транслятором (переводчиком) в машинные коды и запускается на выполнение. Процесс отладки программы начинается с выявления:

.Синтаксических ошибок в тексе;

.Алгоритмических ошибок (неверно составлении или запрограммирован алгоритм), и заканчивается, как правило написанием новой программы, т.к. программу можно усовершенствовать очень много раз, а отлаженную программу лучше уже не изменять.

Для загрузки среды Турбо-Паскаль запускается файл turbo.exe, расположенный в папке BIN.

Положительные черты:

Простота языка позволяет быстро его освоить и создавать алгоритмически сложные программы.

Развитые средства представления структур данных обеспечивает удобство работы как с числовой, так и с символьной и битовой информацией.

Наличие специальных методик создания трансляторов с паскаля упростило их разработку и способствовало широкому распространению языка.

Оптимизирующие средства трансляторов с паскаля позволяют создавать эффективные программы. Это послужило одной из причин использования паскаля в качестве языка системного программирования.

В языке паскаль реализованы идеи структурного программирования, что делает программу наглядной и дает хорошие возможности для разработки и отладки.

В минимальной конфигурации не требует инсталляции.

Процедурный язык.

Недостатки:

Работает под DOS.

Слабая преобразовываемость одних типов в другие.

Малое количество графических команд.

Невозможность работы с хорошим расширением.

Отсутствие функции возведения в степень.

.3 Описание программных модулей

Файл носит название: metod_kasatelnuh;

расширение: pas;

размер: 1,5 байт;

устанавливается: запуском из среды Turbo Pascal;

запуск: 1) Run-Run;

)Ctrl + F9;

)После компиляции программы на Паскале (Run-Run)

создается выполняемый exe - файл. Его можно запустить в двоичным щелчком.

Вывод

В данной курсовой работе был выполнен анализ метода решения нелинейных уравнений - метод касательных (метод Ньютона), выполнен анализ еще нескольких методов решения подобных уравнений. Также разработан алгоритм решения уравнения методом Ньютона, на основании которого и была написана программа в среде Turbo Pasсal.

Было выяснено, что метод касательных удобно применять для решения нелинейных уравнений.

Алгоритм решения задачи достаточно прост и его удобно представить в блок-схемах, на основе которых и составлялась в дальнейшем программа. Объем программы невелик, поэтому в качестве носителя могла использоваться дискета.

Список литературы

1. Алексеев В.Е., Ваулин А.С., Петрова Г.Б. - Вычислительная техника и программирование. Практикум по программированию: Практ.пособие/-М.: Высш.шк., 1991.-400с.

. Вычислительная техника и программирование: Учебник для техн. вузов/ Петров А.В., Алексеев В.Е., Ваулин А.С. и др.-М.: Высш.шк., 1990-479 с.

. Гусев В.А., Мордкович А.Г. - Математика: Справ. материалы: кн.для учащихся-2-е изд.М.:Просвещение, 1990.-416 с.

. Методичні указання (ДонНУ), с.25-30

. А.Гарнаев «Exel, VBA, Internet в экономике и финансах»: Санкт-Перергург,2001 г.

. «Введение в С++» Бьярн Страуструп (электронная версия).

. «Учимся программировать на Pascal»,Ален Голуб,учебник.

. «Turbo Pascal» Валерий Фаронов, Санкт-Петербург,2003.

. «Алгоритмические трюки для программистов», Генри С. Уоррен младший (электронная версия).

. «Использование шаблонов в Pascal» статья на сайте Гречина А.А. 2005 г.

Приложение

(Листинги программы)

metod; crt; xn,xn1,a,b,eps:real; ,m2:integer;f(x:real):real:=x*x*x*x-x*x*x-2*x*x+3*x-3;;f1(x:real):real:=4*x*x*x-3*x*x-4*x+3;;f2(x:real):real;:=12*x*x-6*x-4;;;:=-2;b:=-1;eps:=0.0000000001;m1:=0;:=56;('Ot A=',a,' do B=',b);('Pogrewnost E ',eps:15:10);;f(a)*f2(a)>0xn:=axn:=b;:=xn-f(xn)/f1(xn);abs(xn1-xn)>sqrt(2*m1*eps)/M2 do:=xn1;:=xn-f(xn)/f1(xn);('xn=',xn:15:10,' xn+1=',xn1:15:10,' f(xn+1)=',f(xn1):15:10);;;('Kon.znach');('xn1=',xn1:15:10,'f(xn1)=',f(xn1):15:10);;('Vtoroy koren');:=1;b:=2;eps:=0.0000000001;m1:=0;:=32;('Ot A=',a,' do B=',b);('Pogrewnost E ',eps:15:10);;f(a)*f2(a)>0xn:=axn:=b;:=xn-f(xn)/f1(xn);abs(xn1-xn)>sqrt(2*m1*eps)/M2 do:=xn1;:=xn-f(xn)/f1(xn);('xn=',xn:15:10,' xn+1=',xn1:15:10,' f(xn+1)=',f(xn1):15:10);;;('Kon.znach');('xn1=',xn1:15:10,'f(xn1)=',f(xn1):15:10);;.