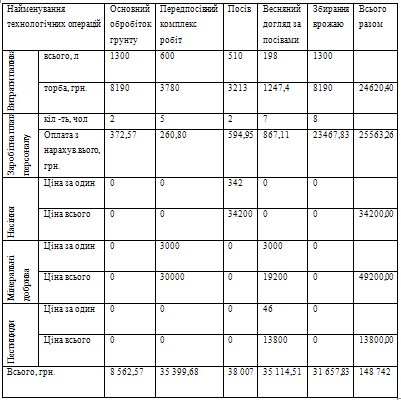
|
Найменування
технологічних операцій
|
Основний обробіток
грунту
|
Передпосівний
комплекс робіт
|
Посів
|
Весняний догляд за
посівами
|
Збирання врожаю
|
Всього разом
|
|
Витрати палив
|
всього, л
|
1300
|
600
|
860
|
372
|
2050
|
|
|
торба, грн.
|
8190
|
4797,45
|
5418
|
2343,6
|
12915
|
33664,05
|
|
Заробітна пата
соналу
|
кіл -ть, чол
|
2
|
5
|
2
|
7
|
8
|
|
|
Оплата з
нарахув.вього грн.
|
372,57
|
260,80
|
349,97
|
1816,02
|
24910,20
|
27709,57
|
|
Насіння
|
Ціна за один
|
0
|
0
|
617
|
0
|
0
|
|
|
Ціна всього
|
0
|
0
|
61700
|
0
|
0
|
61700,00
|
|
Мінеральні добрива
|
Ціна за один
|
0
|
5200
|
0
|
0
|
0
|
|
|
Ціна всього
|
0
|
78000,00
|
0
|
0
|
0
|
78000,00
|
|
Пестициди
|
Ціна за один
|
0
|
0
|
0
|
1434
|
0
|
|
|
Ціна всього
|
0
|
0
|
0
|
39762
|
0
|
39762,00
|
|
Всього, грн.
|
8 562,57
|
83 331,67
|
67 467
|
43 921,62
|
37 825,20
|
241 109
|
Ціна 1 т. кукурудзи 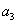 =
1800 грн.
=
1800 грн.
Собівартість 1 т. 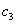 = 482 грн.
= 482 грн.
Врожайність га/т 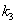 = 5
= 5
Днів посіву 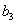 = 10
= 10
Продуктивність сівалки га 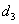 =
32.3
=
32.3
Днів збирання 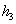 = 20
= 20
Продуктивність комбайна га 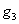 =
12
=
12
4. Озиме жито - 245634.39 грн.
Таблиця 3.4 Витрат на виробництво 100 га озимого жита.

Ціна 1 т. озимого жита 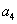 =
1300 грн.
=
1300 грн.
Собівартість 1 т. 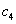 = 614 грн.
= 614 грн.
Врожайність га/т 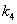 = 4
= 4
Днів посіву 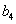 = 15
= 15
Продуктивність сівалки га 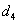 =
35
=
35
Днів збирання  = 10
= 10
Продуктивність комбайна га  =
16
=
16
. Соняшник - 148742.54 грн.
Таблиця 3.5 Витрат на виробництво 100 га соняшнику.
Ціна 1 т. соняшнику 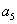 =
3500 грн.
=
3500 грн.
Собівартість 1 т.  = 743 грн.
= 743 грн.
Врожайність га/т 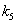 = 2
= 2
Днів посіву 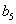 = 15
= 15
Продуктивність сівалки га 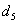 =
22
=
22
Днів збирання 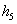 =10
=10
Продуктивність комбайна га 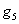 =
30
=
30
6. Ярий ячмінь - 186378 грн.
Таблиця 3.6 Витрат на виробництво 100 га ярового ячменю.
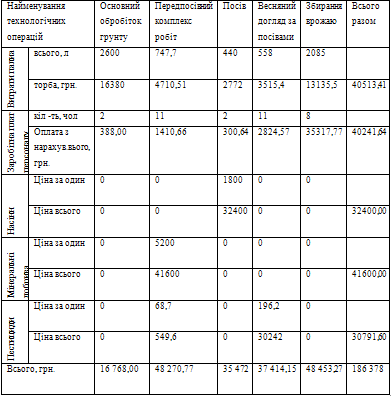
Ціна 1 т. ярового ячменю 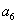 =
1400 грн.
=
1400 грн.
Собівартість 1 т. 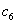 = 934 грн.
= 934 грн.
Врожайність га/т  = 2
= 2
Днів посіву 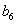 = 12
= 12
Продуктивність сівалки га 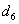 =
37.6
=
37.6
Днів збирання 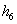 =6
=6
Продуктивність комбайна га 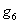 =
15.8
=
15.8
Передбачається, що витрати ресурсів ростуть прямо пропорціонально
обсягу виробництва. Нехай 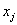 - планований обсяг виробництва j -ої продукції,
- планований обсяг виробництва j -ої продукції,  - кількість гектар засіяних j -ою продукцією. Тоді
допустимим є тільки такий набір вироблюваної продукції x=(x1, x2,., xn), при
якому сума площ засіяних j -ою продукцією не перевершують її запасу:
- кількість гектар засіяних j -ою продукцією. Тоді
допустимим є тільки такий набір вироблюваної продукції x=(x1, x2,., xn), при
якому сума площ засіяних j -ою продукцією не перевершують її запасу:
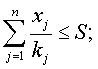 (1)
(1)
Крім того, маємо наступне обмеження по техніці:
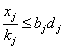 ;(2)
;(2)
Оскільки ми не можемо засіяти більше гектар землі чим це дозволяє
продуктивність сівалки 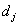 і кількість днів засіву j -ої культури
і кількість днів засіву j -ої культури 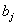 .
.
 ;
(3)
;
(3)
Оскільки озима пшениця і озимий ячмінь мають один і той же час повного
дозрівання і однаковий період збирання 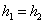 ,
то 4 комбайни не можуть обробити більше посівних площ, чим їм дозволяє їх
продуктивність
,
то 4 комбайни не можуть обробити більше посівних площ, чим їм дозволяє їх
продуктивність 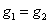 .
.
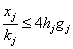 ;
;
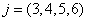 (4)
(4)
комбайни не можуть обмолотити більше ніж їм дозволяють терміни збирання
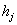 і їх продуктивність
і їх продуктивність  .
.
Обмеження за технологією:
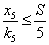 ;
(5)
;
(5)
За технологією виробництва соняшнику цю культуру на одному місці можна
вирощувати 1 раз в 5 років. Тому якщо ми хочемо виробляти цю культуру щороку,
його посівні площі не повинні перевищувати  від
загального запасу землі.
від
загального запасу землі.
Вартість набору продукції x виражається величиною:
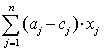 (6)
(6)
Задача планування виробництва ставиться таким чином:
Знайти оптимальний розмір посівних площ, що задовольняє обмеженням (1),
(2), (3), (4), (5), при якому величина (6) набуває найбільшого значення, тобто
дає максимальний прибуток.
3.2 Математичний опис поставленої задачі планування симплекс
методом
Цільова функція - максимум торгівельного прибутку
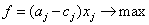
при обмеженнях:
на посівні площі
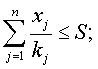 ,
,
по техніці на посів
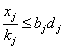 ,
,
по техніці на збирання
 ,
,
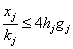 ;
;
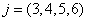 ,
,
за технологією виробництва
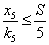
Треба спланувати такий набір вироблюваної продукції x=(x1, x2, x4, x5,
x6), при якому повинні виконаються наступні нерівності, тобто
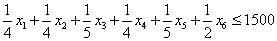 ;
;
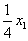
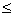 585;
585;
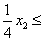 390;
390;
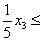 323;
323;
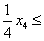 525;
525;
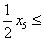 330;
330;
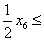 451;
451;
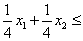 825;
825;
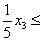 960;
960;
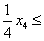 640;
640;
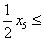 1200;
1200;
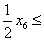 380;
380;
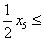 300;
300;
і при цьому повинні виконуватися наступні обмеження: x1, x2, x3, x4,
x5, x6 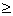 0. Спланований набір вироблюваної продукції x=(x1,
x2, x3, x4, x5, x6) повинен забезпечити максимум вартості цього набору
0. Спланований набір вироблюваної продукції x=(x1,
x2, x3, x4, x5, x6) повинен забезпечити максимум вартості цього набору
{1141x1+1040x2+1318x3+684x4+2757x5+466x6}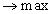
Таким чином, ми отримаємо одинокритерійне завдання, яке є завданням
лінійного програмування (ЗЛП). Воно зводиться до пошуку екстремуму лінійної
функції (ця функція називається або критерієм, або цільовою функцією)
(x)=1141x1+1040x2+1318x3+684x4+2757x5+466x6
за наявності системи лінійних нерівностей, що обмежують область зміни
аргументів цієї функції
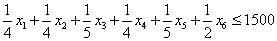 ;
;
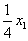
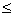 585;
585;
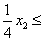 390;
390;
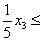 323;
323;
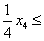 525;
525;
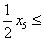 330;
330;
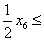 451;
451;
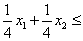 825;
825;
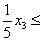 960;
960;
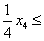 640;
640;
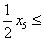 1200;
1200;
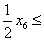 380;
380;
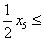 300;,
x2, x3, x4, x5, x6
300;,
x2, x3, x4, x5, x6 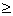 0.
0.
3.3
Рішення поставленої задачі планування виробництва
Опис методу рішення задачі.
Процедура рішення ЗЛП починається з приведення її до канонічної форми,
тобто до стандартної форми завдання, орієнтованої на розроблений саме для цієї
форми метод рішення. Завдання лінійного програмування в канонічній формі має
сенс за умови n>m. В цьому випадку повністю описується область допустимих
рішень (ОДР) ЗЛП, що геометрично є опуклим многогранником в просторі Евкліда
Rn[1]. Опукла фігура, як відомо, характеризується тією властивістю, що, якщо
дві точки X1 і X2 належать цій фігурі, то і увесь відрізок X1X2 належить їй.
Крім того, доведено, що оптимальне рішення ЗЛП завжди лежить на межі ОДР. Тому
справедливий висновок про те, що, принаймні, одна з кутових (опорных) точок
опуклого многогранника ОДР є точкою оптимуму. Для того, щоб визначити
координати опорної точки, усю безліч змінних X={xj}, j=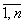 необхідно розділити на дві підмножини
необхідно розділити на дві підмножини
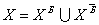 :
:
підмножина базисних змінних
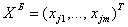 ,
,
при цьому число m базисних змінних дорівнює числу рівнянь (обмежується)
за умови, що рівняння є не-залежними; підмножина  інших
n - m вільних (внебазисных) змінних {xj}, j_Би[1].
інших
n - m вільних (внебазисных) змінних {xj}, j_Би[1].
Кількість можливих варіантів розподілу змінних на базисних і вільних
(число базисів) дорівнює  .
.
Найбільш очевидний метод рішення ЗЛП полягає в тому, щоб для кожного з  базисів знайти координати відповідних опорних точок,
виділити з них точки, що належать ОДР, а потім з них, у свою чергу, вибрати ту,
координати якої максимізували цільову функцію. На відміну від цього методу, що
реалізовує, по суті, ідею повного перебору опорних точок ОДР, відомий
ефективніший так званий симплекс-метод рішення ЗЛП.
базисів знайти координати відповідних опорних точок,
виділити з них точки, що належать ОДР, а потім з них, у свою чергу, вибрати ту,
координати якої максимізували цільову функцію. На відміну від цього методу, що
реалізовує, по суті, ідею повного перебору опорних точок ОДР, відомий
ефективніший так званий симплекс-метод рішення ЗЛП.
У основі симплекс-методу лежить підхід, що включає:
вибір опорної точки, що належить ОДР (вибір початкового допустимого
базису);
перевірку опорної точки на оптимальність;
вибір нового базису, що дозволяє мінімізувати число опорних точок на
траєкторії у разі невиконання умов оптимальності.
Приведення початкового завдання до канонічного виду.
Маємо початкову ЗЛП:
(x)=1141x1+1040x2+1318x3+684x4+2757x5+466x6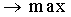
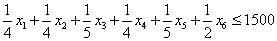 ;
;
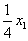
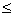 585;
585;
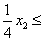 390;
390;
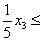 323;
323;
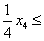 525;
525;
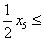 330;
330;
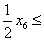 451;
451;
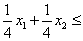 825;
825;
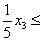 960;
960;
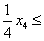 640;
640;
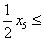 1200;
1200;
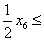 380;
380;
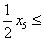 300;,
x2, x3, x4, x5, x6
300;,
x2, x3, x4, x5, x6 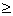 0
0
Приведемо ЗЛП до канонічної форми. Приведення системи обмежень, заданих
у формі нерівностей, до канонічної форми рівності здійснюється за допомогою
відповідного збільшення розмірності вектора X=(x1, x2, x3, x4, x5, x6) з
урахуванням обов'язкової позитивності усіх його складових.
Таким чином, ЗЛП в канонічній формі має вигляд:
max{1141x1+1040x2+1318x3+684x4+2757x5+466x6};
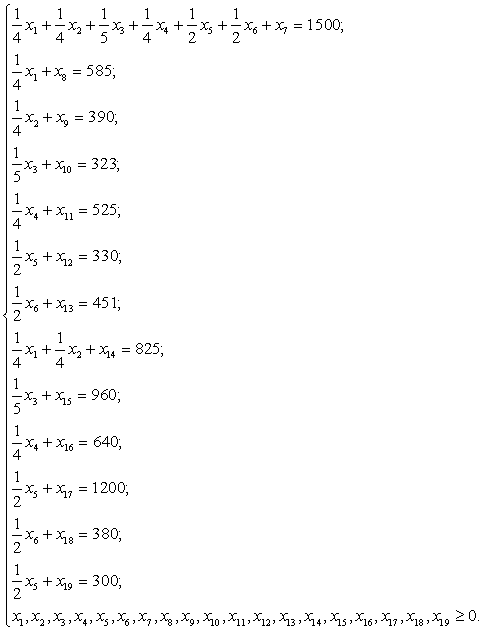 (7
(7
Пошук допустимого базису.
Заповнення симплекс-таблицы.
ЗЛП в канонічній формі можна записати в матричному виді:
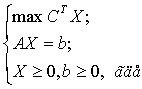 (8)
(8)
b=(1500, 585, 390, 323, 525, 330, 451, 825, 960, 640, 1200,
380, 300) T=(x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12, x13, x14, x15,
x16, x17, x18, x19) T=(1144,1040,1318,686,2757,466,0,0,0,0,0,0,0,0,0,0,0,0,0)

Пошук допустимого базису починається з аналізу стовпців матриці A=(A1,
A2,., A19), використовуваної в записі обмеження (8) канонічної форми ЗЛП. Як
базисні слід вибирати такі 13 змінних, яким відповідає набір стовпців, що
дозволяють скласти одиничну матрицю P=(Aj1, Aj2, Aj3, Aj4, Aj5, Aj6, Aj7, Aj8,
Aj9, Aj10, Aj11, Aj12, Aj13).
Якщо ОДР початкової ЗЛП задана у формі нерівностей типу 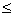 (як в нашому випадку), то початковий базис може бути
сформований з додаткових змінних x7, x8, x9, x10, x11, x12, x13, x14, x15, x16,
x17, x18, x19, обмежень, що вводяться в систему, з метою приведення її до
канонічної форми рівності. В цьому випадку матриця P буде одиничною. Таким
чином, виберемо як початковий базис XБО=(x7, x8, x9, x10, x11, x12, x13, x14,
x15, x16, x17, x18, x19) T, оскільки стовпці A7, A8, A9, A10, A11, A12, A13,
A14, A15, A16, A17, A18, A19 матриці A утворюють одиничну матрицю. Тепер
перейдемо до заповнення симплекс-таблиці. Нехай ЗЛП сформульована в канонічній
формі (7). Ми вибрали базисні змінні x7, x8, x9, x10, x11, x12, x13, x14, x15,
x16, x17, x18, x19. Дозволимо систему нерівностей в (7) відносно базисних
змінних. Система обмежень у формі Такера набере вигляду:
(як в нашому випадку), то початковий базис може бути
сформований з додаткових змінних x7, x8, x9, x10, x11, x12, x13, x14, x15, x16,
x17, x18, x19, обмежень, що вводяться в систему, з метою приведення її до
канонічної форми рівності. В цьому випадку матриця P буде одиничною. Таким
чином, виберемо як початковий базис XБО=(x7, x8, x9, x10, x11, x12, x13, x14,
x15, x16, x17, x18, x19) T, оскільки стовпці A7, A8, A9, A10, A11, A12, A13,
A14, A15, A16, A17, A18, A19 матриці A утворюють одиничну матрицю. Тепер
перейдемо до заповнення симплекс-таблиці. Нехай ЗЛП сформульована в канонічній
формі (7). Ми вибрали базисні змінні x7, x8, x9, x10, x11, x12, x13, x14, x15,
x16, x17, x18, x19. Дозволимо систему нерівностей в (7) відносно базисних
змінних. Система обмежень у формі Такера набере вигляду:
x7=1500 -(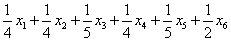 );=585 -(
);=585 -(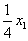 );=390
-(
);=390
-(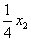 );=323 -(
);=323 -( );=525
-(
);=525
-(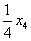 );=330 -(
);=330 -( );=451
-(
);=451
-(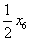 );=825 -(
);=825 -(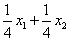 );
(9)=960 -(
);
(9)=960 -( );=640 -(
);=640 -(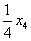 );=1200
-(
);=1200
-( );=380 -(
);=380 -(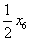 );=300
-(
);=300
-( );
);
Цільову функцію можна представити у виді:
f(x)=f0 -(- 1141x1-1040x2-1318x3-684x4-2757x5-466x6), де f0=0.
Симплекс-таблиця виглядає таким чином:
Таблиця 3.3.1. Початкова симплекс таблиця поставленого завдання

Складена симплекс-таблиця відповідає початковому базису і початковій
опорній точці ОДР. Перехід до чергової опорної точки в процесі пошуку
оптимального рішення супроводжується складанням нової симплекс-таблиці.
Кожна симплекс-таблиця аналізується по критеріях допустимості і
оптимальності базису.
3.3.1
Перевірка ознаки допустимості і оптимальності базису
Ознака допустимості базису :
у опорній точці відповідно до (9) xj=bi, i=7,., 19; j=7,., 19, тому
ознака допустимості базису формулюється як умова bi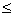 0, i=7,., 19.
0, i=7,., 19.
Ознака оптимальності базису:
Якщо для 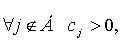 те знайдене рішення оптимальне і єдино.
те знайдене рішення оптимальне і єдино.
Якщо для 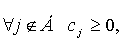 те знайдене рішення оптимальне, але не єдино.
те знайдене рішення оптимальне, але не єдино.
Якщо 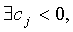 те рішення неоптимальне. В цьому випадку пошук
оптимального рішення триває і необхідно перейти до нової опорної точки.
те рішення неоптимальне. В цьому випадку пошук
оптимального рішення триває і необхідно перейти до нової опорної точки.
Перейдемо до конкретного випадку. У нашому випадку виконується умова
допустимості базису, оскільки b=(1500, 585, 390, 323, 525, 330, 451, 825, 960,
640, 1200, 380, 300) T<0 і bi<0 (i=7,., 19).
Вибраний нами початковий базис XБО=(x7, x8, x9, x10, x11, x12, x13,
x14, x15, x16, x17, x18, x19) T не є оптимальним, оскільки c1=-1144<0,
c2=-1040<0, c3=-1318<0, c4=-686<0, c6=2757<0, c7=466<0. Таким
чином, необхідно здійснити перехід до нової опорної точки (новому базису).
3.3.2
Знаходження дозволяючого елементу в симплекс-таблиці. Формування нового базису
Відповідно до симплекс-методу нова опорна точка вибирається
тільки серед сусідніх, тобто новий базис лише однією змінною відрізняється від
колишнього. Таким чином, формування нового базису здійснюється на базі
колишнього за допомогою виведення з нього одній з базисних змінних xs і вступи
однієї з вільних змінних xr.
Вибір змінної xr. Вибір змінної xr здійснюється за
результатами аналізу коефіцієнтів cj симплекс-таблиці.
Знайдемо
cr=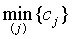 .
.
У нашому випадку min{c1, c2, c3, c4, c5, c6}=c1=-1144 і xr=x1.
Стовпець, який відповідає змінній xr=x1 в симплекс-таблице,
називатимемо таким, що дозволяє.
Вибір змінної xs. Вибір змінної xs проводиться за результатами аналізу
коефіцієнтів air i=1,2,3,4,5,6 дозволяючого стовпця.
Якщо 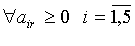 , це означає, що ОДР така, що необмежене збільшення
вільної змінної xr приводить до необмеженого зростання цільової функції (ОДР не
замкнута). Якщо
, це означає, що ОДР така, що необмежене збільшення
вільної змінної xr приводить до необмеженого зростання цільової функції (ОДР не
замкнута). Якщо 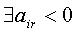 ,
то відповідні базисні змінні xi (i=6,7,8,9,10,11,12,13,14,15,16,17,18,19)
отримують негативні прирости при збільшенні xr=x1. Серед цих змінних xi
необхідно відшукати xs, що досягає нуля при мінімальному значенні приросту xr.
Треба знайти
,
то відповідні базисні змінні xi (i=6,7,8,9,10,11,12,13,14,15,16,17,18,19)
отримують негативні прирости при збільшенні xr=x1. Серед цих змінних xi
необхідно відшукати xs, що досягає нуля при мінімальному значенні приросту xr.
Треба знайти
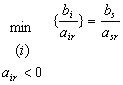
Вибір дозволяючого елементу завершує формування нового базису XБ1, що
відрізняється від колишнього базису однієї змінної xr=x1, тобто замість змінної
x8 в базис XБ1 буде включена змінна x1 : XБ1=(x6, x7, x1, x9, x10, x11, x12,
x13, x14, x15, x16, x17, x18, x19) T.
Для нового базису (нової опорної точки) знову заповнюється
симплекс-таблиця, в якій нові базисні змінні виражені через нові вільні.
3.3.3
Перерахунок симплекс-таблиці
Правила перерахунку :
Дозволяючий елемент замінюється на 1.
Елементи дозволяючого стовпця за винятком asr переписуються
без змін. Елементи дозволяючого рядка
за винятком asr змінюють знак на протилежний. Елементи нової симплекс-таблицы, що
залишилися, обчислюються згідно з наступним правилом: твір відповідного
елементу колишньої таблиці на дозволяючий елемент asr мінус твір елементів, що
знаходяться на іншій діагоналі таблиці. Відповідно до цього правила маємо:
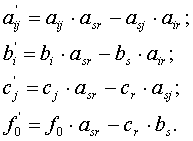
Усі елементи отриманої таблиці необхідно розділити на дозволяючий
елемент asr :

Таблиця 3.3.6.1. Ітерація №1

Б1=(с) T.
Базис XБ1=(x7, x1, x9, x10, x11, x12, x13, x14, x15, x16, x17, x18,
x19) T є допустимим, але не оптимальним. Дозволяючий елемент таблиці a103=0,2
визначає необхідність переходу до базису XБ2=(x7, x1, x9, x3, x11, x12, x13,
x14, x15, x16, x17, x18, x19) T. Приведемо результат перерахунку
симплекс-таблиці для базису XБ2.
Таблиця 3.3.6.2 Ітерація №2
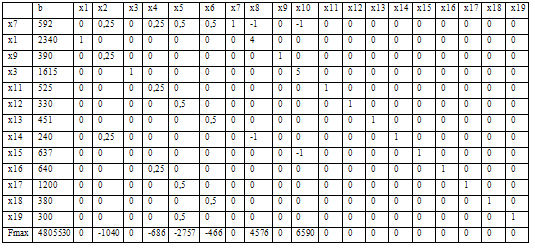
Базис XБ2=(x7, x1, x9, x3, x11, x12, x13, x14, x15, x16, x17, x18, x19)
T є допустимим, але не оптимальним. Дозволяючий елемент таблиці a195=0,5
визначає необхідність переходу до базису XБ3=( x7, x1, x9, x3, x11, x12, x13,
x14, x15, x16, x17, x18, x5) T. Приведемо результат перерахунку
симплекс-таблиці для базису XБ3.
Таблиця 3.3.6.3 Ітерація №3

Базис XБ3=(x7, x1, x9, x3, x11, x12, x13, x14, x15, x16, x17, x18, x5)
T є допустимим, але не оптимальним. Дозволяючий елемент таблиці a142=0,25
визначає необхідність переходу до базису XБ4=(x7, x1, x9, x3, x11, x12, x2,
x14, x15, x16, x17, x18, x5) T. Приведемо результат перерахунку
симплекс-таблиці для базису XБ4.
Таблиця 3.3.6.4 Ітерація №4
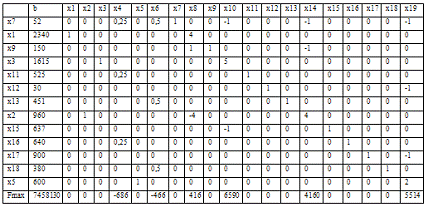
Базис XБ3=(x7, x1, x9, x3, x11, x12, x2, x14, x15, x16, x17, x18, x5) T
є допустимим, але не оптимальним. Дозволяючий елемент таблиці a74=0,25 визначає
необхідність переходу до базису XБ4=(x4, x1, x9, x3, x11, x12, x2, x14, x15,
x16, x17, x18, x5) T. Приведемо результат перерахунку симплекс-таблиці для
базису XБ4.
Таблиця 3.3.6.5 Інтерация №5
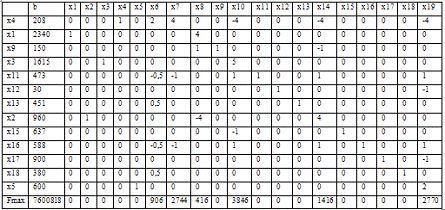
Аналіз таблиці 6 дозволяє зробити висновок про допустимість і
оптимальність базису XБ4=(x4, x1, x9, x3, x11, x12, x2, x14, x15, x16, x17,
x18, x5) T.
4.
Програма для вирішення задачі ЛП симплекс-методом
4.1
Опис
В процесі виконання дипломної роботи був реалізований і
відлагоджений програмний інтерфейс під ОС Windows XP (також протестований під
Windows Vista), вирішальний завдання ЛП симплекс-методом (зокрема поставлене
завдання планування виробництва).
Програма здійснює: рішення завдань ЛП симплекс методом;
збереження і завантаження початкових даних у файл/з файлу; виведення рішення по
кроках; експорт рішення в документ MS Excel; системний код програми написаний в
середовищі об'єктно-орієнтованого програмування С++.
4.2
Графічне представлення програми
Головне вікно програми "Початкові дані":
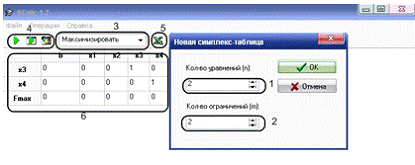
Мал. 5 Головне вікно програми Simplex : 1 - Число змінних, в
нашому випадку кількість вироблюваної продукції. 2 - Число обмежень. 3 -
Цільова функція, в нашому випадку максимізація. 4 - Кнопки для вирішення
завдання . 5 - експорт таблиць в Excel. 6 - Система обмежень у формі Такера.
4.3
Робота з програмою
Приступаємо до введення початкових даних: 1 - поля для
введення обмежень ; 2 - поля для введення набору вироблюваної продукції. 3 -
поля для введення коефіцієнтів цільової функції (у нашому випадку це прибуток
від одиниці продукції ); 4 - натискаємо кнопку "Вирішити". (див. Мал.
6)
Заповнивши усі поля, приступаємо до рішення задачі:
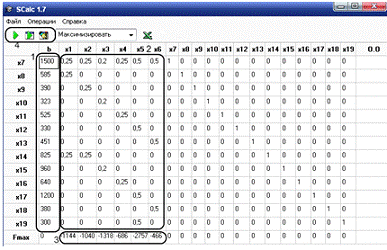
Мал. 6 Робота з програмою
Після натиснення кнопки "Рішення" програма виробляє
необхідні обчислення і автоматично переходить до другого вікна, в якому
відображується покрокове рішення поставленої задачі у виді симплекс таблиць.
У 5 і 6 - можна побачити дозволяючий елемент кожної таблиці,
5 - початкові дані, 6 - кількість ітерацій, 7 - оптимальний набір вироблюваної
продукції, 8 - Відповідь, в нашому випадку максимум цільової функції
(максимальний прибуток) (див. Мал. 7).
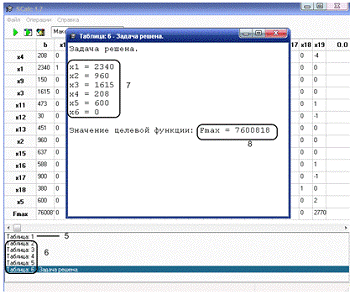
Мал. 7 Робота з програмою
4.4
Схема програми
Логічна структура програми вирішального завдання ЛП симплекс
методом приведена на Мал. 8, Мал. 9, Мал. 10.
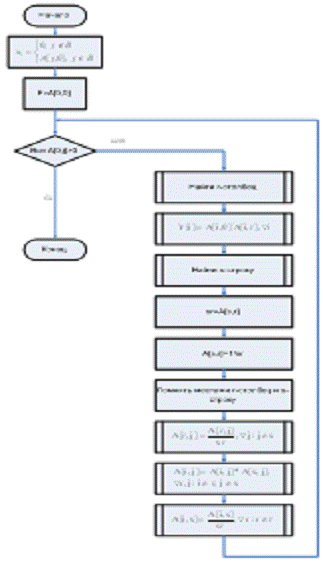
Мал. 8 Симплекс-метод
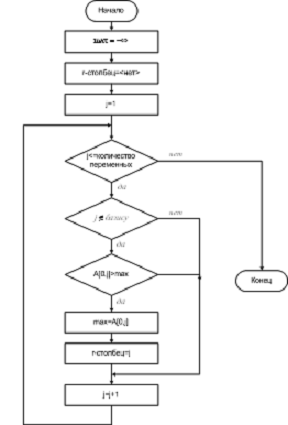
Мал. 9 Пошук r -стовпчика
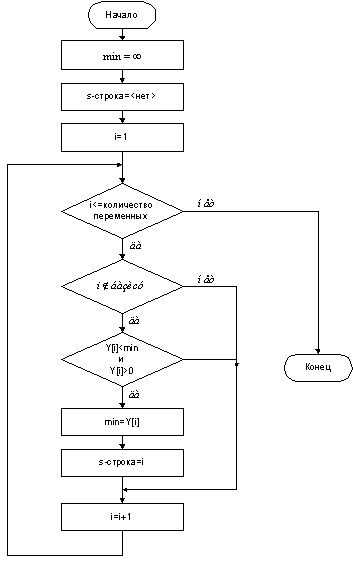
Мал. 10 Пошук s -строки
4.5
Результат рішення задачі планування виробництва
В результаті рішення поставленої задачі симплекс-методом
отримали набір вироблюваної продукції x(2340, 960, 1615, 208, 600, 0), який
задовольняє усім накладеним обмеженням і забезпечує максимальну вартість цього
набору (максимум цільової функції f(x) = 1141x1+1040x2+1318x3+684x4+2757x5+
466x6 = 7600818 грн.). Таким чином, можна оптимально спланувати обсяг
виробництва продукції :
Озимої пшениці треба випустити 2340 тонн
Озимого ячменю - 960 тонн
Кукурудзи - 1615 тонн
Озимого жита - 208 тонн
Соняшнику - 600 тонн
Ярового ячменю - для досягнення максимального прибутку в цих
умовах виробляти не вигідно.
По посівних площедям:
Озимої пшениці треба засіяти 585 га.
Озимого ячменю - 240 га.
Кукурудзи - 323 га.
Озимого жита - 52 га.
Соняшнику - 300 га.
Ярового ячменю - 0 га.
Підприємством ТОВ "ОльвіяЛатІнвест " в 2010 році
було засіяно:
Озимої пшениці - 400 га.
Озимого ячменю - 400 га.
Кукурудзи - 250 га.
Озимому житу - 0 га.
Соняшнику - 350 га.
Ярового ячменю - 100 га.
При реалізації продукції був отриманий прибуток 7165000 грн.,
що на 435818 грн. менше ніж можна отримати при використанні оптимізації
виробництва. Також було засіяно 350 га. соняшнику, що на 50 га. перевищує
технологію виробництва. А значить з часом зменшує продуктивність землі.
Виходячи з цього можна зробити висновок що оптимізація
структури виробництва при плануванні випуску продукції є істотним джерелом
збільшення суми прибутку. А також дозволяє раціонально використовувати земельні
ресурси.
Висновки
Розвиток сучасного суспільства характеризується підвищенням
технічного рівня, ускладненням організаційної структури виробництва,
поглибленням громадського розподілу праці, пред'явленням високих вимог до
методів планування виробничої діяльності. У цих умовах тільки науковий підхід
до економіки підприємств дозволить забезпечити високі темпи розвитку
промисловості. Наукового підходу вимагає і рішення тактичних і стратегічних
завдань.
Нині новітні досягнення математики і сучасної обчислювальної
техніки знаходять усе більш широке застосування як в економічних дослідженнях і
плануванні, так і в інших завданнях. Цьому сприяє розвиток таких розділів
математики як математичне програмування, теорія ігор, теорія масового
обслуговування, а також бурхливий розвиток швидкодіючої
електронно-обчислювальної техніки.
Вже накопичений великий досвід постановки і рішення
економічних і тактичних завдань за допомогою математичних методів. Особливо
успішно розвиваються методи оптимального управління. Економіка і виробництво
розвивається швидко там, де широко використовуються математичні методи.
Після реалізації проекту можна сказати, що усі поставлені
завдання досягнуті. За даними сільськогосподарського підприємства була
побудована економічна модель завдання. Проаналізувавши економічну модель була
виконана математична постановка завдання.
З безлічі методів рішення завдань лінійного програмування був
вибраний універсальний - симплекс-метод. Вивчені його переваги і недоліки.
По вибраному методу реалізована програма на мові С++. Вона
протестована і налагоджена. Розроблена програма зручна для використання не лише
в цьому підприємстві, але і для будь-якого іншого сільськогосподарського
підприємства.
Виконана чисельна реалізація на прикладі
сільськогосподарського підприємства ТОВ "ОльвіяЛатІнвест". Отриманий
оптимальний план виробництва для цього підприємства. Оптимізація виробництва
показала що підприємство може заробляти на 435818 грн. більше, при цьому
раціонально використовувати земельні ресурси.
Список
літератури
1.
Абрамов Л.М., Капустин В.Ф. Математическое программирование. Л., Изд-Ленингр.
ун-та, 1976. - 184 с.
.
Акулич И.Л., "Математическое программирование в примерах и задачах",
Москва "Высшая школа" 1993г.
.
Ашманов С.А. Линейное программирование, Учебное пособие. - М.:Наука, 1981.- 311
с.
.
Баканов М.И., Шеремет А.Д. Теория экономического анализа: Учебник. -4-е изд.,
доп. и перераб. - М.: Финансы и статистика, 2000. - 416 с.
.
Банди Б. Основы линейного программирования: Пер. с англ. - М.: Радио и связь,
1989. -176 с.
.
Вентцель Е.С. Исследование операций: задачи, принципы, методологии. М.: Изд-во
"Наука", 1980.
.
Давыдов Э.Т. Исследование операций.- М.:Высш.шк., 1990. - 130с.
.
Джерод Холлингворс, Дэн Баттерфилд, Боб Свот C++ Builder 5. Руководство
разработчика = C++ Builder 5 Developer's Guide. - М.: "Диалектика",
2001. - С. 884. - ISBN 0-672-31972-1
.
Джаррод Холингворт, Боб Сворт, Марк Кэшмэн, Поль Густавсон Borland C++ Builder
6. Руководство разработчика = Borland C++ Builder 6 Developer's Guide. - М.:
"Вильямс", 2004. - С. 976. - ISBN 0-672-32480-
.
Габасов Р., Кириллова Ф.М. Методы оптимизации. --- Минск: Издательство БГУ им.
В.И. Ленина, 1981. - 352 с.
.
Габасов Р., Кириллова Ф.М. Методы линейного программирования. Ч.2. Транспортные
задачи, Минск, Изд-во БГУ им. В.И. Ленина, 1977. - 240 с.
.
Гасс С.Линейное программирование. - М.: Физматгиз, 1961. - 214с.
.
Гермейер Ю.Б. Введение в теорию исследования операций. - М.: Наука, 1971. -
403с.
.
Гольштейн Е.Г., Юдин Д.Б. Линейное программирование, теория, методы и
приложения. - М.: Наука, 1969. - 236с.
.
Ершов А.Т., Карандаев И.С., Шананин Н.А. Планирование производства и линейное
программирование. МИУ, М., 1981.
.
Зайченко Ю.П. Исследование операций.- Киев: Вища школа, 1975. - 278с.
.
Интрилигатор М. Математические методы оптимизации и экономическая теория.-
М.:Прогресс, 1975. - 396с.
.
Карманов В.Г. Математическое программирование. --- Москва: Наука, Главная
редакция физико-математической литературы, 1986. - 215с.
.
Леоненков А.В. Решение задач оптимизации в среде MS Excel BHV-Санкт-Петербург
ISBN: 5941575033 2005 г.
.
Ляшенко И.Н. Линейное и нелинейное программирование. - Киев: Вища школа, 1975.
- 372 с.
.
Мину М. Математическое программирование. Теория и алгоритмы. М.: Наука, 1990.-
488 с.
.
Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. - М.: Наука,
Главная редакция физико-математической литературы, 1986. - 328с.
.
Схрейвер А. Теория линейного программирования: в 2-х т. Т.2: Пер с англ. - М.:
Мир, 1991. - 342с., ил. Раздел линейное программирование
.
Тынкевич М.А. Экономико-математические методы (исследование операций). Изд. 2,
испр. и доп. - Кемерово, 2000. - 177 с.
.
Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы:
построение и анализ = INTRODUCTION TO ALGORITHMS. - 2-е изд. - М.:
"Вильямс", 2006. - С. 1296. - ISBN 0-07-013151-1
.
Юдин Д.Б., Гольштейн Е.Г. Линейное программирование (Теория, методы и
приложения). -- М.: Наука, Главная редакция физико-математической литературы,
1969. -424 с.
.
Хемди А. Таха Глава 3. Симплекс-метод // Введение в исследование операций =
Operations Research: An Introduction. - 7-е изд. - М.: "Вильямс",
2007. - С. 95-141. - ISBN 0-13-032374-8
Додаток
Лістинг програми
// // Цей файл визначає клас симплекс методу
##include <vcl.h>
##include <list>
##include "CD.cpp"
##ifndef CSM2_H
##define CSM2_HSM
{
//----------------//----------------Симплекс-метод------------------------------CSM
{:( int n, int m );SetBaz( int * baz );SetT( CD ** T
);Show();GetWord();GetTacker();Get_Rap();operator<<=( CSM * csm
);get_CF();** get_ogr(){ return T; }* get_baz(){ return baz; }get_rez(){ return
rez; }get_nm( int* nIn, int* mIn ){ *nIn = n; *mIn = m; }get_ij( int* i, int* j
){ *i = a_i; *j = a_j; }
~CSM( );:int iter; // Число ітераційoptim(); // перевірка
рішення (0 - оптимальне, 1 - не існує, 2 - не оптимальне)n; // Число зміннихm;
// Число обмеженьa_i;a_j; // Координати дозволяючого елементу* baz; // Масив
базисних змінних** T; // Симплекс таблицяrez;
};CSM::iter = 0; // Число ітерацій::CSM( int nIn, int mIn )
{= nIn;= mIn;= new int [m];= new CD * [m + 1]; // m + 1
оскільки ще рядок цільової функції( int i = 0; i < m + 1; i++ )[i] = new CD
[n + 1]; // n + 1 оскільки ще вільний член+= 1;= 2;
}::~CSM( )
{baz;( int i = 0; i < m + 1; i++ )T[i];T;-= 1;
}CSM::SetBaz( int * bazIn )
{( int i = 0; i < m; i++ )[i] = bazIn[i];
}CSM::SetT( CD ** TIn ) // Копіювання таблиці, що входить, і
перевірка рішення з пошуком дозволяючого елементу
{( int i = 0; i < m + 1; i++ )( int j = 0; j < n + 1;
j++ )[i][j] = TIn[i][j];optim();
}CSM::optim()
{_i = a_j = 0; // Ініціалізація координат дозволяючого елементу
// // Перевірка на отрицательность серед вільних членів( int
i = 1; i < m; i++ ) // перевірка вільного члена( T[i][0].get_d() <
T[a_i][0].get_d() ) // Шукаємо мінімальний_i = i;( T[a_i][0].get_d() < 0 )
// Якщо мінімальний елемент негативний (подвійний СМ)
{( int j = 1; j < n + 1; j++ ) // перевірка на наявність
негативних эл-тов в рядку( T[a_i][j].get_d() < 0 ) // є негативні елементи
{_j = j; // Перший негативний елемент; // Вихід з циклу
пошуку
}( a_j == 0 ) return rez = 1; // Немає оптимального рішення
// вихід( int j = a_j + 1; j < n + 1; j++ ) // Прохідний по рядку ще раз для
знаходження мінімального відношення( T[a_i][j].get_d() < 0 ) // Негативний(
fabs( (T[m][j]/T[a_i][j]).get_d() )< fabs( (T[m][a_j]/T[a_i][a_j]).get_d()
)) // Найменше відношення_j = j;rez = 2; // продовження виконань ітерацій //
вихід
}
// // Перевірка на отрицательность серед елементів цільової
функції_j = 1;_i = m;( int j = 2; j < n + 1; j++ ) // Прохідний по рядку
цільової функції( T[m][j].get_d() < T[m][a_j].get_d() ) // Шукаємо
мінімальний_j = j;( T[m][a_j].get_d() < 0 ) // Є негативний елемент в
цільовій функції
{( int i = 0; i < m; i++ ) // Прохідний по стовпцю(
T[i][a_j].get_d() > 0 )
{_i = i; // Перший позитивний елемент; // Вихід з циклу
пошуку
}( a_i == m ) return rez = 1; // Немає оптимального рішення
// вихід( int i = a_i + 1; i < m; i++ ) // Прохідний по стовпцю ще раз для
знаходження мінімального відношення( T[i][a_j].get_d() > 0 ) // Позитивний(
fabs( (T[i][0]/T[i][a_j]).get_d() )< fabs( (T[a_i][0]/T[a_i][a_j]).get_d()
)) // Найменше відношення_i = i;rez = 2; // продовження виконань ітерацій //
вихід
}rez = 0; // оптимальне рішення // вихід
}CSM::operator<<=( CSM * csmIn ) // Тут з попередньої
таблиці виходить нова
{_i = csmIn ->a_i;_j = csmIn ->a_j;
// // Ділимо на дозволяючий елемент дозволяючий рядок і
міняємо базисну змінну( int j = 0; j < n + 1; j++ )[a_i][j] = csmIn
->T[a_i][j] / csmIn ->T[a_i][a_j];
// // Домножаем дозволяючий рядок на эл-т в дозволяючому
стовпці, соотв-щий цьому рядку, і складаємо з цим рядком( int i = 0; i < m +
1; i++)
{( i == a_i) continue;( int j = 0; j < n + 1; j++ )[i][j]
= csmIn ->T[i][j] - T[a_i][j] * csmIn ->T[i][a_j];
}
// // Вводимо нову змінну в базис( int i = 0; i < m; i++
)[i] = csmIn ->baz[i];[a_i] = a_j;optim();
}CSM::get_CF()
{T[m][0];
}CSM::Show( )
{tab;= "БП\tСЧ";( int j = 0; j < n; j++)//
шапка= tab + "\tX" + AnsiString( j + 1 );( int i = 0; i < m + 1;
i++ )
{( i == m ) tab = tab + "\nY";tab = tab +
"\n" + baz[i];( int j = 0; j < n + 1; j++)= tab + "\t" +
T[i][j].get_a();
}
// // ShowMessage(tab);
}CSM::GetWord()
{
// // Таблицяtab;= "\n<table border=3 cellpadding=5
><tr bgcolor=\"#aaaaaa\">";+= "<td
align=\"center\">БП</td><td>СЧ</td>";( int
j = 0; j < n; j++)// шапка
{+= "<td align=\"center\">";= tab +
"X<sub>" + (j+1) + "</sub>";+=
"</td>";
}+= "</tr>";( int i = 0; i < m + 1; i++ )
{+= "<tr>";+= "<td
bgcolor=\"#aaaaaa\" align=\"center\">";( i == m )
tab += "F'";tab = tab + "X<sub>" + baz[i] +
"</sub>";+= "</td>";( int j = 0; j < n + 1;
j++)
{( i == a_i && j == a_j && rez == 2 ) tab +=
"<td bgcolor=\"#cccccc\">";tab += "<td
align=\"center\">";+= T[i][j].get_a();+=
"</td>";
}+= "</tr>";
}+= "</table>";tab;
/*tab;= "БП;СЧ;";( int j = 0; j < n; j++)//
шапка( j == n - 1 ) tab = tab + "X" + AnsiString( j + 1 );tab = tab +
"X" + AnsiString( j + 1 ) + ";";( int i = 0; i < m + 1;
i++ )
{( i == m ) tab = tab + "\nF';";tab = tab +
"\nX" + baz[i] + ";";( int j = 0; j < n + 1; j++)( j ==
n ) tab = tab + T[i][j].get_a();tab = tab + T[i][j].get_a() + ";";
}tab;
*/
}CSM::GetTacker()
{tab;( int i = 0; i < m; i++ )
{+= AnsiString("X") + baz[i] + " = ";+=
T[i][0].get_a() + " - ( " + T[i][1].get_a() + "*X1";( int j
= 2; j < n + 1; j++)
{is_b = false;( int d = 0; d < m; d++ )( j == baz[d] )
{_b = true;;
}( !is_b )+= T[i][j].get_s() + "*X" + AnsiString( j
);
}+= " )\n";
}+= "\nЦелевая функція :";+= "\nF' = " +
T[m][0].get_a() + " - ( " + T[m][1].get_a() + "*X1";( int j
= 2; j < n + 1; j++)
{is_b = false;( int d = 0; d < m; d++ )( j == baz[d] )
{_b = true;;
}( !is_b )+= T[m][j].get_s() + "*X" + AnsiString( j
);
}+= " )\n";tab;
}CSM::Get_Rap()
{Rap;( rez == 0 )
{( T[m][0] == 0 )= "Рішення оптимальне. Штучний базис
отриманий. Далі підставляємо нові бвазисные пременные в цільову
функцію".;Rap = "Рішення оптимальне, але цільова функція не дорівнює
0. штучного базису немає".;
}if( rez == 1 )
{( a_j == 0 ) Rap = AnsiString( "Рішення не існує.
Цільова функція необмежена, оскільки вільний член при X" ) + baz[a_i] +
" негативний, а інші елементи рядки не негативні".;if( a_i == m ) Rap
= AnsiString( "Рішення не існує. Цільова функція необмежена, оскільки
елемент в рядку цільової функції при X" ) + a_j + " негативний, а
інші елементи стовпця не позитивні".;
}if( rez == 2 )
{= AnsiString( "Рішення триває. З базису виводиться
X") + baz[a_i] + " і вводиться X" + a_j + "".;
}Rap;
}
}
##endif // CSM_H
// // Цей файл визначає клас дробу
##include <vcl.h>
##include <math.h>
##ifndef CD_H
##define CD_H
##define PR_COUNT 5000mas[PR_COUNT] = {0};Generate_Prost();CD
// Клас дріб
{:::CD( int = 0, int = 1 );Set( int hi, int lo );Set( double
d );Set( AnsiString d );SetInv( AnsiString d );hi(){ return m_hi; }; //
чисельникlo(){ return m_lo; }; // знаменникget_d(); // повертає десяткове
значенняget_a(); // повертає рядок звичайного дробуget_s(); // повертає рядок
звичайного дробуget_dr();get_cel();get_abs();operator*(CD d);operator*(int
num);operator/(CD d);operator/(int num);operator+(CD d);operator+(int
num);operator -(CD d);operator -(int num);operator=(CD d);operator=(int
num);operator==(CD d);operator==(int num);operator!=(CD d);operator!=(int
num);:m_hi; // чисельникm_lo; // знаменникm_d;overflow;optim();bool gen;
};CD::gen = false;::CD( int hi, int lo )
{( !gen )
{_Prost();= true;
}= false;( hi, lo );
}CD::Set( int hi, int lo )
{= false;( lo == 0 )
{_hi = 0;_lo = 1;false;
}_hi = hi;( m_hi == 0 ) m_lo = 1;
{_lo = lo;();
}true;
}CD::Set( double d )
{= true;_d = d;true;
}CD::Set( AnsiString d )
{pos = 0;( pos = d.LastDelimiter("/"))
{_hi = StrToIntDef( d.SubString( 1, pos - 1 ), 0 );_lo =
StrToIntDef( d.SubString( pos + 1, d.Length() ), 1 );( m_hi, m_lo );
}if( pos = d.LastDelimiter(".))
{( StrToFloat( d ));
}
{_hi = StrToIntDef( d, 0 );( m_hi, 1 );
}();
// // ShowMessage( "m_hi = " + AnsiString(m_hi) +
"\nm_lo = " + m_lo );true;
}CD::SetInv( AnsiString d )
{pos = 0;( pos = d.LastDelimiter("/"))
{_hi = - StrToIntDef( d.SubString( 1, pos - 1 ), 0 );_lo =
StrToIntDef( d.SubString( pos + 1, d.Length() ), 1 );( m_hi, m_lo );
}if( pos = d.LastDelimiter(".))
{( - StrToFloat( d ));
}
{_hi = - StrToIntDef( d, 0 );( m_hi, 1 );
}
// // ShowMessage( "m_hi = " + AnsiString(m_hi) +
"\nm_lo = " + m_lo );true;
}CD::get_d() // повертає десяткове значення
{( overflow ) return m_d;( m_hi ) return
float(m_hi)/m_lo;return 0;
}CD::get_a()
{( overflow ) return FloatToStrF( m_d, ffGeneral, 7, 0 );(
m_lo == 1 ) return AnsiString(m_hi);return AnsiString(m_hi) + "/" +
AnsiString(m_lo);
}CD::get_s()
{( overflow )
{( m_d >= 0 ) return AnsiString( " + " ) +
FloatToStrF( m_d, ffGeneral, 7, 0 );return AnsiString( " - " ) +
FloatToStrF( - m_d, ffGeneral, 7, 0 );
}( m_lo == 1 ) return (m_hi < 0)?AnsiString(" -
") + abs(m_hi) :" + " + AnsiString(m_hi);return ((m_hi <
0)?AnsiString(" - ") + abs(m_hi) :" + " + AnsiString(m_hi))
+ "/" + AnsiString(m_lo);
}CD::get_dr()
{cd;( overflow )
{.Set( m_d - floor(m_d));cd;
}_t r;= ldiv( m_hi, m_lo );( r.rem >= 0 )
{.Set( r.rem, m_lo );
}
{.Set( m_lo + r.rem, m_lo );
}cd;
}CD::get_cel()
{cd;( overflow )
{= floor( m_d );cd;
}( m_hi >= 0 )= ldiv( m_hi, m_lo ).quot;= ldiv( m_hi, m_lo
).quot - 1;cd;
}CD::get_abs()
{cd;( overflow )
{( m_d >= 0 ) cd.Set( m_d );cd.Set( - m_d );cd;
}( m_hi < 0 ) cd.Set( - m_hi, m_lo );cd.Set( m_hi, m_lo
);cd;
}CD::operator+(CD d)
{cd;( overflow || d.overflow )
{.Set( get_d() + d.get_d() );cd;
}.Set( m_hi*d.m_lo + d.m_hi*m_lo, m_lo*d.m_lo );cd;
}CD::operator+(int num)
{cd;( overflow )
{.Set( get_d() + num );cd;
}.Set( m_hi + num*m_lo, m_lo );cd;
}CD::operator -(CD d)
{cd;( overflow || d.overflow )
{.Set( get_d() - d.get_d() );cd;
}.Set(m_hi*d.m_lo - d.m_hi*m_lo, m_lo*d.m_lo );cd;
}CD::operator -(int num)
{cd;( overflow )
{.Set( get_d() - num );cd;
}.Set( m_hi - num*m_lo, m_lo );cd;
}CD::operator*(CD d)
{cd;( overflow || d.overflow )
{.Set( get_d() * d.get_d() );cd;
}.Set( m_hi*d.m_hi, m_lo*d.m_lo );cd;
}CD::operator*(int num)
{cd;( overflow )
{.Set( get_d() * num );cd;
}.Set( m_hi*num, m_lo );cd;
}CD::operator/(CD d)
{cd;( overflow || d.overflow )
{.Set( get_d() / d.get_d() );cd;
}.Set( m_hi*d.m_lo, m_lo*d.m_hi );cd;
}CD::operator/(int num)
{cd;( overflow )
{.Set( get_d() / num );cd;
}.Set( m_hi, m_lo*num );cd;
}CD::operator=(CD d)
{( d.overflow)
{( d.get_d() );*this;
}( d.m_hi, d.m_lo );*this;
}CD::operator=(int num)
{( num, 1 );*this;
}CD::operator==(CD d)
{( overflow || d.overflow )
{get_d() == d.get_d();
}( m_hi == d.m_hi )( m_lo == d.m_lo )true;false;
}CD::operator==(int num)
{( overflow )
{get_d() == num;
}( m_hi == num )( m_lo == 1 )true;false;
}CD::operator!=(CD d)
{( overflow || d.overflow )
{get_d() != d.get_d();
}( m_hi == d.m_hi )( m_lo == d.m_lo )false;true;
}CD::operator!=(int num)
{( overflow )
{get_d() != num;
}( m_hi == num )( m_lo == 1 )false;true;
}CD::optim()
{( overflow ) return;_hi *= m_lo/abs(m_lo); // для знаку_lo =
abs(m_lo);( m_hi ) // далі скорочення дробу
{i = 0;(1)
{( ldiv( m_hi, mas[i] ).rem == 0 && ldiv( m_lo,
mas[i] ).rem == 0 )
{_hi /= mas[i];_lo /= mas[i];
}( (mas[i + 1] > abs(m_hi) && mas[i + 1] >
m_lo) || i + 1 > PR_COUNT - 1 ) break;++;
}( abs(m_hi)> mas[PR_COUNT - 1] || m_lo > mas[PR_COUNT
- 1] )
{= true;_d = double(m_hi)/m_lo;;
}
}
}Generate_Prost()
{is_prost;per;kol = 1;[0] = 2;i = 3;(1)
{_prost = true;( int j = 0; j < kol; j++ )( ldiv( i,
mas[j] ).rem == 0 )
{_prost = false;;
}( is_prost )
{[kol] = i;++;
}( kol >= PR_COUNT ) return;++;
}
/*p;( int i = 0; i < kol; i++ )= p + mas[i] + "
";
// // ShowMessage( p );
//*/
}
##endif // CD_H