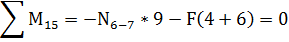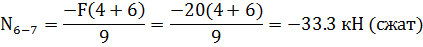Расчет статически определимых стержневых систем на неподвижную нагрузку
РАСЧЕТ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ НА НЕПОДВИЖНУЮ НАГРУЗКУ
ЗАДАНИЕ
Для заданного варианта №10 при размерах по
строке 19 и нагрузке по строке 19 требуется:
. Произвести кинематический анализ систем и,
если необходимо, построить поэтажные схемы.
. Определить опорные реакции и построить эпюры
внутренних усилий.
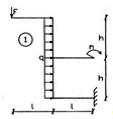
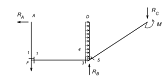
СХЕМА 1
Дано: 
Решение:
Заданная система представлена консольным ломаным
стержнем с жесткой заделкой.
Система статически определима, так как имеет три
неизвестных опорных реакции (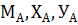
), которые можно
определить, составив три уравнения равновесия.
Эпюру М можно построить без определения опорных
реакций. Для этого необходимо найти значение изгибающих моментов лишь в
нескольких характерных сечениях.
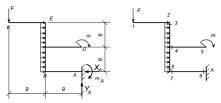
Проводим сечение через точку 2, мысленно
отбрасываем нижнюю часть стержня с заделкой и рассматриваем участок 1-2 как
консольную балку с жесткой заделкой.
Сила F растягивает верхние волокна балки
Момент в точке 3 определим из условия равновесия
узла Е:
Участок 4-5 также рассматриваем как консольную
балку с жесткой заделкой. В точке 2 к балке приложен момент. других нагрузок
нет, поэтому эпюра прямолинейна имеет одну ординату на всем участке.
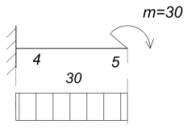
Под действием момента растянуты верхние волокна
участка балки
Через точку 6 проводим сечение и, отбросив
мысленно правую часть с заделкой, помещаем жесткую заделку в точку 6.
Рассматриваем участок балки 3-6 как консольную
балку нагруженную равномерно-распределенной нагрузкой и двумя моментами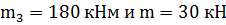 
м.
Растянуты нижние волокна
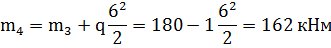
В точке 4 приложен момент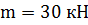 
м
(растягивающий верхние волокна балки), поэтому на эпюре будет скачок:
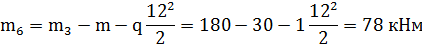
Чтобы определить момент в заделке заданной балки
нужно сложить моменты от всех сил, приложенных к балке:
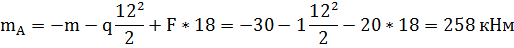
Растянуты верхние волокна участка АВ.
Соединив эпюры участков, получим общую эпюру
моментов:
Построение эпюры поперечных сил:
Эпюру поперечных сил Q будем строить по эпюре
изгибающих моментов М, используя зависимость
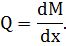
Численное значение Q на участках с линейной
эпюрой М будем определять по формуле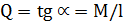 
,
а знак - по направлению вращения оси стержня до совмещения с эпюрой М.
Стержень 1-2:
Стержень 4-5: здесь нет сосредоточенной силы,
приложен только момент, поэтому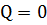 
.
Стержень 7-8:
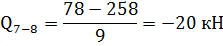
Поперечные силы в стержне 4-6 будем определять
по участкам 6-4 и 4-3ю
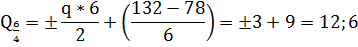
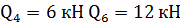
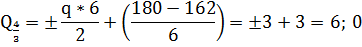
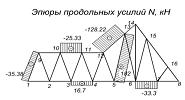
Построение эпюры продольных сил N
Эпюру продольных сил строим по эпюре Q, вырезая
узлы.
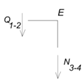
Узел Е:
на стержень 1-2 действует сила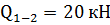 
. Узел должен
уравновешиваться силой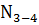 
.
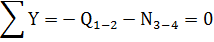
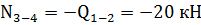
Стержень 3-4 будет сжат.
Узел В:
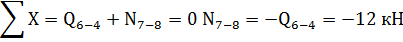
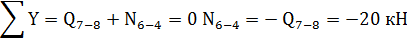
Стержни 6-4 и 7-8 сжаты.
Опорные реакции: 
СХЕМА 2
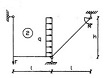
Дано:
Степень статической неопределимости вычисляется
по формуле
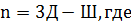
Д=3 - количество дисков, Ш=6 - количество шарниров
,
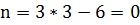Следовательно рама статически определима.
1. Определение опорных реакций.
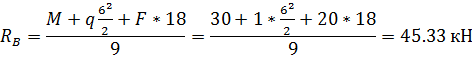
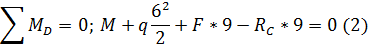
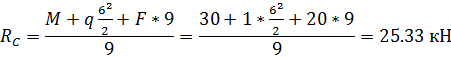
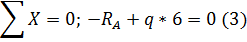
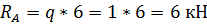
Проверка:
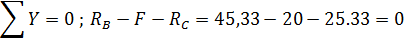
Построение эпюры моментов М:
Разбиваем раму сечениями на участки и строим
эпюру моментов по участкам.
Участок А-1:
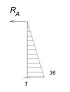
Отбрасываем мысленно правую часть рамы а сечение
1 ставим жесткую заделку
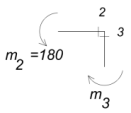
Участок 2-3:
ставим заделку в сечение 3
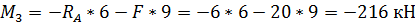
Участок D-4:
заделка в сечении 4
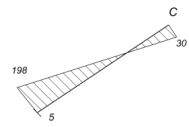
Участок 5-С: заделка в сечении 5
Выполним проверку, составив уравнение равновесия
узла В:
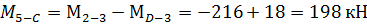
Общий вид эпюры моментов:
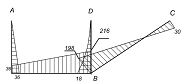
Построение эпюры Q.
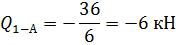
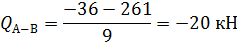
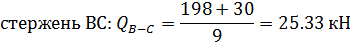
Построение эпюры продольных сил.
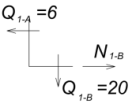
Вырежем узел 1: опора А шарнирно-подвижная,
поэтому продольного усилия в стержне А-1 нет.
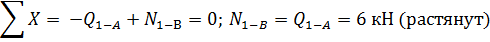
Вырежем узел В: стержень DB консольный, поэтому
продольного усилия в нем нет.
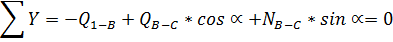
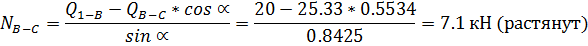
Эпюры Q и N:
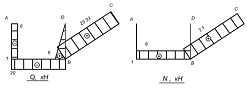
СХЕМА 3
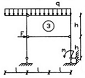
дано: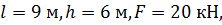 
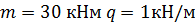
Степень статической неопределимости вычисляется
по формуле
Д=3 - дисков, Ш=3 - количество шарниров, 
число
опорных стержней
,
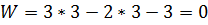Следовательно рама статически определима.
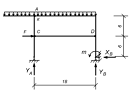
1. Определение опорных реакций.
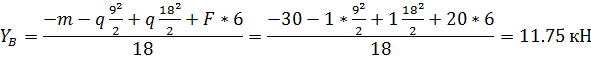
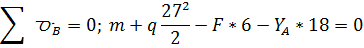
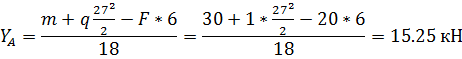
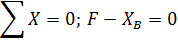
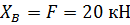
Проверка:
Опорные реакции определены правильно.
Усилие в затяжке определим, составив уравнение
моментов правой или левой частей рамы частей рамы относительно шарнира К:
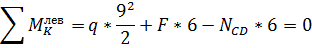
Для проверки составим уравнение равновесия
правой части рамы:
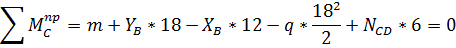
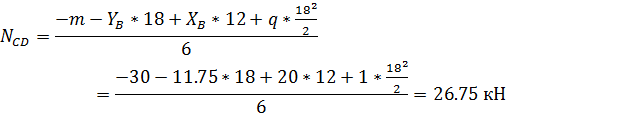
2. Построение эпюры моментов М.
Разбиваем раму сечениями на участки и строим
эпюру моментов по участкам.
участок А3:
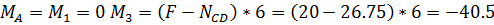
участок Z4:
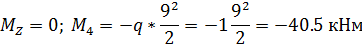
участок 5-6:
участок В-7:
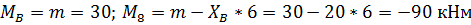
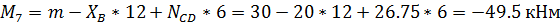
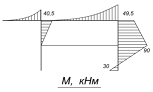
Эпюра поперечных сил Q:
стойки:
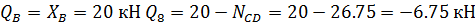
Консоль
ЕК: 
Ригель
КZ: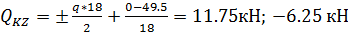 
. Построение эпюры N. Эпюру продольных
усилий будем строить по эпюре Q, рассматривая равновесие узлов
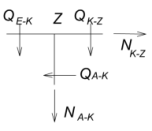
Узел К:
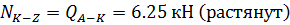
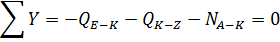
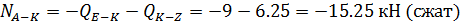
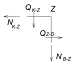
Узел Z:
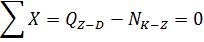
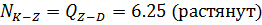
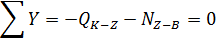
Эпюра продольных сил N
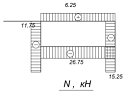
СХЕМА 4
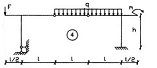
дано: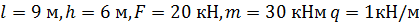 
Степень статической неопределимости вычисляется
по формуле
Д=3- дисков, Ш=2 - количество шарниров,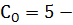 
число
опорных стержней
,
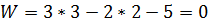Следовательно рама статически определима.
Строим поэтажную схему, для чего разделим
систему на балку и две рамы.
Решаем рамы и балку каждую в отдельности,
начиная с верхней балки.
1. Балка ЕК:
Опорные реакции
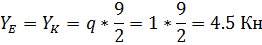
Эпюры М и Q:
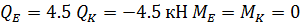
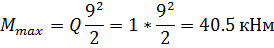
2. Рама ACDE:
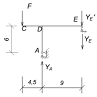
На эту раму кроме заданных нагрузок действует
еще и реактивная сила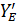 
от веса верхней
балки.
Вычисляем опорные реакции:
Проверка:
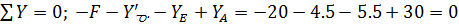
Строим эпюры M и Q.
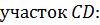
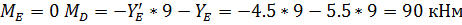
. Рама BKZS:
На раму, кроме заданных нагрузок, действует еще
и реактивная сила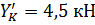 
,
Определим опорные реакции рамы:
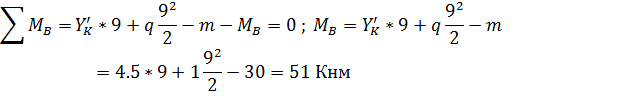
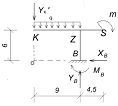
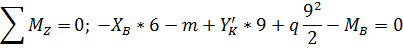
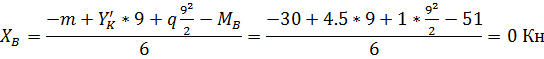
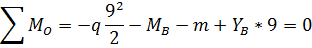
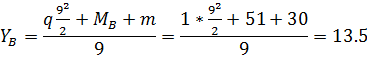Проверим
правильность определения опорных реакций, составив уравнение равновесия.
Моментную точку нужно выбрать так, чтобы в уравнение вошли все проверяемые силы
- это будет точка S:
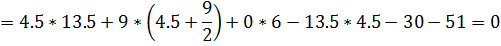
Опорные реакции определены верно.
Строим эпюры М и Q.
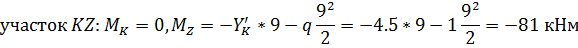
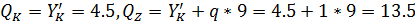
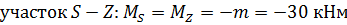
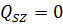
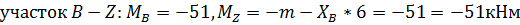
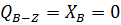
Соединяем эпюры:
Эпюру продольных сил N строим по эпюре Q,
рассматривая равновесие узлов:
Узел С:
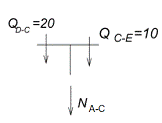
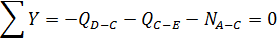
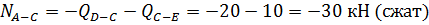
Узел Z:
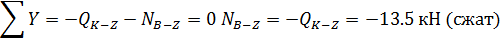
Эпюра продольных усилий:
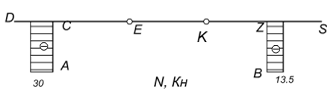
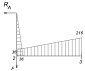
СХЕМА 5
дано: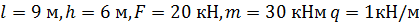
Степень статической неопределимости вычисляется
по формуле
Д=3- дисков, Ш=2 - количество шарниров, 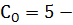число
опорных стержней
,
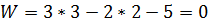Следовательно балка статически определима.
Строим поэтажную схему. В результате получаем
три балки: две вспомогательные - двухопорная DE и консольная EK и двухопорная с
консолями AD.
статический стержневой опорный эпюра
1. Определение опорных реакций.
Опорные реакции определяем для каждой балки
отдельно.
Балка DE:
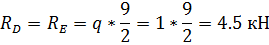
Эпюры М и Q:
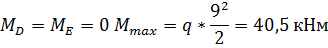
Балка AD: в
точке D на балку действует реактивная сила 
от
веса верхней балки
Опорные реакции:
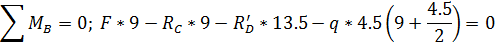
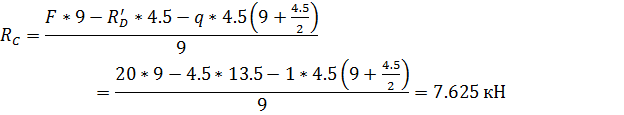
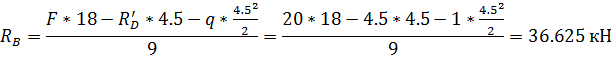
Проверка:
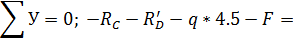
Эпюра М:
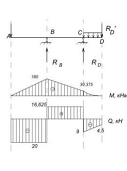
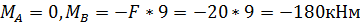
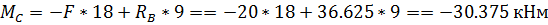
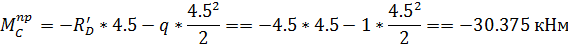
Эпюрa Q:
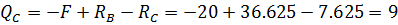
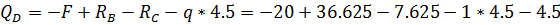
Балка ЕК:
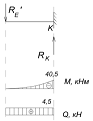
Консольная. На балку действует только одна
реактивная сила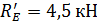 
от веса верхней
балки. Эпюры можно построить, не определяя опорных реакций:
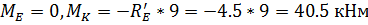
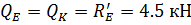
Общий вид эпюры:
СХЕМА 6
дано: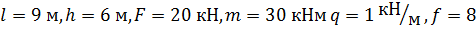 
м
Степень статической неопределимости вычисляется
по формуле
Д=3- дисков, Ш=1 - количество шарниров,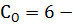 
число
опорных стержней
,
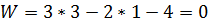Следовательно арка статически определима.
1. Расчет геометрии арки
Пролет арки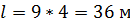 
Радиус окружности
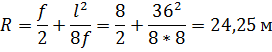
Разбиваем арку сечениями через 4,5 м.
Координаты сечений:
|
№
сечения
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
|
4.5
|
9
|
13.5
|
18
|
22.5
|
27
|
31.5
|
|
|
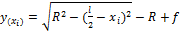
3.89
|
6.27
|
7.58
|
8
|
7.58
|
6.27
|
3.89
|
|
|
0.5567
|
0.3711
|
0.1856
|
0
|
-0.1856
|
-0.3711
|
-0.5567
|
|
|
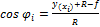
0.8322
|
0.9294
|
0.9820
|
1
|
0.9820
|
0.9294
|
0.8322
|
2. Определение реакций опор.
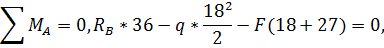
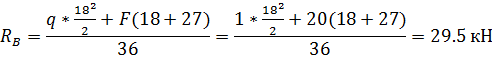
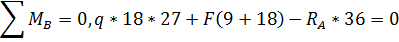
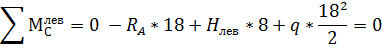
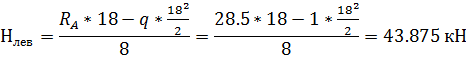
Выполним проверки правильности определения
реакций:
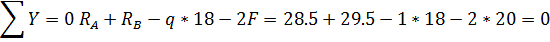
Под схемой арки чертим замещающую балку с теми
же нагрузками. Опорные реакции останутся такими же, как и у арки, нет только
распора. Строим балочные эпюры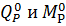 
.
Эпюра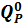 
:
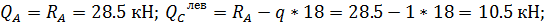
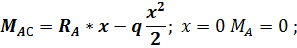
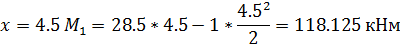
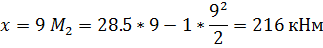
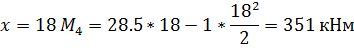
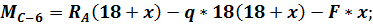
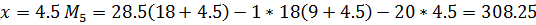
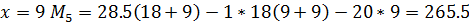
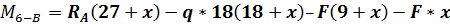
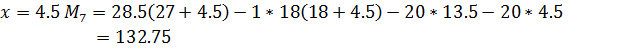
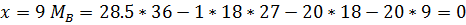
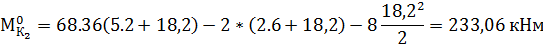
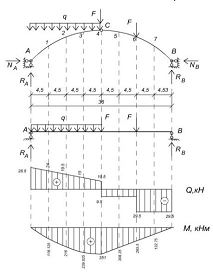
Расчет усилий в сечениях арки ведем в таблице:
№
сеч. x, м y, м tgφк, ед. sinφк, ед. cosφк, ед. Q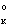
, кНМ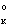, кН.мQ
соsφк, тHa.
sinφк, кНQк=Q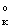
.
сosφк-a.sinφкQ.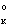
sinφк, кНHa.
|
cosφк, кНNк=-
(Q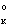.sinφк+ +Ha.cosφк)Ha.yк,
кН.мMк=M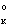--Ha.yк,
кН.м
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11=9-10
|
12
|
13
|
14=12+13
|
15
|
16=8-15
|
|
A
|
0
|
0
|
|
1
|
0
|
28,5
|
0
|
0
|
43,875
|
-43,875
|
28,5
|
0
|
-28,5
|
0
|
0
|
|
1
|
4.5
|
3.89
|
|
0,5567
|
0,8322
|
24
|
118,125
|
19,97
|
24,43
|
-4,46
|
13,36
|
36,51
|
-49,87
|
170,67
|
-52,54
|
|
2
|
9
|
6.27
|
|
0,3711
|
0,9294
|
19,5
|
216
|
18,12
|
16,28
|
1,84
|
7,24
|
40,77
|
-48,01
|
275,1
|
-59,1
|
|
3
|
13.5
|
7.58
|
|
0,1856
|
0,9820
|
15
|
293,625
|
14,73
|
8,14
|
6,59
|
2,78
|
43,08
|
-45,86
|
332,57
|
-38,95
|
|
4
(C)
|
18
|
8
|
|
0
|
1
|
10,5
|
351
|
10,5
|
0
|
10,5
|
0
|
43,875
|
-43,875
|
351
|
0
|
|
|
|
|
|
|
|
-9,5
|
|
-9,5
|
|
-9,5
|
0
|
|
|
|
|
|
5
|
22.5
|
7.58
|
|
-0,1856
|
0,9820
|
-9,5
|
308,25
|
-9,33
|
-8,14
|
-1,19
|
1,76
|
43,08
|
-43,08
|
332,57
|
-24,32
|
|
6
|
27
|
6.27
|
|
-0,3411
|
0,9294
|
-9,5
|
265,5
|
-9,33
|
-16,28
|
-1,19
|
3,24
|
40,77
|
-42,53
|
275,1
|
-9,6
|
|
|
|
|
|
|
-29,5
|
|
-24,42
|
|
-8,14
|
10,06
|
|
-50,83
|
|
|
|
7
|
31.5
|
3.89
|
|
-0,5567
|
0,8322
|
-29,5
|
132,75
|
-24,55
|
-24,43
|
-0,12
|
16,42
|
36,51
|
-52,93
|
170,67
|
-37,95
|
|
B
|
0
|
0
|
|
-1
|
0
|
-29,5
|
0
|
0
|
-43,875
|
43,875
|
29,5
|
0
|
-29,5
|
0
|
0
|
СХЕМА 7
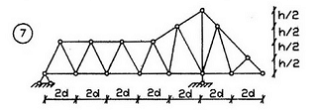
дано: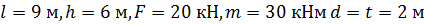 
ширина панели d не задана, но в таблице есть t=2
м. Принимаю её за d. Нагрузка тоже не показана, поэтому загружаю каждый узел
верхнего пояса.
ЕЩЕ: в подобных задачах задают определить усилие
в нескольких стержнях, обычно от 4 до 6, либо в стержнях какой-то панели.
Поэтому определяю усилия в шести стержнях по своему выбору.
Степень статической неопределимости вычисляется
по формуле
Д=1- дисков, Ш=0 - количество шарниров, 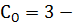число
опорных стержней
,
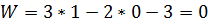Следовательно ферма статически определима.
. Определение опорных реакций:
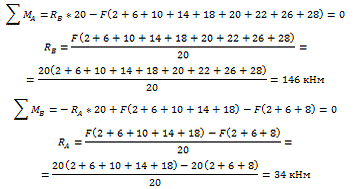
Проверка:
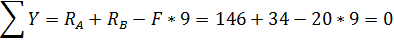
Реакции определены правильно.
. Определение усилий в стержнях.
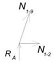
Стержень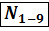 
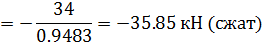
Стержень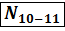 
Проводим сечение 1-1 и составляем уравнение
равновесия правой (или левой) частей фермы относительно моментной точки 3
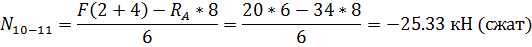
Стержень 
Воспользуемся сечением 1-1. Составим уравнение
равновесия левой части фермы относительно узла 11
Стержень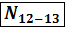 
Проведем сечение 2-2 и составим уравнение
равновесия правой (можно и левой) от сечения части фермы - относительно узла 5
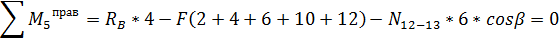
Угол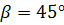 
(можно
определить по чертежу)
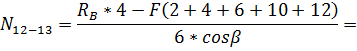
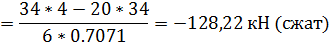
Стержень 
Воспользуемся сечением 2-2. Составим уравнение
равновесия правой части фермы относительно моментной точки 3
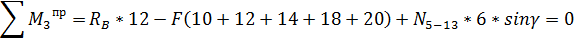
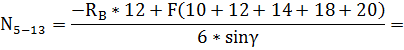
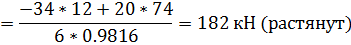
Стержень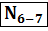 
Проводим сечение 3-3 и составляем уравнение
равновесия для правой части фермы относительно моментной точки 15.
