Деление отрезка пополам, метод деления Гаусса

Деление отрезка пополам, метод деления Гаусса

1. Разработать программное обеспечение для решения нелинейного уравнений методом деления отрезка пополам

Уравнение: x^2+ln(x)=0, e=^-2.

Метод деления отрезка пополам

Отделить корень х^* уравнения f(x) = 0 - значит указать окрестность точки x^*, не содержащую других корней этого уравнения.

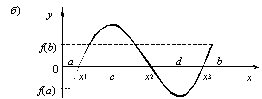
Рис. 1.1

Как известно из анализа, если непрерывная функция f(x) на концах отрезка [a, b] принимает значения разных знаков, т.е. если f(a)×f(b) < 0, то внутри этого отрезка существует, по крайней мере, один корень уравнения f(x) = 0 (рис 1.1). При этом корень x* будет единственным, если f '(x) сохраняет знак внутри интервала (а, b) (рис. 1.1а).

На практике отделение корней уравнения f(x) = 0 на отрезке [а, b] и начинается с проверки условия f(a)×f(b) < 0. Если это условие выполнено, то, следовательно, на (a, b) имеется корень и дальнейшая задача состоит в выяснении его единственности или не единственности.

Для отделения корней практически достаточно провести процесс половинного деления, в соответствии с которым отрезок [a, b] делится на 2,4,8,… равных частей и последовательно определяются знаки функции в точках деления. При этом если в точках деления х_i, х_i+1 выполнено условие f(х_i)×f(х_i+1) < 0, то на интервале (х_i, х_i+1) имеется корень уравнения f(x) = 0. При определении корней всегда стараются найти интервал (х_i, х_i+1) как можно меньшей длины.

Согласно вышеизложенному, получается следующий алгоритм определения корней уравнения f(x) = 0:

) находим участки возрастания и убывания функции f(x) (с помощью производной f ¢(x), если она существует);

) составляем таблицу знаков функции f(x) в стационарных точках (или ближайших к ним), а так же в граничных точках области определения f(x);

) определяем интервалы по правилу x_i = a + (i - 1)×(b - a)/m - 1; i = 1, 2, …, m, на которых f(x) имеет противоположные знаки. Внутри таких интервалов содержится только по одному корню. На рисунке 1.1б интервалы монотонности функции (a, c), (c, d), (d, b), на концах которых функция имеет противоположные знаки. Корнями уравнения f(x) = 0 на отрезке [a, b] в данном случае являются точки x₁, x₂ и x₃.

программа листинг тестирование уравнение

Рис. 1.2 Блок-схема

Тестирование программы

Возьмем значения a = -10, b =5.

Рис. 1.3

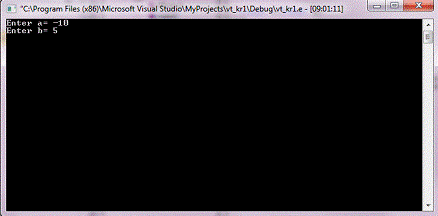
Рис. 1.4

Рис. 1.5

Искомый корень данной функции равен: 0,653076

Листинг программы

#include <iostream>

#include <cmath>namespace std;e=0.01;

f (float x)

{x*x+log(x);

}

main()

{a, b, c;(«Enter a=»); scanf («%f»,&a);(«Enter b=»); scanf («%f»,&b);(b - a > e) {= (a + b) / 2;(f(c) >= 0)= c;= c;

}<<«Otvet: «<< (a + b) / 2 << endl;

}

2. Разработать программное обеспечение для решения системы линейных уравнений методом деления Гаусса

Система уравнений:

x₁+x₂-x₃=-1

x₁+4 x₂+ x₃=5

x₁+ x₂+3 x₃=3

Метод Гаусса

Этот метод является наиболее распространенным методом решения СЛАУ. В его основе лежит идея последовательного исключения неизвестных, в основном, приводящая исходную систему к треугольному виду, в котором все коэффициенты ниже главной диагонали равны нулю. Существуют различные вычислительные схемы, реализующие этот метод. Наибольшее распространение имеют схемы с выбором главного элемента либо по строке, либо по столбцу, либо по всей матрице. С точки зрения простоты реализации, хотя и с потерей точности, перед этими схемами целесообразней применять так называемую схему единственного деления. Рассмотрим ее суть.

Посредством первого уравнения системы (1) исключается х₁ из последующих уравнений. Далее посредством второго уравнения исключается х₂ из последующих уравнений и т.д. Этот процесс называется прямым ходом Гаусса. Исключение неизвестных повторяется до тех пор, пока в левой части последнего n-го уравнения не останется одно неизвестное х_n

a¢_nnx_n = b¢,

где a¢_nn и b¢ - коэффициенты, полученные в результате линейных (эквивалентных) преобразований.

Прямой ход реализуется по формулам

а*_mi = a_mi - ;

b*_m = b_m -

где    m - номер уравнения, из которого исключается x_k;

k - номер неизвестного, которое исключается из оставшихся (n - k) уравнений, а также обозначает номер уравнения, с помощью которого исключается x_k;

i - номер столбца исходной матрицы;

a_kk - главный (ведущий) элемент матрицы.

Во время счета необходимо следить, чтобы a_kk ¹ 0. В противном случае прибегают к перестановке строк матрицы.

Обратный ход метода Гаусса состоит в последовательном вычислении x_n, x_n-1,…, x₁, начиная с (5) по алгоритму

x_n = b¢ / a¢_nn;         .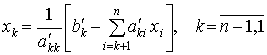

Точность полученного решения оценивается посредством «невязки» (3). В векторе невязки (r₁, r₂,…, r_n)^Т отыскивается максимальный элемент и сравнивается с заданной точностью e. Приемлемое решение будет, если r_max < e. В противном случае следует применить схему уточнения решения.

Уточнение корней

Полученные методом Гаусса приближенные значения корней можно уточнить.

Пусть для системы  найдено приближенное решение , не удовлетворяющее по «невязке». Положим тогда. Для получения поправки d = (d₁, d₂,…, d_n)^Т корня следует рассмотреть новую систему

      или    ,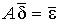

где  - невязка для исходной системы.

Таким образом, решая линейную систему с прежней матрицей А и новым свободным членом = (e₁, e₂,…, e_n)^Т, получим поправки (d₁, d₂,…, d_n).

Рис. 1.6 Блок-схема

Тестирование программы

Для тестирования программы используем заданное уравнение. Получаем следующую матрицу(система) (рис 1.7)

Далее получаем нужные нам корни. Проверяем методом подстановки корней

*(-0,347826)+0,869565-0,826087=-1 à -1,043478+0,43478 = -1

*(-0,347826)+4*0,869565+0,826087=5 à 0,695652+3,47826+0,826087=4,999999

,347826+0,869565+3*0,826087=3 à 0,521739+2,478261=3

Рис. 1.7

Листинг программы

#include <stdio.h>

#include <conio.h>

#include <math.h>

#define №50glavelem (int k, double mas[] [N + 1], int n, int otv[]);main(void)

{mas[N] [N + 1];x[N];otv[N];i, j, k, n;

{(«Vvedite kolichestvo uravneniy sistemy:»);(«%d», & n);(N < n)(«Slishkom bolshoe chislo uravneniy. Povtorite vvod:\n»);

}(N < n);(«Vvedite sistemu:\n»);(i = 0; i < n; i++)(j = 0; j < n + 1; j++)(«%lf», & mas[i] [j]);

(«Sistema:\n»);(i = 0; i < n; i++)

{(j = 0; j < n + 1; j++)(«%7.2f», mas[i] [j]);(«\n»);

}

(i = 0; i < n + 1; i++)[i] = i;(k = 0; k < n; k++)

{(k, mas, n, otv);(fabs (mas[k] [k]) < 0.0001)

{(«Sistema ne imeet edinstvennogo reshenija»);(0);

}(j = n; j >= k; j-)[k] [j] /= mas[k] [k];(i = k + 1; i < n; i++)(j = n; j >= k; j-)[i] [j] -= mas[k] [j] * mas[i] [k];

}

(i = 0; i < n; i++)[i] = mas[i] [n];(i = n - 2; i >= 0; i-)(j = i + 1; j < n; j++)[i] -= x[j] * mas[i] [j];

(«Otvet:\n»);(i = 0; i < n; i++)(j = 0; j < n; j++)(i == otv[j])

{(«%f\n», x[j]);;

}(0);

}

glavelem (int k, double mas[] [N + 1], int n, int otv[])

{i, j, i_max = k, j_max = k;temp;

(i = k; i < n; i++)(j = k; j < n; j++)(fabs (mas[i_max] [j_max]) < fabs (mas[i] [j]))

{_max = i;_max = j;

}

(j = k; j < n + 1; j++)

{= mas[k] [j];[k] [j] = mas [i_max] [j];[i_max] [j] = temp;

}

(i = 0; i < n; i++)

{= mas[i] [k];[i] [k] = mas[i] [j_max];[i] [j_max] = temp;

}

= otv[k];[k] = otv [j_max];

otv [j_max] = i;

Литература

1. Д. Мак-Кракен, У. Дорн. Численные методы М.: Мир. 1977

2.       С.В. Поршев. Вычислительная математика

.        Ю.П. Боглаев Вычислительная математика