Анализ характеристик многослойного образца и синтез многомерного оператора для описания его геометрических и физических свойств
ВЫПУСКНАЯ
РАБОТА БАКАЛАВРА
Тема: Анализ
характеристик многослойного образца и синтез многомерного оператора для
описания его геометрических и физических свойств
Реферат
Отчет 36 с., 1 ч., 13 рис., 3 табл., 6 источников, 2 прил.
КОЭФФИЦИЕНТ ТЕПЛОПРОВОДНОСТИ, КУСОЧНО-ЛИНЕЙНЫЕ ОПЕРАТОРЫ,
КУСОЧНО-ПОСТОЯННЫЕ ОПЕРАТОРЫ, МНОГОСЛОЙНЫЙ ОБРАЗЕЦ.
Объектом исследования является модель многослойного тела, имеющего
области с различными тепловыми характеристиками.
Целью работы является построение оператора для описания геометрических и
физических свойств.
В этой работе было проведено исследование результатов компьютерной
программы, вычисляющей значение коэффициента теплопроводности, в зависимости от
температур и координат тела. Были получены коэффициенты, позволяющие строить
кусочно-линейный и кусочно-постоянный операторы в любой математической среде.
Содержание
Введение
. Обзор методик учета физических и геометрических
характеристик тел
. Многомерные нелинейные операторы
2.1 Обзор кусочно-линейных операторов
2.2 Обзор кусочно-постоянных операторов
3. Методы выделения областей образца с постоянным характером
физических свойств
. Методика синтеза многомерных кусочных операторов
4.1 Кусочно-линейный оператор
.2 Кусочно-постоянный оператор
.3 Реализация математической модели на языке C/C++
5. Сходимость многомерных операторов
. Проведение эксперимента
Вывод
Список литературы
Приложения
физический геометрический оператор математический
Введение
Фундаментальные исследования в области математических, физических,
технических наук и энергетики требуют непрерывного совершенствования и
разработки новых математических моделей для практической реализации сложных
технических объектов. Современные энергетические проблемы требуют
многовариантного развития методов моделирования, анализа и синтеза
агрегированных систем и энергетических конструкций для создания комплексных
методов расчета на основе агрегирования классических моделей теплопроводности,
прочности и др. Этот этап развития моделей и методов требует обобщения классических
математических моделей для расчета энергетических объектов.
Научная новизна состоит в синтезе N-мерных операторов, а также создании оператора, объединяющего
свойства кусочно-линейного и кусочно-постоянного операторов.
1. Обзор
методик учета физических и геометрических характеристик тел
При математическом моделировании процессов теплопроводности можно
руководствоваться методиками, разработанными на основе:
. Аналитические методы решения задач математической физики в
классических и обобщенных подстановках.
. Разностные схемы для уравнений теплопроводности с постоянными,
переменными или разрывными коэффициентами, обладающие свойствами монотонности
. Обобщенные модели и разностные задачи теплопроводности,
учитывающие температурные, температурно-скоростные и температурно-координатные
изменения параметров моделей теплопроводности с применением кусочно-линейных и
кусочно-постоянных операторов.
. Вариационные методы в различных формах, включая метод конечных
или граничных элементов.
Существуют методы моделирования, основанные на применении разностных схем
в рамках классических и обобщенных моделей, а также разностных задач метода
конечных элементов. Классические модели теплопроводности в виде однородных
разностных задач теплопроводности (диффузии) с непрерывными или разрывными
(кусочно-постоянными) коэффициентами позволяют учесть свойства технических
объектов. Частные случаи кусочно-линейных уравнений теплопроводности позволяют
создать однородные разностные схемы, формируемые по одним и тем же рекуррентным
отношениям (без явного выделения точек или линий разрывов по параметрам и
координатам или их производным).
В зависимости от постановки задачи различным образом формируется проблема
краевых (граничных) условий. Если считать, что исследуемые процессы начинаются
с момента времени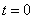 
и протекают до момента времени 
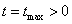, то при решении уравнений
теплопроводности, обычно ставятся краевые задачи. Краевые задачи в таких
системах будем называть краевыми (граничными условиями).
При моделировании весьма важно адекватное формирование краевых условий.
В задачах многослойной теплопроводности особое место занимает условия
сопряжения. При рассмотрении многослойных сред необходимо учитывать условия на
границе контакта двух сред с различными теплофизическими характеристиками -
условия сопряжения. Модели многослойных должны учитывать специфику
моделирования тел сложной формы, состоящих из композита нескольких тел с
различными теплофизическими свойствами.
Для моделирования процессов теплопроводности в сложных конструкциях,
состоящих из нескольких частей, необходимо формулировать разностные задачи для
каждой из частей, согласуя решения на сопрягаемых нагреваемых (охлаждаемых)
поверхностях с помощью условий сопряжения. При этом необходимо учесть следующие
ситуации:
. Совокупность двух тел можно рассматривать как одно тело, но с
разрывным коэффициентом теплопроводности, причем соответствующие модели
теплопроводности имеют адекватный смысл.
. Условия сопряжения не являются единственными вариантами учета
специфики при анализе соединенных тел, а возможны другие модели контакта с
учетом прослойки между сопрягаемыми телами. Эти модели приводят к системе
уравнений с краевыми условиями и условиями сопряжения.
Из приведенного обзора математических моделей теплопроводности следуют
формальные и содержательные характеристики параметров. Разностные задачи для
уравнений теплопроводности с постоянными и переменными коэффициентами являются
важными моделями, позволяющими учесть изменения характеристик многослойных
сред.
Возможны различные варианты учета в уравнениях характеристик сред,
изменяющихся во времени и по координатам, многослойных сред и границ, путем
перехода к соответствующим краевым задачам для квазилинейных уравнений.
2. Многомерные
нелинейные операторы
2.1 Обзор
кусочно-линейных операторов
График кусочно-линейного оператора представлен на рисунке 2.1.1. На
каждом из участков, функция имеет линейный характер.
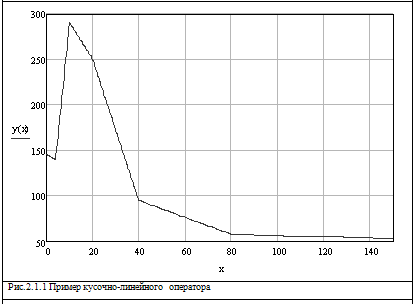
Кусочно-линейный оператор описывается формулой (2.1.1)[2]:
|
|
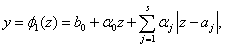
(2.1.1)
|
Запишем систему уравнений, содержащую известные данные:
Будем считать, что коэффициенты
Проведем замену множителей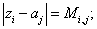 
С учетом введенных замен и ограничений, получим следующую систему
ограничений.
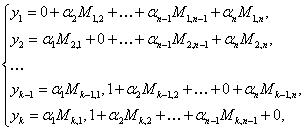
Запишем систему уравнений в матричной форме:
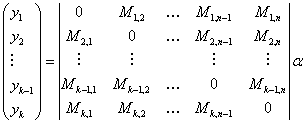
Матрица M будет симметричной относительно
главной диагонали. Главная диагональ всегда нулевая.
Для решения системы уравнений можно воспользоваться одним из методов
решения системы линейных уравнений:
· Метод Крамера
· Метод Гаусса
· Матричный метод (метод с обратной матрицей)
В данной работе будет использоваться третий метод, по причинам
вычислительной простоты и возможности быстрой проверки в любой математической
среде.
Рассмотрим случай, при котором коэффициент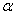 
характеризует неоднородный объект, и 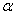зависит от некоторого другого
параметра. Примером такого сложного объекта можно считать многослойное тело, у
которого коэффициент теплопроводности для разных слоев разный. В этом случае
формула 2.1.1 примет вид
|
|
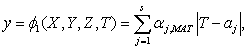
(2.1.2)
|
Где MAT - индекс материала в точке 
, вычисляемый с помощью
кусочно-постоянного оператора, рассматриваемого в следующем параграфе.
2.2 Обзор
кусочно-постоянных операторов
График кусочно-постоянного оператора представлен на рисунке 2.2.1. На
каждом участке, 
имеет постоянное значение, отсюда и название оператора.
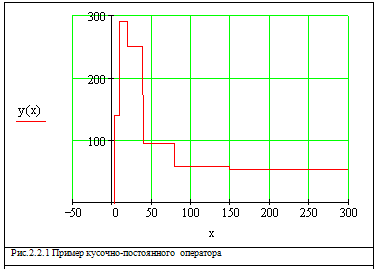
Для преобразования табличных данных к операторному виду, необходимо
выполнить операцию интерполирования. Рассмотрим кусочно-постоянный оператор:
|
|
(2.2.1)
|
Здесь коэффициенты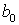 
и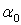 
задают приращение функции и тангенс угла наклона ее
постоянных промежутков,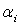 
- приращение отдельных постоянных участков функции, а 
- границы постоянных участков
функции.
Для выполнения операции синтеза коэффициентов выполним ряд ограничений:
будем считать, что коэффициенты 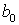и 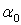будут равны нулю, так как при интерполяции табличных данных
мы имеем дело с набором постоянных участков данных. С учетом ограничений,
уравнение (2.2.1) примет вид:
|
|
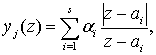
(2.2.2)
|
3. Методы
выделения областей образца с постоянным характером физических свойств
Кусочно-линейный оператор в своем алгоритме использует области с
одинаковым характером свойств. Для использования этого оператора необходимо разбить
всю область на такие участки. Самым простейшим вариантом является двумерный
случай, когда существует две прямоугольные области с разным характером
физических свойств. Такой случай представлен на рисунке 3.1
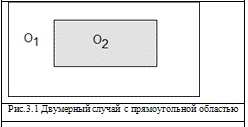
Пусть белая область имеет индекс - 1,а серая - 2.
Разбиение производится по обеим координатам. Кроме координат внутренней
области, задаем граничные значения.
Аналогично можно определять прямоугольные области в трехмерных объектах.
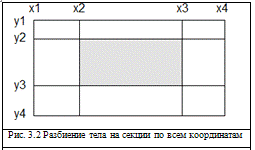
Таким образом, мы получили разбиение по осям. Следующим шагом зададим
каждой секции индекс области. Проще всего это реализовать с помощью таблицы,
столбцы которой - координаты по оси X, строки - координаты разбиения по Y.
Таблица 3.1 Присвоение индексов секциям.
|
X1
|
X2
|
X3
|
X4
|
|
Y1
|
1
|
1
|
1
|
1
|
|
Y2
|
1
|
2
|
1
|
1
|
|
Y3
|
1
|
2
|
1
|
1
|
|
Y4
|
1
|
1
|
1
|
1
|
Более сложным вариантом является случай, когда область представляет собой
фигуру вращения или треугольник.
Рассмотрим разбиение на примере круга. Как и в случае с прямоугольными
областями, происходит разбиение по всем осям, но в данном случае будет больше.
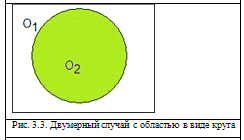
Появляется задача при таком разбиении - определить индекс области в
определенной секции на границе внутренней области. Для решения этой проблемы
сравнивались площади фигуры в секции и площадь секции.
Таким образом, можно выделить области с определенным характером
физических свойств.
Аналогичным образом происходит разбиение образца в трехмерном
пространстве. По каждой из осей происходит разбиение на области с одинаковым
значением параметра. После этого создается таблица со значением индекса в
каждой секции.
4. Методика
синтеза многомерных кусочных операторов
В этой главе рассмотрим методику синтеза многомерных кусочных операторов.
Используя одномерный и двумерный операторы, я постарался выделить общую
методику построения N-мерного
оператора
.1
Кусочно-линейный
оператор
Для синтеза многомерного кусочно-линейного оператора вначале рассмотрим
одномерный оператор.
Одномерный случай:
Методика вывода одномерного кусочно-линейного оператора описана во второй
главе, поэтому в этом разделе будут использоваться формулы без их выведения.
Исходные данные описаны в таблице 5.1.1:
Таблица 5.1.1 Исходные данные в одномерном случае
Вводим матрицу отношения элементов:
Тогда матрица коэффициентов будет высчитываться следующим образом:
И конечная формула выглядит:
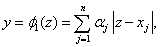
Двумерный случай:
Таблица 5.1.2. Исходные данные двумерного случая
Для каждой переменной построим матрицу разностей
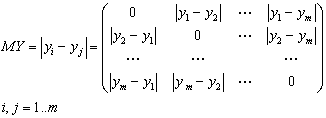
Матрица значений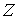 
будет иметь вид:
|
|
|
Искомая матрица коэффициентов для синтеза кусочно-линейных операторов по
одной координате может быть получена вычислением выражения:
|
|
|
Получим конечную матрицу коэффициентов путем умножения матрицы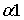 
на инвертированную матрицу 
:
Формула для подсчета кусочно-линейного оператора от двух переменных будет
выглядеть:
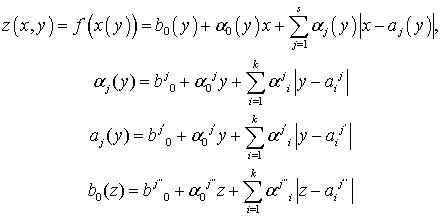
N-мерный
случай:
Исходные данные:
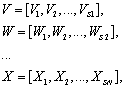
Значение функции:
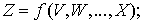
Для каждой переменной 
рассчитаем матрицу разностей элементов:
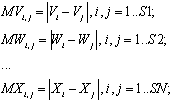
Рассчитываем первую матрицу коэффициентов -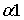
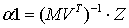
Вторая и последующие матрицы будут зависеть от предыдущих матриц:
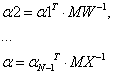
4.2 Кусочно-постоянный оператор
Одномерный случай:
Исходные данные: координаты разбиения по X, значение параметра M в каждой области разбиения:
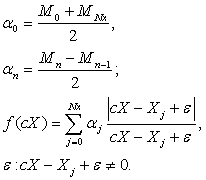
Как видно, вычисление производится в два этапа - вычисление коэффициентов
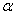и вычисление функции, которая
зависит от одного параметра. В N-мерных
случаях, число коэффициентов и функций будет равно N.
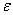подбирается таким образом, чтобы знаменатель не превращался
в ноль, значение этой переменной никак не меняет результат.
Двумерный случай:
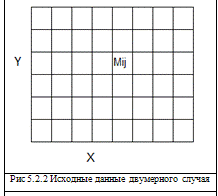
Аналогично с одномерным случаем, исходными данными являются разбиение по
осям, значение параметра в каждой области.
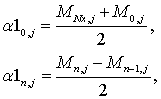
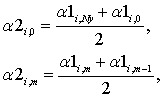
Коэффициент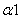 
нужен только для расчета 
, и в дальнейших вычислениях он не
используется.
В двумерном случае используются уже две матрицы параметров 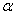и две функции, одна зависит от обеих
координат, другая вызывается в первой, и зависит от одной координаты.
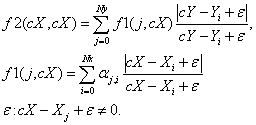
Трехмерный случай:
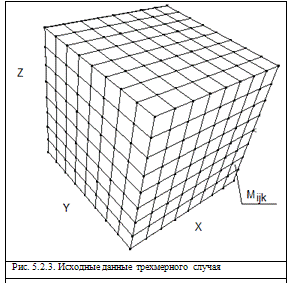
Следуя аналогиям с двумерным оператором, вычислим три 
- матрицы, первая из которых зависит
от матрицы M, следующие зависят только от
предыдущих.
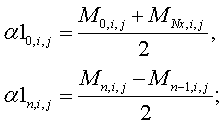
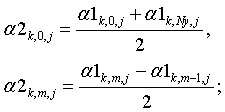
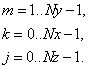
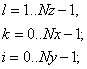
Построим функции:
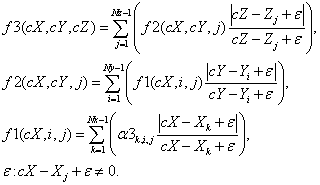
N-мерный
случай,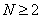
Рассчитываем первую матрицу, использую значения исходной матрицы M:
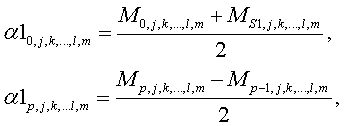
Вторая матрица коэффициентов рассчитывается на основании первой.
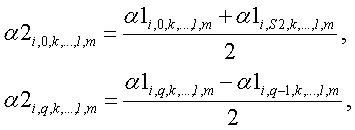
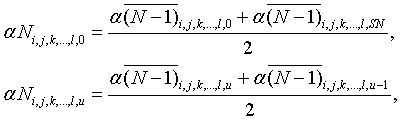
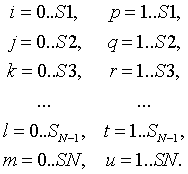
Получили набор массивов коэффициентов, из которых нам потребуется только
последний,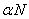 
.
Первая функция использует все координаты.
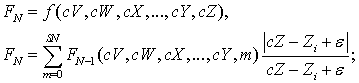
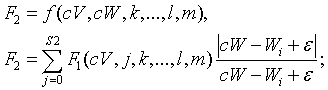
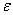подбирается таким образом, чтобы знаменатель не превращался
в ноль, значение этой переменной никак не меняет результат.
.3
Реализация
математической модели на языке C/C++
Поскольку созданный N-мерный
оператор является сложным для вычисления даже простейших задач, целью этой
работы также являлось создание программного комплекса, позволяющего решать
поставленные задачи.
В качестве среды разработки был выбран язык c/c++, в силу
некоторых причин, таких как работа с текстовыми файлами, возможность
использования подключаемых модулей (dll), возможность создания собственного интерфейса взаимодействия между
программой и пользователей.
Структура программы выглядит следующим образом:
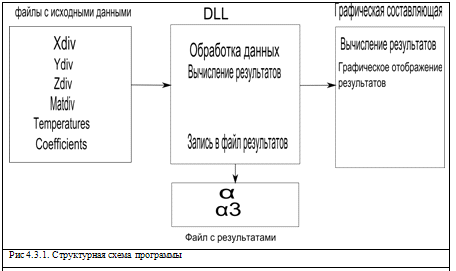
В качестве исходных данных выступают:
· Файлы с таблицами разбиения объекта по осям X,Y,Z.
· Файл с таблицей индексов материалов в каждом секторе разбиения.
· Файл с таблицей шкал температур
· Файл с таблицей коэффициентов каждого материала
После обработки данных в dll,
высчитываются две главные переменные - матрица коэффициентов кусочно-линейного
оператора:
И матрица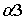 
для расчета значений кусочно-постоянного оператора.
Данные считываются в графический модуль программы, в котором происходят
дальнейшие вычисления для отображения данных.
Создается сетка узлов, в которых будет высчитываться значение
коэффициента теплопроводности в зависимости от температуры.
Программа имеет два режима отрисовки. В первом режиме для каждого
видимого узла, показывается индекс его материала. В таком режиме можно
проверить, насколько точно было проведено разбиение по координатам.
Второй режим предназначен для вывода информации о значении коэффициента
теплопроводности. С помощью цветовой палитры для каждого узла обозначается его
значение теплопроводности - чем темнее цвет, тем больше значение коэффициента
теплопроводности.
Результаты программы отображены в главе "проведение
эксперимента". Код кусочно-линейного и кусочно-постоянного операторов
представлен в приложениях 1 и 2.
5. Сходимость
многомерных операторов
Для оценки эффективности рассмотрим сходимость к точному значению
многомерных операторов.
Введем основные понятия и условие сходимости.
Функция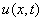 
является решением задачи:
|
|
(5.1)
|
в области D, ограниченной
контуром Г, если она удовлетворяет уравнению (5.1), а также краевым, начальным
или начально-краевым условиям.
Будем использовать два пространства:- пространство непрерывных в D
функций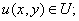 
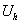- пространство сеточных функций в 
полученное дискретизацией по времени
и координатам исходного U-пространства непрерывных функций в D.
В качестве аналога задачи (5.1) в пространстве сеточных функций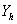 
определен разностный оператор
|
|
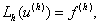
(5.2)
|
Где 
. В пространствах 
введены нормы 
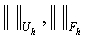соответственно
Определение 1.
Разностная схема является сходящейся, если при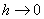 
имеет место:
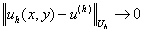
Определение 2.
Если выполнено следующее условие:
,
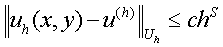где c - постоянная, независящая от h, то имеет место скорость сходимости
к аналитическому решению порядка s.
Определение 3.
Разностная схема называется аппроксимирующей исходную задачу на решении u(x,y), если
и 
при 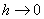. Функция 
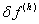называется погрешностью аппроксимации разностной схемы.
Поскольку для анализа сходимости необходимо исследовать условие
где c - постоянная, не зависящая от h, необходимо построить приближенные
представления решений, доставляемые разностными схемами. Аналогичные оценки
используются при анализе скорости сходимости к аналитическому решению заданного
порядка. При исследовании сходимости используются полиномиальные аппроксимации
решений, которые локально адекватны решениям семейств линейных систем.
6. Проведение
эксперимента
Логическим завершением работы можно считать проведение эксперимента с
использованием построенной математической модели.
Для этого эксперимента была создана программа, обрабатывающая исходные
данные, вычисляющая необходимые величины, выводящая их в файл и также
изображающая результаты визуально.
В качестве многослойного объекта была выбрана следующая фигура:
Физически это часть стены, в которой гвоздь держит отделочный материал
комнаты.
Этот эксперимент можно обозначить как исследование теплопроводности
материалов в условиях пожара, мороза, или резкой смены температур.
В результате необходимо получить таблицы коэффициентов для построения
операторов, вывести их в файл, а также построить графическую модель системы.
Исходные данные:
Исходные данные представляются в виде одного столбца, с указанием общего
числа данных в файле. В связи с очень большим количеством данных и отсутствием
удобной формы представления и задаваемых данных, я не буду описывать начальные условия.
Результаты:
. Получена таблица коэффициентов кусочно-линейного оператора: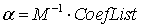 
|
2.825000-0.175000-0.475000
-7.6000001.5500001.550000 5.7000000.4000001.800000 1.5250001.1750000.875000
|
2. Получена таблица 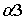для вычисления кусочно-постоянного оператора:
|
1.2500000.0000000.0000000.0000000.0000000.000000
0.3750000.0000000.0000000.0000000.000000-0.125000
0.0000000.0000000.0000000.0000000.0000000.000000
-0.3750000.0000000.0000000.0000000.000000-0.125000
0.0000000.1250000.250000-0.250000-0.1250000.000000
0.0000000.000000-0.1250000.1250000.0000000.000000
0.0000000.125000-0.1250000.125000-0.1250000.000000
0.0000000.0000000.0000000.0000000.0000000.000000
0.0000000.0000000.0000000.0000000.0000000.000000
0.0000000.0000000.0000000.0000000.0000000.000000
0.0000000.0000000.0000000.0000000.0000000.000000
0.0000000.0000000.0000000.0000000.0000000.000000
-0.250000-0.125000-0.2500000.2500000.1250000.000000
-0.1250000.0000000.125000-0.1250000.000000-0.125000
0.000000-0.1250000.125000-0.1250000.1250000.000000
-0.3750000.0000000.0000000.0000000.000000-0.125000
|
Кроме табличных значений коэффициентов мы можем получить графическое
представление о процессе.
На рисунках 6.2 и 6.3 представлена графическая модель объекта.
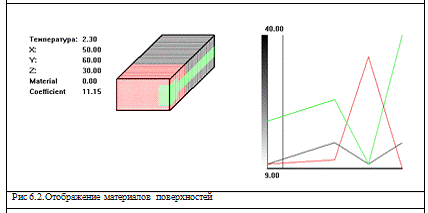
Первая цветовая схема определяет материал в каждой точке тела, и выводит
в виде областей разного цвета. Для этого используется только кусочно-постоянный
оператор.
График справа и данные слева рисунка нужны для второй схемы.
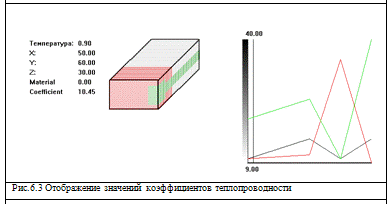
На рисунке 6.3. представлен второй режим - отображения, основной,
выводящий информацию о коэффициенте теплопроводности в точках объекта.
Информация слева показывает текущую температуру, координату заданной точки, а
также номер материала, и значение коэффициента теплопроводности
График справа изображает характер коэффициентов теплопроводности разных
материалов, в зависимости от температуры. Для графика применяется
кусочно-линейный оператор.
И самым важным результатом является параллелепипед в центре. В
зависимости от текущей температуры, и координаты, высчитывается значение
коэффициента теплопроводности. С помощью оттенков цвета показывается значение
коэффициента теплопроводности.
В результате была получена математическая модель, описывающая
геометрические (рис 6.2) и физические (рис 6.3) свойства объекта. Благодаря
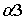коэффициентам и , аналогичную модель можно построить в любой другой математической
среде.
Вывод
В ходе написания работы был проведен анализ методик учета физических и
геометрических характеристик тел. В качестве основной была выбрана методики,
построенная на обобщенной модели теплопроводности учитывающей, температурные,
температурно-скоростные и температурно-координатные изменения параметров
моделей теплопроводности с применением кусочно-линейных и кусочно-постоянных
операторов.
Был проведен анализ кусочно-линейных и кусочно-постоянных операторов. На
основе анализа были синтезированы N-мерные операторы.
Построена математическая модель для расчета коэффициента теплопроводности
произвольного многослойного образца, в зависимости от координат и температуры.
В математической модели использовался одномерный кусочно-постоянный оператор, и
трехмерный кусочно-постоянный.
Была построена математическая модель, реализующая эту математическую
модель
В этой работы был проведен анализ кусочных операторов, с последующим
синтезом N-мерных кусочно-линейных и
кусочно-постоянных операторов.
В качестве эксперимента была выбрана трехмерная модель образца, имеющего
области с различными тепловыми характеристиками. Компьютерная программа смогла
обработать эту модель, и получить трехмерную модель тела, вычисляющая
коэффициент теплопроводности в любой точке, для диапазона температур.
Список литературы
1. В.Н. Козлов, С.В. Хлопин. Математические и
информационные модели теплофизических процессов. Санкт-Петербург, изд.
Политехнического университета, 2010 г. 189 стр.
. В.Н. Козлов, В.Е. Куприянов, В.С. Забородский.
Вычислительные методы синтеза систем автоматического управления. Ленинград,
изд. Ленинградского университета. 1989 г. 224стр.
. Козлов В.Н., Хлопин С.В. Обобщенные модели
теплопроводности. Материалы X Всероссийской конференции по проблемам науки и
высшей школы Cб. Фундаментальные исследования в технических
университетах". Санкт-Петербург. - СПб.: СПбГПУ, 2006. -578 с. Стр. 62-63.
. Козлов В.Н., Магомедов К.А., Хлопин С.В.
Операторно-функицональный метод моделирования тепловых процессов. Материалы
VIII Всероссийской конференции по проблемам науки и высшей школы. Cб.
"Фундаментальные исследования в технических университетах".
Санкт-Петербург. - СПб.: СПбГПУ, 2009г,
394с. Стр. 15-17
. Даугавет И.К. Теория приближенных методов. Линейные
уравнения. Санкт-Петербург, изд. "БХВ-Петербург, 2006 год"
. Самарский А.А, Вабищевич П.Н. Вычислительная
теплопередача, Москва, изд. УРСС, 2010 г.
784 с.
Приложение 1
Листинг кода
кусочно-линейного оператора
void MathR()
{
//результирующая матрица(α=M^(-1)*CoefList)=new
double*[TempSize];(int i=0;i<TempSize;i++)
{[i]=new double [MaterialsSize];
}=new double* [TempSize];//Матрица разниц температур=new
double* [TempSize];//инвертированная матрица M(int i=0;i<TempSize;i++)
{[i]=new double [TempSize];[i]=new double [TempSize];
}(int i=0;i<TempSize;i++)
{(int j=0;j<TempSize;j++)
{
//Расчет
значений[i][j]=fabs(Temperatures[i]-Temperatures[j]);[i][j]=M[i][j];//Создание
копии
}
}(Mtr,TempSize);//Инвертируем копию
//перемнажаем M^(-1) и CoefList:(Mtr,TempSize,TempSize,CoefList,TempSize,MaterialsSize,R);
}
CDesignView::CalcLocalCoef(double X, double Y, double Z,
double cT)
{SUMM=0;//конечный результатiterat=0;//результат за
итерациюMatIndex=(int)Funk3(X,Y,Z);//индекс материала в точке(int
j=0;j<TempSize;j++)
{=CoefList[j][MatIndex]*(cT-Temperatures[j]);+=iterat;
}SUMM;
}
Приложение 2
Листинг кода
кусочно-постоянного оператора
void MathAlpha()
{(int i=0;i<YSize;i++)
{(int j=0;j<ZSize;j++)
{[0][i][j]=(M_at_point[0][i][j]+M_at_point[XSize-1][i][j])/2;(int
n=1;n<XSize;n++)
{[n][i][j]=(M_at_point[n][i][j]-M_at_point[n-1][i][j])/2;
}
}
}(int k=0;k<XSize;k++)
{(int j=0;j<ZSize;j++)
{[k][0][j]=(Alpha1[k][0][j]+Alpha1[k][YSize-1][j])/2;(int
m=1;m<YSize;m++)
{[k][m][j]=(Alpha1[k][m][j]-Alpha1[k][m-1][j])/2;
}
}
}(int k=0;k<XSize;k++)
{(int i=0;i<YSize;i++)
{[k][i][0]=(Alpha2[k][i][0]+Alpha2[k][i][ZSize-1])/2;(int
l=1;l<ZSize;l++)
{[k][i][l]=(Alpha2[k][i][l]-Alpha2[k][i][l-1])/2;
}
}
}
}CDesignView::Funk1(double Xcoord, int cI, int cJ)
{(Xcoord-Xdiv[k]+eps2!=0)//если знаменатель не равен 0
{=Alpha3[k][cI][cJ]*(fabs(Xcoord-Xdiv[k])/(Xcoord-Xdiv[k]+eps2));+=Iterat;
}//иначе применяем другой знаменатель
{+=Alpha3[k][cI][cJ]*(fabs(Xcoord-Xdiv[k])/(Xcoord-Xdiv[k]+eps1));
}
}SUMM;
}CDesignView::Funk2(double Xcoord, double Ycoord, int cJ)
{SUMM=0;//РезультатIterat=0;//результат за одну итерацию(int
i=0;i<YSize;i++)
{(Ycoord-Ydiv[i]+eps2!=0)//если знаменатель не равен 0
{=Funk1(Xcoord,i,cJ)*(fabs(Ycoord-Ydiv[i])/(Ycoord-Ydiv[i]+eps2));+=Iterat;
}//иначе применяем другой знаменатель
{+=Funk1(Xcoord,i,cJ)*(fabs(Ycoord-Ydiv[i])/(Ycoord-Ydiv[i]+eps1));
}
}SUMM;
}CDesignView::Funk3(double Xcoord, double Ycoord, double
Zcoord)
{SUMM=0;//РезультатIterat=0;//результат за одну итерацию(int
j=0;j<ZSize;j++)
{(Zcoord-Zdiv[j]+eps2!=0)//если знаменатель не равен 0
{=Funk2(Xcoord,Ycoord,j)*(fabs(Zcoord-Zdiv[j])/(Zcoord-Zdiv[j]+eps2));+=Iterat;
}//иначе применяем другой знаменатель
{+=Funk2(Xcoord,Ycoord,j)*(fabs(Zcoord-Zdiv[j])/(Zcoord-Zdiv[j]+eps1));
}
}SUMM;
}