Использование ключевых задач в процессе обучения школьников решению задач по геометрии
Использование ключевых задач в процессе обучения школьников
решению задач по геометрии
Введение
Обучение математике - это, прежде
всего, обучение решению задач. Учитель не должен добиваться, чтобы школьники
решали как можно больше однотипных задач.
Решение большинства довольно трудных
задач даже на математических олимпиадах сводится в конечном итоге к умелому
распознаванию небольшого числа идей, отраженных учителем в ключевых задачах.
Кроме того, система ключевых задач позволяет, обосновано дифференцировать
работу учащихся, так как овладение умением решать ключевые задачи гарантирует
выполнение программных требований к их знаниям и умениям. Учащиеся,
интересующиеся математикой, оттолкнувшись от этих задач, свободно переходят к
следующему качественному этапу работы с математическими задачами. Многие
задачи, опубликованные в учебниках, задачниках, методических пособиях в
значительной степени дублируют друг друга, отличаясь лишь обозначениями или
другими не очень существенными деталями, тогда как математическая их сущность -
одна и та же.
Оказывается, по каждой теме
достаточно выделить несколько, обычно не более 3-6 «ключевых» задач; почти все
остальные задачи можно свести к одной из них или их композиции. Какие же задачи
следует считать ключевыми?
Целью данной курсовой работы
является разработка методики и технологии применения ключевых задач при
обучении школьников решению задач по планиметрии в школьном курсе геометрии.
Задачи, которые были поставлены
перед выполнением данной работы:
) Показать эффективность
использования ключевых задач в школьном курсе геометрии;
) Выделить ключевые задачи и
разработать к ним систему задач по темам в школьном курсе планиметрии;
) Разработать план-конспект
урока с использованием ключевых задач.
В первой главе были раскрыты такие
понятия как «ключевая задача темы» и «метод ключевой задачи», представлены
классификация задач по геометрии и методы отбора ключевых задач, рассмотрен
алгоритм подготовки урока решения ключевых задач. Вторая глава посвящена
практическому применению метода ключевых задач.
1. Роль задач в процессе
обучения школьников в школьном курсе геометрии
1.1 Роль задач в
обучении математике
При обучении математике
задачи имеют образовательное, практическое, воспитательное значение.
Образовательное значение
математических задач. Решая математическую задачу, учащийся познает много
нового: знакомится с новой ситуацией, описанной в задаче, с применением
математической теории к ее решению, познает новый метод решения или новые
теоретические разделы математики, необходимые для решения задачи, и т.д. Иными
словами, при решении математических задач учащиеся приобретают математические
знания, повышают своё математическое образование. При овладении методом решения
некоторого класса задач у учащегося формируется умение решать такие задачи, а
при достаточной тренировке - и навык, что тоже повышает уровень математического
образования.
Практическое значение математических
задач. При решении математических задач ученик обучается применять
математические знания к практическим нуждам, готовится к практической
деятельности в будущем, к решению задач, выдвигаемых практикой, повседневной
жизнью. Почти во всех конструкторских расчетах приходится решать математические
задачи, исходя из запросов практики. Исследование и описание процессов и их
свойств невозможно без привлечения математического аппарата, т.е. без решения
математических задач.
Воспитательное значение
математических задач. Прежде всего, задача воспитывает своей фабулой, текстовым
содержанием. Поэтому фабула многих математических задач существенно изменяется
в различные периоды развития общества. Но воспитывает не только фабула задачи,
воспитывает весь процесс обучения решению математических задач. Правильно
поставленное обучение решению математических задач воспитывает у учеников
честность и правдивость, настойчивость и преодоление трудностей, уважение к
труду своих товарищей.
Они развивают логическое
и алгоритмическое мышление учащихся, вырабатывают практические навыки
применения математики, формируют диалектико-материалистическое мировоззрение,
являются основным средством развития пространственного воображения, а также
эвристического и творческого начал.
При обучении
теоретическим знаниям задачи способствуют мотивации введения понятий, выявлению
их существенных свойств, усвоению математической символики и терминологии,
раскрывают взаимосвязи одного понятия с другими.
В процессе изучения
теоремы задачи выполняют следующие функции: способствуют мотивации ее введения;
выявляют закономерности, отраженные в теореме; помогают усвоению содержания
теоремы; обеспечивают восприятие идеи доказательства, раскрывают приемы
доказательства; обучают применению теоремы; раскрывают взаимосвязи изучаемой
теоремы с другими теоремами.
С изменением роли и
места задач в обучении обновляются и видоизменяются и сами задачи. Раньше они
формулировались с помощью слов «найти», «построить», «вычислить», «доказать», в
современной школе чаще используются слова «обосновать», «выбрать из различных
способов решения наиболее рациональный», «исследовать», «спрогнозировать
различные способы решения» и т.д.
Решение задач является
наиболее эффективной формой развития математической деятельности. [1]
1.2 Классификация задач
по геометрии
В современной
методической и психологической литературе принята классификация задач. По
характеру требования:
- задачи на
доказательство;
- задачи на построение;
- задачи на вычисление.
По функциональному
назначению:
- задачи с
дидактическими функциями;
- задачи с
познавательными функциями;
- задачи с развивающими
функциями.
По величине
проблемности:
- стандартные;
- обучающие;
- поисковые;
- ключевые;
- проблемные.
По методам решения:
- задачи на
геометрические преобразования;
- задачи на векторы и
др.
По числу объектов в
условии задачи и связей между ними:
- простые;
- сложные.
По компонентам учебной
деятельности:
-
организационно-действенные;
- стимулирующие;
- контрольно-оценочные.
Кроме того, различают
задачи: стандартные и нестандартные; теоретические и практические; устные и
письменные; одношаговые, дву-шаговые и др.; устные, полуустные, письменные и
т.д. [2]
1.3 Роль ключевых задач
в системе обучающих задач в школьном курсе геометрии
Ключевая задача темы - это задача,
идея решения которой применяется при решении других задач темы.
Метод составления
системы задач, построенной по принципу - каждая задача системы использует
результат решения одной какой-либо (ключевой) задачи, называется методом ключевой
задачи.
Существует две точки
зрения на понятие ключевой задачи. Первая из них состоит в рассмотрении
ключевой задачи как задачи-факта. Зачастую такая ключевая задача оказывается
дополнительной теоремой школьного курса. Вторая точка зрения состоит в
рассмотрении ключевой задачи как задачи-метода. При изучении какой-либо темы
школьного курса можно отобрать определенный минимум задач, овладев методами
решения которых, учащиеся будут в состоянии решить любую задачу на уровне
программных требований по изучаемой теме.
«Ключевая» задача является средством
решения других задач, поэтому ее знание учащимися обязательно. Разворачивающаяся
система задач, с одной стороны, способствует усвоению факта или метода решения,
изложенных в «ключевой» задаче, с другой, позволяет увидеть взаимосвязи
отдельных тем школьного курса математики. Поэтому составленная данным методом
система задач является эффективным средством повторения, обобщения и
систематизации учебного материала.
Анализ различной методической,
математической и педагогической литературы показал, что единого определения
«ключевой (опорной или базисной) задачи» нет. Также как нет и точного сравнения
опорной, ключевой и базисной задачи, но рассматривая различные высказывания, мы
делаем вывод, что эти слова являются синонимами. [3]
Рассмотрим один из
возможных алгоритмов подготовки урока решения ключевых задач,
предложенный Н.И. Зильбербергом:
1. Изучение программы и
определение умений, которые должны быть
сформированы у всех учеников после изучения темы.
2. Систематизация
методов решения задач по изучаемой теме.
3. Отбор ключевых задач
по изучаемой теме.
4. Проработка ключевых
задач по изучаемой теме.
5. Выбор методов решения
ключевых задач, которые будут использоваться при работе с учащимися.
6. Изучение затруднений
и возможных ошибок учащихся при реализации отобранных алгоритмов,
их диагностика, способы предупреждения их
преодоления.
7. Обоснование
последовательности разбора ключевых задач с учащимися.
8. Планирование
проведения урока. [4]
.4 Методы отбора
ключевых задач по изучаемой теме
Отбирать ключевые задачи можно
различными способами, кроме того, возможны различные системы ключевых задач (в
зависимости от особенностей класса, учителя и т.п.). Рассмотрим некоторые
методы выбора ключевых задач.
Первый метод основан на умениях,
которые должны быть сформированы у учащихся после изучения темы. Для отбора
задач требуется просмотреть известные учителю задачи по теме и соотнести их с
умениями, которые планируется сформировать. Далее выбирается минимальное число
задач, овладев умениями решать которые школьник сможет решить любую задачу из
учебника, а также задачи определенного уровня сложности. Эту процедуру выбора
можно представить наглядно. С этой целью составим специальную таблицу (таблица
1.1). В таблице по горизонтали перечислены умения, а по вертикали указаны
номера задач (из учебника или любого задачника). В ходе просмотра задач в соответствующей
строке и столбце будем ставить 1, если решение задачи способствует формированию
умения (оно используется), и 0 в противном случае.
|
Номера задач
|
Умения
|
|
1
|
2
|
4
|
5
|
6
|
7
|
|
162
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
163
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
|
164
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
|
165
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
166
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
Задачи выбираем таким образом, чтобы
их число было 3-6 и были задействованы все умения 1-7. Существенно, чтобы
наиболее сложные умения были задействованы не в одной, а в нескольких задачах,
чтобы задачи не были однотипными как по методам решения, так и по условию,
чтобы уровень их сложности выбирался в соответствии с особенностями
предшествующей подготовки учащихся и учитывал ближайшую зону развития учеников.
Кроме того, при выборе ключевых задач следует опираться на следующие критерии:
. Соответствие программе по
данной теме.
. Степень использования при
изучении последующих тем.
. Затраты времени по обучению
учащихся решению задач.
. Оптимальность алгоритмов
решения задач.
. Возможность поразить
учащихся красотой решения.
Второй метод выделения ключевых
задач можно назвать методом исключения и дополнения. Для его реализации
обращаемся к задачам из учебника. Читаем первую задачу - она первый кандидат на
включение в систему ключевых задач. Переходим к следующей задаче. Здесь
возможно несколько вариантов:
. Она аналогична первой. В
этом случае сравниваем первую и вторую. Учителю предстоит решить, оставить в
списке возможных кандидатов первую или вторую (единого рецепта нет и не должно
быть, решать учителю).
. Она существенно отличается
от первой и не включает первую. В этом случае эту задачу следует добавить к
возможным кандидатам.
. Вторая задача отличается от
первой, но включает в себя первую. Чаще всего это означает, что первую следует
исключить, а вторую включить в число возможных кандидатов.
Далее переходим к следующей задаче и
процедура повторяется. Если проделать это со всеми задачами учебника, то
остается 3-6 задач. Они и будут включены в число ключевых задач, отобранных на
основе учебника. Теперь учителю следует задать себе вопрос: «С моей
профессиональной точки зрения, достаточно ли моим ученикам уметь решать задачи
только из учебника?» Если ответ утвердительный, то процедура выделения ключевых
задач (для этого учителя и класса) окончена. Если же ответ отрицательный, то
выбор ключевых задач следует продолжать, обратившись к дополнительным
источникам.
Следующий способ ключевых задач
основан на методах решения задач по изучаемой теме, которые учитель отобрал для
работы с учащимися. Выбор осуществляется в такой последовательности:
. Изучается набор задач в
учебнике и дополнительных источниках.
. Задачи соотносятся с
методами решения, отобранными для работы с учащимися.
. Выбирается 3-6 задач, при
решении которых будут задействованы все отобранные учителем методы решения
задач.
Важно, что наиболее сложные методы
заложены не в одной, а в нескольких ключевых задачах. Это дает возможность
показать различные варианты реализации метода.
Следующий метод выбора ключевых
задач можно назвать комбинаторным. Для его реализации следует выделить объекты,
которые фигурируют в задачах той или иной темы, рассмотреть возможные
комбинации этих объектов, а потом для наиболее важных комбинаций подобрать
задачу.
Итак, отобраны ключевые задачи и
найдены многие, основанные на различных идеях методы решения. На данном этапе
подготовки урока учителю важно выбрать те решения ключевых задач, которые будут
использованы при работе с классом. Предпочтение отдается тем методам, которые
применимы к более широкому множеству задач.
Теперь следует определить
последовательность ключевых задач, в которой задачи будут разбираться на уроке.
При этом следует учитывать следующие рекомендации:
. Начинать лучше всего с
самых простых ключевых задач.
. Задачи, при решении которых
приходиться выходить за рамки школьной программы, которые наиболее удалены от
обязательных результатов обучения, лучше всего разбирать в конце урока.
. Если при решении какой-либо
ключевой задачи может быть использована другая ключевая задача (или метод ее
решения), то эта задача должна разбираться ранее (в этом случае учащиеся
тренируются в распознавании и применении ключевых задач).
. Самые красивые и яркие
задачи лучше отнести на вторую часть урока, чтобы под влиянием работы с ними
ученики преодолели естественную усталость.
. Желательно чередовать
задачи, требующие обширных записей, с теми, которые не предполагают громоздких
письменных обоснований.
. Те ключевые задачи, которые
как-то связаны с предыдущей темой, лучше включить в число первых, а активно
используемые в последующих темах желательно разбирать позднее. [4]
Основные элементы
метода использования ключевых задач можно сформулировать следующим образом:
) Все задачи
разбираются и записываются на уроке в виде конспекта или в виде опорных схем.
) На первом
этапе, когда дети только знакомятся с понятием «ключевая задача», учитель сам
выделяет систему ключевых задач по разбираемой теме. При этом в зависимости от
подготовленности учащихся, все задачи могут быть разобраны и записаны на одном
уроке, а могут записываться постепенно на нескольких уроках.
) Система
задач, предложенная учителем, может дополняться самими учащимися.
) Наборы ключевых
задач записываются детьми в отдельную тетрадь, которая будет являться
своеобразным справочником по методам решения. К такому справочнику удобно
обращаться при подготовке к контрольным работам, зачётам, а также при
повторении.
) Работа по
отбору ключевых задач ведется непрерывно, система дополняется новыми задачами,
выделенными при решении более сложных задач.
) Учащимся
разрешается на уроке при выполнении заданий пользоваться схемами и таблицами до
тех пор, пока необходимость их использования не отпадёт. При этом хорошо
реализуется принцип дифференцированного подхода в обучении, так как у слабых
учащихся всегда под руками имеется «руководство к действию» в виде схем и
алгоритмов, отражённых в опорном конспекте. А сильные ученики, проанализировав
и обобщив весь материал конспекта в целом, получают возможность оценить весь
«арсенал» различных методов решения. Что позволяет им перейти к
самостоятельному решению комбинированных и творческих задач.
) После
разбора всех ключевых задач, необходимо организовать деятельность учащихся так,
чтобы они научились распознавать и решать как непосредственно сами ключевые
задачи, так и задачи комбинированные, при решении которых используется уже
несколько таких задач. Т.е. обязателен тренинг по распознаванию, применению, а,
следовательно, и заучиванию системы «ключей».
) Для
организации тренинга учитель заранее готовит набор упражнений. Количество
тренировочных работ (обучающего, а не контролирующего плана) зависит от
подготовки класса в целом и каждого учащегося в отдельности.
) Целесообразно
завершить использование полученных знаний зачётом. [5]
2. Практическое
применение метода ключевых задач в школьном курсе геометрии
Приведем системы,
составленные методом «ключевых» задач, которые можно использовать для итогового
повторения курса планиметрии.
Свойства медиан
треугольника.
Ключевые задачи:
1. Медианы в треугольнике пересекаются в одной точке и делятся в
ней в отношении 2:1, считая от вершины.
2. Медиана делит треугольник на два равновеликих.

Пусть ВМ - медиана △АВС. Рассмотрим △АВМ, △МВС (Рисунок. 2.1).
Т.к. для △АВМ и △МВС ВН - высота общая,
то


а, по условию, ВМ -
медиана ⇒ АМ=МС ⇒ 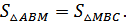
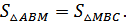
3. Медианы треугольника делят его на шесть равновеликих
треугольников и SABC=3SAOB=3SBOC=3SCOA.

Доказательство.
Пусть ВК, СМ, АН - медианы △АВС, которые
пересекаются в т.О (Рисунок. 2.2). Получим △АОВ, △ВОС, △АОС. Пусть их площади равны соответственно S1, S2, S3. А площадь △АВС равна S.
Рассмотрим △АВК и СВК - они равной
площади, т. к. ВК - медиана.
В △АОС
и ОК - медиана, значит 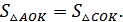
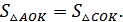
Отсюда
следует, что S2=S3, S3=S1, т.е. SABC=3SAOB=3SBOC=3SCOA
Обозначим площади △МОВ,
△ВОН, △НОС, △СОК, КОА и △АОМ соответственно S1,
S2, S3,
S4, S5,
S6.
Т.к. площади △АОВ,
△ВОС, △АОС равны и площади △АОМ,
△ВОМ равны, значит S1=
S6. Аналогично S2= S3.
Если S1+ S6= S2+ S3 и 2S2=2S1, значит S2=S1. И так далее. Получим,
что все шесть треугольника имеют равные площади и они составляют шестую часть
от площади △АВС.
Задачи
системы:
Задача
1. Две стороны треугольника соответственно равны 6 и 8. Медианы,
проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.
Решение.
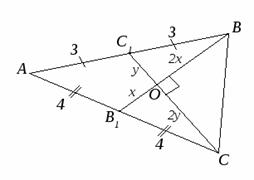
Пусть AB=6, AC=8 (Рисунок. 2.3).
Тогда медианы СС1
и ВВ1перпендикулярны и пересекаются в точке О.
SABC=3SBOC.
SBOC=
 OB∙OC, так как треугольник ВОС прямоугольный.
OB∙OC, так как треугольник ВОС прямоугольный.
По ключевой
задаче: если ВВ1=x, то OB=2x; если OC1=y, то OC=2y. Треугольники ВОС1 и СОВ1 прямоугольные и по
теореме Пифагора имеем
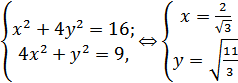
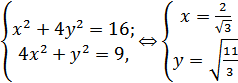 SBOC=
SBOC=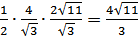
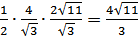 .
.
Тогда SABC=

Ответ: 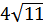
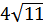 .
.
Задача 2.
В треугольника АВС АА1 и СС1 - медианы, причем АА1=5,
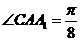 ,
,
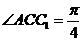 .
Найдите площадь треугольника АВС.
.
Найдите площадь треугольника АВС.
Тогда
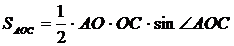 ,
, 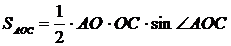 ,
,
 ,
, .
.
Решение. 
ключевой задаче 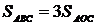 .
.
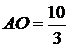 .
Длину стороны ОС найдем по теореме синусов (Рисунок. 2.4):
.
Длину стороны ОС найдем по теореме синусов (Рисунок. 2.4):
|
 ⇒ ⇒ . .
|
Ответ: 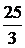 .
.
Задача 3.
Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.
А1, В1,
С1 - середины сторон ВС, АС и АВ соответственно (Рисунок. 2.5).
Пусть 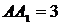 ,
,
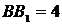 ,
,
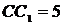 .
Тогда по ключевой задаче
.
Тогда по ключевой задаче 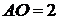 ,
,
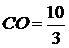 ,
,
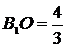 и
и
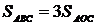 .
Достроим треугольник АОС до параллелограмма, отложив на прямой ВВ1
от точки В1 отрезок B1D, равный В1О.
.
Достроим треугольник АОС до параллелограмма, отложив на прямой ВВ1
от точки В1 отрезок B1D, равный В1О.
|
Тогда  . .
|
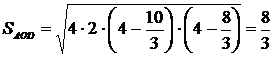 . Следовательно,
. Следовательно,  .
.
Ответ: 
Задача 4. Длины двух сторон треугольника 27 и 29. Длина медианы,
проведенной к третьей стороне, равна 26. Найдите высоту треугольника,
проведенную к стороне длиной 27.
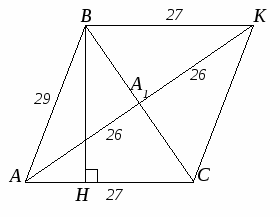
Пусть AB=29, AC=27, медиана AA1=26 (Рисунок. 2.6).
Чтобы найти высоту ВН
достаточно знать площадь треугольника АВС. Чтобы найти площадь треугольника АВС
достроим его до параллелограмма АВКС, продлив медиану АА1.
Тогда SABC=SABK=
 SABKC.
SABKC.
SABK=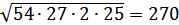
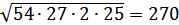 .
.
SABC=
 AC∙BH,
AC∙BH,
=
 ∙27∙BH,
∙27∙BH,
BH=20.
Ответ: 20.
Длина
медианы
Ключевая
задача:
1.
Докажите, что если стороны
АВ, АС и ВС треугольника АВС равны соответственно с, b и а, то длина медианы,
проведенной к стороне ВС, может быть вычислена по формуле
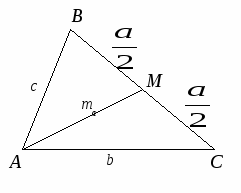
По теореме косинусов имеем:
Треугольник ABM (Рисунок. 2.7):
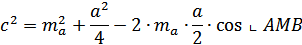
Треугольник АВС:
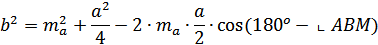
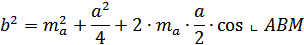
Сложим эти равенства,
получим
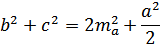
Отсюда
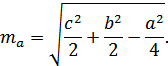
2.
Сумма квадратов медиан треугольника равна 
 суммы квадратов его
сторон.
суммы квадратов его
сторон.
Используя предыдущую
ключевую задачу, получим:
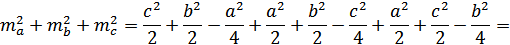
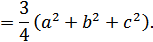
 3.
3.
Сумма квадратов медиан
прямоугольного треугольника, проведенных из вершин острых углов, равна 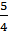
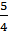 квадрата его
гипотенузы.
квадрата его
гипотенузы.
Пусть АМ, ВН - медианы △АВС
(Рисунок. 2.8).
Из △АСМ:
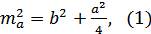
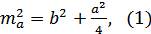
Из △RAH:

Сложим равенство (1) и
(2), получим

Задачи
системы:
Задача
1. Найдите отношение суммы квадратов всех медиан треугольника к
сумме квадратов всех его сторон.
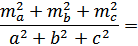
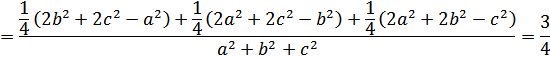
Ответ: 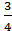
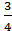 .
.
Задача
2.

. Найдем АС, используя формулу длины медианы (Рисунок. 2.9):


2. Треугольник АВС -
прямоугольный, так как
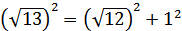
Следовательно,

Ответ: 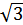
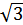 .
.
Задача 3.
Длины двух сторон треугольника равны 16 и 12. Медианы, проведенные к этим
сторонам треугольника, перпендикулярны. Найдите третью сторону треугольника.

Проведем медианы АК и ВМ в
треугольнике АОВ (Рисунок. 2.10). Заметим, что
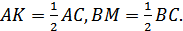
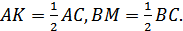
Тогда, согласно третьей
ключевой задаче, запишем:

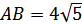
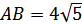
Ответ: 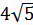
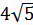 .
.
Медиана,
проведенная к гипотенузе.
Ключевая
задача. В прямоугольном треугольнике длина
медианы, проведенной к гипотенузе, равна ее половине.

Продлим отрезок CD и отметим на луче
отрезок DM=CD, AMBC - четырехугольник (Рисунок. 2.11).
Докажем, что AMBC - прямоугольник.
Рассмотрим △ADM и △CDB, по условию AD=AB, MD=DC; ∠ADM=∠CBD (как вертикальные), значит, △ADM=△CDB (по двум сторонам и углу между ними), следовательно, АМ=ВС.
Так же из △ADC=△BDM следует АС=МВ.
Значит, АМ=ВС, АС=МВ, ∠С=90о, т.е.:
АМВС - прямоугольник.
АВ и МС - диагонали прямоугольника
АМСВ, т.е. АВ=МС, АD=DB=MD=DC, значит
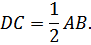
Следствия:
1. Центр описанной около
прямоугольного треугольника окружности лежит на середине гипотенузы.
. Если в треугольнике длина медианы
равна половине длины стороны, к которой она проведена, то этот треугольник -
прямоугольный.
Задачи системы:
Задача 1. Лестница скользит по стенкам угла. Какую траекторию описывает
фонарик, находящийся на средней ступеньке лестницы?
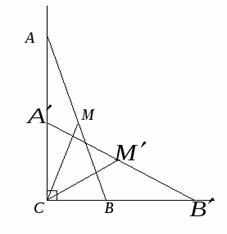
По ключевой задаче 
 (Рисунок. 2.12).
Аналогично,
(Рисунок. 2.12).
Аналогично, 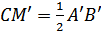
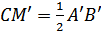 . Так как
. Так как 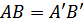
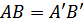 , то
, то 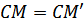
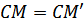 .
.
Множество точек,
отстоящих от точки С на одинаковом расстоянии, лежат на окружности. Таким
образом, фонарик, находящийся на средней ступеньке лестницы, описывает дугу
окружности.
Задача 2.
В трапеции углы при одном из оснований равны 300 и 600,
длина отрезка, соединяющего середины оснований, равна 3. Найдите длины
оснований трапеции и ее площадь, если длина средней линии равна 5.
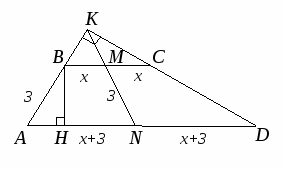
Пусть ⌞BAD=60o,
⌞CDA=30o, тогда продолжения боковых сторон пересекаются под прямым углом
(Рисунок. 2.13).
По ключевой задаче 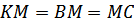
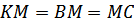 и
и 
 . Пусть
. Пусть 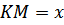
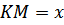 , тогда
, тогда 
 .
.
По свойству средней
линии трапеции: 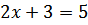
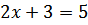 ,
, 
 . Следовательно,
. Следовательно, 
 .
.
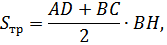


Ответ: 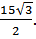
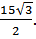
Ключевая задача.
Биссектриса треугольника делит противоположную сторону на отрезки
пропорциональные прилежащим сторонам.

Проведем CF, параллельно
биссектрисе BD (Рисунок. 2.14). Тогда по теореме о пропорциональных отрезках 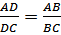
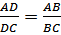 . Треугольник BCF -
равнобедренный.
. Треугольник BCF -
равнобедренный.
Так как углы ∠
 равны как
соответственные при параллельных прямых BD
и CF и секущей AF, углы ∠BCF
и ∠CBD равны как
накрест лежащие при параллельных прямых BD и CF и секущей ВС, ∠ABD=∠CBD по свойству
биссектрисы. Следовательно, BF=BC. Тогда
равны как
соответственные при параллельных прямых BD
и CF и секущей AF, углы ∠BCF
и ∠CBD равны как
накрест лежащие при параллельных прямых BD и CF и секущей ВС, ∠ABD=∠CBD по свойству
биссектрисы. Следовательно, BF=BC. Тогда 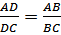
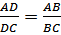 .
.
Задачи системы:
Задача 1.
В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу на
отрезки 3 и 4. Найдите площадь треугольника.
Пусть 
 ,
, 
 (Рисунок. 2.16). Тогда
по свойству биссектрисы
(Рисунок. 2.16). Тогда
по свойству биссектрисы 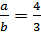
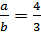 , а по теореме Пифагора
, а по теореме Пифагора 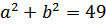
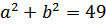 . Решая систему получим:
. Решая систему получим:
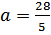
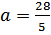 ,
, 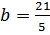
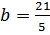 . Вычисляя площадь
треугольника по формуле
. Вычисляя площадь
треугольника по формуле
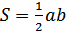
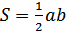 ,
,
получим 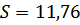
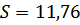 .
.
О т в е т: 11,76.
Задача 2.
В прямоугольном треугольнике проведена биссектриса острого угла. Отрезок,
соединяющий ее с основание с точкой пересечения медиан, перпендикулярен катету.
Найдите острые углы треугольника.
 Пусть
AD - биссектриса прямоугольного треугольника АВС). Точка О - точка
пересечения медиан. Тогда по условию задачи
Пусть
AD - биссектриса прямоугольного треугольника АВС). Точка О - точка
пересечения медиан. Тогда по условию задачи 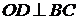 .
.
По свойству медиан 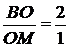 .
.
|
По теореме Фалеса 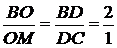 . .
|
|
Так как AD - биссектриса, то 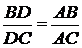 . Следовательно,
. Следовательно, 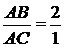 .
.
Так как гипотенуза АВ в
два раза больше катета АС, то 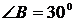 . Следовательно,
. Следовательно, 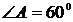 .
.
Ответ: 300;
600.
Задача 3.
В равнобедренный треугольник АВС с основанием АС вписана окружность с центром
О. Луч АО пересекает сторону ВС в точке К, причем 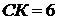 ,
,
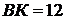 .
Найдите периметр треугольника АВС.
.
Найдите периметр треугольника АВС.
 Так как О - центр
вписанной окружности, то АК - биссектриса треугольника АВС (Рисунок. 2.18).
Тогда
Так как О - центр
вписанной окружности, то АК - биссектриса треугольника АВС (Рисунок. 2.18).
Тогда 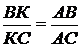 .
Имеем
.
Имеем 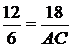 ,
,
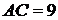 .
.
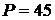 .
.
Задача 4. Найдите стороны треугольника, если медиана и высота, проведенные
из одного угла, делят его на три равные части, а длина медианы равна 10.
 Р
е ш е н и е. Пусть СN - медиана, а СК -
высота (Рисунок. 2.19). Так как СК - высота и биссектриса, то треугольник CNB равнобедренный, следовательно,
Р
е ш е н и е. Пусть СN - медиана, а СК -
высота (Рисунок. 2.19). Так как СК - высота и биссектриса, то треугольник CNB равнобедренный, следовательно, 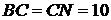 и
и 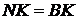 .
.
|
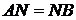 ,
следовательно, ,
следовательно,  . .
|
|
CN
- биссектриса в треугольнике АСК, следовательно, 
Треугольник 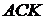 -
прямоугольный, поэтому
-
прямоугольный, поэтому 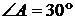 ,
,
 ,
,
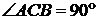 ,
,
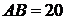 ,
,
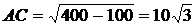 .
.
Ответ: 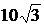 .
.
Длина биссектрисы
Ключевая задача:
.
Длину биссектрисы можно вычислить по формуле: la=
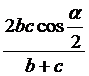 ,
где la - длина биссектрисы, проведенной из
угла A треугольника ABC,
α =
,
где la - длина биссектрисы, проведенной из
угла A треугольника ABC,
α = 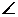 BAC,
b, a - длины сторон треугольника.
BAC,
b, a - длины сторон треугольника.

Пусть площадь △АВС равна S, а площадь △АBD и △CAD равны соответственно S1 и S2 (Рисунок. 2.20).
Тогда S= S1 + S2,
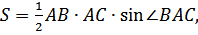
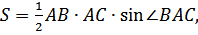
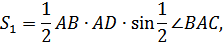
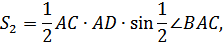
откуда,

Учитывая, что
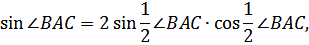
получим
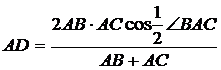 .
.
2.
Длину биссектрисы можно вычислить по формуле: 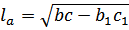
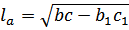 , где
, где 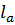
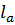 - длина биссектрисы,
проведенной из угла A треугольника ABC,
- длина биссектрисы,
проведенной из угла A треугольника ABC, 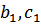
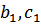 -
-
отрезки, на которые
биссектриса делит сторону BC,
b, a - длины сторон треугольника.

Применим теорему косинусов к △BAD и △CAD, получим
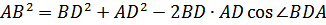
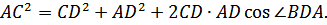
Умножим первое равенство на CD, а второе - на BD и сложим эти равенства
AB2 ∙СD + AC2 ∙BD = BD2 ∙CD + CD2 ∙DB + AD2 ∙(BC+ DC) (1).
Так как биссектриса угла
треугольника делит сторону, противоположную этому углу, на части,
пропорциональные прилежащим сторонам, то
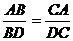 ,
,
откуда
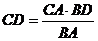 ,
, 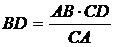 .
.
Подставим эти выражения
в левую часть равенства (1), получим
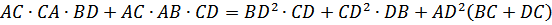
или
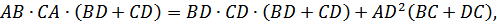
откуда
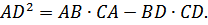
Заключение
обучение школьник геометрия
биссектриса
Анализ использования метода ключевых
задач в обучении показывает, что такой подход дает возможность ликвидировать не
только перегрузку учащихся (решается меньшее число задач, меньше их задается на
дом, заранее известно, какие типы задач подлежат опросу), но и существенно
облегчает труд учителя по планированию уроков, проверке знаний учащихся.
В заключение отметим, что
эффективность урока зависит от:
) знания учителем состава задач по
теме и методов их решения;
) владения методами выделения
ключевых задач и умелой их реализации;
) отсутствия формализма в
требованиях по овладению умениями решать ключевые задачи;
) способности предвидеть
затруднения, типичные ошибки учащихся и выбрать методы их предупреждения;
) умения правильно организовать
контроль за умениями решать ключевые задачи и качественно провести анализ
результатов контроля.
При использовании ключевых задач
происходит наглядное моделирование мыслительного процесса. Таким образом,
реализуется возможность перехода от «школы памяти» к «школе мышления». Пусть
далеко не все ученики могут решить сложнейшую задачу, но понять предлагаемое
решение и воспроизвести его этапы могут все. Учащиеся из пассивных слушателей
превращаются в деятельных, активных участников образовательного процесса.
Навыки и умения, полученные учащимися при выделении и решении непосредственно
ключевых, а также комбинированных задач, создают прочную базу для дальнейшего
изучения предмета на более углублённом уровне. Переход к нестандартным,
творческим задачам становится более актуальным, т.к. на первый план выступает
практическое применение полученных знаний.
1) Готман, Э.Г. Задачи по планиметрии и методы их решения /
Э.Г. Готман. - М.: Мир, 1988. - 264 с.
) Методика преподавания математики в основной школе. Курс
лекций [Электронный ресурс] / Александр Печко. - 2000-2012. - Режим доступа:
http:// rudocs.exdat.com. - Дата доступа: 25.09.2013.
3) Колягин, Ю.М. Методика преподавания математики в средней школе / Ю.М. Колягин. - М.: Мир, 1980. - 375 с.
) Зильберберг, Н.И. Ключевые задачи в обучении математике/
Н.И. Зильберберг, Р.Г. Хазанкин. - М: Мир, 1984. - 179 с.
) Электронная хрестоматия по методике преподавания
математики. Методика обучения решению задач [Электронный ресурс] / Сазанова
Т.А., Дубов А.Г. - 2000-2012. - Режим доступа:
http://fmi.asf.ru/library/book/mpm/index.html. - Дата доступа: 10.10.2013.
6) Пирютко, О.Н. Геометрия в таблицах и задачах: планиметрия:
для школьников / О.Н. Пирютко. - Минск: Аверсэв, 2008. - 122 с.
) Тавгень, О.И. Математика в задачах. Теория и методы
решений. Планиметрия, стереометрия, текстовые задачи / О.И. Тавгень,
А.И. Тавгень. - Минск: Аверсэв, 2005. - 511 с.
) Лисова, М.И. Планиметрия. Итоговое повторение / М.И.
Лисова, О.Н. Пирютко. - Минск: Аверсэв, 2004. - 416 с.
9) Шлыков. В.В. Геометрия: учебное пособие для 9-го класса
учреждений, обеспечивающих получение общего среднего образования (базовый и
повышенный уровни) / В.В. Шлыков. - 2-е издание. - Минск: Народная асвета,
2006. - 205 с.