Исследование термосиловой устойчивости тел с покрытиями
Реферат
ТРЕНИЕ, КАТАСТРОФИЧЕСКИЙ ИЗНОС, ДАВЛЕНИЕ,
ТЕПЛОВОЙ ВЗРЫВ, ТЕРМОСИЛОВАЯ УСТОЙЧИВОСТЬ.
Целью данной работы является исследование износа
покрытия с учетом тепловыделения от трения.
Исследования в работе проводятся аналитическим
методом, схема контакта тел через покрытие была максимально упрощена, что
сделало возможным рассмотреть большое число явлений, происходящих в зоне
контакта.
В результате выполнения данной работы построено
решение несвязной задачи термоупругости в квазистатической постановке. Получены
формулы, позволяющие рассчитать контактную температуру, напряжения и
перемещения в покрытии, а также исследовать связь между давлением и толщиной
слоя в зависимости от времени.
Кроме того получены два условия: «теплового
взрыва» и термосиловой устойчивости покрытия.
Введение
В работе рассматривается задача об истирании
(износе) упругого слоя материала (покрытия). Покрытие нанесено на твердое
(недеформируемое) тело. По поверхности покрытия скользит и давит на него
жесткий штамп (плита). Схема контакта тел через покрытие максимально упрощена,
что сделало возможным рассмотреть большое число явлений, происходящих в зоне
контакта. Учитываются тепловыделение от трения в области контакта,
неоднородность твердости по глубине слоя, зависимость коэффициентов трения и
износостойкости от температуры.
На основе решения несвязанной квазистационарной
задачи термоупругости для слоя изучено явление изнашивания покрытий при
тепловыделении от трения, определены связь контактной температуры с контактным
давлением, определен ресурс трибосопряжения при абразивном режиме износа,
определено условие теплового взрыва.
Рассмотренная в работе модель в первом
приближении может объяснить износ различных движущихся деталей, например,
тонких поршневых колец, вызванный их перегревом.
1. Постановка задачи

Рисунок 1 - Схема контакта плиты (штампа) с
материалом покрытия-слоя
Пусть упругий слой начальной толщины
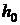 жестко
сцеплен с недеформируемым основанием. В поверхность слоя усилием
жестко
сцеплен с недеформируемым основанием. В поверхность слоя усилием 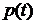 вдавливается
жесткая бесконечная плита. Допустим, что эта плита движется с постоянной
скоростью
вдавливается
жесткая бесконечная плита. Допустим, что эта плита движется с постоянной
скоростью 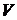 в
направлении оси
в
направлении оси 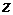 (рисунок) и
в области контакта плиты со слоем возникают силы Кулоновского трения
(рисунок) и
в области контакта плиты со слоем возникают силы Кулоновского трения
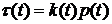 ,
,
где 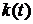 - коэффициент трения, зависящий от
времени.
- коэффициент трения, зависящий от
времени.
Вследствие трения в области контакта
происходит износ поверхности слоя  (то есть толщина слоя меняется со
временем) и выделяется в единицу времени на единицу площади контакта количества
тепла [1]
(то есть толщина слоя меняется со
временем) и выделяется в единицу времени на единицу площади контакта количества
тепла [1]
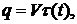 (1.1)
(1.1)
которое приводит к нагреванию
поверхности слоя, а также всей плиты до температуры 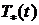 ,
превышающей температуру нижней грани слоя
,
превышающей температуру нижней грани слоя  . Предполагаем, что на нижней грани
слоя поддерживается температура окружающей среды, которую принимаем за начало
отсчета температур, то есть принимаем
. Предполагаем, что на нижней грани
слоя поддерживается температура окружающей среды, которую принимаем за начало
отсчета температур, то есть принимаем  .
.
Таким образом, формируется поток
тепла 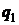 через слой,
равный при
через слой,
равный при  [2]
[2]
 , (1.2)
, (1.2)
где 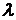 - коэффициент теплопроводности
слоя.
- коэффициент теплопроводности
слоя.
Условие баланса тепла при  , то есть
на поверхности слоя равно
, то есть
на поверхности слоя равно
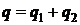 . (1.3)
. (1.3)
Мощность энергии, идущей на износ
поверхностного слоя 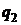 ,
определяется соотношением
,
определяется соотношением
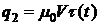 , (1.4)
, (1.4)
где 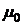 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Будем считать, что 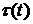 - медленно
меняющаяся функция времени, и процесс теплопроводности через слой является
квазистационарным. Тогда уравнение теплопроводности имеет вид [9]
- медленно
меняющаяся функция времени, и процесс теплопроводности через слой является
квазистационарным. Тогда уравнение теплопроводности имеет вид [9]
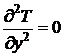 . (1.5)
. (1.5)
2. Определение температуры в зоне
контакта плиты и слоя
Решением (1.5) является
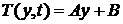 . (2.1)
. (2.1)
Имеем следующие граничные условия
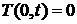 , (2.2)
, (2.2)
 . (2.3)
. (2.3)
Кроме того, в силу соотношений
(1.1)-(1.4) имеем при 
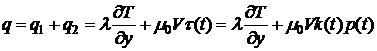 .
.
С другой стороны, согласно (1.1)
имеем
 .
.
Приравнивая правые части, получим
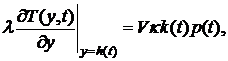 (2.4)
(2.4)
где 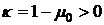 , так как поток тепла положителен.
, так как поток тепла положителен.
Подставим решение (2.1) в граничное
условие (2.2) , найдем, что 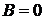 .
.
Из второго граничного условия (2.3)
определим
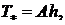 отсюда
отсюда 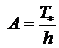 .
.
Следовательно, решение (2.1) примет
вид
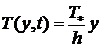 . (2.5)
. (2.5)
Эта функция описывает распределение
температуры внутри слоя, если  - известно.
- известно.
Продифференцируем (2.5) и в
полученной формуле положим  . Тогда формула (2.4) преобразуется
к виду
. Тогда формула (2.4) преобразуется
к виду
 . (2.6)
. (2.6)
Предположим, что коэффициент трения 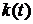 является
линейной функцией контактной температуры
является
линейной функцией контактной температуры 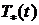 ,то есть
,то есть
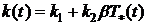 . (2.7)
. (2.7)
где 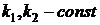 ,
,
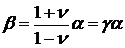 ,
,
 -коэффициент линейного расширения
слоя,
-коэффициент линейного расширения
слоя,
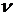 -коэффициент Пуассона.
-коэффициент Пуассона.
Тогда соотношение (2.6) с учетом
(2.7) перепишется в виде

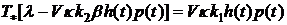 .
.
Отсюда следует формула для
определения температуры в зоне контакта плиты и слоя - покрытия
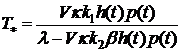 . (2.8)
. (2.8)
Заметим, что должно выполняться
условие
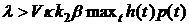 (2.9)
(2.9)
для всех 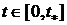 ,
,
где 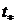 - время, необходимое для полного
истирания слоя (ресурс трибосопряжения),
- время, необходимое для полного
истирания слоя (ресурс трибосопряжения),
 - температура поверхностей плиты и
слоя в зоне контакта (
- температура поверхностей плиты и
слоя в зоне контакта (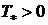 ).
).
Если 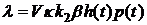 , то
, то 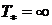 - условие теплового взрыва.
- условие теплового взрыва.
Замечание:
В формуле (2.8) закон изменения
толщины слоя  вследствие
износа считается неизвестным, если сила
вследствие
износа считается неизвестным, если сила 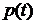 задана. И, наоборот, может быть
задана функция
задана. И, наоборот, может быть
задана функция  , а величина
усилия, вдавливающего жесткую плиту в слой-покрытие, вследствие чего происходит
истирание, неизвестна. Эти функции будут определены позже.
, а величина
усилия, вдавливающего жесткую плиту в слой-покрытие, вследствие чего происходит
истирание, неизвестна. Эти функции будут определены позже.
3. Определение
напряженно-деформированного состояния слоя (НДС)
Так как режим рассматривается
квазистационарный, то в этих уравнениях пренебрежем инерционными членами 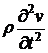 и
и 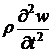 . В
рассматриваемом случае перемещение
. В
рассматриваемом случае перемещение 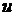 вдоль оси
вдоль оси 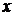 равно нулю,
а перемещения
равно нулю,
а перемещения 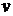 и
и 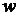 вдоль осей
вдоль осей 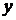 и
и 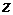 являются
функциями только времени
являются
функциями только времени 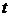 и
координаты
и
координаты 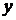 . Поэтому
уравнения Ляме-Неймана упрощаются и имеют вид
. Поэтому
уравнения Ляме-Неймана упрощаются и имеют вид
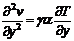 , (3.1)
, (3.1)
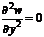 . (3.2)
. (3.2)
Нормальное напряжение 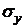 и
касательное
и
касательное 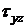 определяются
выражениями [9] (Приложение А)
определяются
выражениями [9] (Приложение А)
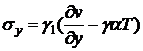 , (3.3)
, (3.3)
 . (3.4)
. (3.4)
Коэффициенты  и
и 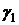 даются
формулами
даются
формулами
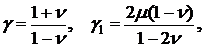 (3.5)
(3.5)
где 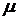 - модуль сдвига слоя,
- модуль сдвига слоя,
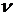 - коэффициент Пуассона,
- коэффициент Пуассона,
 - коэффициент линейного расширения
слоя.
- коэффициент линейного расширения
слоя.
Граничные условия задачи
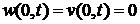 при
при 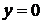 , (3.6)
, (3.6)
 при
при  . (3.7)
. (3.7)
Первое условие (3.6) означает, что
нижняя грань 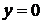 слоя-покрытия
жестко сцеплена с твердым телом. Второе условие означает, что на поверхности
слоя
слоя-покрытия
жестко сцеплена с твердым телом. Второе условие означает, что на поверхности
слоя  заданы
вертикальные усилия
заданы
вертикальные усилия 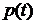 и
касательные усилия
и
касательные усилия 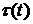 , причем
согласно условиям задачи
, причем
согласно условиям задачи 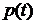 и
и 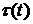 связаны
соотношением
связаны
соотношением 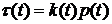 .
.
Подставим выражение для температуры
(2.5) в уравнение (3.1), получим
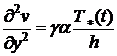 .
.
Дважды проинтегрируем это уравнение,
определим перемещение точек слоя 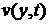 в направлении оси
в направлении оси 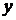
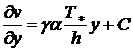 ,
,
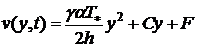 .
.
 .
.
Удовлетворяя граничным условиям
(3.6), найдем
 .
.
Из (3.3), (3.4) и граничных условий
(3.7) получим
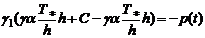 ,
,
отсюда
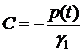 .
.
Из второго граничного условия имеем
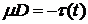 ,
,
отсюда
 .
.
Решение уравнений (3.1) и (3.2)
имеет вид
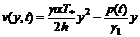 , (3.8)
, (3.8)
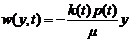 . (3.9)
. (3.9)
При этом функция 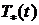 описывается
формулой (2.8)
описывается
формулой (2.8)
Замечание:
Очевидно, что температура и смещения
как внутри, так и на поверхности покрытия зависят от многих параметров: V,
p(t), h(t), k(t), 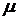 ,
,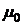 ,
, 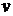 ,
, 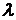 ,
, ,
, 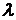 .
.
Вычислим нормальное и касательное
напряжения в точках слоя-покрытия по формулам (3.3) и (3.4) с учетом решений
(3.8),(3.9),
 ,
,
 .
.
4. Условие термосиловой устойчивости
Условие контакта плиты (штампа) со
слоем при  можно
представить в виде
можно
представить в виде
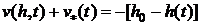 , (4.1)
, (4.1)
где 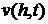 - упругое перемещение (3.8) при
- упругое перемещение (3.8) при  ,
,
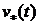 - перемещение плиты в направлении
оси
- перемещение плиты в направлении
оси 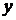 , вызываемое
износом слоя,
, вызываемое
износом слоя,
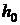 - начальная толщина слоя,
- начальная толщина слоя,
 - толщина слоя, меняющаяся со
временем в силу износа.
- толщина слоя, меняющаяся со
временем в силу износа.
В случае абразивного износа
перемещение 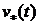 пропорционально
работе сил трения [3], то есть
пропорционально
работе сил трения [3], то есть
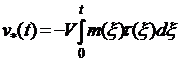 ,
,
Подставим сюда 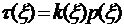 , получаем
, получаем
 , (4.2)
, (4.2)
где 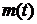 - коэффициент износостойкости.
- коэффициент износостойкости.
Подставим (4.2), (3.8), (2.7) в
(4.1), получим
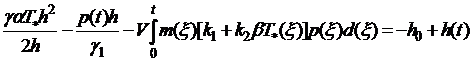 (4.3)
(4.3)
Подставим теперь (2.8) в (4.3),
имеем
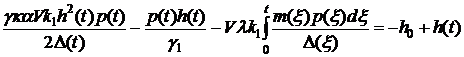 , (4.4)
, (4.4)
где  ,что следует из (2.8).
,что следует из (2.8).
Введем безразмерные величины
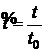 ,
, ,
,
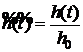 ,
,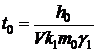 ,
,
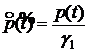 ,
, ,
,
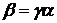 ,
,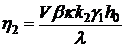 .
.
Тогда уравнение (4.4) запишется в
виде (в дальнейшем знак «~» опускаем для удобства)
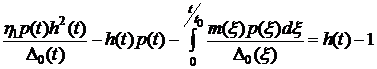 , (4.5)
, (4.5)
 .
.
Замечание:
Величину 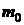 конкретизируем
ниже. Уравнение (4.5) можно рассмотреть при заданных
конкретизируем
ниже. Уравнение (4.5) можно рассмотреть при заданных 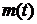 и
и 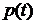 как
уравнение относительно неизвестной функции
как
уравнение относительно неизвестной функции  , а при заданных
, а при заданных 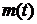 и
и  как
уравнение относительно неизвестной функции
как
уравнение относительно неизвестной функции 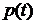 .
.
В обоих случаях это будет нелинейное
интегральное уравнение Вольтерра.
Положим в (4.5) 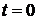 , имеем
, имеем
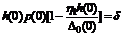 , (4.6)
, (4.6)
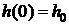 .
.
Величина 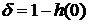 мала и
описывает деформацию слоя в момент времени
мала и
описывает деформацию слоя в момент времени 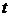 .
.
Предполагаем, что в любой момент
времени 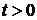 выполняется
выполняется
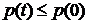 , тогда из
(4.6) с учетом (2.9) и при
, тогда из
(4.6) с учетом (2.9) и при 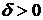 вытекает неравенство
вытекает неравенство

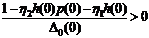 .
.
С учетом  , то есть
, то есть 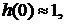 получаем
получаем
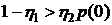 . (4.7)
. (4.7)
Условие (4.7) называется условием
термосиловой устойчивости.
Это условие можно записать в виде
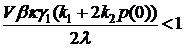
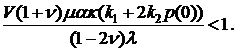
Замечание:
Таким образом, термосиловая
устойчивость покрытия зависит от скорости 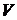 движения плиты, контактирующей с
покрытием, и от свойств материала покрытия: коэффициента Пуассона
движения плиты, контактирующей с
покрытием, и от свойств материала покрытия: коэффициента Пуассона 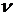 , модуля
упругости слоя
, модуля
упругости слоя 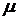 ,
коэффициента линейного расширения
,
коэффициента линейного расширения  и коэффициента теплопроводности
слоя
и коэффициента теплопроводности
слоя 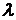 , а также от
коэффициента трения.
, а также от
коэффициента трения.
Решив уравнение (4.5), то есть
определив 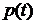 , если
, если  задано, или
задано, или
 при
известном
при
известном 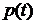 , найдем
контактную температуру
, найдем
контактную температуру  по формуле
(2.8), которую с учетом обезразмеривания, запишем в виде
по формуле
(2.8), которую с учетом обезразмеривания, запишем в виде
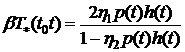 . (4.8)
. (4.8)
5. Вычисление контактного давления
Пусть 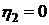
 и
и 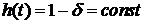 . Так как
. Так как 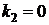 (
(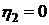 ), то
), то 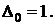 .
Предположим, что в размерных величинах
.
Предположим, что в размерных величинах
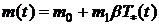 . (5.1)
. (5.1)
Это означает, что коэффициент
износостойкости 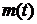 является
линейной функцией температуры
является
линейной функцией температуры  на контакте.
на контакте.
В безразмерных переменных (5.1) с
учетом (4.8) примет вид
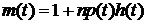 ,
,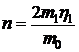 . (5.2)
. (5.2)
Подставим (5.2) в (4.5) и,
пренебрегая малой величиной  в сравнении с единицей, получим
интегральное уравнение для определения
в сравнении с единицей, получим
интегральное уравнение для определения 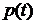 .
.
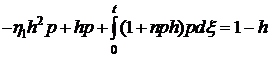
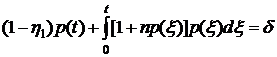 . (5.3)
. (5.3)
Учли, что  .
.
Продифференцируем (5.3), приходим к
дифференциальному уравнению
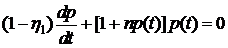 . (5.4)
. (5.4)
Начальное условие получим из (5.3),
полагая 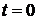
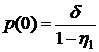 . (5.5)
. (5.5)
Разделим в (5.4) переменные
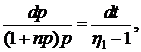
Решим это уравнение методом неопределенных
коэффициентов. Представим

где А,В - неизвестные пока
коэффициенты.
Приведем к общему знаменателю
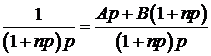 .
.
Имеем
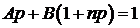 ,
,
Раскроем скобки
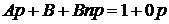 .
.
Приравняем коэффициенты при
одинаковых степенях p
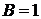 ,
,
 .
.
Отсюда следует
 ,
,
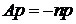 .
.
Таким образом
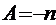 , B =1,
, B =1,
 .
.
Интегрируя, получаем

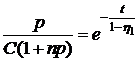 .
.
Положим в этой формуле t=0, из
последнего выражения найдем постоянную C в виде
 ,
,
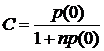 .
.
Окончательно давление будет
определятся выражением
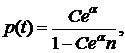
где 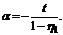
Перепишем это решение уравнения
(5.4) в виде
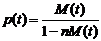 , (5.6)
, (5.6)
где функция М(t) описывается
формулой
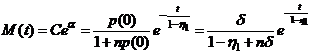 .
.
Здесь учли условие (5.5).
Замечание:
Из этой формулы следует, что
контактное давление 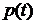 при
при  экспоненциально
убывает, если
экспоненциально
убывает, если  .
.
Таким образом, чтобы толщина
покрытия оставалась постоянной (износ отсутствовал) необходимо, чтобы
контактное давление ослабевало с течением времени.
6. Нахождение закона изменения
толщины покрытия вследствие износа
Пусть 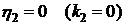 и
и 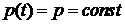 . Допустим, что твердость материала
слоя изменяется по толщине. Коэффициент износостойкости
. Допустим, что твердость материала
слоя изменяется по толщине. Коэффициент износостойкости 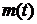 приблизим
линейной функцией
приблизим
линейной функцией  .
.
В размерных величинах
 . (6.1)
. (6.1)
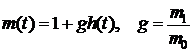 . (6.2)
. (6.2)
Подставим (6.2) в (4.5), получим
интегральное уравнение для определения 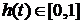
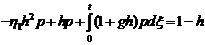 ,
,
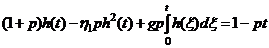 . (6.3)
. (6.3)
Продифференцируем (6.3) по времени t
 . (6.4)
. (6.4)
Начальное условие имеет вид
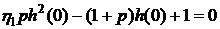 . (6.5)
. (6.5)
Это условие получим из (6.3),
полагая 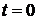 .
.
Из начального условия (6.5)
единственное значение  может быть
определено, если выполняется неравенство
может быть
определено, если выполняется неравенство
 . (6.6)
. (6.6)
В этом можно убедиться, если найдем
корни квадратного уравнения (6.5) 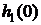 ,
, 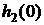 .
.
Уравнение (6.4) перепишем в виде

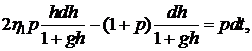
 ,
,
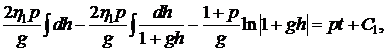
Вычислим интегралы получаем
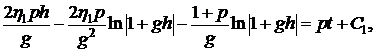
Упростим полученное уравнение
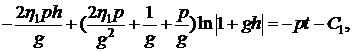
В результате имеем
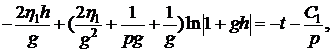
Обозначим
 ,
,
тогда
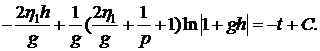
Решением уравнения (6.4) является
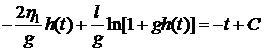 , (6.7)
, (6.7)
 ,
,
а 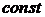
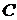 определяется из начального условия
(6.5).
определяется из начального условия
(6.5).
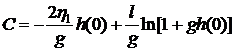
Значение 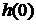 определяется
из начального условия (6.5). Подставляя найденное значение
определяется
из начального условия (6.5). Подставляя найденное значение 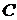 в (6.7),
получим
в (6.7),
получим
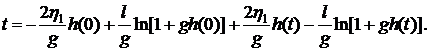 (6.8)
(6.8)
Полагая в (6.8) 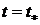 и учитывая
и учитывая 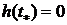 , находим
ресурс трибосопряжения
, находим
ресурс трибосопряжения
 . (6.9)
. (6.9)
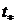 -время, необходимое для полного
истирания покрытия.
-время, необходимое для полного
истирания покрытия.
Рассмотрим случай, когда 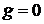 ,
,
Полагая в (6.4) g=0, имеем
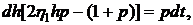
Раскроем скобки
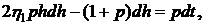
Интегрируем это выражение
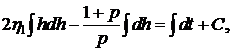
После вычисления интегралов, имеем
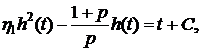 (6.10)
(6.10)
В последнем выражении полагая t=0,
находим

Подставляя найденное значение C в
(6.10), получаем
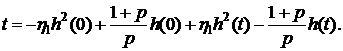
При 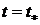 ,
, 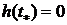
 .
.
Учитывая условие (6.5) последнюю
формулу можно переписать в виде

или в размерных величинах

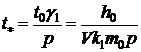 .
.
Учитывая, что [5]
 ,
,
Получим
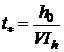 ,
,
где  - интенсивность линейного
изнашивания,
- интенсивность линейного
изнашивания,
 .
.
Замечание:
Отметим, что формулы (6.7), (6.9)
сохраняют силу и в случае, если вместо (6.1) принять для 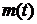 зависимость
(5.1). Необходимо только в них принять
зависимость
(5.1). Необходимо только в них принять  , где
, где  имеет вид (5.2).
имеет вид (5.2).
Для твердосмазочного покрытия ВНИ
ИНП-219 толщины 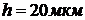 ,
нанесенного на стальную основу и находящегося в контакте с движущейся подложкой
(сталь 1Х17Н2) в условиях трения без смазки, когда
,
нанесенного на стальную основу и находящегося в контакте с движущейся подложкой
(сталь 1Х17Н2) в условиях трения без смазки, когда
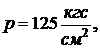
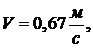
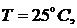
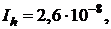
определим 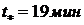 .
.
Вычислим значение 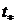 в
безразмерном виде
в
безразмерном виде
Подставляя значения:
 ,
,
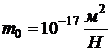 ,
,
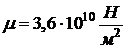 ,
,
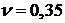 ,
,
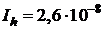
Найдем 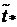
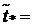
 =6.
=6.
7. Численные расчеты
В предположениях п.5 (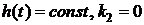 ) будем
считать, что коэффициент износостойкости материала покрытия
) будем
считать, что коэффициент износостойкости материала покрытия 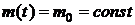 .
.
Уравнение (5.3) примет вид (в
безразмерных параметрах)
 , (7.1)
, (7.1)
Продифференцируем это уравнение,
получим
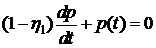 . (7.2)
. (7.2)
Начальное условие для уравнения
получим, полагая в (7.1) 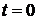
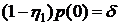
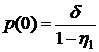 . (7.3)
. (7.3)
Решением уравнения (7.2) является
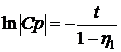 .
.
Отсюда находим
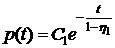 . (7.4)
. (7.4)
Неизвестную 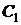 найдем из
начального условия (7.3)
найдем из
начального условия (7.3)
 .
.
Вычислим значение 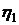
 .
.
Подставляя значения параметров для
твердосмазочного покрытия [9]
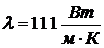 ,
, 

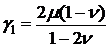 ,
,
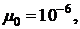
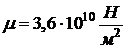 ,
,
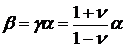 ,
,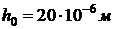 ,
,
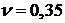 ,
, ,
,
 ,
,
Найдем величину 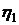
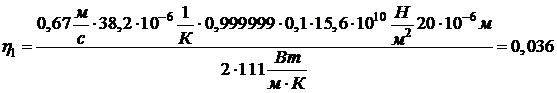 .
.
Получили 
График функции
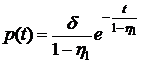
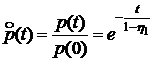 (7.5)
(7.5)
представлен на рисунке Б.1.
Температура в зоне контакта определяется
формулой
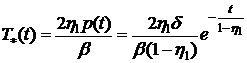 ,
,
график которой построен на рисунке
Б.2.
Смещения в безразмерном виде в зоне
контакта плиты и покрытия 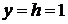
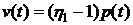 ,
,
 .
.
Графики построены на рисунках Б.3 и
Б.4 соответственно.
В предположениях п.6 ( ) будем
также считать, что коэффициент износостойкости материала покрытия не зависит от
времени
) будем
также считать, что коэффициент износостойкости материала покрытия не зависит от
времени
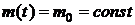 .
.
Тогда уравнение (4.5) примет вид (в
безразмерных параметрах)

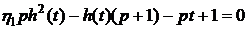 . (7.6)
. (7.6)
Решение может быть определено, если
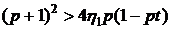 .
.
Решая (7.6), получим
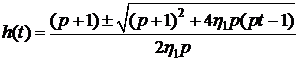 .
.
Из этих двух решений следует выбрать
то, которое удовлетворяет условию  .
.
Удовлетворяющие нашему условию
является следующее решение
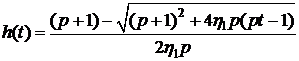 .
.
Из этой формулы видно, что когда 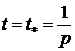 , то
, то 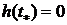 , то есть
покрытие-слой полностью износится.
, то есть
покрытие-слой полностью износится.
Заключение
В работе рассматривается задача об
истирании (износе) упругого слоя материала (покрытия).
Изучена задача о контакте двух
твердых тел через упругое покрытие (слой), при этом одно тело жестко сцеплено с
покрытием, а другое - скользит по покрытию с некоторой скоростью.
Рассмотрено явление изнашивания
покрытий при тепловыделении от трения.
При этом предполагается, что все
процессы во времени медленно меняются, то есть, рассмотрена несвязная задача
термоупругости в квазистатической постановке. Построено решение указанной
задачи. Получены формулы, позволяющие рассчитать контактную температуру,
напряжения и перемещения в покрытии, а также связь между давлением и толщиной
слоя в зависимости от времени.
Получено условие термосиловой
устойчивости покрытия и условие при котором наблюдается явление «теплового взрыва».
Список использованных источников
1. Александров
В.М. О термосиловом взаимодействии деформируемых
2. перекрытий
тел с учетом износа / В. М. Александров // Проблемы машиностроения и надежности
машин. - 1995. - № 5. - С. 70 - 75.
. Александров
В.М. Абразивный износ тонкого мягкого покрытия при нелинейном законе трения с
учетом тепловыделения / В.М. Александров // Изв. вузов. Сев.-Кавказ. регион.
Техн. науки. - 2001. - Спецвыпуск. - С. 11 - 13.
. Александров
В.М. Контактная задача для тел с покрытиями с учетом нелинейного трения, износа
и тепловыделения от трения / В.М. Александров. Изв. РАН. МТТ. - 2003.- № 4. -
С. 128 - 135.
. Хрущов
М.М. Абразивное изнашивание / М.М. Хрушов, М.А. Бабичев. - М.: Наука, 1970. -
251 с.
. Крагельский
И.В. Основы расчетов на трение и износ / И.В. Крагельский, М.Н. Добычин, В.С.
Комбалов. М.: Машиностроение, 1977. - 528 с.
. Подстригач
Я.С. Температурное поле в системе твердых тел, сопряженных с помощью тонкого
промежуточного слоя / Я.С. Подстригач // Инж. - физ. журнал. 1963. - Т. 6. - №
10. - С. 129 -136.
. Александров
В.М. Взаимодействие покрытий тел с учетом деформируемости, износа и
тепловыделения от трения / В.М. Александров, Г.К. Аннакулова // Трение и износ.
- 1992. - Т. 13. - № 1. С. 154 - 160.
. Коваленко
А.Д. Основы термоупругости / А.Д. Коваленко. - Киев: Наук. думка, 1970. - 380
с.
. Полянин
А.Д. Справочник по нелинейным уравнениям математической физики. Точные решения
/ А.Д. Полянин, В.Ф. Зайцев. - М.: Физматлит, 2002. - 432 с.
Приложение А
Вспомогательные формулы
Полная система дифференциальных уравнений,
описывающая движение термоупругой среды [9]
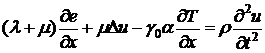 , (А. 1)
, (А. 1)
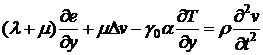 , (А. 2)
, (А. 2)
 . (А. 3)
. (А. 3)
Уравнение теплопроводности с учетом
связанности полей [9]
 . (А. 4)
. (А. 4)
Здесь
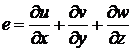 ,
,
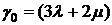 ,
,
где 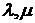 - параметры Ляме,
- параметры Ляме,
 - коэффициент линейного расширения,
- коэффициент линейного расширения,
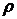 - плотность среды,
- плотность среды,
 - коэффициент теплопроводности,
- коэффициент теплопроводности,
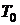 - начальная температура, за которую
обычно принимают температуру окружающей среды,
- начальная температура, за которую
обычно принимают температуру окружающей среды,
 - перемещения точек среды,
- перемещения точек среды,
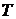 - температура.
- температура.
Граничные условия задачи
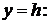

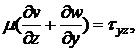
 ,
,
 ;
;
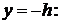
 .
.
Эти граничные условия для задачи о
колебаниях полуограниченного слоя толщины 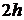 . Нижняя грань слоя жестко сцеплена
с недеформируемым основанием и теплоизолирована, на верхней границе заданы
нормальные
. Нижняя грань слоя жестко сцеплена
с недеформируемым основанием и теплоизолирована, на верхней границе заданы
нормальные 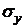 ,
касательные
,
касательные 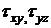 напряжения
и тепловой поток
напряжения
и тепловой поток 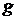 .
.
Здесь  - коэффициент теплопроводности,
- коэффициент теплопроводности,
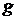 - нормальная компонента вектора
теплового потока.
- нормальная компонента вектора
теплового потока.
Рассмотрим случай, когда перемещение
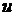 вдоль оси
вдоль оси 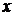 равно нулю,
а перемещения
равно нулю,
а перемещения 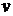 и
и 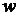 вдоль осей
вдоль осей 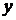 и
и 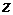 зависят только
от координаты
зависят только
от координаты 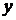 . Если
рассматривается квазистационарная задача, то в уравнениях Ляме-Неймана (1)-(3)
можно пренебречь инерционными членами
. Если
рассматривается квазистационарная задача, то в уравнениях Ляме-Неймана (1)-(3)
можно пренебречь инерционными членами 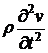 и
и 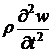 . Тогда получим вместо уравнений
(1)-(3) два уравнения
. Тогда получим вместо уравнений
(1)-(3) два уравнения
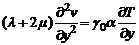 , (А. 5)
, (А. 5)
 (А. 6)
(А. 6)
(ось 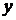 перпендикулярна поверхности среды).
перпендикулярна поверхности среды).
Рассмотрим также несвязанную задачу,
то есть вторым слагаемым в уравнении (4) (вкладом упругих волн) можно
пренебречь.
Кроме того, считаем, что тепловой
процесс является квазистационарным, то есть третьим слагаемым в уравнении (4)
также можно пренебречь. В результате получим
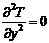 . (А. 7)
. (А. 7)
Дифференциальные уравнения (5)-(7)
являются основными дифференциальными уравнениями, описывающими исходную задачу.
Граничными условиями при данных предположениях
являются
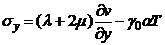 ,
,
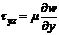 .
.
Заметим, что
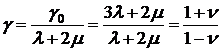 ,
,
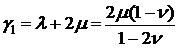 ,
,
где 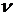 - коэффициент Пуассона.
- коэффициент Пуассона.
То есть граничные условия примут вид
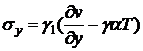 ,
,
 .
.
Приложение Б
Графики
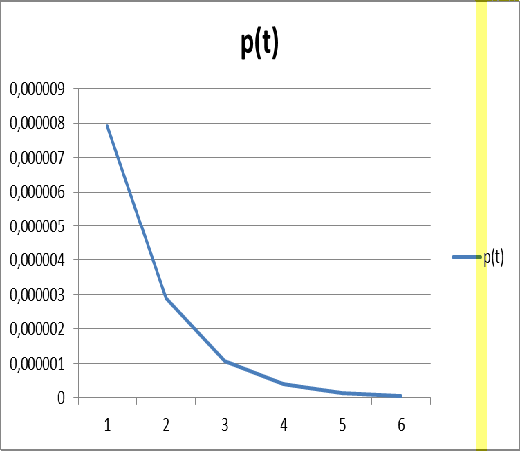
Рисунок Б.1 - Контактное давление
p(t)
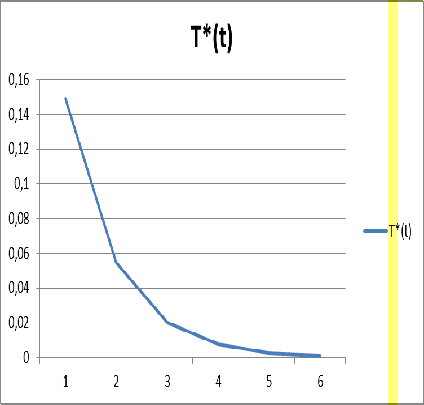
Рисунок Б.2 - Температура поверхностей T*(t)
плита слой термосиловой устойчивость
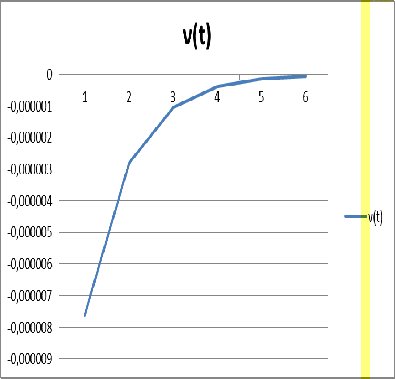
Рисунок Б.3 - Горизонтальное перемещение v(h,t)
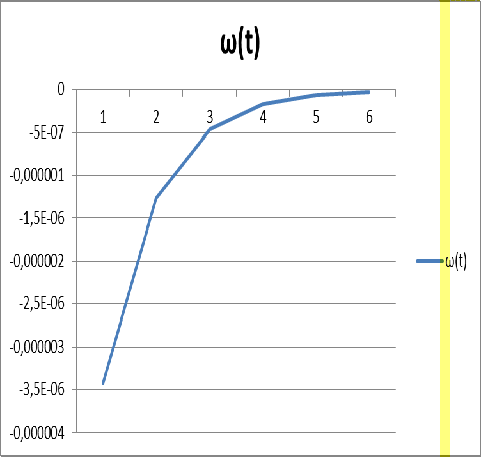
Рисунок Б.4 - Вертикальное перемещение вдоль
w(h,t)