Оценка качества работы системы автоматического регулирования

Оценка качества работы системы автоматического регулирования

Лекция 8 (6 часов)

ОЦЕНКА КАЧЕСТВА РАБОТЫ САР

Показатели качества работы САР

Устойчивость является необходимым, но недостаточным условием работоспособной системы, поскольку она (САР) должна отвечать дополнительным требованиям в статике и динамике для обеспечения хорошего функционирования, т.е. качественной работы. Под качеством САР понимают совокупность требований, прямо или косвенно характеризующих точность ее работы.

Требования в статике ориентированы на точность работы САР в установившихся режимах. При этом обычно необходимо, чтобы установившаяся ошибка САР eуст не превышала заданных допустимых значений.

При анализе динамики САР предъявляются вполне определенные требования по отработке либо наиболее характерных управляющих воздействий, либо наиболее неблагоприятных. К числу неблагоприятных воздействий часто относят скачкообразное воздействие 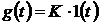. Поскольку мы рассматриваем линейные системы, то изменение величины скачка K влияет только лишь на изменение масштаба по оси ординат, а перерегулирование s, время первого согласования tc, время достижения переходным процессом максимального значения tm, а также время регулирования tp при этом остаются неизменными. Поэтому в качестве скачкообразного воздействия часто принимают единичную функцию Хевисайда .

Нам уже известно, что реакцию САР на единичное воздействие  называют переходной функцией . Следовательно, оценку качества работы САР можно осуществлять по переходной функции.

Разделим задачу оценки качества работы САР на две подзадачи:

1)      Оценка точности работы САР в установившихся режимах;

2)      Анализ качества переходных процессов в САР.

Оценка точности работы САР в установившихся режимах. Коэффициенты ошибок

При рассмотрении вопросов точности будем считать, что на систему с единичной отрицательной обратной связью действует управляющее воздействие, которое изменяется достаточно плавно при больших временах наблюдения (рис.8.1), т.е. так, что существенное значение имеют только первые l производных от  -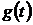

, , …, ,

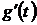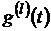а остальные, высшие производные  могут быть приняты равными нулю.

Наиболее полной характеристикой качества системы в установившемся режиме является установившаяся ошибка. Найдем ПФ САР по ошибке:

.

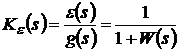Разложим 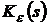 в ряд Маклорена, сходящийся при малых s (т.е. при больших временах t):

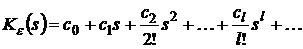,(1)

где коэффициенты ряда c0, c1, c2, … определяются по уравнению [1]:

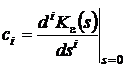,(2)

где значению i=0 соответствует отсутствие дифференцирования.

Действительно, из (1) с помощью (2) можно получить:

;

;

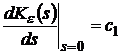Ограничиваясь в (1) первыми l+1 слагаемыми (т.е. пренебрегая производными порядка выше l-го), для изображения ошибки запишем выражение:

,

или, переходя к оригиналам:

.(3)

Коэффициенты c0, c1, …, cl называются коэффициентами ошибок.

Коэффициенты ошибок определяют долевое участие в общей ошибке самого сигнала (c0) и l его производных (c1, c2, …, cl). Если входная 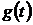 и выходная  величины одной размерности, то c0 есть безразмерная величина, размерность c1 - секунда (с), размерность c2 - с2 и т.д.

Первые три коэффициента ошибки, которыми часто и ограничиваются на практике, имеют специальные названия: c0 - коэффициент позиционной ошибки; c1 - коэффициент скоростной ошибки; c2 - коэффициент ошибки по ускорению.

Примечание. Только что рассмотрен случай, когда на САР действует только управляющее воздействие 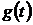, поэтому, строго говоря, выше речь шла о коэффициентах ошибки по управляющему воздействию. В случае действия на САР дополнительного возмущающего воздействия 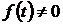 в силу линейности рассматриваемых САР

.

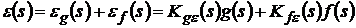При учете второго слагаемого аналогичным образом могут быть введены коэффициенты ошибки по возмущающему воздействию.

Коэффициенты ошибок в статических и астатических САР

Рассмотрим статическую систему (). Как известно, при отработке постоянного управляющего воздействия  (рис.8.2) в ней имеет место установившаяся ошибка

,

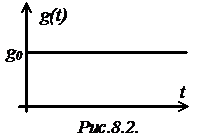
где  - коэффициент усиления разомкнутой САР.

Производные первого и высших порядков сигнала 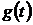 равны нулю:

, , , …

При больших временах t (в т.ч. в установившемся режиме, т.е. при ) установившаяся ошибка, согласно (3), равна

.

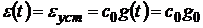Сравнивая последние два выражения для установившейся ошибки, получаем, что коэффициент ошибки

.

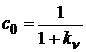Астатические системы (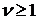), как было показано раньше, постоянный управляющий сигнал  (рис.8.2) отрабатывают без ошибки в установившемся режиме:

.

Следовательно, для любой астатической системы коэффициент ошибки c0 равен нулю:

.        (4)

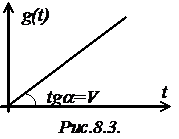
Рассмотрим астатическую систему 1-го порядка (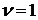). Подадим на ее вход линейно изменяющийся сигнал 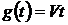 (рис.8.3). Производные: , .

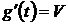Согласно (3) и с учетом свойства (4) астатических САР, установившаяся ошибка может быть записана в виде:

.

Вспоминая понятие добротности по скорости 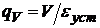, определяем, что коэффициент ошибки c1 в астатической системе 1-го порядка равен

,

где  - коэффициент передачи разомкнутой САР.

Таким образом, в астатической системе 1-го порядка коэффициент ошибки c1 по скорости изменения задающего воздействия есть величина, обратная добротности САР по скорости.

Астатические системы 2-го порядка (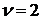) линейно изменяющееся управляющее воздействие 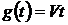 (рис.8.3) отрабатывают без установившейся ошибки, поэтому для них, кроме условия (4),

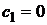.        (5)

Подадим на вход астатической системы 2-го порядка воздействие, изменяющееся в квадратичной зависимости от времени (с постоянным ускорением),  (рис.8.4). Производные , , .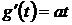

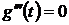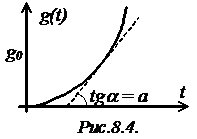
Поэтому установившаяся ошибка с учетом (3) - (5) равна

.

С другой стороны, вспоминая понятие добротности по ускорению , определяем, что коэффициент ошибки c2 в астатической системе 2-го порядка равен

.

Таким образом, в астатической системе 2-го порядка коэффициент ошибки c2 по ускорению изменения задающего воздействия есть величина, обратная половине добротности САР по ускорению.

Для астатических систем более высокого порядка () рассуждения проводятся аналогично.

Определение некоторых коэффициентов ошибок по ЛАЧХ разомкнутой САР

Точность работы САР в установившихся режимах связана с характером изменения ЛАЧХ разомкнутой системе в области низких частот (т.е. с ее наклоном в самой левой области частот). Суть определения коэффициентов ошибок по ЛАЧХ разомкнутой САР 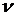-го порядка состоит в определении частоты, при которой низкочастотный участок ЛАЧХ пересечет ось частот, равной

где 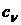 - коэффициент ошибки при отработке управляющего воздействия, представляющего собой кривую 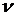-го порядка вида . При этом коэффициенты ошибок c0, c1, …, cn-1 будут равны нулю.

На рис.8.5 изображены начальные (низкочастотные) участки ЛАЧХ статической и астатических (n=1, 2, 3) САР и указаны коэффициенты ошибок при отработке указанного воздействия.

При более сложных (полиномиальных) законах изменения управляющего воздействия следует пользоваться формулами (1) и (2) (что иногда очень затруднительно), либо воспользоваться следующим алгоритмом.

Определение коэффициентов ошибок по передаточной функции САР по ошибке

Пусть имеется ПФ системы по ошибке:

Коэффициенты ошибок в общем виде можно определить, если числитель этой ПФ разделить на знаменатель (по правилу деления полиномов), а затем сравнить полученный результат с равенством (1).

Для удобства выполнения операции деления полиномов рекомендуется члены делимого и делителя располагать в порядке увеличения степени s:

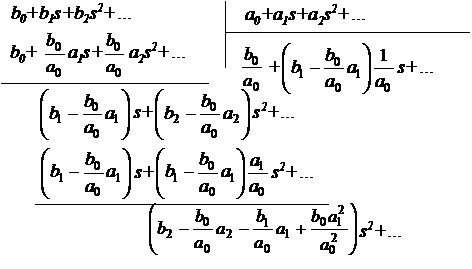
Деление выполняют до тех пор, пока либо остаток не становится равным нулю, либо при достижении нужного количества слагаемых в частном, позволяющих определить необходимые коэффициенты ошибок. Для определения же коэффициентов ошибок полученный результат сравнивается с выражением (1).

Пример. Передаточная функция разомкнутой системы имеет вид:

.

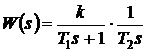Определить коэффициенты ошибок.

Решение. Определяем ПФ замкнутой системы по ошибке:

.

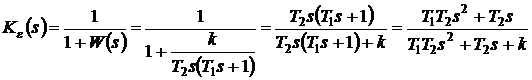Выполняем деление числителя на знаменатель:

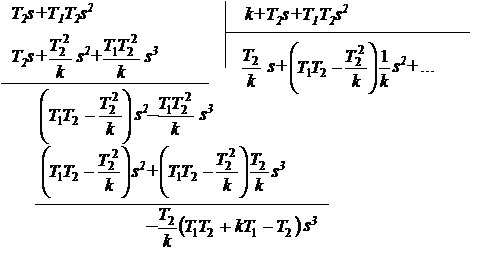
Сравнивая результат деления с (1), определяем:

система автоматический регулирование точность

; ; .

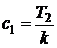Пусть задающее воздействие, действующее на систему, имеет вид:

.

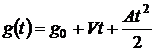Тогда установившаяся ошибка по (3) равна

.

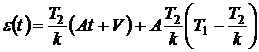Оценка качества переходных процессов

Существуют прямые и косвенные показатели качества в переходном режиме.

К прямым методам относят такие, в которых оценка качества дается по предварительно определенной (аналитически или с помощью математического моделирования) или снятой экспериментально переходной характеристике h(t).

В косвенных методах оценка дается на основе анализа частотных и некоторых др. характеристик системы. Они требуют менее громоздких вычислений, и поэтому более удобны. Косвенные методы подразделяют на корневые, частотные и интегральные.

Все методы оценки качества переходных процессов предполагают априори, что система является устойчивой.

Прямые методы оценки качества переходных процессов

К прямым показателям качества относят время регулирования и перерегулирование, определяемые по переходной характеристике.

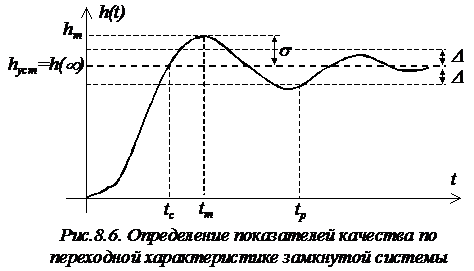
Временем регулирования tp называют время, по истечении которого отклонение выходной величины от установившегося значения не превышает некоторой заданной величины D. Обычно принимают D= (0,01…0,05)hуст.

Перерегулированием s называют максимальное отклонение переходной функции от установившегося значения, выраженное в процентах:

.

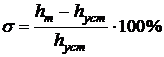В большинстве случаев процесс считается устойчивым, если величина перерегулирования не превышает 10…30%.

Кроме tp и s, иногда в качестве показателей качества рассматривают время первого согласования tс (которое определяет быстродействие системы) и число колебаний Nк выходной величины относительно установившегося значения за время tp (обычно не должно превышать 1…2).

О взаимосвязи ЛАЧХ разомкнутой системы с качеством переходного процесса

Для оценки качества переходного процесса может быть использована связь между характером переходного процесса и формой ЛАЧХ.

Низкочастотная часть ЛАЧХ связана с работой САР в установившихся режимах (при больших временах наблюдения) и характеризует точность работы системы.

Высокочастотный участок ЛАЧХ определяет начальный участок переходного процесса.

Среднечастотная часть ЛАЧХ определяет качество работы системы в переходных режимах. В этой области находится частота среза wС, определяющая быстродействие системы; по значению ЛФЧХ при частоте среза можно определить запас устойчивости по фазе. По значению частоты среза с помощью эмпирических зависимостей можно определить время первого согласования tc, время достижения максимального значения tm и время регулирования tp, т.е. основные параметры переходного процесса. Эти эмпирические зависимости носят название номограмм Честната и Майера [4], и будут использоваться нами в дальнейшем.

Любая работоспособная система имеет среднечастотный участок ЛАЧХ в области частоты среза wС с наклоном -1. Только при этом условии можно получить качественную САР, причем чем больше длина среднечастотного участка с наклоном -1, тем больше вероятность получения качественной системы, с приемлемыми колебательностью и перерегулированием.

Некоторые следствия из анализа номограмм Честната и Майера:

. Смещение ЛАЧХ вдоль оси частот влево или вправо влияет только на быстродействие САР. Чем больше частота среза wС, тем система более быстродействующая:

.

. Если в области высоких частот имеется наклон ЛАЧХ -2, -3, -4 и т.д., то высокочастотный хвост этой ЛАЧХ можно заменить добавлением ЛАЧХ апериодического звена с постоянной времени TS, равной сумме постоянных времени всех апериодических звеньев, частоты сопряжения которых находятся правее частоты среза (рис.8.8).

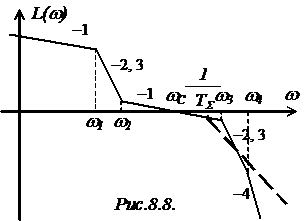
Другими словами, все непрерывные звенья, постоянные времени которых малы (частоты сопряжения выше частоты среза), могут быть заменены апериодическим звеном с передаточной функцией

,

где

Частотные показатели качества переходных процессов

Исходя из того, что качественная САР должна быть прежде всего устойчивой, в качестве частотных показателей качества рассматриваются уже известные нам запас устойчивости по амплитуде А и запас устойчивости по фазе y, а также резонансный максимум АЧХ замкнутой системы Мр и полоса пропускания (рис.8.9).

Запасы устойчивости по амплитуде и по фазе характеризуют близость системы к границе устойчивости и определяются по логарифмическим частотным характеристикам разомкнутой САР. Чем дальше система от границы устойчивости, тем она лучше. В качественных системах запасы устойчивости должны составлять:

А=6…20 дБ                           y=30…60°.

Резонансный максимум является показателем колебательности САР, и, как будет показано ниже, позволяет более удобно оценивать запас устойчивости САР. Резонансный максимум равен отношению максимального значения Amax АЧХ замкнутой системы, которое имеет место при резонансной частоте wр, к ее начальному значению A(0). Другими словами, показатель колебательности есть максимальное отношение амплитуд выходного xmax и входного gmax воздействий, имеющее место при частоте задающего воздействия w=wр, определяемой экспериментальным или расчетным путем:

.

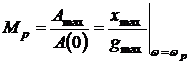Обычно в качественных системах показатель колебательности не должен превосходить значений 1,1…1,5.

Для оценки величины резонансного максимума можно пользоваться эмпирическими формулами связи между запасом устойчивости по фазе и резонансным максимумом:

,

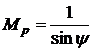а также связи между резонансным максимумом и перерегулированием (s в долях):

               .

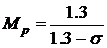Зная время достижения переходной функцией максимального значения

,

можно приближенно с помощью зависимости рис.8.10 [3] определить время первого согласования tc.

.

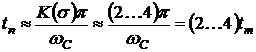Оценка качества работы САР по резонансному максимуму АЧХ замкнутой системы

Определение резонансного максимума по ЧХ разомкнутой САР

Пусть имеется САР, изображенная на рис.8.11.

Частотная (или, как ее еще называют, амплитудно-фазовая) характеристика замкнутой системы:

Амплитудно-частотная характеристика (АЧХ):

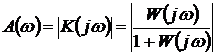                                                   (1)

Примерный вид нормированной АЧХ представлен на рис.8.12.

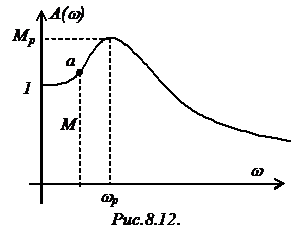
Чем выше резонансный максимум Mp, тем меньше запас устойчивости, и тем больше склонность системы к колебаниям. В реальных САР величина Mp находится в пределах 1,0…1,8.

Возьмем на АЧХ некоторую точку а (рис.8.12), значение АЧХ в ней обозначим через М.

Отобразим точку а на комплексную плоскость частотной характеристики разомкнутой САР. Для этого в формуле (1) подставим :

                                                  (2)

Частотная характеристика разомкнутой САР в точке а может быть определена в виде:

,

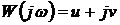и тогда

.                                                  (3)

Решая уравнение (3) относительно u и v, можно прийти к выводу, что линия равных значений М отображается на плоскость ЧХ разомкнутой САР в окружность, уравнение которой:

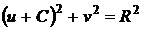,                                                       (4)

где 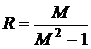 - радиус окружности;  - смещение центра окружности по оси абсцисс.

Построив семейство таких окружностей (рис.8.13) для разных значений 1<М<¥, замечаем, что при M®¥ радиус окружности R®0 и окружность вырождается в точку с координатами (-1; j0). С другой стороны, при М®1 радиус R®¥, и окружность вырождается в линию, параллельную оси ординат и отстоящую от нее на 0,5.

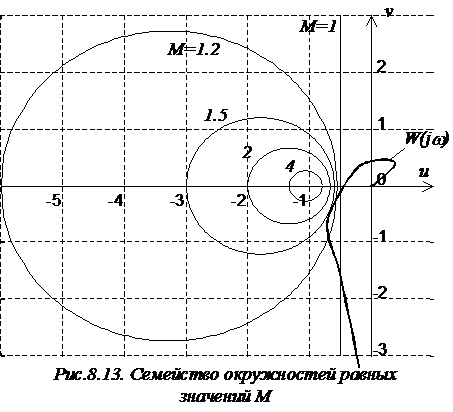
Можно отметить, что для значений 0<M<1 получится семейство окружностей, расположенный справа от прямой М=1  симметрично с первым семейством. При М=0 окружность вырождается в точку, совпадающую с началом координат.

Величина резонансного максимума может быть определена путем нахождения окружности, которой касается ЧХ разомкнутой САР (совпадает только в одной точке). Например, САР, ЧХ которой в разомкнутом состоянии имеет вид W(jw) (рис.8.13) будет иметь резонансный максимум Мр=1.5.

Проектирование САР с заданным уровнем Мр

На практике очень часто ставят задачу: спроектировать систему, для которой Мр будет не больше некоторого заданного значения Mзад. Очевидно, что в общем случае задача будет решена, если обеспечить такой вид ЧХ разомкнутой системы, чтобы ее кривая не заходила внутрь окружности М=Мзад (рис.8.14). Таким образом, окружность М=Мзад ограничивает запретную зону для амплитудно-фазовой характеристики (заштрихована).

Рассмотрим частный случай. Пусть Мзад=2.

Решение.

По заданной величине Мзад определяем координаты радиуса и центра окружности:

; .

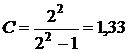Строим окружность с центром в точке (-1,33; 0) радиуса 0,67 (рис.8.15).

Чтобы реальное значение резонансного максимума было меньше заданного, необходимо, чтобы ЧХ разомкнутой САР не заходила в запретную зону, т.е. внутрь окружности.

Пусть точка b принадлежит ЧХ разомкнутой САР. Обозначим угол, который образует вектор А, проведенный из начала координат в точку b, с отрицательным направлением оси u, через m. Очевидно, что угол m равен запасу устойчивости САР по фазе.

Из рис.8.15 следует, что запретная зона может иметь место при значении модуля АЧХ А разомкнутой системы

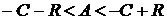
или

.                                                       (5)

Очевидно также, что для любого модуля А существует такой угол m, при котором ЧХ разомкнутой системы не заходит в запретную зону.

Из треугольника ObO1 можно найти выражение для запаса по фазе, при котором ЧХ может попасть в запретную зону:

.                                                        (6)

Используя (6), можно построить называемые m-кривые (рис.8.16) [1], пользуясь которыми, для любого значения модуля А можно найти то значение величины m, при котором обеспечивается требуемое значение резонансного максимума.

Для зависимости (6) можно определить, что максимум будет иметь место при 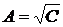, а само значение максимума:

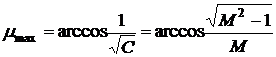.                                      (7)

Если имеются логарифмические частотные характеристики разомкнутой системы, то по имеющимся m-кривым и при заданном значении М можно построить требуемое значение запаса по фазе для каждого значения модуля А, удовлетворяющего условию (5), которое для ЛАЧХ принимает вид:

.                          (8)

В результате можно получить запретную зону для ЛФЧХ. Чтобы показатель колебательности Мр не был больше заданного значения, ЛФЧХ не должна заходить в эту область.

Определим условия, при которых ЛФЧХ гарантированно не заходит в запретную область, на примере типовой ЛАЧХ типа "-2-1-2".

Пусть передаточная функция разомкнутой САР равна

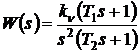,                                                        (9)

причем .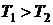

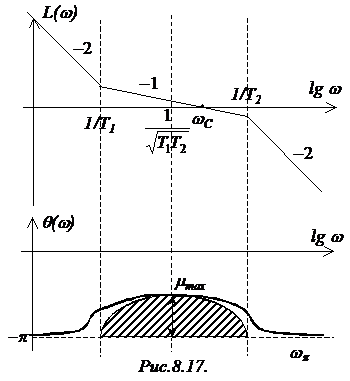
Логарифмические частотные характеристики такой разомкнутой САР представлены на рис.8.17.

Выражение для ЛФЧХ для (9) имеет вид:

где 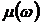 - запас по фазе, который запишем следующим образом:

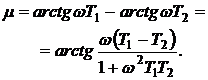                                           (10)

Для зависимости (10) можно определить, что ее максимум будет иметь место при , а само значение максимума:

.                                                   (11)

Таким образом, максимальный запас по фазе определяется только постоянными времени, определяющими участок с наклоном "-1".

В [1] доказано, что значение максимального запаса по фазе (11) будет не меньше предельно допустимого запаса по фазе (7) при условии:

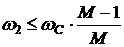
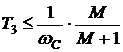
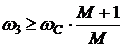                                            (12)

В граничном случае (равенство) ЛФЧХ будет касаться запретной зоны в точке m=mmax. В этом случае будет иметь место максимальное быстродействие системы при заданном уровне Мр.

Таким образом, при выполнении условий (12) для ЛАЧХ разомкнутой системы вида "-2-1-2" требования по величине Мр будут выполнены.

В случае, когда ЛАЧХ разомкнутой системы имеет вид "-2-1-2-3-4…", также можно пользоваться представленными зависимостями, предварительно заменив все апериодические звенья с частотами сопряжения правее частоты среза одним апериодическим звеном с постоянной времени TS, равной сумме постоянных времени этих звеньев.

.
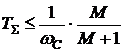