Исследование простейших электронных схем в Electronics Workbench

Исследование простейших электронных схем в Electronics Workbench

Министерство образования Республики Беларусь

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра математического моделирования и управления

Отчет по лабораторной работе

По предмету: Физика ЭВМ

Исследование простейших электронных схем в Electronics Workbench

студента 4 курса 6 группы

Преподаватель

Хорячкин Владимир Викторович

доцент кафедры ТП,

канд. физ.-мат. наук

Минск 2013

Вариант индивидуального задания

Задание 1

Понять назначение и возможности пакета Electronics Workbench. Изучить интерфейс пользователя. Ознакомиться с основными специальными терминами и понятиями.

Задание 2

Исследовать поведение емкости и индуктивности в цепях постоянного (задание 2.1) и переменного тока (задание 2.2). Получить навыки работы с контрольно-измерительными приборами. Научиться читать и собирать простейшие электронные схемы.

1. Емкость и индуктивность в цепях постоянного тока

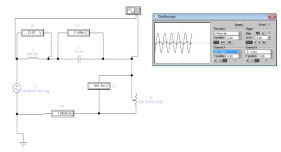
Рисунок 1 - Серия опытов с емкостью в цепях постоянного напряжения

Таблица 1 - Серия опытов с емкостью в цепях постоянного напряжения

Вывод: показания амперметра и вольтметра равны нулю, так как конденсатор в цепях с постоянным током представляет собой разрыв в цепи, что видно из формул:

;

Заменим конденсатор в цепи на катушку индуктивности:

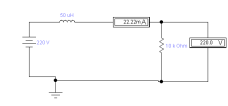
Рисунок 2 - Серия опытов с индуктивностью в цепях постоянного напряжения

Таблица 2 - Серия опытов с индуктивностью в цепях постоянного напряжения

Вывод: в цепи постоянного тока катушка индуктивности имеет лишь небольшое сопротивление, поэтому она не влияет на показания приборов. Значение падения напряжения в цепи совпадает с напряжением источника. Это можно подтвердить формулами:

.

То есть U не меняется. Тогда

.

2. Конденсатор в цепях переменного напряжения

Соберем схему с источником переменного тока и конденсатором.

Рисунок 3 - Схема с источником переменного тока

Определим значение переменного тока, снимем осциллограммы в контрольных точках электронной схемы, определим сдвиг фаз снятых сигналов.

Для начала проведем исследования, изменяя значение емкости конденсатора при фиксированной частоте. Затем - изменяя частоту источника переменного напряжения при фиксированной емкости конденсатора.

Разность фаз вычисляется по следующей формуле

.

Таблица 3 - Серия опытов с емкостью и индуктивностью в цепях переменного напряжения

Вывод: в цепи переменного тока при фиксированном значении частоты источника переменного тока максимальный сдвиг фаз наблюдается при минимальной емкости конденсатора.

Для обоснования полученных результатов используем следующие формулы:

, , .

Вычислим силу тока для самого первого опыта.

Опытным путем с помощью мультиметра был получен такой же результат.

Отметим, что разность фаз с возрастанием частоты или ёмкости становится меньшей. Это объясняется следующей формулой:

,

понятно, что будет верным следующий предельный переход:

.

. Исследовать и сравнить свойства емкостей и индуктивностей в цепях постоянного и переменного напряжений

Рисунок 4 - Схема эксперимента

Таблица 4 - Результаты эксперимента

Вывод: подсчитаем напряжение, которое при правильном проведении опытов мы должны получить, используя приведенные ниже формулы. Будем находить величину напряжения V3 для первого испытания.

.

В нашем случае r = 3 кОм, L = 400 мГн и меняется за счет изменения частоты f от опыта к опыту.

Найдем величину напряжения V3 для испытания №1.

Теоретические данные согласуются с результатом, полученным опытным путем.

Заметим, что во всех опытах с использованием конденсатора значения на вольтметре V4, измеряющем постоянное напряжение, очень малы, а с использованием катушки индуктивности равны 36 В - значению на источнике постоянного напряжения. Также в опытах с катушкой значения напряжения на вольтметре V3 тем меньше, чем больше частота f. Это легко следует из следующей цепочки формул:

4. Исследовать схему делителя напряжения и освоить новые функциональные возможности сложных приборов

1. Исследование схемы делителя напряжения

Таблица 5 - Задания пункта 4.1

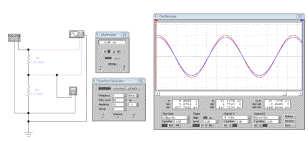
Рисунок 5 - Схема делителя напряжения

Таблица 6 - Результаты измерений

Вывод: в цепи с делителем напряжения на два последовательно соединенных резистора подается высокочастотный переменный ток. Поскольку сопротивления резисторов равны, напряжение источника делится на них поровну, и, как видно на первой осциллограмме таблицы 9, при масштабе каналов осциллографа 2:1 входной и выходной сигналы полностью совпадают. Измерения, представленные на второй осциллограмме в таблице 9, также показывают, что амплитудные значения выходного сигнала 2,98 В в 2 раза меньше, чем амплитуда входного сигнала 5, 96 В. Мультиметр, настроенный на работу с переменным током показывает действующее значение напряжения, которое по определению в  раз меньше амплитудного. При заданном значении амплитудного напряжения на генераторе, равном 6 В, после прохождения через делитель на выходе получаем амплитудное напряжение 3 В, а действующее значение составляет 2,12 В, что хорошо согласуется со значением, измеренным мультиметром и представленном на рисунке 6.

2. Для обоснования полученных результатов воспользуемся следующими функциональными зависимостями:

5. Исследовать схему последовательного колебательного контура

индуктивность напряжение колебательный контур

Для заданных значений RLC найти резонансную частоту контура. Определить добротность и характеристическое сопротивление контура. Выясните поведение тока для относительно малых (f(∆_w0)) и очень больших расстроек (∆_f) частоты генератора от резонансной частоты контура (f_r). То есть, оцените полосу пропускания последовательного колебательного контура.

Рисунок 6 - Схема последовательного колебательного контура

Найдем резонансную частоту контура:

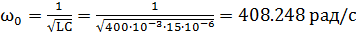
Тогда:

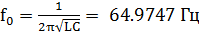
Определим характеристическое сопротивление контура:

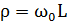
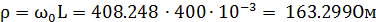
Определим добротность контура:

Коэффициент затухания:

Оценим полосу пропускания. Для этого найдем верхнее и нижнее значение частоты:

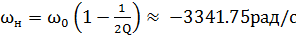
Таблица 7 - Опыт в RLC-цепи

Вывод: в цепи последовательного колебательного контура наблюдается резонанс напряжений при определенной частоте.

Таблица 8