Исследование алгоритма оценивания стохастических динамических систем
Введение
Целью данной работы является исследование
алгоритма оценивания стохастических динамических систем называемого Фильтром
Калмана. Задачей работы помимо исследования алгоритма является реализация его
на языке с++. Объектом оценивания будет являться спутниковые измерения.
Спутниковая система навигации (GNSS,
global navigation
satellite
system) - комплексная
электронно-техническая система, состоящая из совокупности наземного и
космического оборудования, предназначенная для определения местоположения (позиционирования),
а также параметров движения (скорости, направления движения и др.) для
различных целей. Местоположение определяется тремя координатами приёмника
спутниковой навигации в некоторой системе координат. Обычно используются
системы координат ECEF
(Earthcentered & earthfixed,
декартова система координат с началом в точке центра масс Земного шара), WGS84
(World Geodetic
System 1984, сферическая
система координат с началом в точке центра масс Земного шара). Если
местоположение считается в сферической системе координат и третья координата
(высота) неизвестна, то позиционирование является двумерным. Если в процессе
позиционирования координаты приёмника не меняются, то позиционирование
называется статическим. В противном случае говорят о кинематическом
позиционировании.
Система спутниковой навигации включает в себя
орбитальную группировку, состоящую из нескольких (от 2 до 30) спутников,
излучающих специальные радиосигналы, наземную систему контроля, приёмное
клиентское оборудование ("спутниковые навигаторы"), Возможно также
использование системы наземных станций, позволяющих повысить точность
определения координат, системы для передачи пользователям уточнённых координат
и часов спутников.
Местоположение приемника в системе спутниковой
навигации вычисляется пересечением сфер от разных спутников. Радиусы сфер
определяются неточно из-за ионосферной и тропосферной задержек, релятивистского
эффекта, эффекта приема отраженного сигнала и других факторов. Без каких-либо
коррекций точность определения местоположения составляет 30-50 метров.
Важнейшими приложениями спутниковой навигации
являются:
· Картография: построение карт при помощи систем
спутниковой навигации;
· Геодезия, кадастровые работы: с
помощью систем навигации определяются точные координаты границ земельных
участков;
· Навигация: с применением систем
спутниковой навигации осуществляются морская, дорожная, авиационная и другие
виды навигации;
· Спутниковый мониторинг транспорта: с
помощью систем навигации ведется мониторинг за положением, скоростью автомобилей,
контроль за их движением;
· Сотовая связь: в случае, когда
телефон снабжен устройством спутниковой навигации, можно узнать его
местоположение;
· Геофизические измерения: с помощью
систем навигации ведутся наблюдения движений и колебаний литосферных плит.
В каждой области, где используется та или иная
система спутниковой навигации, существуют свои требования к точности нахождения
местоположения. Например, при кадастровых работах необходимо, чтобы ошибка была
не более 10 сантиметров. Напротив, в дорожной навигации, точности в 5 метров
зачастую бывает достаточно. В соответствии с этими требованиями используются
разные датчики и разные методы.
Существует несколько классов методов решения
задач спутниковой навигации. В прошлом наиболее популярны были разностные
методы. Для этих методов необходима как минимум одна наземная станция (т.е.
приёмник, координаты которого известны), находящаяся достаточно близко к месту
измерений. Эти методы позволяют алгебраическими преобразованиями сократить
большинство ошибок, в частности можно сократить ионосферную и тропосферную
задержки, ошибки часов спутников и приёмников. Однако, чем дальше от наземной
станции производится подсчёт, тем меньше точность позиционирования.
Это главный минус разностных методов, но тем не
менее ранее им уделялось большое внимание и практически не рассматривались
абсолютные методы, т.е. методы, использующие лишь один приемник. Но ситуация
начала меняться, когда стали появляться наземные службы, вычисляющие различные
дополнительные данные, такие как точные орбиты спутников, погрешности часов
спутников, атмосферные карты и др. На сегодняшний день самая большая такая
служба - IGS (International
GNSS Service,
[13]), В последнее время стали приобретать популярность методы высокой точности
(point precise
positioning). Этот класс
методов подразумевает учёт максимального числа данных для коррекций различных
ошибок и задержек.
Нахождение местоположения в системе спутниковой
навигации - это нахождение трёх координат. Наряду с этими величинами, можно
замерить ряд относительных параметров при помощи инерциальных датчиков (IMU,
inertial
measurements
unit): акселерометра,
гироскопа и магнетометра. При помощи акселерометра можно измерить три
координаты ускорения, при помощи гироскопа - три координаты угловых скорости,
при помощи магнетометра - три координаты вектора магнитного склонения. Эти
данные также могут быть использованы при решении навигационных уравнений.
Ошибки измерений и их порядки
В этом главе будет представлена в аналитическом
виде значительная часть ошибок и задержек, возникающих при измерении расстояния
от спутника до приемника.
Под ошибкой будем понимать какой-либо сдвиг
координат спутника или часов приёмника и спутников. Задержка - эта ошибка, по
причине которой изменилась скорость прохождения сигнала на каком-либо участке
от спутника до приёмника.
Пусть у нас имеется приемник и несколько
спутников. Пусть имеется общая временная шкала, т.о. время, но которому
выстроены часы спутников и приёмника, В качество общей временной шкалы
практически всегда берут среднее время но Гринвичу (время на нулевом
меридиане). Будем называть псевдодалъностъю величину

• c
- скорость света в вакууме
• t(T2)
- время получения сигнала приемником по часам приемника
• ti(T1)
- время отправления сигнала спутником по часам спутника номер i
Определяя расстояние от i-го
спутника до приёмника, псевдодальность содержит также следующие ошибки: ошибку
синхронизации часов спутника и приемника, задержку сигнала в атмосфере
(тропосфера и ионосфера), релятивистский эффект, инструментальные задержки,
помехи тина "повторных изображений" (multipath),
интерференции и другое.
Учитывая вышеуказанное, получим следующее
выражение для псевдодальности:
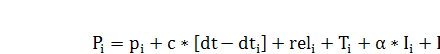 (*)
(*)
где:  геометрическое
расстояние от спутника под номером i,
т.е.
геометрическое
расстояние от спутника под номером i,
т.е.
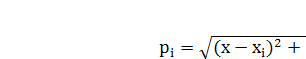
•  изменение часов
приемника от общей временной шкалы;
изменение часов
приемника от общей временной шкалы;
•  изменение часов i-го
спутника от общей временно шкалы;
изменение часов i-го
спутника от общей временно шкалы;
•  тропосферная
задержка;
тропосферная
задержка;
•  характеризует
ионосферную задержку,
характеризует
ионосферную задержку,  множитель, который
выражается через частоту сигнала
множитель, который
выражается через частоту сигнала  ;
;
•  релятивистский
эффект;
релятивистский
эффект;
•  инструментальная
задержка, вызванная помехами спутника, не зависит от частоты;
инструментальная
задержка, вызванная помехами спутника, не зависит от частоты;
•  эффект приема
отраженного сигнала, зависит от частоты;
эффект приема
отраженного сигнала, зависит от частоты;
•  неучтенные ошибки.
неучтенные ошибки.
1. Математические модели
Математи́ческая
модемль
<#"668724.files/image003.gif">(входной
сигнал прибора) с его выходным сигналом  .
.
Так как в реальных условиях погрешность прибора  и
тем самым его выходной сигнал
и
тем самым его выходной сигнал являются
случайными процессами, то и модели должны носить вероятностный характер.
являются
случайными процессами, то и модели должны носить вероятностный характер.
В случаях, когда работа прибора происходит в
непрерывном времени, она может быть описана с помощью системы стохастических
дифференциальных уравнений с фазовыми координатами  (вектор
состояния) и системы функциональных преобразований
(вектор
состояния) и системы функциональных преобразований  от
векторов
от
векторов  :
:
 ,
,
 ,
,

где  n-мерный
вектор-столбец состояния;
n-мерный
вектор-столбец состояния;  m-мерный
вектор измеряемых величин;
m-мерный
вектор измеряемых величин;  m-мерный
вектор выходных сигналов (измеренных величин);
m-мерный
вектор выходных сигналов (измеренных величин);  n-мерная,
n-мерная,
 m-мерная
дифференцируемые функции своих переменных;
m-мерная
дифференцируемые функции своих переменных;  случайные
процессы типа “белый шум”.
случайные
процессы типа “белый шум”.  матрица.
Ковариационные матрицы этих процессов будем считать известными и равными
матрица.
Ковариационные матрицы этих процессов будем считать известными и равными



где  дельта-функция.
дельта-функция.
Матрицы  называются
матрицами интенсивности “белых” шумов. Если модель записать в виде
называются
матрицами интенсивности “белых” шумов. Если модель записать в виде
 ,
,
 ,
,
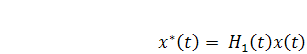
То она называется линейной.
Имеются измерительные приборы, которые работают
дискретно. Кроме того, в некоторых случаях у непрерывных приборов съем
показаний осуществляется в дискретные моменты времени. Для таких приборов
математические модели тоже должны быть дискретными. Для нелинейных систем
дискретная модель имеет вид:
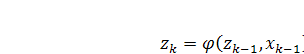 ,
,

где  многомерные
дискретные “белые” шумы с ковариационными матрицами
многомерные
дискретные “белые” шумы с ковариационными матрицами  ,
,
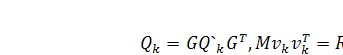 .
.
Для линейных систем дискретная модель
представляется в форме
 ,
,

2. Фильтр Калмана
.1. Общий вид
Определение 1 Фильтр Калмана - эффективный (т.е.
имеющий способ гарантированно достигать результат за конечное число действий)
рекурсивный фильтр, оценивающий вектор состояния динамической системы,
используя ряд неполных и зашумленных измерений. Назван в честь Рудольфа
Калмана.
Чтобы дать более полное определение фильтра
Калмана, необходимо ввести ряд необходимых терминов и обозначений.
Путь имеется некоторый процесс, для которого
существует физическая модель. Пусть также существуют некоторые измерения,
связанные с этим процессом. Фильтр Калмана подразумевает дискретное время, В  ый
момент времени вектор состояний
ый
момент времени вектор состояний  выражается через
вектор состояний
выражается через
вектор состояний го момента времени
го момента времени  :
:


где: •  матрица
физический модели процесса
матрица
физический модели процесса
•  матрица управления
процессом
матрица управления
процессом
•  - вектор управления
размерности
- вектор управления
размерности 
•  - случайный вектор
ошибки размерности
- случайный вектор
ошибки размерности  , характеризующий
ошибку физической модели.
, характеризующий
ошибку физической модели.
•  - ковариационная
матрица процесса z
- ковариационная
матрица процесса z
•  -
ковариационная матрица процесса w
-
ковариационная матрица процесса w
Также в каждый момент времени мы можем получать
измерения. Вектор измерений  связан с вектором
состояний следующим уравнением
связан с вектором
состояний следующим уравнением
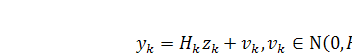 (2)
(2)
где:  -
вектор измерений размерности m
-
вектор измерений размерности m
•  матрица,
характеризующая связь вектора состояний с вектором измерений.
матрица,
характеризующая связь вектора состояний с вектором измерений.
• v - случайный
вектор ошибки размерности m,
характеризующий ошибку измерений.
• 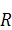 -
ковариационная матрица случайного процесса ошибки измерений.
-
ковариационная матрица случайного процесса ошибки измерений.
• 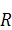 -
ковариационная матрица зависимости процессов w
и v
-
ковариационная матрица зависимости процессов w
и v
Уравнения (1) выдают какой-то физический
процесс, а вектор  есть измерения,
которые мы можем сделать какими-либо приборами. Уравнения (2) показывают связь
вектора состояний с вектором измерений. Матрица B
может быть ненулевой только в случае, когда процессом управляют со стороны. В общем
случае уравнения могут быть нелинейными, однако алгоритм Калмана подразумевает,
что мы всегда их можем линеаризовать.
есть измерения,
которые мы можем сделать какими-либо приборами. Уравнения (2) показывают связь
вектора состояний с вектором измерений. Матрица B
может быть ненулевой только в случае, когда процессом управляют со стороны. В общем
случае уравнения могут быть нелинейными, однако алгоритм Калмана подразумевает,
что мы всегда их можем линеаризовать.
Определение 2 Алгоритмом Калмана называется
следующий двух шаговый алгоритм вычисления состояния динамический системы (1),
(2):
Первый шаг -
предсказание(предикция, экстраполяция)

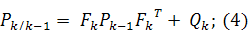
Второй шаг - коррекция:
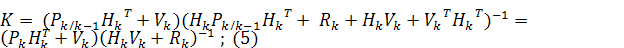
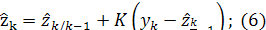

2.2 Свойства условных
вероятностей
Пусть имеются две векторные случайные величины 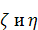 порядка
n и m
соответственно.
порядка
n и m
соответственно.
Пусть далее у них имеется совместная плотность
распределения вероятностей  где x
и y - аргументы
функции плотности, представляющие собой векторы той же размерности, что и
где x
и y - аргументы
функции плотности, представляющие собой векторы той же размерности, что и 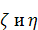 .
.
Условной плотностью распределения случайной
величины 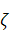 при
условии, что реализация вектора
при
условии, что реализация вектора 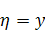 ,
будет функция
,
будет функция
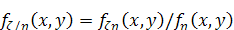 .
.
Условным математическим ожиданием 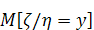 случайного
вектора
случайного
вектора 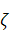 при
условии
при
условии 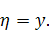 называются
первые моменты от условной плотности распределения
называются
первые моменты от условной плотности распределения 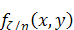
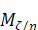 =
=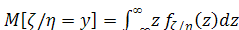 ,
,
где 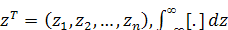 представляет
собой сокращенное обозначение n-кратного
интеграла
представляет
собой сокращенное обозначение n-кратного
интеграла 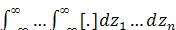 .
.
Из определенных выше выражений вытекает
известная формула для условных математических ожиданий

Которая получается из следующей цепочки
равенств:
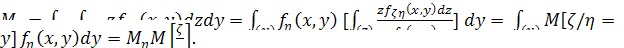
Вторые центральные моменты от функции 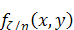 условной
плотности распределения образуют ковариационную матрицу
условной
плотности распределения образуют ковариационную матрицу  условного
распределения
условного
распределения
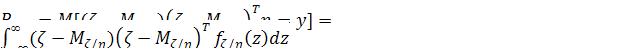 .
.
Рассмотрим теперь следующую задачу. По
реализации случайного вектора  нужно построить
оценки
нужно построить
оценки 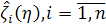 для
элементов неизвестного для наблюдателя случайного вектора
для
элементов неизвестного для наблюдателя случайного вектора 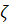 . При этом оценки
. При этом оценки  представляющие
собой фукции от аргумента
представляющие
собой фукции от аргумента  , должны удовлетворять условию
минимума дисперсии для погрешности оценивания
, должны удовлетворять условию
минимума дисперсии для погрешности оценивания

Минимум в последнем соотношении берется по всем
всевозможным видам функции  Докажем, что
функцией на которой реализуется минимум, будет условное математическое ожидание
Докажем, что
функцией на которой реализуется минимум, будет условное математическое ожидание

Доказательство следует из цепочки равенств
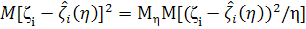 =
= ,
,
Где 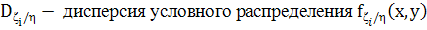 , положительная и не
зависящая от выбора функции
, положительная и не
зависящая от выбора функции 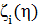 величина.
величина.
Выражение достигает своего минимума при 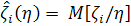 .
.
Итак, оценка 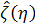 , оптимальная в
смысле наименьшей дисперсии, совпадает с условным математическим ожиданием.
, оптимальная в
смысле наименьшей дисперсии, совпадает с условным математическим ожиданием.
Далее для краткости записи для обозначения
случайных величин 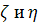 , их плотностей, математических
ожиданий и ковариационных матриц мы будем применять конкретные реализации
, их плотностей, математических
ожиданий и ковариационных матриц мы будем применять конкретные реализации 
Рассмотрим теперь задачу на определение условной
гауссовской плотности вероятности. Пусть задан нормальный случайный вектор 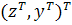 , состоящий из двух
векторов z и y, размерности
которых n и m
соответственно. Математические ожидания
, состоящий из двух
векторов z и y, размерности
которых n и m
соответственно. Математические ожидания  этих
векторов, а также ковариационные матрицы
этих
векторов, а также ковариационные матрицы 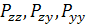 считаются
известными. Также считаем, что
считаются
известными. Также считаем, что  , т.е. случайный вектор y
является невырожденным.
, т.е. случайный вектор y
является невырожденным.
Перейдем к поиску условного математического
ожидания 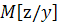 и
условную ковариационную матрицу
и
условную ковариационную матрицу 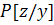 , которые задают условную плотность
вероятности как плотность гауссовского типа.
, которые задают условную плотность
вероятности как плотность гауссовского типа.
Для решения поставленной задачи введем вектор 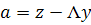 , а матрицу
, а матрицу 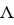 подберем
так, чтобы векторы
подберем
так, чтобы векторы  и
и 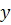 были
некоррелированными
были
некоррелированными
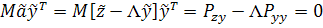 ,
,
где  ;
;
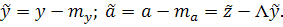
Получаем
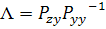
В силу независимости случайных величин  и
и
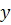 получаем
равенство условного и априорного ожиданий
получаем
равенство условного и априорного ожиданий
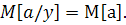
Учитывая, что

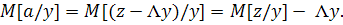
Окончательно получаем выражение для условного
математического ожидания
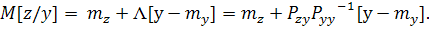 (8)
(8)
Вычислим теперь ковариационную матрицу  условного
нормального распредения. Рассмотрим случайный вектор
условного
нормального распредения. Рассмотрим случайный вектор
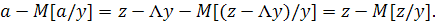
В этом случае ковариационная матрица  может
быть представлена в виде
может
быть представлена в виде
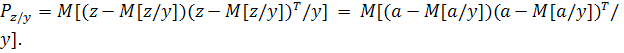
В силу независимости случайных векторов  и
и
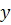 в
последнем выражении от условных математических ожиданий можно перейти к
априорным.
в
последнем выражении от условных математических ожиданий можно перейти к
априорным.
Тогда получим

Итак, определены формулы для нахождения
условного математического ожидания и ковариационной матрицы. Эти формулы будут
необходимы для вывода фильтра Калмана.
2.3 Вывод линейного фильтра
В этой части будет рассмотрен непосредственный
вывод формул (3)-(7). По результатам 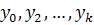 измерений,
проводимых в дискретные моменты времени
измерений,
проводимых в дискретные моменты времени  , необходимо
определить оценки вектора состояний
, необходимо
определить оценки вектора состояний 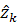 наименьшей
дисперсии процесса (1). Для этого по известным уже измерениям
наименьшей
дисперсии процесса (1). Для этого по известным уже измерениям 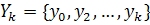 необходимо
определить условное математическое ожидание
необходимо
определить условное математическое ожидание  , которое и
принимается за оптимальную оценку вектора
, которое и
принимается за оптимальную оценку вектора 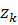 . Оптимальность её
следует из предыдущей главы. Предполагается, что матрицы
. Оптимальность её
следует из предыдущей главы. Предполагается, что матрицы 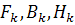 в
соотношениях (1) и (2) и ковариационные матрицы
в
соотношениях (1) и (2) и ковариационные матрицы  известны.
известны.
Кроме условного математического ожидания 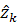 требуется
определить ковариационную матрицу
требуется
определить ковариационную матрицу 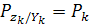 условного
нормального распределения
условного
нормального распределения 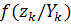 .
.
При решении поставленной задачи предположим, что
к моменту времени 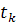 оценка
оценка 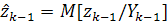 , и ковариационная
матрица
, и ковариационная
матрица  уже
вычислены на предыдущем шаге и нам известны. Из этого предположения с учетом
(1) и (2) следует, что априорные для момента
уже
вычислены на предыдущем шаге и нам известны. Из этого предположения с учетом
(1) и (2) следует, что априорные для момента 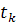 (т.е.
не учитывающие результат
(т.е.
не учитывающие результат  последних
измерений) значения математических ожиданий и ковариационных матриц для
случайных векторов
последних
измерений) значения математических ожиданий и ковариационных матриц для
случайных векторов 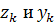 будут равны:
будут равны:
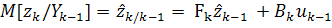 ;
;
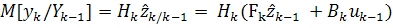 ;
;
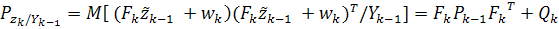 ;
;
Для краткости обозначим 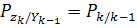 .
.
 M[
M[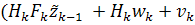 )
)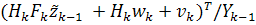 ]
=
]
=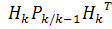 +
+
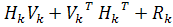 ;
;
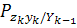 =M
=M
 ]=
]=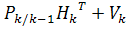 .
.
Из вышеизложенных формул для условных
математических ожиданий и ковариационных матриц на основании выражения (8)
получаем формулу для оценки 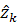 :
:
 +
+ 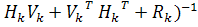 [
[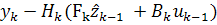 ]=
]=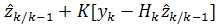 ,
,
где K
задается соотношением:
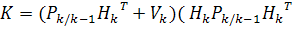 +
+ 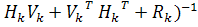 .
.
Формулу для вычисления матрицы  получим
использую выражение
получим
использую выражение
 +
+ 
В дальнейшее будем использовать свойство
ковариационных матриц  .
.  +
+
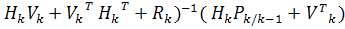 =
=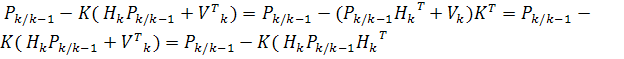 +
+
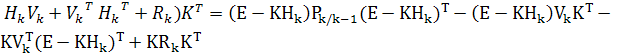 .
.
Формулы (3)-(7) получены.
2.4 Нелинейный фильтр
(дискретный случай)
Рекуррентный оптимальный алгоритм (3)-(7)
является оптимальным для линейных систем (1)-(2).
Однако в случае малого отклонения вектора 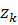 от
его оценки
от
его оценки 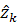 он может быть
применен и для нелинейных систем вида
он может быть
применен и для нелинейных систем вида
a)  ,
,
 ;
;
b)  .
.
где 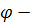 n-мерная
нелинейная функция от n
аргументов, являющихся элементами вектора
n-мерная
нелинейная функция от n
аргументов, являющихся элементами вектора 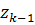 ;
;
 m-мерная
нелинейная функция от n
аргументов, являющихся элементами вектора
m-мерная
нелинейная функция от n
аргументов, являющихся элементами вектора 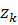 ;
;
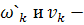 «белые»
шумы.
«белые»
шумы.
Линеаризуем функции 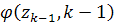 и
и
 около
точки
около
точки 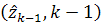 , а функцию
, а функцию 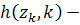 около
точки
около
точки 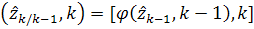 . В таком случае
получим с точностью до малых второго порядка
. В таком случае
получим с точностью до малых второго порядка
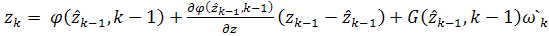 ;
;
 ,
,
где 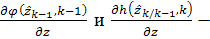 матрицы
частных производных (матрицы Якоби), вычисленные в точках
матрицы
частных производных (матрицы Якоби), вычисленные в точках 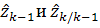 соотвественно.
соотвественно.
Вышеуказанные уравнения являются линейными. Они
могут рассматриваться как уравнения вида (1)-(2), если установить соответствие
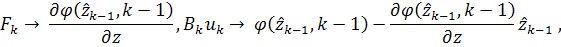
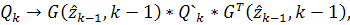
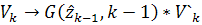 ,
,
 +
+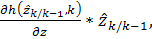

Пользуясь этими отношениями соответствия, из
алгоритма Калмана (3)-(7) получаем алгоритм для оценивания 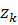
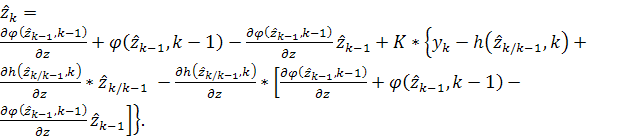
В последнем выражении линейные члены, включающие
в себя матрицы 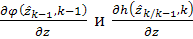 , взаимно сокращаются.
, взаимно сокращаются.
В конечном виде имеем
 (10)
(10)
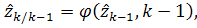
Остальные формулы идентичны формулам (3)-(7),
подставляя в качестве матриц соотношения (9). Алгоритм (10) представляет собой
рекуррентный алгоритм оценивания по Калману для нелинейных дискретных систем.
Такой алгоритм уже не будет строго оптимальным, однако во многих случаях это
алгоритм дает высокую точность оценивания.
2.5 Оценивание по максимуму апостериорной
вероятности (дискретный случай)
Рассмотрим нелинейную дискретную модель вида:
a)  ,
,
 ,
,
b) 
 конечный момент
времени в проведении измерений.
конечный момент
времени в проведении измерений.
По результатам измерений 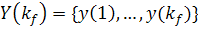 для
множества значений фазовых координат
для
множества значений фазовых координат  требуется
определить оценки
требуется
определить оценки 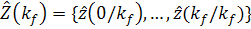 , доставляющие максимум для
апостериорной плотности распределения вероятностей
, доставляющие максимум для
апостериорной плотности распределения вероятностей 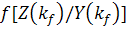 . При этом получение
значений
. При этом получение
значений 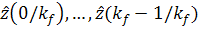 будет
представлять собой процесс сглаживания, а получение оценки
будет
представлять собой процесс сглаживания, а получение оценки 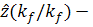 процесс
фильтрации.
процесс
фильтрации.
По формуле Байеса имеем
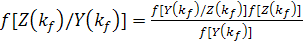 .
.
Из (11, б) следует, что при известном  функция
функция
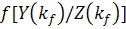 представляет
собой нормальную плотность, так как
представляет
собой нормальную плотность, так как  случайный
нормальный процесс. В таком случае
случайный
нормальный процесс. В таком случае
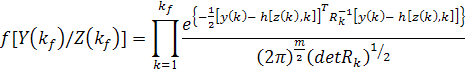
По правилу умножения вероятностей 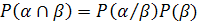 получим,
что
получим,
что

Так как 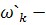 последовательность
независимых нормальных случайных векторов, то
последовательность
независимых нормальных случайных векторов, то  марковский
процесс, и предыдущее соотношение преобразуется к виду:
марковский
процесс, и предыдущее соотношение преобразуется к виду:
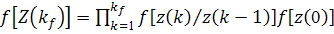
где 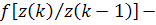 нормальная
условная плотность вероятностей с параметрами: средним
нормальная
условная плотность вероятностей с параметрами: средним  и
ковариационной матрицей
и
ковариационной матрицей 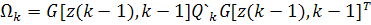 .
.
Поскольку 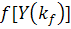 явно
от
явно
от 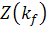 не
зависит, то при максимизации условной плотности (12) ее можно рассматривать как
нормированный множитель.
не
зависит, то при максимизации условной плотности (12) ее можно рассматривать как
нормированный множитель.
В таком виде условная плотность (12) может быть
записана в виде


где 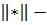 представление
квадратичной формы.
представление
квадратичной формы.
Нахождение величин 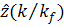 , обеспечивающих
максимум плотности вероятности (13) и представляет процесс нелинейного сглаживания
и фильтрации по критерию максимума апостериорной плотности вероятности.
Плотность (13) с точностью до постоянного множителя A
можно трактовать как плотность распределения вероятностей для всего выборочного
пространства, которое задается совокупной плотностью распределения случайных
величин
, обеспечивающих
максимум плотности вероятности (13) и представляет процесс нелинейного сглаживания
и фильтрации по критерию максимума апостериорной плотности вероятности.
Плотность (13) с точностью до постоянного множителя A
можно трактовать как плотность распределения вероятностей для всего выборочного
пространства, которое задается совокупной плотностью распределения случайных
величин  ,…,
,…, . В статистике такую
плотность принято называть функцией правдоподобия. В таком случае оценки
. В статистике такую
плотность принято называть функцией правдоподобия. В таком случае оценки 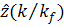 , полученные по
критерию МАВ, можно также трактовать, как оценки максимального правдоподобия.
, полученные по
критерию МАВ, можно также трактовать, как оценки максимального правдоподобия.
Вычисление максимума функции (13) по переменным 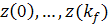 эквивалентно
вычислению минимума функции
эквивалентно
вычислению минимума функции
 .
.
По переменным  при
наложении на указанные переменные уравнений связей
при
наложении на указанные переменные уравнений связей
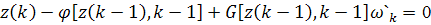 .
.
Задача условной минимизации (14)-(15) может быть
решена методом неопределенных множителей  Лагранжа.
Лагранжа.
При этом методе минимизируемая функция
записывается в виде
 .
.
Если от функции J
вычислить частные производные по  и
приравнять их нулю, то получим следующую систему (16) для оценок и множителей
Лагранжа:
и
приравнять их нулю, то получим следующую систему (16) для оценок и множителей
Лагранжа:
a) 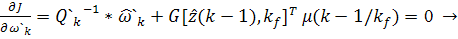
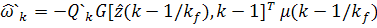 ;
;
b) 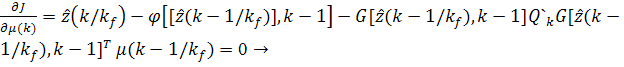
 ;
;
c)  ;
;
Обозначим 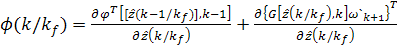 .
.
d) 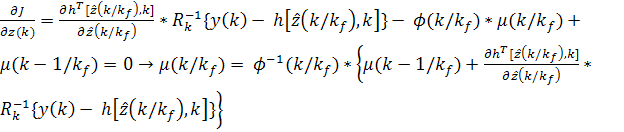 ,
,
для  .
.
e) 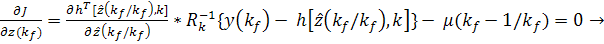
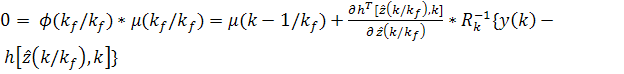 .
.
 нулю, введен
формально это позволяет соотношения (16, d
и e) переписать в
едином виде
нулю, введен
формально это позволяет соотношения (16, d
и e) переписать в
едином виде
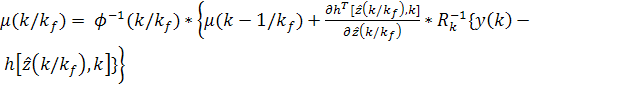 ,
,
для 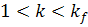 .
.
В интересах дальнейшего изложения удобно сделать
следующую замену переменных
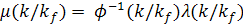
В этом случае уравнения (16, a,d
и e)
a)  (17)
(17)
b) 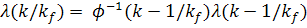 +
+ 0.
0.
Решая тем или иным способ систему нелинейных
алгебраических и уравнений (17), мы получим искомые оценки 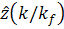 ,
, 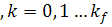 и
вместе с ними множители Лагранжа
и
вместе с ними множители Лагранжа 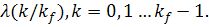 Данная
система имеет порядок
Данная
система имеет порядок 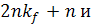 представляет собой
в практическом случае сложную вычислительную задачу. Заметим, что проведение
следующего измерения, когда
представляет собой
в практическом случае сложную вычислительную задачу. Заметим, что проведение
следующего измерения, когда  увеличивается на 1,
заставляет заново решать систему уравнений (17), увеличившуюся на 2n.
увеличивается на 1,
заставляет заново решать систему уравнений (17), увеличившуюся на 2n.
Во многих случаях интерес представляет только
задача фильтрации, когда оцениваются величины  По
этой причине возникает задача рекуррентного перехода от оценки
По
этой причине возникает задача рекуррентного перехода от оценки 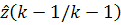 на
предыдущем шаге к оценке
на
предыдущем шаге к оценке 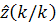 в текущий момент
времени.
в текущий момент
времени.
Указанная задача может быть решена методом
инвариантного погружения. Сущность метода инвариантного погружения здесь
состоит в следующем. Пусть задача (17) для шага 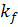 , и мы получили
решения
, и мы получили
решения  и
и
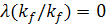 . Одновременно мы
получили и решения
. Одновременно мы
получили и решения 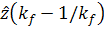 и
и 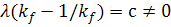 . Предположим, что мы решили бы
задачу, считая шаг
. Предположим, что мы решили бы
задачу, считая шаг 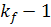 последним, но
величину
последним, но
величину  взяли
равной не нулю, а величине с. Тогда для моментов времени
взяли
равной не нулю, а величине с. Тогда для моментов времени  мы
получили бы оценки, совпадающими с оценками
мы
получили бы оценки, совпадающими с оценками 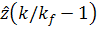 .
.
Дадим определение расширенное решение 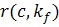 для
системы (17). Так мы будем называть решение
для
системы (17). Так мы будем называть решение  при
условии, что
при
условии, что 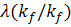 принята равной
принята равной 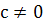 , причем с здесь и
далее рассматривается уже как произвольная величина. В обозначении
, причем с здесь и
далее рассматривается уже как произвольная величина. В обозначении  зависимость
решения от величины c и номера
шага
зависимость
решения от величины c и номера
шага 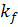 . Естественно, что
. Естественно, что 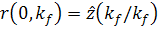 .
.
Из уравнения (17, а) следует, что расширенное
решение от шага 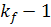 к шагу
к шагу 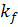 удовлетворяет
соотношению:
удовлетворяет
соотношению:

Из уравнения (17,б) вытекает, что величины 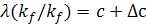 и
и
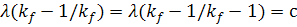 удовлетворяет
соотношению
удовлетворяет
соотношению
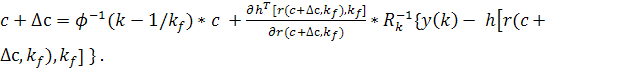
В дальнейших выкладках мы 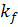 заменим
на
заменим
на 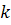 , считая его
последним шагом.
, считая его
последним шагом.
Предыдущие соотношения можно записать в
обобщенном виде
a) 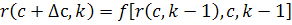 ;
;
b)  .
.
c)
Рассмотрим теперь представление
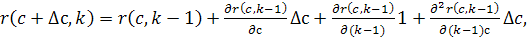
где  ,
,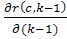 и
и  матрицы
размерности n*n.
матрицы
размерности n*n.
Из (18,б) следует, что

В таком случае из (18)-(19) вытекает уравнение
дискретного инвариантного погружения
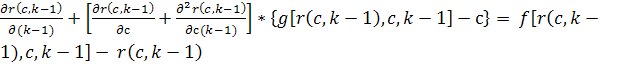
Решение этого уравнения будем искать в следующем
приближении:
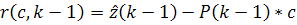 ,
,
где  , а
, а 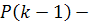 неизвестная
пока симметричная матрица размером n*n.
неизвестная
пока симметричная матрица размером n*n.
Учитывая, что
 ,
,

из (21) и (22) получим:
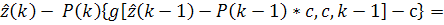
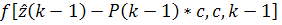 (23)
(23)
Соотношение (23) верно при любых достаточно
малых c. Будем считать, что его левую и
правую часть можно разложить в степенные ряды по переменной c. Если приравнять
друг к другу свободные члены, а также коэффициенты при первых степенях c, то получим
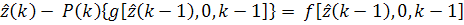

Если в (18) принять с=0, то с учетом (22)
получим
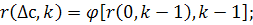

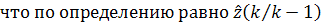
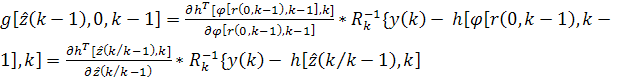
В таком случае уравнение (24) примет вид

Можно заметить уравнение для оценок (26) по
форме совпало с уравнением (10), полученным ранее из условия минимума для
дисперсии оценивания.
Рассмотрим теперь уравнения (25) для матрицы 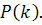 Для
этого нужно вычислить входящие в него производные. На основании (25) ,(18) и
(22)
Для
этого нужно вычислить входящие в него производные. На основании (25) ,(18) и
(22)
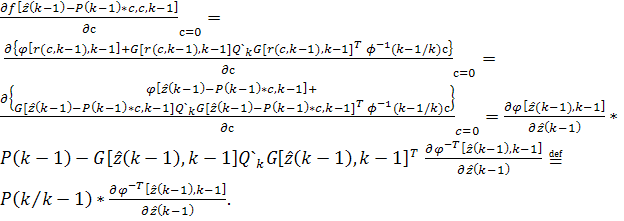
где 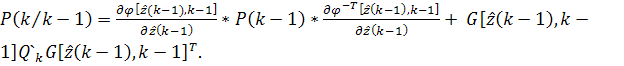
Перейдем к вычислению 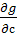 , входящей в (25) . На основании (18)
и (22) получаем
, входящей в (25) . На основании (18)
и (22) получаем
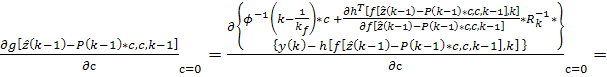

Из (25) следует
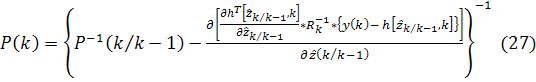
Вычисление  по
формуле (27) требует обращения трех матриц, вычислительные трудности могут
бытьрешены при помощи следующего приема
по
формуле (27) требует обращения трех матриц, вычислительные трудности могут
бытьрешены при помощи следующего приема
Определим матрицу  с
помощью соотношения
с
помощью соотношения
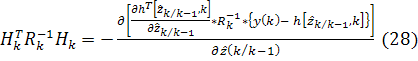
Тогда, опираясь на лемму об обращении
(приложение 1)

Отсюда и (27) получаем формулу для рекуррентного
вычисления матрицы 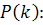
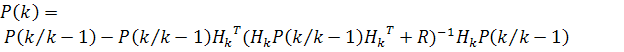
Для нелинейной стохастической дискретной системы
вида (11) получаем окончательно следующую сводку формул для алгоритма
нелинейного фильтрации, оптимального по критерию максимума апостериорной
плотности вероятности
a) 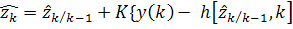 ,
,
где 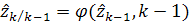 .
.
где 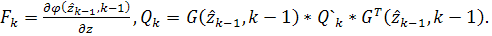
c) 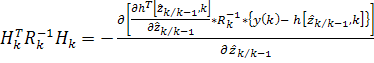 ;
;
d) 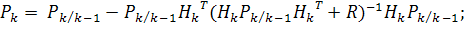
e) 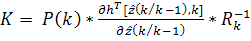 .
.
3. Применение Фильтра
3.1 Пример фильтра,
оценивающего погрешность расстояния
Задача: Пусть из точки О излучается радиосигнал
с длиной волны 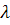 и начальной фазой
и начальной фазой 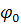 . Напомним, что
уравнение синусоиды «бегущей» вдоль оси
. Напомним, что
уравнение синусоиды «бегущей» вдоль оси  со
скоростью
со
скоростью  имеет вид
имеет вид 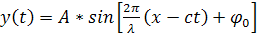 . Тогда в подвижной
точке М, удаленной от точки О на расстояние
. Тогда в подвижной
точке М, удаленной от точки О на расстояние  этот
сигнал будет иметь вид
этот
сигнал будет иметь вид
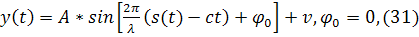
где 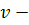 белый
шум интенсивности
белый
шум интенсивности 
Предположим, что на точке М имеются точные часы,
радиоприемник, воспринимающий сигнал 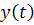 . А также
навигационное устройство (типа счисления пути), с помощью которого можно определять
расстояние
. А также
навигационное устройство (типа счисления пути), с помощью которого можно определять
расстояние 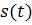 . Предположим, что указанное
расстояние
. Предположим, что указанное
расстояние 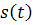 определяется (в
течении времени наблюдений) с постоянной погрешностью
определяется (в
течении времени наблюдений) с постоянной погрешностью 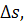 так
что
так
что 
По дискретным наблюдениям 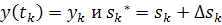 требуется
оптимальным образом оценить расстояние
требуется
оптимальным образом оценить расстояние  .
.
Поставленная задача может быть сформулирована на
языке нелинейной фильтрации, если ввести обозначение 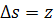 . В таком случае
уравнение состояния и уравнение наблюдения приобретают вид
. В таком случае
уравнение состояния и уравнение наблюдения приобретают вид
a) 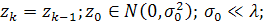
b) 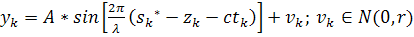
Решим задачу оценивания 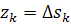 двумя
методами: с помощью алгоритма (10) по критерию минимума апостериорной дисперсии
(МАД) и с помощью алгоритма (30) по критерию максимума апостериорной
вероятности (МАВ).
двумя
методами: с помощью алгоритма (10) по критерию минимума апостериорной дисперсии
(МАД) и с помощью алгоритма (30) по критерию максимума апостериорной
вероятности (МАВ).
Определим значения параметров: 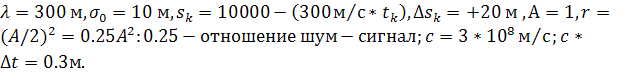
Для первого алгоритма имеем соотношения,
вытекающие из (10) и (31):
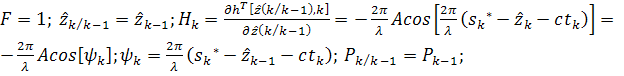
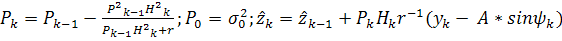 .
.
Для второго алгоритма (оптимального по критерию
МАВ) имеем соотношения
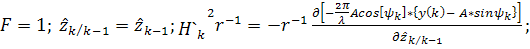

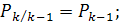
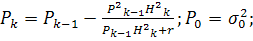
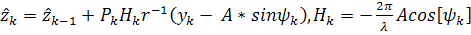 .
.
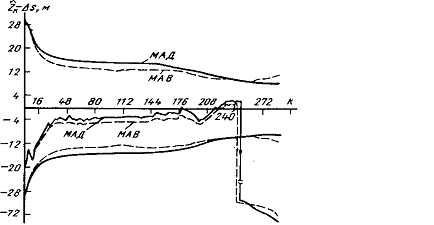
Рис. 1
На рисунке 1 сплошными линиями приведены две
симметричные кривые для величин 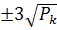 и кривая для
погрешности
и кривая для
погрешности 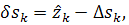 вычисленных по
методу МАД. Пунктирными линиями проведены те же кривые только для метода МАВ.
вычисленных по
методу МАД. Пунктирными линиями проведены те же кривые только для метода МАВ.
Далее приведены графики (рис. 2-4), полученные пакетом
matlab, данных, найденных собственной
программой. На них приведена только 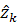 , причем
, причем  не
постоянна, она принимает случайное значение от -10 до +10. Остальные параметры
(длина волны, интенсивность шума и т.д.) остались такими же, как и в примере.
Красные кривые - для оценок, полученных по методу МАД, зеленые - по методу МАВ.
На втором графике имитирован отказ системы на шагах 250-300 (
не
постоянна, она принимает случайное значение от -10 до +10. Остальные параметры
(длина волны, интенсивность шума и т.д.) остались такими же, как и в примере.
Красные кривые - для оценок, полученных по методу МАД, зеленые - по методу МАВ.
На втором графике имитирован отказ системы на шагах 250-300 (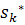 увеличили на 70 м).
увеличили на 70 м).
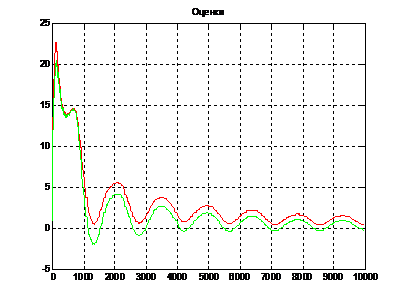
Рис. 2. Оценка без отказа
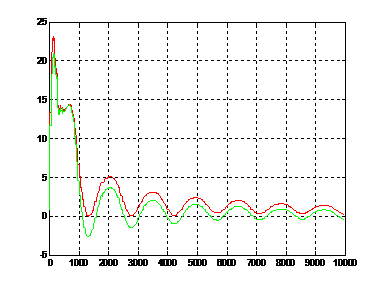
Рис. 3. Оценка со сбоем
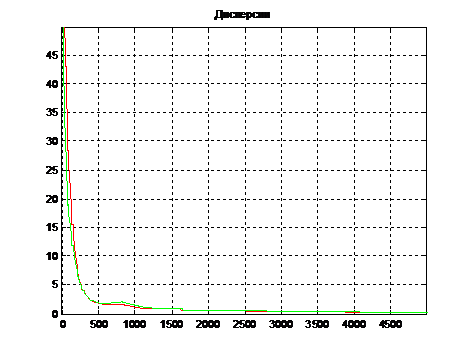
Рис. 4. Дисперсия
На последнем графике показаны значения дисперсии
также для обоих методов (красный - МАД, зеленый - МАВ).
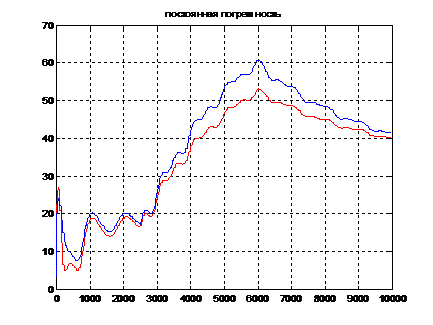
Рис. 5.
На Рис. 5. показаны оценки для обоих методов при
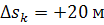 и
отказе системы при k=3000-6000.
Заметно, что при k<3000, оценка стремилась к 20, при k>6000
оценки стали убывать и стремится к 20.
и
отказе системы при k=3000-6000.
Заметно, что при k<3000, оценка стремилась к 20, при k>6000
оценки стали убывать и стремится к 20.
По результатам опытов стоит отметить, что
дисперсия переменной состояния всегда стремится к нулю при количестве
наблюдений стремящихся к бесконечности. Оценка стремится к среднему значению
случайной ошибки, которую в программе можно изменять. Если задать константу, то
оценка соответственно с увеличением количества шага стремится к этой константе.
3.2 Описание программы
Программа состоит из следующих основных частей:
· Model.cpp
содержит функцию void model(double *s_izm, double *y_izm, double *ds, int n,
double v, double var, ofstream &ofst), которая задает стахостическую модель
процесса, указанного в примере в гл. 4.1.. s_izm, y_izm и ds - возвращаемые
массивы расстояния, значения сигнала и погрешности расстояния соответственно. n
- количество измерений, v - дисперсия для сигнала, var - дисперсия для
расстояния.
· Filter.cpp содержит следующие
функции
void FilterMAD(matrix z, double *s, matrix P,
matrix Q, matrix y, matrix R, matrix V, int k, int n, int m, ofstream
&ofst),FilterMAD(double *z, double *s, double *P, double *y, double r,
double k),
void FilterMAV(double *z, double *s,
double *P, double *y, double r, double k)
Первая функция полностью
соответствует алгоритму нелинейной фильтрации по методу МАД. z и y - это вектора,
описанные здесь в виде матриц n*1 и m*1 соответственно для упрощения
элементарных преобразований над матрицами и векторами. z - начальное значение
оцениваемого параметра, s - дальность до объекта, P - начальная ковариационная
матрица, Q,R,V - ковариоционные матрицы шумов, y - измерения, k - количество
измерений, n - размерность вектора z, m - размерность вектора y.
Последние две функции описаны,
исходя из примера гл.4.1. по обоим методам. Значение параметров такое же, как и
в вышеуказанной функции.
· matrix.h и
matrix.cpp - класс, описывающий матрицу и операции над ней. Здесь определены
такие операторы как +, = , *,-, и действия над матрицами: транспонирование,
отыскание обратной матрицы, отыскание определителя.
· main.cpp содержит
инициализацию переменных, работу с файлами, вызов вышеуказанных функций.
Заключение
В рамках данной работы описаны два критерия
оценивания вектора состояния динамической системы.
На основе этих критериев разобраны три случая:
фильтрация линейной системы по критерию МАД, и фильтрация нелинейной системы по
обоим критериям. Заметим, что каждый из фильтров оптимален лишь в рамках своего
метода оценивания. В случае линейной фильтрации оба метода дают одни и те же
рекуррентные соотношения. Нелинейные фильтры по критерию МАД является менее
эффективным, так как приходится линеаризовывать нелинейные функции, а это
существенно влияет на точность.
Данные методы реализованы и протестированы на
одномерном примере. По полученным результатам можно сказать, что оцениваемый
параметр сглаживается к среднему значению, а дисперсия убывает от шага к шагу.
фильтр калман спутниковый сигнал
Список литературы
1. О.А.
Бабич / Обработка информации в навигационных комплексах. - М.: Машиностроение,
1991. - 512 с. - ISBN
5-217-0160-6.
2. Д.Ю.
Першин, А.С. Щербаков / Определение местоположения высокой точности для
одночастотных приемников спутниковой навигации с использлванием инерциальных
датчиков.
. Сайт
#"668724.files/image342.gif"> удовлетворяют
уравнению

Причем 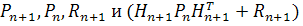 также
существуют.
также
существуют.
Тогда матрица  может
быть найдена по формуле
может
быть найдена по формуле
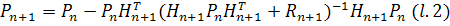
Докажем эту лемму путем выполнения таких
преобразований, которые позволяют из 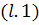 получить
получить
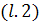 .
.
Умножая 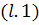 на
на
 , получим
, получим
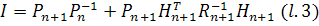
Повторное умножение  на
на
 слева
приводит к равенству
слева
приводит к равенству
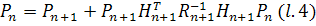
Вновь умножая 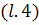 на
на
 , получим
, получим
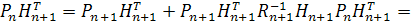
Умножая 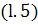 на
на
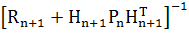 дает
в результате
дает
в результате
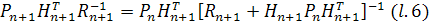
Наконец, умножая это равенство на  , приходим к
следующему равенству
, приходим к
следующему равенству
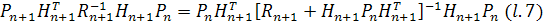
Вычитая 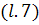 из
из
 , получим
, получим

На основании 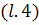 теперь
можно записать
теперь
можно записать
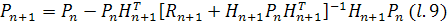
Полученное равенство совпадает с 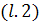 , что и требовалось
доказать.
, что и требовалось
доказать.