Взвешивание, обработка и представление результатов

Взвешивание, обработка и представление результатов

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е. Алексеева

Кафедра «Физика и технология материалов и компонентов электронной техники».

Лабораторная работа №1

«Взвешивание, обработка и представление результатов»

Выполнил: студент группы 10-МТЭ

Печенкин Н.А.

Проверил: Мочалов Г.М.

Н. Новгород

г.

Задание

Изучить принцип взвешивания. Проверить сходимость собственных результатов, а также воспроизводимость результатов измерений, полученных при взвешивании на аналитических и технохимических весах, и воспроизводимость между операторами.

В ходе данной лабораторной работы мы осваиваем методику измерений и обработки результатов. Вычисляем систематические и случайные погрешности, проверяем сходимость собственных результатов, воспроизводимость результатов измерений, полученных при взвешивании на аналитических и технохимических весах, и воспроизводимость между операторами.

1.     
Обзор литературных данных

.1      Определение взвешивания, типы весов, способы взвешивания

Взвешиванием называют определение массы тел с помощью весов. Различают дискретное взвешивание, когда массу каждого тела измеряют отдельно с использованием какого-либо типа весов, и непрерывное взвешивание, когда определяют суммарную массу материала при транспортировке его, например, ленточным транспортером.

Гири характеризуются номинальной массой (обычно от 1 мг до 20 кг) и допускаемыми погрешностями, т. е. допускаемыми отклонениями действительного значения массы от номинального. Гири подразделяют на эталонные, образцовые (для поверочных операций), рабочие и специальные (например, встроенные в весы). Рабочие гири выпускают пяти классов точности: 1-й - для микрохимических и химических анализов и других взвешиваний высшей точности; 2-й - для аналогичных работ высокой точности; 3-й - для технических анализов повышенной точности и взвешивании драгоценных металлов и камней; 4-й - для обычных технических анализов; 5-й - для взвешивания при производственных, хозяйственных и торговых операциях.

Весы и накладные гири для них должны иметь одинаковый класс точности; встроенные гири должны быть подогнаны по массе так, чтобы их суммарная погрешность в любой комбинации не превышала погрешность, допускаемую для весов соответствующего класса точности. Гири изготавливают в виде отдельных мер (поштучно) или наборов (разновесов) различной массы - миллиграммовых, граммовых, килограммовых. Наборы содержат гири, образующие обычно ряд, кратный 1,2,2 и 5 (напр., 1; 2; 2; 5; 10; 20; 20 и 50), реже - ряд, кратный 1,1,1,2 и 5. Наборы гирь 1-го и 2-го классов точности при поверке снабжают свидетельствами с указанием погрешности каждой гири. Гири разных классов точности изготавливают из различных материалов (например, из нержавеющей немагнитной или углеродистой стали, алюминия). Для устранения погрешностей при взвешивании гири подгоняют по массе в организациях, осуществляющих их ремонт и поверку.

Точность взвешивания характеризуется абсолютной и относительной погрешностями и определяется показателями весов, условиями их применения, методами взвешивания и полнотой учета влияния различных источников погрешностей. Наименьшая относительная погрешность (1,2)*10^-9 достигнута при сличении платиновоиридиевых килограммовых эталонов массы.

При взвешивании на весах общего назначения, технологических, а также общелабораторных весах обычной точности применяют только метод простого взвешивания. Согласно ему, массу объекта взвешивания принимают равной массе уравновешивающих его гирь, показаниям по отсчетному устройству весов или алгебраической сумме масс уравновешивающих гирь и показаний по отсчетному устройству. Погрешности гирь, инструментальные погрешности весов, а также влияние окружающей среды и др. не учитываются.

При работе на гирных весах аналитической группы, широко используемых для химических анализов высокой точности (например, при полумикроанализе с погрешностью не более 0,01-0,02 мг), метод простого взвешивания не приводит к удовлетворительным результатам. Поэтому для исключения систематических погрешностей применяют более трудоемкие и требующие больших затрат времени методы точного взвешивания. При этом относительная погрешность уменьшается приблизительно в 2 раза, а при использовании лучших моделей электронных весов погрешности взвешивания не превышают погрешностей, достигнутых при метрологических исследованиях.

Метод двойного взвешивания (метод Гаусса) состоит в повторном прямом взвешивании после перестановки объекта и гирь с одной чашки весов на другую. Масса объекта принимают М = 1/2 (М₁ + М₂), где М₁ и М₂ -результаты двух прямых взвешиваний.

Методы замещения - взвешивание на одном плече (метод Борда) и компенсационный, или нулевой (метод Менделеева). По методу Борда объект взвешивания после уравновешивания его тарным грузом (например, гирями более низкого класса точности) снимают с весов и на чашку помещают столько гирь соответствующего класса, чтобы привести весы в исходное положение равновесия. Массу объекта взвешивания определяют как алгебраическую сумму масс гирь и показаний по шкале весов.

Самый распространенный метод точного взвешивания - метод Менделеева: на одну чашку весов помещают гири в количестве, отвечающем наибольшему пределу взвешивания, а на другую - тарный груз, уравновешивающий гири. Объект взвешивания помещают на чашку с гирями, снимая при этом столько гирь, чтобы весы пришли в исходное положение. Массу объекта находят как сумму масс снятых гирь и показаний по шкале весов. Этот метод реализован в двухпризменных весах.

Выбор метода точного взвешивания определяется конструкцией весов и условиями взвешивания. При особо точных взвешиваниях (например, объектов массой 1-10³ мкг при ультрамикроанализе) используют не только методы точного измерения массы, но и принимают во внимание погрешности гирь и шкал весов, а также воздействие внешних условий (аэростатических и др. сил, атмосферного давления и т. п.). Погрешности, вносимые накладными гирями 1-го и 2-го классов точности, исключаются при точном взвешивании внесением поправок, указанных в свидетельствах на наборы гирь. Погрешность взвешивания из-за влияния аэростатических сил возникает при неравенстве объемов объекта взвешивания и гирь. Согласно закону Архимеда, эту погрешность можно найти по формуле: D= d_в(1/d_г - 1/d_т), где d_в, d_г и d_т - плотность соответственно воздуха, гирь (принятая при поверке) и объекта взвешивания. Для исключения этой погрешности вводят поправки (что особенно необходимо, если d_т и d_г значительно различаются), которые обычно находят из специальных таблиц или графиков.

При взвешивании на микроаналитеских весах с рейтерными шкалами рейтер должен всегда находиться в рабочем положении. Погрешности шкал возникают из-за погрешностей самого рейтера, неправильного нанесения или плохой обработки зарубок шкалы и вследствие неправильной посадки рейтера на коромысло. Для исключения погрешности отсчетной шкалы весов, т. е. разности между номинальным и действительным значениями цены деления, шкалу следует периодически контролировать без нагрузки, при нагрузках, равных наибольшему пределу взвешивания и 0,1 его значения, используя тщательно поверенные гири. Малые изменения цены деления могут быть устранены регулятором положения центра тяжести коромысла; при больших изменениях требуется юстировка весов.

Погрешности, обусловленные электростатическими силами, могут значительно исказить результаты взвешивания, особенно при употреблении сосудов из стекла с высоким содержанием примесей и при низкой относительной влажности воздуха. Это влияние исключается ионизацией воздуха в витринах весов с помощью специальных источников излучений (при всех лабораторных работах, кроме микро- и ультрамикроанализов).

Традиционные гирные весы аналитической группы (прежде всего микро-и ультрамикровесы), а также общелабораторные весы повышенной точности весьма чувствительны к колебаниям и градиентам температуры, воздушным потокам, вибрациям и т. п. Поэтому гири и объекты взвешивания должны иметь температуру, возможно более близкую к температуре в витрине весов, для чего выдерживаются в ней перед измерениями. В витринах весов не рекомендуется размещать поглотители влаги. Помещения для точного взвешивания на всех весах указанных типов должны освещаться люминесцентными лампами или специальными светильниками с теплоотводом, а также термостатироваться и оборудоваться кондиционерами (обычно температура 20 °С при суточных колебаниях ее не более ± 2°С), электронные весы могут эксплуатироваться при более значительных перепадах температур.

.2 Результаты измерений обрабатываются следующим образом

. определение среднего арифметического

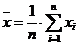
. расчет дисперсии

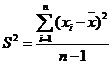
. вычисление среднеквадратичного отклонения (СКО)

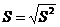
взвешивание измерение погрешность

4. исключение промахов

Для этого в результатах измерения выбирают наибольшее и наименьшее значения (x_exr). Потом исследуют на промахи по 4-м методам

.1 по уровню значимости β

Вычисляют критерий промаха V_крит

_крит =

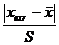
Задаём уровень значимости β, который зависит от количества измерений.

Таблица 1 - значения β для Р=0,95

Если V_крит ≥ β, то значение является промахом.

.2 по 3S-критерию

Если 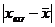>3S, то значение является промахом.

.3 по Q-критерию, где смысл критерия - размах варьирования измеренных величин

Определение размаха осуществляется следующим образом:

=

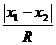
где Q - критерий, R = x_max-x_min - размах варьирования, x₁ - максимальное или минимальное значение, х₂ - наиболее близкое к максимальному или минимальному значению.сравнивается с табличным, если Q>Q_табл, то промах доказан.

Таблица 2 - значения Q для P=0.95

.4 статистический метод

Данный метод обнаружения промахов основан на предположении, что погрешности распределены нормально. Промахом считается то, значение погрешности, которое выше некоторого критического значения. Критические значения погрешности указаны в таблицах. _T - критическое значение - квантиль максимального распределения.

t_max =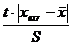

- квантиль-распределитель Стьюдента.

Если t_max> t_T, то результат является промахом.

Таблица 3 - значения t_T и t для P=0.95

. представление результатов измерений

После исключения промаха заново рассчитывают среднеарифметическое значение и СКО.

Затем производят оценку доверительного интервала ε

ε = t·S,

где S - СКО, t - квантиль распределения Стьюдента.

В этом случае определяется случайная погрешность ε. Однако существует и систематическая погрешность θ.

Если θ/S ≤ 0,8, то превалирует ε и действительное число выглядит как 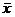±ε.

Если θ/S ≥ 8, то превалирует θ и действительное число выглядит как 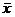±θ.

Если 0,8 ≤ θ/S ≤ 8, то реализуется суммарная погрешность ∆_∑ и действительное число выглядит как ±∆_∑.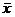

∆_∑ =

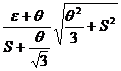
. оценивается воспроизводимость результатов измерений

Результаты считаются воспроизводимыми, если выполняются следующие соотношения:

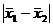<|ε₁|+|ε₂|

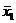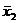где ± ε₁ - действительные значения, полученные в одних условиях, ± ε₂ - действительные значения, полученные в других условиях.

2.     
Экспериментальная часть

Перед началом измерений были проведены следующие подготовительные работы.

На технохимических весах сначала провели юстировку с помощью юстировочных грузиков, двигая их таким образом, чтобы уменьшить отклонение стрелки весов до допустимого значения, которое не должно превышать половину цены деления шкалы. Следующим шагом мы выполнили градуировку шкалы. Для этого мы взяли грузик массой 500 мг, разместили его на одной из чашек весов. Стрелка весов отклонилась, но осталась в пределах шкалы. Далее мы разделили массу грузика на число делений, которое показала стрелка весов. Полученный результат (25 мг) и есть цены деления данных весов. Зная цену деления, мы можем рассчитать неисключенную систематическую погрешность. Разделив 25 мг пополам и округлив результат, получаем θ = 10 мг.

На аналитических весах мы произвели корректировку ноля с помощью горизонтального балансировочного грузика и исключение мультипликативной погрешности с помощью вертикального балансировочного грузика. Цена деления шкалы аналитических весов равна 0.2 мг, следовательно, неисключенная систематическая погрешность составляет 0.1 мг.

Измерения проводились следующим образом. Оператор брал образец, размещал его на левой чашке весов. На правой чашке технохимических весов оператор размещал разновес массой 9 грамм. Затем приводил весы в рабочее состояние, опуская призму с помощью рычажка. Число делений шкалы, полученное при отклонении стрелки от положения равновесия, умножалось на цену деления шкалы. Результат складывался с известной нам массой разновеса на правой чашке весов и записывался в протокол. Аналогичные действия оператор производил и с аналитическими весами,

Результаты измерений представлены в таблицах 4 и 5.

Таблица 4. Результаты измерения образца на технохимических весах

Т.к. результаты отличаются на величину, не превышающую систематическую погрешность, то они не требуют метрологической обработки

Таблица 5. Результаты измерения образца на аналитических весах

.       
Обработка результатов измерений

Взвешивание на технохимических весах

Результаты всех трех измерений совпали, значит отсутствуют случайные погрешности.

Х=9,075г

Систематическая погрешность

θ= 12,5мг

Представление полученного результата

Вычисление относительной погрешности

Е=100Δ/хср

Е=100*10/9080=0,11%

Взвешивание на аналитических весах

Результаты всех трех измерений совпали, значит отсутствуют случайные погрешности.

Х=9,0854г

Систематическая погрешность

θ= 0,1мг

Представление результата

,4±0,1мг

Вычисление относительной погрешности

Е=100Δ/хср

Е=100*0,1/9085,4=0,001%

Проверка на воспроизводимость

Собственная воспроизводимость

Если условие |X1-X2|<| ΔX1|+ |ΔX2| выполняется, значит, результаты воспроизводимы |9080-9085.4|<|10|+|0.1| 5,4<10,1 условие выполняется, следовательно, результаты воспроизводимы

Проверка на воспроизводимость между коллегами

Если условие |X1-X2|<| ΔX1|+ |ΔX2| выполняется, значит, результаты воспроизводимы

Технохимические весы

Мой результат: 9080±10мг

Результат коллеги: 9080±10мг

|9080-9080|<|10|+|10|

<20

условие выполняется, следовательно, результаты воспроизводимы

Аналитические весы

Мой результат: 9085,4±0,1мг

Результат коллеги: 9085,4±0,1мг

|90085,4-9085,4|<|0,1|+|0,1|

<0,2

условие выполняется, следовательно, результаты воспроизводимы

Выводы

В работе исследованы результаты измерений образца, проведенных на аналитических весах. С помощью аналитических весов получена масса образца 9085,4±0,1мг с относительной погрешностью Е=0,001% и с помощью технохимических весов - 9080±10мг с относительной погрешностью Е=0,11%. Исходя из полученных результатов, можно сделать вывод, что аналитические весы являются более точными, чем технохимические.