Анализ статистических данных
Курсовая
работа
по
дисциплине «Статистика»
на тему
Анализ статистических данных
Автор
работы
Е.А.
Созыкина
Введение
статистический
экономический информация риск
Статистические методы являются важной частью
процесса управления. Они позволяют вырабатывать обоснованные стратегические
решения, сочетающие интуицию специалиста с тщательным анализом имеющейся
информации. Использование статистики становится важным преимуществом в
конкурентной борьбе.
Целью данной курсовой работы является изучение категорий
и понятий статистической науки, овладение современным статистическим
инструментарием анализа экономической информации, путем проведения
статистического исследования экономического показателя и анализа полученных
результатов.
В качестве исследуемого экономического
показателя в работе взята урожайность зерновых культур. Такой выбор обусловлен
доступностью статистической информации, а также простотой и значимостью
исследования.
Урожайность - один из основных экономических
показателей сельскохозяйственного производства. Исследование урожайности с
позиций статистической науки позволяет осуществлять прогнозы, оценивать риск и
многое другое. Поэтому анализ урожайности имеет важное практическое значение.
Источником информации для выполнения
исследования служат ежегодные статистические сборники, выпускаемые Челябинским
областным комитетом государственной статистики.
Для достижения цели курсовой работы
предполагается решить ряд задач:
1) определить и проанализировать основные
статистические показатели урожайности,
2) изучить закон распределения и
корреляционной связи, а также количественную оценку риска неурожайности,
) кроме того, работа предполагает
построение, сглаживание и анализ структуры временного ряда, а также выделение
тренда и прогнозирование.
Методы исследования базируются на знании общей
теории статистики и теории вероятностей.
1. Построение
ряда распределения
Проведем статистическое исследование урожайности
зерновых культур в Увельском административном районе. В расчётах будем
использовать данные по фактическому сбору урожая в среднем с 1 га посевной (или
убранной) площади за последние годы, начиная с 1990 года.
Данные по урожайности для Увельского района
занесены в табл. 1.1.
Таблица 1.1 Исходные статистические данные по
урожайности для Увельского района Челябинской области
|
Годы
|
1990
|
1991
|
1992
|
1993
|
1994
|
1995
|
1996
|
1997
|
1998
|
1999
|
2000
|
2001
|
|
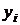 y1 y1
|
y2
|
y3
|
y4
|
y5
|
y6
|
y7
|
y8
|
y9
|
y10
|
y11
|
y12
|
|
|
Урожайн,
ц /га
|
18,5
|
2,4
|
17,2
|
14,6
|
11,4
|
5,6
|
5,8
|
12,1
|
5,5
|
13,2
|
5,7
|
16,3
|
|
Годы
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
|
|
|
|
|
|
|
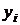 y13y14y15y16y17y18 y13y14y15y16y17y18
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Урожайн,
ц/га
|
14,6
|
11,6
|
6,3
|
15,6
|
15,2
|
11,8
|
|
|
|
|
|
|
Воспользовавшись данными табл. 1.1,
составим ранжированный ряд распределения 
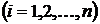 путём
расположения исходных данных в порядке возрастания от
путём
расположения исходных данных в порядке возрастания от 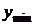 до
до 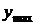
 , (1.1)
, (1.1)
где 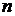 - объём выборки, n=18.
- объём выборки, n=18.
Результаты представить в виде табл.
1.2.
Таблица 1.2 Ранжированный вариационный ряд
|
хi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x9
|
x10
|
|
Урожайность,
ц/га
|
2,4
|
5,5
|
5,6
|
5,7
|
5,8
|
6,3
|
11,4
|
11,6
|
11,8
|
12,1
|
|
хi
|
x11
|
x12
|
x13
|
x14
|
x15
|
x16
|
x17
|
x18
|
|
|
|
Урожайность,
ц/га
|
13,2
|
14,6
|
14,6
|
15,2
|
15,6
|
16,3
|
17,2
|
18,5
|
|
|
Таким образом, мы отсортировали показатели
урожайности в порядке возрастания, составив ранжированный ряд распределения.
2. Расчёт выборочных
параметров ряда распределения
Произведем оценку среднего значения  , дисперсии
, дисперсии  и
среднеквадратического отклонения
и
среднеквадратического отклонения 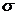 генеральной совокупности с помощью
выборочных параметров
генеральной совокупности с помощью
выборочных параметров  ,
, 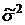 и
и 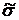 соответственно
по формулам:
соответственно
по формулам:
 ; (2.1)
; (2.1)

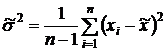 ; (2.2)
; (2.2)
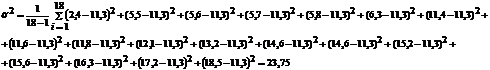
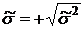 . (2.3)
. (2.3)
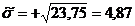
Найдем коэффициент вариации:
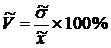 . (2.4)
. (2.4)

Результаты расчёта представлены в
таблице 2.1
Таблица 2.1 Выборочные параметры
ряда распределения
Определим доверительный интервал для генеральной
средней
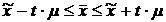 , (3.5)
, (3.5)
где 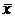 - среднее значение в генеральной
совокупности;
- среднее значение в генеральной
совокупности;
 - средняя ошибка в определении
среднего значения величины
- средняя ошибка в определении
среднего значения величины 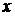 для малой выборки
для малой выборки 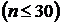 , в нашем
случае n=18
, в нашем
случае n=18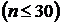 .
.
 =
=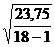 =1,4
=1,4
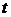 - коэффициент доверия. При
вероятности, равной
- коэффициент доверия. При
вероятности, равной 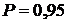 , величина
коэффициента
, величина
коэффициента 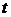 имеет
значение 1,96.
имеет
значение 1,96.
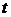 =1,96
=1,96


Таким образом, мы определили диапазон, в котором
с наибольшей вероятностью будет находиться средняя величина генеральной
совокупности.
3. Построение диаграммы
накопленных частоти гистограммы выборки
Построение диаграммы накопленных частот
Диаграмма накопленных частот  является
эмпирическим аналогом интегрального закона распределения (функции
распределения). Построим ее в соответствии с формулой
является
эмпирическим аналогом интегрального закона распределения (функции
распределения). Построим ее в соответствии с формулой
 , (3.1)
, (3.1)
где 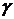 - число элементов в выборке, для
которых значение
- число элементов в выборке, для
которых значение  ;
; 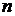 - объём
выборки.
- объём
выборки.
Данные для построения диаграммы
приведены в табл. 3.1, диаграмма представляет собой кумуляту (см. Приложение 1)
Таблица 3.1 Данные для построения диаграммы
накопленных частот
|

|
|
|
0/18
|
0
|

|
|
1/18
|
0,06
|
|
|
2/18
|
0,11
|

|
|
3/18
|
0,17
|
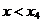
|
|
4/18
|
0,22
|

|
|
5/18
|
0,28
|
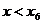
|
|
6/18
|
0,33
|

|
|
7/18
|
0,39
|

|
|
8/18
|
0,44
|

|
|
9/19
|
0,50
|
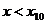
|
|
10/18
|
0,56
|

|
|
11/18
|
0,61
|
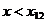
|
|
12/18
|
0,67
|
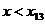
|
|
13/18
|
0,72
|
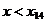
|
|
14/18
|
0,78
|

|
|
15/18
|
0,83
|

|
|
16/18
|
0,89
|
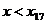
|
|
17/18
|
0,94
|
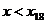
|
|
18/18
|
1
|
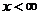
|
Построение гистограммы выборки
Гистограмма 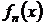 выборки
является эмпирическим аналогом функции плотности распределения
выборки
является эмпирическим аналогом функции плотности распределения  . Для
построения гистограммы
. Для
построения гистограммы
. Определим число интервалов  по формуле
Стерджесса
по формуле
Стерджесса
 , (4.2)
, (4.2)
 =5
=5
2. Определим длину интервала
 . (4.3)
. (4.3)

. Примем за центр интервала середину
области изменения изучаемого признака (центр распределения)


. Подсчитаем количество элементов
(частоту) ряда распределения  , попавшее в каждый интервал.
, попавшее в каждый интервал.
. Подсчитаем относительное
количество элементов (частость)  совокупности, попавших в данный
интервал.
совокупности, попавших в данный
интервал.
. Построим гистограмму,
представляющую собой ступенчатую кривую, значение которой на 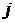 -м интервале
-м интервале
 постоянно и
равно
постоянно и
равно
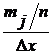 (
( )
)
Результаты расчетов представлены в
таблице 3.2
Таблица 3.2 Данные для построения гистограммы
выборки
По изображению гистограммы выборки (Приложение
2) можно сказать, что изучаемый нами признак имеет нормальный закон
распределения. Проверим данное положение теоретически.
4. Проверка основной гипотезы
распределения
Для проверки гипотезы о нормальном
законе изучаемого распределения, учитывая небольшой ( ) объём
выборки (n=18),
используем следующий критерий. Если выборочные асимметрия
) объём
выборки (n=18),
используем следующий критерий. Если выборочные асимметрия 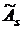 и эксцесс
и эксцесс 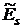 удовлетворяют
неравенствам
удовлетворяют
неравенствам
 ; (4.1)
; (4.1)
и
 , (4.2)
, (4.2)
то изучаемое распределение можно считать
нормальным.
В противном случае гипотезу о нормальном законе
распределения следует отвергнуть или, по крайней мере, считать сомнительной.
Выборочные асимметрию и эксцесс рассчитаем по
формулам
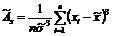 ; (4.3)
; (4.3)
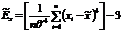 , (4.4)
, (4.4)
где  - элементы выборки;
- элементы выборки;  - выборочное
среднее;
- выборочное
среднее; 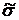 -
среднеквадратическое отклонение выборки;
-
среднеквадратическое отклонение выборки; 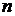 - объём выборки.
- объём выборки.
Дисперсию асимметрии 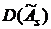 и дисперсию
эксцесса вычислим по формулам
и дисперсию
эксцесса вычислим по формулам
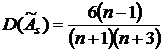 ; (4.5)
; (4.5)
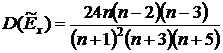 . (4.6)
. (4.6)
Итак,
. Вычислим значения выборочных
асимметрии 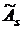 и эксцесса
и эксцесса 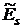
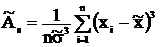

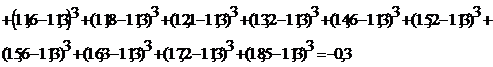
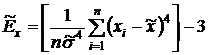
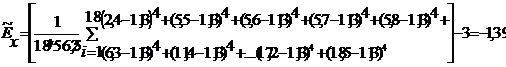
. Найдем дисперсию асимметрии 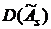 и дисперсию
эксцесса
и дисперсию
эксцесса 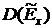 .
.
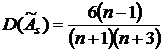

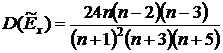

. Сведем результаты расчётов в табл.
4.1.
Таблица 4.1 Данные для проверки основной
гипотезы
|
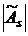  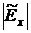 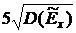 Выполнение
критерия Выполнение
критерия
|
|
|
|
|
|
0,3
|
1,5
|
1,39
|
3,84
|
Да
|
Результатом проверки гипотезы является ее
принятие.
. ПОСТРОЕНИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Эмпирическая функция распределения  носит
ступенчатый характер (см. Приложение 1). Подберем плавную (теоретическую)
кривую распределения
носит
ступенчатый характер (см. Приложение 1). Подберем плавную (теоретическую)
кривую распределения  , наилучшим
образом описывающую эмпирические данные распределения
, наилучшим
образом описывающую эмпирические данные распределения  , то есть
осуществим выравнивание функции
, то есть
осуществим выравнивание функции  . Для этого воспользуемся методом
наименьших квадратов (МНК), согласно которому сумма квадратов отклонений
эмпирических данных от теоретических обращается в минимум:
. Для этого воспользуемся методом
наименьших квадратов (МНК), согласно которому сумма квадратов отклонений
эмпирических данных от теоретических обращается в минимум:
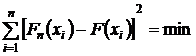 . (5.1)
. (5.1)
В случае нормального закона теоретическая
функция распределения имеет вид
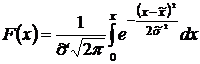 , (5.2)
, (5.2)
где  и
и 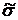 - уточнённые в результате
выравнивания выборочные среднее и среднеквадратическое отклонение.
- уточнённые в результате
выравнивания выборочные среднее и среднеквадратическое отклонение.
Выравнивание эмпирической функции распределения
проведено с помощью компьютерной программы «Stat
1» .
Полученные в результате расчёта на
ПЭВМ уточнённые параметры  ,
, 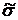 , а также
значения аргумента
, а также
значения аргумента 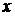 и
соответствующие им расчётные значения функции
и
соответствующие им расчётные значения функции  занесены в табл. 5.1.
занесены в табл. 5.1.
Рассчитанное с помощью программы
среднее значение 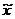 принадлежит
доверительному интервалу, рассчитанному в п. 2:
принадлежит
доверительному интервалу, рассчитанному в п. 2:  .
.
На диаграмму накопленных частот,
отраженную в Приложении 1, нанесем точки, соответствующие расчетным значениям 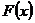 , соединим
их плавной линией. Полученное эмпирическим путем изображение функции
распределения схоже с графиком выровненной функции.
, соединим
их плавной линией. Полученное эмпирическим путем изображение функции
распределения схоже с графиком выровненной функции.
Таблица 5.1 Данные для выравнивания эмпирической
функции распределения
|
Уточнённые
значения параметров распределения
|
|
|
 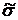   0123456789 0123456789
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,07
|
3,69
|
13,62
|
 0 0
|
0,001
|
0,003
|
0,006
|
0,014
|
0,027
|
0,050
|
0,084
|
0,135
|
0,202
|
|
|
|
|
 10 10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
|
|
|
|
|
 0,287 0,287
|
0,386
|
0,492
|
0,599
|
0,699
|
0,786
|
0,856
|
0,909
|
0,945
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Построение и анализ
корреляционной функцииряда распределения
Величина урожайности 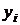 для каждого
года
для каждого
года  является
случайной величиной. Значения
является
случайной величиной. Значения 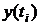 , рассматриваемые в течение
нескольких лет, образуют последовательность случайных величин (случайную
функцию, или случайный процесс)
, рассматриваемые в течение
нескольких лет, образуют последовательность случайных величин (случайную
функцию, или случайный процесс) 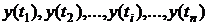 . Между любыми двумя случайными
величинами из этой последовательности может существовать связь. Для
характеристики такой связи служит корреляционная функция
. Между любыми двумя случайными
величинами из этой последовательности может существовать связь. Для
характеристики такой связи служит корреляционная функция 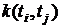 . Она
является функцией промежутка
. Она
является функцией промежутка 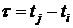 между ними, т.е.
между ними, т.е.
 .
.
Среднее значение корреляционной
функции 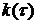 для каждого
для каждого
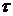 может быть
получено с помощью формулы
может быть
получено с помощью формулы
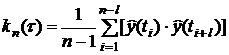 , (6.1)
, (6.1)
где 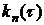 - оценка (среднее значение)
корреляционной функции
- оценка (среднее значение)
корреляционной функции 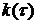 ;
;
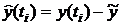 и
и  - центрированные случайные величины
соответственно для периодов времени
- центрированные случайные величины
соответственно для периодов времени  и
и 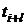 ,
, 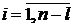 ;
;
 - длина рассматриваемого интервала
времени;
- длина рассматриваемого интервала
времени;
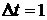 год - величина шага;
год - величина шага;
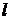 - число шагов (
- число шагов (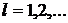 );
);
 - выборочное среднее случайной
величины
- выборочное среднее случайной
величины 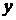 ;
;
 - объём выборки.
- объём выборки.
Этой формулой рекомендуется
пользоваться при 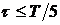 (где
(где  - интервал
наблюдения случайной величины
- интервал
наблюдения случайной величины 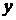 ), тогда рассчитаем
), тогда рассчитаем 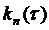 для
для  =3,6.
=3,6.
Своё максимальное значение
корреляционная функция (6.1) принимает при 
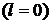
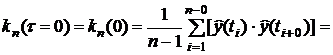
 , (6.2)
, (6.2)
где  - дисперсия случайной величины
- дисперсия случайной величины 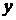 .
.

При 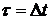


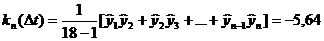
При 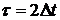
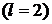

При 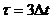
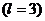
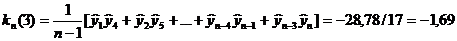
Разделив 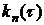 на своё
максимальное значение
на своё
максимальное значение 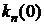 , получим
нормированную корреляционную функцию (коэффициент корреляции)
, получим
нормированную корреляционную функцию (коэффициент корреляции) 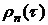
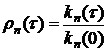 . (6.3)
. (6.3)
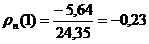 ,
,
 ,
,

Результаты вычислений занесем в табл. 6.1.
Таблица 6.1 Расчёт эмпирической корреляционной
функции
Проведем выравнивание
экспериментальных данных нормированной эмпирической корреляционной функции 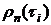 с помощью
компьютерной программы «Stat 2». Данные, полученные с
помощью программы, представлены в табл. 6.2.
с помощью
компьютерной программы «Stat 2». Данные, полученные с
помощью программы, представлены в табл. 6.2.
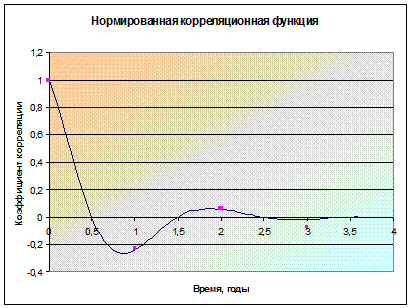
В Приложении 3 изображены
рассчитанные с помощью вычислительной программы значения функции 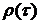 и отмечены
точки эмпирической корреляционной функции
и отмечены
точки эмпирической корреляционной функции 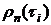 . По графику можно наблюдать
циклический, затухающий характер теоретической нормированной корреляционной
функции. Мы рассматривали функцию в пределах трех лет, если продлить график
функции, можно увидеть, что она будет приближаться к оси абсцисс. Точки
корреляционной функции, полученные эмпирическим путем соответствуют
теоретическим данным кривой.
. По графику можно наблюдать
циклический, затухающий характер теоретической нормированной корреляционной
функции. Мы рассматривали функцию в пределах трех лет, если продлить график
функции, можно увидеть, что она будет приближаться к оси абсцисс. Точки
корреляционной функции, полученные эмпирическим путем соответствуют
теоретическим данным кривой.
Таблица 6.2 Расчёт теоретической нормированной
корреляционной функции
|
б
|
в
|
ф
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
0,7
|
0,8
|
0,9
|
1,0
|
1,1
|
|
|
1,424
|
3,142
|
с(ф)
|
1,000
|
0,825
|
0,608
|
0,383
|
0,175
|
0,000
|
-0,132
|
-0,217
|
-0,259
|
-0,264
|
-0,241
|
-0,199
|
|
|
ф
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2,0
|
2,1
|
2,2
|
2,3
|
|
|
с(ф)
|
-0,146
|
-0,092
|
-0,042
|
0,000
|
0,032
|
0,052
|
0,062
|
0,064
|
0,058
|
0,048
|
0,035
|
0,022
|
|
|
ф
|
2,4
|
2,5
|
2,6
|
2,7
|
2,8
|
2,9
|
3,0
|
3,1
|
3,2
|
3,3
|
3,4
|
3,5
|
3,6
|
|
с(ф)
|
0,010
|
0,000
|
-0,008
|
-0,013
|
-0,015
|
-0,015
|
-0,014
|
-0,012
|
-0,008
|
-0,005
|
-0,002
|
0,000
|
0,002
|
7. Линейная диаграмма
исходного временного ряда
Урожайность, наблюдаемую в течение определённого
периода времени, можно рассматривать как числовые значения статистического
показателя в последовательные моменты времени, т.е. в виде временного ряда или
ряда динамики.
Построим исходный временной ряд 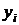
 в виде
линейной диаграммы (Приложение 4).
в виде
линейной диаграммы (Приложение 4).
. Статические
показатели временного ряда
Вычислим основные показатели временного ряда.
1. Абсолютный прирост (цепной и базисный)
определяется как разность между двумя уровнями динамического ряда
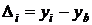 , (8.1)
, (8.1)
где индекс  заменим
заменим
для цепного абсолютного прироста b = i - 1;
для базисного абсолютного прироста b
= 1.
2. Темп роста (цепной и базисный) рассчитаем по
формуле
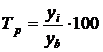 (%). (8.2)
(%). (8.2)
. Темп прироста (цепной и базисный)
найдем из выражения
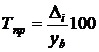 (%) . (8.3)
(%) . (8.3)
. Абсолютное значение одного
процента прироста (цепного или базисного) равно
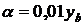 . (8.4)
. (8.4)
Результаты расчёта приведены в табл.
8.1.
Таблица 8.1 Аналитические характеристики
временного ряда урожайности зерновых
|
Годы
|
Урожайность,
ц /га
|
Абсолютный
прирост 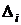 ,ц /гаТемп роста ,ц /гаТемп роста  ,
(%)Темп прироста ,
(%)Темп прироста  , (%)Абсолютное
Значение 1 % прироста , (%)Абсолютное
Значение 1 % прироста 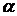 , (ц /га) , (ц /га)
|
|
|
|
|
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
|
1990
|
18,5
|
18,50
|
0,00
|
-
|
100,00
|
-
|
0,00
|
0,000
|
0,185
|
|
1991
|
2,4
|
-16,10
|
-16,10
|
12,97
|
12,97
|
-87,03
|
-87,03
|
0,185
|
0,185
|
|
1992
|
17,2
|
14,80
|
-1,30
|
716,67
|
92,97
|
616,67
|
-7,03
|
0,024
|
0,185
|
|
1993
|
14,6
|
-2,60
|
-3,90
|
84,88
|
78,92
|
-15,12
|
-21,08
|
0,172
|
0,185
|
|
1994
|
11,4
|
-3,20
|
-7,10
|
78,08
|
61,62
|
-21,92
|
-38,38
|
0,146
|
0,185
|
|
1995
|
5,6
|
-5,80
|
-12,90
|
49,12
|
30,27
|
-50,88
|
-69,73
|
0,114
|
0,185
|
|
1996
|
5,8
|
0,20
|
-12,70
|
103,57
|
31,35
|
3,57
|
-68,65
|
0,056
|
0,185
|
|
1997
|
12,1
|
6,30
|
-6,40
|
208,62
|
65,41
|
108,62
|
-34,59
|
0,058
|
0,185
|
|
1998
|
5,5
|
-6,60
|
-13,00
|
45,45
|
29,73
|
-54,55
|
-70,27
|
0,121
|
0,185
|
|
1999
|
13,2
|
7,70
|
-5,30
|
240,00
|
71,35
|
140,00
|
-28,65
|
0,055
|
0,185
|
|
2000
|
5,7
|
-7,50
|
-12,80
|
43,18
|
30,81
|
-56,82
|
-69,19
|
0,132
|
0,185
|
|
2001
|
16,3
|
10,60
|
-2,20
|
285,96
|
88,11
|
185,96
|
-11,89
|
0,057
|
0,185
|
|
2002
|
14,6
|
-1,70
|
-3,90
|
89,57
|
78,92
|
-10,43
|
-21,08
|
0,163
|
0,185
|
|
2003
|
11,6
|
-3,00
|
-6,90
|
79,45
|
62,70
|
-20,55
|
-37,30
|
0,146
|
0,185
|
|
2004
|
6,3
|
-5,30
|
-12,20
|
54,31
|
34,05
|
-45,69
|
-65,95
|
0,116
|
0,185
|
|
2005
|
15,6
|
9,30
|
-2,90
|
247,62
|
84,32
|
147,62
|
-15,68
|
0,063
|
0,185
|
|
2006
|
15,2
|
-0,40
|
-3,30
|
97,44
|
82,16
|
-2,56
|
-17,84
|
0,156
|
0,185
|
|
2007
|
11,8
|
-3,40
|
-6,70
|
77,63
|
63,78
|
-22,37
|
-36,22
|
0,152
|
0,185
|
Определим другие показатели ряда динамики.
5. Средний уровень ряда  , дисперсия
, дисперсия 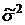 ,
среднеквадратическое отклонение
,
среднеквадратическое отклонение 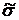 и коэффициент вариации
и коэффициент вариации  .
.

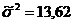

 %
%
6. Средний (цепной и базисный) прирост
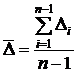 . (8.5)
. (8.5)
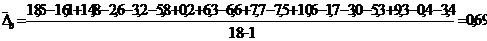

. Средний темп роста, рассчитываемый
по формуле средней геометрической.
Цепной средний темп роста
 (%) . (8.6)
(%) . (8.6)
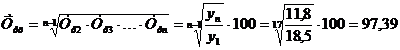 (%)
(%)
Базисный средний темп роста
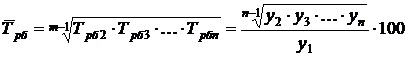 (%). (8.7)
(%). (8.7)
 (%)
(%)
8. Средний темп прироста (цепной и
базисный)
 . (8.8)
. (8.8)
 %,
%,
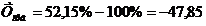 %.
%.
. Границы варьирования 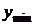 и
и 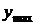 , которые
определяют пределы колебания уровней анализируемого ряда динамики.
, которые
определяют пределы колебания уровней анализируемого ряда динамики.
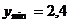 ,
, 
10. Размах вариации
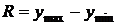 . (8.9)
. (8.9)
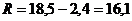
11. Коэффициент выровненности
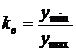 . (8.10)
. (8.10)

12. Среднее абсолютное отклонение, которое
показывает, на сколько ежегодно в среднем изменялась урожайность
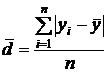 . (8.11)
. (8.11)

. Мода  . Определим
графически моду по гистограмме выборки. (см.Приложение 2).
. Определим
графически моду по гистограмме выборки. (см.Приложение 2). 
. Медиана 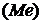 . При чётном
числе членов ряда распределения (n=18) номер медианы определяется как
. При чётном
числе членов ряда распределения (n=18) номер медианы определяется как 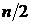 :
:

Значения рассчитанных показателей
занесены в табл. 8.2.
Таблица 8.2 Статистические
показатели временного ряда
|
 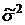 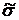    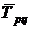  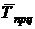 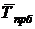  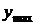 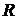 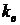 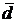 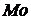 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,07
|
13,62
|
3,69
|
43,1
|
0,69
|
-7,62
|
97,39
|
52,15
|
-2,61
|
-47,85
|
2,4;
18,5
|
16,1
|
0,13
|
3,96
|
14,6
|
Из таблиц 8.1 и 8.2 можно сделать вывод об
изменениях показателей временного ряда для урожайности. Урожайность колеблется
в больших пределах (от 2,4 ц/га до 18,5 ц/га), имея размах вариации R=16.1,
при этом средняя величина составляет 12,07 ц/га, а наиболее часто встречающиеся
показатели - 14,6 ц/га. Цепной средний темп роста - высокий показатель, он
близок к 100%, а средний темп прироста по отношению к базисному году -
отрицательный.
9.
Проверка гипотезы о стационарности временного ряда
Для ответа на вопрос о
стационарности ряда для урожайности разобьем ряд по времени на две части: до
1999г. и после 1999г. Для стационарного ряда средние уровни по этим частям не
должны существенно отличаться: 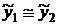 .
.
 ,
,
 .
.
Выполним статистическую проверку по
F-критерию Фишера гипотезы о равенстве дисперсий в сравниваемых частях ряда
(нулевую гипотезу):
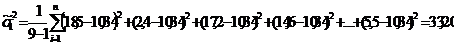
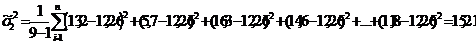
 ,
,
так как 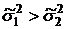 ,
следовательно, условие
,
следовательно, условие  соблюдается.
соблюдается.
Чтобы отвергнуть нулевую гипотезу,
нужно доказать существенность расхождения между дисперсиями 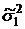 и
и 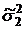 при
выбранном уровне значимости
при
выбранном уровне значимости 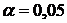 .
.
Сравним фактическое значение  с табличным
с табличным
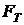 , взятого из
таблицы F-распределения Фишера при числе степеней свободы
, взятого из
таблицы F-распределения Фишера при числе степеней свободы
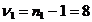
 ,
,
где  и
и  - число уровней в каждой части
временного ряда.
- число уровней в каждой части
временного ряда.
В данном случае, 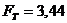 , т.е.
, т.е. 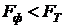 ,
следовательно, гипотеза о равенстве дисперсий подтверждается.
,
следовательно, гипотеза о равенстве дисперсий подтверждается.
В этом случае проверку равенства
средних уровней  и
и  осуществляем
по t-критерию Стьюдента
осуществляем
по t-критерию Стьюдента
 , (9.2)
, (9.2)
где 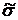 - оценка среднеквадратического
отклонения генеральной дисперсии временного ряда, которую определяем по формуле
- оценка среднеквадратического
отклонения генеральной дисперсии временного ряда, которую определяем по формуле
 , (9.3)
, (9.3)
так как имеет место равенство обеих частей
временных рядов.

В соответствии с формулой (9.2),

Далее сравним полученное фактическое
значение t-критерия Стьюдента 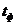 , с табличным
, с табличным  при уровне
значимости
при уровне
значимости 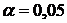 и числе
степеней свободы
и числе
степеней свободы  .
.
 =2,12, следовательно,
=2,12, следовательно, 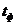 <
< , а это
значит, что различия между средними уровнями
, а это
значит, что различия между средними уровнями  и
и  признаются несущественными.
признаются несущественными.
Результаты расчётов приведены в
табл. 9.1.
Таблица 9.1 Данные для проверки
гипотезы о постоянстве среднего уровня временного ряда
|
       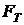   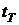 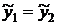
|
|
|
|
|
|
|
|
|
|
|
|
|
9
|
9
|
10,34
|
12,26
|
33,20
|
15,21
|
2,18
|
3,44
|
6,39
|
0,64
|
2,12
|
Да
|
По таблице 9.1 можно сделать вывод о том, что
гипотеза о равенстве дисперсий в сравниваемых частях ряда (нулевая гипотеза)
подтверждена, что показывает несущественность различий между средними уровнями
урожайности в двух частях ряда, их можно считать примерно равными. Равенство
средних уровней указывает на отсутствие у временного ряда тенденции к развитию
- такой ряд можно считать стационарным.
О стационарности временного ряда
также говорит вид корреляционной функции 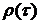 , т.к. с ростом
, т.к. с ростом 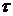 она
стремится к нулю. Графически она представляет собой синусоиду с затухающими
колебаниями: при
она
стремится к нулю. Графически она представляет собой синусоиду с затухающими
колебаниями: при 
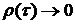 . Поэтому исследуемый временной ряд
является стационарным и функция урожайности
. Поэтому исследуемый временной ряд
является стационарным и функция урожайности  эргодична.
эргодична.
. Сглаживание
временного рядаметодом скользящей средней
Проведем операцию сглаживания для
устранения случайных отклонений экспериментальных значений исходного временного
ряда 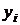 методом
скользящей средней. При сглаживании с помощью трёхчленной средней по значениям
первых трёх уровней
методом
скользящей средней. При сглаживании с помощью трёхчленной средней по значениям
первых трёх уровней  и
и 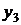 рассчитываем
среднюю (сглаженную) величину для уровня
рассчитываем
среднюю (сглаженную) величину для уровня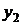 по формуле
по формуле
 . (10.1)
. (10.1)

Затем по следующей тройке уровней 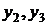 и
и 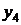 найдем
среднюю величину для уровня
найдем
среднюю величину для уровня 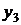
 (10.2)
(10.2)

Крайние точки ряда 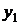 и
и  сглаживают
по специальным формулам. Для уровня
сглаживают
по специальным формулам. Для уровня 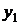 сглаженное значение равно
сглаженное значение равно
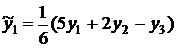 . (10.3)
. (10.3)
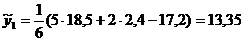
Для уровня  сглаженное
значение находится по формуле
сглаженное
значение находится по формуле
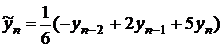 , (10.4)
, (10.4)
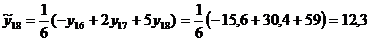
где 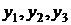 и
и 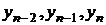 - уровни в начале и в конце
исходного ряда;
- уровни в начале и в конце
исходного ряда;
Результаты расчёта сглаженных значений
временного ряда занесены в таблицу 10.1.
Таблица 10.1 Результаты сглаживания временного
ряда методом скользящей средней
|
Годы
|
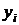 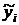
|
|
|
1990
|
18,5
|
13,35
|
|
1991
|
2,4
|
12,7
|
|
1992
|
17,2
|
11,4
|
|
1993
|
14,6
|
14,40
|
|
1994
|
11,4
|
10,53
|
|
1995
|
5,6
|
7,60
|
|
1996
|
5,8
|
7,83
|
|
1997
|
12,1
|
7,80
|
|
1998
|
5,5
|
10,27
|
|
1999
|
13,2
|
8,13
|
|
2000
|
5,7
|
11,73
|
|
2001
|
16,3
|
12,20
|
|
2002
|
14,6
|
14,17
|
|
2003
|
11,6
|
10,83
|
|
2004
|
6,3
|
11,17
|
|
2005
|
15,6
|
12,37
|
|
2006
|
15,2
|
14,20
|
|
2007
|
11,8
|
12,3
|
В Приложении 4 изображена графически
представленная сглаженная функция временного ряда, которая позволяет устранить
случайные отклонения экспериментальных значений исходного временного ряда 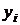 .
.
11. Аналитическое
выравнивание временного рядас помощью линейной функции
Для получения математической модели, выражающей
общую тенденцию (тренд) изменения уровней временного ряда, проведем его
аналитическое выравнивание. Суть выравнивания заключается в замене сглаженных
уровней ряда уровнями, вычисленными на основе определённой аппроксимирующей
функции.
Рассмотрим выравнивание сглаженного с помощью
трёхчленной скользящей средней временного ряда линейной функцией (линейным
трендом)
 , (11.1)
, (11.1)
где  - выровненные уровни временного
ряда;
- выровненные уровни временного
ряда;
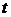 - порядковый номер периода времени
(фактор времени).
- порядковый номер периода времени
(фактор времени).
Параметры  и
и  тренда
(11.1) рассчитываем по методу наименьших квадратов. МНК позволяет определить
параметры модели (11.1), при которых минимизируется сумма квадратов отклонений
выровненных уровней
тренда
(11.1) рассчитываем по методу наименьших квадратов. МНК позволяет определить
параметры модели (11.1), при которых минимизируется сумма квадратов отклонений
выровненных уровней 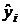 от уровней
сглаженного временного ряда
от уровней
сглаженного временного ряда 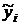
 . (11.2)
. (11.2)
Для упрощенного поиска параметров уравнения
(11.1) необходимо отсчёт времени производить так, чтобы сумма факторов времени
временного ряда удовлетворяла условию
 . (11.3)
. (11.3)
Так как число уровней временного
ряда чётное, то периоды времени, относящиеся к середине ряда, имеют номера 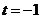 и
и  . Более
ранние значения фактора времени ряда нумеруются
. Более
ранние значения фактора времени ряда нумеруются 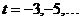 , а более поздние
, а более поздние  и т.д.
Таким образом, выполнится условие (11.3):
и т.д.
Таким образом, выполнится условие (11.3):
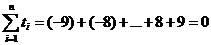
Тогда параметры уравнения (11.1)
найдем по следующим формулам:
 ; (11.4)
; (11.4)
 , (11.5)
, (11.5)
Далее найдем значения выровненных
уровней временного ряда 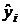 :
:
 -9
-9 ,
,
 -8=11,3+0,08*(-8)=10,66,
-8=11,3+0,08*(-8)=10,66,
 -7=11,3+0,08*(-7)=10,74,
-7=11,3+0,08*(-7)=10,74,
 -6=11,3+0,08*(-6)=10,82,
-6=11,3+0,08*(-6)=10,82,
 -5=11,3+0,08*(-5)=10,9,
-5=11,3+0,08*(-5)=10,9,
 -4=11,3+0,08*(-4)=10,98,
-4=11,3+0,08*(-4)=10,98,
 -3=11,3+0,08*(-3)=11,06,
-3=11,3+0,08*(-3)=11,06,
 -2=11,3+0,08*(-2)=11,14,
-2=11,3+0,08*(-2)=11,14,
 -1=11,3+0,08*(-1)=11,22,
-1=11,3+0,08*(-1)=11,22,
 1=11,3+0,08*1=11,38,
1=11,3+0,08*1=11,38,
 2=11,3+0,08*2=11,46,
2=11,3+0,08*2=11,46,
 3=11,3+0,08*3=11,54,
3=11,3+0,08*3=11,54,
 4=11,3+0,08*4=11,62,
4=11,3+0,08*4=11,62,
 5=11,3+0,08*5=11,7,
5=11,3+0,08*5=11,7,
 6=11,3+0,08*6=11,78,
6=11,3+0,08*6=11,78,
 7=11,3+0,08*7=11,86,
7=11,3+0,08*7=11,86,
 8=11,3+0,08*8=11,94,
8=11,3+0,08*8=11,94,
 9=11,3+0,08*9=12,02.
9=11,3+0,08*9=12,02.
Определив эти параметры, получаем (11.2):

Среднюю ошибку аппроксимации временного ряда
линейным трендом определим как величину среднеквадратического отклонения
выровненных уровней ряда от сглаженных
 , (11.6)
, (11.6)
где 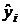 и
и 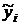 - соответственно выровненные и
сглаженные уровни временного ряда.
- соответственно выровненные и
сглаженные уровни временного ряда.
Результаты расчётов сведены в таблицу 11.1
Таблица 11.1 Результаты выравнивания временного
ряда с помощью линейной функции
|
Годы
|
  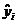 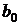 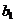  , ц/га , ц/га
|
|
|
|
|
|
|
1990
|
-9
|
13,35
|
10,58
|
11,3
|
0,08
|
2,21
|
|
1991
|
-8
|
12,70
|
10,66
|
|
|
|
|
1992
|
-7
|
11,40
|
10,74
|
|
|
|
|
1993
|
-6
|
14,40
|
10,82
|
|
|
|
|
1994
|
-5
|
10,53
|
10,9
|
|
|
|
|
1995
|
-4
|
7,60
|
10,98
|
|
|
|
|
1996
|
-3
|
7,83
|
11,06
|
|
|
|
|
1997
|
-2
|
7,80
|
11,14
|
|
|
|
|
1998
|
-1
|
10,27
|
11,22
|
|
|
|
|
1999
|
1
|
8,13
|
11,38
|
|
|
|
|
2000
|
2
|
11,73
|
11,46
|
|
|
|
|
2001
|
3
|
12,20
|
11,54
|
|
|
|
|
2002
|
4
|
14,17
|
11,62
|
|
|
|
|
2003
|
5
|
10,83
|
11,7
|
|
|
|
|
2004
|
6
|
11,17
|
11,78
|
|
|
|
|
2005
|
7
|
12,37
|
11,86
|
|
|
|
|
2006
|
8
|
14,20
|
11,94
|
|
|
|
|
2007
|
9
|
12,30
|
12,02
|
|
|
|
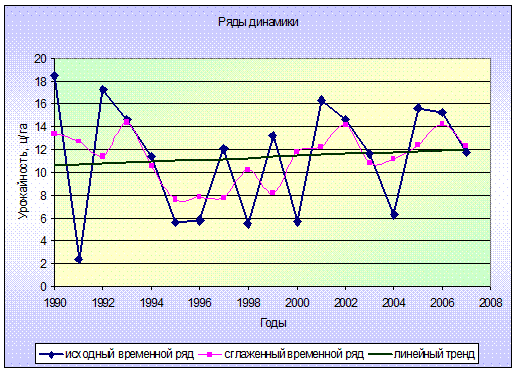
График выровненного временного ряда изображен в
Приложении 4. Исходя из графика, видно, что, благодаря сглаживанию временного
ряда, сокращаются большие разрывы между значениями. Графическое изображение
сглаженного временного ряда более наглядно представляет результаты
исследования. Выровненный временной ряд показывает общую тенденцию изменения
урожайности за рассматриваемый период, поэтому конкретные значения по ней
определить нельзя. По линии тренда можно судить об увеличении урожайности в
последние годы.
12.
Экспоненциальное сглаживание временного ряда
Сущность данного метода заключается в
сглаживании исходного временного ряда с помощью взвешенной скользящей средней,
в которой веса распределяются по экспоненциальному закону. Это позволяет
построить такое описание ряда, при котором более поздним наблюдениям придаются
бьльшие веса по сравнению с ранними.
В расчётах экспоненциальной средней зададим
начальные условия, которые находятся по следующим формулам:
Начальное значение экспоненциальной средней 1-го
порядка
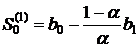 . (12.1)
. (12.1)
Начальное значение экспоненциальной средней 2-го
порядка
 , (12.2)
, (12.2)
где
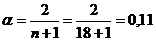 . (12.3)
. (12.3)
Таким образом,
 ,
,

Затем найдем текущие значения экспоненциальных
средних 1-го и 2-го порядка для чего используют реккурентные формулы (12.4) и
(12.5)
 ; (12.4)
; (12.4)
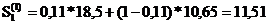 ,
,
 =0,11*2,4+0,89*11,51=10,51,
=0,11*2,4+0,89*11,51=10,51,
 =0,11*17,2+0,89*10,51=11,25,
=0,11*17,2+0,89*10,51=11,25,
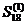 =0,11*11,8+0,89*11,55=11,58.
=0,11*11,8+0,89*11,55=11,58.
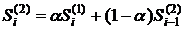 , (12.5)
, (12.5)
 =0,11*11,51+0,89*10,01=10,18,
=0,11*11,51+0,89*10,01=10,18,
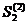 =0,11*10,51+0,89*10,18=10,21,
=0,11*10,51+0,89*10,18=10,21,
 =0,11*11,25+0,89*10,21=10,33,
=0,11*11,25+0,89*10,21=10,33,
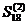 =0,11*11,58+0,89*10,73=10,82,
=0,11*11,58+0,89*10,73=10,82,
Результаты расчёта экспоненциальных средних
представлены в табл. 12.1.
Графическое изображение экспоненциально
сглаженных кривых показывает, что кривая 2-го порядка является более плавной,
чем кривая 1-го порядка. Это объясняется тем, что кривая 2-го порядка
сглаживается на основе уже выровненной функции 1-го порядка. В Приложении 5 для
наглядности изображены 4 временных ряда: исходный ряд; ряд, сглаженный методом
скользящей средней; ряд, сглаженный методом экспоненциальной средней 1-го
порядка и ряд, сглаженный методом экспоненциальной средней 2-го порядка
Таблица 12.1 Результаты сглаживания временного
ряда методом экспоненциальной средней
|
Год
|
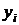  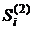
|
|
|
|
1990
|
18,50
|
11,51
|
10,18
|
|
1991
|
2,40
|
10,51
|
10,21
|
|
1992
|
17,20
|
11,25
|
10,33
|
|
1993
|
14,60
|
11,62
|
10,47
|
|
1994
|
11,40
|
11,59
|
10,59
|
|
1995
|
5,60
|
10,93
|
10,63
|
|
1996
|
5,80
|
10,37
|
10,60
|
|
1997
|
12,10
|
10,56
|
10,60
|
|
1998
|
5,50
|
10,00
|
10,53
|
|
1999
|
13,20
|
10,35
|
10,51
|
|
2000
|
5,70
|
9,84
|
10,44
|
|
2001
|
16,30
|
10,55
|
10,45
|
|
2002
|
14,60
|
11,00
|
10,51
|
|
2003
|
11,60
|
11,06
|
10,57
|
|
2004
|
6,30
|
10,54
|
10,57
|
|
2005
|
15,60
|
11,10
|
10,63
|
|
2006
|
15,20
|
11,55
|
10,73
|
|
2007
|
11,80
|
11,58
|
10,82
|
13.
Прогнозирование временного ряда на основе экспоненциального сглаживания
При экспоненциальном сглаживании
существует возможность построения прогнозных оценок 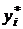 уровней
временного ряда. Построим прогноз на 1 год.
уровней
временного ряда. Построим прогноз на 1 год.
 (13.1)
(13.1)
Параметры 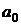 и
и  уравнения
(13.1) найдем из выражений
уравнения
(13.1) найдем из выражений
 ; (13.2)
; (13.2)
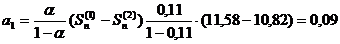 . (13.3)
. (13.3)
Таким образом, можно найти
прогнозное значение на 2008 год по формуле (13.1):
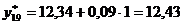
Результаты расчёта параметров 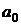 и
и  , а также
прогнозного значения уровня временного ряда (урожайности)
, а также
прогнозного значения уровня временного ряда (урожайности) 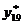 приведены в
табл. 13.1.
приведены в
табл. 13.1.
Фактическое значение  =11,5 .
=11,5 .
Определим абсолютную 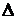 и
относительную
и
относительную  ошибки
прогноза по формулам
ошибки
прогноза по формулам
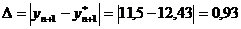 ; (13.4)
; (13.4)
 (%). (13.5)
(%). (13.5)
В таблице 13.1 представлены
результаты расчета параметров 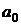 и
и  , а также прогнозного значения
уровня временного ряда (урожайности)
, а также прогнозного значения
уровня временного ряда (урожайности)  для 2008 года.
для 2008 года.
Таблица 13.1 Определение прогнозного значени
урожайности
|
|
|
|
|
|
|
|
|
|
|
|
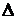 ,
ц/га ,
ц/га
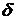 ,
% ,
%
|
|
|
0,11
|
11,58
|
10,82
|
12,34
|
0,09
|
12,43
|
0,93
|
8,09
|
Прогнозное значение и реальные данные близки,
ошибка прогноза составляет 0,93 ц/га в абсолютном значении и 8,09%. Данные
погрешности не являются существенными в масштабах исследуемого района.
Следовательно, можно говорить о верности произведенных эмпирических вычислений.
14. Количественная
оценка риска
Под риском обычно понимают возможность
наступления одного или нескольких случайных событий, являющихся причиной
отклонения полученного результата от ожидаемого значения.
Оценим риск неурожайности 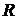 с помощью
коэффициента вариации
с помощью
коэффициента вариации  . Чем больше
величина показателя вариации, тем выше рассеяние и больше риск.
. Чем больше
величина показателя вариации, тем выше рассеяние и больше риск.
 , (14.1)
, (14.1)
Рассчитаем значение коэффициента
вариации урожайности для последних четырёх лет.
Возьмём 2007 год, рассчитаем для
него коэффициент вариации (уровень риска):
 (%).
(%).
Выборочное среднее урожайности за
предшествующий пятилетний период:
 .
.
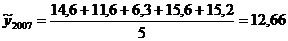
Выборочное среднеквадратическое
отклонение урожайности за тот же период

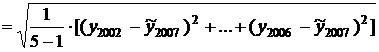
=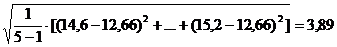
Таким образом,
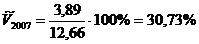 , (14.5)
, (14.5)
Далее рассчитаем коэффициент вариации для 2006,
2005, 2004 годов.
 ,
,
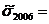
 4,09,
4,09,
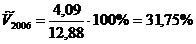 ;
;
 ,
,
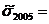 4,78,
4,78,
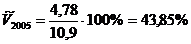 ;
;
 ,
,
 ,
,
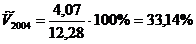 .
.
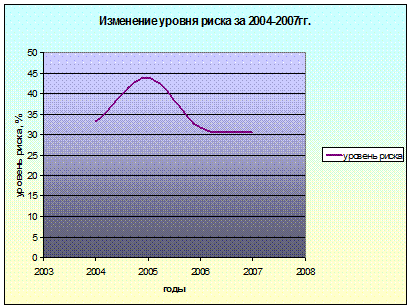
Результаты расчётов представлены в табл. 14.1,
линейная диаграмма изменения уровня риска за последние четыре года - Приложении
6.
Таблица 14.1 Расчёт уровня риска неурожайности
|
Годы
|
2004
|
2005
|
2006
|
2007
|
|
Уровень
риска  ,
(%)33,1443,8531,7530,73 ,
(%)33,1443,8531,7530,73
|
|
|
|
|
Диаграмма изменения уровня риска показывает, что
наиболее высокой степени за 4 года риск неурожайности достигает в 2005 году.
Заключение
Цель данной курсовой работы была достигнута путем
решения, поставленных в начале работы задач. В ходе исследования были
определены и изучены статистические показатели урожайности: среднее значение
урожайности за исследуемый период, мода, медиана, темпы роста и прироста,
проведен анализ полученных результатов, изучены законы распределения и
корреляционной связи, дана количественная оценка риска неурожайности, проведено
сглаживание и выравнивание временного ряда, а также спрогнозировано значение
урожайности на год вперед.
В работе графически представлены полученные
результаты, по котрым можно судить о характер и тенденции изменения некоторых
показателей.
Статистические расчеты позволяют не только
правильно исследовать, но и решить таким образом поставленные проблемы и
использовать результаты анализа в профессиональной деятельности.
Библиографический
список
1. Матвеев Б.А. Анализ
статистических данных. Учебное пособие к курсовой работе. - Челябинск:
Издательство ЮУрГУ, 2007
. Исходные данные по
урожайности: Фактический сбор урожая пшеницы в сельскохозяйственных
организациях
. Данные для оценки прогноза:
Данные по урожайности для определения ошибки прогноза
. Программа для вычислений Stat1
. Программа для вычислений Stat2
ПРИЛОЖЕНИЯ
Приложение 1

Приложение 2

Приложение 3
Приложение 4
Приложение 5

Приложение 6