Умови лінійної залежності та незалежності функцій

Умови лінійної залежності та незалежності функцій

Умови лінійної залежності та незалежності функцій

1. Теоретичні визначення для рішення задач оцінки залежності чи незалежності системи функцій однієї змінної

1.1 Лінійна залежність чи незалежність функцій по визначенню

Нехай маємо кінцеву систему з 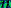 функцій , визначених на на проміжку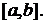

Функції  називають лінійно залежними на інтервалі , якщо існують постійні 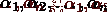, не всі рівні нулю, тобто

.

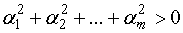такі, що для всіх значень 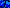 із цього на проміжку  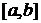справедлива тотожність

 (1.1)

Якщо ж ця тотожність виконується тільки при , то функції  називають лінійно незалежними на на проміжку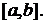

1.2 Лінійна залежність чи незалежність функцій по визначнику матриці Грама

Нехай маємо кінцеву систему з 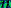 функцій , визначених на проміжку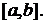

Визначимо інтеграли попарних добутків функцій (евклідів простір) наступним чином:

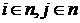 () (1.2)

Матрицею Грама зветься матриця, складена із попарних добутків функцій 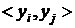 згідно (1.3), а її визначник називається визначником матриці Грама для системи з 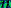 функцій .

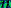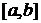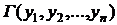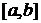Для того, щоб система з  функцій  була лінійно залежна на проміжку , необхідно та достатньо, щоб її визначник Грама  дорівнював нулю. Якщо визначник Грама на проміжку  не дорівнює нулю, то роблять висновок про лінійну незалежність системи функцій.

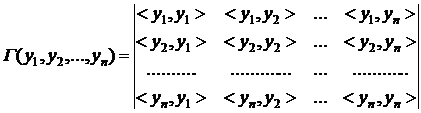 (1.3)

Визначник матриці Грама для деякої системи векторів дорівнює нулю тоді і тільки тоді, коли вектори лінійно залежні. Визначник Грама для лінійно незалежних векторів додатний.

.3 Лінійна залежність чи незалежність функцій по визначнику матриці Вронського

Нехай маємо кінцеву систему з 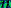 функцій , визначених на проміжку 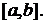 Нехай функції  мають похідні -го порядку.

Матриця, складена із рядків функцій та їх похідних за формою (1.4), називається матрицею Вронського, а визначник цієї матриці - визначником Вронського.

Визначником Вронського W (x; y₁(x), y₂(x),…, y_n(x)) називається визначник матриці, перший рядок якої утворений функціями y₁(x), y₂(x),…, y_n(x) на проміжку [a, b], а наступні рядки утворені похідними від функцій попереднього рядка:

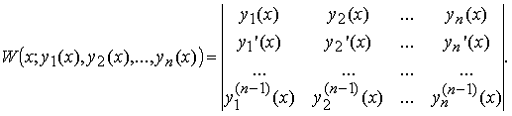 (1.4)

Справедливо наступна необхідна умова лінійної залежності функцій.

Якщо функції y₁(x), y₂(x),…, y_n(x) лінійно залежні на проміжку [a; b], то їх визначник Вронського тотожно дорівнює нулю на цьому проміжку: W (x; y₁(x), y₂(x),…, y_n(x)) ≡ 0 на [a; b]. Важливо розуміти, що зворотне твердження невірно. Визначник Вронського лінійно незалежної системи функцій також може бути тотожно дорівнювати нулю.

Справедливо наступна необхідна умова лінійної залежності функцій: якщо функції y₁(x), y₂(x),…, y_n(x), лінійно залежні на проміжку [a; b], то їхній визначник Вронського тотожно звертається в нуль на цьому проміжку:

(x; y₁(x), y₂(x),…, y_n(x)) ≡ 0.

Однак, якщо визначник Вронского функцій відмінний від нуля хоча б в одній крапці відрізка [a; b], те функції лінійно незалежні. Це останнє твердження - достатня умова лінійної незалежності функцій.

Визначник Вронського використовують для дослідження лінійної залежності функцій: якщо хоча б в одній точці W (x; y₁(x), y₂(x),…, y_n(x)) ≠ 0, то функції y₁(x), y₂(x),…, y_n(x), лінійно залежні на [a; b].

Якщо ж W (x; y₁(x), y₂(x),…, y_n(x)) ≡ 0, то варто продовжити дослідження лінійної залежності функцій. Наприклад, по визначенню.

1.4 Основні алгоритми розрахунку визначників матриць для проведення аналізу за визначниками Грама та Вронського

Числовою матрицею (або просто матрицею) називається прямокутна таблиця чисел. Окремі числа цієї таблиці називаються елементом матриці. Елементи матриці А позначають символом a_ik, де і - номер рядка, а k - номер стовпця, в якому стоїть вибраний елемент.

Якщо матриця містить n рядків і m стовпців, тоді говорять, що матриця має розмірність nxm. Особливо часто доводиться мати справу з матрицями, у яких число рядків дорівнює числу стовпців. Такі матриці називаються квадратними. Число рядків (а, звідси, і число стовпців) квадратної матриці називається порядком матриці.

1. Визначники матриць другого порядку

Для квадратної матриці вводиться нове поняття - визначник матриці. Визначник квадратної матриці будемо позначати символом det A і визначимо його індуктивним шляхом.

Визначником матриці 1-го порядку (тобто матрицею, яка складається із одного елементу, одного числа) називається саме число, яке утворює задану матрицю.

Визначником матриці 2-го порядку 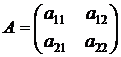 називається число, обчислене по такому правилу: det A=a₁₁a₂₂-a₁₂a₂₁.

Діагональ квадратної матриці, яка йде від лівого верхнього елементу таблиці до правого нижнього, називається головною діагоналлю матриці. Діагональ, яка йде від правого верхнього елементу до лівого нижнього, називається побічною діагоналлю матриці.

Таким чином, для обчислення матриці 2-го порядку потрібно із добутку елементів, які знаходяться на головній діагоналі матриці, відняти добуток елементів, які знаходяться на побічній діагоналі.

Для визначника матриці 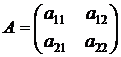 вводиться символ .

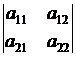Таким чином,

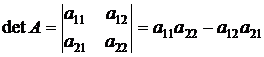                       (1.5)

Із означення (1.5) легко отримати ряд властивостей визначників матриць, які застосовуються при практичних розрахунках визначників матриць.

Властивість 1. При перестановці рядків матриці на місце стовпців і навпаки визначник матриці не змінюється.

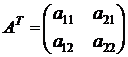Нехай задана матриця , а матриця  отримана із А перестановкою рядків на місце стовпців (така матриця А^Т називається часто транспонованою по відношенню до матриці А). Тоді

 (1.6)

Властивість 2. При перестановці двох стовпців (або рядків) абсолютне значення визначника матриці не змінюється, а знак змінюється на протилежний.

Нехай задана матриця 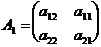, отримана із А перестановкою стовпців. Тоді

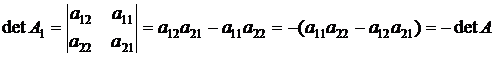
Властивість 3. Якщо матриця має два однакових стовпця (рядка), тоді визначник матриці дорівнює нулю.

Властивість 4. Якщо всі елементи будь-якого стовпця (рядка) матриці домножити на одне і те ж число, тоді визначник матриці виявиться домноженим на те ж число.

Властивість 5. Якщо всі елементи будь-якого стовпця (рядка) матриці дорівнюють нулю, тоді визначник матриці дорівнює нулю.

Властивість 6. Нехай всі елементи будь-якого стовпця (рядка) матриці А представляють собою суму двох елементів і нехай відповідні стовпці матриць А₁ і А₂ складаються із таких елементів:

, ,

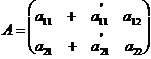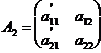
тоді

A=det A₁+detA₂

Властивість 7. Визначник матриці не змінюється, якщо до елементів будь-якого стовпця (рядка) матриці додати величини, пропорційні елементам другого стовпця (рядка).

Нехай  і .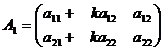

Тоді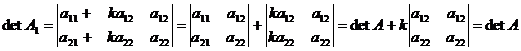

. Визначники матриць третього порядку

Нехай задана будь-яка матриця порядку n

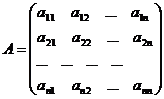 (1.7)

Виберемо довільний елемент a_ik цієї матриці і викреслимо із матриці А той рядок і той стовпець, в яких міститься цей елемент, (тобто викреслимо і-ий рядок та k-ий стовпець). Тоді отримаємо матрицю (n-1) - го порядку.

Будемо називати її субматрицею матриці А, що відповідає елементу a_ik та позначимо її символ D_ik

Визначник субматриці D_ik назвемо мінором матриці А, що відповідає елементу a_ik, та позначимо символом М_ik.

Звідси

М_ik=det D_ik. (1.8)

Нехай вихідна матриця А була матрицею 3-го порядку. Тоді дев`ять її можливих субматриць D₁₁, D₁₂, D₁₃, D₂₁, D₂₂, D₂₃, D₃₁, D₃₂, D₃₃, які відповідають різним елементам матриці А, будуть матрицями 2-го порядку.

Визначення. Визначником матриці 3-го порядку

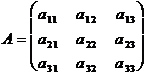
називається число, визначене за таким правилом:

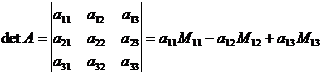 (1.9)

 ,

тоді

₁₁=det D₁₁=a₂₂a₃₃-a₂₃a₃₂₁₂=det D₁₂=a₂₁a₃₃-a₂₃a₃₁₁₃=det D₁₃=a₂₁a₃₂-a₂₂a₃₁

ЗвідсиA=a₁₁(a₂₂a₃₃-a₂₃a₃₂) - a₁₂(a₂₁a₃₃-a₂₃a₃₁)+a₁₃(a₂₁a₃₂-a₂₂a₃₁)A=a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₁₁a₂₃a₃₂-a₁₂a₂₁a₃₃-a₁₃a₂₂a₃₁ (1.10)

Як видно із одержаної формули, визначник матриці 3-го порядку представляє собою алгебраїчну суму шести доданків. Кожний доданок є добутком трьох елементів по одному із кожного рядка і кожного стовпця. Перший із доданків, взятих зі знаком «+», представляє собою добуток елементів, розташованих на головній діагоналі матриці. Останні два містять елементи, розташовані у вершинах трикутників з основою, паралельною головній діагоналі (Рис. 1).

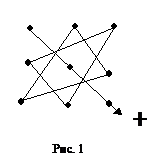
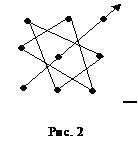
Добутки, які входять зі знаком «-», містять елементи, розташовані на побічній діагоналі, та елементи, розташовані у вершинах трикутників з основою паралельною побічній діагоналі (Рис. 2).

Всі властивості, встановлені для визначників матриць 2-го порядку, мають місце і для визначників 3-го порядку.

3. Визначники матриць вищих порядків

Визначники матриць 4-го і більш високих порядків будемо вводити аналогічно визначникам матриць 3-го порядку. Нехай задана матриця

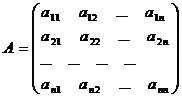
Визначення. Визначником матриці А порядку n називається число, обчислене за таким правилом:

 (1.11)

У відповідності зі сказаним раніше в цій формулі M_ik є мінор матриці А, який відповідає елементу a_ik, тобто визначник субматриці Д_ik, одержаний із матриці А викреслюванням і-того рядка і k-го стовпця.

Правило (1) є очевидним узагальненням правила (2, § 3). Воно дає можливість звести обчислення визначників матриць 4-го порядку до обчислень визначників 3-го порядку і т.ін.

Обчислення визначника матриці високого порядку по формулі (1.11) - операція досить трудомістка. А тому важливо, використовуючи властивості визначників матриць, скоротити обчислення.

Приймемо наступні два твердження про властивості визначників матриць порядку n (ці властивості були перевірені для визначників матриць 2-го порядку, а властивість 1 також і для матриць 3-го порядку).

Властивість 1. При перестановці рядків матриці на місце стовпців визначник матриці не змінюється

Властивість 2. При перестановці двох рядків (або стовпців) матриці абсолютне значення визначника матриці не змінюється, а знак змінюється на протилежний.

Перша властивість дає можливість всі положення, встановлені для рядків матриці, переносити на її стовпці. Із нього, наприклад, виходить, що можливо визначник матриці обчислювати і по формулі

A = a₁₁M₁₁ -a₂₁M₂₁+… + (-1)^n-1 a_n1M_n1 (1.12),

тобто виконувати розклад визначника матриці не тільки по елементах першого рядка, але і по елементах першого стовпця. На основі даних тверджень виведемо основну формулу для розкладу визначника матриці по елементах будь-якого рядка або стовпця:

A=(-1)ⁱ⁺¹a_i1M_i1+(-1)ⁱ⁺²a_i2M_i2+ … +(-1)ⁱ⁺ⁿa_inM_in= (-1)^1+ka_1kM_1k+(- 1)^2+ka_2kM_2k+ … +(-1)^n+k a_nkM_nk (1.13)

Перша частина твердження представляє собою розклад визначника по елементах і-го рядка, друга половина - розклад по елементах k-го стовпця.

Визначення. Алгебраїчним доповненням елементу а_ік матриці А називається мінор М_ік цієї матриці, помножений на (-1)^і+к:

Алгебраїчне доповнення елементу а_ік матриці А позначається, як правило, символом А_ік. Отже,

А_ік=(-1)^і+кМ_ік (1.14)

Тепер формулу розкладу (1.13) можна записати в такому вигляді

=a_i1A_i1+a_i2A_i2+ … +a_inA_in=a_1kA_1k+a_2kA_2k+ … +a_nkA_nk (1.15)

Визначник матриці дорівнює сумі добутків елементів будь-якого рядка (або стовпця) матриці на відповідне алгебраїчне доповнення.

Властивість 3. Якщо матриця має два однакових рядка (або стовпця), тоді визначник матриці дорівнює нулю.

Властивість 4. Якщо всі елементи будь-якого рядка (або стовпця) матриці помножить на одне і те ж число, тоді визначник матриці стане помноженим на те ж число.

Властивість 5. Якщо всі елементи будь-якого рядка (або стовпця) матриці дорівнюють нулю, тоді визначник матриці дорівнює нулю.

Властивість 7. Визначник матриці не зміниться, якщо до елементів будь-якого рядка (або стовпця) матриці додати величини, пропорційні елементам другого рядка (стовпця) тієї ж матриці.

2. Практичні розрахунки залежності та незалежності системи функцій

.1 Завдання 1

Дослідити на лінійну залежність систему 4-х функцій:

, х, х², х³

по визначенню та за допомогою визначника Грама

Рішення:

. Область допустимих значень х для заданої системи функцій - .

2. Відповідно, задачею дослідження є виявлення того, що система функцій на проміжку значень = :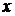

або

а) α₁·1 + α₂·x + α₃·x²+ α₄·x³ 0. - якщо існують постійні, не всі одночасно рівні нулю

, тобто лінійно залежна по визначенню;

або

б)  - тільки при , тобто лінійно незалежна по визначенню;

. Доведемо лінійну незалежність на всій числовій осі системи функцій 1, x, x², x³ по визначенню.

Справді, рівність  може виконуватися для всіх 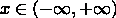 тільки за умови, що . Якщо ж хоч одне із цих чисел не дорівнює нулю, то в лівій частині рівності будемо мати багаточлен ступеня не вище третього, а він може звернутися в нуль не більш, ніж при трьох значеннях 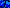 з даного інтервалу.

Допустимо противне, тобто допустимо, що існують постійні α₁, α₂, α₃, α₄, не рівні нулю одночасно й такі, що для всіх x справедливо

α₁·1 + α₂·x + α₃·x²+ α₄·x³ = 0.

Остання рівність для всіх x можливо тоді й тільки тоді, коли багаточлен α₁·1 + α₂·x + α₃·x²+ α₄·x³ тотожно дорівнює нулю, тобто тоді і тільки тоді, коли α₁= α₂= α₃= α₄= 0.

Ця остання рівність суперечить припущенню що постійні α₁, α₂,…, α_n+1, не дорівнюють нулю одночасно. Твердження доведене.

. Досліджуємо лінійну незалежність на всій числовій осі системи функцій 1, x, x², x³ з використанням визначника Вронського W (x; 1, x, x², x³) системи функцій 1, x, x², x³:

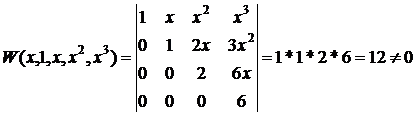
Визначник Вронського на всій числовій осі відмінний від нуля, отже функції 1, x, x², x³ лінійно незалежні на всій числовій осі.

5. Побудуємо визначник матриці Грама. Для цього визначимо згідно (1.2) інтеграли попарних добутків функцій наступним чином:

перша строка

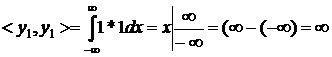
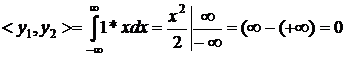
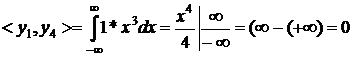
- друга строка

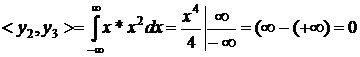
третя строка

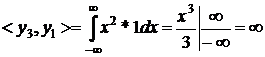
четверта строка

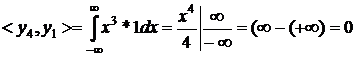
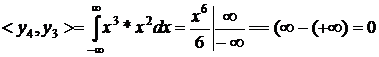
Властивість 3. Якщо матриця має два однакових рядка (або стовпця), тоді визначник матриці дорівнює нулю.

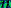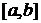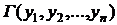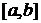Для того, щоб система з  функцій  була лінійно залежна на проміжку , необхідно та достатньо, щоб її визначник Грама  дорівнював нулю. Якщо визначник Грама на проміжку  не дорівнює нулю, то роблять висновок про лінійну незалежність системи функцій.

Висновки завдання 1 - досліджуєма система функцій:

а) за визначенням - лінійно незалежна;

б) за визначником Вронського - лінійно незалежна;

в) за визначником Грама - лінійно залежна.

Функції 1, x, x², x³ лінійно незалежні на будь-якому інтервалі (a, b). Їхня лінійна комбінація  - багаточлен ступеня  - не може мати на (a, b) більше трьох корінь, тому рівність = 0 для 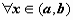можливо тільки при .

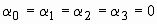.2 Завдання 2

Дослідити на лінійну залежність систему 2-х функцій:

xsinx, xcosx

по визначенню та за допомогою визначника Грама

Рішення:

. Область допустимих значень х для заданої системи функцій - .

2. Відповідно, задачею дослідження є виявлення того, що система функцій на проміжку значень = :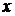

або

а) α₁·(xsinx) + α₂· (xcosx) 0. - якщо існують постійні

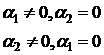, не всі одночасно рівні нулю, тобто лінійно залежна

по визначенню;

або

б) α₁·(xsinx) + α₂· (xcosx) 0 - тільки при , тобто лінійно незалежна по визначенню;

. Досліджуємо систему функцій за визначенням, перетворюючи вихідний вираз наступним чином:

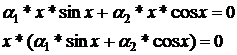
таким чином, точка 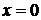 - особлива точка системи функцій.

Вираз:

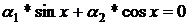 перетворюємо з врахуванням

в форму

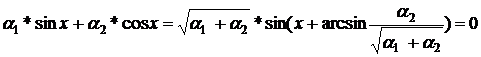
це рівняння на всьому проміжку 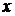=  має постійні рішення (які не залежить від 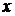) тільки , тобто система функцій xsinx, xcosx лінійно незалежна по визначенню;

4. Досліджуємо лінійну незалежність на всій числовій осі системи функцій xsinx, xcosx з використанням визначника Вронського W (x; xsinx, xcosx) системи функцій xsinx, xcosx:

Враховуючи перші похідні заданих функцій:

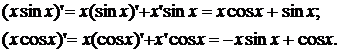
Будуємо визначник Вронського та проводимо обчислення:

Отриманий визначник Вронського на всій числовій осі відмінний від нуля (за виключенням точки - нуль), отже функції xsinx, xcosx лінійно незалежні на всій числовій осі (за виключенням точки - нуль).

По визначнику Вронського - система функцій xsinx, xcosx - лінійно незалежна.

. Побудуємо визначник матриці Грама. Для цього визначимо згідно (1.2) інтеграли попарних добутків функцій наступним чином:

перша строка

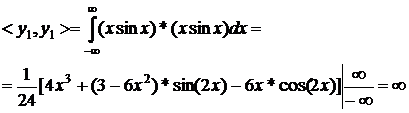
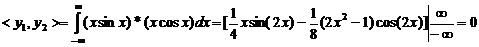
друга строка

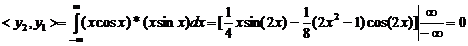
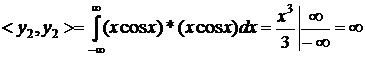
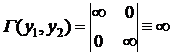
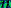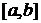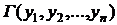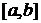Для того, щоб система з  функцій  була лінійно залежна на проміжку , необхідно та достатньо, щоб її визначник Грама  дорівнював нулю. Якщо визначник Грама на проміжку  не дорівнює нулю, то роблять висновок про лінійну незалежність системи функцій.

По визначнику Грама - система функцій xsinx, xcosx - лінійно незалежна.

Висновки завдання 2 - досліджуєма система функцій:

а) за визначенням - лінійно незалежна;

б) за визначником Вронського - лінійно незалежна;

в) за визначником Грама - лінійно незалежна.

.3 Завдання 3

Дослідити на лінійну залежність систему 3-х функцій:

4-х, 2х + 3, 6х + 8

по визначенню та за допомогою визначника Грама.

Рішення:

. Область допустимих значень х для заданої системи функцій - .

2. Відповідно, задачею дослідження є виявлення того, що система функцій на проміжку значень = :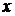

або

а) α₁·(4-х) + α₂·(2х + 3) + α₃·(6х + 8) 0. - якщо існують постійні, не всі одночасно рівні нулю

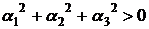, тобто лінійно залежна по визначенню;

або

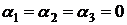б) α₁·(4-х) + α₂·(2х + 3) + α₃·(6х + 8) 0 тільки при , тобто лінійно незалежна по визначенню;

. Проведемо дослідження системи функцій по визначенню:

отримаємо

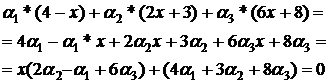
або на проміжку 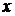значень =  існує певна кількість значень 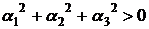 рішення системи рівнянь (які не залежать від )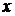

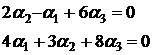
що свідчить про лінійну залежність заданої системи функцій.

4. Досліджуємо лінійну незалежність на всій числовій осі системи функцій

-х, 2х + 3, 6х + 8 з використанням визначника Вронського W (x; 4-х, 2х + 3, 6х + 8) системи функцій 4-х, 2х + 3, 6х + 8:

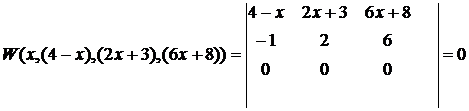
Властивість 5. Якщо всі елементи будь-якого рядка (або стовпця) матриці дорівнюють нулю, тоді визначник матриці дорівнює нулю.

Визначник Вронського на всій числовій осі дорівнює нуля, отже функції 4-х, 2х + 3, 6х + 8 є лінійно залежними на всій числовій осі.

. Побудуємо визначник матриці Грама. Для цього визначимо згідно (1.2) інтеграли попарних добутків функцій наступним чином:

перша строка

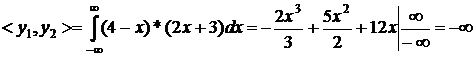
друга строка

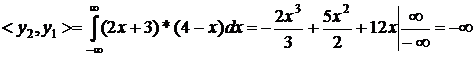
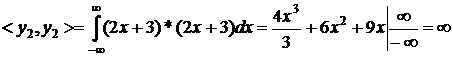
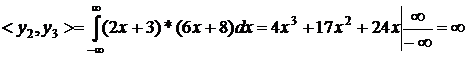
третя строка

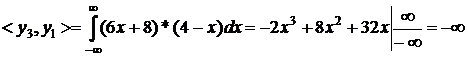
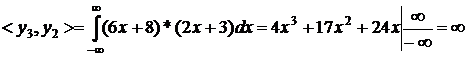
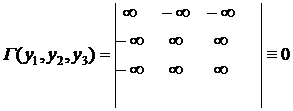
Властивість 3. Якщо матриця має два однакових рядка (або стовпця), тоді визначник матриці дорівнює нулю.

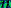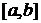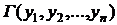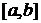Для того, щоб система з  функцій  була лінійно залежна на проміжку , необхідно та достатньо, щоб її визначник Грама  дорівнював нулю. Якщо визначник Грама на проміжку  не дорівнює нулю, то роблять висновок про лінійну незалежність системи функцій.

По визначнику Грама - система функцій 4-х, 2х + 3, 6х + 8 - лінійно залежна.

Висновки завдання 3 - досліджуєма система функцій:

а) за визначенням - лінійно залежна;

б) за визначником Вронського - лінійно залежна;

в) за визначником Грама - лінійно залежна.

.4 Завдання 4

Дослідити на лінійну залежність систему 2-х функцій:

ln x⁴, ln 5x

по визначенню та за допомогою визначника Грама

Рішення:

При рішенні використовуємо визначення властивостей логарифмічної функції. Логарифмом позитивного числа N (N>0) по підставі (b > 0, b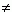 1) називається показник ступеня x, у якbq потрібно звести b, щоб одержати N.

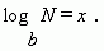
Основні властивості логарифмів.

1) log 1 = 0, тому що b ⁰ = 1.

2) Логарифм добутку дорівнює сумі логарифмів співмножників:

log (ab) = log a + log b.

3) Логарифм частки дорівнює різниці логарифмів ділимого й дільника:

log (a / b) = log a - log b.

4) Логарифм ступеня дорівнює добутку показника ступеня на логарифм її підстави:

log (b ^k) = k · log b

2. Область допустимих значень х для заданої системи функцій - інтервал .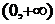

. Відповідно, задачею дослідження є виявлення того, що система функцій на проміжку значень = :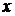

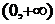або

а)  - якщо існують постійні (незалежні від 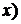 коефіцієнти, не всі одночасно рівні нулю,

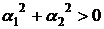, то лінійно залежна по визначенню;

або

б) - тільки при постійних (незалежних від 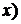 , тобто лінійно незалежна по визначенню.

. Досліджуємо систему функцій за визначенням, перетворюючи вихідний вираз наступним чином:

 (4.1)

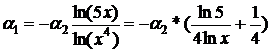
таким чином, на інтервалі значень 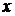=  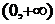пари коефіцієнтів 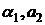, що обертають рівність (4.1) в нуль існують, але вони функціонально пов’язані із змінною 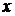= 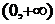, тобто не є постійними.

Відповідно, рівняння (4.1) на всьому проміжку 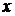=  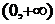має постійні рішення (які не залежать від 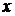) тільки , тобто система функцій 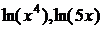 є лінійно незалежною по визначенню.

. Досліджуємо лінійну незалежність на всій числовій осі системи функцій 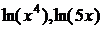 з використанням визначника Вронського W (x;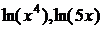) системи функцій :

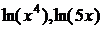Враховуючи перші похідні заданих функцій:

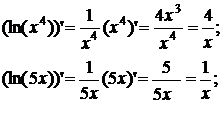
Будуємо визначник Вронського та проводимо обчислення:

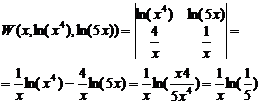
Отриманий визначник Вронського на всьому проміжку 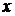=  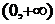відмінний від нуля, отже функції  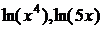лінійно незалежні на всьому проміжку 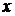= 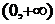. По визначнику Вронського - система функцій 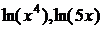 - лінійно незалежна.

5. Побудуємо визначник матриці Грама. Для цього визначимо згідно (1.2) інтеграли попарних добутків функцій наступним чином:

перша строка

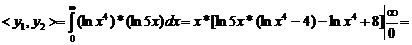
друга строка

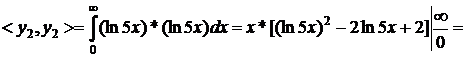
Оскільки обрахування визначених інтегралів на проміжку 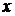=  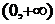є самостійною дослідницькою задачею, замінимо проміжок інтегрування на дуже великий 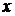= , в якому дозволяє провести інтегрування інтерактивна система з отриманням результату до 10¹⁶[].

- перша строка

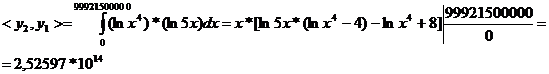
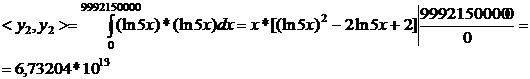
відповідний визначник Грама виглядатиме наступним чином

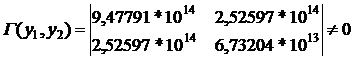
Висновки

Згідно меті та завданню в курсовій роботи проведене узагальнення теоретичних матеріалів щодо визначення і методів дослідження лінійної залежності та незалежності функцій та проведене практичне дослідження лінійної залежності (незалежності) систем функцій однієї змінної за визначенням і з використанням визначників матриць Вронського та Грама згідно завданню.

Особливістю ідентифікації лінійної залежності та лінійної незалежності довільного набору функцій однієї змінної є дослідницький характер застосування визначників матриць Вронского та Грама, згідно якому необхідно кожну систему функцій, яка імітує розв’язки однорідного диференціального рівняння досліджувати послідовно за 3-ма методами:

по визначенню - рішенням єдиного вихідного рівняння з декількома змінними методами математичної логіки, оскільки пошук математичного рішення неможливий за відсутністю необхідної кількості рівнянь;

методом визначника матриці Грама в строках якої розташовані комбінації визначених інтегралів від кожної змінної функції в вихідному рівнянні:

а) Визначник матриці Грама для деякої системи функцій дорівнює нулю тоді і тільки тоді, коли вектори лінійно залежні;

б) Визначник Грама для лінійно незалежних функцій додатний.

методом визначника Вронського в строках якого розташовані послідовні похідні вищого порядку від змінних функцій в вихідному рівняння:

а) необхідна умова лінійної залежності функцій - визначник Вронського тотожно дорівнює нулю при всіх ,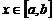

б) достатня умова лінійної незалежності розв’язків - визначник Вронського  не дорівнює нулю в жодній точці .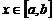

Тільки одночасна ідентифікація 3-ма методами дає впевненість в лінійній незалежності чи лінійній залежності систем досліджуваних функцій.

Список літератури

залежність функція вронський грам

1. Боярчук А.К. Математический анализ: введение в анализ, производная, інтеграл: Справочное пособие по высшей математике, т. 1 / И.И. Ляшко, А.К. Боярчук, Я.Г. Гай, Г.П. Головач. - М.: Эдиториал УРСС, 2001. - 360 с.

. Боярчук А.К. Дифференциальные уравнения в прмерах и задачах: Справочное пособие по высшей математике, т. 5 / А.К. Боярчук, Г.П. Головач. - М.: Эдиториал УРСС, 2001. - 384 с.

. Двайт Г.Б. Таблицы интегралов и другие математические формулы. / Г.Б. Двайт, Пер. с англ. Н.В. Леви, под. ред. К.А. Семендяева - М.: Издательство «Наука», 1964. - 226 с.

. Кадильникова Т.М., Запорожченко О.Є., Бас Т.П. Вища математика в прикладах та задачах. Частина I: Навч. посібник. - Дніпропетровськ: НМетАУ, 2010. - 92 с.

. Літнарович Р.М. Алгебра матриць. Курс лекцій. МЕГУ, Рівне, 2007, - 112 с.

. Сясєв А.В. Диференціальні рівняння: Навч. посіб. (Гриф МОНУ) ‒ Д.: Вид-во ДНУ. 2007. - 358 с.

. http://matematikam.ru/ - Справочный Интернет-сайт онлайн - калькулятора по вычислению неопределенных и определенных интегралов, Москва, 2012