Теория и методика обучения школьников векторному методу (стереометрия)
Министерство образования и науки
Российской Федерации
ГОУ ВПО Нижегородский Государственный
Педагогический Университет
Факультет математики, информатики,
физики
Кафедра теории и методики обучения
математике
ДИПЛОМНАЯ РАБОТА
Теория и методика обучения школьников
векторному методу (стереометрия)
Выполнила:
Мыслякова Т.И.
Научный руководитель:
доктор пед. наук, профессор
Т.А. Иванова
Нижний Новгород, 2009 г.
Содержание
Введение
Глава 1. Теоретические и методические особенности изучения
векторного метода в школьном курсе геометрии
.1 История возникновения и становления аналитических методов
.2 Различные подходы к определению понятия вектора в
математике и в школьном курсе математики
.3 Обучение решению задач как психологическая и методическая
проблема
.4 Методика обучения векторному методу решения афинных задач
в геометрии
Глава 2. Методика изучения темы «Векторы в пространстве» в 10
классе
.1 Логико-дидактический анализ «Векторы в пространстве» в 10
классе
.2 Методика формирования умений, составляющих суть векторного
метода решения геометрических задач
.3 Методика обучения векторному методу решения содержательных
геометрических задач
.4 Описание опытной работы
Заключение
Список литературы
Приложение
Введение
Актуальность. В соответствии с концепцией Российского образования и, в
частности, математического одной из задач обучения, развития и воспитания
учащихся в средней школе является достижение следующих двух главных целей
образования: воспитать личность, способную адаптироваться в быстро меняющихся
условиях жизни и способную одновременно изменять эти условия. Соответственно,
усилия школы должны быть сосредоточены в двух направлениях: создание условий
для развития интеллекта и формирование творческих качеств личности обучающихся.
Одной из приоритетных целей математического образования в рамках
выделенных направлений является «формирование представлений о математике как
универсальном языке науки, средстве моделирования явлений и процессов, об идеях
и методах математики» [23, с. 3].
Векторный метод является одним из основных методов геометрии. С его
помощью можно эффективно решить ряд аффинных и метрических задач планиметрии и
стереометрии, ряд прикладных задач физики и астрономии.
Так же изучение векторного метода представляет собой самостоятельный
познавательный интерес, т.к. на его основе имеется возможность корректно ввести
метод координат на плоскости и в пространстве.
Необходимо отметить, что в школьном курсе математики тема «Векторы», а
вместе с ней векторный метод, появилась относительно недавно, в начале
шестидесятых годов прошлого века. Тем не менее, практически сразу же понятие
вектора стало одним из ведущих понятий школьного курса математики, а векторный
метод -одним из основных способов решения задач и доказательства теорем.
В любом школьном учебнике изложение темы «Векторы» состоит из двух
этапов: изучение векторов и векторного метода 1) в планиметрии; 2) в
стереометрии.
Изучение темы «Векторы в пространстве» дает возможность учащимся получить
представление о широте применения векторов в различных областях человеческой
деятельности, познакомиться с некоторыми фактами развития векторного
исчисления, усвоить систематизированные сведения о векторах в пространстве,
научиться проводить аналогии между плоскими и пространственными конфигурациями
векторов, применять векторный метод для изучения плоских и пространственных
форм, при решении задач.
Изучением темы «Векторы. Векторный метод решения задач» в разные периоды
времени занимались многие ученые-физики, математики и методисты (К. Вессель, Р.
Декарт, Ж. Арган, З.А. Скопец, А.Н. Колмогоров, А.Д. Александров, В.А Гусев,
Ю.М Калягин, Т.А. Иванова). В настоящее время существует несколько подходов к
определению понятию вектора, определены операции с векторами, очерчен круг
задач, решаемых векторным методом, выделены умения, входящие в состав
векторного метода. Разработаны частные методики по обучению учащихся векторам
и, в частности, векторному методу. Все они основаны на идее основного
назначения векторов - использование алгебраического аппарата для решения
геометрических задач.
Не смотря на все это, многие специалисты отмечают, что некоторые учителя,
студенты, а тем более школьники, затрудняются в применении векторного метода к
решению содержательных задач.
Сказанное позволяет выделить существующее противоречие между
необходимостью обучения учащихся векторному методу решения геометрических задач
и недостаточному уделению внимания этому на практике. Разрешение этого
противоречия особенно актуально при изучении темы «Векторы в пространстве» в 10
классе, поскольку в теории и методике обучения математике даются, в основном,
рекомендации для изучения векторного метода на плоскости. Между тем, при
изучении стереометрии круг задач, решаемых с помощью векторов, значительно
расширяется.
Таким образом, сформулированное выше противоречие определило актуальность
проблемы нашей работы, которая состоит в его разрешении посредством
обоснованной разработки методических рекомендаций по обучению учащихся
векторному методу решения геометрических задач в теме «Векторы в пространстве».
Цель исследования - выявить теоретико-методические условия изучения
векторного метода решения геометрических задач и разработать научно
обоснованные методические рекомендации по обучению учащихся этому методу.
Объект исследования - процесс обучения геометрии в старших классах
общеобразовательной школы;
Предмет исследования - методическая система обучения учащихся векторному
методу решения задач.
Гипотеза исследования: Если целенаправленно обучать школьников умениям и
действиям, входящих в состав векторного метода, формулировать частные эвристики
по решению отдельных типов задач, то это будет способствовать эффективному
усвоению учащимися этого метода
Для достижения поставленной цели и проверки выдвинутой гипотезы
необходимо было решить следующие задачи:
. Провести анализ психолого-педагогической и научно-методической
литературы по проблеме исследования с целью выявления условий успешного
овладения школьниками векторного метода решения геометрических задач;
. Провести анализ программных документов, школьных учебников по теме
«Векторы в пространстве»;
. Выявить теоретико-методическую концепцию, на основе которой можно
разрабатывать методические рекомендации изучения векторного метода решения
задач в школьном курсе геометрии;
4. Разработать методические рекомендации для успешного овладения
учащимися векторного метода;
5. Провести опытную проверку разработанных методических
рекомендаций.
Для решения поставленных задач использовались следующие методы:
изучения и анализ литературы по исследуемой проблеме;
беседа с учителями математики в старших классах общеобразовательной
школы;
тестирование учащихся;
опытная работа.
Методологической основой исследования послужили: концепция развивающего
обучения (В.В. Давыдова, Д.Б. Эльконина); основные положения деятельностного
подхода; методические рекомендации по изучению темы «Векторы в пространстве»
(Т.А. Ивановой, З.А. Скопеца, В.А. Гусева, Г.И. Саранцева).
Новизна исследования заключается в методических рекомендациях по теме
«Обучение школьников решению задач векторным методом», которые основаны на идее
целенаправленной предварительной работы по формированию умений, необходимых для
успешного овладения учащимися этого метода.
Положения, выносимые на защиту:
. Вектор является одним из фундаментальных понятий современной
математики. В настоящее время существует несколько подходов к определению этого
понятия.
. Векторный метод является эффективным методом решения геометрических
задач и доказательства теорем;
. Для успешного овладения школьниками векторным методом решения
содержательных геометрических задач необходимо обучать их умениям и действиям,
входящих в его состав;
. Сущность векторного метода состоит в том, что условие и требование
задачи записывается в векторной форме, а ее решение состоит в переходе от условия
к требованию на основе законов векторной алгебры.
Апробация основных положений и результатов исследования осуществлялась
автором в личном опыте работы с учащимися 10 класса МОУ Хвощевской средней
школы Богородского района Нижегородской области в период педагогической
практики, в выступлении перед студентами V курса на семинарских занятиях.
Структура дипломной работы определена ее логикой и решением задач
исследования. Работа состоит из введения, двух глав, заключения, списка
литературы, приложения.
вектор математика геометрия школьный
Глава 1. Теоретические и методические особенности изучения векторного
метода в школьном курсе геометрии
Эта глава посвящена изложению теоретического материала, касающегося
изучению векторного метода в школе. Прежде чем начать изучение какой-либо темы,
необходимо обратиться к истории ее возникновения. Именно поэтому главу 1 мы
начнем с исторической справки о возникновении векторного метода. Далее проведем
анализ различных подходов к определению понятия вектора в математике, в
школьном курсе математики. Для того чтобы выявить методическую концепцию по
изучению школьниками векторного метода решения задач, проанализируем
психолого-педагогическую литературу по проблеме обучения школьников решению
задач, и учебно-методическую литературу по обучению собственно векторному
методу.
.1 История возникновения и становления аналитических методов
Интерес к векторам и векторному исчислению пробудился у математиков в 19
веке в связи с потребностями механики и физики. Однако истоки исчисления с
направленными отрезками возникли в далеком пришлом. В Древней Греции,
пифагорейцы, открыв иррациональные числа, которые нельзя выразить дробями (Ö2, Ö5,…), пришли к выводу, что не всякую
величину можно выразить дробями. Вследствие этого математики того времени
попытались свести вопросы арифметики и алгебры к решению задач геометрическим
путем. Таким образом, было положено начало геометрической теории отношений
Евдокса (408-355 гг. до н.э.), а позднее «геометрической алгебре».
В работе Евклида «Начала» сложение и вычитание сводились к сложению и
вычитанию отрезков, умножение - к построению прямоугольников на отрезках,
соответствующих по длине множителям, а деление - к операции «приложения»
геометрических фигур.
В последствии в 16-17 вв. геометрическая алгебра из-за ограниченности
своих средств исследования стала тормозом развития науки.
Однако, геометрическое исчисление сыграло значительную роль в развитии
математики, в том числе и для теории векторов, послужив истоком развития этой
теории.
Еще в работе «Механические проблемы», созданной в школе Аристотеля,
введен термин «сложение движений», т.е. скоростей, и сформулировано правило
параллелограмма. Его использовал Архимед в работе «О спиралях», а позже -
Птолемей. Астрономы средневекового Востока, развивая теорию Птолемея, постоянно
использовали «сложение движений».
В 1587 г. был опубликован на голландском языке трактат фламандского
ученого С. Стевина (1548-1620) «Начала статики». В нем автор, рассматривая
сложение сил, приходит к выводу, что для нахождения результата сложения двух
сил, действующих под углом 90°, необходимо воспользоваться «параллелограммом сил», при этом для
обозначения сил С. Стевин ввел стрелки. Иначе говоря, С. Стевин впервые ввел
сложение двух векторов, перпендикулярных друг другу. Далее, Стевин в «Основах
статики» и Валлис (1616-1703) в «Механике» сформулировали правила
параллелограмма и параллелепипеда для сложения направленных отрезков, которыми
они изображали силы, скорости, ускорения.
В конце 16- начале 17 в. многие ученые - физики, в том числе Леонардо да
Винчи, Галилео Галилей, пользовались направленными отрезками для наглядного
представления сил. Формулируя свои законы движения планет, Кеплер по существу
рассматривает направленный отрезок, началом которого является Солнце, а конец
совпадает с движущейся точкой.
Однако в рассматриваемую эпоху в естествознании еще не оформилось четко
понятия векторной величины, а идеи алгебраических действий с направленными
отрезками лишь зарождались.
Исторически развитие векторного исчисления шло тремя путями:
геометрическим (исчисление отрезков), физическим (исследование векторных
величин, встречаемых в естествознании), и алгебраическим (расширение понятия
операции при создании современной алгебры).
Начала исчисления направленных отрезков были впервые изложены норвежцем
Каспаром Весселем в мемуаре «Опыт об аналитическом представлении направления и
его применениях, преимущественно к решению плоских и сферических
многоугольников», опубликованном в «Трудах Датской Академии наук» в 1799 г. Вессель
создал свой труд, исходя из чисто практических задач - облегчить труд
геодезиста-землемера.
Вессель впервые представил комплексные числа как направленные отрезки. Он
ввел операции умножения и деления направленных отрезков на основе операций с
комплексными числами.
Так, результатом умножения отрезков z1 и z2, где z1=r1(cosa+isina), z2=r2(cosb+isinb), является отрезок z1×z2=r1×r2(cos(a+b)+isin(a+b)). При этом отрезок z1
поворачивался на угол b, а
его длина r1 умножалось на число r2.
Векторную алгебру на плоскости (или двумерное векторное пространство)
Вессель строит почти так же, как она изложена в наших учебниках. Для
иллюстрации приведем его определение суммы нескольких векторов, следующее за
определением суммы двух направленных отрезков: «Чтобы сложить более двух
отрезков, нужно следовать тому же правилу: располагаем их так, чтобы конец
первого совпадал с началом второго, а конец второго совпадал с первой точкой
третьего и т. д., затем соединяем отрезком ту точку, где первый отрезок
начинается с той точкой, где последний отрезок заканчивается, и называем этот
последний отрезок суммой всех данных отрезков». Причем он подчеркивает, что в
расширенное понятие сложения включен как частный случай и старый смысл этого
действия, т.е. «Если складываемые отрезки одинаково направлены, то это
определение суммы вполне согласуется с обычным сложением».
Вессель также строит исчисление направленных отрезков в пространстве
(трехмерное векторное пространство) и, развивая оригинальную «алгебру вращения
сферы», применяет ее к решению сферических треугольников и многоугольников.
«Опыт» Весселя свидетельствует о том, что именно удовлетворение потребностей
прикладной геометрии привело к развитию векторного исчисления.
Об этом говорят и философские воззрения великих ученых о роли математики
в исследовании явлений природы. Система координат Р. Декарта основана на его
концепции единой математики, объединяющей геометрию и алгебру. Развивая мысли
Декарта о матемизации естествознания, Лейбниц писал: «Алгебра выражает величину
необходим ещё иной, чисто геометрический анализ, непосредственно выражающий
положение». Лейбниц говорил о построении геометрического исчисления, изучающего
направленные отрезки, их длины, углы между ними. Эти мысли стали исходной
точкой для многих геометрических работ.
Видное
место в истории векторного исчисления занимает книга Карно «Геометрия
положения» (1803). В ней автор вводит понятие геометрического количества, под
которым он подразумевает в основном направленный отрезок, и занимается
действиями над ориентированными фигурами, в частности отрезками. До него
положительные и отрицательные отрезки рассматривались лишь в пределах одной
прямой, он же ввел отрезки, имеющие любое направление, и фактически проложил
путь к векторному исчислению. Некоторые введенные Карно термины и символы, в
частности обозначение вектора с помощью черты наверху (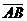 ,
, 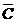 ),
сохранились и поныне.
),
сохранились и поныне.
В
1835 г. Дж. Белаватис в «Теории эквиполентности» ввел свободные векторы, назвав
эквиполентными направленные отрезки с равной длиной и совпадающими
направлениями.
В
сочинении по аналитической и проективной геометрии «Барицентрическое
исчисление» (1827) немецкий математик А. Мебиус в известной мере продолжил труд
Карно и систематизировал его идеи. Автор впервые представлял геометрическое
количество АВ в виде разности точек: В - А.
Швейцарский
математик Жан Арган (1768-1822) написал в 1806 г. «Опыт о способе изображения
мнимых количеств в геометрических построениях». Арган ставит и корректно решает
задачу построения исчисления направленных отрезков, которые он называет
«направленными линиями». Примерно в то же время появился и ряд других работ (М.
Бюэ, Дж. Уоррена и др.), в которых делаются попытки обобщения алгебраических
понятий таким образом, чтобы «числами» и «величинами» охватить отрицательные и
комплексные числа, и направленные отрезки.
В
математике эта теория окончательно утвердилась после «курса алгебраического
анализа» (1821) О. Коши и «Теории биквадратичных вычетов» (1832) Гаусса.
Дальнейшее
развитие векторного исчисления связано с исследованиями гиперкомплексных
числел, с помощью которых можно было бы изучать повороты направленных отрезков
в пространстве.
Представители
английской школы символической алгебры Дж. Пикок (1791-1858), Д. Грегори
(1813-1844), А.Де Морган (1806-1874), Дж. Гревс (1806-1870) получили ряд
интересных результатов, изучая триплеты, т.е. выражения вида
t=a+bi+cj,
где
i2=-1,
j2=-1, a, b, c - действительные числа.
Однако
им не удавалось так задать операции с триплетами, чтобы наряду с умножением
была бы выполнима операция деления, кроме деления на нуль. У. Гамильтон в
течение нескольких лет изучал операции с триплетами. Проделав громадные
вычисления, он убедился, что на множестве триплетов систему с делением построить
невозможно, и перешел к исследованию кватернионов, т.е. выражений вида
w=a+bi+cj+dk,
где i2=j2=k2=-1,
ij=-ji=k, jk=-kj=I, ki=-ik=j, a,b,c,d -
действительные числа.
В
своем труде «Лекции о кватернионах» Гамильтон дал строгое изложение алгебры
комплексных чисел и создал учение, которое явилось одним из алгебраических
источников развития современного векторного исчисления. В работе автор впервые
вводит термины «вектор» (от лат. vector - «несущий или ведущий, влекущий, переносящий»),
«скаляр», скалярное и векторное произведения, а так же определяет операции с
векторами в трехмерном пространстве. Он писал: «Шаг от точки А к точке В можно
рассматривать как работу по транспортировке или переносе подвижной точки из
начального положения в конечное».
Теорию
кватернионов развил и усовершенствовал математик и физик П. Тэт (1831-1901),
посвятивший теории кватернионов и ее приложениям к физике 70 своих работ. В
1867 г. в «Элементарном трактате по теории кватернионов» Тэт впервые дал
векторное изложение аналитической геометрии. В главе «Геометрия прямой и
плоскости» Тэт предложил те задачи, которые и сейчас входят в учебники: найти
уравнение прямой, проходящей через две данные точки; найти длину
перпендикуляра, опущенного из данной точки на плоскость; найти условие того,
что четыре данные точки лежат в одной плоскости, и т.д.
Грассман
в труде «Учение о протяженности» (1844 г.) впервые излагает учение об n-
мерном евклидовом пространстве, которое как частный случай включает теорию
векторов на плоскости и в трехмерном пространстве. Векторы, названные автором
палочками, он обозначал жирными буквами латинского алфавита. Скалярное
произведение векторов, названное им внутренним произведением, он обозначал a | b;
векторное произведение, внешним произведением, он обозначал [a, b].
Во
второй половине 19 в. идеи векторного исчисления получили свое развитие, в
основном, в области физики. Так, Сен-Венан (1797-1886), опираясь на труды
Валлиса и Стевина, в работе «О геометрических суммах и разностях и их
применении для упрощения изложения механики» (1845 г.) разработал теорию
сложения и вычитания направленных отрезков. Джемс Кларк Максвелл (1831-1879),
один из создателей теории электромагнитного поля, применил в своем «Учении об
электричестве и магнетизме» векторное исчисление. «Ценность идеи вектора
несказанна», - писал Максвелл Тэту. Из разбухшего аппарата теории кватернионов
он выбрал то, что необходимо для векторного исчисления, и тем самым создал
удобный инструмент, который широко использует современная физика.
Однако
современный вид придали векторному исчислению в конце 19 в. американский физик,
один из основателей химической термодинамики и статической механики - Дж. Гиббс
(1839-1903), Грассман, и английский физик О. Хевисайд (1850-1925), применивший
векторы в своей «Электромагнитной теории».
В
последней четверти 19 в. происходит слияние, синтез трех путей
(геометрического, алгебраического и физического) исторического развития и трех
источников формирования векторного исчисления. Векторное исчисление становится
независимой ветвью математики.
В
современной математике раздел, в котором излагается учение о действиях с
векторами, называют векторной алгеброй, так как эти действия имеют много
свойств с алгебраическими действиями. Наряду с ней Гамильтон создал и векторный
анализ, изучающий переменные векторы - векторные функции, и определил
производные скалярной функции по векторному аргументу (градиент) и некоторые
виды производных вектор-функций векторного аргумента - дивергенцию и роторы.
История
векторного анализа подчеркивает неразрывную связь отдельных областей математики
- алгебры, геометрии, математического анализа, теории функций комплексного
переменного. Созданные в 16 в. для решения алгебраических уравнений комплексные
числа в 19 в. стали образцом для открытия теории гиперкомплексных чисел,
которая вскоре привела ученых к теории кватернионов и к векторному исчислению.
Векторный анализ, построенный как математический аппарат для изучения
электричества и магнетизма, стал научной базой для развития физических теорий,
что в последствии привело к созданию тех благ цивилизации, которыми сейчас
пользуется человечество.
1.2 Различные подходы к определению понятия вектора в математике и в
школьном курсе математики
Вектор является одним из фундаментальных понятий современной математики.
Эволюция этого понятия осуществлялась благодаря широкому использованию его в
различных областях математики, механики, а так же в технике.
Уже на уроках физики в 7 классе изложение материала ведется с широким
привлечением векторного аппарата. Понятно, что это заставляет задуматься,
прежде всего, над тем, как наиболее естественно ввести в курс математики
средней школы понятие вектора, как эффективнее применять его при изложении
теории и решении задач, как рассматривать основные действия над векторами.
Известно, что существует несколько подходов к ведению этого понятия.
В учебнике Л.Я. Куликова по алгебре [17] «n-мерным вектором над полем F (где F-поле
скаляров) называется любой кортеж из n элементов поля F».
При таком подходе вектор обычно записывается в виде строки или столбца.
Например, (α1, α2,…,
αn), где αi-скаляры.
Вводится определение равных векторов.
Определение1:
Векторы (α1, α2,…, αn) и (β1,β2,…, βn)
называются равными, если αi=βi, 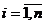 .
.
Так
же на множестве n-мерных векторов определены операции сложения,
умножения вектора на скаляр.
Определение
2: Суммой векторов (α1, α2,…, αn) и (β1,β2,…, βn)
называется вектор (α1+β1,α2+β2,…, αn+βn).
Определение
3: Произведением скаляра λ
на вектор (α1, α2,…, αn)
называется вектор (λα1, λα2,…, λαn).
Определение
4: Вектор (0,0,…,0) называется нулевым вектором и обозначается символом 0.
Нулевой вектор является нейтральным элементом относительно сложения.
Определение
5: Вектор (-1)(α1, α2,…, αn)
называется вектором, противоположным вектору а=(α1, α2,…, αn), и
обозначается символом - а.
Очевидно
а+(-а)=0.
В
теории линейной алгебры можно встретить другой, абстрактный подход. Например, в
учебном пособии [4] вектор определяется как элемент векторного пространства V,
который обладает рядом свойств:
) (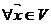 ) 1×
) 1×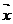 =
=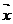 ;
;
) (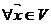 ) 0×
) 0×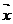 =
=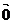 ;
;
) (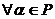 ) a×
) a×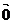 =
=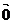 ;
;
) (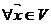 ) (-1)×
) (-1)×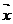 = -
= - 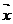
В данном случае определение вектора вводится аксиоматически, через
систему свойств.
В качестве векторных пространств в смысле этого определения можно
привести следующие:
. V2-множество векторов на плоскости. Тогда V2- векторное пространство над |R.
. С - векторное пространство над |R, Q. |R-векторное пространство над Q.
3.
Нулевое векторное пространство V={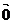 } над Р.(
} над Р.(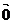 +
+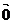 =
=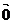 , a×
, a×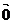 =
=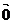 ).
).
Анализируя
оба подхода к определению понятия вектора, лежащих в основе линейной алгебры,
можно сделать вывод, что в данном случае геометрия полностью заменяется
алгеброй, а все арифметические операции над векторами сводятся к аналогичным
операциям над числами.
В
геометрии к определению понятия вектора другой подход:
«Вектор
- геометрический объект, характеризующийся направлением и длиной».
Кроме
того, существуют различные конкретизации.
I. Предметом
векторного исчисления служит вектор как множество сонаправленных отрезков,
имеющих одинаковую длину.
Соответственно
этому подходу векторы рассматривают с точностью до их положения (т.е. не
различая равных векторов, получающихся друг из друга параллельным переносом). В
этом смысле векторы называют свободными. Таким образом, свободные векторы
вполне определяются заданием его длины и (если он не нулевой) направления.
Равные векторы, не совпадающие по положению, рассматриваются как различные
конкретные изображения одного и того же свободного вектора.
Данный
подход имеет ряд преимуществ. Во-первых, он упрощает понятие равенства, а
во-вторых, однозначно определяет операции для свободных векторов. Так, сумма
двух свободных векторов есть определенный свободный вектор, тогда как, к
примеру, суммой двух направленных отрезков служит любой из направленных
отрезков, полученных соответствующим построением. Тем не менее, этот подход
осложняется большим числом оговорок. Например, из начального курса физики
хорошо известно, что сила может быть изображена направленным отрезком. Но она
не может быть изображена вектором в смысле этого определения, поскольку силы,
изображаемые равными направленными отрезками, производят, вообще говоря,
различные действия. (Если сила действует на упругое тело, то изображающий её
отрезок не может быть перенесен даже вдоль той прямой, на которой он лежит).
II. В основу
теории движения заложено понятие вектора как параллельного переноса.
Параллельным
переносом называется такое движение, при котором точки смещаются по
параллельным прямым на одно и то же расстояние в одном и том же направлении.
Действительно, задать параллельный перенос - это все равно, что задать длину (а
именно расстояние, на которое смещаются все точки) и направление (а именно,
направление, в котором смещаются все точки), а задать длину и направление - все
равно, что задать свободный вектор.
В
этом случае сложение векторов соответствует сочетанию (композиции) параллельных
переносов.
Такое
определение вектора позволяет устранить противоречия с теоретико-множественной
точки зрения на понятие равенства, которое возникло при традиционном
определении вектора как направленного отрезка. Кроме того, такой подход к
введению понятия вектора является логически безупречным, но, между тем, он
недостаточно нагляден.
III. В
аналитической геометрии вектор определяется как направленный отрезок.
«Пара
точек называется упорядоченной, если про эти точки известно, какая из них
первая, а какая-вторая» [4, с. 15].
Определение
1: Отрезок, концы которого упорядочены, называется вектором. Нулевой вектор -
вектор, у которого начало и конец вектора совпадают.
Определение 2: Векторы называются коллинеарными, если существует такая
прямая, которой они параллельны.
Определение 3: Расстояние между началом и концом вектора называется его
длиной.
Определение 4: Два вектора называются равными, если они коллинеарные,
одинаково направлены и имеют равные длины.
При данном подходе операции сложения векторов и умножения вектора на
число определяются следующим образом:
Определение
5: Пусть даны 2 вектора 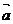 и
и 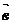 . Суммой
. Суммой 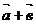 называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора 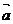 в конец вектора
в конец вектора 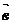 , при
условии, что вектор
, при
условии, что вектор 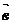 приложен к концу вектора
приложен к концу вектора 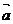 .
.
Определение
6: Пусть даны вектор 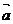 и число a. Обозначим их
модули соответственно через |
и число a. Обозначим их
модули соответственно через |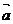 | и |a|. Произведением a
| и |a|. Произведением a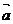 называется вектор, который коллинеарен вектору
называется вектор, который коллинеарен вектору 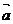 , имеет длину, равную |a|×|
, имеет длину, равную |a|×|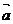 |, и направление
такое же, как у вектора
|, и направление
такое же, как у вектора 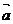 , если a>0, и
противоположное, если a<0.
, если a>0, и
противоположное, если a<0.
Операция вычитания векторов определяется как операция, обратная сложению.
Определение
7: Разностью 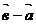 называется вектор, который в сумме с вектором
называется вектор, который в сумме с вектором 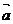 составляет вектор
составляет вектор 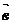 .(разность
двух векторов, приведенных к общему началу, есть вектор, идущий из конца «вычитаемого»
вектора в конец «уменьшаемого»).
.(разность
двух векторов, приведенных к общему началу, есть вектор, идущий из конца «вычитаемого»
вектора в конец «уменьшаемого»).
Данный подход к определению понятия вектора нагляден, но неоднозначно
определяет результат операций над векторами.
Анализируя представленные подходы, необходимо отметить, что векторы,
представляемые параллельными переносами, перемещением точек, направленными
отрезками являются лишь изображения векторов, но не сами векторы в их общем
понятии.
Приведем еще один подход к определению понятия вектора, автором которого
является Вейль. Этот подход составляет основу векторного изложения геометрии
[5].
Вейль
относит вектор к числу первоначальных неопределяемых понятий. К ним же
относится и понятие суммы векторов (некоторое правило, которое каждым двум
векторам  и
и 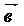 однозначно
сопоставляет вектор
однозначно
сопоставляет вектор  +
+ 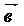 ),
умножение вектора на число, скалярное произведение векторов
),
умножение вектора на число, скалярное произведение векторов
Свойства
арифметических операций над векторами автор описывает через систему аксиом. Он
выделяет 5 групп аксиом.
группа:
аксиомы сложения
.1. (" и
и 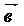 )
) 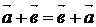 ;
;
.2. (" ,
, 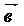 ,
, 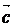 )
) 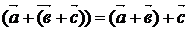 ;
;
.3. ($!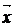 )("
)(" )
)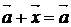 ; вектор
; вектор 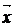 принято
обозначать
принято
обозначать 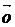 и называть нулевым вектором.
и называть нулевым вектором.
.4. (" )($!
)($!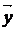 )
)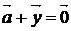 ; вектор
; вектор 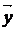 принято
обозначать
принято
обозначать 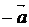 и называть вектором, противоположным вектору
и называть вектором, противоположным вектору  .
.
2 группа: аксиомы умножения вектора на число
2.1.
(" k, l,  )
) 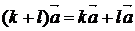 ;
;
.2.
(" k,  ,
, 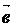 )
) 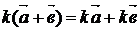 ;
;
.3.
(" k, l,  )
) 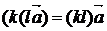 ;
;
.4.
(" )
)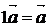
группа:
аксиомы размерности
.1.
Существует три линейно независимых вектора;
.2.
любые 4 вектора линейно зависимы
группа:
аксиомы скалярного умножения векторов
.1.
(" ,
, 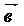 )
) 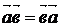 ;
;
.2..
(" k,  ,
, 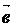 )
) 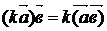 ;
;
.3.
(" ,
, 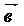 ,
, 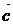 )
) 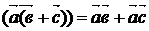 ;
;
.4.
("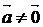 )
)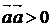 ; умножение вектора
; умножение вектора  на себя
называется скалярным квадратом и обозначается
на себя
называется скалярным квадратом и обозначается  2. Длиной вектора
2. Длиной вектора  называется
число
называется
число 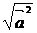 .
.
Все
4 группы аксиом справедливы для множества R3 - множества всех векторов. Кроме этого множества
Вейль рассматривает непустое множество Е3, элементами которого
являются точки. Точка, как и вектор, относится к числу неопределяемых понятий.
К ним же относится и некоторое правило, которое каждой упорядоченной паре А, В
ставится в соответствии вектор 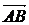 .
.
В
связи с этими понятиями Вейль приводит 5 группу аксиом: аксиомы точек:
.1.
(" т. А, В, С) 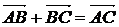
.2.
(" т. А,  ) ($В)
) ($В) 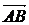 =
=
.3..
(" т. А, В) 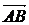 =
=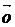 ÞА=В
ÞА=В
На
основе приведенных определений и аксиом Вейль вводит различные основные понятия
геометрии, доказывает теоремы.
Такой
подход к определению понятия вектора достаточно громоздкий. Кроме того, при
таком подходе затруднено понятие результата выполнения арифметических действий
над векторами. Тем не менее, этот подход обладает рядом преимуществ: при
векторном изложении некоторые теоремы геометрии доказываются значительно проще,
чем при традиционном изложении.
Итак,
в математике существуют различные подходы к определению понятия вектора. Каждый
из них имеет преимущества и недостатки. Однако никакой из них не может быть
«перенесен» в школьный курс геометрии без должных оговорок.
Рассмотрим специфику изложения темы «Векторы» в различных школьных
учебниках по геометрии.
Прежде всего, обратимся к истории. Как же предполагалось изучать векторы?
В учебном пособии [10] под редакцией А.Н. Колмогорова вектор определялся
как параллельный перенос плоскости: «Параллельным переносом (вектором)
называется отображение плоскости на себя, при котором все точки плоскости изображаются
в одном и том же направлении на одно и то же расстояние».
Это определение обладает тем важным преимуществом, что параллельный
перенос представляет свободный вектор, и потому все векторные операции с ним
определяются как однозначные. При таком определении вектора векторное
исчисление может быть изложено без противоречий и смешения понятий.
Однако если обратиться к задачам, предлагаемым в учебнике, то сразу
видно, что в них фигурируют направленные отрезки, а не переносы плоскости или
пространства.
В следующем пособии для 9-10 классов [11] (под редакцией З.А. Скопеца),
вектор определяется уже как параллельный перенос пространства. «Параллельным
переносом, определяемым парой (А, В) несовпадающих точек, называется
преобразование пространства, при котором каждая точка М отображается на такую
точку М1, что луч ММ1 сонаправлен с лучом АВ, расстояние ½ММ1½равно расстоянию ½АВ½». Таким образом, вектор вводился как множество пар
точек, задающих один и тот же перенос.
В последнем издании учебника под редакцией А.Н. Колмогорова явно вводится
понятие свободного вектора, и перенос привлекается только как его изображение.
В результате изложение оказалось существенно лучше, чем в других учебниках для
6-8 классов того времени, без путаницы и ошибок.
В перестройке школьного курса геометрии, происходящей в середине 80-х
годов ХХ века, одним из центральных моментов оказалось коренное изменение
понятия о векторе. Вектор, определяемый как параллельный перенос плоскости или
пространства, был заменен направленным отрезком: на место отображения плоскости
или пространства на себя поставлена фигура с «отмеченной» точкой (один конец
отрезка «отмечен» как начало).
Проведем обзор введения понятия вектора в современных учебниках.
В учебнике А.В. Погорелова [21] изложение темы начинается следующим
образом: «Вектором мы будем называть направленный отрезок. Направление вектора
определяется указанием его начала и конца… Для обозначения векторов будем
пользоваться строчными латинскими буквами а, b, c,… Можно так же обозначить вектор указанием его начала и
конца. При этом начало вектора ставится на первое место» [21, c. 117].
«Абсолютной величиной (или модулем) вектора называется длина отрезка,
изображающего вектор».
Проведем анализ данного подхода. Назвав направленный отрезок вектором,
автор не объяснил, не определил, что называется направленным отрезком. Поэтому
и конкретное определение вектора отсутствует. Говорится только о направлении
вектора - «отмечается стрелкой», хотя «стрелка» - это не геометрическое
понятие.
При введении обозначений не понятно, что называется началом и концом
вектора. Это происходит оттого, что опять же не дано определение направленного
отрезка, который «направлен» тем, что указан порядок его концов.
Модулем вектора названа «длина отрезка, изображающего вектор». Таким
образом, выходит, что направленный отрезок, который назван вектором, изображает
вектор. Получается некоторого рода тавтология. (Направленный отрезок и есть
изображение вектора, а не сам вектор, как его понимают в векторном исчислении.)
Далее определяется равенство векторов - направленных отрезков: они равны,
если совмещаются параллельным переносом. Перенос же был определен ранее
формулами х¢=х+а, у¢=у+b в прямоугольных координатах. Однако, то, что это определение
не зависит от выбора системы координат, не оговаривается. Таким образом,
принципиальный момент независимости определения от выбора системы координат
оказался скрытым.
Затем вводятся координаты вектора, и операции с векторами определяются
через операции с их координатами; исходный геометрический смысл этих операций
отодвигается на второй план, так что получается искаженное представление
векторного исчисления, которое создано и применяется как геометрическое
исчисление, чтобы обходиться, насколько возможно, без координат.
К тому же получается непоследовательность: понятие вектора определяется
посредством наглядного образа направленного отрезка, а в определении действий
этот образ не используется. Кроме того, координаты задают не вектор как
направленный отрезок, а свободный вектор: у всех равных векторов координаты
одни и те же. Поэтому фактически определяются операции со свободными векторами.
Таким образом, вместо исчисления векторов подается исчисление пар чисел с
геометрической интерпретацией.
Так
координаты вытесняют геометрию. Этот факт хорошо прослеживается при
формулировке теорем и их доказательств. Например, при доказательстве того, что
векторы 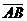 и
и 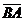 противоположно
направлены, используют координаты (пользуются правилом умножения вектора на
число, в частности на -1), тогда как ответ был бы очевиден, если геометрически
определено, что значит противоположно направленные векторы (но такое
определение не дано).
противоположно
направлены, используют координаты (пользуются правилом умножения вектора на
число, в частности на -1), тогда как ответ был бы очевиден, если геометрически
определено, что значит противоположно направленные векторы (но такое
определение не дано).
Положительным
моментом является рассмотрение физического приложения векторов в § 95 -
«Сложение сил». В нем вводится равнодействующая нескольких сил, и определяется
их изображение. Приведен пример решения задачи из физики.
В
задачном материале А.В. Погорелов рассматривает следующие виды заданий:
Доказательство
равенства векторов;
Доказательство
перпендикулярности векторов;
Вычисление
угла между векторами.
Основным
теоретическим базисом при решении этих задач являются определения равенства
векторов и скалярного произведения векторов. Надо отметить, что аппаратом
решения заданий становятся формальные действия с координатами, т.е.
геометрическое приложение векторов опускается.
Также
автор предлагает 2 содержательные задачи. Их требование - найти угол между
прямыми.
В
учебнике Л.С. Атанасяна и др. [8] вектор так же определяется как направленный
отрезок, но изложение строится иначе, чем в учебнике А.В. Погорелова.
В
параграфе «Понятие вектора» п.1 начинается так: «Многие физические величины,
например сила, перемещение материальной точки, скорость, характеризуются не
только своим числовым значением, но и направлением в пространстве. Такие
физические величины называются векторными величинами или векторами».
Далее,
после приведения примера изображения силы в физике, говорится: «Отвлекаясь от
конкретных свойств физических векторных величин, мы приходим к геометрическому
понятию вектора… Определение. Отрезок, для которого указано, какой из его
концов считается началом, а какой - концом, называется направленным отрезком
или вектором.
Недостаток
этого изложения состоит в том, что дается два понятия вектора без должных
оговорок. Однако авторы не могут оставить определение вектора как направленного
отрезка. В конце §1 они делают важное замечание.
«Замечание.
Равные векторы, отложенные от разных точек, часто обозначают одной и той же
буквой. Иногда про такие векторы говорят, что это один и тот же вектор, но
отложенный от разных точек». По сути, здесь говорится о свободном векторе. Но
само определение этого понятия не вводится.
Описав
сложение векторов по правилу треугольника, когда первое слагаемое 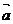 откладывается от точки А, так что
откладывается от точки А, так что 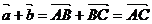 , авторы пишут: «Докажем, что если… точку А, от
которой откладывается вектор
, авторы пишут: «Докажем, что если… точку А, от
которой откладывается вектор 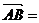
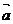 ,
заменить другой точкой А1, то вектор
,
заменить другой точкой А1, то вектор 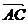 заменится
равным ему вектором
заменится
равным ему вектором 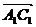 ». Таким образом, сумма представляется неоднозначной:
ее представляют бесконечно много (хотя и равных) направленных отрезков. Это
вносит некоторую неопределенность, хотя и логично с точки зрения подхода,
изложенного в данном учебнике.
». Таким образом, сумма представляется неоднозначной:
ее представляют бесконечно много (хотя и равных) направленных отрезков. Это
вносит некоторую неопределенность, хотя и логично с точки зрения подхода,
изложенного в данном учебнике.
Так
же недостаток изложения состоит еще в том, что в учебнике некоторые важнейшие
свойства векторов принимаются без доказательства, хотя их можно было бы
доказать доступно для учащихся. Так, свойствам произведения вектора на число
дается только геометрическая интерпретация.
Задачный
материал в учебнике Л.С. Атанасяна направлен на осознание, осмысление вводимых
дидактических единиц. Он служит своеобразным пропедевтическим курсом для
решения задач векторным методом.
Содержательных
задач в главе немного, но они разнотипны. Ключевые из них решены в учебнике.
В
учебнике И.Ф. Шарыгина [31] вектор так же определяется через направленный
отрезок: «Рассмотрим на плоскости две точки А и В. Обозначим через 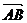 вектор АВ, понимая под этим направленный отрезок АВ,
т.е. отрезок, у которого точка А является началом, а точка В концом».
вектор АВ, понимая под этим направленный отрезок АВ,
т.е. отрезок, у которого точка А является началом, а точка В концом».
Автор
не вводит определения сонаправленных и коллинеарных векторов, поэтому понятие
равенства состоит из двух утверждений: «Два вектора 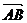 и
и 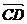 ,
расположенные на одной прямой, считаются равными, если равны отрезки АВ и CD,
т.е. равны длины этих векторов, а лучи АВ и CD задают
одинаковые направления.
,
расположенные на одной прямой, считаются равными, если равны отрезки АВ и CD,
т.е. равны длины этих векторов, а лучи АВ и CD задают
одинаковые направления.
Если
же векторы 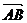 и
и 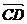 не
расположены на одной прямой, то они считаются равными, если четырехугольник АВDC
является параллелограмом».
не
расположены на одной прямой, то они считаются равными, если четырехугольник АВDC
является параллелограмом».
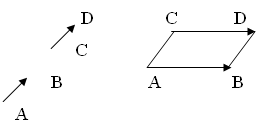
Такое
определение достаточно сложно для понимания учащимися. Каждый раз при
доказательстве равенства векторов требуется достраивание до четырехугольника,
что не всегда удобно, и показывать, что он является параллелограммом.
Далее
говорится: «Таким образом, мы можем вектор не только перемещать вдоль
соответствующей прямой, но и переносить его начало в любую точку плоскости».
Тем самым автор высказывает идею о свободном векторе.
Так
же, как и А.В. Погорелов, И.Ф. Шарыгин вводит координаты вектора, и на их
основе определяет операции с векторами.
В
связи с этим, и основным способом решения задач по учебному пособию И.Ф.
Шарыгина становится выражение векторов через координаты, произведение с ними
арифметических действий.
Автор
предлагает задания на отработку понятия скалярного произведения векторов. Он
приводит следующие виды метрических задач:
- найти угол между прямой и плоскостью;
- найти угол между плоскостями;
доказательство того факта, что сумма косинусов двугранных углов
любого тетраэдра не больше двух;
доказательство того, что все три угла между биссектрисами
плоских углов трехгранного угла одновременно либо острые, либо прямые, либо
тупые.
Также И.Ф. Шарыгин предлагает для решения достаточное количество
содержательных задач, методом решения которых может стать векторный.
В учебнике А.Д. Александорова [2] понятие вектора вводится аналогично
подходу, изложенному у Л.С. Атанасяна.
«Величины, которые характеризуются не только численным значением, но и
направлением, называются векторными величинами или векторами. Численное
значение вектора называется его модулем».
Далее автор выделяет пункт «Направленные отрезки».
«…Если тело переместилось из точки А в точку В, то это перемещение
естественно изобразить отрезком, направленным из точки А в точку В…У
направленного отрезка указан порядок концов.» После этого автор обращает
внимание учащихся на то, что направленный отрезок - лишь изображение вектора, а
не сам вектор в общем понимании.
В отличие от Л.С. Атанасяна, А.Д. Александров доказывает, что отношение
равенства на множестве векторов обладает отношением эквивалентности, выделяя
тем самым следующие свойства:
1. Каждый вектор равен самому себе.
2. Если
вектор 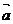 равен вектору
равен вектору 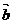 , то
, то 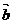 равен
равен 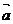 .
.
. Два
вектора, равные третьему вектору, равны.
Однако, в отличие от остальных авторов, А.Д. Александров не вводит
понятие компланарных векторов. Он определяет следующие способы разложения
вектора: по прямой и плоскости, по трем прямым. Предлагает для решения задачи
на отработку этих умений.
Кроме того, А.Д. Александров приводит задачи на геометрическую
интерпретацию векторов:
- Отложить вектор, равный сумме двух или более данных;
- Отложить вектор, равный разности двух векторов;
Доказать векторные равенства, пользуясь изображением
параллелепипеда.
Анализируя представленные подходы, можно сделать вывод, что все авторы в
той или иной степени стремятся дать определение свободного вектора. Это
делается у различных авторов по-разному. Дело в том, что если понимать вектор
как любой из равных направленных отрезков, то нужно только определить, что
значит, что эти отрезки одинаково направлены, а это можно определить достаточно
просто, через сонаправленные лучи, например, как сделано в учебнике А.Н.
Колмогорова. (Но в этом учебнике транзитивность сонаправленности не доказана.)
В учебнике Л.С. Атанасяна и др. полного определения нет, а у А.В. Погорелова
оно опирается на понятие параллельного переноса, определение которого сложно,
поскольку использует координаты.
В заключении приведем цитату из статьи А.Д. Александрова: «Определение
вектора как направленного отрезка, рассматриваемого с точностью до выбора
начала, может показаться настолько расплывчатым и не подходящим под
установившиеся стандарты определений. Но оно выражает то, как в
действительности понимают вектор, и потому на самом деле применяют, а не так,
что дается определение, заучивается, а затем применяется другое определение.
Определения нужны не для заучивания, а для уточнения понимания. Нужно
добиваться не пустого заучивания, а действенного, т.е. работающих в применениях
понимания» [3, с. 45].
1.3 Обучение решению задач как психологическая и методическая проблема
С выдвижением понятия вектора в число ведущих идей школьного курса
геометрии векторный метод стал одним из основных методов решения геометрических
задач. Поэтому перед выявлением специфики векторного метода, разработки
конкретной методики обучения школьников решению математических задач,
необходимо проанализировать само понятие задач, их роль и место в обучении
математике.
Задачи играют огромную роль в жизни человека. Задачи, которые ставит
перед собой человек, и задачи, которые ставят перед ним другие люди и
обстоятельства жизни, направляют всю его деятельность, всю его жизнь. Поэтому
проблемы, связанные с этим понятием, занимают значительное место во многих
науках. Например, в психологии исследуются процессы решения задач и особенности
этих процессов при решении отдельных их видов. Предметом исследования дидактики
и частных методик являются вопросы использования решений задач в обучении.
Выявим существенные дидактические, психологические и методические аспекты
задач применительно к обучению математике.
В обучении математике задачи играют большую роль. Эта роль определяется,
с одной стороны, тем, что конечные цели этого обучения сводятся к овладению
учащимися методами решения определенной системы математических задач. С другой
стороны, она определяется и тем, что полноценное достижение целей обучения
возможно лишь с помощью решения учащимися системы учебных и математических
задач, которые являются важнейшим средством формирования у школьников системы
основных математических знаний и способов деятельности.
Кроме того, «от эффективности использования задач в обучении математике
во многом зависит не только качество обучения, воспитания и развития учащихся
средней школы, но и степень их практической подготовленности к последующей за
обучением деятельности в любой сфере производства, народного хозяйства,
культуры, личных и общественных взаимоотношений» [24, с.5].
Чтобы раскрыть еще большую значимость математических задач в школьном
обучении, попробуем выявить роль и место задач во всей системе школьного
математического образования, в единстве реализуемых при этом целей обучения,
воспитания и развития учащихся.
Выявление роли и места задач в современном обучении математике диктует
целесообразность изучения дидактически направленной характеристики важнейших
компонентов математического развития учащихся, которые должны формироваться в
процессе школьного обучения, выявления основных функций задач в системе
развивающего и воспитывающего обучения математике; характеристики самого
понятия учебной задачи и психолого-дидактических особенностей процесса ее
решения.
В различных областях знания (психология, педагогика, математика, методика
математики) проблему содержания понятия «задача» исследовали Г.А. Балл, Ю.М.
Калягин, Л.М. Фридман, В.И. Крупич, А.Ф. Эсаулов, Н.А. Менчинская и многие
другие. Каждый из них дает свою точку зрения на рассматриваемую проблему.
Приведем несколько определений понятия задачи:
Примером наиболее широкой трактовки понятия задачи является определение,
данное Я.А. Пономаревым, как «состояние возмущения взаимодействующей системы».
А.Ф. Эсаулов определяет задачу как более или менее определенную систему
информационных процессов, несогласованное или даже противоречивое отношение
между которыми вызывает потребность в их преобразовании. Суть решения как раз и
заключается в поисках преодоления путей такого несогласования.
С.О. Шатуновский предлагает рассматривать задачу как изложение требования
«найти» по «данным» вещам другие «искомые вещи», находящиеся друг к другу и к
данным вещам в указанных состояниях.
В методике математике под задачей принято понимать «задание, которое
должен выполнить субъект, или вопрос, на который он должен найти ответ,
опираясь на указанные условия и все вытекающие из них следствия» [28, с. 158].
Из приведенных примеров различных трактовок понятия задачи, можно сделать
вывод, что понятие задачи достаточно сложно и многогранно.
Г.И. Саранцев считает, что основное отличие в подходах к содержанию этого
понятия состоит в том, что авторы по-разному подходят к отношению между
субъектом и задачей. Одни из них рассматривают задачу как ситуацию, в которой
действует субъект, в других трактовках субъект не включается в понятие задачи.
Таким образом, он подчеркивает, что для задачи характерны две стороны:
объективная и субъективная. К первой относятся предмет действия, требование,
место в системе задач, логическая структура решения задачи, определенность и
неопределенность условия и т.д., ко второй - способы и средства решения.
К понятию «задача» тесно примыкает понятие процесса решения задачи.
В свою очередь, по мнению психологов, процесс решения задач тесно взаимосвязан
с процессом мышления. Многие исследования показывают, что именно в ходе решения
задач самым естественным образом можно формировать у школьников элементы
творческого, логического и алгоритмического мышления.
Необходимо отметить, что умственное развитие учащихся является одной из
основных задач обучения математике. Многие авторы связывают его именно с
развитием математического мышления. В соответствии с этим возникает вопрос, что
представляет собой математическое мышление, каковы его специфические черты.
«Чаще всего математическое мышление рассматривается в соответствии со
спецификой математики, которая состоит в особенностях ее абстракций (Ж. Адамар,
Б.В. Гнеденко, А.Н. Колмогоров, А.И. Маркушевичи др.)» [28, c.82]. В их работах сущность понятия
математического мышления ассоциируется с понятием математических способностей.
Выделяется огромное число черт математических способностей: сила
абстрагирования, оперирование абстракциями, геометрическая интуиция, четкое
логическое рассуждение, гибкость мышления, математическая интуиция,
анализирование, синтез, стремление к рациональности решения, лаконизм,
оригинальность мышления и др. Все эти способности можно развивать в процессе
решения задач. Поэтому наша цель на данном этапе - выявить такие условия обучения
решению задач, при которых максимально эффективно будут развиваться
перечисленные нами математические способности.
«Эффективность обучения находится в прямой зависимости от уровня
активности ученика в познавательной деятельности, степени его самостоятельности
в этом процессе, что, в свою очередь определяется познавательными интересами
школьников (Ю.К. Бабанский, М.А. Данилов, А.В. Усова, Г.И. Щукина и др.)» [25,c.11]. Источником их развития теория
познания считает противоречия в самом процессе познания человеком
действительности, фиксируемые посредством категории проблемы. Поэтому развитие
творческих мыслительных способностей и познавательной самостоятельности
учащихся невозможно вне проблемных ситуаций. Необходимо внедрение
проблемно-развивающего обучения. Задачи при таком обучении служат основным
средством активизации знаний и способов действий. Они используются для
раскрытия содержания понятий, теорем, способов умственной деятельности ученика,
а также для формирования умений и навыков. В решение таких задач важно включать
этапы анализа задачи и обсуждения решения.
В процессе анализа задачи должны устанавливаться предметная область
задачи, все ее элементы, характер каждого элемента (постоянный или переменный,
известный или неизвестный и т.д.). Также необходимо вычленение из задачи всех
отношений, которыми связаны элементы предметной области. Это позволит выбрать
правильный подход к решению задачи.
В процессе анализа проделанного решения выявляются преимущества и
недостатки решения, проводятся поиски лучшего решения, устанавливаются и
закрепляются в памяти учащихся те приемы, которые были использованы в данном
решении, выделяются условия возможности применения этих приемов. Все это будет
в наилучшей степени способствовать превращению решения задач в могучее
обучающее средство.
Рассмотрев роль и место задач в обучении математике, осталось определить
функции математических задач.
В настоящее время решение математических задач используется для разных
функций.
Л.М. Фридман под функцией решения задачи понимает «проектируемые учителем
изменения в деятельности и психике учащихся, которые должны произойти в
результате решения ими этих задач» [30, с.151].
Одной из основных функций в обучении математике он считает функцию
формирования и развития у учащихся общих умений решений любых математических (в
том числе и прикладных) задач.
Общее умение по решению задач следует отличать от частных умений решения
задач определенного вида. Частные умения формируются на основе усвоения
учащимися теоретических знаний, пользуясь которыми учащиеся производят операции
и действия, входящие целостным элементом в формируемое умение.
Общее же умение решения математических задач пока формируется совсем
иначе: часто стихийно, а не в результате целенаправленного систематического
обучения. Считается, что эти умения могут возникнуть лишь благодаря решению
большого количества математических задач. А в результате, большинство учащихся,
встретившись с задачей незнакомого или малознакомого вида, не знают, с чего
начать решение.
Формирование общих умений решения математических задач осуществляется
таким образом, что учащиеся не получают никаких особых знаний, лежащих в основе
этих умений. Поэтому представления учащихся о задачах, их элементах и
структуре, о сущности и механизмах их решения является весьма смутными, а
зачастую просто неверными. Притом эти представления по мере перехода в старшие
классы отнюдь не улучшаются, т.к. они формируются часто стихийно, в результате
случайной информации и редкой рефлексии на свои действия в процессе решения многочисленных
задач.
Это происходит потому, что действующие программы по математике не
предусматривают изучения каких-либо теоретических основ о задачах и их решении.
В то же время, теоретические знания о задачах и их решении нужны учащимся для
того, чтобы они могли производить решение разнообразных задач сознательно и
целенаправленно, а не только лишь на основе подражания по аналогии с ранее
решенными задачами.
«Общие знания о задачах и механизмах их решения нужны для того, чтобы
решение задач принимало наиболее познавательный эффект, чтобы процесс их
решения превратился в подлинный метод обучения учащихся определенным знаниям и
навыкам» [30, c.154].
В отличие от Л.М. Фридмана Ю.М. Колягин к главным функциям задач относит
воспитывающую и развивающую функции. К числу важнейших воспитывающих функций
задач он относит «формирование у школьников диалектико-материалистического
мировоззрения, познавательного интереса и творческих задатков, воспитание
чувства патриотизма, эстетическое воспитание и т.д.» [24, с.11].
В частности, автор поясняет, что в процессе применения математики к
решению любой практической задачи, можно показать школьникам, что математика,
отражая явления реальной действительности, является мощным средством ее
познания. Предложение учащимся задачи с избыточной или неполной информацией
воспитывает у них готовность к практической деятельности. Рассмотрение изящного
решения той или иной математической задачи способствует эстетическому
воспитанию школьников.
Применение в обучении математике задач с воспитывающими функциями
способствует, по мнению Ю.М. Колягина, формированию у школьников интереса к
решению задач, что в свою очередь является эффективным средством приобщения
школьников к учебной математической деятельности творческого характера.
Как же должен строиться процесс обучения решению задач?
В методической литературе встречаются разделения задач по различным
основаниям.
Л.М. Фридман предлагает разделить все задачи на два вида:
) задачи на усвоение учебного материала (учебные задания);
) задачи на применение изученного учебного материала.
Задачи первого типа следует решать непосредственно в процессе изучения
учебного материала, и при этом все ученики решают одни и те же задачи. Число
таких задач невелико. Задачи же второго типа даются учащимся спустя некоторое
время. При этом выдается список всех рекомендуемых задач, которые они могут
решать.
Автор считает, что такая организация решения задач в процессе обучения
математике позволяет, кроме всего прочего, решить проблему длительного и
многократного повторения и закрепления изученного учебного материала и методов
решения задач.
К.И. Нешков и А.Д. Семушин выделяют следующие типы задач:
ü Задачи с дидактическими функциями;
ü Задачи с познавательными функциями;
ü Задачи с развивающими функциями.
Первые, по их мнению, предназначены для облегчения усвоения уже изученных
теоретических сведений. В процессе решения задач с познавательными функциями,
углубляются знания учащихся по отдельным разделам математики, школьники
знакомятся с важнейшими теоретическими сведениями, методами решения задач.
Задачи с развивающими функциями - это задачи, содержание которых расширяет
основной курс математики, способствует повышению уровня сложности нескольких
изученных ранее вопросов.
Опыт показывает, что наиболее приемлемым является выделение следующих
видов задач:
- По характеру требования - на вычисление или нахождение; на
доказательство или объяснение; на построение или преобразование;
- По отношению к способам решения - стандартные и нестандартные;
По характеру объектов - математические и реальные (или с
практически содержанием).
Очевидно, что отнесение задачи к группе задач с той или иной функцией не
является классификацией, поскольку одна и та же задача для различных субъектов
и в разных ситуациях может нести разные функции. Однако выделение функций задач
имеет смысл, т.к. учитывая цели обучения, важно, чтобы в системе задач по
конкретной теме присутствовали задачи с каждой из названных функций.
Итак, характерная для настоящего времени тенденция к повышению роли
проблемного обучения свидетельствует о том, что решение задач правомерно
занимает все более ведущее место в обучении математике, нередко определяя его
формы и методы, в которых основной акцент ставится на самостоятельное и
творческое усвоение школьниками учебного материала, на формирование их
математического развития, целостного развития личности и развития всех
психических процессов (воли, эмоций, памяти, воображения, представлений и
т.д.).
При обучении учащихся решению задач необходимо изучать с ними сами
задачи, их структуру и особенности, характер используемых общих методов
решения, их структуру деятельности по решению задач.
При этом главными объектами усвоения следует считать общие схемы
деятельности по решению задач, общие методы и способы моделирования задач.
Решение же отдельных задач должно быть лишь средством для такого обучения.
При обучении учащихся общим методам решения задач необходимо выделять
действия, составляющие суть этого метода. Подготовительная работа перед
решением определенного класса задач каким-либо методом должна быть направлена
на овладение учащимися этими действиями. Причем этот процесс должен приобрести
целенаправленный и управляемый характер.
В связи с вышеизложенным перед нами встает ряд проблем. Какие действия
составляют суть векторного метода? Как строить процесс обучения этим действиям?
Какую методику следует избрать при обучении учащихся собственно векторному
методу решения геометрических задач? Для ответа на поставленные вопросы
необходимо проанализировать методическую литературу по теме «Обучение
школьников векторному методу решения геометрических задач».
.4 Методика обучения векторному методу решения аффинных задач в геометрии
Проблемой методики обучения учащихся векторному методу занимались многие
ученые-методисты: В.А. Гусев, Г.Л. Луканин, Г.И Саранцев, З.А. Скопец, Т.А.
Иванова и другие.
Авторы учебного пособия [13] предлагают рассматривать вектор как
параллельный перенос плоскости (пространства). Однако при доказательстве теорем
и решении задач с помощью векторов используют определение вектора как
направленного отрезка.
При обучении учащихся векторному методу В.А. Гусев, Ю.М. Колягин и Г.Л.
Луканин дают следующие методические рекомендации [13, c.43]:
) необходимо заинтересовать учащихся, показав им эффективность
использования векторного метода на специально подобранных задачах;
)следует обучить учащихся некоторым эвристикам (системе определенных
правил, помогающих найти ключ к решению задачи), которые помогут создать у них
навык в его применении;
В частности, при обучении решению аффинных задач авторы указывают на
возможность формулирования следующих эвристик:
|
Что требуется доказать (на
геометрическом языке)
|
Что достаточно доказать (на
векторном языке)
|
|
а½êb
|
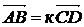 , [AB] Ìa, [CD] Ìb, k- число , [AB] Ìa, [CD] Ìb, k- число
|
АÎа, ВÎа, СÎа (три точки принадлежат одной прямой) А)
установить справедливость одного из следующих равенств 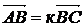 , или
, или 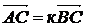 , или
, или 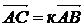 ;
;
Б)
доказать равенство 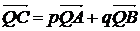 , где p+q=1, Q-произвольная точка;
, где p+q=1, Q-произвольная точка;
В)
доказать равенство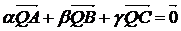 ,
,
|
где 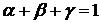 , Q-произвольная точка , Q-произвольная точка
|
СÎ[АВ], ½АВ½: ½СВ½=m:n (деление отрезка в данном отношении) А) 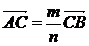
|
Б) 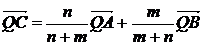 , где Q-произвольная точка , где Q-произвольная точка
|
) обучать векторному методу стоит на достаточно простых по
геометрическому содержанию задачах, чтобы не отвлекать внимание учащихся на
трудности чисто геометрического содержания;
) следует указать учащимся, что векторный метод не является универсальным,
к решению некоторых задач он может быть неприменим или малоэффективен.
З.А. Скопец в статье [26] кроме аффинных задач без векторных данных
(содержательных геометрических задач) рассматривает также еще два вида задач:
) задачи на доказательство и вычисление, для решения которых требуется
рассматривать векторно-параметрическое задание прямой и плоскости;
) Задачи, в содержание которых уже включены векторы.
Автор обращает большое внимание на решение задач различными методами
(векторным и конструктивным), подчеркивая важность их сопоставления для
развития математического мышления учащихся.
Более подробные методические рекомендации по обучению школьников
векторному методу решения геометрических задач, в частности при изучении темы
«Векторы в пространстве», дает Т.А. Иванова в учебных пособиях [6, 7].
Автор условно делит материал главы IV учебника [9] «Векторы в пространстве» на три самостоятельных
блока:
. Понятие вектора в пространстве. Сложение и вычитание векторов.
Умножение вектора на число.
. Компланарные векторы. Разложение вектора по трем некомпланарны
векторам.
. Применение векторов к решению геометрических задач.
Материал первого блока представляет собой систематизацию и обобщение на
пространство известных учащимися операций над векторами. Поэтому при его
рассмотрении необходимо усилить долю самостоятельной работы учащихся.
Материал второго блока является новым для десятиклассников и очень
важным. Поэтому наиболее целесообразной формой изучения теории представляется
школьная лекция.
Знакомству учащихся с новым для них методом решения геометрических задач
также следует посвятить лекцию, на которой учитель раскрывает сущность
векторного метода.
Т.А. Иванова в пособии [6] приводит следующие методические рекомендации к
построению отдельных уроков темы.
Как уже отмечалось, на первых уроках изучения векторов в пространстве с
учащимися необходимо повторить соответствующий материал планиметрии. Это можно
сделать следующим образом:
1) Решением упражнений на повторение (как устно, так и письменно, в
алгебраической форме и геометрически);
2) Заслушиванием докладов учащихся (необходимые записи при этом
производить в левой половине доски и листа тетради);
) Записью основных формул векторов на плоскости.
После повторения учитель сообщает, что аналогично можно ввести (доказать)
то или иное понятие (теорему) для пространства. Необходимые записи проводятся в
правой половине доски и листа тетради.
При этом, в зависимости от уровня знаний учащихся, форма изложения нового
материала может быть различной. Если класс средний, то возможна обобщающая
лекция с элементами эвристической беседы. Ее план:
. Понятие вектора в пространстве. Модуль вектора. Коллинеарные векторы.
Сонаправленные и противоположно направленные векторы. Равные векторы.
. Сложение и вычитание векторов.
. Умножение вектора на число.
Полученные основные результаты для пространства заносятся в таблицу:
Таблица 1
|
Векторы на плоскости и в
пространстве
|
|
1.определение
|
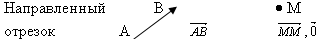
|
|
2. Длина
|
Длина отрезка АВ
|
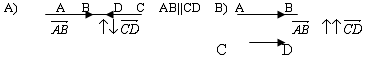
|
|
4.Равные векторы
|
(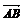 = =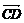 ) Û1) ) Û1) 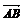 ¯ ¯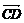 , 2)АВ=CD , 2)АВ=CD

|
|
5 Сложение векторов
|

|
6.
Вычитание векторов 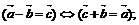
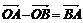
|
Теорема: 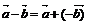
|
7.
умножение вектора на число 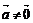 ,
, 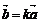 Û1)
Û1)  и
и  коллинеарные,
коллинеарные,
)½ ½=½
½=½ ½½k½
½½k½
Дома учащиеся, пользуясь учебником, более детально изучают каждый вопрос,
заучивают определения, разбирают доказательства теорем. К каждому пункту лекции
решают задачи из учебника.
В подготовленном классе можно предложить учащимся самостоятельно найти
ответы на выделенные выше вопросы. Для этого класс можно разбить на три группы,
каждая из которых готовит ответ на один вопрос и решает соответствующие задачи.
В классе заслушиваются эти ответы, после чего учитель подводит итоги урока и, в
частности, с помощью таблицы 1 систематизирует весь рассмотренный материал.
Приступая к построению уроков-практикумов, важно помнить, что «основная
дидактическая цель каждого урока по решению задач по материалам первых двух
блоков состоит в формировании умений и навыков, необходимых для решения
содержательных геометрических задач векторным методом» [6, с.16].
Охарактеризуем кратко эти умения.
К таким умениям, в первую очередь, относится владение векторными
формулами и законами векторной алгебры. Это умение достигается в процессе
решения простейших дидактических упражнений. Поскольку при решении
геометрических задач средствами векторов необходимы умения в преобразовании
векторных выражений, то при получении основных векторных выражений, то при
получении основных векторных формул следует приучать учащихся пользоваться ими
в “обе стороны”.
В то же время полезно предложить учащимся составлять на отдельном листе
таблицу основных векторных формул (таблица 2). Ее можно начать составлять уже в
8 классе.
Таблица 2
|
Основные формулы векторной
алгебры
|
|
1
|
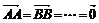
|
|
2
|
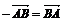
|
|
3
|
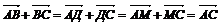
|
|
4
|
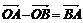
|
|
5
|
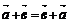
|
|
6
|
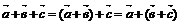
|
|
7
|
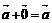
|
|
8
|
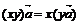
|
|
9
|
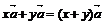
|
|
10
|
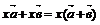
|
|
11
|
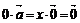
|
|
12
|
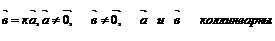
|
|
13
|

|
Следующим необходимым условием подготовки учащихся к решению задач с
помощью векторов является умение переводить геометрическое свойство на
векторный язык и обратно. Начинать вырабатывать его следует с самых первых
уроков изучения темы. Так, решая первые дидактические упражнения, важно
обращать внимание учащихся на имеющуюся взаимосвязь геометрических фактов и их
соответствующую векторную запись. Для этого можно составить “словарь перевода”
геометрических свойств фигур на язык векторов (таблица 3). Словарь заполняется
в результате теоретического материала, решения устных упражнений и задач. При
этом нужно иметь в виду, что одному и тому же геометрическому факту может
соответствовать несколько векторных формул, но все эти соотношения будут
равносильны.
Таблица 3
|
Словарь “перевода”
геометрических свойств фигур на язык векторов
|
|
Геометрическое свойство
|
Векторная запись
|
|
1
|
А=В
|
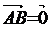
|
|
2
|
А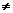 В В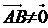
|
|
|
3
|
М АВ АВ 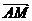 =к =к 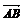 или или 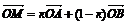
|
|
|
4
|
М-середина АВ
|
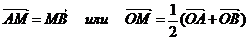
|
|
5
|
М-точка пересечения медиан DАВС
|
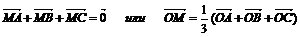
|
|
6
|
АВСD-параллелограмм
|
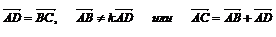
|
|
7
|
MÎ (ABC)
|
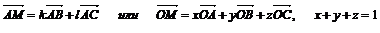
|
|
8
|
KM || (ABC)
|
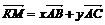
|
|
9
|
(ABC) || (A1B1C1)
|
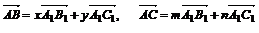
|
Одновременно учащимся следует показывать, как полученные соотношения
используются при решении задач познавательного характера, в которых сочетаются
геометрические факты, свойства фигур и векторы. Эти задачи условно можно
разбить на три группы:
ü Доказательство векторных соотношений, связанных с
определенной геометрической фигурой.
ü Доказательство геометрических свойств фигур на основе данных,
выраженных в векторной форме.
ü Смешанные задачи.
Материал второго блока, «Компланарные векторы», может быть изучен в форме
школьной лекции. Ее план:
1. Определение компланарных векторов.
2. Сложение векторов по правилу параллелепипеда.
. Признак и свойство (критерий) компланарных векторов.
. Разложение вектора по трем некомпланарным векторам
К понятию компланарных векторов можно подвести учащихся, используя модель
и изображение параллелепипеда.
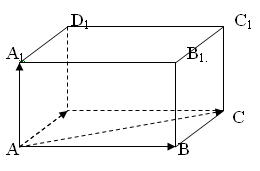
Основная дидактическая цель урока «Применение векторов к решению
геометрических задач» - познакомить учащихся с новым для них аналитическим
методом решения задач, разъяснить сущность решения геометрических задач с
помощью векторов, дать примерную схему решения. Исходя из этого, наиболее
приемлемой формой урока является школьная лекция.
Первая задача по обучению новому методу не должна содержать громоздких
выкладок, но должна наглядно иллюстрировать суть этого метода. Это позволит
ученикам самостоятельно выделить основные этапы решения геометрической задачи
векторным методом:
1. Прочитав и проанализировав условие, выполнить рисунок.
2. Согласно условию и требованию задачи, ввести в рассмотрение
векторы.
. Выразить через них векторы, необходимые для решения.
. «Перевести» условие и требование задачи на язык векторов.
. С помощью преобразований над полученными векторными
соотношениями придти от условия задачи к требованию.
. Полученному векторному выражению дать геометрическое толкование.
Обобщающий урок по теме можно провести в форме семинара. Цель этого урока
- выяснить, какие виды задач можно решать с помощью изученного материала о
векторах, сравнить векторный метод решения задач с традиционным,
геометрическим.
Анализ решения задач разными методами позволит выявить учащимися
достоинства и недостатки аналитических и конструктивных методов решения задач.
Под руководством учителя ученики должны придти к выводу, что преимущество
векторного метода состоит в том, что он позволяет избежать далеко не всегда
очевидных дополнительных построений, а приведенная ранее схема решения задач
этим методом дает определенные ориентиры решающему.
Подводя итог урока, происходит обсуждение аффинных видов задач, решаемых
с помощью векторов:
1) доказательство параллельности отрезков и прямых, прямых и
плоскостей, плоскостей;
2) доказательство компланарности трех прямых;
) установление принадлежности точки прямой (плоскости);
) вычисление отношения длин параллельных отрезков;
) доказательство того, что три прямые пересекаются в единственной
точке.
Итак, при обучении школьников векторному методу решения геометрических
задач следует обучать их умениям, входящим в его состав. К таким умениям
относятся следующие:
) преобразование векторного выражения, используя законы векторной алгебры;
2) представление вектора в виде суммы или разности нескольких
векторов, произведения вектора на число.
3) перевод геометрического свойства фигуры на векторный язык;
) перевод векторной записи на геометрический язык,
В процессе обучения учащихся выделенным умениям целесообразно составить
таблицу основных векторных равенств, словарь «перевода» геометрических свойств
фигур на векторный язык.
При решении простейших дидактических упражнений на отработку этих умений
совместно с учащимися необходимо формулировать эвристики применения того или
иного полученного факта в новых ситуациях.
При обучении учащихся собственно векторному методу необходимо выделить
алгоритм (схему) решения содержательных задач с помощью векторов. Целесообразно
так же решить ряд задач несколькими способами, на примере которых наглядно
прослеживаются преимущества и недостатки векторного метода.
Следует привлекать прикладные задачи, задачи из смежных дисциплин, при
решении которых применение векторного метода будет наиболее эффективно.
Проанализировав научную, учебно-методическую, психолого-педагогическую
литературу по теме «Решение задач векторным методом», можно сделать следующие
выводы:
1. Исторически векторное исчисление развивалось как аппарат решения задач
физики и естествознания. Однако постепенно понятие вектора стало одним из
фундаментальных понятий современной математики.
. В настоящее время в математике существуют различные подходы к
определению понятия вектора. Основой линейной алгебры служит понятие вектора
как совокупности скаляров некоторого поля Р. В геометрии вектор определяется,
как множество сонаправленных отрезков, имеющих равную длину.
Кроме того, создана теория (аксиоматика Вейля), в которой вектор является
основным неопределяемым понятием, а свойства операций над векторами описываются
системой аксиом.
. В школьных учебниках по геометрии встречается два подхода к определению
понятия вектора. Это вектор как параллельный перенос и вектор как направленный
отрезок. Однако в том и другом случае для решения задач используется модель
вектора как направленного отрезка.
. Векторы определяют один из основных методов школьного курса геометрии -
векторный метод. Его применение эффективно позволяет решать ряд аффинных и
метрических задач стереометрии и планиметрии.
. Умение решать задачи является одним из основных показателей уровня
математического развития, глубины усвоения учебного предмета. Психологи
отмечают, что для успешного овладения учащимися этим умением необходимо
целенаправленно обучать их общим методам решения задач.
6. При обучении учащихся общим методам решения задач необходимо выделять
действия, составляющие суть этого метода.
. В методической литературе [6] к основным умениям, составляющих суть
векторного метода относят:
владение основными векторными формулами и законами векторной алгебры;
умение раскладывать вектор по векторам исходного базиса;
умение переводить геометрическое свойство фигур на «векторный» язык и
обратно.
. В процессе обучения учащихся выделенным умениям целесообразно составить
таблицу основных векторных равенств, словарь «перевода» геометрических свойств
фигур на векторный язык.
. При решении простейших дидактических упражнений на отработку этих
умений совместно с учащимися необходимо формулировать эвристики применения того
или иного полученного факта в новых ситуациях.
. Высокая степень сформированности указанных умений и навыков является
базой для успешного решения задач с геометрическим содержанием векторным
методом.
11. При обучении учащихся собственно векторному методу необходимо
выделить алгоритм (схему) решения содержательных задач с помощью векторов.
Целесообразно так же решить ряд задач несколькими способами, на примере которых
наглядно прослеживаются преимущества и недостатки векторного метода.
. Следует привлекать прикладные задачи, задачи из смежных дисциплин, при
решении которых применение векторного метода будет наиболее эффективно.
Глава 2. Методика изучения темы «Векторы в пространстве» в 10 классе
Эта глава посвящена изложению основных методических рекомендаций по
изучению темы «Векторы в пространстве». В первом параграфе проведем
логико-дидактический анализ этой темы по учебному пособию Л.С. Атанасяна,
выделим ключевые задачи, сформулируем цели изучения данной темы и рассмотрим
один из вариантов ее планирования. Во втором и третьем параграфе дадим
методические рекомендации по обучению школьников умениям, входящим в состав
векторного метода, и собственно векторному методу; приведем разработки
отдельных уроков по теме. В заключении опишем опытную проверку разработанных
методических рекомендаций.
.1 Логико-дидактический анализ темы «Векторы в пространстве»
Проанализировав содержание главы IV по учебному пособию Л.С. Атанасяна и других [9], можно
сделать следующие выводы:
. В теме можно выделить 2 группы понятий:
а) Понятие вектора в пространстве, определения равных и коллинеарных
векторов, сложение и вычитание векторов, умножение вектора на число.
Особенность этого содержания состоит в том, что представляет собой
систематизацию и обобщение на пространство известных учащимся операций над
векторами. Поэтому при его рассмотрении нужно усилить долю самостоятельной
работы учащихся.
б) Определение компланарных векторов. Этот материал является новым для
учащихся, поэтому очень важным. Он требует отработки по полной схеме работы с
новым определением.
Логическая структура перечисленных определений не нова для учащихся. Все
понятия представлены в вербальной и графической форме. Существование объектов,
относящихся к понятиям вектора, равных и коллинеарных векторов, считается
очевидным по аналогии с соответствующими понятиями планиметрии. Существование
суммы и разности двух или нескольких векторов доказывается их построением.
Имеются широкие возможности для продолжения формирования умений подводить
под понятие и выводить следствия.
. Теорем в главе не много. В зависимости от новизны изучаемого материала
их также можно разделить на 2 группы:
а) теорема об отложении от точки вектора, равного данному; теоремы о
независимости суммы векторов от выбора точки и от порядка сложения векторов;
законы сложения векторов и умножения вектора на число.
Формулировка этих теорем и способы их доказательства не новы для
учащихся, так как аналогичны соответствующим теоремам из планиметрии. Поэтому
автор учебника предлагает доказать эти утверждения самостоятельно.
б) новыми для учащихся являются теорема о разложении вектора по трем
некомпланарным векторам, критерий компланарности векторов, а также правило
параллелепипеда. Доказательства этих теорем приводится в учебнике. Они являются
необходимыми для изучения, поскольку идея их доказательства будет использована
при решении задач векторным методом.
При доказательстве всех вышеперечисленных теорем в качестве
общелогического метода используется синтетическиий, в качестве частного -
векторный.
. В теме имеются объективные предпосылки для формирования приема
аналогии, поскольку понятия вектора и операций над векторами на плоскости
аналогичны соответствующим понятиям в пространстве. Аналогичны также понятия
равных и коллинеарных векторов. Значит, возможно использование метода укрупнения
дидактических единиц.
Имеются также необходимые возможности для формирования умений
анализировать, синтезировать, обобщать и т.д.
. Поскольку есть аналогия с определениями понятий, формулировками теорем,
изученных в планиметрии, то есть возможность для «открытия» учащимися
соответствующих выводов для пространства. Методы доказательства теорем также
могут быть предложены учащимися.
. Есть возможности для формирования действий моделирования, т.к. в теме
происходит иллюстрация применения определений понятий, теорем и правил.
. В задачном материале темы достаточное количество дидактических
упражнений и задач на комплексное применение знаний. Все они направлены на
формирование умений и навыков, необходимых для решения геометрических задач
векторным методом. Это такие умения:
а) овладение основными векторными формулами и законами векторной алгебры.
В процессе решения простейших дидактических упражнений такого типа (№№328,
335-337, 347, 350-354) учащиеся должны научится преобразовывать векторные
выражения.
б) умение переводить геометрические свойства фигур на векторный язык и
обратно (№№331, 338 342, 348).
в) умение раскладывать вектор по данным векторам (№№ 320-326, 329-324,
348, 349).
В качестве ключевых задач можно предложить такие: №№ 328,322, 329, 332, 341,
346, 336, 349.
. Также имеется достаточное количество задач на осознание новых понятий
темы (компланарные векторы, разложение вектора по трем некомпланарным).
В качестве ключевых задач этой группы можно предложить следующие: №№ 356,
362, 366, №359 (направлена на комплексное применение полученных знаний и знаний
из физики).
. В конце задачного материала автор предлагает несколько содержательных
задач, которые можно решить двумя методами (конструктивным и векторным).
Проанализировав разные способы решения одной и той же задачи, учащиеся должны
выделить преимущества и недостатки аналитических и конструктивных методов.
Ключевые задачи этого раздела: №№ 372, 375, 395 (разные типы аффинных
задач, к решению которых может быть применен векторный метод: №372-принадлежность
трех точек одной прямой; №375-доказательство параллельности прямых;
№395-доказательство компланарности трех прямых).
Учитывая все вышеизложенное, проведя логико-дидактический анализ главы IV учебника [9] «Векторы в
пространстве», можно предложить следующие учебные задачи изучения темы:
. Формирование у школьников представлений о предмете математики, о
методах математики (в частности - аналитическом);
. Формирование у школьников представлений о векторах в пространстве, об
операциях над ними;
. Формирование у школьников основных умений, содержащих суть векторного
метода;
. Формирование у школьников эвристических, логических и конструктивных
умений, связанных:
с «открытием » определений и теорем на основе аналогии;
с применением векторного метода к решению задач.
В результате изучения темы ученик знает;
понятие вектора в пространстве;
определения коллинеарных, компланарных и равных векторов;
свойства операций над векторами;
критерий компланарности векторов; теорему о разложении вектора по трем
некомпланарным векторам;
суть векторного метода в пространстве;
ученик понимает, что:
понятия вектора на плоскости и в пространстве аналогичны;
доказательство критерия компланарности трех векторов в стереометрии
аналогично доказательству теоремы о разложении вектора по двум неколлинеарным
векторам в планиметрии;
при доказательстве единственности коэффициентов разложения необходимо
применить метод «от противного»;
ученик умеет:
пользоваться таблицей основных векторных равенств;
осуществлять перевод геометрических свойств фигур на векторный язык и
обратно;
раскладывать вектор по базису;
ученик применяет:
прием аналогии при «открытии» определений и теорем;
векторный метод при решении содержательных задач.
В соответствии с программой по математике на изучение темы «Векторы в
пространстве» отводится 12 часов. Поэтому может быть предложен следующий
вариант тематического планирования темы:
|
№ п/п
|
Тема урока. Тип урока
|
Основные задачи
|
|
1-2
|
Понятие вектора в
пространстве. Действия над векторами. (Обобщающая лекция)
|
1.Обобщить и
систематизировать знания учеников по теме «Векторы на плоскости и в
пространстве». 2.Составить совместно с учащимися обобщающую таблицу.
3.Формировать умения в применение приема аналогии.
|
|
3-4
|
Решение задач
(уроки-практикумы)
|
1.Формировать умения и навыки,
необходимые для решения содержательных задач векторным методом. 2.Продолжить
заполнение таблиц основных векторных равенств и словаря перевода.
|
|
5
|
Компланарные векторы.
Разложение вектора по трем некомпланарным векторам (Урок-лекция)
|
1.«Открыть» совместно с
учащимися определение компланарных векторов, критерий компланарности трех
векторов, теорему о разложении вектора по трем некомпланарным векторам.
2.Формировать умения в формулировании предложений, обратных данным, в
применении анализа, синтеза, метода от противного, приема аналогии при
доказательстве теорем.
|
|
6
|
Решение задач (урок
усвоения теории)
|
1.Диагностика знаний,
полученных на предыдущих уроках. 2.Формировать умения в применении критерия
компланарности векторов, теоремы о разложении вектора по трем некомпланарным
векторам.
|
|
7
|
Решение задач.
(Урок-практикум)
|
Формировать у учащихся
умение раскладывать вектор по данным векторам, необходимое для решение задач
векторным методом.
|
|
8
|
Применение векторов к
решению геометрических задач. (Урок-лекция)
|
1.Выявить совместно с
учащимися типы афинных задач, решаемых векторным методом. 2. «Открыть» план
решения задач векторны методом.
|
|
9-10
|
Решение задач
(уроки-практикумы)
|
1.Формировать умение
применять векторный метод при решении содержательных задач. 2. Выявить
совместно с учащимися преимущества и недостатки векторного метода.
|
|
11
|
Векторы в пространстве.
(Урок обобщения и систематизации знаний).
|
Организовать осмысление
знаний, полученных при изучении темы
|
|
12
|
Контрольная работа.
|
Выявить уровни усвоения
фактического материала и соответствующего теме векторного метода решения
задач.
|
.2 Методика формирования умений, составляющих суть векторного метода
решения геометрических задач
К умениям, составляющим суть векторного метода относят следующие:
а) овладение основными векторными формулами и законами векторной алгебры;
б) умение раскладывать вектор по данным векторам;
в) умение переводить геометрические свойства фигур на векторный язык;
г) умение давать векторной записи геометрическую интерпретацию.
Отсюда следует перечень типов задач, способствующих овладению векторного
метода:
) на преобразование векторных выражений;
) на переход от соотношения между геометрическими свойствами фигур к
соотношению между векторами;
) на переход от векторной записи свойства фигуры к её геометрической
интерпретации;
) на разложение вектора по данным векторам:
представление вектора в виде суммы (разности) нескольких векторов,
представление вектора как произведения вектора на число,
выражение вектора через три некомпланарных.
Все эти типы задач в достаточном количестве имеются в учебнике. Ключевые
из них выделены в пункте 2.1.
При организации уроков-практикумов важно продумать систему вопросов к
этапу анализа каждой задачи. Учащиеся должны осознать, какой прием использован
при решении данной задач, как в дальнейшем можно использовать тот или иной
факт.
Таким образом, учащиеся под руководством учителя должны выделить общий
алгоритм решения задач для каждого из выделенных типов 1)-4). Например, чтобы
решить задачу на перевод геометрического свойства фигуры на векторный язык,
необходимо:
. Записать векторное выражение, логически «вытекающее» из определения
данного геометрического свойства,
. Записать равносильную задачу,
. Преобразовать с помощью законов векторной алгебры.
Важно обращать внимание учащихся на то, что одному и тому же
геометрическому факту может соответствовать несколько векторных формул, но все
эти соотношения равносильны между собой. При решении конкретной задачи следует
выбирать ту векторную формулу, которая наиболее соответствует условию и
требованию задачи.
При решении задач на преобразование векторных выражений требуется
выполнить следующую последовательность действий:
. Раскрыть скобки,
. Сгруппировать векторы таким образом, чтобы к каждой паре векторов можно
было применить или сложение векторов по правилу треугольника, или правило
разности двух векторов с общим началом.
Для более эффективного выполнения учащимися данных типов упражнений
необходимо составить с ними таблицы основных векторных формул и словарь
перевода геометрических свойств фигур на векторный язык.
Так как задач, необходимых для успешного овладения выделенных умений,
требуется решить достаточно много, то следует использовать принципы
варьирования задач. Это позволит ученикам выделить взаимосвязи между задачами
данной темы.
При отборе содержания к урокам-практикумам в теме «Векторы в
пространстве» можно использовать следующие принципы варьирования задач:
1. Изменение условия задачи,
2. Изменение требования задачи,
. Рассмотрение взаимно-обратных задач теорем (целесообразно при
составлении словаря перевода),
. Построение цикла взаимосвязанных задач, когда решение одной
задачи опирается на результат или решение предшествующей
Результатом проведения уроков практикумов по выделенной методике должно
стать формулирование частных эвристик к уроку «Применение векторного метода к
решению геометрических задач».
Проиллюстрируем сказанное на примерах.
Пример 1. Уроки № 3,4 по теме «Векторы в пространстве» (2ч.)
Тема урока: «Применение свойств операций над векторами к решению задач»
Тип урока: урок решения задач
Форма проведения урока: урок-практикум
Учебные задачи урока:
. Формировать у учащихся следующие умения и навыки, необходимые для
решения содержательных задач векторным методом:
а) преобразовывать векторные равенства, используя законы векторной
алгебры.
б) переводить геометрические свойства фигур на векторный язык;
в) переводить векторную запись свойства фигуры на геометрический язык.
Диагностируемые цели:
В результате ученик
· Знает
основные векторные формулы;
свойства действий над векторами;
· Умеет
пользоваться таблицей основных векторных равенств;
преобразовывать векторные равенства;
представлять вектор в виде алгебраической суммы нескольких векторов;
· Понимает
- что одному геометрическому свойству фигуры может соответствовать
несколько векторных записей, но все они равносильны;
Ход урока
|
Педагогическая деятельность
учителя
|
Учебная деятельность
учеников
|
|
I. Мотивационно-ориентировочный этап.
|
|
Что мы с вами изучали на
прошлом уроке? - Сформулируйте определение понятия «вектора в пространстве»
|
Понятие вектора в
пространстве. Действия над векторами. 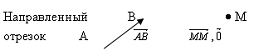
|
|
- Какие действия с
векторами в пространстве мы изучали? - Перейдем к решению задач. - Пусть дана
призма АВСDA1B1C1D1
|
- Сложение векторов,
вычитание векторов, умножения вектора на число.
|
|
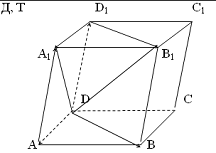
|
|
|
|
-Запишите,
чему будет равна сумма векторов 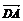 и
и 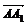
-Какое
правило сложения здесь прменимо? -Чему равна сумма векторов 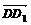 и
и 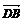 ?
?
Какое
правило сложения вам еще известно?
Приведите
свои примеры.
Как
найти результат суммы векторов 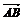 и
и 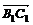 ?
?
На
основании каких теоретических фактов мы смогли заменить вектор 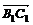 вектором
вектором 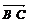 ?
?
Какие
векторы называются равными?
Чему
равна разность векторов 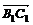 и
и 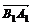 ?
?
Как
направлен результирующий вектор разности ?
Верно.
Отметим точку М-середину АВ. Выразите вектор 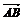 через
вектор
через
вектор 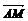 .
.
Выразите
вектор 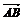 через вектор
через вектор 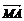 .
.
Какими
между собой являются векторы 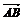 ,
, 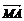 ,
, 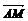 .
.
Какая
теорема о коллинеарных векторах вам известна?
Пусть
теперь дан параллелепипед АВСDA1B1C1D1.
и некоторое выражение:
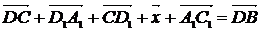 .
.
Необходимо
найти вектор 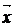 , начало и конец которого являются вершинами
параллелепипеда.
, начало и конец которого являются вершинами
параллелепипеда.
Что
сначала необходимо выполнить?
Что
мы будем применять при преобразовании векторного выражения.
Верно.
Для того, чтобы решить эту задачу, нам сначало необходимо преобразовать
векторное выражение, используя свойства операций над векторами.
Как
вы дукмаете, какова же тема нашего сегодняшнего урока?.
Оперативно-познавательный этап
Чтобы
применить к выражению законы векторной алгебры, необходимо сгруппировать
векторы.
Как
это можно сделать в данном случае?
Какие
правила вы использовали?
Итак,сформулируйте
окончательный результат.-Итак, выделите основные этапы решения данной задачи.
Верно.
Итак, чтобы преобразовать векторное выражение. Необходимо векторы данного
выражения преобразовать специальным образом. Посмотрим этот принцип на примере
еще ряда задач
правило
треугольника
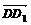 +
+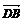 =
=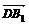 (по правилу параллелограмма)
(по правилу параллелограмма)
Правило
многоугольника.
{приводят
свои примеры}
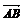 +
+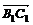 =
=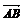 +
+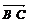 =
=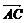
Т.к
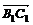 и
и 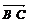 -равные
векторы.
-равные
векторы.
Два
вектора называются равными, если они сонаправлены и имеют одинаковую длину.
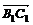 -
-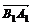 =
=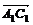
Он
направлен из конца второго вектора к началу первого.
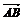 =2
=2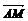
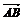 =-2
=-2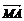
Коллинеарными
Если
векторы  и
и 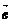 -коллинеарны,
и
-коллинеарны,
и  ¹
¹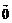 , то существует числотакое, что
, то существует числотакое, что 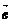 =k
=k
Преобразовать
векторное выражение.
Свойства
операций над векторами
«Решение
задач на применение свойств операций над векторами»
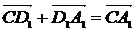
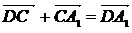
Сложение
векторов по правилу треугольника
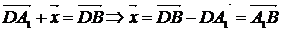
.
Преобразование векторного выражения, используя принцип группировки;
|
2. Нахождение искомого
вектора как разность двух векторов
|
|
Задача
№ 333. В пространстве даны четыре точки А, В, С, D. Назовите
вектор с началом и концом в данных точках, равный сумме векторов: а) 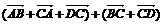
Каким
свойством вы воспользовались при преобразовании данного выражения?
Каким
способом еще можно преобразовать данное выражение?
Какие
свойства использовали в этом случае?
Б)(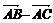 )+
)+ 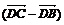
Чем
вы воспользовались при преобразовании выражений, стоящих в скобках?
На
основании какого факта вы перешли к третьему равенству?
В
предыдущих заданиях нам были даны выражения, состоящие из действий над
некоторыми векторами. Что требовалось найти?
Попробуйте
сформулировать обратное задание.
Выразите
вектор 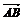 в виде алгебраической суммы векторов
в виде алгебраической суммы векторов 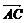 ,
, 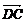 ,
, 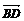 .
.
Как
по-другому можно представить эти векторы, чтобы в результате их суммы получить
вектор 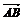 ?
?
Верно.
Как теперь преобразовать данное выражение, чтобы вернуться к исходным векторам?
Теперь
аналогичным образом выразите вектор 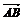 через
векторы
через
векторы 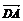 ,
, 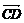 ,
, 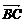 .
.
Итак,
если нам требуется преобразовать векторное выражение, чем мы можем
воспользоваться?
Если
необходимо представить данный вектор с помощью нескольких векторов, что мы
должны будем сделать?
Чем
мы можем при этом воспользоваться?
Хорошо.
Давайте теперь попробуем решить следующую задачу.
Пусть
точка М принадлежит АВ. О -произвольная точка пространства. Докажите, что 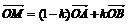 Сначало необходимо сгруппировать векторы таким
образом, чтобы можно было применить законы векторной алгебры.
Сначало необходимо сгруппировать векторы таким
образом, чтобы можно было применить законы векторной алгебры.
Имеем,
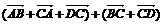 =
=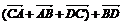
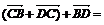
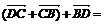
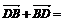
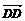 =
=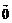
переместительным
законом сложения векторов
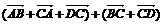 =
=
=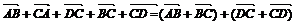 +
+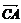 =
=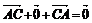
Сочетательный
закон сложения векторов, переместительный закон, свойство сложения вектора с
нулевым вектором.
(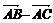 )+
)+ 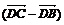 =
=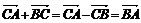
Таблицей
основных векторных равенств.
Т.к
векторы 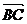 и
и 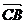 противоположные,
то
противоположные,
то 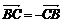
Вектор,
являющийся результатом этих операций
Дан
вектор. Необходимо выразить его с помощью операций над несколькими векторами.
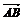 =
=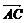 -
-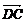 -
-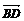
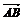 =
=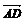 +
+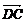 +
+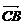 =-
=-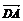 -
-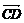 -
-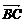 =
=
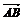 =-(
=-(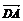 +
+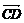 +
+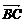 )
)
|
- Свойствами операций над
векторами -Попытаться представить этот вектор в виде суммы некоторых
векторов, затем преобразовать полученное выражение с учетом исходных.
-Таблицей основных векторных равенств.
|
|
|

|
-Что
значит на векторном языке М ÎАВ? -Как можно представить
вектор 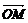 ?
?
Какие
векторы необходимо выразить, чтобы получить искомое выражение? Как это можно
сделать?
Какими
свойствами вы пользовались при преобразовании последнего выражения?
А
как вы думаете, каким числом может быть k. Почему?
А
если точка М является серединой отрезка АВ. Каким в этом случае будет k и какой
вид примет доказанное нами выражение?
Сформулируйте
окончательный результат.
Давайте
попробуем доказать это утверждение. Какие векторные соотношения можно
составить, учитывая, что М-середина АВ.
Как
моно представить эти векторы чтобы получить векторы, участвующие в требовании
задачи.
Какое
равенство можно получить, учитывая, что АМ=ВМ?
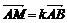
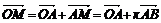
Представить
вектор 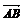 как разность векторов
как разность векторов 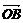 и
и 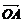
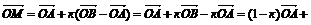
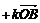 ч.т.д.
ч.т.д.
Первым
и вторым распределительными закономи операции умножения вектора на число.
0<K<1, так как М принадлежит отрезку АВ, и вектор 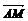 по длине должен быть меньше вектора
по длине должен быть меньше вектора 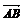 .
.
Если
М- середина АВ, то 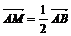 , т.е. k=
, т.е. k= .
.
Тогда
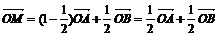
Если
М- середина АВ, то 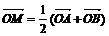
- 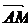 =
= 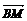 .
.
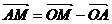
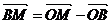
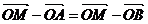
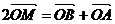
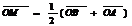
Итак,
мы с вами решили 2 задачи, которые относятся к типу задач на перевод
геометрического свойства фигуры на векторный язык.Какие взаимосвязи мы
выделили? -Какова идея решения этих задач? М ÎАВ, О-произвольная точкаÞ 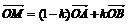
М-
середина АВ, то 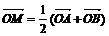
|
-Записать векторное
выражение, которое следует из определения геометрического свойства фигуры;
преобразовать это векторное выражение, используя законы векторной алгебры
|
Верно.
Попробуем решить обратный тип задач: на перевод векторной записи на
геометрический язык. Сформулируйте Обратные задачи к рассмотренным. - Докажем
второе утверждение.Что значит М-середина АВ. -Как на векторном языке можно
представить это условие? 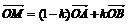 .
Доказать, что МÎАВ
.
Доказать, что МÎАВ
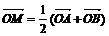 .
Доказать, что М-середина АВ.
.
Доказать, что М-середина АВ.
АМ=МВ
Вернемся
к исходному равенству. Как можно выразить векторы ОА и ОВ через векторы АМ и
МВ) -итак, выделите шаги решения задачи на переход от векторной записи к
соответствующему ей геометрическрму свойству фигуры -Аналогично можно доказать
принадлежность точки М отрезку АВ, исходя из равенства 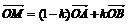
Итак,
мы получили 2 утверждения.
Каждое
из которых можно доказать в обе стороны. Запишем полученные нами утверждения в
Словарь перевода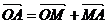
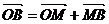
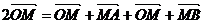
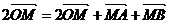
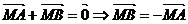 или
или 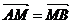
Значит,
М -середина АВ
Записать
равносильную задачу (требование задачи (геометрическое свойство фигуры)
перевести на векторный язык);
|
Решить полученную задачу,
Преобразовав исходное векторное выражение; Полученному результату дать
геометрическую интерпретацию
|
|
|
{Записываются полученные
выражения в словарь перевода}
|
|
- Как вы думаете, какие
задачи можно решать с помощью полученных условий? -Верно. Рассмотрим задачу №
341. Основанием четырехугольной пирамиды с вершиной Р является трапеция
АВСD. Точка О - середина средней линии трапеции. Докажите, что 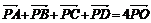 -Задачи, в которых сказано либо о принадлежности
точки отрезку, либо о середине какого-либо отрезка. -Задачи, в которых сказано либо о принадлежности
точки отрезку, либо о середине какого-либо отрезка.
|
|
|
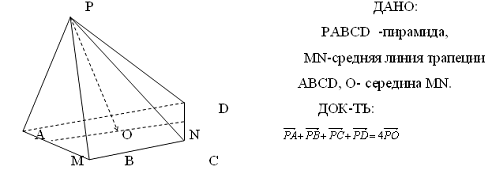
|
-Для
того, чтобы получить конечный результат нам необходимо ввести векторы. Какое
условие задачи мы можем перевести на «векторный» язык? -Что удобно выбрать в
качестве произвольной точки О? -Какой вид примет выражение? -Чем является
отрезок MN? -Сделайте вывод о свойстве точек М и N. -Какие выражения тогда мы
получим? -Итак, Что нам помогло при решении данной задачи?
- О- середина МN -Точку Р. 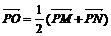
Средней
линией трапеции.
М-середина
АВ, N-середина DC
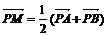
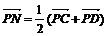
Тогда,
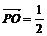 (
(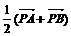 +
+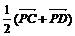 ).
).
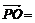
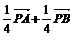 +
+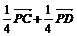 или
или
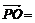
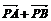 +
+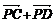
Ч.т.д
|
-Связь условия середины
отрезка с векторным выражением.
|
|
|
III. Рефлексивно-оценочный
этап.
|
-
Итак, как вы думаете, какова же была цель нашего урока? - С какими же типами
задач мы сегодня познакомились? -Какие задачи вызвали у вас затруднения?
-Какие показались интересными? -Какова идея решения задачи на преобразование
векторных выражений? -Как можно решить задачу на представление вектора через
другие. -Какова деятельность по решению задач на переход от геометрического
свойства фигуры на векторный язык? -Как
решаются обратные задачи: на перевод векторной записи на геометрический
язык. -К каким задачам можно применить доказанные нами утверждения о
середине отрезка и о принадлежности точек отрезку? -Верно. Всем спасибо за
работу. Записываем домашнее задание Д/з 1уровень.№№ 337, 346 2 уровень: Пусть
М - точка пересечения медиан DАВС О - произвольная точка
пространства. Доказать: 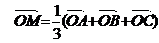 -Научиться решать задачи, в решении которых
используются свойства операций над векторами.
-Научиться решать задачи, в решении которых
используются свойства операций над векторами.
Задачи
на преобразование векторных выражений; на представление вектора через другие
векторы; на перевод геометрического свойства фигуры на векторный язык, на
пререход от векторной записи к геометрическому свойству фигуры.
{ответы
детей}
Использовать
группировку векторов таким образом, чтобы к группе векторов можно было
применить законы векторной алгебры
Представить
исходный вектор в виде суммы данных векторов (или их противоположных),
преобразовать полученную сумму с учетом данных векторов.
Записать
векторное выражение, которое следует из определения геометрического свойства
фигуры;
Преобразовать
это векторное выражение, используя законы векторной алгебры до получения
доказываемого векторного выражения.
|
-Записать равносильную задачу (требование задачи
(геометрическое свойство фигуры) перевести на векторный язык); Решить
полученную задачу, Преобразовав исходное векторное выражение; Полученному
результату дать геометрическую интерпретацию -Задачи, в условиях которых
говорится о середине какого-либо отрезка; или о точке, разбивающий данный
отрезок в заданном отношении.
|
|
Пример 2. Фрагмент урока №6 по теме «Векторы в пространстве»
Тема урока: «Применение векторов к решению геометрических задач»
Учебные задачи урока:
. Формировать у учащихся умение применять полученные теоретические факты
при решении задач
. Формировать у учащихся умение раскладывать вектор по трем
некомпланарным векторам, необходимое при решении содержательных задач векторным
методом;
. Выделить совместно с учащимися типы содержательных задач, при решении
которых используется критерий компланарности векторов.
В результате ученик:
· Знает
- типы задач, к которым может быть применен критерий компланарности
векторов;
· Умеет
- применять критерий компланарности трех векторов к решению задач,
раскладывать вектор по трем некомпланарным векторам, используя
соответствующую теорему;
находить сумму трех некомпланарных векторов по правилу параллелепипеда
Ход урока
|
Педагогическая деятельность
учителя
|
Учебная деятельность
учеников
|
|
Учитель предлагает решить
Задачу №356 Отрезок EF соединяет середины ребер АВ и CD
тетраэдра ABCD. Докажите, что 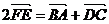 .
Компланарны ли векторы FE, BA, DC. .
Компланарны ли векторы FE, BA, DC.
|
|
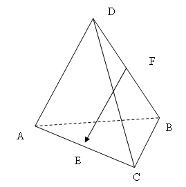
|
ДАНО: АВСD -
тетраэдр; Е,F-середины сторон АС и DB. ДОК-ТЬ: 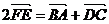
|
-Какие
условия задачи мы можем перевести на векторный язык? -С помощью какого
векторного выражения мы представим данные условия? -Как теперь можно выразить
вектор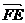 , учитывая требование задачи
, учитывая требование задачи
Как
по-другому можно записать это равенство?
Е,F-середины
сторон АС и DB
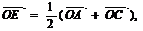
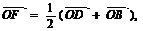
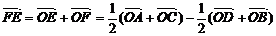
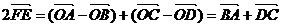
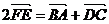
-Что
значит эта запись? -Т.к. векторы компланарны, то согласно второму определению
отрезки (прямые) параллельны некоторой плоскости. Как же можно
переформулировать требование данной задачи, чтобы в нем не участвовали векторы?
-Попробуйте выделить идею решения сформулированной задачи. -Верно. Итак, для
доказательства параллельности трех прямых некоторой плоскости мы будем
использовать определение и критерий компланарных векторов. Попробуем теперь
выяснить, можно ли применить компланарность векторов к решению следующей
задачи: Доказать, что 4 точки A. B, C, D лежат в одной плоскости.  - Что для этого нам нужно ввести в рассмотрение?
-При каком же условии точки A, B, C, D будут лежать в одной плоскости? - Как тогда запишется
векторное выражение? -Итак, мы показали, что если A, B, C, D
лежат в одной плоскости, то
- Что для этого нам нужно ввести в рассмотрение?
-При каком же условии точки A, B, C, D будут лежать в одной плоскости? - Как тогда запишется
векторное выражение? -Итак, мы показали, что если A, B, C, D
лежат в одной плоскости, то 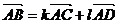 .
Сформулируйте и докажите обратное утверждение.
.
Сформулируйте и докажите обратное утверждение.
Верно.
Как можно объединить эти 2 задачи в одну.
Итак,
мы с вами доказали взаимосвязь геометрического свойства фигуры (принадлежность
4-х точек одной плоскости) и его векторной записи. Запишем полученное
утверждение в словарь перевода.
Сформулируем
вывод: Чтобы доказать, что 4 точки лежат в одной плоскости, необходимо…-Что
векторы  ,
,  ,
, 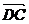 -компланарны.
-компланарны.
Доказать,
что прямые FA, BA, DC параллельны некоторой плоскости.
Необходимо
перейти от прямых к их направляющим векторам, и доказать, что они компланарны.
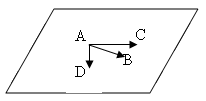
Векторы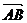 ,
, 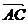 и
и 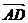 .
.
Если
векторы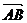 ,
, 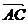 и
и 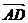 компланарны.
компланарны.
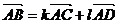
-Если
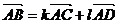 , то A, B, C, D принадлежат одной плоскости.
, то A, B, C, D принадлежат одной плоскости.
Доказательство:
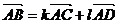 Þ(по критерию компланарности векторов)
Þ(по критерию компланарности векторов)
 ,
, 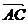 и
и 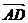 лежат в
одной плоскости ÞA, B, C, D
принадлежат одной плоскости A, B, C, D принадлежат одной плоскости Û
лежат в
одной плоскости ÞA, B, C, D
принадлежат одной плоскости A, B, C, D принадлежат одной плоскости Û 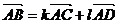
|
-Показать, что 3 вектора,
определяемые этими точками, компланарны.
|
|
|
{Аналогичная работа
проводится по решению задачи на доказательство параллельности прямой и
плоскости. В конце урока делается общий вывод: какие задачи модно решать,
используя компланарнось векторов}
|
.3 Методика обучения векторному методу решения содержательных
геометрических задач
Векторный метод является одним из аналитических методов решения
геометрических задач и доказательства теорем. Сущность его состоит в том, что
условие и требование задачи записываются в векторной форме, а ее решение
состоит в переходе от условия к требованию на основе законов векторной алгебры.
Векторный метод относится к методам алгоритмического типа, т.к. можно
выделить общую схему решения геометрических задач векторным методом.
Этот план включает следующие пункты:
. Прочитав и проанализировав условия, выполнить рисунок
2. Согласно условию и требованию задачи, ввести в рассмотрение
векторы
. Выразить через них векторы, необходимые для решения задачи
. «Перевести» условие и требование задачи на язык векторов
. С помощью преобразований над полученными векторными
соотношениями придти от условия задачи к требованию.
6.Полученному векторному соотношению дать геометрическое истолкование
Поэтому, при организации урока по обучению учащихся векторному методу
необходимо учитывать технологию работы с алгоритмом, разработанную в теории и
методике обучения математики.
Имеется 3 различных возможностей построения данного урока:
. Повторить с учащимися умения, входящие в состав векторного метода;
затем сообщить им тему урока, сформулировать в готовом виде схему решения задач
векторным методом, и далее отрабатывать этот алгоритм на примере решения ряда
задач.
. Вспомнить с учащимися алгоритм решения задач векторным методом из
планиметрии, по аналогии найти план решения стереометрических задач векторным
методом.
. В результате совместного поиска учителем и учащимися решения
стереометрической содержательной задачи выделить план решения этой задачи векторным
методом; обобщить алгоритм для всех задач.
Нам представляется более целесообразным третий подход, т.к. организация
такого урока соответствует основному принципу деятельностного подхода:
включение ученика в целесообразно организованную деятельность.
Урок должен включать в себя три основных блока:
мотивационно-ориентировочный, оперативно-познавательный и
рефлексивно-оценочный.
На этапе актуализации необходимо повторить с учащимися умения,
необходимые для решения задач векторным методом:
переводить геометрическое свойство фигур на векторный язык и обратно;
преобразовывать векторное выражение,
представлять вектор через другие,
На отработку этих умений были направлены предыдущие уроки-практикумы.
В качестве создания проблемной ситуации можно предложить решить задачу,
которая известными методами решается достаточно трудно. Отсутствие решения
предложенной задачи послужит мотивацией к дальнейшей деятельности.
После изучения векторного метода учащиеся должны усвоить типы задач,
решаемых с помощью векторов. Для этого целесообразно постепенно составлять
систематизирующую таблицу (приложение 1).
Полезно в конце изучения темы выделить преимущества и недостатки
векторного метода. Это можно сделать, решив ряд задач двумя методами (векторным
и конструктивным).
Подобная организация работы будет способствовать более эффективному
усвоению учащимися векторного метода решения геометрических задач.
Приведем конспект урока № 8 по теме «Векторы в пространстве» (1 ч.)
Тема урока: «Применение векторов к решению геометрических задач»
Тип урока: урок изучения нового
Форма проведения урока: школьная лекция.
Учебные задачи урока:
1. «Открыть» совместно с учащимися план решения задач векторным
методом.
2. Выявить совместно с учащимися типы аффинных задач, решаемых
векторным методом.
Диагностируемые цели:
В результате ученик:
· Знает
план решения стереометрических задач векторным методом;
некоторые типы задач, решаемых с помощью векторов;
· Умеет
пользоваться таблицей основных векторных равенств и словарем перевода при
решении задач
· Понимает, что некоторые пункты плана решения задач векторным
методом можно менять (пропускать).
Подготовка к уроку: Учитель на урок приносит карточки с заданиями для
каждого ученика, плакат с записанной схемой решения геометрических задач
векторным методом. Таблица векторных равенств и словарь перевода уже вывешены в
классе.}
Ход урока
|
Педагогическая деятельность
учителя
|
Учебная деятельность
учеников
|
I. Мотивационно
- ориентировочный этап. Форма проведения: самостоятельная работа {Учитель
раздает карточки с заданиями. Ученики их выполняют (записи ведут на карточках).
Затем ученики в паре меняются выполненными работами. Осуществляется
взаимопроверка} Задание №1. Найти: 1) 
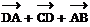
) 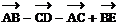
)
Выразите 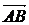 через
через 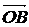 и
и 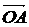
Задание
№2
|
Записать на языке векторов
1)М - середина АВ 2) АВ, CD, EF - лежат в одной плоскости.
|
|
-Предлагаю вам решить
задачу № 375. Дан тетраэдр DABC. Точки К, М - середины АВ и CD.
Докажите, что середины отрезков КС, KD, MA, MB
являются вершинами некоторого параллелограмма.
|
|
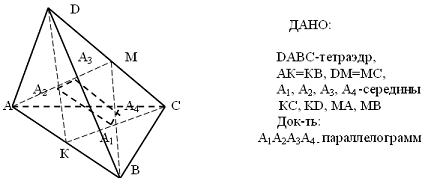
|
|
- Предлагаю решить эту
задачу известными вам способами. На обдумывание дается 2 минуты. - Какими
способами вы пробовали решить задачу? Что у вас получилось?
|
{Отвечают на вопрос,
аргументируя вызвавшее затруднение}
|
|
-Какую общую тему мы
изучаем на протяжении последних уроков?
|
-Векторы в пространстве
|
|
Какой метод, связанный с
применением векторов, мы рассматривали в планиметрии? -Как вы думаете, можно
ли применить векторный метод, чтобы решить стереометрическую задачу?
|
Векторный -Наверное, можно
|
|
-Верно, в пространстве, как
и на плоскости, при решении задач может быть реализован векторный метод.
-Итак, сформулируйте тему нашего урока.
|
Векторный метод решения
стереометрических задач
|
|
-Какова же в связи с темой цель нашего урока?
|
- Открыть способ решения
задач векторным методом
|
|
{Тема урока записывается на
доске и в тетрадях}
|
|
II Операционно-познавательный
этап.
|
-Вернемся
к решению сформулированной задачи. -Что значит на векторном языке: доказать,
что A1A2A3A4 - параллелограмм?
-Чем вы воспользовались при ответе на данный вопрос? -Что означает второе
условие на геометрическом языке? -Выполняется ли это условие? Почему? -Таким
образом, что нам достаточно проверить? -Итак, мы должны выразить векторы 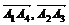 . Как это можно сделать?
. Как это можно сделать?
Необходимо
ввести в рассмотрение векторы, но не произвольно, а учитывая условие задачи.
Известно,
что точка М - середина DC. Как этот факт записать с помощью векторов?
Верно.
Начнем оформление задачи.- 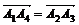 ,
, 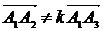
Словарем
«перевода» геометрических свойств фигур на векторный язык -А1, А2,
А3 не лежат на одной прямой -Выполняется. Т.к. в противном случае АВ
было бы параллельно DC, что невозможно 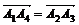
|
-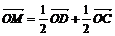
|
|
|
Учитель, привлекая
учеников, проводит решение у доски, показывает образец оформления, учащиеся в
тетрадях (записи ведутся в 2 колонки) Вторая колонка заполняется после
решения задачи
|
1)
М - середина DCÞ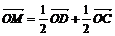
К-середина
АВÞ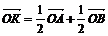
А1-серединаКСÞ 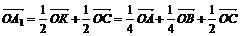
А4-середина
МВÞ
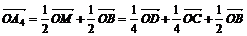
А2-середина
АМÞ
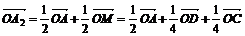
А4-середина
МВÞ
|
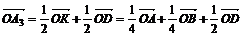 1. Ввели векторы. 2. «Перевели» условие и требование
задачи на векторный язык. 1. Ввели векторы. 2. «Перевели» условие и требование
задачи на векторный язык.
|
|
2.)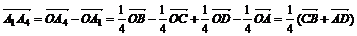
Выразить
векторы, не-
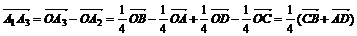
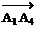 =
=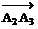
|
 3. Выразили векторы, необходимые для решения.
4.Перешли от условия к требованию задачи. 5. «Перевели» векторное выражение
на геометрический язык 3. Выразили векторы, необходимые для решения.
4.Перешли от условия к требованию задачи. 5. «Перевели» векторное выражение
на геометрический язык
|
|
|
-Давайте проанализируем
решение задачи и составим план решения задач векторным методом. -С чего мы
начали решение данной задачи? -Как мы это сделали?
|
-Ввели в рассмотрение
векторы. -Учитывая условия задачи
|
|
Продолжая беседу
аналогичным образом, заполняется вторая колонка. После проведенного анализа
учитель вывешивает заранее подготовленную схему: Прочитав и проанализировав
условия, выполнить рисунок Согласно условию и требованию задачи, ввести в
рассмотрение векторы Выразить через них векторы, необходимые для решения
задачи «Перевести» условие и требование задачи на язык векторов С помощью
преобразований над полученными векторными соотношениями придти от условия
задачи к требованию. Полученному векторному соотношению дать геометрическое
истолкование}
|
|
-Учитывая, что A1A2A3A4
- параллелограмм, составьте на
основе этой задачи новые, изменив требование задачи. -Хорошо. Сделайте вывод,
какие задачи мы можем попытаться решить, используя векторный метод? -Верно.
Рассмотрим еще один вид задач, которые можно решить с помощью векторного
метода. Перейдем к решению задачи №395. Докажите, что если точки пересечения
медиан треугольников АВС и А1В1С1 совпадают,
то прямые АА1, ВВ1, СС1 параллельны
некоторой плоскости. -С чего начнем
решение этой задачи?
|
-Доказать, что А1А2½½А3А4, А2А3½½А1А4, А1А2=А3А4,
А2А3=А1А4 -Доказательство факта,
что данная фигура - параллелограмм, доказательство параллельности прямых,
доказательство равенства двух отрезков С построения чертежа
|
|
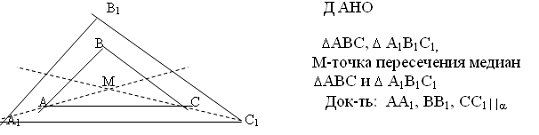
|
|
|
|
|
-Что
значит, прямые АА1, ВВ1, СС1½½a? -Как можно на векторном языке представить данный
факт? -Верно. Нам надо попытаться выразить один вектор через два остальных.
-Что нам еще необходимо сделать, согласно плану решения. {Учитель оформляет
задачу на доске под диктовку учащихся} -Это значит, направляющие
их векторы компланарны {Обращаются к словарю перевода} -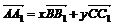
|
-Ввести в рассмотрение
векторы, учитывая условия задачи.
|
1.
М-медиана DАВС Þ 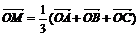
М-медиана
DА1В1С1 Þ 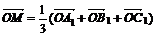
. 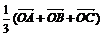 =
=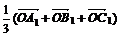 Þ
Þ 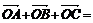
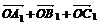
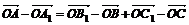 ,
,
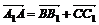 , т.е.
, т.е. 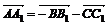
. 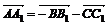 Þ АА1, ВВ1,
СС1½½a
Þ АА1, ВВ1,
СС1½½a
|
ч.т.д.
|
|
-Какой вид задач мы еще
смогли решить, используя векторный метод? -Что нам для этого потребовалось
установить? -Какой теоретический факт лежал в основе доказательства? -Какие
виды задач можно ещё решить, используя критерий компланарности векторов? {На
предыдущем уроке рассматривался данный вопрос} -Посмотрите на решение задачи
№372 (с.95). Докажите, что диагональ АС1 параллелепипеда АВСDA1В1C1D1 проходит через точки пересечения медиан
треугольников A1BD и CB1D1 и делится этими точками на три равных отрезка. -
Что необходимо установить в этой задаче в общем случае (используя термины
«точка», «прямая»)? -Какое теоретическое положение используется в решении
задачи при доказательстве этого факта? -В каком отношении точка М1
делит отрезок АС?
|
-Доказательство параллельности
трех прямых некоторой плоскости -Что направляющие векторы этих прямых
компланарны -Критерий компланарности 3-х векторов. - Доказательство факта,
что 4 точки лежат в одной плоскости; доказательство параллельности прямой и
плоскости. {Дается 1 мин. для ознакомления с решением задачи} -Необходимо
доказать принадлежность точек прямой. -критерий коллинеарности 2-х векторов -1:3
|
|
-Выделите еще один тип
задач, решаемых векторным методом. -Верно. Таким образом, мы выделили ещё два
типа задач, решаемых векторным методом: установление принадлежности точек
прямой и нахождение отношений длин отрезков. III.
Рефлексивно-оценочный этап. -Итак, какова была цель нашего урока? -Каковы
этапы решения задач мы с вами выделили?
|
-Найти, в каком отношении
делит отрезок точка, принадлежащая этому отрезку -Найти способ решения задач
векторным методом 1. Прочитав и проанализировав условия, выполнить рисунок 2.
Согласно условию и требованию задачи, ввести в рассмотрение векторы 3.
Выразить через них векторы, необходимые для решения задачи 4. «Перевести»
условие и требование задачи на язык векторов 5. С помощью преобразований над
полученными векторными соотношениями придти от условия задачи к требованию.
6. Полученному векторному соотношению дать геометрическое истолкование
|
|
-Чем вы можете
воспользоваться при решении задачи на этапах 2, 3, 5? -А чем на этапах 4 и
6? -Заметим, что выделенная нами схема является примерной. В зависимости от
содержания задания часть из этих этапов может быть проведена «мысленно»,
«перевод» может осуществляться не сразу, а постепенно по ходу решения и т.д.
-Какие типы задач можно попытаться решить, используя векторы? -Какие теоремы
используются в решении данных задач? -Как вы думаете, чем мы с вами будем
заниматься на следующих уроках? Д\З: №398
|
-Таблицей основных
векторных равенств -Словарем «перевода» геометрических свойств фигур на язык
векторов -Доказательство параллельности прямых, прямой и плоскости, трех
прямых некоторой плоскости; установление принадлежности 3-х точек одной
прямой -Критерий компланарности 3-х векторов, критерий коллинеарности 2-х
векторов. -Решать задачи векторным методом.
|
Пример 2. Уроки № 8,9 по теме «Векторы в пространстве» (2ч.)
Тема урока: «Применение векторов к решению геометрических задач»
Тип урока: урок решения задач
Форма проведения урока: урок-практикум
Учебные задачи урока:
. Формировать у учащихся умение применять векторный метод при решении
содержательных задач.
. Выявить совместно с учащимися типы аффинных задач, решаемых с помощью
векторов.
. Выявить совместно с учащимися преимущества векторного метода.
Диагностируемые цели:
После урока ученик
Знает
типы аффинных задач, решаемых с помощью векторов;
основные преимущества векторного метода решения геометрических задач
перед конструктивными методами.
Умеет
применять векторный метод к решению содержательных задач
Понимает
важность изучаемой темы.
Ход урока
|
Педагогическая деятельность
учителя
|
Учебная деятельность
учеников
|
|
I. Мотивационно-ориентировочный этап
|
|
{Вызывается ученик для
проверки домашнего задания. Пока ученик готовиться, учитель проводит устный
опрос}
|
-Какова
была тема нашего прошлого урока? - -Какие типы задач можно попытаться решить,
используя векторы? -Какие факты используются при доказательстве? -Сформулируйте
критерий коллинеарности двух векторов. -В каких ещё задачах, рассмотренных
нами, используется критерий коллинеарности векторов? -Какие типы задач мы еще
рассматривали? -Что для этого необходимо установить? -Сформулируйте критерий
компланарности 3-х векторов. -Теперь давайте проверим решение домашней задачи. -Применение
вектора к решению задач. -Доказательство параллельности прямых. -Определение
равных векторов, критерий коллинеарности 2-х ненулевых векторов. 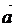 и
и  коллинеарны,
коллинеарны,
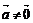 Û
Û  =
= k
k
Доказательство
принадлежности точек прямой; вычисление отношений длин отрезков, на которые
делит точка данный отрезок.
Доказательство
параллельности 3-х прямых данной плоскости.
Что
направляющие векторы этих прямых компланарны.
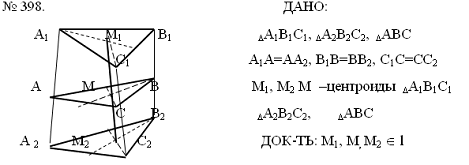 ДОКАЗАТЕЛЬСТВО: 1. М1 - центроид DА1В1С1Þ
ДОКАЗАТЕЛЬСТВО: 1. М1 - центроид DА1В1С1Þ 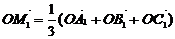
М
- центроид DАВСÞ 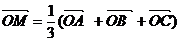
М2
- центроид DА2В2С2Þ 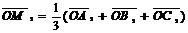
. 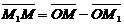 Þ
Þ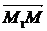 =
=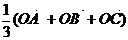 -
-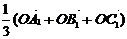 =
=
=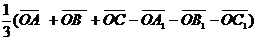
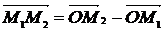 Þ
Þ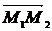 =
=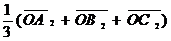 -
-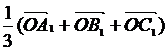 =
=
=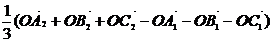
.
А-середина А1А2 Þ 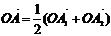
В-середина
В1В2 Þ 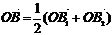
С-середина
С1С2 Þ 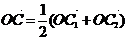
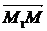 =
=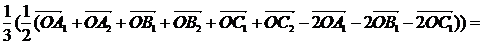
=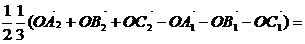
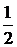
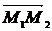
Значит,
точки М, М1, М2 лежат на одной прямой (по определению
коллинеарных векторов, критерию коллинеарности 2-х ненулевых векторов)
|
{В ходе проверки домашнего
задания повторяются этапы решения задач векторным методом, выясняется тип
данной задачи (известный учащимся), теоретический базис решения}
|
|
-Перейдем к решению задачи
№390.
|
|
|
Дан прямоугольный
параллелепипед АВСDA1B1C1D1, в котором АВ=AD=a, AA1=2a.
В вершинах В1 и D1
помещены заряды q, а в вершине А - заряд 2q. Найдите
абсолютную величину результирующей напряженности электрического поля в точке
А1. 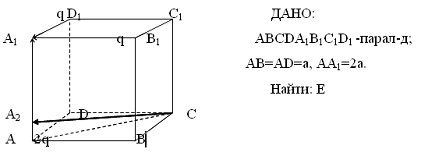
|
-Что
значит, на векторном языке найти абсолютную величину результирующей
напряженности электрического поля? -Как находится вектор 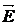 напряженности электрического поля?
напряженности электрического поля?
В
каких точках по условию задачи находятся точечные заряды?
В
каждом случае вектор напряженности свой. Найдем эти напряженности.
Как
же найти вектор результирующей напряженности в точке А1?-Найти длину
результирующего вектора.
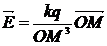 , где
О-точка, в которой помещен заряд, М-точка, в которой создается электрическое
поле.
, где
О-точка, в которой помещен заряд, М-точка, в которой создается электрическое
поле.
В
точках А, В1, D1.
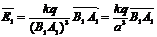
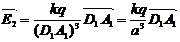
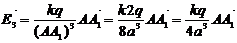
Как
сумму напряженностей 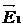 ,
,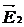 ,
,
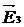 .
.
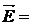
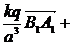
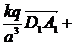
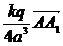 =
=
=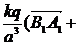
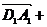
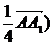 =
=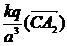
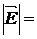
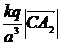 ,
, 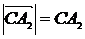
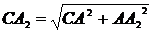 =
=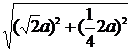 =
=
=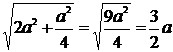
|
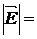 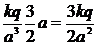
|
|
|
Итак, мы с вами рассмотрели
решение 2-х задач (из геометрии и из физики). Что общего можно сказать об
этих задачах? -Верно. Как вы думаете, какова тема нашего сегодняшнего урока?
|
-К решению обеих задач был
применен векторный метод. -Решение задач векторным методом.
|
|
II Операционно-познавательный этап
|
|
-Предлагаю вам разделиться
на 3 группы и решить предложенную задачу.
|
|
|
{Учитель организует три
группы (в каждой группе ученики с разной степенью обученности)} Список задач:
Задача №1. Не параллельные отрезки АА1, ВВ1, СС1
параллельны плоскости a. Докажите, что отрезок ММ1, где М и М1
точки пересечения медиан треугольников АВС и А1В1С1
так же параллелен плоскости a. Задача №2 Докажите, что три
отрезка, соединяющие середины боковых ребер тетраэдра с серединами
противоположных сторон основания, проходят через одну точку и делятся ей
пополам. Задача№3: Дан параллелепипед АВСDA1B1C1D1. Точки P, Q центры
граней A1B1C1D1
и ВВ1С1С,
точка М принадлежит ребру В1С1 и В1М : МС1=2
:1. Докажите, что точка М принадлежит плоскости APQ. {Ученики
в группах в течение 10 мин. обсуждают решение задачи, производят его
оформление (один человек от группы у доски, другие в тетрадях). Потом
ученики, оформлявшие задачу у доски, по очереди объясняют приведенное решение
(остальные ученики кратко фиксируют план решения). После каждой задачи всем
классом обсуждаются полученные итоги задачи, а участники группы комментируют
затруднения, возникшие в процессе её решения}
|
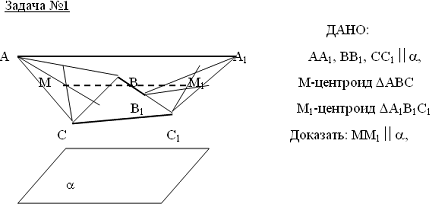 РЕШЕНИЕ: 1. Выберем в плоскости a произвольные
неколлинеарные векторы
РЕШЕНИЕ: 1. Выберем в плоскости a произвольные
неколлинеарные векторы  и
и 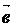
.
АА1 çêa Þ 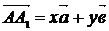
ВВ1
çêa Þ 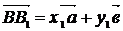
СС1
çêa Þ 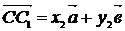
х,
х1, х2; у, у1, у2 попарно различны,
т.к. АА1, ВВ1, СС1 попарно не параллельны.
.
М-центроид DАВСÞ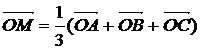
М1-центроид
DА1В1С1Þ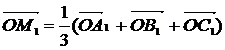
-Итак,
каково было требование задачи? -Что для этого потребовалось установить? -На
каком теоретическом факте основывано решение данной задачи? -Какие
геометрические соотношения интерпретировались на «векторный язык» в процессе
решения? -Итак, какой тип задач, к решению которых может быть применен
векторный метод, вы можете выделить в данном случае? -Верно. Обратимся к
решению второй задачи. -Доказать параллельность отрезка плоскости. -Вектор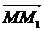 разложим по некоторым векторам плоскости a
разложим по некоторым векторам плоскости a
На
критерии компланарности 3-х векторов
Параллельность
прямой и плоскости, Точка пересечения медиан треугольника.
|
-Установление
параллельности прямой и плоскости.
|
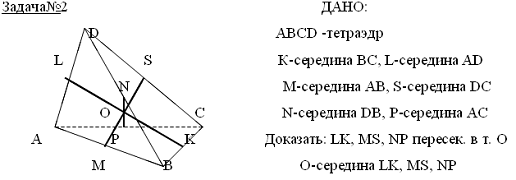 РЕШЕНИЕ:
РЕШЕНИЕ:  3. Пусть О3-середина
PN. Аналогично получаем,
3. Пусть О3-середина
PN. Аналогично получаем, 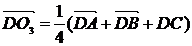
|
Из 1, 2, 3 имеем 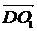 = =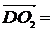 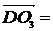 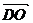 Þ LK,
MS, NP пересек. в т. О, где О-середина LK,
MS, NP/ Ч.т.д. Þ LK,
MS, NP пересек. в т. О, где О-середина LK,
MS, NP/ Ч.т.д.
|
|
-К какому типу задач вы
можете отнести рассмотренную сейчас задачу? -Верно. На каких теоретических
фактах основано доказательство? -Будет ли иметь место доказанный факт для
правильного тетраэдра? -Перейдем к решению последней задачи
|
-Доказательство факта, что
три прямые пересекаются в одной точке. -На формуле середины отрезка, теореме
о единственности разложения вектора по трем некомпланарным векторам, лемме о
коллинеарных векторах. -Да, т.к. данное утверждение доказано для произвольной
треугольной пирамиды.
|
Задача
№3 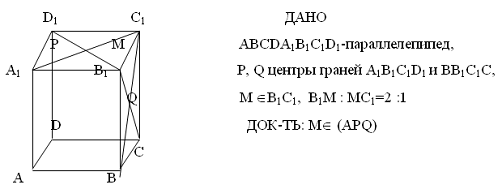 РЕШЕНИЕ: 1.
Пусть векторы
РЕШЕНИЕ: 1.
Пусть векторы 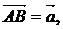
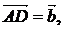
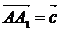 .
.
.
Тогда 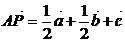 ,
, 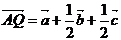 ,
, 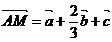
. 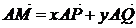
Для
этого необходимо, чтобы система была совместна. 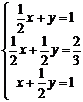 Þх=
Þх=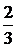 , у=
, у=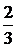
|
Значит, 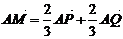 Þ МÎ (АPQ)
ч.т.д Þ МÎ (АPQ)
ч.т.д
|
|
-Итак, что необходимо было
установить в данной задаче? -Какие теоретические факты были положены в основу
доказательства? -Попробуйте изменить требование задачи так, чтобы решение
осталось неизменным. -Итак, сделайте вывод, задачи какого ещё типа можно
эффективно решить, используя векторный метод? -Давайте рассмотрим другой
метод решения данной задачи (конструктивный). Что необходимо построить для
доказательства принадлежности точки М плоскости (АPQ)? -Какую
часть сечения необходимо показать на рисунке, учитывая условия задачи?
-Верно. Для этого необходимо построить вспомогательную плоскость А1АQ.
{учитель у доски выполняет построения (см. рис. ниже), комментирует,
записывает этапы построения} Она пересечет плоскость (А1В1С1)
по прямой А1Q1, где Q1ÎB1C1, QQ1ïïAA1. -Каково взаимное расположение прямых A1Q1 и AQ? -Как в таком случае построить точку пересечения
таких прямых? -Пусть A1Q1 и AQ пересекаются в точке Х. Что вы можете сказать о
принадлежности точки Х плоскостям (АPQ) и (А1В1С1)?
-Итак, Х - общая точка плоскостей (АPQ) и (А1В1С1).
Какая еще точка, отмеченная на рисунке, принадлежит этим плоскостям? -
Постройте линию пересечения этих плоскостей. -Пусть (АPQ)
пересекает В1С1 в точке М1, а А1D1 в точке Х1. Что нам необходимо
установить, чтобы доказать принадлежность точки М плоскости сечения? -Как
это можно проверить?
|
-Принадлежность точки
плоскости. -Критерий компланарности векторов; теорема о единственности
разложения вектора по трем некомпланарным. -Доказать, что точки А, P, Q, M
лежат в одной плоскости. -Доказательство принадлежности точки плоскости, 4-х
точек одной плоскости -Сечение параллелепипеда АВСDA1B1C1D1
плоскостью (АPQ).
-Линию пересечения плоскостей (АPQ) и (А1В1С1)
-Они пересекаются, так как лежат в одной плоскости и не являются
параллельными. {Выполняют построение.} - Х Î(АPQ)
и (А1В1С1), т. к. принадлежит лежащим в них
прямым A1Q1 и AQ. -Точка Р {Выполняют построение} -Что точки М и М1
совпадают. -Необходимо проверить выполнимость условия В1М1
: М1С1=2:1
|
|
{Производится оформление
решения, этапы построения сечения были записаны ранее}
|
 5. Q1M1-средняя
линия треугольника A1XX1 (Q1середина В1С1, Q1M1ïïA1Х1)Þ Q1M1=
5. Q1M1-средняя
линия треугольника A1XX1 (Q1середина В1С1, Q1M1ïïA1Х1)Þ Q1M1=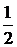 A1X1
A1X1
6.
D A1XР=D М1С1РÞ М1С1= A1X1=2 Q1M1
. Q1-середина В1С1 Þ M1С1=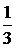 В1С1 или В1М1
: М1С1=2:1.
В1С1 или В1М1
: М1С1=2:1.
|
Это означает, что М=М1Þ МÎ (АPQ)
Ч.т.д
|
|
-Давайте сравним 2 метода
решения одной задачи. Какой вам показался более простым? Почему? -Что вы
скажете о необходимости выполнения рисунка в том и другом случае? -Как мы
строим процесс решения задач векторным методом? -Верно. Поэтому применение
векторного метода при решении задач дает некий ориентир решаемому, в то время
как конструктивный метод требует более трудоемкой работы на этапе поика
решения. Ш.Рефлексивно-оценочный этап -Итак, сформулируйте, какими основными
преимуществами обладает векторный метод решения геометрических задач по
сравнению с геометрическим? -А что вы можете отнести к его недостаткам?
-.Верно, далеко не любую задачу можно решить, используя векторный метод. К
каким-то классам задач векторный метод либо вовсе неприменим, либо является
малоэффективным. -Мы с вами на протяжении нескольких уроков выделяли типы
задач, к которым может быть применен векторный метод., составляли систематизирующую
таблицу {приложение1}. Какие классы задач нами были рассмотрены? - Решение
этих задач опирается на аффинные операции над векторами (сложение векторов,
умножение вектора на число) и их свойства. Пока мы не можем с помощью
векторов решать метрические задачи (на нахождение длины отрезков, величины
углов и т.д.) Для этого нужно изучить новую операцию над векторами (скалярное
произведение). Её мы изучим в 11 классе. А пока попробуйте сформулировать
вывод, почему нам необходимо изучать векторы и векторный метод решения
геометрических задач? Д/з №397, 399(Выписать в таблицу новый тип задач)
|
-Векторный метод, т.к. он
является более рациональным. -При конструктивном методе решения рисунок
необходим, т.к. на нем производятся дополнительные простроения, необходимые в
процессе решения. При решении задач векторным методом рисунок играет
вспомогательную роль. -Опираясь на алгоритм решения задач векторным методом.
-Векторный метод имеет алгоритм решения задач, позволяет избежать
дополнительных построений. - Векторный метод не является универсальным
методом решения геометрических задач. -Доказательство параллельности
прямых; трех прямых и плоскости; прямой и плоскости. Доказательство
принадлежности трех точек одной прямой, 4-х точек одной плоскости. Доказательство
того, что три прямые пересекаются в единственной точке. Вычисление отношения,
в котором данная точка делит исходный отрезок {ответы учеников}
|
2.4 Описание опытной работы
Опытная проверка по разработанной системе уроков проводилась в период с 9
марта по 7 апреля 2009 года в 10 классе МОУ Хвощевской СОШ под руководством
учителя математики - Мишиной Евгении Николаевны.
Цель опытной проверки: обосновать актуальность проводимого исследования;
подтвердить или опровергнуть его гипотезу: «Если, начиная с первых уроков
изучения темы «Векторы» целенаправленно обучать учащихся умениям, необходимым
для решения задач векторным методом, то это будет способствовать эффективному
усвоению учащимися этого метода».
Достижение поставленной цели реализовывалось в три этапа.
Цель первого, констатирующего этапа - обосновать актуальность проводимого
исследования.
Для этого были выбраны следующие методы исследования: беседа с учителями
математики, тестирование учащихся.
В результате беседы с учителями математики были выявлены следующие типы
упражнений, характерные для темы «Векторы», при выполнении которых ученики
испытывают трудности:
ü разложить вектор по 2-м неколлинеарным (3-м некомпланарным)
векторам;
ü выразить вектор через другие, используя определение и законы
сложения и умножения векторов;
ü представить геометрическое свойство фигуры на «векторный»
язык;
ü решить содержательную задачу векторным методом.
Для получения более объективной информации среди учеников 10 класса была
проведена входная диагностика в форме тестирования. Цель тестирования: выявить
уровень остаточных знаний учащихся по теме «Векторы на плоскости».
Тестовые задания были составлены на основе методических рекомендаций
учебного пособия [27, с.82-90].
. Этап планирования тестовых заданий.
|
Лист требований по теме
«Векторы на плоскости», 8-9 класс.
|
|
Элементы содержания
|
Кол-во заданий
|
Вид деятельности
|
|
Понятие вектора. Нулевой
вектор. Длина вектора
|
3
|
Знает и понимает
|
|
Коллинеарные векторы
(сонаправленные/ противоположно направленные)
|
2
|
Знает, понимает
|
|
Определение понятия равных
векторов
|
1
|
Знает, понимает, умеет
применять
|
|
Теорема об откладывании
вектора от данной точки
|
1
|
Знает, понимает, умеет
применять
|
|
Сложение векторов по
правилу треугольника, параллелограмма, многоугольника
|
3
|
Знает, понимает, умеет
применять
|
Законы
сложения: 1. 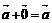
. 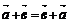
|
3. 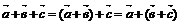 3Знает, понимает, умеет применять 3Знает, понимает, умеет применять
|
|
|
|
Определение разности
векторов
|
1
|
Знает, понимает, умеет
применять
|
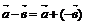 2Знает, понимает, умеет применять 2Знает, понимает, умеет применять
|
|
|
|
Определение произведения
вектора на число
|
2
|
Знает, понимает, умеет
применять
|
Свойства
операции произведения вектора на число: 1.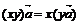
.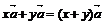
|
3.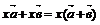 3Знает, понимает, умеет применять 3Знает, понимает, умеет применять
|
|
|
|
Лемма о коллинеарных
векторах
|
1
|
Знает, понимает, умеет
применять
|
|
Теорема о разложении
вектора по двум неколлинеарным векторам
|
1
|
Знает, понимает, умеет
применять
|
|
Применение векторов к
решению задач
|
1*
|
Умеет применять векторный
метод при решении содержательных задач
|
|
ИТОГО:
|
23+1*
|
|
Таким образом, минимальное количество заданий обязательного уровня
подготовки по теме «Векторы на плоскости» равно 24.
. Найдем число заданий теста, учитывая коэффициент К1-критерий полноты
отображения учебного материала.
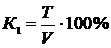 , ,
Где Т-число заданий в тесте,
V-объем
контролируемого материала.
Чтобы отображение проверяемого материала было полное, необходимо, чтобы
40% £ К1 £ 70%. В нашем случае получаем:
0,4
£  £ 0,7 £ 0,7
,6
£ Т £ 16,8
Пусть
тест будет содержать 10 заданий.
1. Определим процент заданий по видам деятельности (Знает и понимает
10%, применяет в знакомой ситуации-40%, применяет в измененной ситуации-30%,
применяет в новой ситуации - 10%).
|
Виды деятельности
|
Число заданий
|
Максимальное число баллов
|
|
Знает и понимает 20%,
|
0,2*10=2
|
2*1=2
|
|
применяет в знакомой ситуации-40%
|
0,4*10=4
|
4*1=4
|
|
применяет в измененной
ситуации-30%
|
0,3*10=3
|
3*2=6
|
|
применяет в новой ситуации
- 10%).
|
0,1*10=1
|
1*4=4
|
|
ИТОГО
|
10
|
16
|
2. Определим процент заданий по уровню сложности (Б, П, В) в соответствии
с критерием К3- коэффициента соответствия содержания теста содержанию
стандарта.
|
Уровень сложности
|
Число заданий
|
Процент заданий
|
|
Базовый
|
2+4=6
|
60%
|
|
Повышенный
|
3
|
30%
|
|
Высокий
|
1
|
10%
|
.Составим тестовые задания на основе выделенной спецификации.
II.
Содержание теста
Инструкция. В заданиях №№ 1-3 обведите кружком букву (несколько букв),
соответствующую правильному ответу.
Задание №1.
Выберите рисунок с изображением равных векторов
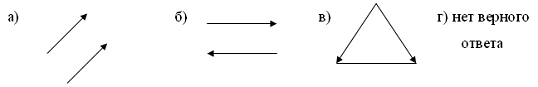
Эталон ответа а)
Задание №2
АВСD -
параллелограмм. Найдите сумму векторов 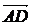 и и 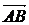 . .
а)
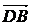 б) б) 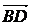 в) в) 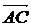 г) нет верного ответа г) нет верного ответа
Эталон ответа в)
Задание №3.
АВСD-прямоугольник
со сторонами 4 и 3 см. Найдите длину вектора 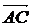 . .
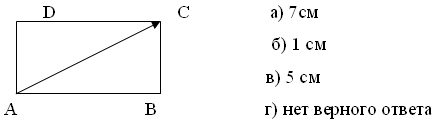
Эталон
ответа в)
Инструкция. В заданиях №4,5 запишите ответ в специально отведенное место.
Задание №4.
Преобразуйте
векторное выражение 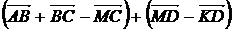
ОТВЕТ:
Эталон ответа 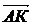 . .
Задание №5
Выразите
вектор (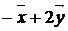 ) через векторы ) через векторы  и и 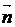 , если , если 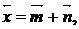 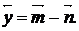
ОТВЕТ:
Эталон ответа 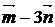
Задание №6
В треугольнике АВС точка Р делит медиану АМ в отношении 1:3, считая от
вершины А. Поставьте вместо многоточия такое число, чтобы равенство было
верным.
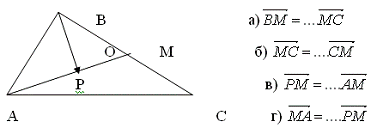
Эталон
ответа а)1; б)-1; в)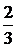 ; г)-1,5. ; г)-1,5.
Инструкция.
Запишите ответ в специально отведенное место.
Задание
№7.
В
треугольнике АВС 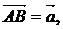 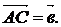 Точка
О-середина медианы АМ (см. рисунок к предыдущей задаче). Выразите вектор Точка
О-середина медианы АМ (см. рисунок к предыдущей задаче). Выразите вектор 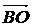 через векторы через векторы  и и 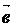 . .
ОТВЕТ:
Эталон ответа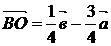
Инструкция. Для записи ответов на задания 8-10 используйте прилагаемый
бланк ответов. Запишите сначала номер выполняемого задания, а затем решение.
Задание №8.
М
- середина отрезка АВ, О - произвольная точка. Выразите вектор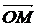 через векторы через векторы 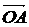 и и 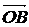 . .
Эталон
ответа
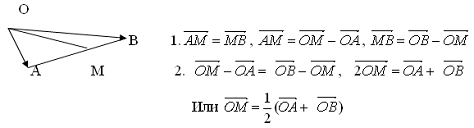
Задание №9
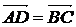 , , 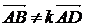 . Что представляет собой фигура АВСD. . Что представляет собой фигура АВСD.
Эталон ответа
Возможны 2 случая
1)
Векторы 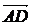 и и 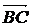 лежат на
параллельных прямых, 2) на одной прямой. лежат на
параллельных прямых, 2) на одной прямой.
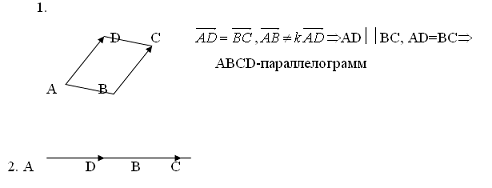
Тогда
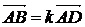 , что противоречит второму условию задачи , что противоречит второму условию задачи
Итак,
АВСD -параллелограмм.
Задание №10
Дан параллелограмм АВСD.
Точки P,Q, R, S - середины сторон АВ, ВС, СD, DA соответственно. Прямые PC, QD, RA, SB пересекаются в точках К, L, M, N. Докажите, что КLMN-параллелограмм.
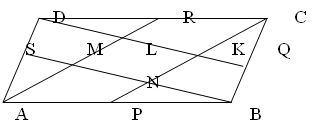
Эталон ответа.
1. Пусть
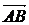 = = , , 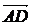 = =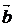 . .
. 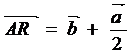 , , 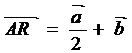 = =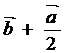
. 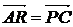 ÞAR½½PC, ÞAR½½PC,
. Аналогично,
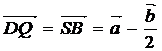 Þ DQ½½SB Þ DQ½½SB
. Имеем,
ML½½NK, MN½½LKÞMNKL-параллелограмм
Таким образом, тест включал в себя 10 вопросов, каждый из которых
соответствовал одному из трех уровней усвоения знаний: 1 уровень - фактическое
знание учебного материала проверяемой темы (формулировка основных определений
понятий, теорем); 2 уровень - понимание, умение применять теоретические факты в
стандартных ситуациях; 3 уровень - умение применять «новые» факты в измененных
ситуациях (умение применять векторный метод при решении содержательных
геометрических задач). В тестировании принимало участие 12 учеников 10 класса,
отсутствующих не было.
Приведем результаты проведенного тестирования:
|
Номер задания
|
Ответили верно
|
Ответили неверно
|
Не приступили к заданию
|
|
1
|
12 (100%)
|
-
|
-
|
|
2
|
12
|
-
|
-
|
|
3
|
11
|
2
|
-
|
|
4
|
9
|
3
|
-
|
|
5
|
10
|
2
|
-
|
|
6
|
8
|
3
|
1
|
|
7
|
7
|
3
|
2
|
|
8
|
7
|
2
|
3
|
|
9
|
5
|
4
|
3
|
|
10
|
2
|
6
|
4
|
Анализ результатов тестирования позволил сделать следующие выводы:
. Учащиеся достаточно хорошо владеют теоретическим материалом темы
«Векторы на плоскости»: различают основные отношения между парами векторов, их
взаимосвязь; формулируют теоремы-законы сложения векторов и произведения
вектора на число. Успешно справляются с заданиями, в которых требуется
преобразовать векторное равенство, построить результат сложения векторов по
правилам треугольника и параллелограмма.
. Около половины учащихся испытывает трудности при выполнении упражнений
на представление вектора через другие, на разложение вектора по двум
неколлинеарным векторам, а также на установлении взаимосвязи геометрических
свойств фигур с их векторной записью.
. Большая часть класса затрудняется в применении векторного метода к
решению содержательных геометрических задач.
Таким образом, проведенный анализ результатов тестирования позволил
выделить противоречие между необходимостью владения умениями, входящими в
состав векторного метода и недостаточным уровнем их сформированности у учащихся
в период изучения темы «Векторы на плоскости».
Выделенное противоречие позволило обосновать актуальность проводимого
исследования и сформулировать его гипотезу, а именно: целенаправленное обучение
школьников умениям, входящим в состав векторного метода, будет способствовать
эффективному усвоению ими собственно векторного метода решения содержательных
задач.
На втором, поисковом, этапе эксперимента решались следующие задачи:
) Проведение логико-дидактического анализа темы «Векторы в
пространстве» по учебному пособию [9] (параграф 2.1);
2) Разработка методических рекомендаций по обучению школьников векторному
методу, основанных на идее целенаправленной предварительной работы по
формированию умений, необходимых для успешного овладения учащимися этого
метода.
) Разработка системы уроков по теме в соответствии с планированием.
Конспекты 5 уроков приведены в параграфах 2.2 и 2.3.
На третьем, формирующем, этапе была осуществлена апробация разработанных
методических рекомендаций в личном опыте при обучении учащихся 10 класса МОУ
Хвощевской СОШ теме «Векторы в пространстве».
На этапе контролирующего эксперимента была проведена контрольная работа в
форме тестирования, аналогичная работе перед изучением данной темы.
Цель тестирования: выявить у учащихся 1) уровень усвоения теоретического
материала темы «Векторы на плоскости», 2) степень сформированности умения
применять векторный метод к решению задач различного уровня.
Тест так же содержал 10 вопросов, каждый из которых соответствовал одному
из трех уровней усвоения знаний. (Методика составления этого теста аналогична
рассмотренной выше).
Приведем содержание теста.
Инструкция. Обведите кружком букву, соответствующую правильному ответу.
Задание №1
Дан параллелепипед АВСDA1B1C1D1. Назовите вектор, равный сумме
векторов
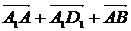
а)
А1D
б)
А1С
в)
С1А
г)
А1С1
Эталон
ответа б)
Инструкция
Обведите ответ «да» или «нет» в клеточке таблицы ответов.
Задание
№2
Установите,
являются ли следующие утверждения истинными (ответ «да») или ложными (ответ
«нет»).
|
Два коллинеарных вектора
являются компланарными
|
да
|
нет
|
|
Два произвольных вектора
не являются компланарными
|
да
|
нет
|
|
Три вектора, из которых два
являются коллинеарными, компланарны
|
да
|
нет
|
|
Три произвольных вектора не
всегда являются компланарными
|
да
|
нет
|
Эталон ответа да-нет-да-да
Инструкция. В заданиях № 3-7 запишите ответ в специально отведенное
место.
Задание №3
В
параллелепипеде АВСDA1B1C1D1 точка К
- середина АВ, АМ : МD =2:3. 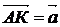 , , 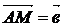 . Выразите вектор . Выразите вектор 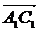 через
векторы через
векторы  и и 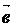 . .
ОТВЕТ:
Эталон ответа 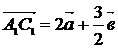
Задание №4.
Преобразуйте
векторное выражение 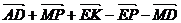
ОТВЕТ:
Задание№5
Дана
треугольная призма ABCDA1B1С1.
Укажите вектор 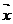 , начало и конец которого совпадают с вершинами
призмы, такой, что: , начало и конец которого совпадают с вершинами
призмы, такой, что: 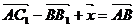
ОТВЕТ:
Задание
№6
Основанием
пирамиды с вершиной О является параллелограмм АВСD, диагонали
которого пересекаются в точке М. Разложите вектор 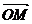 по векторам по векторам 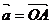 , , 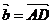 , , 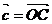
ОТВЕТ:
Задание№7
Дан
параллелепипед АВСDA1B1C1.
Разложите вектор 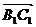 по векторам по векторам 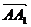 , , 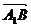 , , 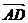 . .
ОТВЕТ:
Инструкция. Для записи ответов на задания 8-10 используйте прилагаемый
бланк ответов. Запишите сначала номер выполняемого задания, а затем решение.
Задание №8
Доказать,
что если т.М Î (АВС), то 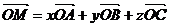 , х+y+z=1 , х+y+z=1
Задание
№9
Даны
треугольники АВС и А1В1С!. И две точки Р и О
пространства. Известно, что 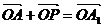 , , 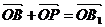 , ,  .
Докажите, что стороны треугольника А1В1С соответственно
равны и параллельны стронам треугольника АВС, .
Докажите, что стороны треугольника А1В1С соответственно
равны и параллельны стронам треугольника АВС,
Задание
№10.
Точки
А, В, С, D не принадлежат одной плоскости. Точки М, N, P, Q
-середины отрезков АВ, ВС, CD, DA. Докажите, что точки пересечения медиан треугольников
АВР, ВСQ, CDM, DAN принадлежат одной плоскости.
Рассмотрим полученные результаты:
|
Номер задания
|
Ответили верно
|
Ответили неверно
|
Не приступили к заданию
|
|
1
|
12 (100%)
|
-
|
-
|
|
2
|
11
|
1
|
-
|
|
3
|
11
|
1
|
-
|
|
4
|
10
|
2
|
-
|
|
5
|
10
|
2
|
-
|
|
6
|
11
|
1
|
-
|
|
7
|
9
|
3
|
-
|
|
8
|
8
|
4
|
-
|
|
9
|
8
|
3
|
1
|
|
10
|
7
|
3
|
2
|
Анализ приведенных результатов показал, что учащиеся в достаточной мере
овладели умениями и навыками, необходимых при решении задач векторным методом,
что способствовало значительному увеличению доли учащихся, решивших
содержательную задачу векторным методом.
Таким образом, содержание эксперимента и интерпретация его результатов
позволили сделать вывод о правильности выдвинутой гипотезы: предложенные
методические рекомендации по формированию у учащихся умений и навыков, входящих
в состав векторного метода способствуют эффективному усвоению учащимися
собственно векторного метода решения содержательных задач.
Заключение
В процессе исследования, в соответствии с его целями и задачами, были
получены следующие основные выводы и результаты:
. Анализ учебно-методической литературы показал, что методика обучения
школьников векторному методу очень широко обсуждается методистами, но, тем не
менее, учащиеся до сих пор испытывают трудности в применении этого метода к
решению задач и доказательству теорем. Между тем, векторные доказательства чаще
оказываются более предпочтительнее традиционных.
2. Анализ психолого-педагогической и научно-методической литературы
показал, что для успешного овладения учащимися общего метода решения задач,
необходимо обучать их умениям и действиям, входящим в состав этого метода. К
умениям и действиям, составляющих суть векторного метода относят следующие:
умение преобразовывать векторные выражения;
умение переводить геометрическое свойство фигуры на векторный язык и
обратно;
умение выражать вектор через другие.
. В соответствии с этими положениями разработаны методические
рекомендации по обучению учащихся векторному методу решения геометрических
задач на базе 10 класса в рамках темы «Векторы в пространстве», сформулированы
частные эвристики по решению отдельных типов задач темы.
. Была осуществлена опытная проверка разработанных методических
рекомендаций в 10 классе МОУ Хвощевской средней школы Богородского района
Нижегородской области. В качестве проверки эффективности применения
разработанных методических рекомендаций было проведено тестирование учащихся.
. Содержание эксперимента и интерпретация его результатов позволили
сделать вывод о правильности выдвинутой гипотезы.
Вышесказанное позволяет утверждать, что цель исследования достигнута,
гипотеза подтверждена.
Список литературы
1. Автономова Т.В., Аргунов Б.И. Основные понятия и методы
школьного курса геометрии: Кн. Для уч-ля. -М.: Просвещение, 1988.
2. Александров А.Д. и др. Геометрия для 8-9 кл.: Учеб.
пособие для учащихся шк. и классов с углуб. изуч. мат-ки / А.Д. Александров,
А.А. Вернер, В.И. Рыжик. - М.: Просвещение, 1991.
. Александров А.Д. Так что же такое вектор? //
Математика в школе. - 1984.- №5.
. Беклемишев Д.В. Курс аналитической геометрии и
линейной алгебры. -М, 2003.
. Болтянский В.Г., Волович М.В. Векторное изложение
геометрии. - М.: Просвещение, 1982.
. В помощь учителю математики: Методические
рекомендации к изучению отдельных тем. - Н. Новгород: НГПУ, 1994.
. В помощь учителю математики: Методические
рекомендации по решению геометрических задач аналитическими методами. -
Горький: ГГПИ им. Горького, 1985.
. Геометрия: учеб. для 7-9 кл. сред. шк./Л.С.
Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. - М.: Просвещение, 1990.
. Геометрия: учеб. для 10-11 кл. сред. шк./Л.С.
Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.-М.:Просвещение, 1992.
. Геометрия. Учеб. пособие для 7-го кл. сред. школы.
Под. ред. А.Н. Колмогорова. Изд. 5-е.-М.:Просвещение, 1976.
. Геометрия. Учеб. пособие для 9-10 кл. сред. школы.
Под. ред. З.А. Скопеца. - М.: Просвещение, 1976.
. Глейзер Г.И. История математики в школе 9-10
классов.: Пособие для учителей.-М.:Просвещение, 1983.
. Гусев В.А., Калягин Ю.М., Луканин Г.Л. Векторы в
школьном курсе геометрии.: Пособие для учителей.-М., 1976.
. Дорофеева А.В. Из истории векторного исчисления.//
Математика в школе. - 1998. - №2.
. Иванова Т.А., Серова Н.А. Выпускная квалификационная
работа по теории и методике обучения математике: Учебно-методическое пособие.
Н. Новгород: НГПУ, 2006.
. Концепция модернизации математического
образования.//www.edu.rin.ru
. Куликов Л.Я. Алгебра и теория чисел: Учеб. пособие
для педагогических институтов.-М.,1979.
. Менчинская Н.А. Проблемы учения и умственного
развития школьника: Избранные психологические труды. - М.: Педагогика, 1989.
. Методика преподавания математики в средней школе.
Частная методика. Сост. В.И. Мишин. - М.: Просвещение, 1987.
. Педагогика: Учеб. пособие для студентов пед. вузов и
пед. колледжей/Под. ред. П.И. Пидкасистого. - М: Педагогическое общество
России, 2001
. Погорелов А.В. Геометрия: Учеб. для 7-11 кл.
общеобразоват. Учреждений.-6-е изд-е. - М.:Просвещение, 1996.
. Потоскуев Е.В. Векторно-координатный метод при
решении стереометрических задач//Математика в школе. - 1995. - №1
. Программы для общеобразовательных школ, гимназий,
лицеев: Математика 5-11 кл./ Сост. Г.М. Кузнецова, Н.Г. Миндюк. - М., 2002.
. Роль и место задач в обучении математике: Сборник
научных трудов/В.А.Оганесян, В.В. Пикан: Под ред. Ю.М. Колягина. - М.: НИИ школ
МП РСФСР, 1978.
. Саранцев Г.И. Упражнения в обучении математике. -
М.: Просвещение, 1995.
. Скопец З.А. Векторное решение стереометрических
задач//Преподавание геометрии в 9-10 классах. -М.: Просвещение, 1980.
. Современные средства оценивания результатов
обучения: Учебное пособие/ Е.Н. Перевощикова, А.В. Поршнев, А.В. Юхова, Е.Ю.
Клюева: Под ред. проф. Е.Н. Перевощиковой. - Н. Новгород: НГПУ, 2007.
. Теоретические основы обучения математике в средней
школе: Учебное пособие/Т.А. Иванова, Е.Н. Перевощикова, Т.П. Григорьева, Л.И.
Кузнецова; Под ред. проф. Т.А. Ивановой. - Н.Новгород:НГПУ, 2003.
. Уч. Стандарты школ России. Госуд. Стандарты общего,
основного и среднего (полного) общего образования. Книга 2. Математика.
Естеств-науч. Дисциплины (Под ред. В.С. Леднева, Н.Д. Никандрова, М.Н.
Лазутовой).-М.: «Тц Сфера», «Прометей», 1998.
. Фридман Л.М. Психолого-педагогические основы
обучения математике в школе: Учителю математики о пед. Психологии. - М.:
Просвещение, 1983
. Шарыгин И.Ф. Геометрия 7-9 кл.: Учеб. для
общеобразоват. учеб. завед.-5-е изд-е.-М.:Дрофа, 2001.
. Шарыгин И.Ф. Геометрия 10-11 кл.: Учеб. для
общеобразоват. учеб. завед.-3-е изд-е., стереотип.-М.:Дрофа, 2001
. Якушина Е.В. Об изучении векторов в планиметрии и
стереометрии.//Математика в школе.- 1996, №3.
Приложение 1
Типы задач, решаемых векторным методом
|
Что требуется доказать (на
геометрическом языке)
|
Что достаточно доказать (на
векторном языке)
|
|
а½êb
|
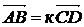 , [AB] Ìa, [CD] Ìb, k- число , [AB] Ìa, [CD] Ìb, k- число
|
|
АÎа, ВÎа, СÎа (три точки принадлежат одной прямой)
|
установить справедливость
одного из следующих равенств 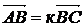 , или , или 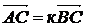 , или , или 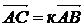 ; ;
|
|
СÎ[АВ], ½АВ½: ½СВ½=m:n (деление отрезка в данном отношении)
|
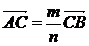
|
|
а½êa
|
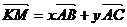 где [КМ]Ìа, т.А, В,
С Îa, так, что где [КМ]Ìа, т.А, В,
С Îa, так, что 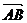 ≠к ≠к
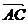
|
|
а, b, c ½êa
|
 , где [AB] Ìa, [CD]
Ìb, MSÌс , где [AB] Ìa, [CD]
Ìb, MSÌс
|
|
А, В, С, D Îa
|
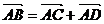
|
MÎa 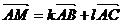 где т.А, В, С Îa, так, что где т.А, В, С Îa, так, что
|
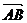 ≠к ≠к 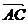
|
|
|
[AB] ½ê[CD] |AB| :|CD| = m:n
|
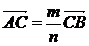
|
Похожие работы на - Теория и методика обучения школьников векторному методу (стереометрия)
|