Решения комбинаторных задач теории графов с помощью теоремы Пойа
Введение
Решение многих задач перечисления графов
сводится к подсчету числа классов эквивалентностей. Эффективный метод решения
таких задач базируется на известной теореме Пойа. Теорема (теория) Редфилда -
Пойа - классический результат перечислительной комбинаторики. Впервые эта
теорема была получена и опубликована Редфилдом в 1927 году, но работа была
сочтена весьма специальной и осталась незамеченной. Пойа независимо доказал то
же самое в 1937 году, но оказался куда более успешным популяризатором - так, например,
в первой же публикации он показал применимость этого результата к перечислению
химических соединений.
Актуальность теоремы Пойа: Далеко не всегда
удаётся чисто аналитическим путём получить явную формулу для количества классов
эквивалентности. Во многих задачах количество перестановок, входящих в группу,
может быть слишком большим для ручных вычислений, и вычислить аналитически
количество циклов в них не представляется возможным. Тогда для вычисления
количества циклов используется теорема Пойа.
Цель курсовой работы : изучить основные свойства
групп подстановок и метод решения комбинаторных задач теории графов с помощью
теоремы Пойа.
Задачи: 1) изучить такие основополагающие
понятия теории графов и теории групп, как граф, группа подстановок и ее цикловой
индекс; 2) рассмотреть определение эквивалентности, порождаемой группой
подстановок, и доказать лемму Бернсайда о числе классов такой эквивалентности;
3) разобрать определение перечня конфигурации и доказать теорему Пойа; 4)
разобрать примеры и решить задачи.
Глава 1. Основные понятия теории графов и теории
групп
.1 Основные понятия графа
теория граф теорема пойа
Граф - это совокупность непустого множества
вершин и множества пар вершин (связей между вершинами). С формальной точки
зрения граф представляет собой упорядоченную пару G = (V, Е) множеств, первое
из которых состоит из вершин, или узлов, графа, а второе - из его ребер. Ребро
связывает между собой две вершины. Графы часто описывают множество близких
ситуаций. Самым привычным примером служит карта автодорог, на которой
изображены перекрестки и связывающие их дороги. Перекрестки являются вершинами
графа, а дороги - его ребрами. Иногда наши графы ориентированы (подобно улицам
с односторонним движением) или взвешены - каждой дороге приписана стоимость
путешествия по ней (если, например, дороги платные). Когда мы изучим язык
графов подробнее, аналогия с картой автодорог станет еще более глубокой.
Граф может быть ориентированным или нет. Ребра
неориентированного графа, чаще всего называемого просто графом, можно проходить
в обоих направлениях. В этом случае ребро - это неупорядоченная пара вершин,
его концов. В ориентированном графе, или орграфе, ребра представляют собой
упорядоченные пары вершин: первая вершина - это начало ребра, а вторая - его конец.
[1]
На рисунке 1 изображено графическое
представление неориентированного (а) и ориентированного (б) графов вместе с их
формальным описанием.
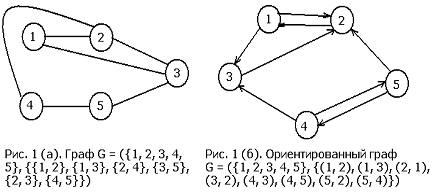
Подграфом называется часть графа, образованная
подмножеством вершин вместе со всеми ребрами (дугами), соединяющими вершины из
этого множества. Если из графа удалить часть ребер (дуг), то получим частичный
граф. Две вершины называются смежными, если они соединены ребром (дугой).
Смежные вершины называются граничными вер шинами соответствующего ребра (дуги),
а это ребро (дуга) - инцидентным соответствующим вершинам.
Путем называется последовательность дуг (в
ориентированном графе), такая, что конец одной дуги является началом другой
дуги. Простой путь - путь, в котором ни одна дуга не встречается дважды.
Элементарный путь - путь, в котором ни одна вершина не встречается дважды.
Контур - путь, у которого конечная вер шина совпадает с начальной вершиной.
Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если
последние заданы). [3]
Граф, для которого  из
следует,
из
следует,  называется
симметрическим. Если из
называется
симметрическим. Если из  следует, что
следует, что  то
соответствующий граф называется антисимметрическим.
то
соответствующий граф называется антисимметрическим.
Цепью называется множество ребер (в
неориентированном графе), которые можно расположить так, что конец (в этом
расположении) одного ребра является началом другого. Другое определение: цепь -
последовательность смежных вершин. Замкнутая цепь называется циклом. По
аналогии с простым и элементарным путем, можно определить соответственно
простые и элементарные цепь и цикл. Любой элементарный цикл является простым,
обратное утверждение в общем случае неверно. Элементарная цепь (цикл, путь,
контур), проходящая через все вершины графа называется гамильтоновой цепью
(соответственно - циклом, путем, контуром). Простая цепь (цикл, путь, контур),
содержащая все ребра (дуги) графа называется эйлеровой цепью (соответственно -
циклом, путем, контуром).
Если любые две вершины графа можно соединить
цепью, то граф называется связным. Если граф не является связным, то его можно
разбить на связные подграфы, называемые компонентами. Связностью графа
называется минимальное число ребер, после удаления, которых граф становится
несвязным. Для ориентированных графов, если любые две вершины графа можно
соединить путем, то граф называется сильно связным. Известно , что: связность
графа не может быть больше, чем [2m /n], где [x] - целая часть числа x;
существуют графы с n вершинами и m ребрами, имеющие связность [2m /n]; в сильно
связном графе через любые две вершины проходит контур. Связный граф, в котором
существует эйлеров цикл, называется эйлеровым графом. В неориентированном графе
степенью вершины i называется число di инцидентных ей ребер.
Очевидно, dj < n - l , i eX . Граф, степени всех вершин которого
равны n - 1, называется полным. Граф, все степени вершин которого равны,
называется однородным. [2]
Связный граф является эйлеровым тогда и только
тогда, когда степени всех его вершин четны (теорема Эйлера). Обозначим щ -
число вершин, имеющих степень k, k = 0, 1, 2,... . Известно, что:
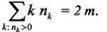
Для ориентированных графов для каждой вершины
можно ввести два числа - полу степень исхода 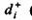 (число
выходящих из нее вершин) и полу степень захода
(число
выходящих из нее вершин) и полу степень захода
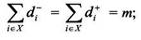
(число
входящих в нее для эйлерова графа имеет место: d = di, вершин). В
дальнейшем, если не оговорено особо, будем рассматривать графы без петель, то
есть без дуг, у которых начальная и конечная вершины совпадают. Известно, что: 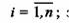 эйлеров
граф является объединением контуров, попарно не имеющих общих ребер.
эйлеров
граф является объединением контуров, попарно не имеющих общих ребер.
Деревом
называется связный граф без простых циклов, имеющий не менее двух вершин. Для
дерева m = n-1, а число висячих вершин равно
 .
.
Легко
показать, что в дереве любые две вершины связаны единственной цепью.
Прадеревом
называется ориентированное дерево, у которого одна из вершин, называемая
корнем, не имеет заходящих дуг, а степени захода остальных вершин равны
единице.
Плоским
(планарным) называется граф, который можно изобразить на плоскости так, что
различным вершинам соответствуют различные кружки и никакие два ребра не имеют
общих точек, отличных от их границ (не пересекаются). Для плоского графа
существует понятие грани - части плоскости, ограниченной ребра ми и не
содержащей внутри себя ни вершин, ни ребер. Для простоты определения грани в
дальнейшем в основном будем рассматривать графы без висячих вершин. Например,
дерево имеет всего одну внешнюю грань - всю плоскость. Степенью грани
называется число ее граничных ребер (висячие ребра считаются дважды). Обозначим
- число граней плоского графа, pk - число его граней, имеющих
степень k, q, i - степень 2-ой грани. Можно показать, что имеет место
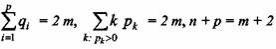
формула
Эйлера. Данные выражения являются необходимыми условиями  существования
плоских графов с заданными наборами чисел.
существования
плоских графов с заданными наборами чисел.
Любому
связному плоскому графу G можно поставить в соответствие двойственный ему
связный плоский граф G, определяемый следующим образом: каждой грани графа G
соответствует вершина графа G*, каждому ребру V графа G ,
являющемуся граничным для граней z1 и z2, соответствует
ребро V* графа G*, соединяющее соответствующие граням z
1 и z2 вершины. Понятие двойственного графа тесно связано с
понятием двойственности в линейном программировании.
.2
Группы подстановок
Группой
называется множество элементов (конечное или бесконечное), на котором задана
операция умножения , которая удовлетворяет следующим четырём аксиомам:
Замкнутость
группы относительно операции умножения. Для любых двух элементов группы
существует третий, который является их произведением:

Ассоциативность
операции умножения. Порядок выполнения умножения несущественен:
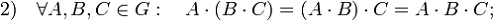
Существование
единичного элемента. В группе существует некоторый элемент E, произведение
которого с любым элементом A группы даёт тот же самый элемент A:

Существование
обратного элемента. Для любого элемента A группы существует такой элемент A−1,
что их произведение даёт единичный элемент E:
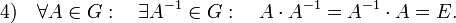
Аксиомы
группы никак не регламентируют зависимость операции умножения от порядка
сомножителей. Поэтому, вообще говоря, изменение порядка сомножителей влияет на
произведение. Группы, для которых произведение не зависит от порядка
сомножителей, называют коммутативными или абелевыми группами. Для абелевой
группы:
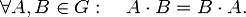
Абелевы
группы, довольно редко встречаются в физических приложениях. Чаще всего группы,
имеющие физический смысл, являются не абелевыми:
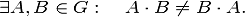
Непустое
подмножество A множества Г называют подгруппой группы Г, если оно удовлетворяет
следующим двум условиям:
Бинарная
операция не выводит за пределы подмножества A;
Для
любого элемента x из A обратный к нему элемент x−1 также лежит в A.
Пусть
A - некоторая подгруппа группы Г. Правым классом смежности группы Г по
подгруппе A называется множество вида Ax = {y·x | y из A}, где x - произвольный
элемент из Г (аналогично определяются левые классы смежности). Известно также
утверждение о том, что если A - подгруппа группы Г, то группу Г можно разложить
в объединение правых (левых) классов смежности по подгруппе A.
Рассмотрим
теперь множество X = {1, 2, …, n}. Подстановкой называется взаимно однозначное
отображение a: X → X. Умножением подстановок будем называть их
композицию. Пусть A - некоторая совокупность подстановок множества X, замкнутая
относительно операции умножения. Тогда A является группой подстановок на
множестве объектов X. Порядок группы A, обозначаемый |A|, есть число
подстановок A, а степень группы - это число n элементов в множестве объектов X.
[3]
Наиболее
важными для нас примерами группы подстановок являются симметрическая группа Sn
- группа всех подстановок на множестве из n объектов, и знакопеременная группа
An - группа всех четных подстановок. Чтобы определить понятие четной
подстановки введем понятие транспозиции.
Транспозицией
называется подстановка, меняющая два элемента местами друг с другом и
оставляющая остальные элементы на своих местах. Можно показать, что любая
подстановка раскладывается в произведение транспозиций. Подстановка называется
четной, если число транспозиций, в которые раскладывается подстановка, четно.
Пусть A - группа подстановок с множеством объектов X = {1, 2, …, n}. Циклом
длины k называется подстановка, обозначаемая (i1, i2, …,
ik), которая переводит i1 в i2, i2
в i3, …, ik в i1. Известно, что каждая подстановка
a может быть представлена в виде произведения непересекающихся циклов.
Например,
3 = {(1)(2)(3), (12)(3), (13)(2),
(23)(1), (123), (132)} или A3 = {(1)(2)(3), (123), (132)}.
Существует
естественная связь между группами подстановок и графами. Рассмотрим два графа G1
и G2. Взаимно однозначное отображение, a множества вершин графа G1
на множество вершин графа G2, сохраняющее смежность, называют
изоморфизмом. Если G1 = G2, то a называется автоморфизмом
графа. Совокупность всех автоморфизмов графа G, обозначаемая Г(G), образует
группу, называемую группой графа G, или группой автоморфизмов графа G. Таким
образом, элементы группы Г(G) являются подстановками, действующими на множестве
вершин графа. Рассмотрим граф G, изображенный на рисунке 2.
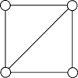
Рис.
2
Его
четыре вершины составляют множество X целых чисел 1, 2, 3, 4. Заметим, что
следующий список подстановок 1 = (1)(2)(3)(4)2 =
(1)(3)(24)3 = (13)(2)(4)4 = (13)(24)
включает
все подстановки множества X, сохраняющие отношение смежности в графе G. К
примеру, вершины 1 и 4 смежны в G. Подстановка (13)(2)(4) преобразует вершины 1
и 4 в вершины 3 и 4, и эти образы 3 и 4, также являются смежными. Таким
образом, подстановка (13)(2)(4) сохраняет смежность вершин 1 и 4.
Так
как совокупность подстановок в этом списке замкнута относительно операции
умножения, то она образует группу. [2]
.3
Цикловые индексы группы подстановок
Пусть
A - группа подстановок с множеством объектов X = {1, 2, …, n} и a - некоторая
подстановка из этой группы. Для каждого k = 1, 2, …, n через jk(a)
обозначим число циклов длины k в разложении подстановки a в произведение
непересекающихся циклов.
Тогда
цикловой индекс группы A, обозначаемый Z(A) или Z(A, s1, s2,
…, sn), представляет собой многочлен от переменных s1, s2,
…, sn, определяемый формулой

Рассмотрим
для примера симметрическую группу S3. Заметим, что тождественная
подстановка (1)(2)(3) имеет три единичных цикла дающих слагаемое s13. Три
подстановки (1)(23), (2)(13) и (3)(12) имеют каждая по единичному циклу и по
одному циклу длины 2, так что получается одно слагаемое 3s1s2.
Наконец, подстановки (123) и (132) вносят 2s3. Таким образом, имеем
Z(S3) = (1/3!)(s13 + 3s1s2 + 2s3).
Для вычисления циклового индекса симметрической группы Sn введем понятие
разбиения числа и рассмотрим несколько утверждений. [2] Назовем разбиением
натурального числа n его представление в виде суммы некоторых натуральных
чисел. Заметим, что каждая подстановка a на n объектах может быть связана с
определенным разбиением числа n, имеющим для каждого k = 1, 2, …, n точно jk(a)
частей, равных числу k. Будем задавать разбиение числа n посредством вектора
(j)
= (j1, j2, …, jn),
где
jk - число частей разбиения, равных k. Итак,
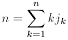
Пример
|
4
= 1 + 1 + 1 + 1
|
(4,
0, 0, 0)
|
|
4
= 1 + 1 + 2
|
|
4
= 2 + 2
|
(0,
2, 0, 0)
|
|
4
= 1 + 3
|
(1,
0, 1, 0)
|
|
4
= 4
|
(0,
0, 0, 1)
|
Глава 2. Лемма Бернсайда о числе классов
эквивалентности
.1 Определение эквивалентности, порождаемой
группой подстановок
Определение: Если множество А={1,2,…,n}
постоянно, то взаимнооднозначное отображение р:А→А называется
подстановкой, которая обозначается:

где ik
= p(k).
Произведение двух подстановок есть их последовательное исполнение.
Множество подобных подстановок, определенных на
множестве А с операциями умножения подстановок и взятия обратной подстановки
образуют симметрическую группу Sn
с единицей:
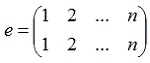
которая есть тождественная подстановка. Заметим,
что симметричная группа Sn
не коммутативна и содержит n!
элементов.
Пусть Sn
есть симметрическая группа подстановок, определенных на множестве Х={1,2,…,n}.
Утверждение: Всякая конечная группа порядка n(число
элементов в группе) изоморфна некоторой подгруппе симметрической группы Sn.
Пусть G=(p0=e,p1,…,pr}
есть некая группа подстановок, определенная на множестве X={1,2,…,n}
с единицей p0=e
(тождественной подстановкой).
Введём отношение X~Y
на Х так, чтобы X~Y
⇔
∃p∈G
(p(x)=y)
X~Y
есть отношение эквивалентности, то есть он удовлетворяет трем аксиомам:
. X~X
. X~Y
⇒
Y~X
. X~Y
и Y~Z
⇒
X~Z
Замечание: Отношение X~Y
индуцирует разбиение множества Х на попарно непересекающиеся классы
эквивалентных между собой элементов.
Определение: Класс эквивалентности в множестве Х
по отношению к соотношениям X~Y
называется орбитой группы подстановок G.
Длина орбиты есть число её элементов.
Замечание: Для ∀а∈Х
множество А(а)={р0(a)=a,
р1(a),…,рn-1(a)}
перечисляет все элементы, эквивалентные а, и потому множество А(а) есть орбита
группы G.
Замечание: Орбита О замкнута относительно ∀
функции р(х)∈G,
то есть ∀a∈O
∀P∈G
р(a)∈O.
Утверждение: ∀O={i1,…,iu}
группа подстановок G для ∀
элемента с∈О орбита О=А(с)={р0(с)=с,
р1(с),…,рn-1(с)}
Следствие: Все орбиты группы подстановок G
исчерпываются орбитами вида А(а).
Замечание: Множество Х={1,2,…,n}
распадается в сумму попарно непересекающихся между собой орбит группы G.[1]
.2 Лемма Бернсайда
Уильям Бернсайд сформулировал и доказал эту
лемму (без указания авторства) в одной из своих книг (1897 год), но историки
математики обнаружили, что он не был первым, кто открыл её. Коши в 1845 году и
Фробениусу в 1887 году также была известна эта формула. По-видимому, лемма была
столь хорошо известна, что Бернсайд просто опустил указание авторства Коши.
Поэтому эта лемма иногда называется леммой не Бернсайда. Это название не столь
туманно, как кажется: работа Бернсайда была столь плодотворной, что большинство
лемм в этой области принадлежит ему.
В теории групп лемма Бернсайда связывает
количество орбит в подгруппе симметрической группы с цикловой структурой
элементов этой подгруппы. Существует несколько вариантов леммы: упрощенный,
весовой, ограниченный и т. д. Лемма Бёрнсайда лежит в основе доказательства
теоремы Редфилда - Пойа.
Упрощенный вид:
Пусть G
- конечная группа, действующая на множестве X.
Для любого элемента g из G
будем обозначать Xg
через множество элементов X,
оставляемых на месте g.
Лемма Бернсайда даёт формулу числа орбит группы G,
обозначаемого |X/G|:
|X/G|=.
Число орбит (натуральное число или
бесконечность) равно среднему количеству точек, оставляемых на месте элементом
из G.
Доказательство
Доказательство основано на подсчёте числа
элементов одного множества двумя способами:


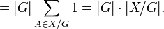
Весовой вид:
 [3]
[3]
где 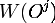 -
вес орбиты
-
вес орбиты  (вес любого её
представителя),
(вес любого её
представителя),  - вес элемента.
- вес элемента.
Глава 3. Определение конфигурации и теорема Пойа
.1 Определение перечня конфигурации
Конфигурация - конечное множество точек, прямых,
плоскостей, связанных между собой взаимными инцидентностями. К. могут быть как
плоскими, так н пространственными.
Плоская конфигурация - конечная система рточек и
gпрямых на плоскости, расположенных таким образом, что всякая точка системы
инцидентна с одним и тем же числом упрямых этой системы, а всякая прямая
инцидентна с одним и том же числом p точек этой системы. Минимальная система
точек данной К., из к-рой вся К. может быть получена путем инциденций пар точек
с прямыми и пересечений пар прямых, наз. системой образующих данной К. Числа р,
g,g, p связаны соотношением pg=gp, a К. обозначается символом (р, g, gp). К.,
содержащая одинаковое число точек и прямых, обозначается символом ( р у).
Автоморфизмом конфигурации называется
отображение конфигурации на себя, при котором точки конфигурации переходят в
точки, прямые - в прямые этой же конфигурации, и при этом ни одна инцидентность
не пропадает, и не добавляется новых. Конфигурация называется правильной, если
группа автоморфизмов этой конфигурации транзитивна.
Которая может быть определена также как конечная
частичная плоскость. Возможность существования некоторой конфигурации
определяется из геометрических и комбинаторных соотношений между количеством
точек и прямых и количеством взаимных инциденций. Конфигурация задается и с
помощью абстрактных схем, на таблице (рис. 3) указаны инцидентности
(обозначенные крестиком) четырех точек, вершин Аi, и четырех
плоскостей, граней Di тетраэдра. После того как некоторая
конфигурация определена абстрактно, возникает вопрос о ее реализации, т. е. о
возможности построения всех инциденций по данной системе образующих.
Реализуемость конфигурации, как конечной частичной плоскости, означает
возможность изоморфного отображения ее на некоторую под плоскость какой-либо
плоскости. [1]
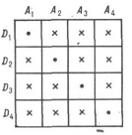
Рис. 3
.2 Теорема Пойа
Многие проблемы перечисления формулируются так,
что ответ можно дать, найдя формулу для числа орбит (систем транзитивности),
определяемых группой подстановок. Часто орбитам приписываются веса; Пойа
показал, как получить формулу, перечисляющую орбиты в соответствии с весами и
зависящую от циклической структуры подстановок данной группы. Обращение теоремы
Пойа связано с обобщением хорошо известной перечислительной формулы,
принадлежащей Бернсайду.
Теорема. Пусть А - группа подстановок,
действующая на множестве X с орбитами Q1, Q2, …, Qn, и 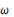
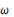 - функция, приписывающая веса каждой
орбите (весовая функция). Более того,
- функция, приписывающая веса каждой
орбите (весовая функция). Более того, 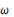
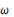 определяется на X так, что
определяется на X так, что 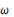
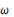 (x)=
(x)= 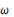
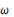 (
(
 i), если х
i), если х
 i. Тогда
сумма весов орбит равна: (1)
i. Тогда
сумма весов орбит равна: (1)
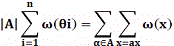
Доказательство
Мы уже видели, что порядок |А|
группы A равен |А
(х)|- |
 (х)| для любого х из X, где А(х) -
стабилизатор элемента х. Кроме того, поскольку весовая функция постоянна на
элементах данной орбиты, то
(х)| для любого х из X, где А(х) -
стабилизатор элемента х. Кроме того, поскольку весовая функция постоянна на
элементах данной орбиты, то

для каждой орбиты 
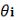 . Сопоставляя эти факты, находим,
что
. Сопоставляя эти факты, находим,
что

Суммируя по всем орбитам, имеем
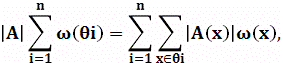
откуда сразу следует (1).
Традиционную форму леммы Бернсайда
теперь можно установить как следствие этой теоремы. Пусть для подстановки а,
представленной в виде произведения непересекающихся циклов, jk(
 ) обозначает число циклов длины k.
) обозначает число циклов длины k.
Следствие (2) (лемма Бернсайда).
Число N (А) орбит группы подстановок А равно
Все классические проблемы
перечисления, к которым применяется теорема Пойа, имеют одну и ту же общую
форму. Пусть дана область определения D, множество
значений R и весовая
функция 
 , определенная на R. В качестве
примера можно взять весовую функцию
, определенная на R. В качестве
примера можно взять весовую функцию 
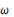 , приписывающую каждому r
, приписывающую каждому r
 R упорядоченную пару
R упорядоченную пару 
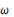 (r) = (
(r) = (
 r,
r,
 r) неотрицательных целых чисел.
Объекты, подлежащие счету, - это функции, действующие из D в R. Для завершения
постановки проблемы надо условиться о том, когда две функции из RD
рассматриваются как неразличимые (эквивалентные). Это достигается указанием
группы А, действующей на D; при этом две функции считаются
эквивалентными, когда они принадлежат одной и той же орбите из ЕА,
где Е - тождественная группа степени |R|.
r) неотрицательных целых чисел.
Объекты, подлежащие счету, - это функции, действующие из D в R. Для завершения
постановки проблемы надо условиться о том, когда две функции из RD
рассматриваются как неразличимые (эквивалентные). Это достигается указанием
группы А, действующей на D; при этом две функции считаются
эквивалентными, когда они принадлежат одной и той же орбите из ЕА,
где Е - тождественная группа степени |R|.
Задержимся на минуту и
проиллюстрируем эти идеи на «проблеме ожерелья». Рассмотрим ожерелья, скажем, с
4 бусинками, в которых одни бусинки красные, а другие синие. Два таких ожерелья
считаются эквивалентными, если их можно сделать «конгруэнтными» с сохранением
цветов бусинок. Здесь D - множество ячеек (мест), в которых
могут находиться бусинки, R - множество {красная бусинка, синяя
бусинка}, а функция f 
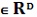 - приписывание бусинок каждому
месту (каждый ячейке) на ожерелье. В этом примере группа А - диэдральная группа
D4; весовую
функцию
- приписывание бусинок каждому
месту (каждый ячейке) на ожерелье. В этом примере группа А - диэдральная группа
D4; весовую
функцию 
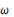 можно определить равенствами
можно определить равенствами 
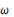 (красная бусинка) (1, 0) и
(красная бусинка) (1, 0) и 
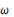 (синяя бусинка) = (0,1).
(синяя бусинка) = (0,1).
Следуя интуитивной терминологии
Пойа, элементы области определения D будем
называть местами, элементы множества значений - фигурами, функции -
конфигурациями, а группу подстановок А-группой конфигураций. Припишем вес 
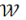 (f) каждой
функции f
(f) каждой
функции f

 RD:
RD:
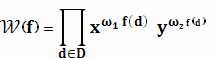

Легко видеть, что все функции из
данной орбиты множества RD,
определяемой группой ЕА, имеют один и тот же вес, так что вес орбиты
можно определить как вес любой функции из нее.
Если в (2) написать Z(A)=Z(A; a1, a2, …,ad), то для
любой функции
h (х, у)Z(A,h (х, y))=Z (A; h (х, y),h(x2, у2),
..., h(xd, yd)). (3)
Теорема (теорема перечисления Пойа)
Перечисляющий ряд для конфигураций
получается подстановкой перечисляющего ряда для фигур в цикловой индекс группы
конфигураций, т. е.
C(x,y)=Z(A,c(x,y)).
Доказательство
Пусть 
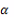 - подстановка в группе А и ᾶ -
соответствующая подстановка в степенной группе ЕА. Предположим
сначала, что f-
конфигурация, остающаяся неподвижной при действии ᾶ, и £ - цикл
длины k в
разложении
- подстановка в группе А и ᾶ -
соответствующая подстановка в степенной группе ЕА. Предположим
сначала, что f-
конфигурация, остающаяся неподвижной при действии ᾶ, и £ - цикл
длины k в
разложении 
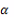 на непересекающиеся циклы. Тогда f(d)=f(£d) для
каждого элемента d в представлении £, так что
все элементы, переставляемые при помощи £ должны иметь один и тот же
образ при f. Обратно,
если элементы каждого цикла подстановки б имеют один и тот же образ при
конфигурации f, то ᾶ оставляет f
неподвижной. Таким образом, все конфигурации, остающиеся неподвижными при
действии ᾶ, получаются
с помощью независимого выбора элемента г из R для каждого
цикла £ подстановки
б и проверки равенства f(d)=r для всех
элементов d,
переставляемых циклом £. Тогда если
щ(r) = (т, п),
где m=щ1r и n=щ2r, и £ имеет длину
k, то цикл £ вносит
множитель
на непересекающиеся циклы. Тогда f(d)=f(£d) для
каждого элемента d в представлении £, так что
все элементы, переставляемые при помощи £ должны иметь один и тот же
образ при f. Обратно,
если элементы каждого цикла подстановки б имеют один и тот же образ при
конфигурации f, то ᾶ оставляет f
неподвижной. Таким образом, все конфигурации, остающиеся неподвижными при
действии ᾶ, получаются
с помощью независимого выбора элемента г из R для каждого
цикла £ подстановки
б и проверки равенства f(d)=r для всех
элементов d,
переставляемых циклом £. Тогда если
щ(r) = (т, п),
где m=щ1r и n=щ2r, и £ имеет длину
k, то цикл £ вносит
множитель 
 в произведение, задающее сумму весов
в произведение, задающее сумму весов

 . Следовательно, так как
. Следовательно, так как

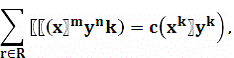
то для каждого б из А

Суммируя обе части этого соотношения
по всем подстановкам б из А (или, что то же самое, по всем б из ЕA) и деля обе
части на |А| =|ЕА|, получаем
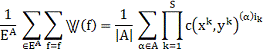 (4)
(4)
Правая часть этого равенства есть Z(A,
с(х, у)). Чтобы показать, что левая часть есть С(х, у), применим тот вариант
леммы Бернсайда, который дается теоремой (2). Сначала заметим, что для
степенной группы ЕA
сумма весов орбит равна
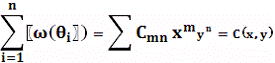

Но, как следует из формулы (1), левые части в
(4) и (5) совпадают, так что Z(A,
с(х, у)) = С(х, у); теорема доказана.
Возвращаясь к упомянутой выше проблеме ожерелья
с четырьмя бусинками, заметим, что цикловой индекс диэдральной группы D4
равен
Z(D4) = 
 (
(
 2а4), (6)
2а4), (6)
а перечисляющий ряд для фигур имеет
вид с(х, y)=x1y0+x°yl=х+у.
Подставляя х+у в (6) и учитывая (3), находим
Z(D4,x + y) = 
 {(x + y)4
+ 2 (х + у)2 (x2 + y2) + 3(х2
+ у2)2+2(х4 + у4)} =
{(x + y)4
+ 2 (х + у)2 (x2 + y2) + 3(х2
+ у2)2+2(х4 + у4)} =
х4 + x3y + 2х2у2
+ ху3 + у4. (7)
Коэффициент при хmуn в (7) равен
числу различных ожерелий с четырьмя бусинками, из которых m красные и n синие. Эти
6 раз личных ожерелий показаны на рис. 4.
Случайно оказывается, что ожерелья
можно также перечислить, используя в качестве перечисляющего ряда для фигур 1+x вместо х+у.
При этом красная бусинка имеет вес 1, а синяя бусинка - вес 0. Тогда в
многочлене Z(D4, 1+x)=х4+х3+2х2+х+1
коэффициент при хт равен числу ожерелий с т красными бусинками и,
следовательно с 4-m синими бусинкам.

Рис. 4
Следствие: Если А - группа
подстановок, действующая на X, то число индуцированных группой А орбит
п-подмножеств множества X равно коэффициенту при хп в Z(A, 1+х).
В приложениях теоремы перечисления
Пойа часто встречаются определенные группы подстановок. Приведем формулы для
цикловых индексов пяти важных групп подстановок. В формулах (8) и (9)
суммирование ведется по всем разбиениям (j) числа р. В
(10) 
 (k) есть
-функция Эйлера, ее значение при k
(k) есть
-функция Эйлера, ее значение при k
 равно числу положительных целых
чисел, меньших k и взаимно простых с k, причем по
определению
равно числу положительных целых
чисел, меньших k и взаимно простых с k, причем по
определению 
 (1) = 1. Итак
(1) = 1. Итак
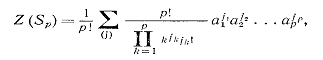 (8)
(8)
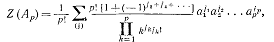 (9)
(9)
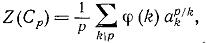 (10)
(10)
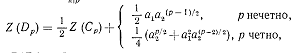
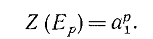
Существует несколько очень полезных
формул, позволяющих по цикловым индексам Z{A) и Z(B) групп А и
В вычислять цикловые индексы суммы А+В, произведения АхВ, композиции А [В] и
степенной группы ВА. Под Z(A)[Z(B)] мы понимаем
многочлен, полученный заменой каждой переменной ah в Z(A)
многочленом, который строится из многочлена Z(B) с помощью
умножения всех индексов переменных из Z(B) на число k.
Z(A + B) =
Z(A)Z(B),
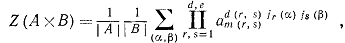
Где d (r, s) и m (r, s) обозначают
соответственно наибольший общий делитель и наименьшее общее кратное чисел г и s;
Z(A[B])=Z(A)[Z(B)],

где (
 и
и


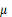 - известная теоретико-числовая
функция. [2]
- известная теоретико-числовая
функция. [2]
.3 Решения задач
Задание 1
Пусть G - множество
всех подстановок граней тетраэдра, которые могут быть получены его вращениями.
Найти цикловой индекс группы G.
Решение:
PG=(
 +8x1x3 + 3
+8x1x3 + 3
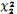 )/12. Здесь можно воспользоваться
тем, что двойственным к тетраэдру правильным многогранником является сам
тетраэдр.
)/12. Здесь можно воспользоваться
тем, что двойственным к тетраэдру правильным многогранником является сам
тетраэдр.
Задание 2
Пусть G -множество
тех подстановок вершин куба, которые могут быть получены его вращениями. Найти
цикловой индекс группы G.
Решение:
вращения куба можно разбить на пять
частей:
) тождественное;
) 3 поворота на 180
 вокруг прямых, соединяющих центры
противоположных граней;
вокруг прямых, соединяющих центры
противоположных граней;
) 6 поворотов на 90° вокруг прямых,
соединяющих центры противоположных граней;
) 6 поворотов на 180° вокруг прямых,
соединяющих середины противоположных ребер;
) 8 поворотов на 120° вокруг прямых,
соединяющих противоположные вершины.
Подстановка 1) дает 8 циклов длины
1. Подстановка 2) дает 4 цикла длины 2. Подстановка типа 3) дает 2 цикла длины
4. Подста- новка типа 4) дает 4 цикла длины 2. Подстановка типа 5) дает 2 цикла
длины 1 и 2 цикла длины 3. Поэтому
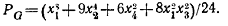
Задание 3
Доказать, что цикловой индекс
симметрической группы Sn равен
коэффициенту при zn в разложении
exp {zx1 + z2x2/2 + z3x3/3 + ...}.
Решение
ехр(zx1+ 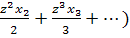
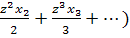 =
= 
Коэффициент при zn
получается суммированием выражений
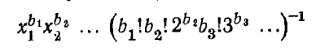
по всевозможным целым неотрицательным числам b1,
b2,
... , удовлетворяющим условию b1+2b2+3b3+…=n.
[4]
Заключение
В работе рассмотрены основное понятие графа -
совокупность конечного числа точек (вершины) и попарно соединяющих некоторые из
этих вершин линий (ребра или дуги графа). Были решены задачи с использованием
графов, приведены примеры различных задач из других областей науки и техники.
Список используемой литературы
1. Белов В.В., Воробьев Е.М.,
Шаталов В.Е. Теория графов. - М.: ВШ, 1976. с 9-18, 239-243, 245-248.
. Харари Ф. Теория графов. - М.:
Мир, 1973. с 21-26, 211-216.
. Калужнин Л.А., Сущанский В.И.
Преобразования и перестановки. - М.: Наука, 1985. с 50-63, 81-85