Решение линейных уравнений
1. Теоретическая часть
1.1 Основные виды линейных интегральных уравнений
Под интегральным уравнением понимается уравнение, содержащее
неизвестную функцию у (х) под знаком определенного интеграла. В дальнейшем мы
ограничимся рассмотрением линейных интегральных уравнений, в которые
неизвестная функция входит лишь в первой степени (линейно).
Приведем некоторые наиболее часто встречающиеся типы
интегральных уравнений. Уравнение вида
 (1)
(1)
где  (ядро) и f(х) - известные функции, называется интегральным уравнением
Фредгольма первого рода. Уравнение вида
(ядро) и f(х) - известные функции, называется интегральным уравнением
Фредгольма первого рода. Уравнение вида
у (х)-
 (2)
(2)
где  - числовой параметр, носит название
интегрального уравнения Фредгольма второго рода.
- числовой параметр, носит название
интегрального уравнения Фредгольма второго рода.
Параметр  вводится по следующим соображениям: при
данном значении
вводится по следующим соображениям: при
данном значении  интегральное уравнение (2) не всегда
имеет решения. Варьируя параметр
интегральное уравнение (2) не всегда
имеет решения. Варьируя параметр  , можно добиться того, чтобы решение уравнения (2) существовало.
Параметр
, можно добиться того, чтобы решение уравнения (2) существовало.
Параметр  можно также ввести в левую часть
уравнения Фредгольма первого рода (1).
можно также ввести в левую часть
уравнения Фредгольма первого рода (1).
Если в (2) f(х) 0, то получается однородное уравнение
0, то получается однородное уравнение
у (х)=
 (3)
(3)
допускается нулевое (тривиальное) решение у≡0. Те
значения параметра λ, при которых однородное
интегральное уравнение (3) имеет нетривиальные решения, называются собственными
значениями (собственными числами) ядра К (x, s), или соответствующего
уравнения (2), а отвечающие им нулевые решения - собственными функциями.
Основной результат теории следующий (теорема Фредгольма): 1) если λ не есть собственное значение ядра К (x, s), то соответствующее
неоднородное интегральное уравнение Фредгольма (2) с регуляторным ядром К (x, s) и непрерывным свободным
членом f(x) имеет единственное непрерывное решение у(х)
(а≤х≤b), 2), если же λ есть собственное значение, то уравнение (2) или не имеет решений,
или же допускает бесчисленное множество их.
В приложениях важную роль играют уравнения Фредгольма второго
рода с симметричным ядром К (x, s), т.е. таким, что
 =
=  .
.
Симметрическое ядро обладает следующими свойствами:
· для всякого симметрического ядра
существует по меньшей мере одно собственное значение;
· все собственные значения симметрического
ядра действительны;
· собственные функции  (х) и
(х) и  (х) симметрического ядра, соответствующие различным собственным
значениям
(х) симметрического ядра, соответствующие различным собственным
значениям  и
и 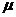 (
(

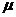 ),
ортогональны между собой на основном промежутке (а, b), т.е.
),
ортогональны между собой на основном промежутке (а, b), т.е.

Пример 1. Пусть простой замкнутый кусочно-гладкий контур
 (Г)
(Г)
ограничивает конечную область G. Тогда функция u (х, у), дающая решение
соответствующей задачи Дирихле т.е. такая, что
 при (x, y)
при (x, y)  G= f (t) при (х, у)
G= f (t) при (х, у)  Г
Г
(f, (t) - известная функция), может быть представлена в виде

и функция  удовлетворяет интегральному уравнению
удовлетворяет интегральному уравнению
πµ(s)+

ядро которого есть
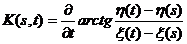 .
.
В частности, например, для эллипса

будем иметь

В приложениях встречаются также интегральные уравнения вида
 (4)
(4)
у (х)-
 (5)
(5)
которые носят названия интегральных уравнений Вольтерра
соответственно первого и второго рода. Вводя функцию

уравнения Вольтерра (4) и (5) можно записать в виде
соответствующих уравнений Фредгольма с ядром 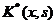 . Таким образом, теория уравнений Вольтерра сводится к теории
уравнений Фредгольма; однако в некоторых случаях уравнения Вольтерра полезно
изучать независимо.
. Таким образом, теория уравнений Вольтерра сводится к теории
уравнений Фредгольма; однако в некоторых случаях уравнения Вольтерра полезно
изучать независимо.
Примером уравнения Вольтерра первого рода является обобщенное
уравнение Абеля

 (6)
(6)
где  - известная непрерывно дифференцируемая
функция. Решение уравнения (6) дается формулой
- известная непрерывно дифференцируемая
функция. Решение уравнения (6) дается формулой

в чем можно убедиться непосредственно.
Заметим, что если ядро  и
и  - непрерывно дифференцируемые функции,
причем
- непрерывно дифференцируемые функции,
причем 
 0 при
0 при  , то уравнение Вольтерра первого рода (4)
сводится к уравнению Вольтерра второго рода (5). Действительно, дифференцируя
уравнение (4) по x, будем иметь
, то уравнение Вольтерра первого рода (4)
сводится к уравнению Вольтерра второго рода (5). Действительно, дифференцируя
уравнение (4) по x, будем иметь

отсюда
( ),
),


К линейным интегральным уравнениям может быть приведено
большое количество задач математической физики.
В основном мы это будут интегральное уравнение Фредгольма
второго рода и частично уравнение Вольтерра второго рода (для краткости в
дальнейшем мы их будем именовать просто уравнениями Фредгольма и Вольтерра).
Основными проблемами здесь являются следующие:
1. нахождение приближенного или точного решения неоднородного
интегрального уравнения при заданном значении параметра  ;
;
. нахождение собственных значений и соответствующих
собственных функций однородного интегрального уравнения.
1.2 Метод последовательных приближений
Рассмотрим уравнение Фредгольма
у(х)=  +
+ 
 (1)
(1)
где  и
и  непрерывны.
непрерывны.
Будем искать решение в форме степенного ряда
 (2)
(2)
Подставляя выражение (2) в интегральное уравнение (1) и
приравнивая коэффициенты при одинаковых степенях параметра  , будем иметь
, будем иметь
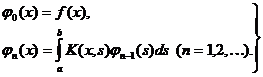 (3)
(3)
Пусть  и
и  в области
в области  .
.
Из формул (3) по индукции получаем  Поэтому сходимость ряда (2) будет обеспечена, если
Поэтому сходимость ряда (2) будет обеспечена, если
y(x)
 n(x)=
n(x)=
 k
k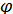
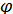 k(x),
k(x),
мы получим приближенное решение интегрального уравнения (1) с
погрешностью

 n=
n=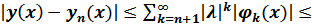
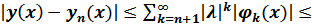
≤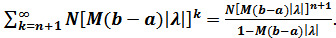
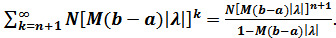 (4)
(4)
Формула (2) дает аналитическое относительно  решение уравнения Фредгольма (1) в
окрестности точки
решение уравнения Фредгольма (1) в
окрестности точки  = 0. Из формул (3) вытекает, что решение
(2) можно
= 0. Из формул (3) вытекает, что решение
(2) можно
записать в виде
 (6)
(6)
Коэффициенты  , так называемые итерированные ядра, могут
быть последовательно найдены по формулам
, так называемые итерированные ядра, могут
быть последовательно найдены по формулам
(x, s)=K (x, s)
Kn(x,
s)=
 (n=2, 3,…).
(n=2, 3,…).
Функция  называется резольвентой уравнения (1) и
при малых
называется резольвентой уравнения (1) и
при малых 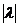 определяется степенным рядом (6). Пользуясь
аналитическим продолжением, резольвенту
определяется степенным рядом (6). Пользуясь
аналитическим продолжением, резольвенту  можно продолжить на всю комплексную плоскость параметра
можно продолжить на всю комплексную плоскость параметра  , за исключением собственных значений
, за исключением собственных значений  (особые точки), которые являются
(особые точки), которые являются
полюсами резольвенты. Тогда формула (5) дает решение интегрального
уравнения (1) при любом 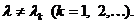
Рассмотрим теперь соответствующее уравнение Вольтерра
у(х)=  +
+ 
 (7)
(7)
где  . Полагая
. Полагая
 , (8)
, (8)
аналогично предыдущему получим
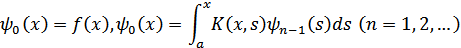
Отсюда
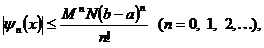 (9)
(9)
где


Следовательно, ряд (8) сходится при любом  и дает единственное решение уравнения
(7). Погрешность приближенного решения
и дает единственное решение уравнения
(7). Погрешность приближенного решения

1.3 Решение интегрального уравнения методом
конечных сумм
Метод основывается на приближенном вычислении определенного
интеграла с помощью некоторой квадратурной формулы
 (1)
(1)
где  - абсциссы точек отрезка
- абсциссы точек отрезка  - числовые коэффициенты, не зависящие от
выбора функции
- числовые коэффициенты, не зависящие от
выбора функции 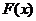 , и
, и 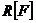 - остаточный член (ошибка) формулы (1).
- остаточный член (ошибка) формулы (1).
Обычно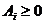 и
и  ,
,
Например, в случае равноотстоящих точек  , где
, где 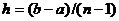 , будем иметь:
, будем иметь:
1. для формулы
прямоугольников:

2. для общей формулы
трапеций:

3. для общей формулы
Симпсона при 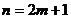 :
:
Пусть теперь дано интегральное уравнение Фредгольма второго
рода
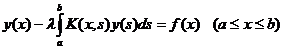 . (2)
. (2)
Выбирая точки  и вводя обозначения:
и вводя обозначения:
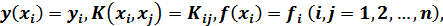
На основании формулы (1) будем иметь
 (3)
(3)
где  - соответствующие ошибки. Отбрасывая в
системе (3) величины
- соответствующие ошибки. Отбрасывая в
системе (3) величины  для приближенных значений
для приближенных значений  решения
решения  в узлах
в узлах получим линейную алгебраическую систему
получим линейную алгебраическую систему
 . (4)
. (4)
Вводя символ Кронекера
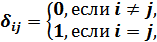
и учитывая, что
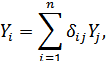
систему (4) можем записать в виде
 (4’)
(4’)
Если
 , (5)
, (5)
то система (4’) имеет единственное решение  которое можно найти методом Гаусса или
другими методами, разработанными для решения систем алгебраических линейных
уравнений.
которое можно найти методом Гаусса или
другими методами, разработанными для решения систем алгебраических линейных
уравнений.
Найдя 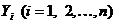 , для решения
, для решения  получаем из уравнения (2) приближенное
аналитическое выражение
получаем из уравнения (2) приближенное
аналитическое выражение
 (6)
(6)
Различные между собой корни  алгебраического уравнения
алгебраического уравнения  представляют собой, вообще говоря, приближения собственных
значений ядра
представляют собой, вообще говоря, приближения собственных
значений ядра  . Если
. Если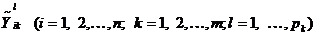 - соответствующие ненулевые решения однородной системы
- соответствующие ненулевые решения однородной системы
 , (7)
, (7)
Метод конечных сумм может быть применен также к интегральному
уравнению Фредгольма первого рода

В этом случае приближенные значения  решения
решения  в узлах
в узлах 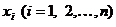 будут определяться из системы
будут определяться из системы
 (8)
(8)
Особенно просто применение метода конечных сумм для решения
интегрального уравнения Вольтерра второго рода
y(x)-λ

которое можно рассматривать как уравнение Фредгольма второго рода.
Здесь  = 0 при j>i, и, следовательно, соответствующая
система (4) имеет вид
= 0 при j>i, и, следовательно, соответствующая
система (4) имеет вид
 . (9)
. (9)
Получилась линейная система с треугольной матрицей. Если
 , (10)
, (10)
1.4 Метод коллокации
Рассмотрим интегральное уравнение
 (1)
(1)
Будем искать приближенное решение уравнения (1) в виде
функции определенного вида
 (2)
(2)
со свободными параметрами  (неопределенные
коэффициенты). Подставляя выражение (2) в уравнение (1), получим невязку
(неопределенные
коэффициенты). Подставляя выражение (2) в уравнение (1), получим невязку
R
 (3)
(3)
Если у является точным решением, то, очевидно, невязка  =0. Поэтому стараются подобрать параметры
=0. Поэтому стараются подобрать параметры  так, чтобы n невязка
так, чтобы n невязка  была в определенном смысле возможно
малой. Минимизировать невязку
была в определенном смысле возможно
малой. Минимизировать невязку  можно различными способами. Обычно для простоты выкладок берут
функцию
можно различными способами. Обычно для простоты выкладок берут
функцию 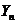 , линейно зависящую от параметров
, линейно зависящую от параметров 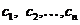 . Найдя параметры
. Найдя параметры 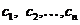 , получают приближенное решение (2).
, получают приближенное решение (2).
Отметим одно обстоятельство. Если невязка  получилась малой, то она близка к невязке
получилась малой, то она близка к невязке
 =0, даваемой точным решением y. Но если два оператора
=0, даваемой точным решением y. Но если два оператора  и R[y] имеют
близкие значения, то отсюда, вообще говоря, не следует, что функции
и R[y] имеют
близкие значения, то отсюда, вообще говоря, не следует, что функции 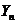 и у близки между собой в обычном смысле.
Поэтому возникает математическая задача: по известной невязке
и у близки между собой в обычном смысле.
Поэтому возникает математическая задача: по известной невязке оценить погрешность
оценить погрешность  приближенного решения
приближенного решения 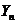 . Но это трудная проблема, связанная с
глубокими теоремами функционального анализа, и мы ее оставим без рассмотрения.
. Но это трудная проблема, связанная с
глубокими теоремами функционального анализа, и мы ее оставим без рассмотрения.
 (4)
(4)
Если справедливо равенство (4), то данным методом решение у можно
найти с любой степенью точности, взяв достаточно большое число параметров 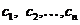 .
.
Перейдем теперь к изложению одного из конкретных методов
построения приближенного решения 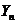 .
.
Положим
 (5)
(5)
где  - известные функции (координатные функции)
и
- известные функции (координатные функции)
и 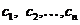 - неопределенные коэффициенты, причем
функции
- неопределенные коэффициенты, причем
функции  линейно независимы. Заметим, что, в
частности, можно полагать
линейно независимы. Заметим, что, в
частности, можно полагать  . Подставляя выражение (5) в левую часть
уравнения (1), получим невязку
. Подставляя выражение (5) в левую часть
уравнения (1), получим невязку
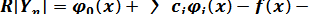

 (6)
(6)
где
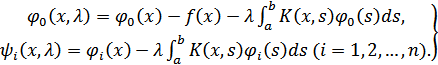
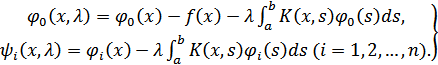 (7)
(7)
Согласно методу коллокации требуем, чтобы невязка  обращалась в нуль в заданной системе
точек
обращалась в нуль в заданной системе
точек 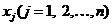 из отрезка [а, b] (точки коллокации),
т.е. полагаем, что
из отрезка [а, b] (точки коллокации),
т.е. полагаем, что

где 
Отсюда на основании формулы (6) для определения коэффициентов 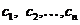 получаем алгебраическую линейную систему
уравнений
получаем алгебраическую линейную систему
уравнений

Если определитель этой системы 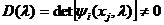 , то из системы можно однозначно определить величины
, то из системы можно однозначно определить величины 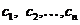 и, следовательно, найти приближенное
решение
и, следовательно, найти приближенное
решение  по формуле (5).
по формуле (5).
Приравнивая нулю определитель 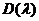 , получим уравнение
, получим уравнение 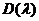 =0, из которого, вообще говоря, можно найти приближенные значения
=0, из которого, вообще говоря, можно найти приближенные значения  первых собственных чисел ядра
первых собственных чисел ядра  .
.
Если положить  то вместо нашей системы будем иметь однородную систему
то вместо нашей системы будем иметь однородную систему
 (9)
(9)
Найдя ненулевые решения 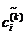 (
( ) системы (8), получим для ядра
) системы (8), получим для ядра  приближенные собственные функции
приближенные собственные функции
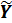
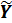 n(k)(x)=
n(k)(x)=
 i(k)
i(k)

отвечающие его собственному значению  .
.
1.5 Метод наименьших квадратов
Для уравнения
 (1)
(1)
полагаем
 (2)
(2)
где  - известные функции и
- известные функции и 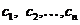 -неопределенные коэффициенты, причем
-неопределенные коэффициенты, причем 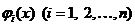 линейно независимы.
линейно независимы.
Подставляя (2) в левую часть уравнения (1), получим невязку
 (3)
(3)
Заметим, что если 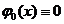 , то
, то  и, следовательно,
и, следовательно, 
 . Так как
. Так как 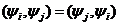 то матрица системы (8) симметрическая.
Вместо интегрального метода наименьших квадратов можно воспользоваться точечным
способом наименьших квадратов.
то матрица системы (8) симметрическая.
Вместо интегрального метода наименьших квадратов можно воспользоваться точечным
способом наименьших квадратов.
Метод наименьших квадратов применяется также для приближенного
нахождения собственных значений и собственных функций ядра  , аналогично тому как это делается для
метода коллокации. А именно, полагая f(x)
, аналогично тому как это делается для
метода коллокации. А именно, полагая f(x)  0 и
0 и 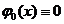 , откуда
, откуда 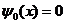 , определяем приближенные значения
собственных чисел из алгебраического уравнения.
, определяем приближенные значения
собственных чисел из алгебраического уравнения.
1.6 Метод моментов
Пусть
 (1)
(1)
Аналогично предыдущему, будем искать приближенное решение
уравнения (1) в виде конечной суммы

 , (2)
, (2)
интегральный уравнение линейный коллокация
где 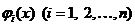 -некоторые известные линейно независимые
функции (координатные функции) и
-некоторые известные линейно независимые
функции (координатные функции) и 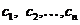 - неопределенные коэффициенты. Подставляя выражение (2) в левую
часть уравнения (1), получим невязку
- неопределенные коэффициенты. Подставляя выражение (2) в левую
часть уравнения (1), получим невязку

 (3)
(3)
Согласно методу моментов коэффициенты  определяются из условия ортогональности
невязки ко всем координатным функциям
определяются из условия ортогональности
невязки ко всем координатным функциям  . Это дает систему уравнений
. Это дает систему уравнений

или, в силу (3),

 (4)
(4)
где

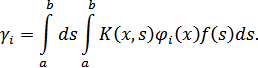
Если определитель системы (4)  отличен от нуля, то из этой системы можно однозначно определить
коэффициенты
отличен от нуля, то из этой системы можно однозначно определить
коэффициенты 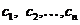 . Тогда формула (2) даст приближенное
решение интегрального уравнения (1). Из уравнения
. Тогда формула (2) даст приближенное
решение интегрального уравнения (1). Из уравнения  =0 приближенно находятся собственные
значения
=0 приближенно находятся собственные
значения  ядра К (х, s).
ядра К (х, s).
Найдя ненулевые решения однородной линейной системы

 j(
j(
 (i=1, 2,…, n),
(i=1, 2,…, n),
легко построить приближенные собственные функции 
 , отвечающие данному собственному значению
, отвечающие данному собственному значению  . Заметим, что метод моментов по идее
совпадает с методом Галеркина.
. Заметим, что метод моментов по идее
совпадает с методом Галеркина.
Пример 1. Найти первые два собственных значения интегрального
уравнения
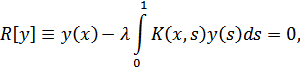
где

 (5)
(5)
На основании (5) имеем

Положим  . Тогда
. Тогда

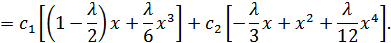
Ортогонализируя невязку R[Y], будем иметь систему

или


После упрощения получим систему

 (6)
(6)
Приравнивая пулю определитель системы (6), получим уравнение
дня определения собственных значений:

полученные из решения соответствующей краевой задачи:

 +
+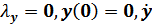
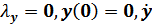 (1)=0.
(1)=0.
Таким образом, погрешность 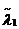 равна примерно
равна примерно 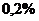 ,
, 
В заключение заметим, что рассмотренные методы минимизации
невязки применимы также к решению нелинейных интегральных уравнений. Имеются
также другие методы решения интегральных уравнений, например метод Монте-Карло.
2.
Практическая часть
2.1 Задача
2.1.1
Постановка задачи
Решить интегральное уравнение методом конечных сумм и методом
моментов. В методе моментов использовать функции  , k = 0, 1, 2,…, n:
, k = 0, 1, 2,…, n:
 .
.
2.1.2
Алгоритм решения
Имеем интегральное уравнение вида
у (х)-
 ,
,
где  , а = 0, в = 1, f(x) = 1/8 (x + 8), ядро К = 1 +
, а = 0, в = 1, f(x) = 1/8 (x + 8), ядро К = 1 +  .
.
. Метод конечных сумм
1) задаемся числом разбиений n = 6, тогда
 ;
;
2) выбираем равноотстоящие узлы
x1= 0, x2 = 0,2, x3
= 0,4 x4=0,6, x5=0,8, x6=1, t1 = 0,
t2 = 0,2, t3 = 0,4, t4=0,6, t5=0,8,
t6=1.
3) Рассчитываем значения Кij = K(xi, tj), i, j, = 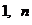
) Рассчитываем значения fi = f(xi), i = 1, n
) Коэффициенты формулы Симпсона

) Составляем 6 уравнений



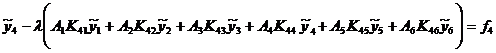


) Решаем систему относительно  i = 1, 6
i = 1, 6
) Приближенное решение находим по формуле

) Также находим приближенное решение для числа разбиений n = 4 и n = 6
10) Находим погрешность  по формуле
по формуле

11) Находим погрешность  по формуле
по формуле
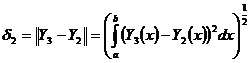
) Сравнивая  и
и  , делаем вывод: если
, делаем вывод: если  <
< , то задача решена правильно.
, то задача решена правильно.
Заключение
В результате выполнения курсовой работы мною был изучен
теоретический материал по решению линейных интегральных уравнений. Были
подробно рассмотрены такие численные методы решения линейных интегральных
уравнений как метод последовательных приближений, метод конечных сумм, метод
вырожденных ядер, метод коллокации, метод наименьших квадратов и метод моментов.
Список литературы
1.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение
функций, дифференциальные и интегральные уравнения. М.: Наука, 1967
.
Калиткин Н.Н. Численные методы. М: Наука, 1978.
.
Сборник задач по математике для втузов. В 4-х частях. Под ред. Ефимова А.В.,
Поспелова А.С. (2001-2003)
.
Турчак Л.И. Основы численных методов. М: Физматлит, 2002.
.
Кунцман Ж. Численные методы. М.: Наука, 1979