Приобретение навыков работы с тензорной алгеброй
Контрольная
работа
Приобретение
навыков работы с тензорной алгеброй
Оглавление
Введение
.
Геометрия гравитационных полей
.
Предположение об однородности и изотропии пространств. Классификация
пространств
.
Уравнения Эйнштейна
.
Геометрические характеристики пространств
.1
Геометрические характеристики пространства метрики типа || по Бьянки
.2
Геометрические характеристики пространства метрики открытой вселенной Фридмана
.
Поиск решения для открытой вселенной Фридмана
Вывод
Литература
Введение
Одним из выдающихся открытий в физике является
общая теория относительности Альберта Эйнштейна, основной побудительной
причиной к созданию которой была эстетическая неудовлетворённость Эйнштейна к
сложившейся к тому времени физической картине мира. То было начало двадцатого
века... Теория, которая произвела огромный научный переворот, также продолжает
вызывать и множество споров. Как и все молодые теории, для подтверждения её
существования и истинности её предположений, был проведён ряд тестов как прямых,
так и косвенных. К косвенным относятся опыты, подтверждающие эвристические
принципы, принятые Эйнштейном за основу теории. Это, например, уточнение
равенства инертной и гравитационной масс, то есть принципа эквивалентности,
выполненные венгерским физиком Лорандом фон Этвёшем в 1889-1908 гг. и
американским исследователем Робертом Дикке в 1964 г. К числу косвенных
подтверждений теории Эйнштейна можно причислить и открытое американским
астрономом Эдвином Хабблом расширение вселенной, и обнаруженное его соотечественниками
Арно Пензиасом и Робертом Уилсоном реликтового излучения , заполняющего
вселенную. Но всё-таки это всего лишь косвенные аргументы в пользу теории
Эйнштейна. Так, из принципа эквивалентности не вытекают уравнения Эйнштейна,
напротив - сам принцип является следствием уравнений. Прямые наблюдения
подтвердили эффекты, непосредственно связанные с уравнениями Эйнштейна.
Учёным давно было известно, что из-за влияния
поля тяготения других планет и по ряду других причин Меркурий движется не
просто по эллипсу, а по эллипсу, который сам медленно поворачивается. Это
явление называется прецессией перигелия Меркурия. Были попытки объяснить такой
поворот при помощи поправок попытки объяснить такой поворот при помощи поправок
к Ньютоновской теории, однако эта теория не смогла полностью объяснить этот
эффект. Также Леверье предполагал что между Солнцем и Меркурием существует
неизвестная планета, которая своим притяжением и вызывает данную аномалии. Но
это предположение оказалось неверным, потому что никто эту планету так и не
обнаружил, наверно лишь потому, что её просто не существует. Учёные бы ещё
долго пытались проделать тщетные попытки объяснить такое смещение орбиты
Меркурия. Но тут пришла на помощь теория Эйнштейна, согласно которой получилось
вычислить не только правильные значения прецессии перигелия Меркурия, но и
соответствующее наблюдениям направление прецессии. К тому же эффект в общей
теории относительности возникает совершенно естественно, без всяких ухищрений и
подгонки числовых данных для приведения теоретических результатов в
соответствие с результатами наблюдений.
Согласно Эйнштейну, наличие больших масс материи
приводит к изменению свойств пространства. Описание явления тяготения
принципиально меняется. По Ньютону, это движение под действием силы тяготения,
по Эйнштейну, это свободное движение тел в искривлённом пространстве-времени.
Загадка движения Меркурия находит при этом естественное объяснение - ведь
Меркурий, находясь ближе к солнцу, чем другие планеты, движется в гораздно
более сильном гравитационном поле. Такие веские доводы о верности теории ещё
раз, но уже практически, подтверждают верность теории Эйнштейна.
Так, общая теория относительности не только
расширяет Ньютоновскую теорию движения, но и существенно дополняет её, тем
самым увеличивая область применения механики.
1. Геометрия гравитационных полей
Основное свойство гравитационных полей - все
тела в них движутся одинаковым образом, вне зависимости от их массы. Это
свойство позволяет рассмотреть гравитационное поле как некоторую неинерциальную
систему отсчёта. Например, если рассматривать движение в некоторой равномерно
ускоренной системе отсчёта, то свободно движущиеся в ней тела будут обладать,
относительно этой системы, постоянным ускорением, равным и противоположным по
направлению ускорению самой системы отсчёта. Таким же является движение в
однородном постоянном гравитационном поле. Так, равномерно ускоренная система
отсчёта, эквивалентна постоянному однородному полю. Такой подход к изучению
полей был назван принципом эквивалентности.
В зависимости от эквивалентности поля некоторой
системе отсчёта, различают “истинные” (поля, эквивалентные инерциальным
системам отсчёта) и поля, эквивалентные неинерциальным системам отсчёта. В
инерциальной системе отсчёта в декартовых координатах интервал определяется
формулой
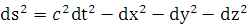
при преобразовании Лоренца этот интервал
сохраняет тот же вид. В неинерциальной же системе отсчёта, например в
равномерно вращающейся, если провести соответствующее преобразование координат,
то интервал примет вид

где величины  определяют
метрику данного пространства-времени
определяют
метрику данного пространства-времени 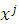 и
являются компонентами метрического тензора, которые в инерциальной декартовой
системе координат примут вид
и
являются компонентами метрического тензора, которые в инерциальной декартовой
системе координат примут вид
 ,
, 
остальные компоненты равны нулю. Такую систему
координат принято называть Галилеевой.
Есть главное отличие между “истинными” полями и
полями, которым эквивалентны неинерциальные системы отсчёта. При наличии “истинного”
гравитационного поля пространство-время таково, что величины  никаким
преобразованием координат не могут быть приведены во всём пространстве к их
Галилееву виду, при другом поле - могут. Так вот, такое пространство-время, при
котором метрика не может быть приведена к Галилеевой, называют кривым, другое -
плоским.
никаким
преобразованием координат не могут быть приведены во всём пространстве к их
Галилееву виду, при другом поле - могут. Так вот, такое пространство-время, при
котором метрика не может быть приведена к Галилеевой, называют кривым, другое -
плоским.
Общая теория относительности (ОТО) -
геометрическая теория тяготения, в которой гравитация рассматривается как
проявление искривления пространства-времени. Одной из главнейших её задач
является определение компонент метрического тензора, которые в совокупности
задают геометрические свойства пространства-времени, по известному
распределению источников энергии-импульса в рассматриваемой системе четырёхмерных
координат. Также знание метрики позволяет рассчитать движение частиц
гравитационного поля, что равносильно знанию свойств поля тяготения в данной
системе.
В этой работе рассматриваются различные
геометрические характеристики некоторых кривых метрических пространств.
эйнштейн гравитационный фридман однородность
2. Предположение об однородности и изотропии
пространств. Классификация пространств
Как всем давным-давно известно: звёзды
распределены по пространству неравномерно, они сконцентрированы в звёздных
системах - галактиках. Но при рассмотрении Вселенной в больших масштабах,
следует отвлечься от этой неравномерности. Так, под плотностью масс, нужно
понимать усреднённую массу пространства по рассматриваемой области, размеры
которой велики по сравнению с расстояниями между галактиками.
Существует ряд астрономических данных, не
противоречащих предположению об однородности и изотропии пространств: данные об
изотропии реликтового излучения, данные о примерно одинаковом распределении
галактик в пространстве. Такое отношение к пространству даёт вполне адекватное
представление о нынешнем состоянии вселенной, о её эволюции в прошлом,
естественно, в больших масштабах.
Однородность и изотропия пространства говорят
что можно выбрать такое мировое время, что в каждый его момент метрика
пространства была одинакова как во всех точках, так и по всем направлениям.
Рассмотрим метрику изотропного пространства,
исключая возможность зависимости от времени. Введём элемент расстояния в
пространстве в виде:

обозначив 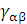 -
трёхмерный метрический тензор. Кривизна пространства полностью определяется его
трехмерным тензором кривизны. В случае полной изотропии тензор кривизны,
очевидно, должен выражаться только через метрический тензор так что в силу
своей симметрии по паре индексов
-
трёхмерный метрический тензор. Кривизна пространства полностью определяется его
трехмерным тензором кривизны. В случае полной изотропии тензор кривизны,
очевидно, должен выражаться только через метрический тензор так что в силу
своей симметрии по паре индексов
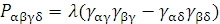 ,
,
где 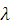 -постоянная.
Тензор Риччи равен:
-постоянная.
Тензор Риччи равен:
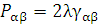 ,
,
а скалярная кривизна:
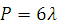 .
.
Свойства кривизны изотропного пространства
определяются только одной постоянной. Соответсвенно этому есть три различных
случая пространственной метрики:
) 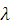 >0
- пространство постоянной положительной кривизны;
>0
- пространство постоянной положительной кривизны;
) 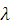 <0
- пространство постоянной отрицательной кривизны;
<0
- пространство постоянной отрицательной кривизны;
) 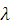 =0
- пространство с кривизной, равной нулю.
=0
- пространство с кривизной, равной нулю.
3. Уравнения Эйнштейна
Одним из важнейших событий в гравитационной
механике стало открытие Эйнштейном при участии Гильберта уравнений
гравитационного поля в ОТО, связывающее между собой метрику искривлённого
пространства-времени со свойствами заполняющей его материи:
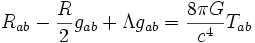
) 
тензор Риччи (тензор кривизны)- упрощенный в
силу своей антисимметричности по паре ближних индексов тензор Римана
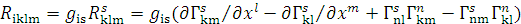 ,
,
который характеризует кривизну данного
пространства. Этот тензор симметричен: 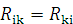 .
.
) Упрощая 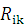 ,
получим инвариант
,
получим инвариант
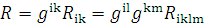
скалярная кривизна пространства. Таким образом,
скалярная кривизна есть след тензора Риччи.
) gik - компоненты метрического тензора, которые
являются функциями координат, симметричных по своим индексам: 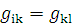 .
.
4) Λ - космологическая
постоянная - физическая постоянная, характеризующая свойства вакуума. Она была
введена Эйнштейном для того, чтобы уравнения допускали космологическое пространственно
однородное статическое решение. Λ меньше
чем 10 − 29 г/см3 поэтому часто ей можно пренебречь.
) Tab - тензор энергии-импульса материи. Это
симметричный тензор второго ранга, который описывает плотность и поток энергии
и импульса полей материи, и определяющий взаимодействие этих полей с
гравитационным полем
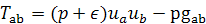
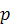 - давление;
- давление;
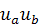 -произведение
компонент вектора 4-скорости;
-произведение
компонент вектора 4-скорости;
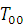 - объёмная
плотность энергии;
- объёмная
плотность энергии;
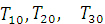 - плотности
компонент импульса, умноженные на c (скорость света);
- плотности
компонент импульса, умноженные на c (скорость света);
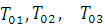 - компоненты потока
энергии, делённые на c (скорость света);
- компоненты потока
энергии, делённые на c (скорость света);
Подматрица 3x3 из чисто пространственных
компонент
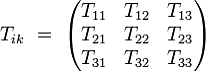
есть тензор напряжений. В механике жидкости
диагональные её компоненты соответствуют давлению, а прочие составляющие -
тангенциальным усилиям (напряжениям или в старой терминологии - натяжениям),
вызванным вязкостью.
) c - скорость света в вакууме - физическая
константа, предельная скорость движения частиц и распространения
взаимодействий.
) G - гравитационная постоянная Ньютона.
Численно она равна модулю силы тяготения, действующей на точечное тело
единичной массы со стороны другого такого же тела. 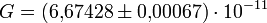 [м³·с−2·кг−1],
или [Н·м²·кг−2
].
[м³·с−2·кг−1],
или [Н·м²·кг−2
].
) 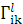 -
символы Кристоффеля. Они выражают изменение компонент вектора при его
параллельном переносе так что
-
символы Кристоффеля. Они выражают изменение компонент вектора при его
параллельном переносе так что

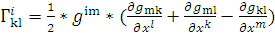
) Величина  ,
стоящая в левой части уравнений Эйнштейна, называется тензором Эйнштейна, это
симметричный тензор второго ранга в n-мерном пространстве, то есть содержит n(n
+ 1) / 2 независимых компонентов. Для 4-мерного пространства: 10 независимых
компонент.
,
стоящая в левой части уравнений Эйнштейна, называется тензором Эйнштейна, это
симметричный тензор второго ранга в n-мерном пространстве, то есть содержит n(n
+ 1) / 2 независимых компонентов. Для 4-мерного пространства: 10 независимых
компонент.
Решить уравнение Эйнштейна - значит найти вид
метрического тензора gμν пространства-времени.
Задача ставится заданием граничных условий и написанием тензора
энергии-импульса Tμν, который
может описывать как точечный массивный объект, распределённую материю или
энергию, так и всю Вселенную целиком.
Основные задачи этой работы:
. Вычислить метрики и другие
геометрические характеристики для построения характеристик космологических
пространств.
. Найти решение, соответствующее
изотропному пространству отрицательной кривизны - открытой модели вселенной
Фридмана.
4. Геометрические характеристики пространств
.1 Геометрические характеристики пространства
метрики типа || по Бьянки
Рассмотрим метрику типа || по Бьянки:
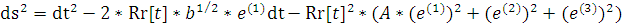
где 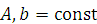 ,
,
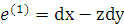 ,
,
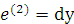 ,
,
 ;
;
Оцифруем координаты 4-пространсва:
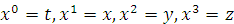
Тогда некоторая точка 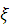 в
4-пространстве будет иметь вид
в
4-пространстве будет иметь вид 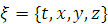 ;
;
a) Метрический
тензор 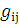 строим
в виде
строим
в виде
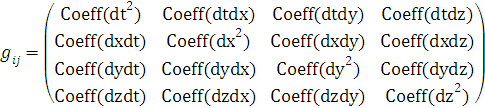
где Coeff(*) -коэффициент при соответствующем
произведении.
Он будет иметь вид:

метрический тензор, заданный
ковариантными компонентами;
б) Для вычисления компонент символов символов
Кристоффеля
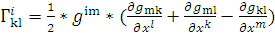
вычислим контравариантные компоненты
метрического тензора, матрица представления которого есть обратная матрица
представления ковариантных компонент метрического тензора, то есть
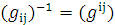 , тогда:
, тогда:


в) Теперь посчитаем символы Кристоффеля по
формуле:
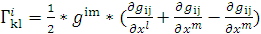 , получим:
, получим:
 ;
;
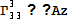 ;
;
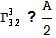 ;
;
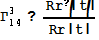 ;
;
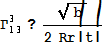 ;
;
 ;
;
 ;
;
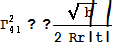 ;
;
 ;
;
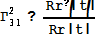 ;
;
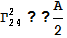 ;
;
 ;
;
 ;
;
 ;
;
г) Вычислим тензор Риччи по формуле
 , получим
, получим
 ;
;
 ;
;
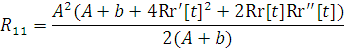 ;
;
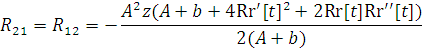
 ;
;

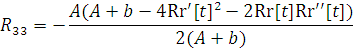 ;
;
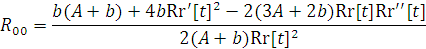
д) Скалярная кривизна 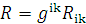 ,
итого
,
итого
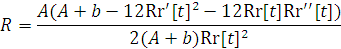
е) Тензор Эйнштейна принимает вид ( ):
):
 ;
;
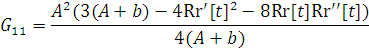 ;
;
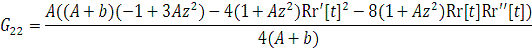
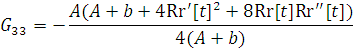 ;
;
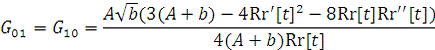 ;
;
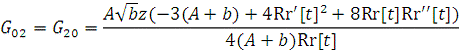 ;
;
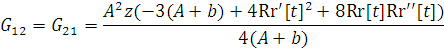
.2 Геометрические характеристики пространства
метрики открытой вселенной Фридмана
Рассмотрим метрику, соответствующую изотропному
пространству отрицательной кривизны:
Для удобства решения воспользуемся вместо
времени величиной 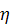 , определяемой
соотношением:
, определяемой
соотношением: 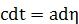 , тогда метрика
преобразуется к виду:
, тогда метрика
преобразуется к виду:
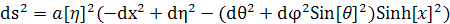
Оцифруем координаты:
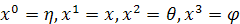 , тогда некоторая
точка этого пространства будет иметь вид:
, тогда некоторая
точка этого пространства будет иметь вид: 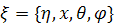
а) метрический тензор будет иметь вид
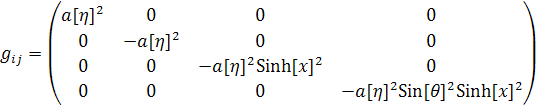
б) матрица контравариантных компонент
метрического тензора:
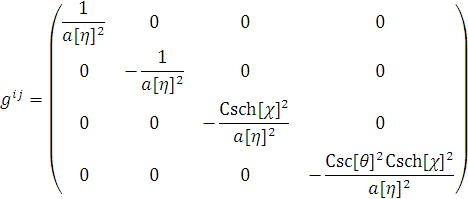
в) Тогда символы Кристоффеля:
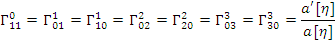
 ;
;
 ;
;
 ;
;
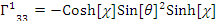 ;
;
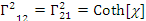 ;
;
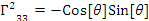 ;
;
 ;
;
 ;
;
г) Вычислим тензор Риччи

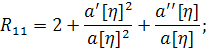
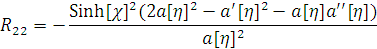
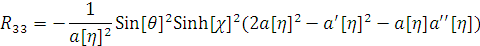 ;
;
д) Скалярная кривизна
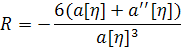 ;
;
е) Тензор Эйнштейна принимает вид
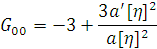
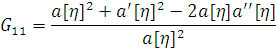
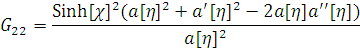
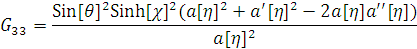
5. Поиск решения для открытой вселенной Фридмана
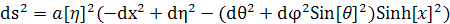
метрика открытой вселенной Фридмана.
Метрический тензор
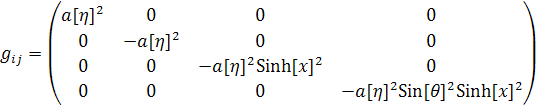
Составим, для начала, уравнения Эйнштейна для
данной метрики:
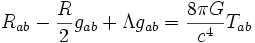
В силу малости космологического члена, то его
наличие не будет сказываться существенным образом на гравитационных полях в не
слишком больших областях пространства-времени. Поэтому пренебрежём им, тогда
уравнение будет иметь вид:
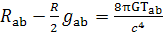
Поскольку в выбранной нами системе отсчёта,
связанной с каждой точкой пространства, материя неподвижна, то компоненты
вектора 4-скорости по пространственным координатам равны нулю:
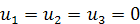
и в силу равенства:
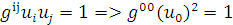
выполняется

Если материя распределена в пространстве в виде
отдельных макроскопических тел, то при определении создаваемого ею
гравитационного поля можно рассматривать эти тела как материальные частицы,
обладающие определёнными массами, не интересуясь вовсе их внутренним строением.
Считая скорости тел сравнительно малыми по сравнению со скоростью света c,
можно положить просто 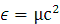 , где
, где 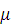 -
сумма масс тел к единице объёма. По той же причине давление, создаваемое этими
телами мало по сравнению с
-
сумма масс тел к единице объёма. По той же причине давление, создаваемое этими
телами мало по сравнению с 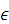 , поэтому им можно
пренебречь: p=0. Итак, для описания современного состояния вселенной в терминах
рассматриваемой модели, мы воспользуемся уравнением состояния “пылевидной ”
материи:
, поэтому им можно
пренебречь: p=0. Итак, для описания современного состояния вселенной в терминах
рассматриваемой модели, мы воспользуемся уравнением состояния “пылевидной ”
материи:
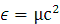 ; p=0.
; p=0.
Тогда, вычисляя тензор энергии-импульса, получим
его равным:
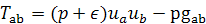 =
= 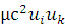
Получили уравнение Эйнштейна:
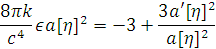
Положим 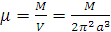 ,
тогда
,
тогда 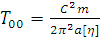 ,
остальные компоненты тензора энергии-импульса равны нулю.
,
остальные компоненты тензора энергии-импульса равны нулю.
Тогда мы получили систему четырёх уравнений
Эйнштейна



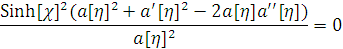

Эта система 4-х дифференциальных уравнений с
одной неизвестной.
Решить первое уравнение и проверим, выполняется
ли тождество для других. Получим:
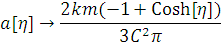
Получили зависимость радиуса кривизны от
времени, который меняется монотонно, возрастая от нуля до бесконечности.
Плотность материи соответственно монотонно убывает. Следовательно можно сказать
что Вселенная, заданная этой моделью нестационарна.
Вывод
Результатом проведённой работы стало овладение
навыками тензорной алгебры, конкретно: поиск космологических решений для кривых
пространств разных метрик, вычисление их геометрических характеристик. Также
было проверенно и подтверждено решение Фридмана для модели открытой вселенной.
Для проведения различных родов вычислений, в том
числе и тензорных, была использована вычислительная система Mathematica.
Были получены навыки построения и осмысления
одной из важнейших задач ОТО - нахождение космологических решений кривых
пространств.
Литература
1.
Ландау Н.Д., Лифшиц Е.М. Теория поля. Теоретическая физика. Том 2 / Л.П.
Питаевский - Москва, ФИЗМАТЛИТ, 2006.
.
ШариповР.А. Классическая электродинамика и теория относительности. Уфа: БашГУ,
1997
.
Цзю X., Гоффман В. (ред.) Гравитация и относительность. М.: Мир, 1965
.
Эйнштейновский сборник 1977. М.: Наука, 1980