Применение параллельных методов решения систем линейных уравнений ленточных матриц
Применение параллельных
методов решения систем линейных уравнений ленточных матриц
1.
Параллельные методы решения СЛАУ с ленточными матрицами
К решению систем линейных алгебраических уравнений сводятся
многочисленные практические задачи (по некоторым оценкам более 75% всех задач).
Можно с полным основанием утверждать, что решение линейных систем является
одной из самых распространенных и важных задач вычислительной математики.
Конечно, существует много методов и современных пакетов
прикладных программ для решения СЛАУ, но для того, чтобы их успешно
использовать, необходимо разбираться в основах построения методов и алгоритмов,
иметь представления о недостатках и преимуществах используемых методов.
Часто возникает необходимость в решении СЛАУ с матрицами, которые
являются слабо заполненными, т.е. содержат много нулевых элементов. В то же
время эти матрицы имеют определенную структуру. Среди таких систем выделим
системы с матрицами ленточной структуры, в которых ненулевые элементы
располагаются на главной диагонали и на нескольких побочных диагоналях, т.е. 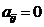 , если
, если 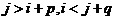 , где
, где 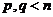 , числа
, числа 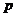 и
и 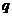 называют шириной верхней и нижней
полуленты, тогда
называют шириной верхней и нижней
полуленты, тогда 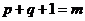 - ширине ленты матрицы (пример одного из
видов матриц в Приложении 1).
- ширине ленты матрицы (пример одного из
видов матриц в Приложении 1).
Подобные системы уравнений возникают в задаче сплайн-интерполяции,
при решении дифференциальных уравнений. Для решения задач с трехдиагональными
матрицами существуют специальные методы.
1.1 Метод прогонки для решения СЛАУ с
3-х-диагональными матрицами
1.1.1
Описание метода «прямой прогонки»
Рассмотрим очень простой и эффективный алгоритм решения
систем линейных уравнений с трехдиагональными матрицами, получивший название
метода прогонки. Пусть
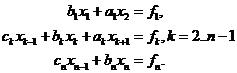 (1.1)
(1.1)
Уравнения этой системы, за исключением первого и последнего,
связывает три неизвестные величины (трехчленные уравнения). С помощью
эквивалентных (т.е. не нарушающих справедливости исходных уравнений)
преобразований можно перейти к системе двухчленных уравнений, связывающих две
последовательные неизвестные. Покажем это с помощью метода индукции.
Первое уравнение уже является двучленным. Исключая с помощью
первого уравнения неизвестного  во втором уравнении, получим также двучленное уравнение.
Продолжая этот процесс, допустим, что
во втором уравнении, получим также двучленное уравнение.
Продолжая этот процесс, допустим, что 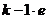 уравнение приведено к виду
уравнение приведено к виду
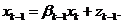 (1.2)
(1.2)
Исключая с помощью (1.2) неизвестную 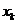 в
в 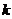 -м уравнении, получим
-м уравнении, получим

Это - двучленное уравнение. Оно принимает вид (1. 2), если
положить
 (1. 3)
(1. 3)
 (1. 4)
(1. 4)
А так как первое уравнение уже имеет двучленный вид, то
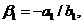
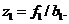 (1. 5)
(1. 5)
Таким образом, рекуррентные соотношения (1. 3) - (1. 5) полностью
определяют прогоночные коэффициенты 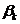 ,
, 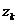 (
(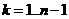 ). Уравнение (1. 2) при
). Уравнение (1. 2) при 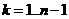 позволяет определить
позволяет определить 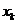 (
(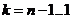 ), если известно
), если известно 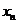 . Для этого последнее уравнение системы
(1. 1) сделаем формально трехчленным, вводя в рассмотрение
. Для этого последнее уравнение системы
(1. 1) сделаем формально трехчленным, вводя в рассмотрение 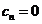 . Сопоставляя тогда уравнение (1. 2) при
. Сопоставляя тогда уравнение (1. 2) при 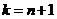 и уравнения (1. 3) при
и уравнения (1. 3) при 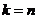 , видим, что
, видим, что
 (1. 6)
(1. 6)
Соотношениями (1. 2) - (1. 6) метод прогонки определяется
полностью. Рекуррентные соотношения (1. 3) - (1. 6) называют прямой прогонкой.
и рекуррентные соотношения (1. 2) - (1. 6) - обратной прогонкой.
Общее число операций в методе прогонки равно 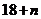 , т.е. пропорционально числу уравнений.
Такие методы решения СЛАУ называют экономичными.
, т.е. пропорционально числу уравнений.
Такие методы решения СЛАУ называют экономичными.
В случае решения СЛАУ с ленточными матрицами система уравнений (1.
1) имеет векторный вид
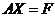 (1. 7)
(1. 7)
где 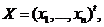
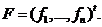 Равенства (покомпонентные) (1. 2) можно записать в виде
Равенства (покомпонентные) (1. 2) можно записать в виде
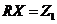 (1. 8)
(1. 8)
где 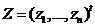 , а верхняя двухдиагональная матрица
, а верхняя двухдиагональная матрица 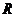 связана коэффициентами
связана коэффициентами 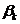 :
:
Кроме того, соотношения (2. 4) также представимы в векторной
форме:
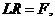 (1. 9)
(1. 9)
где
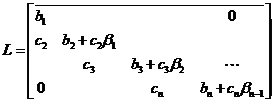
есть нижняя двух диагональная матрица. Сравнение равенств (1. 7) и
(1. 8), (1.9) при произвольном 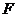 приводит (для невырожденной матрицы
приводит (для невырожденной матрицы 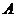 ) к треугольному разложению матрицы
) к треугольному разложению матрицы 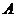 :
:
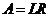 (1. 10)
(1. 10)
Из этого следует, что прогонка является реализацией (для
трехдиагональных систем уравнений) метода исключения Гаусса, который и основан
на разложении матрицы на треугольные множители.
Реализация метода
Постановка задачи: рассмотрим систему из 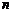 линейных алгебраических уравнений вида
(1.1). В матричном виде система может быть представлена, как
линейных алгебраических уравнений вида
(1.1). В матричном виде система может быть представлена, как 
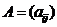 и есть вещественная матрица размера
и есть вещественная матрица размера 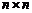 ;
; 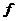 и
и 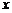 - вектора из
- вектора из 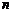 элементов.
элементов.
Будем искать значения вектора неизвестных 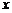 , при которых выполняются все уравнения
системы.
, при которых выполняются все уравнения
системы.
Предположим, что выполнено
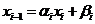 (1. 12)
(1. 12)
Подставим (1. 12) в  -е уравнение системы, получим
-е уравнение системы, получим
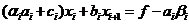 (1. 13)
(1. 13)
Сравнивая (1. 13) и выражение 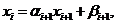 получим
получим
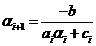
 (1. 14)
(1. 14)
Из первого уравнения  находим
находим

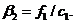
Затем вычисляем 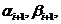 используя (1. 14) при
используя (1. 14) при 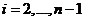 .
.
Определим 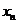 из последнего уравнения
из последнего уравнения
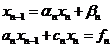

Используя 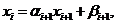 находим все
находим все 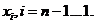
Для реализации алгоритма метода прогонки следует создать модуль с
процедурой, параметрами которой должны являться порядок системы, массивы
коэффициентов P, Q. Результатом должен быть массив решения Y в точках основной
сетки.
Метод прогонки состоит в вычислении прогоночных коэффициентов.
Каждое неизвестное 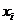 выражается через
выражается через  с помощью прогоночных коэффициентов
с помощью прогоночных коэффициентов 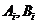 , заданными формулами метода.
, заданными формулами метода.
1.1.2
Метод «встречной прогонки»
Комбинация левой и правой прогонок дает метод встречной
прогонки, который допускает распараллеливание на 2 потока, в ходе которого
первый поток выполняет левую прогонку, второй поток - правую.
Разделим систему между двумя потоками - первый будет оперировать
уравнениями с номерами 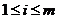 , второй - уравнениями
, второй - уравнениями 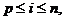
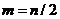 . В первом потоке вычисляются коэффициенты
. В первом потоке вычисляются коэффициенты 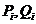 при
при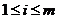
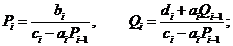
во втором потоке - вычисляются коэффициенты 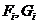 , при
, при 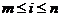 .
.

При 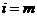 проводится сопряжение решений в форме:
проводится сопряжение решений в форме:
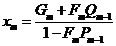
находим значение 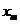 из системы
из системы
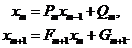
В первом потоке находим 
 при
при 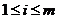 , а во втором все
, а во втором все 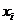 при
при  .
.
Прогонку называют корректной, если знаменатели прогоночных
коэффициентов  не обращаются в нуль, и устойчивой, если
не обращаются в нуль, и устойчивой, если 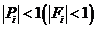 при всех
при всех  .
.
С помощью встречной прогонки мы сокращаем объем работы в двое,
высчитывая прогоночные коэффициенты до 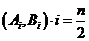 . И в это же время начитаем проводить те же вычисления в обратном
порядке, начиная с
. И в это же время начитаем проводить те же вычисления в обратном
порядке, начиная с  . Прогоночные коэффициенты обратной
прогонки обозначим как
. Прогоночные коэффициенты обратной
прогонки обозначим как 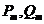 .
.
Таким образом, мы находим решения системы независимо.
Для распараллеливания программы не достаточно модифицировать ее
код, необходимо распределить «роли» на процессоры. Метод встречной прогонки
возможно распараллелить только на 2 процессора, что уже победа, ведь метод
прямой прогонки в чистом виде совершенно непригоден для распараллеливания.
Для удобного анализа результатов программы исходные данные
вводятся в файл под названием «in», а результаты получаем в файле «out».
1.2
Метод циклической редукции
.2.1 Описание
Рассмотрим еще один подход к решению трехдиагональных систем,
которые мы теперь будем записывать в виде
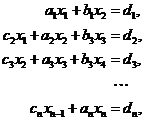 (2.1)
(2.1)
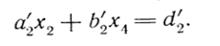
Проделаем то же самое с уравнениями 3, 4 и 5: вычтем из уравнения
4 надлежащие кратные уравнений 3 и 5, чтобы получить новое уравнение

Система (2.2) - это трехдиагональная система относительно
переменных 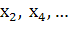
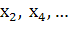 , и описанный только что процесс можно повторить. В результате
получится новая система, в которую входят лишь переменные
, и описанный только что процесс можно повторить. В результате
получится новая система, в которую входят лишь переменные 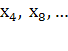
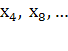 Будем продолжать действовать указанным образом, пока дальнейшая
редукция не станет невозможной. В частности, при
Будем продолжать действовать указанным образом, пока дальнейшая
редукция не станет невозможной. В частности, при 
 редукция закончится единственным финальным уравнением. Решив его,
начнем обратную подстановку. Она схематически иллюстрируется для
редукция закончится единственным финальным уравнением. Решив его,
начнем обратную подстановку. Она схематически иллюстрируется для 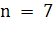
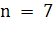 рисунком 2, который представляет собой продолжение рис. 1. Три
уравнения на рис. 2 получены после первого шага редукции, показанного на рис.
1; они комбинируются, порождая финальное уравнение относительно единственного
неизвестного
рисунком 2, который представляет собой продолжение рис. 1. Три
уравнения на рис. 2 получены после первого шага редукции, показанного на рис.
1; они комбинируются, порождая финальное уравнение относительно единственного
неизвестного 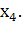
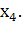
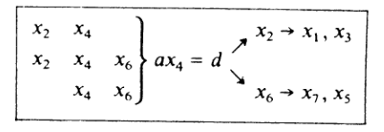
Решив его, мы можем затем решить относительно 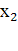
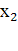 и
и 
 первое и последнее уравнения редуцированной системы. После этого
первое и последнее уравнения редуцированной системы. После этого 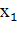
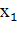 и
и 
 можно определить из первого и последнего уравнений исходной
системы. Наконец,
можно определить из первого и последнего уравнений исходной
системы. Наконец, 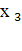
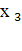 и
и 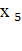
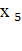 можно найти из третьего и пятого исходных уравнений.
можно найти из третьего и пятого исходных уравнений.
Если 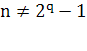
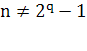 , то редукцию можно закончить системой с небольшим числом
переменных. Решив ее, начнем обратную подстановку. Альтернативный вариант
предусматривает добавление к системе некоторого количества фиктивных уравнений
вида
, то редукцию можно закончить системой с небольшим числом
переменных. Решив ее, начнем обратную подстановку. Альтернативный вариант
предусматривает добавление к системе некоторого количества фиктивных уравнений
вида 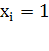
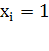 , чтобы общее число переменных стало равно
, чтобы общее число переменных стало равно 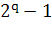
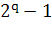 для некоторого числа
для некоторого числа 
 .
.
Описанный процесс известен под названием циклической или
нечетно-четной редукции.
1.2.2
Параллельная реализация
Хотя в те времена, когда он был изобретен, параллельные вычисления
вовсе не имелись в виду, этот процесс обладает немалым параллелизмом. Заметим,
прежде всего, что операции, ведущие к новым уравнениям для 
 , независимы и могут выполняться одновременно. Предположим, что
имеются
, независимы и могут выполняться одновременно. Предположим, что
имеются 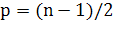
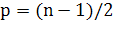 процессоров и применяется схема хранения, показанная на рис. 3.
процессоров и применяется схема хранения, показанная на рис. 3.

Тогда процессоры могут параллельно выполнять операции, порождающие
первую редуцированную систему относительно неизвестных с четными номерами. В
конце этого шага каждый процессор будет содержать коэффициенты в точности
одного нового уравнения, и до начала следующего шага каким-то процессором
должны быть пересланы коэффициенты двух дополнительных уравнений. Один из
естественных способов состоит в том, что каждый «средний» процессор получает
такую информацию по схеме

Процессоры с нечетными номерами теперь прекращают работу, а
процессоры с четными номерами производят следующий шаг исключения. Процесс
продолжается, и после каждого шага примерно половина остающихся процессоров
переходит в разряд пассивных; заключительное комбинирование трех уравнений,
порождающее одно уравнение с единственным неизвестным, выполняется каким-то
одним процессором. Отметим, что всего в редукции 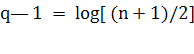
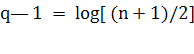 параллельных шагов. При обратной подстановке порядок действий по
существу обращается. Финальное уравнение решается одним процессором, и с каждым
новым шагом число активных процессоров возрастает.
параллельных шагов. При обратной подстановке порядок действий по
существу обращается. Финальное уравнение решается одним процессором, и с каждым
новым шагом число активных процессоров возрастает.
В более реалистическом случае в каждый процессор до начала
редукции будут загружены несколько строк и работа процессоров будет
высокоэффективной, за исключением последних этапов, когда потребуются пересылки
данных и, как и прежде, все больше процессоров будут становиться пассивными.
Каждая следующая итерация прямого и обратного хода зависит от
предыдущей. Распараллеливание по уровням проводить нельзя.
Исключение и восстановление переменных на каждом уровне можно
проводить независимо. Можно выполнить распараллеливание на уровне вложенных
циклов.
.3
Решение СЛАУ с 5 ти-диагональной матрицей
.3.1
Описание метода
Метод прогонки является частным случаем метода Гаусса и
применяется к системам с трех-пятидиагональной матрицей. Такие системы часто
встречаются при численном решении краевых задач для дифференциальных уравнений
второго порядка, при моделировании некоторых инженерных задач.
Если при решении использовать метод Гаусса, то расчет можно
организовать таким образом, чтобы не включать нулевые элементы матрицы. Этим
самым экономится требуемая память и уменьшается объем вычислений.
При нахождении решения краевых задач для уравнений более
высокого порядка мы рассмотрим способ непосредственной аппроксимации исходной
дифференциальной задачи. В этом случае мы приходим к системе уравнений следующего
вида:
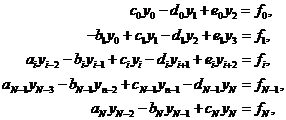
 (3.1)
(3.1)
Такого вида системы возникают при аппроксимации краевых задач для
обыкновенных дифференциальных уравнений четвертого порядка, а также при
реализации разностных схем для уравнений в частных производных. Матрица 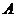 системы (3.1) является пятидиагональной
квадратной матрицей размерности
системы (3.1) является пятидиагональной
квадратной матрицей размерности  и имеет не более
и имеет не более 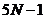 ненулевых элементов.
ненулевых элементов.
Для решения системы (3.1) метод исключения Гаусса. Учитывая
структуру системы (3.1), легко получим, что обратный ход метода Гаусса должен
осуществляться по формулам
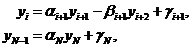
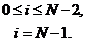 (3.2)
(3.2)
Для реализации (3.2) необходимо задать 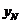 , а также определить коэффициенты
, а также определить коэффициенты 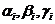 используя первое уравнение (3.2), выразим
используя первое уравнение (3.2), выразим
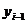 и
и 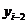 . Получим
. Получим
 (3.3)
(3.3)
для 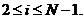
Подставляя (3.3) в третье уравнение (3.1), получим
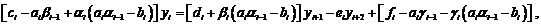
при 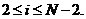
Сравнивая это выражение с первым уравнением (3.2), видим, что если
положить
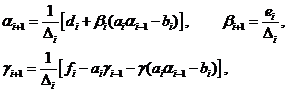 (3.4)
(3.4)
где обозначено  , то уравнения системы (3.1) для
, то уравнения системы (3.1) для 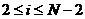 будут удовлетворены.
будут удовлетворены.
Рекуррентные соотношения (3.4) связывают 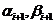 и
и  с
с 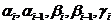 и
и 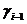 . Поэтому, если будут заданы
. Поэтому, если будут заданы 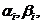 и
и 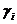 для
для  , то по формулам (3.4) последовательно можно найти коэффициенты
, то по формулам (3.4) последовательно можно найти коэффициенты 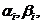 и
и 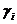 для
для 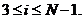
Найдем 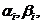 и
и 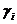 для
для  . Из первого уравнения (3.1) и (3.2) для
. Из первого уравнения (3.1) и (3.2) для 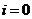 непосредственно получим
непосредственно получим
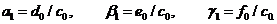 (3.5)
(3.5)
Далее подставляя значение (3.3) при 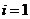 во вторую строчку (3.1), получим
во вторую строчку (3.1), получим
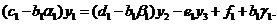 (3.6)
(3.6)
Следовательно, второе уравнение (2.3.1) будет выполнено, если
положить
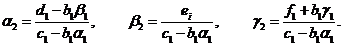 (3.7)
(3.7)
Итак, используя (3.4) - (3.7) можно найти 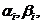 и
и 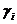 для
для 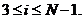 Осталось определить
Осталось определить 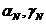 и
и 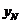 , входящие в формулу (3.2).
, входящие в формулу (3.2).
Воспользуемся для этого четвертым и пятым уравнениями (3.1).
Подставляя (3.3) при 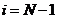 в четвертое уравнение, найдем, что
в четвертое уравнение, найдем, что  и
и 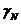 определяются по формулам (3.4) для
определяются по формулам (3.4) для 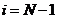 . Найдем теперь
. Найдем теперь 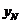 . Для этого подставим
. Для этого подставим 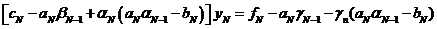 или
или  где
где 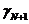 определяется по формуле (3.4) при
определяется по формуле (3.4) при 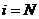 .
.
Объединяя полученные выше формулы, запишем алгоритм правой
прогонки для системы (3.1) в следующем виде:

где
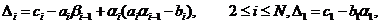
находятся прогоночные коэффициенты 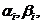 и
и 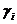 ;
;
неизвестные  находятся последовательно по формулам
находятся последовательно по формулам

Алгоритм построен.
1.3.2
Модификация, позволяющая эффективное решение системы
Метод прогонки состоит из прямого и обратного хода. Его
параллельная реализация напрямую при использовании декомпозиции расчетной
области оказывается невозможной, так как этот метод предусматривает
многократный проход от одного угла расчетной области к другому через всю
область.
Однако, существует способ решения этой проблемы. Главная идея
состоит в следующем: прямой и обратный ход прогонки организуются не по всей
области, а по подобластям, получившимся в результате декомпозиции расчетной
области. На границах «разрезов», или фиктивных границах, ставятся условия
первого рода, то есть полагается, что значение, прилежащее к границе «разреза»
с внешней стороны, точно известно. В действительности же, это значение
рассчитывается соседним процессом и нуждается в постоянной синхронизации, то
есть получении от соседнего процесса.
СЛАУ с пятидиагональной матрицей дает систему уравнений с
тремя прогоночными коэффициентами в отличие от трехдиагональной, что
увеличивает размер программы и время ее работы.
2. Результаты численного эксперимента
Для того, что бы ответить на поставленные в начале работы
вопросы, численные эксперименты будут проводиться на трех ПК с разными техническими
характеристиками.
ПК1
процессор: Pentium 4 1,7 GHz
оперативная память: 1,00 Гб
ПК2
процессор: Pentium Duai-Core CPU 2,10 GHz 2,10 GHz
оперативная память: 4,00 Гб (доступно 2,97 Гб)
ПК3
процессор: Intel Core i5-3210M CPU 2,5 GHz 2,5
GHz
- оперативная память: 4,00 Гб
Сразу оговорим, что тестирование проводилось на компьютерах
обычных пользователей, на которых были запущены системные процессы, утилиты,
антивирусы и т.п., поэтому одна и та же программа на одном и том же ПК в разный
момент времени может иметь разную продолжительность выполнения, следовательно,
полученные данные приблизительные.
Сравним результаты тестирования при изменении размерности
матрицы от 30000 до 3800000.
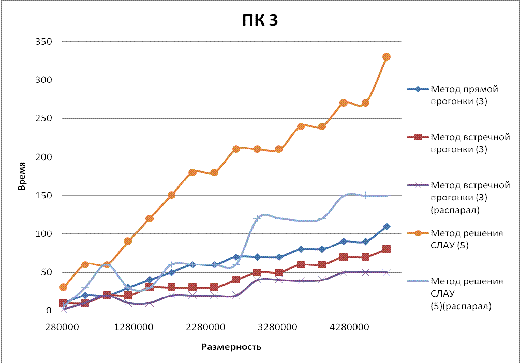
Как и ожидалось, ПК с самыми слабыми характеристиками
потратил наибольшее количество времени на решение СЛАУ. Так как ПК1 может
работать только с одним потоком, разница между простой встречной прогонкой и
распараллеленной несущественна (1,3%). Но по отношению с методом прямой
прогонки встречная сокращает время решения задачи на 31%.
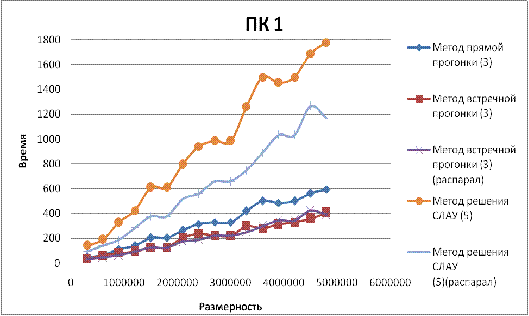

Результаты тестирования на ПК 2 показывают, что метод
встречной прогонки улучшает показатели на 29%, а при распределении по потокам
на 44%.
Заключение
В данной работе рассмотрены одни из самых эффективных методов
решения СЛАУ для ленточных матриц и их модификации. Полученные результаты
доказывают, что современные технологии, доступные даже простым пользователям,
дают большие ресурсы для улучшения результатов - сокращения времени работы
программы.
В работе реализованы методы решения СЛАУ с трех- и
пятидиагональными матрицами. Как оказалось, прямой метод прогонки неудобен для
распараллеливания. Представленные модификации алгоритма - встречная прогонка,
сами по себе дают хорошие результаты. Разделив процессы с учетом возможностей
нескольких процессоров, мы увидели значительное сокращение времени работы
программы.
Проведя численные эксперименты на ПК с разными техническими
возможностями, мы убедились, что увеличение количества процессоров
действительно приводит к сокращению времени счета, но более чем в  раз, а при модификации алгоритма и
распараллеливании на программном уровне значительно больше (среднее время
решения СЛАУ в Приложении 7).
раз, а при модификации алгоритма и
распараллеливании на программном уровне значительно больше (среднее время
решения СЛАУ в Приложении 7).
|
Кол-во раз
сокращения времени при переходе от однопроцессорной конфигурации к
2х-процессорной
|
|
Метод прямой
прогонки (3)
|
Метод встречной
прогонки (3)
|
Метод встречной
прогонки (3) (распарал)
|
Метод решения
СЛАУ (5)
|
Метод решения
СЛАУ (5) (распарал)
|
|
2,79514081
|
2,57557252
|
3,38900204
|
2,807692308
|
3,391304348
|
|
Кол-во раз
сокращения времени при переходе от однопроцессорной конфигурации к
4х-процессорной
|
|
Метод прямой
прогонки (3)
|
Метод встречной
прогонки (3)
|
Метод встречной
прогонки (3) (распарал)
|
Метод решения
СЛАУ (5)
|
Метод решения
СЛАУ (5) (распарал)
|
|
5,32842105
|
5,1121212
|
8,246485261
|
5,32842105
|
7,903703704
|
Метод циклической редукции обладает наибольшим параллелизмом,
чем реализованные в дипломной работе методы, и может быть распараллелен для
произвольного количества процессоров, что должно дать еще более существенные
результаты.
Получив результаты численных экспериментов, стало абсолютно
ясно, что параллельные методы решения СЛАУ с ленточными матрицами очень
эффективны. Их развитие и применение, безусловно, поднимет на новый уровень
нашу науку и различные отрасли промышленности.
Список источников
уравнение
матрица ленточный параллельный
1. В.П.
Ильин, Ю.И. Кузнецов Трехдиагональные матрицы и их приложения. Москва: Наука
1985 - с. 50-51, 62-64.
. Харви
Дейтел, Пол Дейтел Как программировать на С. Санкт-Петербург: СГТУ 2004 - с. 87
- 419.
. Баркалов
К.А. Параллельные численные методы. Метод прогонки. М.: Мир1975 - с. 56-63,
134-137.
. Материалы
учебного курса «Параллельные численные методы» от Intel
http://software.intel.com/ru-ru/articles/courseware_parallel_computation_numerical_methods
. Белов
С.А., Золотых Н.Ю. Численные методы линейной алгебры Н. Новгород, ННГУ 2005 -
с. 97-101.
. Акимова
Е.Н. Параллельный алгоритм решения систем уравнений с пятидиагональными
матрицами и исследование его устойчивости // Вестник ННГУ. 2009. №2. с.
135-140.
. Дж.
Ортега Введение в параллельные и векторные методы решения линейных систем.
Москва: Мир 1991 - с. 151 -154.
. А.А.
Самарский Методы решения сеточных уравнений. Москва: Наука. 1978 - с. 97 - 99.
. Есаулов
А.О., Старченко А.В. Параллельная реализация явного метода Н.И. Булеева
http://old.lvk.cs.msu.su/files/mco2005/esaulov.pdf с. 4-7.