Оцінка для найкращих наближень деяких лінійних комбінацій аналітичних функцій
МІНІСТЕРСТВО
ОСВІТИ ТА НАУКИ УКРАЇНИ
Кам’янець-Подільський
національний університет
Кафедра
диференціальних рівнянь та прикладної математики
ДИПЛОМНА РОБОТА
«Оцінка для найкращих наближень деяких лінійних
комбінацій аналітичних функцій»
аналітичних функцій»
студентки
52 групи фізико-математичного факультету
спеціальності
№7.010103 (Педагогіка і методика середньої освіти. Математика і основи
інформатики)
Швець
Оксани Ростиславівни
Науковий
керівник:
кандидат
фізико-математичних наук, доцент кафедри диференціальних рівнянь та прикладної математики
Сорич
В. А.
Кам’янець-Подільський,
2009
Зміст
§1. Перелік умовних
позначень 3
§2. Короткий огляд
результатів та історичні відомості. Постановка задачі. 6
§3. Класи функцій 154
§4. Відношення
порядку для 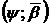 -похідних 231
-похідних 231
§5. Оцінка для найкращих
наближень деяких лінійних комбінацій аналітичних функцій 26
Висновок 59
Список використаних джерел 61
§1.
Перелік умовних позначень
 -
квантор загальності: “для кожного” “для будь-якого”;
-
квантор загальності: “для кожного” “для будь-якого”;
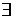 -
квантор існування: “існує”;
-
квантор існування: “існує”;
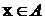 -
елемент х належить множині А;
-
елемент х належить множині А;
 -
елемент х не належить множині А;
-
елемент х не належить множині А;
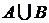 -
об’єднання множин А і В;
-
об’єднання множин А і В;
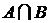 -
перетин множин А і В;
-
перетин множин А і В;
 - множина
А міститься в множині В;
- множина
А міститься в множині В;
N- множина всіх натуральних чисел;
Z
- множина всіх цілих чисел;
R
- множина всіх дійсних чисел;
C
- множина всіх комплексних чисел;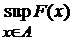 - точна
верхня межа значень функціонала F на множині A;
- точна
верхня межа значень функціонала F на множині A;
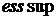 -
суттєва точна верхня межа;
-
суттєва точна верхня межа;
sign - величина, що дорівнює 1, якщо
- величина, що дорівнює 1, якщо 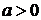 ,дорівнює
-1 якщо
,дорівнює
-1 якщо 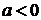 і дорівнює 0, якщо
і дорівнює 0, якщо 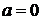 ;
;
 -
норма в лінійному нормованому просторі;
-
норма в лінійному нормованому просторі;
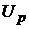 -
одинична куля в просторі
-
одинична куля в просторі 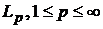 ;
;
 -
одинична куля в просторі
-
одинична куля в просторі 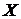 ;
;
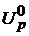 -
множина вигляду
-
множина вигляду  ;
;
С -
простір неперервних  −періодичних функцій
−періодичних функцій 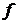 з нормою
з нормою  ;
;
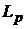 -
простір
-
простір  −періодичних вимірних і суттєво обмежених (при
−періодичних вимірних і суттєво обмежених (при 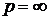 ) або сумовних у р−ому степені функцій
) або сумовних у р−ому степені функцій 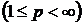 з нормою
з нормою
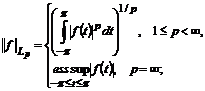 ;
;
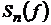 -
сума Фур’є функції
-
сума Фур’є функції 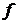 ;
;
 -
тригонометричний поліном порядку п;
-
тригонометричний поліном порядку п;
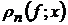 -
відхилення від функції її часткових сум Фур’є
-
відхилення від функції її часткових сум Фур’є  ;
;
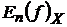 -
найкраще наближення функції тригонометричними поліномами порядку п-1 у
метриці простору
-
найкраще наближення функції тригонометричними поліномами порядку п-1 у
метриці простору 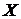 ;
;
 -
найкраще наближення множини
-
найкраще наближення множини 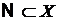 тригонометричними
поліномами порядку п-1 у метриці простору
тригонометричними
поліномами порядку п-1 у метриці простору 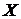 ;
;
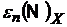 -
наближення множини
-
наближення множини 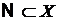 частинними сумами Фур’є порядку п-1 у метриці
простору
частинними сумами Фур’є порядку п-1 у метриці
простору 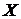 ;
;
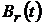 -
ядра Бернуллі
-
ядра Бернуллі 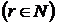 ;
;
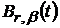 -
ядра Вейля−Надя:
-
ядра Вейля−Надя: 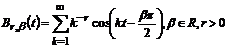 ;
;
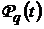 -
ядра Пуассона;
-
ядра Пуассона;
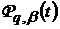 -
узагальнені ядра Пуассона:
-
узагальнені ядра Пуассона: 
 ;
;
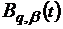 -
бігармонічні ядра Пуассона:
-
бігармонічні ядра Пуассона:
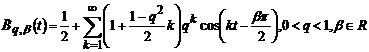 ;
;
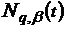 -
ядра Неймана:
-
ядра Неймана: 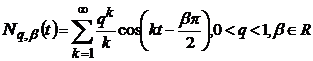 ;
;
 -
ядра вигляду:
-
ядра вигляду: 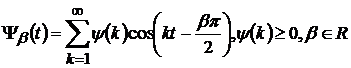 ;
;
 -
ядра вигляду:
-
ядра вигляду: 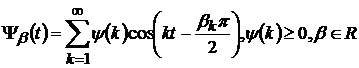 ;
;
 -
ядра вигляду:
-
ядра вигляду:
 ;
;
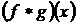 -
згортка функцій
-
згортка функцій 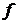 і
і  :
:
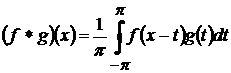 ;
;
 -
-
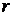 -та похідна функції
-та похідна функції 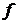 ;
;
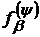 -
-
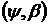 похідна функції
похідна функції 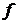 ;
;
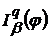 -
інтервал Пуассона функції
-
інтервал Пуассона функції  ;
;
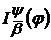 -
-
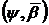 −інтервал функції
−інтервал функції  ;
;
 -
повний еліптичний інтеграл першого роду:
-
повний еліптичний інтеграл першого роду:
 ;
;
 -
класи Соболєва:
-
класи Соболєва: 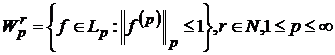 ;
;
 -
класи Вейля−Надя:
-
класи Вейля−Надя:
 ;
;
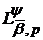 -
класи вигляду:
-
класи вигляду:  ;
;
 -
класи вигляду:
-
класи вигляду:  ;
;
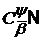 -
класи неперервних функцій вигляду:
-
класи неперервних функцій вигляду: 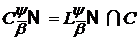 ;
;
§2.
Короткий огляд результатів та історичні відомості. Постановка задачі
Майже у всіх галузях математики важливу роль відіграють
задачі про апроксимацію (наближення) більш складніших об’єктів менш
складнішими. Теорія наближень має справу в основному з наближенням окремих
функцій чи класів функцій за допомогою заданих підпросторів, що складаються із
функцій, що є в деякому розумінні більш простими ніж ті, що апроксимуються.
Для періодичних функцій та їх класів найчастіше в ролі таких
підпросторів вибирають множини тригонометричних поліномів заданого порядку п,
або деякі підмножини цієї множини.
Найпростішим таким тригонометричним многочленом порядку п, що
може відтворювати функцію 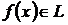 , природно вибрати частинну суму порядку п ряду
Фур’є функції
, природно вибрати частинну суму порядку п ряду
Фур’є функції  , її називають сумою Фур’є функції і позначають:
, її називають сумою Фур’є функції і позначають:
 .(1)
.(1)
Якщо 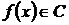 , то за величину похибки заміни
, то за величину похибки заміни  сумою Фур’є беруть норму їх різниці в просторі С,
тобто величину
сумою Фур’є беруть норму їх різниці в просторі С,
тобто величину
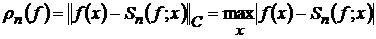 (2)
(2)
Поряд із сумами Фур’є в якості наближуючиx
агрегатів використовуються і інші тригонометричні многочлени. Це викликано тим,
що в окремих випадках суми Фур’є функції збігаються до неї дуже повільно, а то
і взагалі розбіжні, навіть якщо наближаюча функція вибрана із простору С.
Приклади неперервних функцій, ряди Фур’є яких розходяться в окремих точках,
були відомі ще Дюбуа−Реймонду (1876р.). Вказаний факт націлює знаходити
способи побудови послідовностей таких наближаючи поліномів, які вже рівномірно
збігаються до функції на всьому просторі С.
Зрозуміло, що найбільш вдалою в розумінні швидкості збіжності до  є послідовність операторів
є послідовність операторів 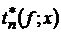 , яка кожній функції ставить у відповідність її
многочлен найкращого наближення
, яка кожній функції ставить у відповідність її
многочлен найкращого наближення  ,
тобто многочлен, що задовольняє умову
,
тобто многочлен, що задовольняє умову

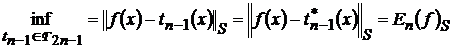 (3)
(3)
в метриці простору 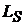 .
.
Але, на жаль, оператори 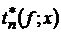 на
всьому просторі
на
всьому просторі 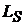 (зокрема на С) не є лінійними. Це в значній
мірі ускладнює їх побудову, дослідження, а отже, і використання.
(зокрема на С) не є лінійними. Це в значній
мірі ускладнює їх побудову, дослідження, а отже, і використання.
Вибір сум Фур’є в якості наближаючих поліномів часто є в деякому
розумінні оптимальним або ж близьким до нього. Перші результати оцінок
відхилень сум Фур’є від заданих неперервних функцій були отримані ще в період
становлення теорії наближення функцій. В 1909 р. А. Лебег
довів, що
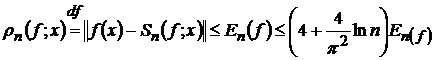 ,(4)
,(4)
де 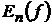 - найкраще наближення функції
- найкраще наближення функції  тригонометричними поліномами
тригонометричними поліномами 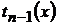 степеня не вищого за
степеня не вищого за 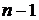 в
рівномірній метриці С, а
в
рівномірній метриці С, а 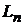 -
константи Лебега:
-
константи Лебега:
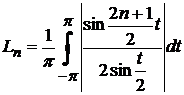 .(5)
.(5)
В поєднанні з теоремами Джексона про оцінки величин 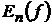 нерівність Лебега (4) містить велику кількість ранніх
результатів по оцінках величин
нерівність Лебега (4) містить велику кількість ранніх
результатів по оцінках величин  та
не зменшує свого значення і в теперішній час: вона є точним по порядку та
зручна в застосуваннях. Наприклад, якщо функція
та
не зменшує свого значення і в теперішній час: вона є точним по порядку та
зручна в застосуваннях. Наприклад, якщо функція  має
похідну порядку r, обмежену, припустимо, одиницею, то
має
похідну порядку r, обмежену, припустимо, одиницею, то 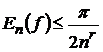 (див., напр., [6, с. 102], і тоді з (4) отримаємо
(див., напр., [6, с. 102], і тоді з (4) отримаємо
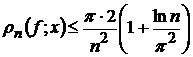 .(6)
.(6)
Нерівності Лебега (4) на всьому класі С неперервних функцій є
точними по порядку. Більше того, в ньому константу  зменшити неможливо,тобто у множині С
нерівність (4) є асимптотично точною. В той же час існують важливі підмножини
неперервних функцій, для яких співвідношення (4) виявляється неточним навіть по
порядку.
зменшити неможливо,тобто у множині С
нерівність (4) є асимптотично точною. В той же час існують важливі підмножини
неперервних функцій, для яких співвідношення (4) виявляється неточним навіть по
порядку.
Щодо просторів 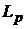 , то ще на початку ХХ століття було відомо, що при
, то ще на початку ХХ століття було відомо, що при 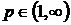 оператори, які відображають довільну функцію
оператори, які відображають довільну функцію 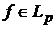 в її частинну суму Фур’є є рівномірно обмеженими.
Звідси випливає:
в її частинну суму Фур’є є рівномірно обмеженими.
Звідси випливає: 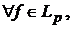
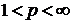 ,
,
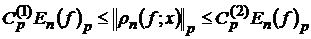 ,(7)
,(7)
де  - величина найкращого наближення функції
- величина найкращого наближення функції  тригонометричними многочленами в метриці простору
тригонометричними многочленами в метриці простору 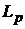 .
.
В теорії наближення розглядають поведінку величин 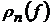 на деякій множині функцій
на деякій множині функцій 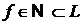 . Позначимо
. Позначимо 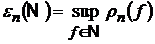 .
Знайти точне значення величини
.
Знайти точне значення величини 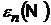 при
кожному натуральному п надзвичайно складна задача, тому намагаються
встановити асимптотичну поведінку цієї величини при
при
кожному натуральному п надзвичайно складна задача, тому намагаються
встановити асимптотичну поведінку цієї величини при  . Початок розв’язування задач більш глибокого
дослідження величин
. Початок розв’язування задач більш глибокого
дослідження величин 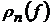 відноситься до 30 − 40-х років ХХ століття та
пов’язане з іменами А. М. Колмогорова та С. М Нікольського. В 1935 р. А. М.
Колмогоров [1] розглянув величину
відноситься до 30 − 40-х років ХХ століття та
пов’язане з іменами А. М. Колмогорова та С. М Нікольського. В 1935 р. А. М.
Колмогоров [1] розглянув величину
 ,
,
і показав, що при 

де 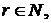 а
а 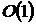 -
величина рівномірно обмежена по п. Потім Пінкевич [2]
довів, що дана рівність залишиться в силі і у випадку класу
-
величина рівномірно обмежена по п. Потім Пінкевич [2]
довів, що дана рівність залишиться в силі і у випадку класу 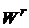 , де
, де  і
не обов’язково ціле, тобто для класів функцій, диференційованих по Вейлю.
Нікольський С. М. поширив дані результати на класи
і
не обов’язково ціле, тобто для класів функцій, диференційованих по Вейлю.
Нікольський С. М. поширив дані результати на класи 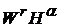
 −періодичних функцій, у яких існують і є неперервними
похідні до r−го порядку
−періодичних функцій, у яких існують і є неперервними
похідні до r−го порядку 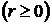
 включно,
причому
включно,
причому 
і на більш загальні класи 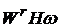 ,
які визначаються опуклими модулями неперервності
,
які визначаються опуклими модулями неперервності  .
Зокрема С. М. Нікольський встановив, що для довільних чисел r та
.
Зокрема С. М. Нікольський встановив, що для довільних чисел r та 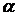 ,
,  ,
,  справедлива рівність
справедлива рівність
 .
.
Окрім
цього, він розв’язав аналогічну задачу і для випадку, коли замість сум 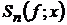 беруться суми Фейєра
беруться суми Фейєра 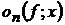 . Ці
дослідження Колмогорова −Нікольського поклали початок новому напрямку в
теорії наближення функцій і підсумовування рядів Фур’є. Результати цих
досліджень поширювали на більш ширші класи функцій, а за агрегати наближення
розглядалися тригонометричні поліноми
. Ці
дослідження Колмогорова −Нікольського поклали початок новому напрямку в
теорії наближення функцій і підсумовування рядів Фур’є. Результати цих
досліджень поширювали на більш ширші класи функцій, а за агрегати наближення
розглядалися тригонометричні поліноми 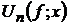 ,
породжені різними методами
,
породжені різними методами 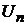 підсумовування
рядів Фур’є.
підсумовування
рядів Фур’є.
Задача
про відшукання асимптотичних рівностей для величин 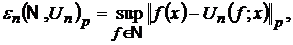
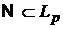 - фіксований
клас
- фіксований
клас  −періодичних функцій із простору
−періодичних функцій із простору 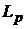 , стала однією з найбільш важливих в теорії наближень
функцій та в теорії підсумовування рядів Фур’є. Якщо в явному вигляді знайдена
функція
, стала однією з найбільш важливих в теорії наближень
функцій та в теорії підсумовування рядів Фур’є. Якщо в явному вигляді знайдена
функція 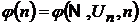 така, що при
така, що при 
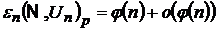 , то кажуть, що розв’язана задача Колмогорова−Нікольського.
, то кажуть, що розв’язана задача Колмогорова−Нікольського.
Після приведених вище робіт А. М. Колмогорова, С. М. Нікольського, В.
Т. Пінкевича про асимптотичні рівності у відповідних задачах Колмогорова−Нікольського
аналогічні результати для різних лінійних методів підсумовування рядів Фур’є (методи
Фур’є, Фейєра, Фавара, Валле−Пуссена, Рісса, Чезаро, Зігмунда та ін.) та
на різних функціональних класах отримали багато видатних математиків ХХ−сторіччя:
О. I. Степанець, В. К. Дзядик, О. В. Єфімов, М. П.
Корнєйчук, В. П. Моторний, Б. Надь. С. Б. Стєчкін, С. О. Теляковський та інші.
У 80 − 90-х роках ХХ сторіччя О. І. Степанцем був розроблений
новий підхід до класифікації періодичних функцій, що базувався на поняттях 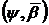 −похідної та
−похідної та  −інтеграла,
який дозволив здійснювати досить тонку класифікацію надзвичайно широких множин
періодичних функцій. За відносно невеликий проміжок часу для запроваджених О.
І. Степанцем та його учнями класів було отримано розв’язки цілого ряду задач
теорії наближення функцій, які до цього були відомі для класів Вейля−Надя.
При цьому результати, які отримано для вказаних класів, з одного боку мають
загальний характер, а з другого - виявляють цілу низку нових ефектів, які у
шкалах раніше відомих класів навіть поміченими не можуть бути.
−інтеграла,
який дозволив здійснювати досить тонку класифікацію надзвичайно широких множин
періодичних функцій. За відносно невеликий проміжок часу для запроваджених О.
І. Степанцем та його учнями класів було отримано розв’язки цілого ряду задач
теорії наближення функцій, які до цього були відомі для класів Вейля−Надя.
При цьому результати, які отримано для вказаних класів, з одного боку мають
загальний характер, а з другого - виявляють цілу низку нових ефектів, які у
шкалах раніше відомих класів навіть поміченими не можуть бути.
Отже, дослідження асимптотичних властивостей на введених О. І.
Степанцем класах періодичних функцій: найкращих наближень тригонометричними
поліномами, наближень за допомогою лінійних методів підсумовування рядів Фур’є,
зокрема, сум Фур’є та інші є важливими і актуальними.
Задача одночасного наближення періодичних функцій та їх похідних сумами
Фур’є у постановці, аналогічній до розглядуваної у дипломній роботі бере свій
початок із статті [3]. В ній за величину, яка характеризує відхилення лінійної
комбінації функцій із класу 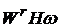 та
їх похідних розглядається верхня межа функціонала
та
їх похідних розглядається верхня межа функціонала
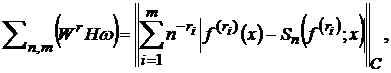
тобто величина
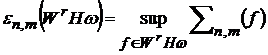 ,
,
де 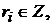
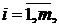
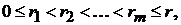
 - довільний модуль неперервності.
- довільний модуль неперервності.
Якщо функція  належить класу
належить класу 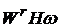 ,
то її похідна порядку ri
,
то її похідна порядку ri 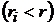 ,
буде знаходитись в класі
,
буде знаходитись в класі 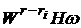 . Тому із результатів роботи [4] для величини
. Тому із результатів роботи [4] для величини 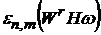 ми можемо отримати асимптотичну нерівність
ми можемо отримати асимптотичну нерівність

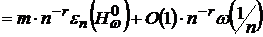 ,
,
де - величина добре відома в науковій літературі (див.,
напр., [5]), а
- величина добре відома в науковій літературі (див.,
напр., [5]), а 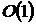 -
рівномірно обмежена по п величина.
Така оцінка величини
-
рівномірно обмежена по п величина.
Така оцінка величини 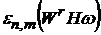 є, взагалі кажучи, неточною. В дійсності, як показав
О. І Степанець,
є, взагалі кажучи, неточною. В дійсності, як показав
О. І Степанець,

де m0 - кількість
парних, а m1
-кількість непарних чисел в наборі 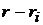
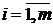 ,
, 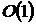 -
величина рівномірно обмежена по n.
-
величина рівномірно обмежена по n.
Пізніше задачі наближення лінійної комбінації функцій та іх похідних
лінійними методами підсумовування рядів Фур’є розв’язані були на класах Степанця.
Ним самим та його учнями: Н. М. Сорич, В. А. Сорич, Н. М.
Задерей, В. В. Дрозд, І. В. Соколенко.
Дана дипломна робота присвячена дослідженню швидкості наближення
лінійної комбінації інтегралів Пуассона частковими сумами Фур’є на класах  − диференційованих функцій, (
− диференційованих функцій, ( −інтегралів) високої гладкості, і зокрема на
класах інтегралів Пуассона.
−інтегралів) високої гладкості, і зокрема на
класах інтегралів Пуассона.
Інтегралом Пуассона функції  називають
функцію
називають
функцію  , що задається рівністю
, що задається рівністю
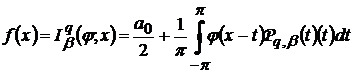 ,
,
де 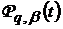 - ядро Пуассона вигляду
- ядро Пуассона вигляду
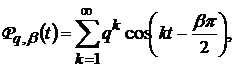
 ,
,
а 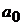 - вільний член ряду Фур’є функції
- вільний член ряду Фур’є функції  . Класи функцій
. Класи функцій  і
і
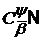 ,породжені ядрами Пуассона
,породжені ядрами Пуассона  (тобто при
(тобто при  ,
,
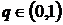 ) будемо позначати відповідно через
) будемо позначати відповідно через 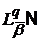 і
і 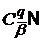 ,а
відповідні
,а
відповідні 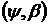 −похідні
−похідні  -а через
-а через  і
називати
і
називати 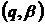 −похідними.
−похідними.
Одиничні кулі в 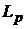 позначимо через
позначимо через 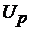
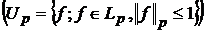 . Величина
. Величина  -
найкраще наближення у просторі
-
найкраще наближення у просторі 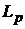 тригонометричними
поліномами порядку не вищого за
тригонометричними
поліномами порядку не вищого за 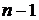 .
.
Нехай, нарешті,
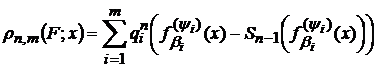 ,(8)
,(8)
де 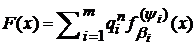 - лінійна комбінація
- лінійна комбінація 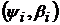 −
похідних.
−
похідних.
В дипломній роботі досліджується величина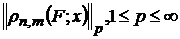 . Основні результати роботи отримано для класів
. Основні результати роботи отримано для класів  , у випадку, коли послідовності
, у випадку, коли послідовності 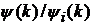 належать до множини
належать до множини 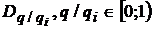 , тобто задовольняють умову
, тобто задовольняють умову  . Основна ідея, на якій базуються результати дипломної
полягає в тому, що величина
. Основна ідея, на якій базуються результати дипломної
полягає в тому, що величина  для
лінійної комбінації вигляду (8) при
для
лінійної комбінації вигляду (8) при 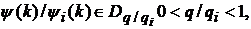 ,
та
,
та 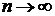 поводиться
приблизно так саме, як і аналогічна лінійна комбінація ядер Пуассона. Це
дозволяє, зокрема, задачі про отримання асимптотичних рівностей
поводиться
приблизно так саме, як і аналогічна лінійна комбінація ядер Пуассона. Це
дозволяє, зокрема, задачі про отримання асимптотичних рівностей 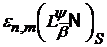 і
і  зводити
до аналогічних задач для величин
зводити
до аналогічних задач для величин 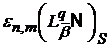 і
і
 відповідно.
відповідно.
§
3. Класи функцій
Нехай  -
-  −періодична,
сумова функція із середнім значенням на періоді рівним нулю, тобто
−періодична,
сумова функція із середнім значенням на періоді рівним нулю, тобто
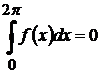
і
 (9)
(9)
ряд Фур’є функції  ,де
,де

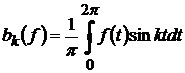
коефіцієнти ряду Фур’є функції  .
.
Якщо функцію  можна
можна 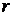 раз
неперервно диференціювати, то інтегруючи
раз
неперервно диференціювати, то інтегруючи 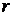 раз
за частинами та враховуючи періодичність функції
раз
за частинами та враховуючи періодичність функції  та
її похідних, k−ту гармоніку ряду можна подати наступним чином
та
її похідних, k−ту гармоніку ряду можна подати наступним чином
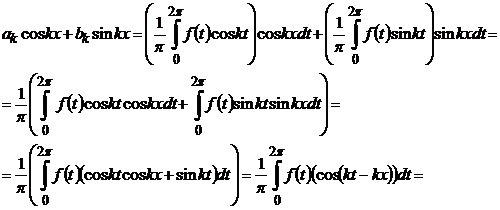
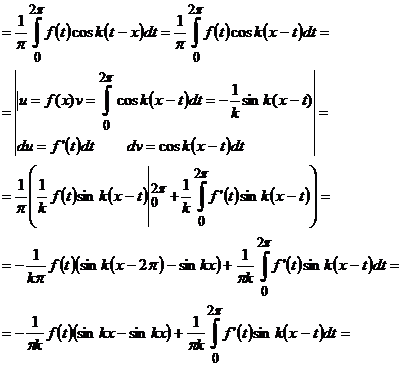
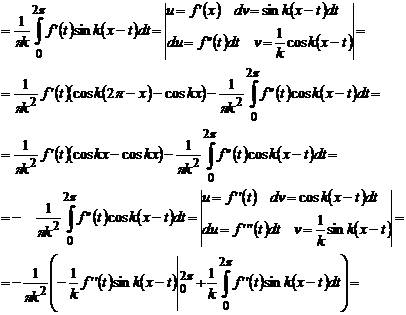
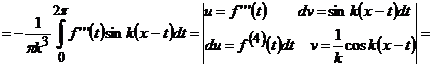

так що
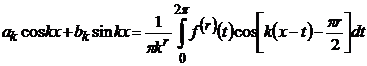 (10)
(10)
Нехай далі, сумова функція  є
такою, що має абсолютно неперервні похідні до
є
такою, що має абсолютно неперервні похідні до 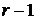 -го
порядку включно, а
-го
порядку включно, а  знаходиться в просторі
знаходиться в просторі 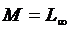 суттєво
обмежених на осі функцій, норма в якому задається рівністю
суттєво
обмежених на осі функцій, норма в якому задається рівністю
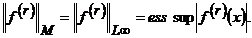
Підставивши вираз (10) в співвідношення
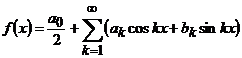
і враховуючи, що ряд Фур’є можна інтегрувати почленно, одержимо для  інтегральний вигляд:
інтегральний вигляд:
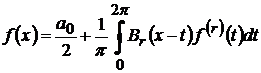 (11)
(11)
В такому випадку функцію  називають
згорткою функції
називають
згорткою функції 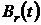 та
та 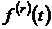 і
позначають іноді
і
позначають іноді 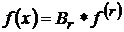 , де
, де 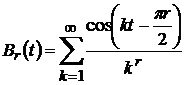 ,(r=1,2,…)
- ядро Бернуллі.
,(r=1,2,…)
- ядро Бернуллі.
Якщо 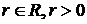 , а функція
, а функція  записується
у вигляді
записується
у вигляді
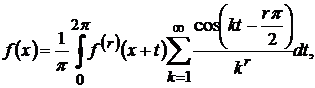
де 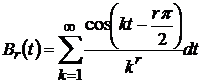 - узагальнене ядро Бернуллі, то
- узагальнене ядро Бернуллі, то
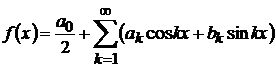
називають згорткою функції  та
та
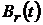 .
.
Якщо деяка функція  подається
через ряд Фур’є у вигляді
подається
через ряд Фур’є у вигляді
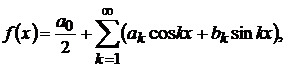
то 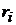 −ю або ж
−ю або ж 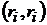
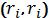 похідною
цієї функції
похідною
цієї функції  називають функцію
називають функцію 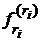 ,
для якої справедлива рівність
,
для якої справедлива рівність

Функцію 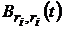 будемо називати, аналогічно як і вище,
ядром Бернуллі, а похідну
будемо називати, аналогічно як і вище,
ядром Бернуллі, а похідну 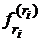 -
-
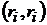 похідною функції
похідною функції  у
розумінні Вейля.
у
розумінні Вейля.
Якщо згортка функції f(x) має вигляд
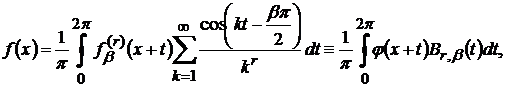
то функцію  називають ядром Бернуллі, а функцію
називають ядром Бернуллі, а функцію  називають
називають 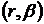 −похідною
функції
−похідною
функції  у розумінні Вейля-Надя і часто записують
у розумінні Вейля-Надя і часто записують 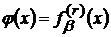 . При цьому, у випадку належності функції
. При цьому, у випадку належності функції  множині
множині 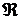 ,
де наприклад,
,
де наприклад, 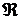 - множина
- множина  −періодичних
суттєво обмежених функцій
−періодичних
суттєво обмежених функцій  (t) з нормою
(t) з нормою  що
не перевищує одиниці, множину таких функцій
що
не перевищує одиниці, множину таких функцій 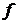 називають
класом Вейля−Надя і позначають
називають
класом Вейля−Надя і позначають 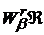
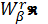 .
.
Нехай далі  - довільна фіксована функція натурального аргументу k,
а
- довільна фіксована функція натурального аргументу k,
а  - фіксоване дійсне число. Припустимо, що ряд
- фіксоване дійсне число. Припустимо, що ряд
 (12)
(12)
є рядом Фур’є деякої сумовної функції. Цю функцію позначимо через 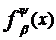 і назвемо (ψ,β -похідною функції
і назвемо (ψ,β -похідною функції . Тоді якщо
. Тоді якщо
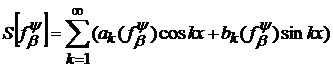 ,
,
то
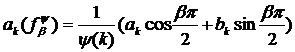

Тому з (9) одержимо
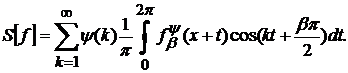 (13)
(13)
Множину функцій  , що задовольняють такій умові, будемо позначати,
користуючись роботою [3, гл. Ι, §7], через
, що задовольняють такій умові, будемо позначати,
користуючись роботою [3, гл. Ι, §7], через 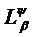 .
.
Функцію  називають згорткою
називають згорткою  -періодичних
сумовних функцій
-періодичних
сумовних функцій 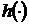 i
i 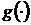 ,
якщо її можна подати у вигляді
,
якщо її можна подати у вигляді
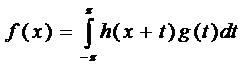
що символічно записують так: 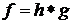 .
При цьому функцію
.
При цьому функцію 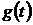 називають ядром згортки.
називають ядром згортки.
Якщо ряд
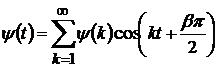 (14)
(14)
на всьому періоді збігається і рядом Фур’є деякої сумової функції 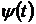 , то функції з множини
, то функції з множини 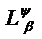 як
показано в [3], можна майже скрізь подати у вигляді
як
показано в [3], можна майже скрізь подати у вигляді
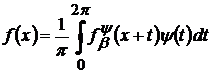 (15)
(15)
тобто вони є згортками ядра  з
функціями
з
функціями 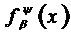 . Останні у роботі [3] названі (ψ,β)-похідними функцій
. Останні у роботі [3] названі (ψ,β)-похідними функцій  .
.
Через C позначимо простір  -періодичних
функцій норма яких має вигляд
-періодичних
функцій норма яких має вигляд

Через 
 позначимо простір сумовних
позначимо простір сумовних  -періодичних функцій степеня р, норма яких
подається у вигляді
-періодичних функцій степеня р, норма яких
подається у вигляді
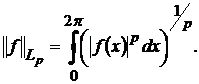
Через 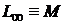 - простір
- простір  -
періодичних вимірних та суттєво обмежених функцій з нормою
-
періодичних вимірних та суттєво обмежених функцій з нормою

Функція  розглядається в дипломній роботі з простору
розглядається в дипломній роботі з простору  або ж з простору
або ж з простору 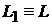
 −періодичних сумовних на
−періодичних сумовних на 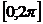 функцій
функцій  з
нормою
з
нормою

Через 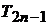 позначимо підпростір тригонометричних поліномів
позначимо підпростір тригонометричних поліномів

де  степеня не вище за
степеня не вище за 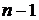 .
.
Величину 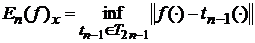 , де
, де 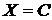 ,
або
,
або 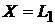 називають найкращим наближенням функцій f, а
величину
називають найкращим наближенням функцій f, а
величину
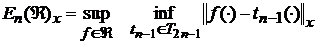
найкращим наближенням класу 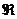 тригонометричними
поліномами степеня не вище за
тригонометричними
поліномами степеня не вище за 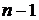 в
метриці простору X.
в
метриці простору X.
§4. Відношення порядку для 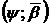 - похідних
- похідних
Нехай 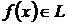 . Як і вище
. Як і вище
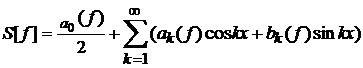
її ряд Фур’є. Нехай, далі, 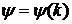 і
і
 - довільні функції натурального аргументу.
- довільні функції натурального аргументу.
Припустимо, що ряд
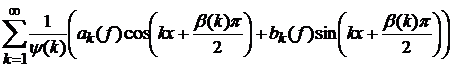
є рядом Фур’є деякої функції із L. Цю функцію позначимо через 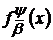 і назвемо
і назвемо 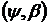 −похідною
функції
−похідною
функції  , а множину функції
, а множину функції  ,
що задовольняють таким умовам, позначимо через
,
що задовольняють таким умовам, позначимо через 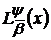
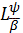 .
Якщо
.
Якщо 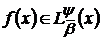 і при цьому
і при цьому 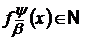
 ,
де
,
де 
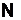 -
деяка підмножина із L, то будемо говорити, що
-
деяка підмножина із L, то будемо говорити, що  належить до класу.
належить до класу. 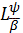
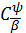
Якщо 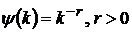 і
і 
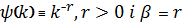 класи
співпадають із відомими вже класами (зокрема
класи
співпадають із відомими вже класами (зокрема 
 ),
що визначаються r-тою похідною в розумінні Вейля, які в свою чергу, при
),
що визначаються r-тою похідною в розумінні Вейля, які в свою чергу, при 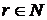
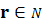 переходять
в класи r-раз диференційованих функцій; якщо при цьому
переходять
в класи r-раз диференційованих функцій; якщо при цьому 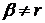
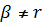 отримуємо
класи Вейля-Надя
отримуємо
класи Вейля-Надя 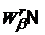
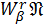 .
.
Класи 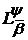 та
та 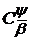 були
введені в [7], дивись також в [8].
були
введені в [7], дивись також в [8].
В цьому параграфі введемо запозичивши із [7] відношення порядку для 
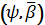 -похідних,
що дозволяють вказати аналоги “молодших” похідних для функцій із множин
-похідних,
що дозволяють вказати аналоги “молодших” похідних для функцій із множин 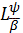
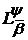 .
.
Означення 1. Нехай
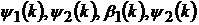
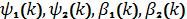 -
довільні послідовності дійсних чисел. Скажемо, що пара
-
довільні послідовності дійсних чисел. Скажемо, що пара 
 L передує парі
L передує парі 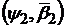
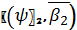 ,
якщо
,
якщо 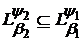 . В цьому випадку будемо писати
. В цьому випадку будемо писати 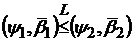 . Якщо
. Якщо 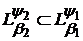 ,
то пишемо
,
то пишемо  .
.
Таким чином, “меншим” парам відповідають більші множини.
Теорема 1. (Степанець О.І.) Якщо функція  належить до
належить до 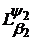 і
і

 ,
то у неї існує похідна
,
то у неї існує похідна 
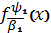 ,
яка знаходиться в множині
,
яка знаходиться в множині 
 .
При цьому
.
При цьому

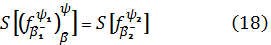 (16)
(16)
Із приведеної теореми, зокрема, випливає: якщо  .
.

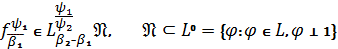 (17)
(17)
для довільної функції 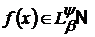
 .
Зрозуміло, що “самий малий” порядок задає пара, у якої
.
Зрозуміло, що “самий малий” порядок задає пара, у якої  і
і 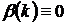
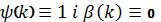 ,
оскільки в цьому випадку
,
оскільки в цьому випадку 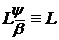
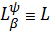 .
Розглядаючи множини
.
Розглядаючи множини 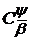 та бажаючи забезпечити неперервність “молодших”
похідних, зауважимо, що ця властивість тісно пов’язана із властивостями
множини, що містить
та бажаючи забезпечити неперервність “молодших”
похідних, зауважимо, що ця властивість тісно пов’язана із властивостями
множини, що містить 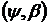
 −похідні,
у зв’язку із цим введемо ще одне поняття.
−похідні,
у зв’язку із цим введемо ще одне поняття.
Означення 2. Нехай  -
як і раніше довільні послідовності вільних чисел. Будемо говорити, що пара
-
як і раніше довільні послідовності вільних чисел. Будемо говорити, що пара 
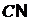 −передує парі
−передує парі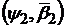 ,
та писати, якщо із включення
,
та писати, якщо із включення 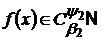 ,
випливає, що
,
випливає, що 
 .
.
Якщо 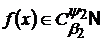
 і
і
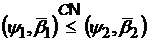
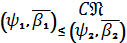 ,
то за означенням
,
то за означенням 
 і
тим більше
і
тим більше 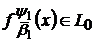
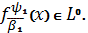 .
(Отже в цьому випадку буде виконуватись рівність (16), в наслідок якої
отримаємо співвідношення(17)),
.
(Отже в цьому випадку буде виконуватись рівність (16), в наслідок якої
отримаємо співвідношення(17)),
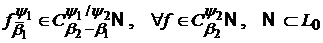
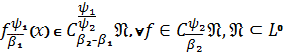 .(18)
.(18)
Зрозуміло, що не довільні пари  і
і
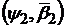
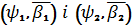 ,
пов’язані співвідношеннями
,
пов’язані співвідношеннями 
 чи
чи
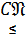
 .
.
Наприклад 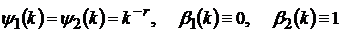
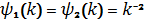
 .
.
Розглянемо функцію
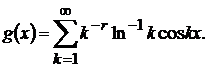
Добре відомо, див., наприклад, [9, гл.V, §1], що ряд є рядом Фур’є
деякої сумовної функції, а ряд 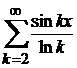
 не
може бути таким. А тому функція
не
може бути таким. А тому функція 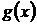 має
має
 −похідну і немає
−похідну і немає 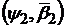
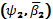 −похідної,
тобто
−похідної,
тобто 
 і
і
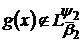 .
.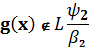
Аналогічно можемо зробити висновок, що функція

знаходиться в 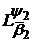
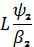 і
не належить до
і
не належить до 
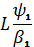 .
.
Таким чином ні співвідношення  ,
ні протилежне йому немає місця.
,
ні протилежне йому немає місця.
Приведений факт міг би бути недоліком, якби нашою ціллю було
впорядкування множини пар послідовностей. Насправді ж він лише засвідчує
різноманітність множин 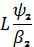
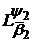 .
.
Разом із тим можна вказати достатньо прості умови, що забезпечують L та
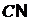 - передування таких пар.
- передування таких пар.
Теорема 2. (Степанець О.І.) Нехай 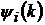
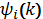 та
та

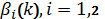 -
довільні послідовності дійсних чисел. Тоді, якщо для пари
-
довільні послідовності дійсних чисел. Тоді, якщо для пари 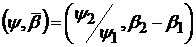
 ряд
ряд
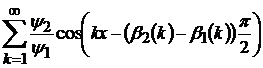
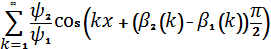 (19)
(19)
є рядом Фур’є деякої сумовної функції 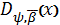
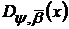 ,
то
,
то

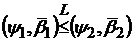 (20)
(20)
Розглянемо, далі, згортку функцій 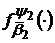 і
і
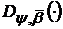


Оскільки 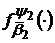 і
і 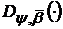
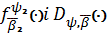 сумовні,
то див., наприклад [6] такою ж буде і їх згортка - функції
сумовні,
то див., наприклад [6] такою ж буде і їх згортка - функції 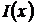
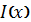 ,
а також у випадку
,
а також у випадку 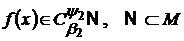
 ,
зокрема
,
зокрема 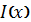
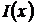 буде
неперервною функцією.
буде
неперервною функцією.
Приведемо приклад реалізації умов теореми 2.
Нехай 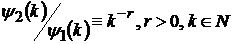
 , а
, а 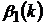 та
та 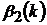 приймають фіксовані значення
приймають фіксовані значення 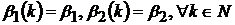
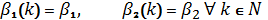 ,
так, що
,
так, що 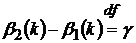
 .
В цьому випадку (див. класи Вейля-Надя) ряд (19) є рядом Фур’є сумовної
функції. Отже в приведеному випадку завжди буде виконуватись співвідношення
(20).
.
В цьому випадку (див. класи Вейля-Надя) ряд (19) є рядом Фур’є сумовної
функції. Отже в приведеному випадку завжди буде виконуватись співвідношення
(20).
Зокрема, при 
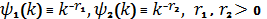 із
теореми 2 випливає, що при виконанні умови
із
теореми 2 випливає, що при виконанні умови 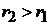
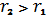 ,
пара
,
пара 
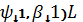 L та
L та
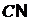 - передує парі
- передує парі 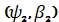
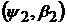 при
довільних значеннях
при
довільних значеннях 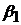 і
і 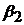
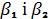 .
Пригадуємо, що як показують приклади функцій
.
Пригадуємо, що як показують приклади функцій 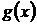 та
та
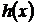 , при
, при 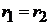
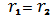 ці
факти в загальному випадку вже місця не мають.
ці
факти в загальному випадку вже місця не мають.
§5. Оцінка для найкращих наближень
деяких лінійних комбінацій аналітичних функцій
Нехай 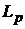 ,
, 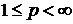 -
простір
-
простір  -періодичних сумовних на
-періодичних сумовних на 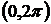 в
в 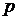
 -му
степені функцій
-му
степені функцій  , в якому норма визначена за допомогою рівності
, в якому норма визначена за допомогою рівності

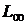 -
простір
-
простір  -періодичних вимірних і суттєво обмежених функцій
-періодичних вимірних і суттєво обмежених функцій  із нормою
із нормою  ;
;
С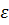 - простір неперервних на всій дійсній осі
- простір неперервних на всій дійсній осі  -періодичних функцій
-періодичних функцій  із
нормою
із
нормою  .
.
Нехай N
 .
Через
.
Через 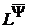 N будемо позначати клас сумовних
N будемо позначати клас сумовних  −періодичних функцій
−періодичних функцій 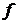 , які допускають зображення у вигляді згортки
, які допускають зображення у вигляді згортки
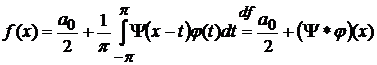 ,
,
 ,(21)
,(21)
де 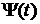 - фіксоване ядро із
- фіксоване ядро із 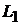
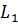 з
рядом Фур’є
з
рядом Фур’є
 ,
,
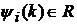 ,
, 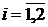 ,
,
 , (22)
, (22)
а 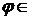 N. При цьому будь-яку функцію
N. При цьому будь-яку функцію , що зображується у вигляді (21) будемо називати
, що зображується у вигляді (21) будемо називати  −інтегралом функції
−інтегралом функції 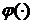
 і
позначати
і
позначати 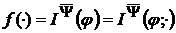 ; функцію
; функцію 
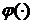 в
інтегральному зображенні (21) домовимось називати
в
інтегральному зображенні (21) домовимось називати  −похідною функції
−похідною функції  і
позначати
і
позначати 
 (див.,
напр., [15]).
(див.,
напр., [15]).
Через 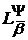 N позначимо клас сумовних
N позначимо клас сумовних  −періодичних функцій
−періодичних функцій  вигляду
вигляду
 ,
(23)
,
(23)
де 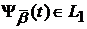 і
і
 ,
,
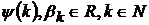 ,(24)
,(24)
а 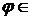 N. При цьому будь-яку функцію
N. При цьому будь-яку функцію 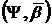 , що зображується у вигляді (23), будемо називати
, що зображується у вигляді (23), будемо називати 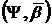
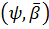 −інтегралом
функції
−інтегралом
функції 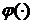 і позначати
і позначати 
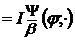 ;
;
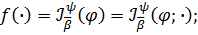 функцію
функцію 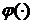 у
зображенні (23) називають
у
зображенні (23) називають 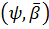
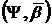 -
похідною функції
-
похідною функції 
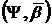 і
позначають
і
позначають 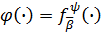
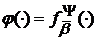 .
У випадку, коли
.
У випадку, коли 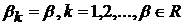 класи
класи 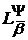 N
позначимо через
N
позначимо через 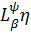
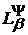 N.
Зрозуміло, що при виконанні умов
N.
Зрозуміло, що при виконанні умов
 ,
,
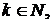 (25)
(25)
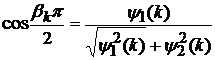 ,
,
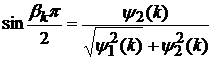 ,
, 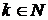 ,(26)
,(26)
класи 
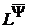 N
і
N
і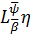
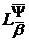 N співпадають (див., напр., [14, с. 33]).
N співпадають (див., напр., [14, с. 33]).
При кожному фіксованому 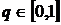
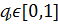 позначимо
через
позначимо
через 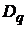
 множину
послідовностей
множину
послідовностей 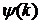 ,
, 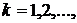 що
задовольняють умову
що
задовольняють умову
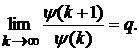 (27)
(27)
На протязі усієї роботи будемо вважати, що коефіцієнти Фур’є  і
і 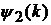 ядра
ядра
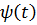
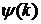 у
формулі (21) такі, що послідовність
у
формулі (21) такі, що послідовність  ,
,
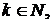 належить множині
належить множині 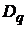 ,
,
 . У цьому випадку функціональні класи
. У цьому випадку функціональні класи 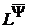 N (як і
N (як і 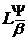 N,
N,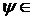
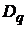 ,
,  )
складаються із
)
складаються із 
 -періодичних
аналітичних на дійсній осі функцій
-періодичних
аналітичних на дійсній осі функцій 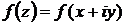 ,
що допускають регулярне продовження в смугу
,
що допускають регулярне продовження в смугу 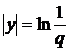
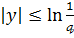 (див.,
напр., [14, с. 35]).
(див.,
напр., [14, с. 35]).
Важливим у подальшому прикладом ядер вигляду (24), коефіцієнти яких
задовольняють умову (27), є ядра
 ,
,
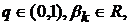
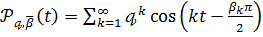 (28)
(28)
які при 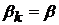
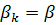 є
відомими ядрами Пуассона і позначаються через
є
відомими ядрами Пуассона і позначаються через 
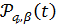 .
Класи
.
Класи 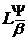 N, що породжуються ядрами (28), позначимо через
N, що породжуються ядрами (28), позначимо через 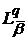 N, а відповідні
N, а відповідні 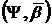 -інтеграли
-інтеграли
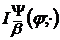
 -
через
-
через  .
.
Якщо N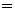
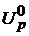 ,
,
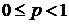 , де
, де 
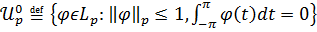 ,
класи
,
класи 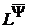 N
N і
і 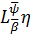
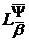 N
домовимося позначати, відповідно, через
N
домовимося позначати, відповідно, через 
 і
і
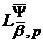
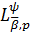 .
.
Нехай 
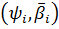 ,
,
 - пари послідовностей дійсних чисел, L- передуючих парі
- пари послідовностей дійсних чисел, L- передуючих парі  :
: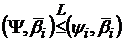
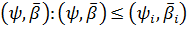 (див., напр., [8, с. 5]), тобто має місце включення
(див., напр., [8, с. 5]), тобто має місце включення 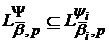
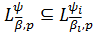 .
.
Нехай далі числа 
 підпорядковані
умові
підпорядковані
умові 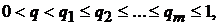
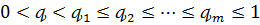 а
а
 . Позначимо через
. Позначимо через 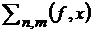
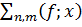 наступну
суму
наступну
суму
 ,
,

де 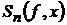
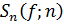 -
частинна сума степеня
-
частинна сума степеня 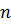
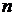 ряду
Фур’є функції
ряду
Фур’є функції 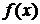
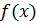 ,
а
,
а  ,
, 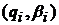
 -
похідні функції
-
похідні функції 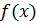
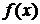 в
сенсі Степанця, які означаються наступним чином. Якщо
в
сенсі Степанця, які означаються наступним чином. Якщо  є рядом Фур’є функції
є рядом Фур’є функції 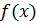
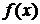 ,
то
,
то
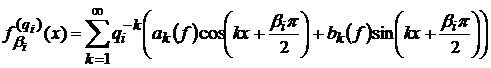 .
.
Нехай 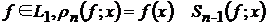
 .
.
В роботі досліджується відхилення лінійної комбінації інтегралів
Пуассона та типу Пуассона від їх сум Фур’є. А саме величини

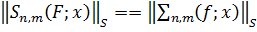 ,
де
,
де
 ,
,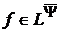 N, (29)
N, (29)
- деякі фіксовані підмножини з 
 ,
,
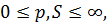 а також величини
а також величини
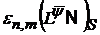
 ,(30)
,(30)
 ,
,
 , (30′)
, (30′)
Будемо розглядати також відповідні величини
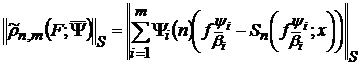 ,
(31)
,
(31)

з метою отримання для них асимптотичних рівностей, коли 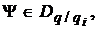
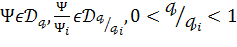
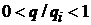 і
і 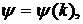
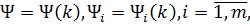

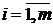 визначаються рівністю (25).
визначаються рівністю (25).
Зауважимо, що у випадку подання функції 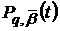
 у
вигляді (28) лінійна комбінація
у
вигляді (28) лінійна комбінація 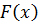
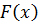 в
(29) (див., напр., [14, с. 36]), подається наступним чином
в
(29) (див., напр., [14, с. 36]), подається наступним чином
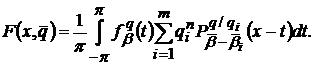 (32)
(32)
Якщо ж функція 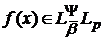
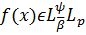 при
при
 що задовольняє умові (27),
що задовольняє умові (27), 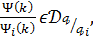 відповідна лінійна комбінація
відповідна лінійна комбінація 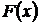
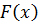 запишеться
запишеться

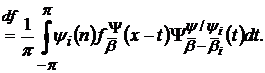
 (32′)
(32′)
Основна ідея роботи відображена в приведеній лемі, суть якої в тому, що
величина 
 для
лінійної комбінації вигляду (32′) при
для
лінійної комбінації вигляду (32′) при 
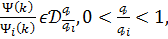 при
при
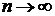
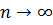 поводиться
приблизно так само, як і лінійна комбінація вигляду (32). Це дозволяє, зокрема,
зводити задачу отримання асимптотичних рівностей величин
поводиться
приблизно так само, як і лінійна комбінація вигляду (32). Це дозволяє, зокрема,
зводити задачу отримання асимптотичних рівностей величин 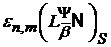 до аналогічних задач для величин
до аналогічних задач для величин 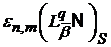 .
.
В деяких важливих випадках для величин 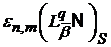 асимптотичні рівності відомі. В таких випадках
з’являється можливість виписати асимптотичні рівності і для величин
асимптотичні рівності відомі. В таких випадках
з’являється можливість виписати асимптотичні рівності і для величин 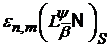 . Зокрема, таким шляхом, відштовхуючись від відомих
результатів С.М. Нікольського [10], С.Б. Стєчкіна [11], О.І. Степанця, А.С.
Сердюка [12] вдається отримати асимптотичні рівності для величин
. Зокрема, таким шляхом, відштовхуючись від відомих
результатів С.М. Нікольського [10], С.Б. Стєчкіна [11], О.І. Степанця, А.С.
Сердюка [12] вдається отримати асимптотичні рівності для величин 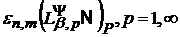
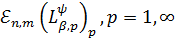 ,
при довільних послідовностях
,
при довільних послідовностях 
 .
Причому є випадки, які раніше не були досліджені. Методи досліджень використані
в цій роботі запозичені із робіт [11], [12].
.
Причому є випадки, які раніше не були досліджені. Методи досліджень використані
в цій роботі запозичені із робіт [11], [12].
Наступна теорема встановлює зв’язок між нормами у просторі 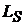 залишків ряду Фур’є
залишків ряду Фур’є 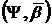
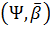 -інтегралів
-інтегралів
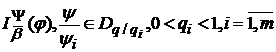
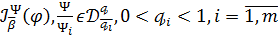 і
залишків ряду Фур’є інтегралів
і
залишків ряду Фур’є інтегралів  .
.
Теорема 3. Нехай 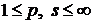
 і
і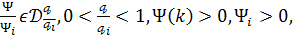
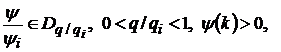
 ,
, 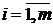 .
.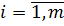 Тоді для довільної функції
Тоді для довільної функції 
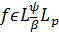 при
при

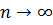 справедлива
рівність
справедлива
рівність
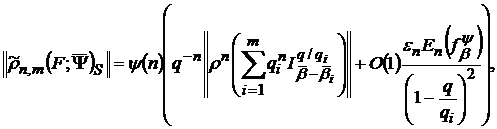 (33)
(33)
в якій  ,
, 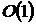 -
величина рівномірно обмежена відносно параметрів
-
величина рівномірно обмежена відносно параметрів 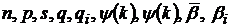
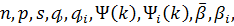 а
а
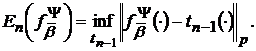
Доведення теореми 3 базується на наступному твердженні, що відтворює
результат отриманий в роботі [12, с. 379].
Лема. Нехай 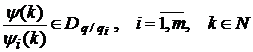
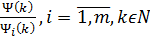 -
довільні числові послідовності із
-
довільні числові послідовності із 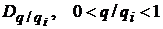
 .
.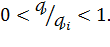 Тоді для будь-якої послідовності дійсних чисел
Тоді для будь-якої послідовності дійсних чисел 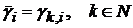
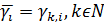 виконується
рівність
виконується
рівність
 (34)
(34)
при цьому для величин 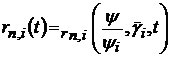
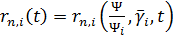 ,
починаючи з деякого номера
,
починаючи з деякого номера 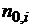
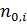 ,
справедлива оцінка
,
справедлива оцінка
 (35)
(35)
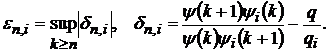 (35′)
(35′)
Доведення. Маємо при довільному 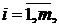
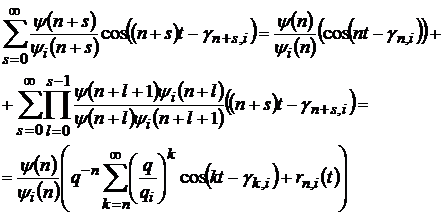
де
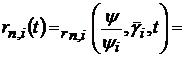
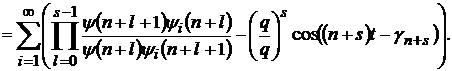 (36)
(36)
Доведемо нерівність (35). Внаслідок (36) маємо
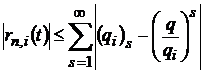 ,(37)
,(37)
де
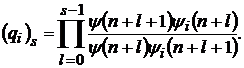 (38)
(38)
У випадку, коли 
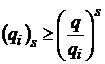 ,
,
 .
.
Якщо ж 
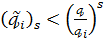 ,
то в силу опуклості функції
,
то в силу опуклості функції 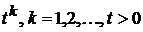
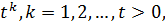

 (39)
(39)
Таким чином, завжди
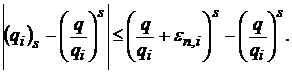 (40)
(40)
Із співвідношень (27) та (35′)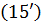 можна зробити висновок, що послідовність
можна зробити висновок, що послідовність 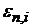
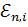 є
монотонно спадною, а тому розпочинаючи з деякого номера
є
монотонно спадною, а тому розпочинаючи з деякого номера 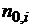 ,
, 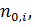
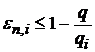 .
.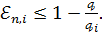 Звідки, враховуючи (37) і (40), при
Звідки, враховуючи (37) і (40), при 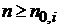
 знаходимо
знаходимо
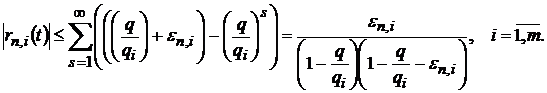
Лема доведена.
Доведення теореми 3. Нехай 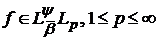 .
. Тоді в силу (32′)
Тоді в силу (32′)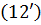 та (27) майже всюди має місце
та (27) майже всюди має місце
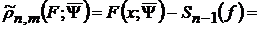
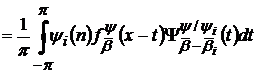 ,(41)
,(41)
де 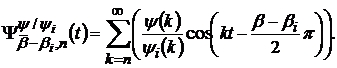
Позначивши 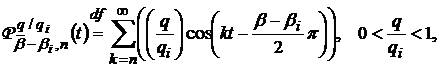 та використавши (41) і (34) приходимо до висновку, що
майже всюди
та використавши (41) і (34) приходимо до висновку, що
майже всюди
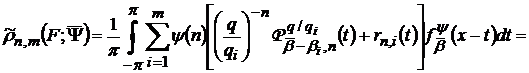

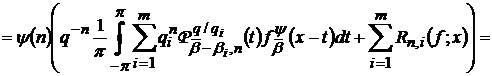

 ,(42)
,(42)
де 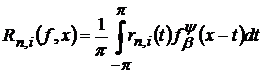 функції
функції 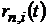
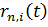 задається
співвідношенням (36) при
задається
співвідношенням (36) при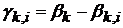
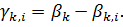
Покажемо, що для довільного тригонометричного многочлена 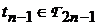
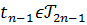 простору
тригонометричних многочленів степеня не вище
простору
тригонометричних многочленів степеня не вище 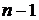
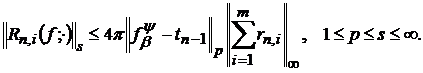 (43)
(43)
Використавши нерівність Хаусдрорфа - Юнга для згорток [13, с. 67]
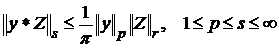 ,
,
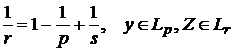 ,
,
при 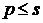
 отримаємо
отримаємо
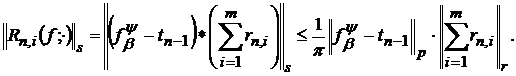 (44)
(44)
Оскільки в даному випадку 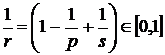
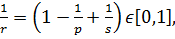 то
то
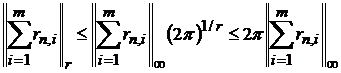 .(45)
.(45)
Якщо порівняти оцінки (44) і (45), маємо
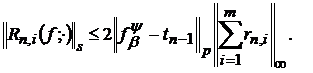 (46)
(46)
Нехай тепер 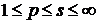 . В силу нерівності Гельдера
. В силу нерівності Гельдера
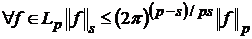 ,
,
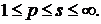
Тому
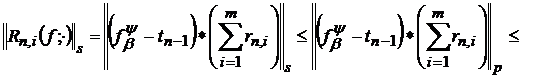
 (47)
(47)
і формула (43) є наслідком оцінок (46) та (47).
Вибравши в ролі  многочлен
многочлен 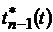
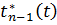 найкращого
наближення в просторі
найкращого
наближення в просторі 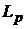 функції
функції 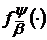 ,
а також використовуючи нерівність (35), отримаємо наступну оцінку:
,
а також використовуючи нерівність (35), отримаємо наступну оцінку:
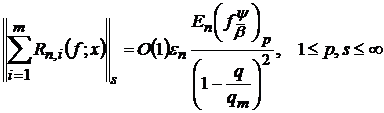 ,
(48)
,
(48)
де 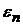 та
та 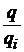 -
числа, на яких досягаються максимальні значення послідовностей в (35′).
Об’єднуючи формули (42) та (48), отримаємо рівність (33).
-
числа, на яких досягаються максимальні значення послідовностей в (35′).
Об’єднуючи формули (42) та (48), отримаємо рівність (33).
Якщо 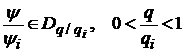
 то
в силу ознаки Даламбера збіжності числових додатних рядів ряд
то
в силу ознаки Даламбера збіжності числових додатних рядів ряд  збігається абсолютно та рівномірно. Отже, якщо
збігається абсолютно та рівномірно. Отже, якщо 
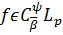 ,
, то рівність (32′), а разом, і рівності (41) та
(42) мають місце в кожній точці
то рівність (32′), а разом, і рівності (41) та
(42) мають місце в кожній точці 
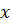 .
А тому із приведених міркувань випливає наступне твердження.
.
А тому із приведених міркувань випливає наступне твердження.
Теорема 3′. Нехай 
 і
і
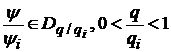 ,
, 
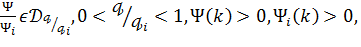

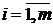
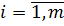 .
Тоді для довільної функції
.
Тоді для довільної функції 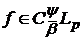
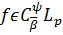 при
при
 справедлива рівність
справедлива рівність
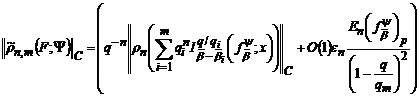 ,(33′)
,(33′)
в якій  ,
, 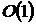 -
величина рівномірно обмежена відносно
-
величина рівномірно обмежена відносно 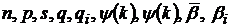 .
.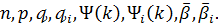
Розглядаючи верхні межі обох частин співвідношення (33) на класах 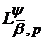
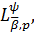 а
співвідношення
а
співвідношення 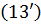 (33′) - на класах
(33′) - на класах 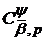
 та
врахувавши, що
та
врахувавши, що
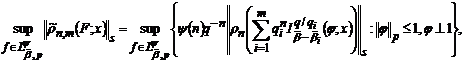
отримаємо наступне твердження.
Теорема 4. Нехай 
 і
і
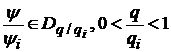 ,
, 

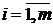 .
.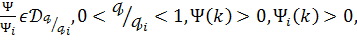 Тоді при
Тоді при 
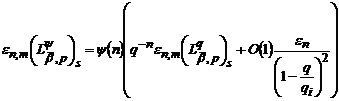 ,(49)
,(49)
 (50)
(50)
Наступні міркування багато в чому запозичені із роботи [12, с. 383].
Відповідно до означення множин 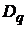 (див.
(27)), з того, що
(див.
(27)), з того, що 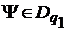
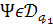 ,
а
,
а 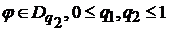
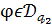 ,
випливає, що
,
випливає, що 
 при
при
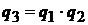
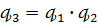 (зокрема,
якщо
(зокрема,
якщо 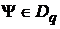
 ,
а
,
а 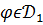
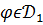 ,
то
,
то 
 .
Звідси маємо, що множині
.
Звідси маємо, що множині 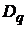
 ,
,
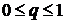 належать довільні послідовності вигляду
належать довільні послідовності вигляду 
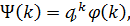 де
де
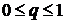 і
і 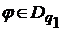
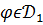 .
З іншого боку, якщо
.
З іншого боку, якщо 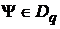 ,
, 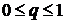 ,
то подаючи
,
то подаючи  у вигляді
у вигляді 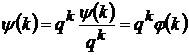
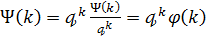 ,
де
,
де  ,
,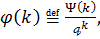 переконуємося, що
переконуємося, що 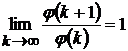 .
.
Внаслідок сказаного справедливе твердження.
Твердження 1. Для того, щоб послідовність 
 належала
множині
належала
множині 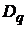
 ,
,
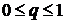
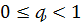 ,
необхідно і досить, щоб мало місце подання
,
необхідно і досить, щоб мало місце подання 
 ,
в якому
,
в якому 
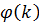 -
деяка послідовність із
-
деяка послідовність із 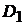
 .
.
Зокрема, до 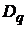
 ,
,
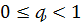
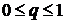 ,
належать послідовності
,
належать послідовності 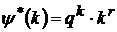 ,
,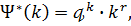
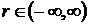
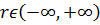 ;
;
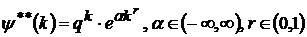
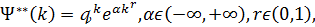 та
ін.
та
ін.
У випадку, коли 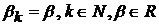
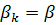 ,
,
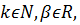 як було зауважено ядра
як було зауважено ядра  є
ядрами Пуассона
є
ядрами Пуассона
 .(51)
.(51)
Класи 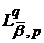
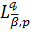 в
цьому випадку позначимо через
в
цьому випадку позначимо через 
 .
.
В 1946 р. С.М. Нікольський [10, с. 221-223] знайшов асимптотичні
рівності для величин 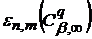
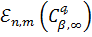 і
і

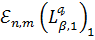 у
випадку наближення одного із класів, тобто якщо
у
випадку наближення одного із класів, тобто якщо 
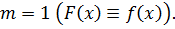
Наступне твердження відтворює результат С.М. Нікольського із уточненим
С. Б. Стєчкіним [11, с. 139] залишковим членом.
Теорема А. Нехай 
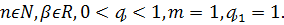 Тоді
при
Тоді
при 
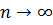 мають
місце асимптотичні рівності
мають
місце асимптотичні рівності
 (52)
(52)
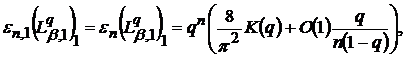 (52′)
(52′)
в яких 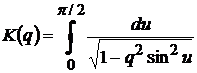 - повний еліптичний інтеграл першого роду, а
- повний еліптичний інтеграл першого роду, а 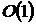 - величина, рівномірно обмежена відносно параметрів
- величина, рівномірно обмежена відносно параметрів 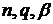 .
.
Із теореми 2 на випадок 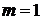 теореми
А, отримуємо наступне твердження
теореми
А, отримуємо наступне твердження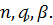
Теорема 5. Нехай класи 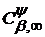
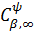 і
і
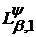
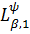 породжені
ядром
породжені
ядром
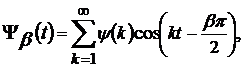 (53)
(53)
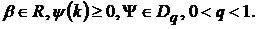
Тоді при 
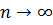 мають
місце асимптотичні рівності
мають
місце асимптотичні рівності
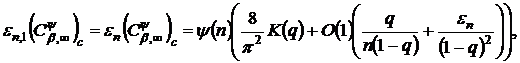 (54)
(54)
 (54′)
(54′)
в яких
 ,
,
а 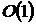 - величина рівномірно обмежена відносно параметрів
- величина рівномірно обмежена відносно параметрів 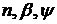 .
.
Зауваження 1. Асимптотичні рівності (54) і (54′) залишаються справедливими,
якщо в теоремі 3 умову 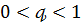
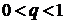 замінити
умовою
замінити
умовою 
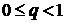 .
.
Справді, формально поклавши 
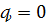 та
побачивши, що
та
побачивши, що  , оцінки (54) та (54′) запишемо у вигляді
, оцінки (54) та (54′) запишемо у вигляді
 (55)
(55)
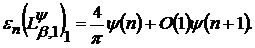 (55′)
(55′)
Істинність асимптотичних рівностей (55) і (55′) для
для 
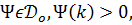 випливає,
наприклад, із [15, с. 1103-1104].
випливає,
наприклад, із [15, с. 1103-1104].
Умови теореми 5 задовольняють ядра Пуассона бігармонічного рівняння
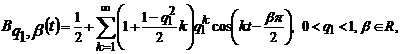 (56)
(56)
а також ядра Неймана
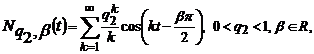 (57)
(57)
Легко перевірити, що для коефіцієнтів 
 ядер
ядер
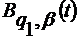 і
і 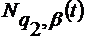
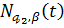
 (58)
(58)
Таким чином, із теореми 5 та співвідношень (58) отримаємо таке
твердження.
Наслідок 1. Нехай класи 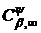
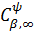 і
і
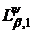
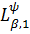 породжені
ядром
породжені
ядром 
 вигляду
(56),
вигляду
(56), 
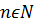 .
Тоді при
.
Тоді при 
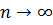 мають
місце асимптотичні рівності
мають
місце асимптотичні рівності
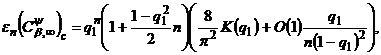
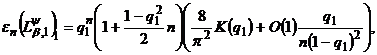
в яких величина 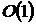 рівномірно обмежена відносно
рівномірно обмежена відносно  .
.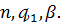
Наслідок 2. Нехай класи 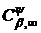
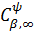 і
і
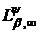
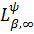 породжені
ядром
породжені
ядром 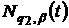
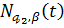 вигляду
(57),
вигляду
(57), 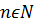
 .
Тоді при
.
Тоді при 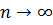
 мають
місце асимптотичні рівності
мають
місце асимптотичні рівності

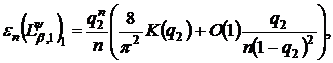
в яких величина 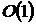 рівномірно обмежена відносно
рівномірно обмежена відносно 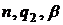 .
.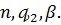
Якщо вважати, далі, що 
 ,
то умовам теореми 3 задовольняють ядра
,
то умовам теореми 3 задовольняють ядра

а для коефіцієнтів 
 такого
ядра
такого
ядра 
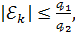 і
має місце
і
має місце
Наслідок 3. Нехай класи 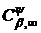
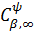 і
і
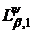
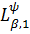 породжені
ядром
породжені
ядром
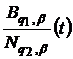
 .(59)
.(59)
Тоді при 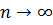
 мають
місце асимптотичні рівності
мають
місце асимптотичні рівності
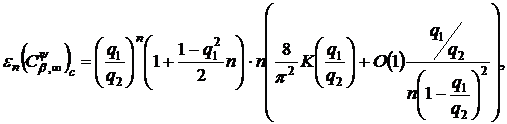
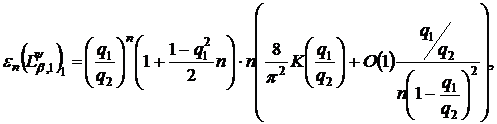
в яких величина 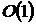 - рівномірно обмежена відносно
- рівномірно обмежена відносно 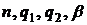 .
.
Аналізуючи доведення теореми A, що міститься в [11, с.
139-142], можна переконатися, що методи використані в ньому дають можливість
отримати асимптотичні оцінки величин 
 і
і
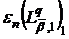
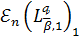 для
класів
для
класів 
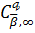 і
і
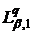
 ,
породжених ядрами
,
породжених ядрами 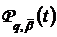
 вигляду
(28), у яких
вигляду
(28), у яких 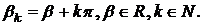
 При
цьому вигляд отриманих оцінок у порівнянні з випадком
При
цьому вигляд отриманих оцінок у порівнянні з випадком 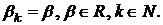
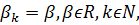 не
зміниться. А саме, справедлива наступна теорема.
не
зміниться. А саме, справедлива наступна теорема.
Теорема Б. Нехай 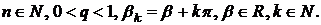
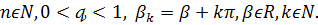 Тоді
при
Тоді
при 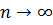
 мають
місце асимптотичні рівності
мають
місце асимптотичні рівності
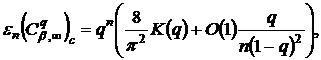 (60)
(60)
 (60′)
(60′)
в яких 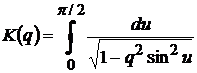 ,а
,а 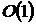 -
величина, рівномірно обмежена відносно параметрів
-
величина, рівномірно обмежена відносно параметрів 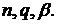
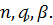
Співставивши теореми 4 та Б у випадку 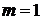
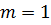 можна
прийти до наступного аналогу теореми 5.
можна
прийти до наступного аналогу теореми 5.
Теорема 5′. Нехай класи 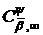
 і
і
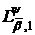
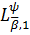 породжені
ядром
породжені
ядром
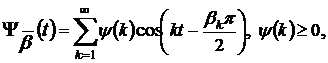 у
якого
у
якого 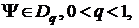
 .
.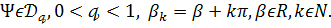 Тоді при
Тоді при 
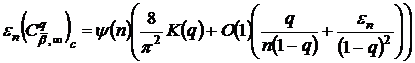 ,(61)
,(61)
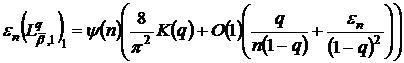
де 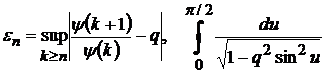
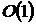 -
величини, рівномірно обмежені відносно параметрів
-
величини, рівномірно обмежені відносно параметрів 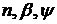 .
.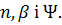
Розглянемо тепер наближення лінійної комбінації аналітичних функцій що
подаються у вигляді інтегралів Пуассона, тобто у вигляді рівності (32).
Має місце
Теорема 6. Нехай  Тоді при
Тоді при 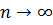
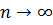 для
величини в (30) при
для
величини в (30) при 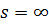
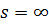 має
місце співвідношення
має
місце співвідношення
 (62)
(62)
де 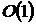 - величина, рівномірно обмежена відносно
- величина, рівномірно обмежена відносно 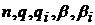 ,
,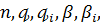 а
а 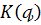
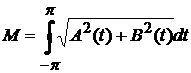 ,
,
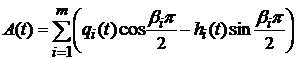 ,
,
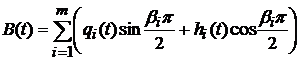 ,
,
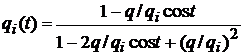 ,
,

В даній частині роботи досліджуватимемо найкраще наближення
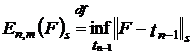 функції
функції  в метриці простору
в метриці простору 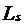 тригонометричними
многочленами степеня
тригонометричними
многочленами степеня 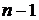 , де
, де  подається
у вигляді (32) та характеризує лінійну комбінацію інтегралів Пуассона. При
цьому сама ж материнська (початкова) функція
подається
у вигляді (32) та характеризує лінійну комбінацію інтегралів Пуассона. При
цьому сама ж материнська (початкова) функція 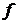 береться
з простору
береться
з простору  . Цікавитимуть нас також і величини
. Цікавитимуть нас також і величини
 та
та
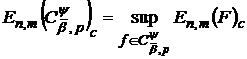 ,
,
з метою отримання для них асимптотичних рівностей.
Наступна теорема встановлює зв’язок між найкращими наближеннями в
метриці простору 
 інтегралів
інтегралів  при
при
 і найкращими наближеннями інтегралів
і найкращими наближеннями інтегралів  при
при 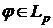 .
.
Теорема 7. Нехай  ,
, 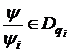 ,
,
 ,
, 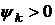 ,
,
 ,
, 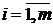 .
Тоді для довільної
.
Тоді для довільної 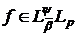 при
при  має
місце рівність
має
місце рівність  ,(63)
,(63)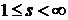 .
.
Якщо ж  , то
, то
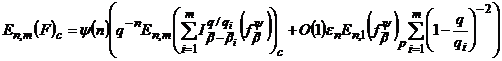 ,(63′)
,(63′)
де 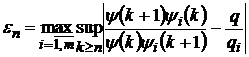 ,
, 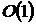 ― величина, рівномірно обмежена відносно
― величина, рівномірно обмежена відносно 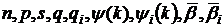 .
.
Доведення. Доведемо спочатку рівність (63). В силу співвідношень
двоїстості: [6, с. 42]
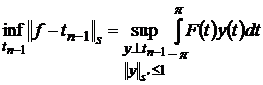 ,
,  ,
, 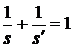 .(64)
.(64)
Тому, враховуючи (42) і (64), отримаємо

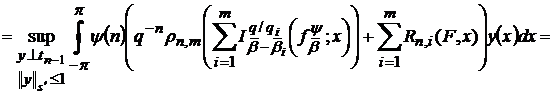
 (65)
(65)
де 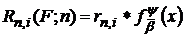 , а функції
, а функції  ― функція, що визначається формулою (61) при
― функція, що визначається формулою (61) при 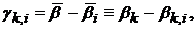
 .
.
Використовуючи нерівність Гельдера, оцінку (48), для довільного 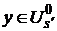 знаходимо
знаходимо
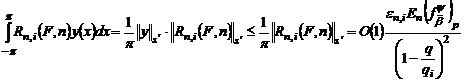 ,
,
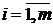 .
(66)
.
(66)
Таким чином, в силу (65) та (66) маємо
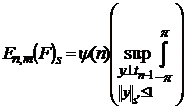
і для доведення рівності (63) залишається зауважити, що в силу (37)
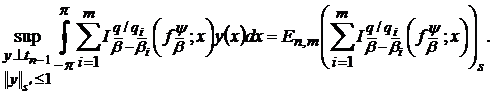 (67)
(67)
Доведення рівності (63′) аналогічне доведенню рівності (63). В
цьому випадку співвідношення двоїстості має вигляд [6, с. 41]
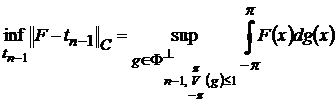 ,(68)
,(68)
де
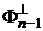 ― множина функцій
― множина функцій 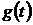 обженої варіації на
обженої варіації на 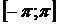 ,
які задовольняють умову
,
які задовольняють умову
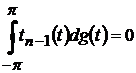
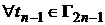 .
.
Враховуючи співвідношення (42) і (61), маємо

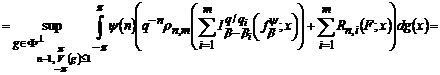
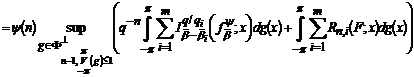 .(69)
.(69)
Але із урахуванням (73)
 ,
, , (70)
, (70)
тому із (69) і (70) випливає
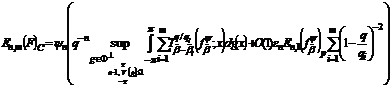 .(71)
.(71)
Застосувавши співвідношення (17) до першого доданку правої частини
рівності (35), переконаємося у справедливості (63′). Теорема доведена.
Перейшовши до верхніх меж обох частин співвідношень (63) і (63′)
на класах  і
і 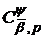 та
враховуючи, що
та
враховуючи, що
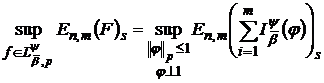 ,
,
приходимо до наступного твердження.
Теорема 8. Нехай  і
і  ,
,
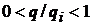 ,
, 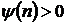 ,
,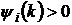 ,
, 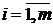 .
Тоді при
.
Тоді при 
 ,
,
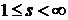 ,(72)
,(72)
 ,(72′)
,(72′)
де  ,
, 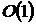 ― величина рівномірно обмежена відносно
― величина рівномірно обмежена відносно 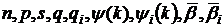 .
.
Величини 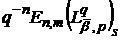 ,
,  ,
і
,
і 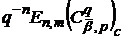 при
при  є
обмеженими зверху і знизу деякими додатними константами, залежними, можливо
лише від
є
обмеженими зверху і знизу деякими додатними константами, залежними, можливо
лише від  ,
, 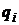 ,
,
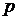 і
і  .
Оцінка зверху величини
.
Оцінка зверху величини 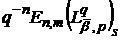 випливає з того, що
випливає з того, що 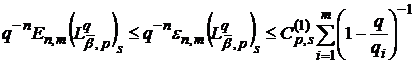 (див. (50)). Щоб отримати потрібну оцінку знизу,
досить побачити, що функція
(див. (50)). Щоб отримати потрібну оцінку знизу,
досить побачити, що функція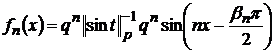 належить
належить  ,
,  ,
і для неї найкраще наближення в просторі
,
і для неї найкраще наближення в просторі 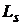 ,
,
 , серед многочленів
, серед многочленів  буде
забезпечувати многочлен, тотожно рівний нулю (див., наприклад, означення 3.3.3
і 3.3.4 із [6, с. 56]).
буде
забезпечувати многочлен, тотожно рівний нулю (див., наприклад, означення 3.3.3
і 3.3.4 із [6, с. 56]).
Таким чином
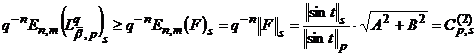 ,
,
де 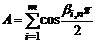 ,
,  ,
,
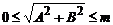 ,
,
отже
 ,(73′)
,(73′)
 ,
,
 ,
, 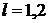 .
.
Здійснивши такі ж міркування, отримаємо
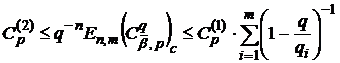 ,
,  ,
, 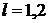 .
.
Оскільки
послідовність 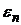 прямує до нуля при
прямує до нуля при  ,
то враховуючи (72) і (73′) у випадках, коли відомі асимптотичні рівності
для величин
,
то враховуючи (72) і (73′) у випадках, коли відомі асимптотичні рівності
для величин 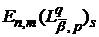 і
і 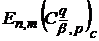 співвідношення
(72) і (72′) дають можливість записати асимптотичну рівність для величин
співвідношення
(72) і (72′) дають можливість записати асимптотичну рівність для величин 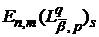
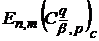 .
.
При  Крейном М. Г. в [16]
та при
Крейном М. Г. в [16]
та при 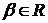 Шевалдіним В. Т
в [17] знайдені точні значення величин
Шевалдіним В. Т
в [17] знайдені точні значення величин  і
і 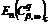 ,
, 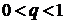 ,
,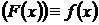 .
.
Теорема
В. Нехай 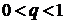 ,
, 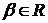 ,
, 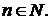 Тоді
Тоді
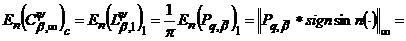
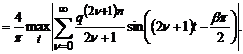 (74)
(74)
Із рівностей (74) випливає  ,
,
 .(75)
.(75)
Співвідношення
(75), а також теорема 8 дають можливість сформулювати наступне твердження.
Теорема
9. Нехай 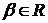 ,
,  ,
, 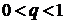 ,
, 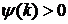 . Тоді
при
. Тоді
при  мають місце асимптотичні рівності
мають місце асимптотичні рівності
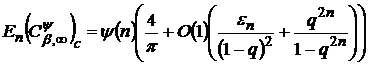 ,(76)
,(76)
 ,(77)
,(77)
де
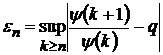 ,
,  ― рівномірно обмежені величини відносно
― рівномірно обмежені величини відносно 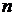 ,
,
 ,
, 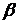 ,
та
,
та  .
.
Аналізуючи доведення теореми В, що міститься в [17, с. 128 - 129], можна переконатись, що рівності (75) будуть справедливими також, якщо замість 
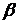 ,
що фігурує в означенні класів
,
що фігурує в означенні класів  та
та
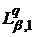 і ядра
і ядра  ,
розглядати послідовність
,
розглядати послідовність 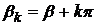 ,
, 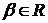 ,
,
 , тобто справедлива теорема.
, тобто справедлива теорема.
Теорема Г. Нехай 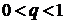 ,
, 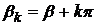 ,
,
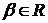 ,
,  .
Тоді
.
Тоді 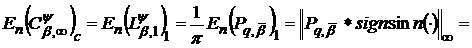
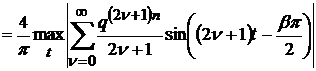 .(78)
.(78)
Співставляючи теореми 8 і Г, отримуємо наступне твердження.
Теорема 9′. Нехай 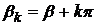 ,
,
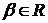 ,
,  ,
,
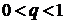 ,
, 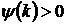 ,
,
 . Тоді при
. Тоді при  мають
місце асимптотичні рівності
мають
місце асимптотичні рівності
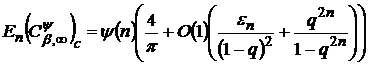 ,(79)
,(79)
 ,(79′)
,(79′)
де
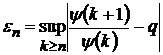 ,
,  ― рівномірно обмежені величини відносно
― рівномірно обмежені величини відносно 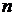 ,
,
 ,
, 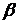 ,
та
,
та  .
.
Зауваження 2. Теореми 9 та 9′ доведені в роботі [12].
Висновок
В дипломній роботі я досліджувала верхні межі найкращих
наближень деяких лінійних інтегралів Пуассона та типу Пуассона в метриках
просторів С і L1 на класах згорток періодичних функцій, що можуть бути
регулярно продовжені у фіксовану смугу комплексної площини. А саме величини ―
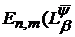 N)S =
N)S = .
.
Основні результати містяться в
Теорема 7. Нехай  ,
,  ,
,
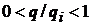 ,
, 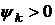 ,
,
 ,
, 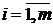 .
Тоді для довільної
.
Тоді для довільної 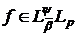 при
при  має
місце рівність
має
місце рівність
математична функція асимптотичний апроксимація
 ,
,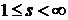 .
.
Якщо ж  , то
, то
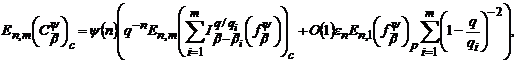 де
де
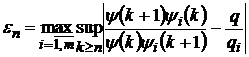 ,
,
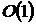 ― величина, рівномірно обмежена відносно
― величина, рівномірно обмежена відносно 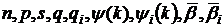 .
.
Теорема 8. Нехай  і
і  ,
,
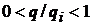 ,
, 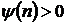 ,
,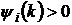 ,
, 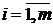 .
Тоді при
.
Тоді при 
 ,
,
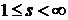 ,
,
 ,
,
де  ,
, 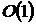 ― величина рівномірно обмежена відносно
― величина рівномірно обмежена відносно 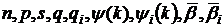
В дипломній роботі встановлені також асимптотичні рівності відхилень
найкращих наближень лінійних комбінацій і в деяких інших випадках параметрів,
що входять в означення відповідних класів аналітичних функцій.
Список
використаних джерел
1. Колмогоров А. МZur Crrossenordnuny des Restliedes
Fouriershen Reihen differenzierbaren Funktionen //Ann. Muth. − 1935. −
36. − 3.521-526.
2. Пинкевич В. Т. О порядке остаточного члена ряда Фурье
функций, дифференцируемых в смысле Вейля //Изд. АН СССР, сер. математика, 1940.−Т.
4−№5, с. 121-528
. Степанец А. И. Одновременное приближение периодических функций и их
производных суммами Фурье //Докл. АН СССР.−1980. − 254, №3. −
с. 543-544.
. Никольський С. М. Ряд Фурье функцій с данным
модулем непрерывности //Докл. Ан СССР. − 1946. − 52, №3.−с. 191-193.
5. Степанец А. И. Равномерные приближения
тригонометрическими полиномами. - К.: Наук. Думка, 1981, - 340 с.
6. Корнейчук Н. П. Экстремальные задачи теории приближения.
- М.: Наука, 1976. - 320 с.
. Степанец А. И. Классификация периодических
функций и приближение их елементов суммами Фурье. - Киев, 1983. - 57 с. (ПрепрУ/АНУССР. Институт математики,
83. 10).
8. Сорич Н.Н. Одновременное приближение
периодических функцій и их производных суммами Фурье. - Киев, 1985. - с. 22-63.
- (Препр. //АН УССР. Институт математики, 85.7).
9. А. Зигмунд. Тригонометрические ряды, т. 1. гл.1.
10. Никольский С.М. Приближение функций тригонометрическими
полиномами в среднем //Изв. АН СССР. сер. мат. - 1946. - 10, №3. - с. 207-256.
11. Стечкин С. Б. Оценка остатка ряда Фурье для
дифференцируемых функций // Тр. мат. ин-та АН СССР. - 1980. - 145. - с.
126-151.
12. Степанец А. И., Сердюк А. С. Приближение суммами Фурье
и наилучшие приближения на классах аналитических функций //Укр. мат. журн. -
2000. - 52, №3 - с. 375-395.
13. Зигмунд А. Тригонометрические ряды: В 2-х т. - М.:
Мир, 1967. - т.1. - 615 с.
14. Степанец А. И. Классификация и приближение периодических
функций. - Киев: Наук.
думка, 1987. - 268 с.
15. Степанец А. И.
Скорость сходимости рядов Фурье на классах 
 -интегралов
//Укр. мат. журн. - 1997. - 49,
№8. - с. 1069-1113.
-интегралов
//Укр. мат. журн. - 1997. - 49,
№8. - с. 1069-1113.
16. Крейн М. Г. К теории
наилучшего приближения периодических функций //Докл. АН СССР. - 1938. - 18,
№4-5. - с. 245-249.
17. Шевалдин В. Т.
Поперечники классов сверток с ядром Пуассона //Мат. заметки. - 1992. - 51, №6.
- с. 126-136.