Оптимизация транспортных перевозок
Введение
В последние годы все большее
значение приобретает математический подход к задачам планирования.
С помощью методов прикладной
математики (в частности линейного программирования) решаются такие проблемы,
как оптимизация транспортных перевозок, задача о наилучшем использовании сырья,
наилучшем плане работы вычислительного комплекса, и многие другие задачи.
Решение этих задач позволит значительно снизить экономические затраты на
реализацию и эксплуатацию соответствующих проектов. Таким образом, задачи
прикладной математики имеют самое обширное применение в жизни.
В данной курсовой работе необходимо
решить ряд вышеописанных задач, используя методы линейного программирования и
безусловной оптимизации.
1.
Линейное программирование
1.1 Построение математической
модели ЗЛП
График по варианту задачи линейного
программирования:
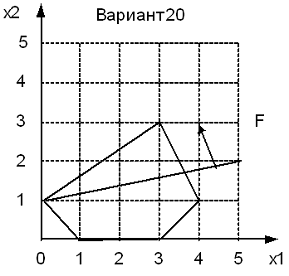
Получение уравнения
целевой функции.
Для наглядности обозначим вершины
буквами:
A (1,0); B (0,1); C (3,3); D (4,1); E (3,0); F (1,0); H (5,2)
Выбираем две точки прямой (0,2)
(5,4) и по уравнению прямой находим уравнение целевой функции:
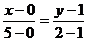
x1=5x2
- 5; x1 - 5x2 + 5=0;
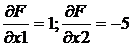
Поскольку направление
справочной стрелки и градиента не совпадают, то целевая функция имеет вид:
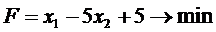
Получение системы
линейных ограничений
Найдем уравнения прямых
по формуле:

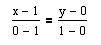
AB:
x1
+ x2 ≥ 1

BC:
x1
- 3x2 ≥
-3
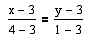
CD:
x1
- x2 ≥
-9
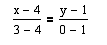
DE:
x1
+x2 ≥ -3
 :1
≥ 0
:1
≥ 0
Составим математическую
модель ЗЛП:
F
= x1 - 5x2 +5 → min1 + x2 ≥
1
x1
- 3x2 ≥ -3
-2x1 - x2 ≥
-9
x1
+x2 ≥ -3
x1,
x2 ≥ 0
.2 Получение решения ЗЛП
графическим методом
Как видно из графика,
оптимальная точка области решений, при которой целевая функция стремится к
минимуму - точка C (3,3). Значение целевой
функции в этой точке: F
= -7.
1.3 Решение ЗЛП
алгебраическим методом
Имеем математическую
модель ЗЛП:
F
= x1 - 5x2 +5
→ min
x1
+ x2 ≥
1
x1
- 3x2 ≥
-3
x1
- x2 ≥
-9
x1
+ x2 ≥
-3
x1,
x2 ≥ 0
Вводим дополнительные
переменные и переходим к каноническому равенству:
F
= x1 - 5x2 +5 → min
x1 + x2
- x3 = 1 x3 = -1 + x1 + x2
2x1 - 3x2
- x4 = -3 x4 = 3 + 2x1 - 3x2
-2x1 - x2
- x5 = -9 ↔ x5 = 9 - 2x1 - x2
-x1 + x2
- x6 = -3 x6 = 3 - x1 + x2
xj ≥ 0,
j = 1,6
Базисными являются x3, x4, x5, x6; свободными - x1, x2.
Решением будет служить < 0, 0,
-1, 3, 9, 3 >, являющееся недопустимым. Выведем x3 из базисных в свободные переменные, а x1 переведём в базисные, чтобы избавиться от недопустимости в
значениях переменных. Тогда система уравнений примет следующий вид:
x1 = 1 - x2 + x3
x4 = 5 - 5x2 + 2x3
x5 = 7 + x2
- 2x36 = 2 + 2x2 + x3= 6 - 6x2 +
x3 → min
Полученное решение < 0, 9, 8, 24,
0, 12 > может быть выбрано в качестве опорного.
Переведем в базис переменную x2, а в свободные - x4:
x2 = 1 - 1/5x4 + 2/5x3
x1 = 0 + 1/5x4 - 8/5x3
x5 = 8 - 1/5x4 - 1/5x3
x6 = 4 - 2/5x4 - 7/5x3
F = 0 + 6/5x4 - 7/5x3
Переводим в базис переменную x3, а в свободные - x5:
x3 = 5 - 11/8x4 - 5/8x5
x1 = 3 - 1/8x4 - 3/5x5
x2 = 3 - 1/4x4 - 1/4x5
x6 = 3 - 3/8x4 + 1/8x5
F = -7 + 7/5x4 + 7/8x5
Решение < 3, 3, 5, 0, 0, 3>, F = -7 является допустимым и оптимальным (так как целевую функцию уже
нельзя улучшить). Так как результат совпал с результатом, полученным при
решении графическим методом, делаем вывод, что решение верно.
1.4 Решение ЗЛП методом
симплекс-таблицы
Имеем математическую модель:
F = x1 - 5x2 +5 → min
x1 + x2 ≥
1
x1 - 3x2
≥ -3
-2x1 - x2 ≥ -9
x1 + x2 ≥ -3
x1, x2 ≥ 0
Выбираем подходящее опорное решение
и преобразовываем его для создания симплекс-таблицы:
x3 = -1 - (-x1 - x2)
x4 = 3 - (-2x1 + 3x2)
x5 = 9 - (2x1 + x2)
x6 = 3 - (x1 - x2)
F = 5 - (-x1 + 5x2)
|
b
|
X1
|
X2
|
|
X3
|
-1
|
|
-1
|
|
-1
|
|
|
|
1
|
|
-2/3
|
|
1/3
|
|
X4
|
3
|
|
-2
|
|
3
|
|
|
|
1
|
|
-2/3
|
|
1/3
|
|
X5
|
9
|
|
2
|
|
1
|
|
|
|
-1
|
|
2/3
|
|
-1/3
|
|
X6
|
3
|
|
1
|
|
-1
|
|
|
|
1
|
|
-2/3
|
|
1/3
|
|
F
|
5
|
|
-1
|
|
5
|
|
|
|
-5
|
|
10/3
|
|
-5/3
|
|
b
|
X1
|
X4
|
|
X3
|
0
|
|
-5/3
|
|
1/3
|
|
|
|
5
|
|
5/8
|
|
5/32
|
|
X2
|
1
|
|
-2/3
|
|
1/3
|
|
|
|
2
|
|
1/4
|
|
-1/12
|
|
X5
|
8
|
|
8/3
|
|
-1/3
|
|
|
|
3
|
|
3/8
|
|
-1/8
|
|
X6
|
4
|
|
1/3
|
|
1/3
|
|
|
|
-1
|
|
-1/8
|
|
1/24
|
|
F
|
0
|
|
7/3
|
|
-5/3
|
|
|
|
-7
|
|
-7/8
|
|
7/24
|
|
b
|
X5
|
X4
|
|
X3
|
5
|
|
5/8
|
|
11/32
|
|
|
|
|
|
|
|
|
|
X2
|
3
|
|
1/4
|
|
1/4
|
|
|
|
|
|
|
|
|
|
X1
|
3
|
|
3/8
|
|
-1/8
|
|
|
|
|
|
|
|
|
|
X6
|
3
|
|
-1/8
|
|
9/24
|
|
|
|
|
|
|
|
|
|
F
|
-7
|
|
-7/8
|
|
-33/24
|
|
|
|
|
|
|
|
|
Получено решение:
Х=(3,3,5,0,0,3) F=-7
1.5 Определение
допустимого решения ЗЛП методом введения искусственного базиса
Имеем математическую модель:
F = x1 - 5x2
+5 → min1 + x2 ≥ 1
x1 - 3x2
≥ -3
-2x1 - x2 ≥ -9
x1 + x2 ≥ -3
x1, x2 ≥ 0
Вводим дополнительные переменные Е:
Е1 = 1 - x1 - x2 + x3
Е2 = 3 + 2 x1 - 3 x2 - x4
Е3 = 9 - 2 x1 - x2 - x5
Е4 = 3 - x1 + x2 - x6
F = x1 - 5x2 +5 → min

Е1 = 1 - (x1 + x2
- x3)
Е2 = 3 - (- 2x1 + 3 x2
+ x4)
Е3 = 9 - (2 x1 + x2
+ x5)
Е4 = 3 - (x1 - x2
+ x6)
F
= x1 - 5x2 +5 → min= 16 - (2x1 +
4 x1 - x3
+ x4 + x5
+ x6)
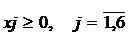
Решаем задачу с помощью
симплекс-таблицы.
|
b
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
|
E1
|
1
|
|
1
|
|
1
|
|
-1
|
|
0
|
|
0
|
|
0
|
|
|
|
1
|
|
1
|
|
1
|
|
-1
|
|
0
|
|
0
|
|
0
|
|
E2
|
3
|
|
-2
|
|
3
|
|
0
|
|
1
|
|
0
|
|
0
|
|
|
|
-3
|
|
-3
|
|
-3
|
|
3
|
|
0
|
|
0
|
|
0
|
|
E3
|
9
|
|
2
|
|
1
|
|
3
|
|
0
|
|
1
|
|
0
|
|
|
|
-1
|
|
-1
|
|
-1
|
|
1
|
|
0
|
|
0
|
|
0
|
|
E4
|
3
|
|
1
|
|
-1
|
|
0
|
|
0
|
|
0
|
|
1
|
|
|
|
1
|
|
1
|
|
1
|
|
-1
|
|
0
|
|
0
|
|
0
|
|
f
|
16
|
|
2
|
|
4
|
|
-1
|
|
1
|
|
1
|
|
1
|
|
|
|
-4
|
|
-4
|
|
-4
|
|
4
|
|
0
|
|
0
|
|
0
|
|
F
|
5
|
|
-1
|
|
5
|
|
0
|
|
0
|
|
0
|
|
0
|
|
|
|
-5
|
|
-5
|
|
-5
|
|
5
|
|
0
|
|
0
|
|
0
|
|
b
|
X1
|
E1
|
X3
|
X4
|
X5
|
Х6
|
|
X2
|
1
|
|
1
|
|
1
|
|
-1
|
|
0
|
|
0
|
|
0
|
|
|
|
0
|
|
5/3
|
|
-1
|
|
1/3
|
|
1/3
|
|
0
|
|
0
|
|
E2
|
0
|
|
-5
|
|
-3
|
|
3
|
|
1
|
|
0
|
|
0
|
|
|
|
0
|
|
5/3
|
|
-1
|
|
1/3
|
|
1/3
|
|
0
|
|
0
|
|
E3
|
8
|
|
1
|
|
-1
|
|
1
|
|
1
|
|
0
|
|
|
|
0
|
|
5/3
|
|
1
|
|
1/3
|
|
1/3
|
|
0
|
|
0
|
|
Е4
|
4
|
|
2
|
|
1
|
|
-1
|
|
0
|
|
0
|
|
1
|
|
|
|
0
|
|
5/3
|
|
-1
|
|
1/3
|
|
1/3
|
|
0
|
|
0
|
|
f
|
12
|
|
-2
|
|
-4
|
|
3
|
|
1
|
|
1
|
|
1
|
|
|
|
0
|
|
5
|
|
3
|
|
-1
|
|
-3
|
|
0
|
|
0
|
|
F
|
0
|
|
-6
|
|
-5
|
|
5
|
|
0
|
|
0
|
|
0
|
|
|
|
0
|
|
25/3
|
|
5
|
|
5/3
|
|
5/3
|
|
0
|
|
0
|
|
b
|
X1
|
E1
|
E2
|
X4
|
X5
|
X6
|
|
X2
|
1
|
|
2/3
|
|
1
|
|
1/3
|
|
1/3
|
|
0
|
|
0
|
|
|
|
2
|
|
1/8
|
|
0
|
|
1/24
|
|
1/24
|
|
1/8
|
|
0
|
|
X3
|
0
|
|
5/3
|
|
0
|
|
1/3
|
|
1/3
|
|
0
|
|
0
|
|
|
|
5
|
|
5/8
|
|
0
|
|
5/24
|
|
5/24
|
|
5/8
|
|
0
|
|
E3
|
8
|
|
8/3
|
|
0
|
|
1/3
|
|
1/3
|
|
1
|
|
0
|
|
|
|
3
|
|
3/8
|
|
0
|
|
1/8
|
|
0
|
|
0
|
|
3/8
|
|
E4
|
4
|
|
1/3
|
|
0
|
|
1/3
|
|
1/3
|
|
0
|
|
1
|
|
|
|
1
|
|
1/8
|
|
0
|
|
1/24
|
|
1/24
|
|
1/8
|
|
0
|
|
f
|
12
|
|
3
|
|
-1
|
|
1
|
|
-2
|
|
1
|
|
1
|
|
|
|
6
|
|
3/4
|
|
0
|
|
1/4
|
|
1/4
|
|
3/4
|
|
0
|
|
F
|
0
|
|
7/3
|
|
0
|
|
5/3
|
|
5/3
|
|
0
|
|
0
|
|
|
|
-7
|
|
7/8
|
|
0
|
|
7/24
|
|
7/24
|
|
7/8
|
|
0
|
|
b
|
Е3
|
E1
|
Е2
|
X4
|
X5
|
X6
|
|
X2
|
3
|
|
1/4
|
|
0
|
|
1/4
|
|
1/4
|
|
1/4
|
|
0
|
|
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
Х3
|
5
|
|
5/8
|
|
-1
|
|
1/8
|
|
1/8
|
|
5/8
|
|
0
|
|
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
Х1
|
3
|
|
3/8
|
|
0
|
|
1/8
|
|
1/8
|
|
3/8
|
|
0
|
|
|
|
0
|
|
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
E4
|
3
|
|
1/8
|
0
|
0
|
|
3/8
|
|
3/8
|
|
1/8
|
|
1
|
|
|
|
3
|
|
|
|
0
|
|
3/24
|
|
3/8
|
|
1/8
|
|
1
|
|
f
|
3
|
|
9/8
|
|
-1
|
|
5/8
|
|
3/8
|
|
1/8
|
|
1
|
|
|
|
-3
|
|
1/8
|
|
0
|
|
3/8
|
|
3/8
|
|
1/8
|
|
-1
|
|
F
|
-7
|
|
7/8
|
|
0
|
|
33/24
|
|
33/24
|
|
7/8
|
|
0
|
|
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
0
|
|
b
|
Е3
|
E1
|
Е2
|
X4
|
X5
|
Е4
|
|
X2
|
3
|
|
1/4
|
|
0
|
|
1/4
|
|
1/4
|
|
1/4
|
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х3
|
5
|
|
5/8
|
|
-1
|
|
1/8
|
|
1/8
|
|
5/8
|
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х1
|
3
|
|
3/8
|
|
0
|
|
1/8
|
|
1/8
|
|
3/8
|
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х6
|
3
|
|
1/8
|
|
0
|
|
3/8
|
|
3/8
|
|
1/8
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f
|
0
|
|
-1
|
|
-1
|
|
-1
|
|
0
|
|
0
|
|
-1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F
|
-7
|
|
7/8
|
|
0
|
|
33/24
|
|
33/24
|
|
7/8
|
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдено решение <3,3,5,0,0,3>,
F=-7. Это решение найдено
правильно, кроме того, оно оптимальное (как видно по коэффициентам целевой
функции). Таким образом, сравнив полученный результат с теми значениями,
которые были выявлены при использовании графического и алгебраического методов,
можно сделать вывод о правильности данного решения.
2.
Целочисленное линейное программирование
Решить задачу целочисленного
линейного программирования, используя метод ветвей и границ.



Получено целочисленное
решение: Xopt =
< 0,1>, F = 4
3. Целочисленное
линейное программирование с булевскими переменными
|
Вариант
|
Проект
|
Расходы (млн. грн. в год)
|
Прибыль (млн. грн)
|
|
|
1-й
год
|
2-й год
|
3-й год
|
|
|
20
|
1
|
7
|
6
|
6
|
25
|
|
2
|
8
|
4
|
7
|
35
|
|
3
|
9
|
9
|
8
|
20
|
|
4
|
6
|
8
|
9
|
15
|
|
5
|
4
|
7
|
5
|
10
|
|
Доступный капитал
|
30
|
30
|
30
|
|
Составим математическую модель
данной ЗЛП с булевскими переменными:
F=25x1 + 35x2
+ 20x3 + 15x4 + 10x5
x1 + 4x2
+ 9x3 + 8x4 + 7x5 ≤ 30
x1 + 7x2
+ 8x3 + 9x4 + 5x5 ≤ 30
Запишем вычисления в
таблицу:
|
x1
|
x2
|
x3
|
x4
|
x5
|
Ф.О.
|
1
|
2
|
3
|
Ц.Ф.
|
|
0
|
0
|
0
|
0
|
0
|
0
|
+
|
+
|
+
|
0
|
|
0
|
0
|
0
|
0
|
1
|
10
|
+
|
+
|
+
|
10
|
|
0
|
0
|
0
|
1
|
0
|
15
|
+
|
+
|
+
|
15
|
|
0
|
0
|
0
|
1
|
1
|
25
|
+
|
+
|
+
|
25
|
|
0
|
0
|
1
|
0
|
0
|
20
|
+
|
+
|
+
|
|
|
0
|
0
|
1
|
0
|
1
|
30
|
+
|
+
|
+
|
30
|
|
0
|
0
|
1
|
1
|
0
|
35
|
+
|
+
|
+
|
35
|
|
0
|
0
|
1
|
1
|
1
|
45
|
+
|
+
|
+
|
45
|
|
0
|
1
|
0
|
0
|
0
|
35
|
+
|
+
|
+
|
|
|
0
|
1
|
0
|
0
|
1
|
45
|
+
|
+
|
+
|
|
|
0
|
1
|
0
|
1
|
0
|
50
|
+
|
+
|
+
|
50
|
|
0
|
1
|
0
|
1
|
1
|
60
|
+
|
+
|
+
|
60
|
|
0
|
1
|
1
|
0
|
0
|
70
|
+
|
+
|
+
|
70
|
|
0
|
1
|
1
|
0
|
1
|
55
|
+
|
+
|
+
|
|
|
0
|
1
|
1
|
1
|
0
|
70
|
+
|
+
|
+
|
|
|
0
|
1
|
1
|
1
|
1
|
80
|
+
|
+
|
+
|
80
|
|
1
|
0
|
0
|
0
|
0
|
25
|
+
|
+
|
+
|
|
|
1
|
0
|
0
|
0
|
1
|
35
|
+
|
+
|
+
|
|
|
1
|
0
|
0
|
1
|
0
|
40
|
+
|
+
|
+
|
|
|
1
|
0
|
0
|
1
|
1
|
50
|
+
|
+
|
+
|
|
|
1
|
0
|
1
|
0
|
0
|
45
|
+
|
+
|
+
|
|
|
1
|
0
|
1
|
0
|
1
|
55
|
+
|
+
|
+
|
|
|
1
|
0
|
1
|
1
|
0
|
60
|
+
|
+
|
+
|
|
|
1
|
0
|
1
|
1
|
1
|
70
|
+
|
+
|
+
|
|
|
1
|
1
|
0
|
0
|
0
|
60
|
+
|
+
|
+
|
|
|
1
|
1
|
0
|
0
|
1
|
70
|
+
|
+
|
+
|
|
|
1
|
1
|
0
|
1
|
0
|
75
|
+
|
+
|
+
|
|
|
1
|
1
|
0
|
1
|
1
|
85
|
+
|
+
|
+
|
85
|
|
1
|
1
|
1
|
0
|
0
|
80
|
+
|
+
|
+
|
|
|
1
|
1
|
1
|
0
|
1
|
90
|
+
|
+
|
+
|
90
|
|
1
|
1
|
1
|
1
|
0
|
95
|
+
|
+
|
+
|
95
|
|
1
|
1
|
1
|
1
|
1
|
105
|
-
|
-
|
-
|
105
|
Максимальной прибыли предприятие
достигнет при реализации проектов
1, 2, 3, 4
X = (1,1,1,1,0); F=95
4. Поиск глобального экстремума функции
Минимизировать функцию 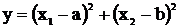 ,
где a = 4, b = 7. Начальная точка
,
где a = 4, b = 7. Начальная точка 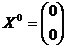 .
Применить метод движения по симплексу. Начальные условия: размер стороны
симплекса a=2;
коэффициент уменьшения стороны симплекса g=10; критерий окончания
поиска
.
Применить метод движения по симплексу. Начальные условия: размер стороны
симплекса a=2;
коэффициент уменьшения стороны симплекса g=10; критерий окончания
поиска
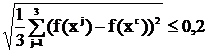

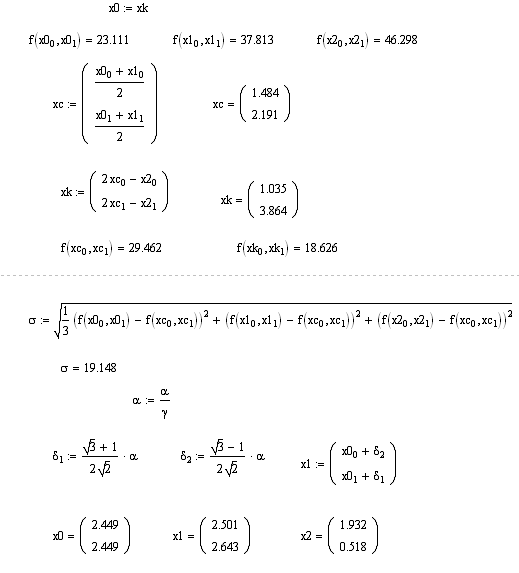

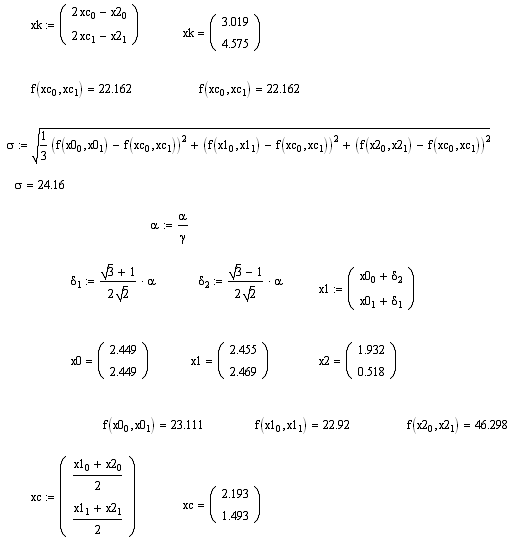

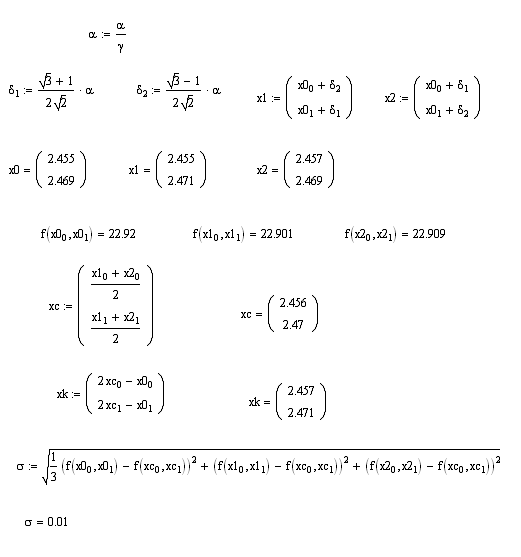

Ответ:
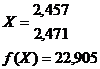
5. Метод градиентного
спуска
Выполнить поиск минимума
функции 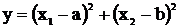 ,
где a = 4, b = 7 методом
градиентного спуска.
,
где a = 4, b = 7 методом
градиентного спуска.
Начальные условия:
значение шага t0=0,5;
коэффициент уменьшения
шага a=2;
критерий окончания
поиска 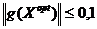 ;
;
начальная точка 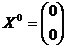
)
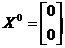
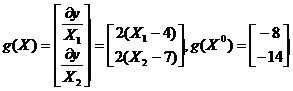
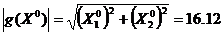
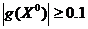

)
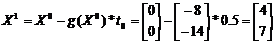

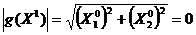

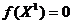
6.
Одномерная минимизация
Требуется:
выполнить поиск минимума
заданной функции методом дихотомии (3 итерации);
уточнить интервал поиска
методом Фибоначчи (3-4 итерации);
завершить поиск методом
квадратичной аппроксимации.
Метод дихотомии
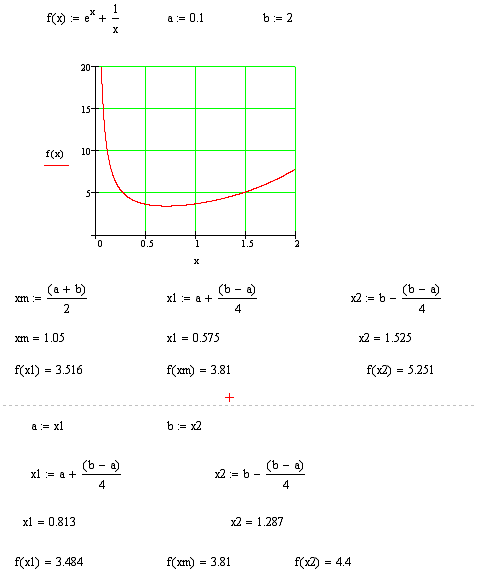

|
k
|
ak
|
x1k
|
xmk
|
x2k
|
bk
|
f(x1)
|
f(xm)
|
f(x2)
|
|
0
|
0.1
|
0.575
|
1.05
|
1.525
|
2
|
3.516
|
3.81
|
5.251
|
|
1
|
0.575
|
0.813
|
1.05
|
1.287
|
1.525
|
3.484
|
3.81
|
4.4
|
|
2
|
0.813
|
0.931
|
1.05
|
1.169
|
1.287
|
3.612
|
3.81
|
4.074
|
|
3
|
0.931
|
0.991
|
1.05
|
1.109
|
1.169
|
3.702
|
3.81
|
3.934
|
Заключение
В ходе курсовой работы были
углублены теоретические знания по дисциплине, а также приобретены и закреплены
практические навыки решения задач линейного и нелинейного программирования и
оценке эффективности работы применяемых алгоритмов.
Для задач линейного программирования
были заданы одни и те же исходные данные, поэтому полученные ответы каждого
пункта одинаковые. Оптимальный план для данной ЗЛП: Х = < 3, 3 5, 0, 0,
3>, значение целевой функции F=-7.
Для задачи целочисленного линейного
программирования было получено следующее оптимальное целое решение: Х =
<0,1>. F = 4.
Задача целочисленного линейного
программирования с булевскими переменными была решена с помощью Метода Баллаша.
Получили следующее решение: X = (1,1,1,1,0); F=95.
С помощью метода движения по
симплексу решена задача поиска глобального экстремума. Получен следующий ответ:
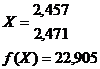
По методу градиентного
спуска был найден экстремум функции  и он составил:
и он составил:
 (x) = 0
(x) = 0
Задача одномерной
минимизации решена тремя методами: метод дихотомии (первые 4 итерации), метод
Фибоначчи (вторые 4 итерации), и завершен поиск методом квадратичной
аппроксимации. Получен ответ:
Х = 0.638, F(x) = 3.43.
Список литературы
программирование
булевский градиентный транспортный
1. М.У. для выполнения курсового проекта по дисциплине
«Прикладная математика»