Модель межотраслевой экономики – модель Леонтьева

Модель межотраслевой экономики – модель Леонтьева

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Нижегородский государственный университет им. Н.И. Лобачевского»

Специальность «Государственное и муниципальное управление»

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: Основы математического моделирования социально-экономических процессов

Выполнил студент 2 курса заочной формы обучения

г. Шахунья

г.

ЗАДАНИЕ №1

Модель межотраслевой экономики - модель Леонтьева.

Задача 1. Даны коэффициенты прямых затрат aij и конечный продукт Yi для двухотраслевой экономической системы. Данные приведены в таблице.

.        Определить коэффициенты полных затрат, вектор валового выпуска, межотраслевые поставки продукции;

.        Проверить продуктивность матрицы коэффициентов прямых затрат;

.        Составить и заполнить таблицу межотраслевого баланса.

.        Найти матрицу косвенных затрат.

Подставив данные варианта m = 4, n = 4, получим:

Из таблицы получаем:

0,4 0,1          1000

А= 0,3 0,4    ,                     Y=            900 .

Найдем матрицу полных затрат:

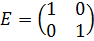
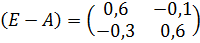
Находим определитель:

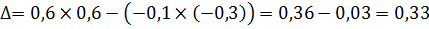
А также матрицу миноров:

А затем матрицу алгебраических дополнений:

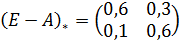
И соответствующую ей транспонированную матрицу:

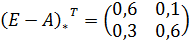
Что позволяет найти обратную матрицу - матрицу полных затрат:

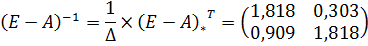
Так как все элементы матрицы полных затрат неотрицательны, а также сумма элементов матрицы А по всем строкам и столбцам <1, то матрица коэффициентов прямых затрат является продуктивной.

Найдем вектор валового выпуска:

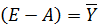
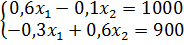
Помножив первое уравнение на 6 и сложив первое уравнения со вторым, получим:

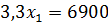
Откуда найдем:

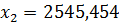
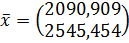
Межотраслевые поставки считаем по формуле:

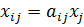
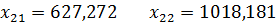
В итоге таблица межотраслевого баланса выглядит следующим образом:

Найдем матрицу косвенных затрат:

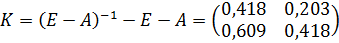
ЗАДАНИЕ №2

Линейное программирование. Задача оптимального производства продукции

Задача 2. Предприятие планирует выпуск двух видов продукции: I и II. На производство расходуется три вида сырья: A, B и C. Потребность aij на каждую единицу j-го вида продукции i-го вида сырья, запас bi соответствующего вида сырья и прибыль cj от реализации единицы j-го вида продукции заданы таблицей:

затрата индексный решение excel

Подставив данные варианта, получим:

Целевая функция решения имеет следующий вид:

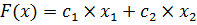
Система ограничений на целевую функцию:

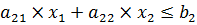
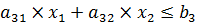
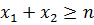
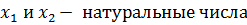
Воспользовавшись сервисом «поиск решения» в программе MS Excel, получим оптимальный план производства продукции:

Определим максимальное значение целевой функции F(X) = 6x1 + 5x2 при следующих условиях-ограничений.

x1 + 2x2≤36+ x2≤11

x1 + 5x2≤40+ x2≥4

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

x1 + 2x2 + 1x3 + 0x4 + 0x5 + 0x6 = 36

x1 + 1x2 + 0x3 + 1x4 + 0x5 + 0x6 = 11

x1 + 5x2 + 0x3 + 0x4 + 1x5 + 0x6 = 40

x1 + 1x2 + 0x3 + 0x4 + 0x5-1x6 = 4

Введем искусственную переменную: в 4-м равенстве вводим переменную x7;

x1 + 2x2 + 1x3 + 0x4 + 0x5 + 0x6 + 0x7 = 36

x1 + 1x2 + 0x3 + 1x4 + 0x5 + 0x6 + 0x7 = 11

x1 + 5x2 + 0x3 + 0x4 + 1x5 + 0x6 + 0x7 = 40

x1 + 1x2 + 0x3 + 0x4 + 0x5-1x6 + 1x7 = 4

Для постановки задачи на максимум целевую функцию запишем так:

(X) = 6x1+5x2 - Mx7 → max

Из уравнения выражаем искусственную переменную:

= 4-x1-x2+x6

которую подставим в целевую функцию:

(X) = (6+M)x1+(5+M)x2+(-M)x6+(-4M) → max

Решим систему уравнений относительно базисных переменных:, x4, x5, x7,

Полагая, что свободные переменные равны 0, получим первый опорный план:= (0,0,36,11,40,0,4)

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее, 4-ая строка является ведущей. Разрешающий элемент равен 1 и находится на пересечении ведущего столбца и ведущей строки.

Получаем новую симплекс-таблицу:

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x6, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai6 и из них выберем наименьшее, 1-ая строка является ведущей. Разрешающий элемент равен 4 и находится на пересечении ведущего столбца и ведущей строки.

Получаем новую симплекс-таблицу:

Итерация №2.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее, 2-ая строка является ведущей. Разрешающий элемент равен 1/2 и находится на пересечении ведущего столбца и ведущей строки.

Получаем новую симплекс-таблицу:

Индексная строка не содержит отрицательных элементов - найден оптимальный план. Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым. Оптимальный план можно записать так:

= 7

x2 = 4

F(X) = 5•4 + 6•7 = 62

Для решения графическим методом заменим неравенства уравнениями и построим их на координатной плоскости. Область решений обозначена штриховкой.

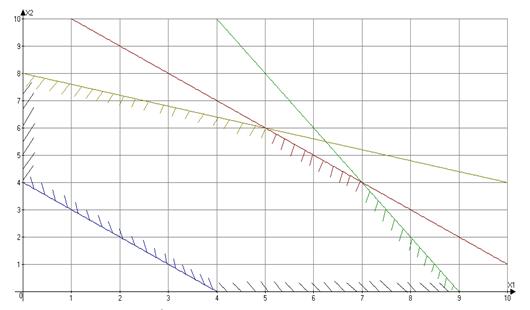
Добавим на график целевую функцию (на графике обозначена пунктирной линией):

Будем искать максимальное значение a, при котором целевая функция касается многоугольника решений. Получилось a=62 для значений x1 = 7 и x2 = 4.

Литература

1.      Красс М.С., Чупрынов Б.П. Математика для экономистов. - СПб.: Питер,2004.

.        Орлова И. В., Половников В.А. Экономико-математические методы и модели. - М.: Вузовский учебник, 2009.

.        Замков О.О. и др. Математические методы в экономике. - М.: Дело и сервис, 2009.

.        Шапкин А. С. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями. - М.: «Дашков и К0», 2006.