Принятие решений в условиях риска. Выбор варианта производимого товара

Принятие решений в условиях риска. Выбор варианта производимого товара

Российский Экономический Университет им. Г.В. Плеханова

Инженерно-экономический факультет

Кафедра технологических инноваций

Курсовая работа

По дисциплине

«Методы оптимизации»

На тему:

«Принятие решений в условиях риска. Выбор варианта производимого товара»

Выполнил:

Студент гр. 7461-2 ИЭФ

Левчук Игорь

Преподаватель:

Кулаго А.Е.

Москва

Содержание

Введение

.        Принятие решений в условиях риска

.1.     Математическая модель ЗПР в условиях риск

.2 Критерий ожидаемого выигрыша. Необходимость введения отклонения от ожидаемого выигрыша

.3 Нахождение оптимального решения по паре критериев (М,Ϭ)

. Задача принятия решений в условиях риска. Выбор производимого товара

Заключение

Список литературы

Введение

Целью курсовой работы является решение задачи принятия решений в условиях риска. Для решения этой задачи будут использоваться математические методы. В качестве примера рассматриваем фирму, производящую различные товары в летний сезон. Необходимо определить производство каких товаров является наиболее оптимальным при определенных погодных условиях. Рассмотрим также, как влияет склонность к риску предпринимателя на конечное решение.

.Принятие решений в условиях риска

.1 Математическая модель ЗПР условиях риска

Построение реализационной структуры задачи принятия решения сводится к заданию функции реализации F(x, y). Формально функция реализации есть функция двух переменных x и y, но эти переменные входят в нее неравноправно, что является отражением неравноправия управляющей системы и среды. Дело в том, что управляющая система всегда имеет определенную цель, поэтому ее поведение носит целенаправленный характер; что касается среды, ее поведение может носить как целенаправленный, так и случайный характер. Принятие решения в условиях риска характеризуется тем, что поведение среды носит случайный характер, причем в этой случайности имеются закономерности стохастического типа. В общем случае это проявляется в том, что существует некоторая вероятностная мера, в соответствии с которой возникают те или иные состояния среды. При этом принимающий решение имеет определенную информацию о вероятностях появления состояний среды, которая по своему характеру может быть весьма разнообразной. Скажем, если имеется всего три возможных состояния среды A, B, C, то дополнительная информация о появлении этих состояний может заключаться, например, в сообщении о том, что состояние A является наименее вероятным, а состояние C - наиболее вероятным; или что вероятность A больше, чем вероятность C; или что вероятность C составляет более 50% и т.п.

Изучение математической модели ЗПР в условиях риска предполагает, кроме задания функции реализации, задание некоторой дополнительной информации о вероятностях состояний среды. Наиболее простой для анализа случай - когда эта дополнительная информация представлена в виде вероятностной меры на множестве состояний среды. Если множество состояний среды Y конечно, Y = {1, . . . , m}, то вероятностная мера на нем может быть задана вероятностным вектором, то есть вектором y = (y1, . . . , ym), где yi ≥ 0 и∑yi=1 (здесь yi есть вероятность наступления состояния j = 1, . . . , m). Считаем, что оценочная структура ЗПР задается в виде оценочной функции.

В данной курсовой работе предметом изучения будут задачи принятия решений, в которых целевая функция (функция выигрыша) представлена в виде таблицы - матрицы выигрышей ‖||aij|| (i= 1, …n; j = 1, …m) и, кроме того, принимающему решение (игроку) известен вероятностный вектор у =(y1, . . . , ym). Такая задача принятия решения (также можно назвать игрой с природой) задается следующей таблицей:

При выборе альтернативыi, игрок знает, что он получит один из выигрышей ai1, . . . , aimс вероятностями y1, . . . , ym, соответственно. Таким образом, исходом для принимающего решение при выборе им альтернативыi будет являться случайная величина

عi =[ai1,…,aim; y1,…,ym].Следовательно, сравнение двух альтернатив i1 и i2 сводится здесь к сравнению соответствующих им случайных величин عi1 и عi2.

В качестве примера приведем выбор варианта продаваемого товара. Фирма А может выставить на продажу один из товаров T1 или Т2, а фирма В - один из товаров Т1*, Т2*,Т3*. Товары Т1 и Т1* являются конкурирующими (например, тетради и блокноты), товары Т1 и Т3*- сопутствующими (например, тетради и ручки); остальные пары товаров являются практически нейтральными. Прибыль (в некоторых денежных единицах) фирмы А зависит от сочетания товаров, выставляемых на продажу обеими фирмами. . Известно, что фирма В выставляет на продажу товар Т3* в 3 раза реже, чем Т1*и в 4 раза реже, чем Т2*. Какой товар следует выставить на продажу фирме А?

Рассмотрим эту задачу как задачу принятия решения для фирмы А, при этом вышестоящая таблица будет матрицей выигрышей. В качестве состояний среды здесь выступают виды товаров, выставляемых на продажу фирмой В. Вероятности этих состояний могут быть найдены из указанного соотношения частот следующим образом. Пусть х - доля случаев, в которых выставляется на продажу товар Т3*. Тогда для товара Т1* доля случаев, в которых он выставляется на продажу, составляет 3х, а для товара Т2*-4х. Так как х + 3х + 4х = 1, то х = 1/8, откуда вероятности состояний Т1*, Т2*, Т3*равны, соответственно 3/8, 4/8 и 1/8. Получаем в итоге задачу принятия решения в условиях риска, заданную таблицей :

.2 Критерий ожидаемого выигрыша. Необходимость введения отклонения от ожидаемого выигрыша

Итак, принятие решения в условиях риска сводится к сравнению между собой случайных величин. Как известно из теории вероятностей, наиболее естественной числовой характеристикой случайной величины عявляется ее математическое ожидание (МО), обозначаемое далее через Мع. Если для задачи принятия решений в условиях риска в качестве критерия для сравнения альтернатив взять математическое ожидание соответствующей случайной величины (или просто говоря ожидаемый выигрыш), то оптимальной следует считать альтернативу, максимизирующую ожидаемый выигрыш. Для описанного выше примера имеем: МعТ1 = 8*3/8 + 18*4/8 + 40 *1/8= = 17, МعТ2 =18*3/8+15*4/8+14*1/8= 16. Таким образом, здесь оптимальной по указанному критерию будет альтернатива Т1.

Можно ли согласиться с тем, что альтернатива Т1 лучше, чем Т2? Как известно из теории вероятностей, математическое ожидание Мع случайной величины ع представляет собой число, к которому приближается среднее значение этой случайной величины при большом числе испытаний. Таким образом, в игре с природой ориентация на математическое ожидание выигрыша есть фактически ориентация на средний выигрыш, который получится при многократном повторении этой игры (в предположении, что условия игры не изменятся). Разумеется, если в действительности игра повторяется многократно, то критерий среднего выигрыша (скажем, в экономических задачах - средней прибыли) можно считать оправданным. Однако разумно ли ориентироваться на этот критерий при единичном испытании? Вернемся к примеру .Здесь МعТ1 = 20,5, МعТ2 = 20.Безусловно, выигрыш в 17 денежных единиц лучше, чем выигрыш в 16денежных единиц, однако при выборе альтернативы Т1 мы ведь получим не 17 денежных единиц, а один из выигрышей: 8, 18 или 40; точно также при выборе альтернативы Т2 мы получим не 16, а один из выигрышей 18, 15 или 14. Составим таблицу, в которой указаны отклонения возможных выигрышей от их ожидаемых значений и вероятности этих отклонений.

Из этой таблицы видно, что альтернативы Т1 и Т2, имея близкие значения ожидаемых выигрышей, по-разному ведут себя в плане возможных отклонений от ожидаемых выигрышей. Отсюда можно сделать следующий вывод: для задачи принятия решений в условиях риска критерий ожидаемого выигрыша не является адекватным и должен быть трансформирован с учетом возможных отклонений случайной величины от ее среднего значения. В теории вероятностей в качестве меры отклонения случайной величины от ее среднего значения (меры "разброса") обычно берется дисперсияDع или среднеквадратичное отклонение (СКО) Ϭ =√Dع. Напомним, что формально дисперсия определяется как математическое ожидание квадрата отклонения случайной величины от ее ожидаемого значения:Dع=M(ع-Mع)2.

Технически удобней здесь использовать среднеквадратичное отклонение Ϭ, так как при изменении масштаба измерения Ϭ изменяется пропорционально.

Для задач принятия решений в условиях риска будем рассматривать в качестве показателя риска среднеквадратичное отклонение Ϭ.

.3 Нахождение оптимального решения по паре критериев (М,Ϭ)

принятие решение риск ожидание

Сказанное выше можно подытожить следующим образом для задач принятия решений в условиях риска выбор альтернативы ع приводит к случайной величине عi, которая может быть охарактеризована парой показателей (Мi,Ϭi), где Mi-Mعi - ожидаемый выигрыш и Ϭi =√Dعi- показатель риска. Теперь мы можем приступить к решению основной задачи - построению адекватного критерия сравнения альтернатив.

Фактически здесь получается задача 2-критериальной оптимизации, где в качестве частных критериев выступают M и Ϭ. Рассмотрим два метода решения данной задачи

)Наиболее заманчивым является "соединение" указанных двух критериев в единый (обобщенный) критерий. Попробуем в качестве обобщенного критерия взять

q(M,Ϭ)=M-λϬ

где λ - некоторая постоянная; фактически критерий представляет собой взвешенную сумму частных критериев M и Ϭ с весовыми коэффициентами 1 и −λ. При λ> 0 оценка случайной величины с помощью обобщенного критерия будет меньше, чем ее среднее значение, что является характерным для осторожного человека, то есть не склонного к риску человека. Напротив, при λ< 0 оценка критерия будет больше, чем ее среднее значение, что характеризует человека, склонного к риску. Наконец, при λ = 0 оценка критерия случайной величины совпадает с ее средним значением (то есть возможные отклонения случайной величины от ее среднего значения игнорируются) - это характеризует человека, безразличного к риску. В качестве основного мы будем далее рассматривать случай, когда принимающий решение не склонен к риску, то есть λ> 0.

В чем же будет содержательный смысл обобщенного критерия при λ> 0?В этом случае увеличение критерия q может происходить как за счет увеличения λ, так и за счет уменьшения λ. Таким образом, для человека не склонного к риску, критерий отражает стремление к увеличению ожидаемого выигрыша и уменьшению риска отклонения от него. При этом показатель λ характеризует субъективное отношение принимающего решение к риску: чем больше λ, тем в большей степени он несклонен рисковать; таким образом, λ можно рассматривать как субъективный показатель меры несклонности к риску (субъективный показатель осторожности).

Учет риска отклонения от ожидаемого значения выигрыша при использовании критерия производится следующим образом. Ожидаемый выигрыш уменьшается или увеличивается (в зависимости от того- имеется несклонность или склонность к риску) на величину, равную произведению показателя риска Ϭ (представляющего собой объективную характеризацию меры риска), на субъективный показатель λ, характеризующий отношение принимающего решение к риску.

Что можно сказать о мере склонности или несклонности к риску по величине показателя λ? Например: большая ли несклонность к риску у человека, для которого λ = 3? Для ответа на этот вопрос воспользуемся известным в теории вероятностей неравенством Чебышева. Пусть принимающий решение не склонен к риску. Так как оценкой случайной величины ع служит число M − λϬ, то "неприятность" для принимающего решение наступает тогда, когда ع<M-λϬ. Оценим вероятность этого события. В этом случае выполняется M-ع>λϬ, следовательно |ع − M| >λϬ. В силу неравенства Чебышева вероятность последнего соотношения будет меньше, чем Dع/(λϬ)2 = Ϭ2/(λ2Ϭ2) = 1/λ2. Итак, вероятность того, что случайная величина ع примет значение, меньшее ее оценки M-λϬ, не превосходит 1/λ2.

Мы можем предположить, если λ= 3, то вероятность того, что случайная величина "неопустится" ниже оценки M − 3Ϭ, будет не менее 1 − 1/9, то есть почти90%. Такую степень риска можно считать невысокой, то есть значение λ= 3 соответствует "достаточно большой степени осторожности"(или" достаточно высокой несклонности к риску").

Далее нужно выяснить - как устанавливается предпочтение альтернатив по обобщенному критерию . Будем считать, что принимающий решение не склонен к риску (λ> 0). Как мы установили выше, в этом случае он стремится увеличить ожидаемый выигрыш и уменьшить риск, то есть критерий M будет здесь позитивным, а критерий Ϭ - негативным. Пусть(ai) - некоторое множество альтернатив, каждая из которых характеризуется парой показателей (Mi, Ϭi). Зафиксируем какие-то две альтернативы ai1 = (Mi1, Ϭi1) и ai2 = (Mi2, Ϭi2). Находим критерии q1и q2. Возможны два случая.

а) Альтернативы ai1 и ai2сравнимы по Парето. Пусть, например,ai1>ai2. Тогда Mi1 ≥ Mi2 и Ϭi1 ≤ Ϭ2(причем хотя бы одно неравенство строгое), значит Mi1-λϬi1>Mi2-λϬi2, то есть q(ai1)>q(ai2). Таким образом, в этом случае независимо от меры несклонности принимающего решение к риску (то есть от значения показателя λ> 0) альтернатива ai1будет более предпочтительной, чем альтернатива ai2(этот факт записывается в виде ai1 ai2).

b) Альтернативы ai1 и ai2 несравнимы по Парето. Пусть, например,Mi1 >Mi2, тогда Ϭi1 >Ϭi2(то есть больший ожидаемый выигрыш здесь всегда сопровождается большим риском). Условие Mi1-λϬi1>Mi2-λϬi2 равносильно тому, что λ<(Mi1-Mi2)/(Ϭi1-Ϭi2). Таким образом, в этом случае

1 ai2; λ<(Mi1-Mi2)/(Ϭi1-Ϭi2)

ai 2 ai 1; λ>(Mi1-Mi2)/(Ϭi1-Ϭi2)

При решении многокритериальной задачи принятия решений основная проблема при определении оптимальной альтернативы состоит в выборе одной альтернативы из множества оптимальных по Парето альтернатив. Эта проблема легко решается (в случае конечного Парето-оптимального множества), если произведено полное ранжирование Парето-оптимальных альтернатив по предпочтению. Так как любые две Парето-оптимальные альтернативы не сравнимы по Парето, то для них выполнено условие b). В этом случае предпочтение между альтернативами ai1 и ai2 будет зависеть от того, выполняются ли вышестоящие условия. В то же время, предпочтения между Парето-оптимальными альтернативами будут носить "единообразный" характер, когда одно из условий выполнено для всех i1, i2,при которых альтернативы ai1 и ai2оптимальны по Парето. Формально это обстоятельство можно выразить следующим образом. Положим λ’=min{(Mi1-M12)/(Ϭi1-Ϭi2)}; λ*=max{(Mi1-Mi2)/(Ϭi1-Ϭi2), где операторы min и max распространяются на такие пары индексов(i1, i2), для которых альтернативы ai1, ai2оптимальны по Парето и Mi1 >Mi2(а, следовательно, Ϭi1 >Ϭi2). Назовем λ’ нижней границей несклонности к риску, λ*- верхней границей несклонности к риску (всегда выполняется λ’<λ*). Нf основании b), получаем для человека, не склонного к риску, следующее

) Если у принимающего решение его субъективный показатель несклонности к риску меньше нижней границы (λ<λ’), то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию q совпадает с ранжированием по показателю ожидаемого выигрыша M (то есть более предпочтительной будет та альтернатива, для которой больше ожидаемый выигрыш);

) Если у принимающего решение его субъективный показатель несклонности к риску больше верхней границы (λ>λ*), то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию q совпадает с ранжированием по показателю риска Ϭ (более предпочтительной будет та альтернатива, для которой меньше риск).

Таким образом, для принятия решений в условиях риска применение обобщенного критерия сводит проблему нахождения оптимального решения к проблеме установления для принимающего решение его меры несклонности (или склонности) к риску. В связи с этим возникает законный вопрос: существует ли эта мера вообще? Заметим, что этот вопрос относится не к математике, а к психологии, так как склонность (или несклонность) к риску является субъективно-психологическим качеством человека. Многие психологи отвечают на этот вопрос утвердительно; при этом предлагается определять показатель склонности (или несклонности) индивидуума к риску из наблюдений за тем, как этот индивидуум принимает решения в рискованных ситуациях - как естественных, так и искусственных. В заключение обсуждения использования обобщенного критерия для задач принятия решений в условиях риска сделаем несколько замечаний.

Согласно а) максимальное значение обобщенного критерия q всегда достигается на Парето-оптимальной альтернативе. Это позволяет найти одну (или несколько) оптимальных по Парето альтернатив по значениям критерия q. Конечно, если число альтернатив невелико, то задача нахождения какой-то Парето-оптимальной альтернативы может быть легко решена непосредственно. Однако дело существенно осложняется, когда имеется большое число альтернатив (несколько сотен и более). В этом случае удобством характеризации каждой альтернативы одним числом - величиной обобщенного критерия - не следует пренебрегать.

Основной недостаток критерия qсостоит в том, что он базируется на предположении постоянства меры несклонности к риску для данного лица, принимающего решение (что означает постоянство локального коэффициента замещения между критериями M и Ϭ. Вместе с тем, для большинства людей их мера склонности (или несклонности) к риску меняется в зависимости от величины ожидаемого выигрыша и степени риска. Долю оптимизма здесь привносит то обстоятельство, что для установления ранжирования альтернатив достаточно знать не точное значение показателя λ, а некоторый содержащий его интервал.

Типичным примером проявления несклонности к риску является участие во всякого рода страхованиях. Обратный пример- проявление склонности к риску - покупка лотерейного билета, стоимость которого больше ожидаемого (то есть среднего) выигрыша в этой лотерее.

Следует сказать, что, как правило, бизнесмены при решении серьезных деловых вопросов предпочитают не рисковать (то есть проявляют несклонность к риску). Хотя нередко среди бизнесменов встречается и противоположный тип.

) Рассмотрим теперь для Задачи принятия решений в условиях риска методы нахождения оптимального решения, основанные на отношении доминирования по Парето). Будем считать, что принимающий решение не склонен к риску; тогда критерий ожидаемого выигрыша будет позитивным, а критерий риска - негативным. Предположим, что требуется выбрать одну (оптимальную) альтернативу из заданного множества допустимых альтернатив (ai), каждая из которых характеризуется парой показателей (Mi,Ϭi). Изобразим на координатной плоскости точки с координатами (Mi,Ϭi) (рис.1). Содержательно условие доминирования по Парето ai1>ai2 означает, что для альтернативы ai1 получается такой же (или больший) ожидаемый выигрыш, что и для альтернативы ai2, но с меньшим (или таким же) риском. Например, a2>a3, a9>a3, a4>a5, a8>a9 и т.д. В данном примере множество Парето-оптимальных альтернатив есть {a1, a4, a7, a8}; окончательный выбор оптимальной альтернативы должен производится из этого множества. Здесь есть два подхода:1-й подход заключается в том, что рациональный анализ заканчивается указанием множества Парето-оптимальных альтернатив и окончательный выбор оптимальной альтернативы из этого множества производит принимающий решение на основе неформальных дополнительных соображений. Рассмотрим теперь вкратце 2-й подход, когда производятся некоторые процедуры сужения множества Парето-оптимальных альтернатив.

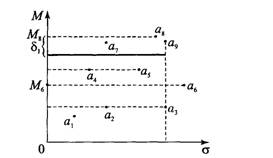
Рис.1

а) Субоптимизация связана с выбором одного критерия и назначением нижних границ по остальным критериям. Для нашей задачи более "осязаемым" является критерий ожидаемого выигрыша, поэтому логичным является проведение субоптимизации следующим образом: назначить нижнюю границу по критерию M и оптимизировать (в данном случае - минимизировать) оставшийся критерий Ϭ. Например, если взять в качестве нижней границы критерия ожидаемого выигрыша значение M6, то оптимальной будет альтернатива a4, так как среди альтернатив, удовлетворяющих условию Mi ≥ M6, она является наименее рискованной.) Лексикографическая оптимизация предполагает упорядочение критериев по относительной важности. Пусть, например, M - важнейший критерий. Так как максимальное значение по критерию M имеет единственная альтернатива a8, то она и будет являться оптимальной. Здесь наглядно проявляется недостаток метода лексикографической оптимизации: учет фактически одного (важнейшего) критерия. Указанный недостаток связан с необходимостью введения жесткого приоритета критериев и может быть снят за счет ослабления "жесткости" приоритетов следующим образом. Назначим некоторую "уступку"δ1 по важнейшему критерию и на первом шаге отберем те альтернативы, для которых оценка по первому (важнейшему) критерию отличается от максимальной оценки не более, чем на δ1. После этого назначаем "уступку"δ2 для 2-го по важности критерия и среди отобранных на первом шаге альтернатив выбираемте, для которых оценка по 2-му критерию отличается от максимальной не более, чем на δ2 и т.д.

Например, в нашем случае возьмем в качестве "уступки" по критерию ожидаемого выигрыша величину δ1. Тогда результатом выбора на первом шаге будут альтернативы {a7, a8, a9}. Среди них наилучшей по 2-му критерию является альтернатива a7 - она и будет оптимальной. Таким образом, несколько снизив требования по критериюM, мы значительно улучшили оценку по критерию Ϭ (то есть некоторое уменьшение ожидаемого выигрыша привело к существенному снижению риска).

Недостаток изложенного метода "последовательных уступок" состоит в необходимости получения дополнительной информации от принимающего решение о величине "уступки" по каждому критерию(кроме последнего).

. Задача принятия решений в условиях риска. Выбор производимого товара

Фирма Х может выпускать продукцию одного из следующих пяти видов: зонтики(з), куртки(к), плащи(п), сумки(с), шляпы(ш). Глава фирмы должен принять решение - какой из этих видов продукции выпускать в течение предстоящего летнего сезона. Прибыль фирмы зависит от того, каким будет лето - жарким, дождливым или умеренным, и определяется нижестоящей таблицей. Выбор какого варианта производства будет оптимальным?

При отсутствии дополнительной информации о состояниях среды эта задача будет задачей выбора решения в условиях неопределенности, и ее решение возможно при принятии какой-либо гипотезы о поведении среды. Если принимающий решение имеет информацию о вероятностях наступления холодной, теплой и умеренной зимы, то указанная задача становится задачей принятия решения в условиях риска. В нашем случае необходимая дополнительная информация может быть взята из статистических данных (наблюдений за погодой в данной местности). Предположим, что вероятность холодной, теплой и умеренной зимы равна, соответственно, 0.2; 0.5; 0.3. Тогда получаем задачу принятия решений в условиях риска, заданную таблицей

Найдем ожидаемые выигрыши, соответствующие альтернативамз = 85·0.2+34·0.5+26·0.3 = 41,8; MС = 60*0.2+37·0.5+40·0.3 = 42,5;к = 60·0.2+22·0.5+57·0.3 = 40,1; Mш = 50·0.2+30·0.5+45·0.3 = 38,5;п = 64·0.2+29·0.5+30·0.3 = 36,3;

Далее, определим дисперсии случайных величин عп, в, عш, عС, عб, (здесь удобно использовать следующее свойство дисперсии: Dع=Mع2-(Mع)2).

DعЗ=7225*0,2+1156*0,5+676*0,3-1747,24=478,56

DعК=3600*0,2+484*0,5+3249*0,3-1608,01=328,69

DعП=4096*0,2+841*0,5+900*0,3-1317,69=192,01

Dعс=3600*0,2+1369*0,5+1600*0,3-1806,25=78,25

DعШ=2500*0,2+900*0,5+2025*0,3-1482,25=75,25

Среднеквадратичные отклонения рассматриваемых случайных величин таковы:

ϬЗ=√478,56 = 21,9;

ϬК=√328,69=18,1;

ϬП=√192,01=13,9;

ϬС =√78,25=8,8;

ϬШ =√75,25=8,7;

Составим таблицу значений критериев М и Ϭ для каждой альтернативы.

Представим рассматриваемые альтернативы точками на координатной плоскости переменных (М,Ϭ)(рис.2), находим Парето-оптимальное множество{с,ш,к}. Окончательный выбор оптимальной альтернативы должен производиться из этого множества. Сужение Парето-оптимального множества (в идеале - до одного элемента)может быть произведено только при наличии дополнительной информации о соотношении критериев М и Ϭ; в частности, такое сужение может быть произведено методом субоптимизации или методом лексикографической оптимизации - как это схематично ранее.

Рис.2

Попробуем найти оптимальное решение при помощи обобщенного критерия q. Здесь

q(з) = 41,8-21,9λ,

q(К) = 40,1 - 18,1λ,

q(П) = 36,3 - 13,5λ,

q(С) = 42,5 - 8,8λ,

q(Ш) = 38,5 - 8,7λ,

Для установления ранжирования Парето-оптимального множества {с, ш,к}по обобщенному критерию q найдем вначале нижнюю и верхнюю границы меры несклонности к риску. Имеем:

(Мк-МШ)/(Ϭк-ϬШ)=(40,1-38,5)/(18,1-8,7)=0,17

(Мк-Мс)\(Ϭк-Ϭс)=(40,1-42,5)/(18,1-8,8)=-0,26

отсюда λ’= min(-0,26;0,17;40) = -0,26, λ* = max(-0,26;0,17;40) =40. Таким образом, интервал (-∞,+∞) разбивается на три интервала:( -∞,-0,26) - зона склонности к риску (зона малой осторожности); (40, +∞) - зона большой несклонности к риску (зона большой осторожности); [-0,26,40] - зона неопределенности.

Получаем:

)Если для принимающего решение его мера несклонности к риску -∞ ≤ λ < -0,26, то для него ранжирование множества Парето-оптимальных альтернатив совпадет с их ранжированием по величине ожидаемого выигрыша: СКШ (знаком обозначается предпочтение по величине обобщенного критерия q); при этом оптимальной будет альтернатива С;

) Если для принимающего решение его мера несклонности к риску λ >40, то для него ранжирование множества Парето-оптимальных альтернатив совпадет с их ранжированием по показателю риска: ШСК ; при этом оптимальной будет альтернатива Ш .

Рассмотрим теперь случай, когда мера несклонности принимающего решение к риску попадает в зону неопределенности. Возьмем, например, λ = 2. Тогда q(к) = 40,1-21.9 · 2 = -3,7; q(С) = 42,5 - 8,8 · 2 = 34,9; q(Ш) = 38,5 −8,7 · 2 = 21.1. Получаем ранжирование СШК . Таким образом, в этом случае предпочтение для пары (К,Ш) определяется по величине ожидаемого выигрыша, а для пары (Ш,С) - по величине риска.

Заключение

Проведя исследования, я установили, что если предприниматель склонен к риску, то лучшей альтернативой для него будет выпуск сумок.

Если же предприниматель осторожен, он старается минимизировать риски, то лучшая альтернатива - шляпы. Однако, стоит заметить, что разница в величине отклонения с сумками минимальна.

В случае, когда предприниматель безразличен к риску, лучшей альтернативой для выпуска являются также сумки.

Список литературы

1)Розен В.В., Математические модели принятия решений в экономике, Москва, Высшая школа, 2002.

)Орлов А.И., Теория принятия решений, Москва, Март, 2004.

3)Балабанов И.Т. Риск-менеджмент. - Москва. Финансы и статистика, 2001.

)Лапуста М.Г., Шаршукова Л.Г. Риски в предпринимательской деятельности. - Москва, ИНФРА-М, 2003.

)Ступаков В.С., Токаренко Г.С. Риск-менеджмент. - Москва.: Финансы и статистика, 2005.

)Шапкин А.С. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. - Москва, Дашков и Ко, 2004.

7) Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю., Моделирование рисковых ситуаций в экономике и бизнесе, Москва, Финансы и статистика, 2000

8) http://nto.immpu.sgu.ru/sites/default/files/3/__17007.pdf

)http://www.elitarium.ru/2010/06/29/prinjatie_reshenijj_neopredelennost.html