Контрпримеры в курсе математического анализа

Контрпримеры в курсе математического анализа

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

СТЕРЛИТАМАКСКИЙ ФИЛИАЛ

ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

"БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ"

Физико-математический факультет

Кафедра математического анализа

Курсовая работа

"Контрпримеры в курсе математического анализа "

Выполнил: студент группы ФИ-21

Кидрячев Айсуак Анурович

Кандидат физ.-мат. наук

Каримов Руслан Халикович

Стерлитамак 2013

Содержание

Введение

1. Контрпримеры в дифференциальном исчислении

2. Контрпримеры в интегральном исчислении

Заключение

Список литературы

Введение

Есть много неверных утверждений, кажущихся на первый взгляд верными. Для опровержения такого рода утверждений нужно построить соответствующий пример; такие примеры называют контрпримерами. Например: "Истинно ли утверждение S ?"-это, пожалуй, наиболее типичный для математики вопрос, когда утверждение имеет вид: "Каждый элемент класса А принадлежит также классу В: А  В". Доказать, что подобное утверждение истинно, - значит доказать включение А  В. Доказать, что оно ложно,- значит найти элемент класса А, не принадлежащий классу В, иными словами, привести контрпример. Например, если утверждение S таково: "Каждая непрерывная функция дифференцируема в некоторой точке", то множества А и В состоят соответственно из всех непрерывных функций и всех функций, дифференцируемых в некоторых точках. Известный же пример Вейер-штрасса непрерывной, но нигде не дифференцируемой функции f является контрпримером для включения А  В, поскольку f является элементом А, не принадлежащим В. Рискуя впасть в чрезмерное упрощение, можно сказать, что математика (за исключением определений, утверждений и выкладок) состоит из двух частей - доказательств и контрпримеров, а математические открытия состоят в нахождении доказательств и построении контрпримеров. Большая часть математических книг посвящена доказательству верных утверждений.

Вообще говоря, примеры в математике бывают двух типов - иллюстративные примеры и контрпримеры. Первые показывают, почему то или иное утверждение имеет смысл, а вторые - почему то или иное утверждение лишено смысла. Можно утверждать, что любой пример является в то же время контрпримером для некоторого утверждения, а именно для утверждения, что такой пример невозможен. Не желая придавать термину контрпример столь универсальный смысл, но допускаем, что его значение достаточно широко, чтобы включить в себя все примеры, роль которых не ограничивается иллюстрацией верных теорем. Так, например, полином как пример непрерывной функции не есть контрпример, но полином как пример неограниченной или непериодической функции является контрпримером. Подобным же образом класс всех монотонных функций на ограниченном замкнутом интервале как класс интегрируемых функций не есть контрпример, однако этот же самый класс как пример функционального, но не векторного пространства является контрпримером.

1. Контрпримеры в дифференциальном исчислении

В некоторых примерах этого параграфа термин производная будет применяться и к бесконечным пределам

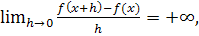
Однако термин дифференцируемая функция используется лишь в том случае, если функция имеет конечную производную в каждой точке своей области определения. Функция называется бесконечно дифференцируемой, если она имеет (конечную) производную любого порядка в каждой точке области определения.

Показательная функция с основанием е будет обозначаться символом е^x или ехр(x).

Предполагается, что все множества, включая области определения и множества значений функций, являются подмножествами. В противном случае будет сделано соответствующее уточнение.

Пример 1. Функция, не являющаяся производной. Функция 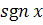 и вообще всякая функция с разрывом в виде скачка не является производной никакой функции, поскольку она не обладает свойством Коши принимать все промежуточные значения, а это свойство присуще не только непрерывным функциям, но и производным. Ниже приводится пример разрывной производной.

Пример 2. Дифференцируемая функция с разрывной производной.

Рассмотрим функцию

f(x)≡

Ее производная

разрывна в точке х = 0.

Пример 3. Разрывная функция, всюду имеющая производную (не обязательно конечную). Для того чтобы такой пример стал возможен, надо расширить определение производной так, чтобы оно включало значения . Тогда разрывная функция sgn х имеет производную

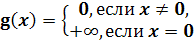
Пример 4. Дифференцируемая функция, производная которой не сохраняет знака ни в какой односторонней окрестности экстремальной точки.

Функция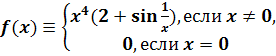

имеет абсолютный минимум в точке х = 0. А ее производная

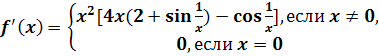
в любой односторонней окрестности нуля принимает как положительные, так и отрицательные значения. Функция f не является монотонной ни в какой односторонней окрестности точки х = 0.

Пример 5. Дифференцируемая функция, производная которой положительна в некоторой точке, но сама функция не монотонна ни в какой окрестности этой точки.

Функция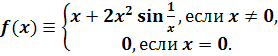

имеет производную, равную

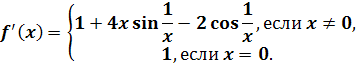
В любой окрестности нуля производная f'(х) имеет как положительные, так и отрицательные значения.

Пример 6. Функция, производная которой конечна, но не ограничена на замкнутом интервале.

Рассмотрим функцию

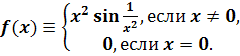
Ее производная

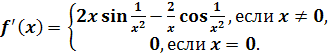
не ограничена на [ - 1, 1].

Пример 7. Функция, производная которой существует и ограничена, но не имеет (абсолютного) экстремума на замкнутом интервале.

Функция

имеет производную

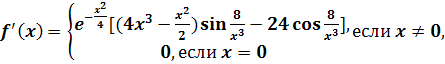
В любой окрестности нуля эта производная имеет значения, как угодно близкие к 24 и - 24. С другой стороны, для 0 < h ≡|x |≤ 1 имеем

поэтому из неравенства 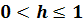 следует, что

Следовательно, множество значений функции f ' на [ - 1, 1] имеет точную верхнюю грань, равную 24, и точную нижнюю грань, равную - 24, и ни одна из этих граней не достигается.

Пример 8. Всюду непрерывная, но нигде не дифференцируемая функция. Функция | х | всюду непрерывна, но не дифференцируема в точке х = 0. С помощью сдвига этой функции можно определить всюду непрерывную функцию, которая не дифференцируема в каждой точке произвольно заданного конечного множества. В этом параграфе мы приведем пример, использующий бесконечное множество сдвигов функции | х | .

Покажем, что функция нигде не дифференцируема. Пусть а - произвольное действительное число, и пусть для всякого натурального п число h_п, равное 4^-n или 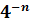, выбрано так, что |f_я(a+ h_n) - f_n(a)|==| h_я|. Тогда величина |f_т(a + h_n) - f_m(a)| имеет одинаковое значение |h_n| для всех т≤ п и равна нулю для т > п. Тогда разностное отношение (f(а + h_n) - f(а))/h_n является целым числом, которое четно при четном п и нечетно при нечетном п. Отсюда следует, что предел

Приведенный пример является модификацией примера, построенного Б. Л. Ван дер Варденом в 1930 г. Первый же пример непрерывной нигде не дифференцируемой функции был построен К. В. Т. Вейерштрассом (немецкий математик, 1815 - 1897 г.):

контрпример производная дифференцируемый функция

где а - целое нечетное число, а число b таково, что . В настоящее время известны примеры непрерывных функций, которые ни в одной точке не имеют даже односторонней конечной или бесконечной производной.

Функция настоящего примера не является монотонной ни на каком интервале. Более того, существует пример функции всюду дифференцируемой и нигде не монотонной. Конструкция этого примера очень сложна и приводит к функции, которая всюду дифференцируема и имеет плотное множество относительных максимумов и плотное множество относительных минимумов.

Пример 9. Дифференцируемая функция, для которой теорема о среднем не имеет места. В этом примере мы снова вынуждены обратиться к комплекснозначной функции. Функция

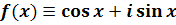
действительного переменного х всюду непрерывна и дифференцируема. Однако не существует такого интервала [а, b], а < b, для которого при некотором 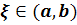 справедливо равенство

Если предположить, что это равенство возможно, то, приравнивая квадраты модулей (абсолютных значений) обеих его частей, мы получим равенство

,

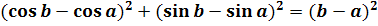которое после элементарных преобразований примет вид

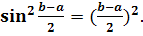
Но так как не существует положительного числа h, такого, что 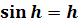, то мы получили противоречие.

Пример 10. Бесконечно дифференцируемая функция f(х), положительная при положительных х и равная нулю при отрицательных х.

Функция

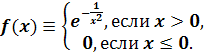
бесконечно дифференцируема, а все ее производные в точке х = 0 равны 0.

Пример 11. Бесконечно дифференцируемая функция, положительная в единичном интервале и равная нулю вне его.

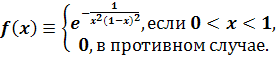
Пример 12. Бесконечно дифференцируемая функция, равная 1 на [1, 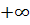) равная 0 на ( 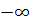, 0] и строго монотонная на [0, 1].

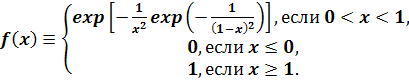
Пример 13. Бесконечно дифференцируемая монотонная функция f, такая, что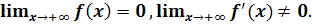

Если не требовать монотонности, то тривиальным примером такой функции будет, например, . Построим пример монотонной функции, обладающей указанным свойством. Положим f(х) равной 1 для х ≤ 1 и равной 1/п на замкнутых интервалах [2п-1, 2п] для n=1, 2. На оставшихся промежуточных интервалах вида (2n, 2n+1) определим f(х) с помощью функции примера 12, применяя горизонтальные и вертикальные сдвиги и умножение на соответствующие отрицательные множители.

2. Контрпримеры в интегральном исчислении

Определение интеграла Римана функции f, заданной на замкнутом интервале [а, b], а также элементарные свойства этого интеграла предполагаются известными. То же самое предполагается относительно основных несобственных интегралов, а в примере 14-относительно интеграла Римана- Стильтьеса.

В некоторых примерах параграфа важное значение имеет понятие множества меры нуль. Множество А  R называется множеством меры нуль, если для всякого ԑ > О существует открытое покрытие множества А счетной совокупностью открытых интервалов, длины которых образуют бесконечный сходящийся ряд с суммой, меньшей е. Ядро всякого множества меры нуль пусто. Говорят, что некоторое утверждение справедливо для почти всех точек или почти всюду, если множество всех точек, для которых это утверждение не имеет места, является множеством меры нуль. Для того чтобы функция f, заданная на замкнутом конечном интервале [а, b], была интегрируема по Риману на этом интервале, необходимо и достаточно, чтобы она была ограничена и почти всюду непрерывна.

Пример 1. Ограниченная функция, не интегрируемая по Риману на конечном замкнутом интервале. Характеристическая функция множества Q всех рациональных чисел, рассматриваемая на замкнутом интервале [0,1], не интегрируема по Риману на нем.

Пример 2. Функция f, для которой   

хотя оба интеграла существуют в смысле Римана.

Функция

определена в замкнутой верхней полуплоскости . Для любого фиксированного значения у эта функция является непрерывной функцией переменного х, а для любого фиксированного значения х - непрерывной функцией переменного у. Однако как функция двух переменных она разрывна в точке (0, 0) (в этом можно убедиться, полагая у = х²). Интегрируя, получаем

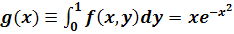
для всякого действительного х (включая х = 0), и, следовательно,  для всякого действительного х (включая х = 0). Если 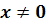, то

Если же x = 0, то, принимая во внимание, что  для всех у (включая у = 0), имеем

Следовательно,

Отметим, что все интегралы, которые встречались в данном примере, - собственные, так как подинтегральные функции являются непрерывными функциями переменной интегрирования.

Пример 3. Функция, интегрируемая по Риману и не имеющая примитивной ни на каком интервале. Если положить A = Q∩[0, 1], то функция f будет интегрируема на [0, 1], так как она монотонна на этом интервале. Однако эта функция не имеет примитивной ни на каком подинтервале из [0,1], поскольку множество точек ее скачков всюду плотно в интервале [0. 1].

Пример 4. Функция, имеющая на замкнутом интервале, но не интегрируемая на нем по Риману. Функция f имеет (конечную) производную g(х) в каждой точке х некоторого замкнутого интервала l. Однако функция g не ограничена, а поэтому не интегрируема по Риману.

Два предыдущих примера (примеры 3 и 4) представляют особый интерес в связи с основной теоремой интегрального исчисления. Первый вариант этой теоремы таков: если функция f(х) (i) интегрируема на интервале [а, b] и (ii) имеет F(х) на этом интервале (F'(х) = f(х) для ), то интеграл Римана функции f(х) можно вычислить по формуле 

Второй вариант гласит: если функция f(х) непрерывна на интервале [а, b], то справедливы утверждения (i) и (ii) с 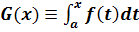, причем для всякой F(х) имеет место формула: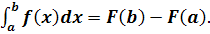

Наконец, третий вариант этой теоремы можно сформулировать так: если f(х) интегрируема на [а, b], а функция F(х) непрерывна на [а, b] и имеет производную F'(х), равную f(х) во всех точках интервала [а, b], за исключением, быть может, конечного числа точек, то интеграл Римана функции f(х) можно вычислить по формуле :

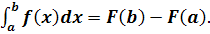
Пример 5. Интегрируемая по Риману функция со всюду плотным множеством точек разрыва. Этим свойством обладает функция примера 3, которая к тому же является монотонной.

Функция также обладающая этим свойством, однако она нигде не монотонна. Для этой функции:

Пример 6. Функция f, для которой 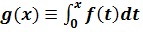  всюду дифференцируема, однако  на всюду плотном множестве. Если f - функция (см. также предыдущий пример), то 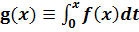  является тождественным нулем и, следовательно,  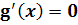для всех х. Поэтому равенство  справедливо лишь для иррациональных x.

Пример 7. Две различные полунепрерывные функции, "расстояние" между которыми равно нулю. В этом случае расстояние d между двумя функциями f и g, интегрируемыми на [а, b], определяется как интеграл от абсолютной величины их разности:

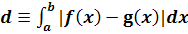
Если f - полунепрерывная функция предыдущего примера, а функция g - тождественный нуль, то f (х) и g(х) не равны во всех рациональных точках х (и, следовательно, f и g, несомненно, являются различными функциями), в то время как определенное выше расстояние d между этими функциями равно нулю.

Пример 8. Интегрируемая по Риману функция, множество точек разрыва которой совпадает с произвольно заданным множеством типа F_σ и меры нуль. Пусть А - заданное множество типа F_σ и меры нуль: А =A₁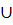A₂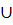 . . . , где А₁, А₂, . . . - замкнутые подмножества некоторого интервала [а, b], причем А_п  A_n+1 для п=1, 2 ..... Далее, пусть А₀ обозначает пустое множество . Определим функцию / следующим образом:

Если с ϵ А, то f разрывна в этой точке. Действительно, пусть с ϵ А_n\ А_n-1. Поскольку А_n\ А_{n- 1} является множеством меры нуль, то у него нет внутренних точек, и, следовательно, с является предельной точкой множества, на котором f принимает значения, отличающиеся от 2^-n по крайней мере на 2^-n-1 . Если же с  А, то f непрерывна в этой точке. В самом деле, пусть задано ԑ > 0. Выберем такое N. что 2^-N < ԑ. После этого возьмем такую окрестность точки с, которая не содержит ни одной точки множеств А₁, А₂ ..... А_N. Тогда в этой окрестности .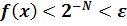

Пример 9. Две функции, интегрируемые по Риману, композиция которых не интегрируема по Риману. Пусть f(x) ≡ 1 для 0 < x ≤ 1 и f(0) ≡ 0. Далее, пусть g - сужение функции f примера 15 параграфа 2 на замкнутый интервал [0, 1]. Тогда f(g(х)) является сужением на [0, 1] характеристической функции множества Q всех рациональных чисел. Эта функция равна 1, если х рационально, и равна 0, если х иррационально.

Пример 10. Не интегрируемая по Риману ограниченная функция, являющаяся пределом возрастающей последовательности интегрируемых по Риману функций. Рассмотрим последовательность {g_n} функций. Если ограничиться замкнутым интервалом [0, 1], то эта последовательность является возрастающей последовательностью интегрируемых по Риману функций, т. е. для каждого х ϵ [0, 1], g_n(х)≤g_п+1(х) при n =1, 2..... Положим   для x ϵ [0, 1].

Тогда g является сужением на замкнутый интервал [0, 1] характеристической функции множества Q всех рациональных чисел, и, следовательно, g не интегрируема по Риману на [0, 1].

Пример 11. Расходящийся несобственный интеграл, имеющий конечное главное значение в смысле Коши. Несобственный интеграл 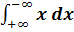   расходится, но его главное значение в смысле Коши равно нулю:

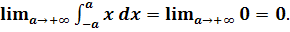
Пример 12. Сходящийся несобственный интеграл 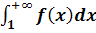 подинтегральная функция которого положительна, непрерывна и не стремится к нулю при . Положим g(п)≡ 1 для всякого целого n > 1, а на замкнутых интервалах [n-n^{- 2}, n] и [n, n + п ^-2] функцию g определим как линейную и равную нулю в концевых нецелых точках. Наконец, в тех точках х ≥ 1, где g(х) еще не определена, положим g(х)≡ 0. Тогда функция

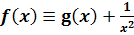
положительна и непрерывна для х ≥ 1, равенство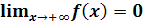

не имеет места, а несобственный интеграл

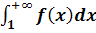
Если опустить требование положительности функции, то простым примером, который удовлетворяет оставшимся требованиям, является интеграл

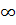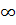Пример 13. Сходящийся на интервале [0, +) несобственный интеграл, подинтегральная функция которого не ограничена на любом интервале вида [а, +), где а>0. Этим условиям удовлетворяет несобственный интеграл

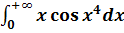
Можно построить такой же пример с положительной и всюду непрерывной подинтегральной функцией. При этом можно воспользоваться методом, подобным тому, который был применен в предыдущем примере, полагая g(п) ≡ п и рассматривая замкнутые интервалы [n - n^-3, n]и[n, n + n^-3].

Пример 14. Функции f и g, такие, что интеграл Римана - Стильтьеса от f относительно g существует на [а, b] и [b, с], но не существует на [а, с].

Положим

и пусть а = 0, b = 1 и с = 2. Тогда

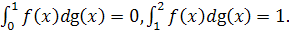
Но поскольку f и g имеют общую точку разрыва х =1, то интеграл

не существует.

Заключение

Данная курсовая работа посвящена контрпримерам в курсе математического анализа. В процессе его реализации были рассмотрены несколько теорем и задач доказываемые при помощи контрпримера. Главной проблемой является то что при встрече с некоторыми вопросами и моментами, не имея достаточного опыта, легко можно дать неправильный ответ или же неправильно представить истинную суть задачи.

В первой главе были рассмотрены контрпримеры в разделе дифференцирование. В начале главы были приведены основные понятия являющиеся существенным в данной главе. Далее были рассмотрены примеры задач и теорем доказываемые при помощи контрпримера.

Во второй главе так же в начале были рассмотрены основные понятия по теме Интеграл Римана, а далее были предложены примеры контрпримеров по данной теме.

Список литературы

1.      Ильин В. А., Позняк Э. Г. Основы математического анализа Часть I: М.: Физматлит, 2005. С. 210-234.

.        Г. И. Архипов, В. А. Садовничий, В. Н. Чубариков. Лекции по математическому анализу : учеб. для вузов - 5-е изд., испр. Дрофа, 2005. с. 145-182.

.        Дороговцев А. Я. Математический анализ. Краткий курс в современном изложении (2-е издание). Киев: Факт, 2005. с. 287- 305.

.        Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. ( В 3-х томах ). - М.: Физматлит, 2008. с. 307-338.

.        Сакс С. , Теория интеграла, Москва : Факториал Пресс, 2006г. с. 209

.        Гелбаум Б., Олмстед Д., Контрпримеры в анализе. серия: Физико-математическое наследие: математика изд -во "ЛКИ", 2010 г. с. 49 -62.

.        Лебег А. Интегрирование и отыскание примитивных функций, М, - Л. , 1934. с. 302-310.

.        Гельфанд И.М. , Лекция по линейной алгебре, М., изд -во "Добросвет", 2010г. с. 378.

.        Хаусдорф Ф., Теория множества, М., изд -во "ЛКИ", 2010. с. 407.