|
1 масив ( 7 тис.
га)
|
2 масив ( 8 тис.
га)
|
3 масив ( 9 тис.
га)
|
|
Буряк
|
х11
|
х12
|
х13
|
|
Морква
|
х21
|
х22
|
х23
|
|
Картопля
|
х31
|
х32
|
х33
|
Тоді обмеженість площ полів дає систему нерівностей:
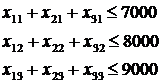
Враховуючи задану врожайність, буряку буде вирощено (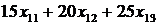 ) ц, моркви - (
) ц, моркви - ( ) ц, картоплі - (
) ц, картоплі - (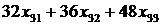 ) ц.
) ц.
За планом передбачено зібрати не менше як 80000 ц буряку, 50000 ц
моркви і 70000 ц картоплі, тобто:
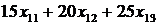 ≥ 80000
≥ 80000
 ≥ 50000
≥ 50000
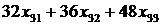 ≥ 70000
≥ 70000
Площа не може бути від’ємною, тому: 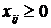 ,
,
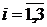 ,
, 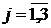 .
.
За 1 ц буряку господарство одержує прибуток 20 у.о., за 1 ц моркви - 25
у.о. і за 1 ц картоплі - 15 у.о. Тоді прибуток від реалізації вирощених овочів
(цільова функція) запишеться у вигляді:
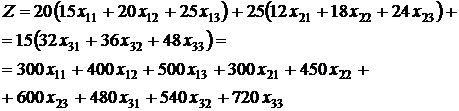
Прибуток необхідно максимізувати, тобто 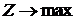 .
.
Одержуємо задачу лінійного програмування в стандартній формі:
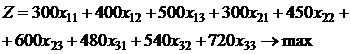
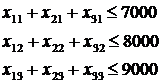
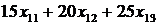 ≥ 80000
≥ 80000
 ≥ 50000
≥ 50000
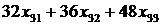 ≥ 70000
≥ 70000
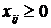 ,
,
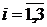 ,
, 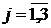 .
.
Задача 2. Графічним методом визначити оптимальний план задачі
лінійного програмування
2 х1 + х2 ≤ 10
х1 + 2 х2 ≥ 2
- х1 + 3 х2 ≤ 3 Z = 4 х1 + 3 х2 →
mах (mіn)
х1 ≥ 0, х2 ≥ 0
Розв’язання:
Спочатку побудуємо многокутник розв’язків; що визначається
системою обмежень.
Для цього побудуємо граничні прямі, рівняння яких отримуємо,
змінив знаки нерівностей на знак “=”. Потім визначаємо півплощину, яка
відповідає кожній нерівності. Для цього в нерівність підставляємо координати
будь-якої точки, наприклад, початку координат (х1=0; х2=0).
Якщо отримаємо вірну нерівність, то шукана півплощина містить цю точку, інакше
- не містить. Потрібну півплощину позначаємо стрілками. Перетин даних
півплощин, який лежить в першій чверті (х1 ≥ 0; х2 ≥
0) і дає шуканий многокутник розв’язків.
Будуємо граничні прямі і визначаємо потрібні півплощини:
(1)
х1 + х2 = 10 - пряма проходить через
точки (2; 6) і (5; 0)
х1 + х2 < 10 => 0 + 0 = 0 < 10
вірно, тобто шукана півплощина містить точку (0; 0), і тому лежить нижче від
прямої (1).
(2)
х1 + 2 х2 = 2 - пряма проходить через
точки (0; 1) і (2; 0)
х1 + 2 х2 > 2 => 0 + 0 = 0 >
2, не вірно, півплощина лежить вище від (2).
(3)
х1 + 3 х2 = 3 - пряма проходить через
точки (0; 1) і (3; 2)
х1 + 3 х2 < 3 => 0 + 0 = 0 < 3, вірно, півплощина лежить
нижче від (3).
Перетин цих півплощин в першій чверті - це чотирикутник АВСD.
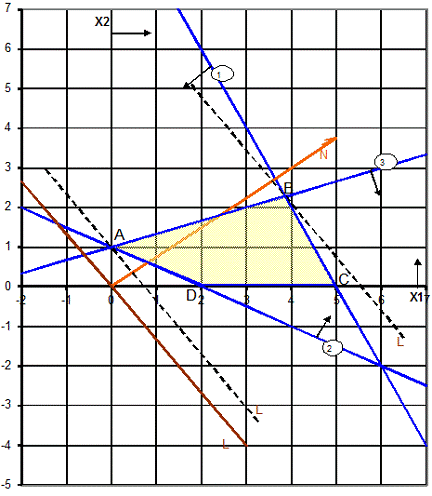
Далі будуємо вектор - градієнт N, який складається з коефіцієнтів
цільової функції Z = 4 х1 + 3 х2, тобто N = (4; 3). Цей вектор визначає напрям
зросту функції Z , тобто її значення збільшується в напрямі вектора N і зменьшується в протилежному
напрямі. Потім будуємо пряму рівня (позначимо її буквою L) перпендикулярно до вектора N в початку координат. Вона має
рівняння Z = 0.
Починаємо зміщувати (пересувати) пряму L паралельно самій собі в напрямі
вектора N. Перша зустрінута вершина
многокутника - точка А(0; 1) - буде точкою mіn. Остання зустрінута вершина
многокутника - точка В - буде точкою mах.
Таким чином, при х1 = 0; х2 = 1 функція Z досягає свого мінімального
значення:
mіn = 4 х1
+ 3 х2 = 4 · 0 + 3 · 1 = 3
Знаходимо координати точки В, розв’язуючи сумісно рівняння прямих, на
перетину яких вона лежить, тобто рівняння (1) і (3) :
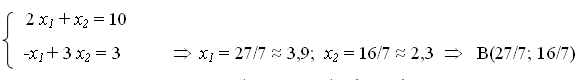
Таким чином, при х1 = 27/7 ; х2 = 16/7 функція Z досягає свого максимального
значення:
mах = 4 х1
+ 3 х2 = 4 · 27/7 + 3 · 16/7 = 156/7 ≈ 22,3.
Відповідь: Zmіn = 3 при х1 = 0; х2
= 1; mах = 156/7 при х1 = 27/7; х2 = 16/7.
Задача 3. Розв’язати задачу лінійного програмування
симплексним методом
= -х1 - 2 х2 + 2 х3 (mіn)
х1 + х2 + х3 = 10
х1 - х2 ≤ 2
хj ≥ 0 j =1,2,3.
Розв’язання:
Приводимо задачу до каноничного вигляду: додаємо до лівої
частини нерівності нову додатну змінну х4 ≥ 0.
= -х1 - 2 х2 + 2 х3 →
mіn
х1 + х2 + х3 = 10
х1 - х2 + х4 = 2
хj ≥ 0 j =1,2,3,4.
Система обмежень містить одиничну матрицю, тому для розв’язку
використовуємо звичайний симплекс-метод.
Векторна форма запису даної задачі така: Z =C•х → max
х1A1 +х2A2 + х3A3 + х4A4 = A0, х ≥ 0
Тут С = (С1, C2, C3, C4) = (-1, -2, 2, 0) - коефіцієнти цільової функції Z.
A0 = 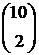 ; A1 =
; A1 = 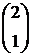 ; A2 =
; A2 = 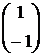 ; A3 =
; A3 =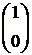 ; A4 =
; A4 =  ;
;
Ця задача має опорний план X1=(0, 0, 10, 2), визначаємий системою двох одиничних
векторів A3, A4.
Складаємо першу симплекс - таблицю:
Таблиця 1
|
і
|
Баз
|
Сбаз
|
A0
|
-1
|
-2
|
2
|
0
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
|
1
|
A3
|
2
|
10
|
2
|
1
|
1
|
0
|
|
2
|
A4
|
0
|
2
|
1
|
-1
|
0
|
1
|
|
3
|
|
Δj
|
20
|
5
|
4
|
0
|
0
|
Перевірку опорного плану на оптимальність будемо проводити по
рядку і = 3.
Умова оптимальності в задачі на mіn - це відсутність в останньому
(індексному) рядку додатних оцінок. Працюємо за наступним алгоритмом:
1.
Переглядаємо
знаки всіх оцінок Δj. Якщо всі Δj ≤ 0, то план оптимальний.
2.
Якщо не
всі Δj ≤
0, то серед значень Δj > 0 обираємо найбільше. Цей
стовпець буде направляючим стовпцем. Направляючим рядком буде рядок, в якому
досягається min серед відношень елементів
стовпця A0 до елементів направляючого стовпця.Тоді елемент, який
стоїть на перетину направляючого рядка і направляючого стовпця, буде головним
елементом.
3.
За
допомогою головного елемента переходимо до наступної симплекс - таблиці,
виконуючи перетворення Жордано-Гауса:
Усі елементи направляючого рядка ділимо на головний елемент.
Значення решти елементів в нової таблиці дорівнює старому значенню мінус
добуток відповідних елементів направляючого рядка і направляючого стовпця,
поділений на головний елемент.
4.
Повертаємось
до кроку 1.
Серед дельт є додатні: 5, 4. За направляючий стовпчик візьмемо А1, оскільки max(|5|, |4|)=5. За направляючий візьмемо
2-й рядок, оскільки min(10 / 2, 2 / 1)=2 / 1. Головний елемент = 1. Переходимо до
таблиці II.
Таблиця 2
|
і
|
Баз
|
Сбаз
|
A0
|
-1
|
-2
|
2
|
0
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
|
1
|
A3
|
2
|
6
|
0
|
3
|
1
|
-2
|
|
2
|
A1
|
-1
|
2
|
1
|
-1
|
0
|
1
|
|
3
|
Δj
|
10
|
0
|
9
|
0
|
-5
|
X2=(2, 0, 6, 0).
План X2 не є оптимальним. Серед дельт є додатні: 9 > 0. За направляючий стовпчик візьмемо А2. За направляючий візьмемо 1-й рядок, оскільки в другому стоїть від’ємне
число.
Таблиця 3
|
і
|
Баз
|
Сбаз
|
A0
|
-1
|
-2
|
2
|
0
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
|
1
|
A2
|
-2
|
2
|
0
|
1
|
1/3
|
-2/3
|
|
2
|
A1
|
-1
|
4
|
1
|
0
|
1/3
|
1/3
|
|
3
|
Δj
|
-8
|
0
|
0
|
-3
|
1
|
X3=(4, 2, 0, 0).
План X3 не є оптимальним, тому що серед дельт є додатні: 1 > 0. За направляючий стовпчик візьмемо А4. За направляючий візьмемо 2-й рядок.
Таблиця 4
|
і
|
Баз
|
Сбаз
|
A0
|
-1
|
-2
|
2
|
0
|
|
|
|
|
A1
|
A2
|
A3
|
A4
|
|
1
|
A2
|
-2
|
10
|
2
|
1
|
1
|
0
|
|
2
|
A4
|
0
|
12
|
3
|
0
|
1
|
1
|
|
3
|
Δj
|
-20
|
-3
|
0
|
-4
|
0
|
X4=(0, 10, 0, 12).
В таб. 4 в рядку і = 3 немає додатмних оцінок в стовпцях A1
- A4, тому цей план є оптимальним, він міститься в стовпці A0
:
х1 = 0; х2 = 10; х3 = 0 ; х4
= 12 (додаткова змінна).mіn = -20.
Відповідь: Zmіn = -20 при х1 = 0; х2 = 10; х3
= 0.
Задача 4. Записати двоїсту задачу до поставленої задачі
лінійного програмування. Розв’язати одну з задач симплексним методом і
визначити оптимальний план іншої задачі
 (1)
(1)
Розв’язання:
Спочатку треба перевірити, чи записана дана задача у відповідному
вигляді. Якщо цільова функція задачі максимізується, то всі обмеження
нерівності повинні мати знак 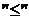 ,
а якщо мінімізується, то знак
,
а якщо мінімізується, то знак 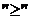 .
Якщо деяка нерівність не відповідає цій умові, то її треба помножити на (-1),
при цьому знаки всіх коефіцієнтів і зак нерівності змінюється на протилежний.
Дана задача - це задача на знаходження mах цільової функції Z, тому всі
нерівності повинні мати знак “≤”. В задачі (1) перша і друга нерівність
мають знак
.
Якщо деяка нерівність не відповідає цій умові, то її треба помножити на (-1),
при цьому знаки всіх коефіцієнтів і зак нерівності змінюється на протилежний.
Дана задача - це задача на знаходження mах цільової функції Z, тому всі
нерівності повинні мати знак “≤”. В задачі (1) перша і друга нерівність
мають знак  , тому множимо їх на(-1):
, тому множимо їх на(-1):
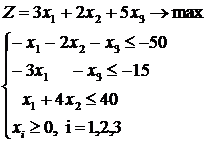 (1’)
(1’)
Будуємо двоїсту задачу:
. Так як цільова функція прямої задачі (1) була Z →
mах, то в двоїстої буде →
mіn.
. Якщо цільова функція задачі максимізується, то всі
обмеження - нерівності повинні мати знак “≤”, а якщо мінімізується, то
знак “≥”, тобто в двоїстої задачі знаки будуть “≥”.
. Коефіцієнти цільової функції Z (x) = 3 х1 + 2 х2 +
5 х3 прямої задачі будуть вільними членами системи обмежень двоїстої
задачі (тобто числа 3; 2; 5), і навпаки: вільні члени системи обмежень прямої
задачі будуть коефіцієнтами цільової функції двоїстої задачі ( тобто числа -50;
-15; 40).
. Матриця коефіцієнтів обмежень двоїстої задачі є
транспонованою відносно матриці коефіцієнтів обмежень прямої задачі.
5. Якщо в задачі (1) було три змінні (х1
, х2, х3) і три обмеження, то в двоїстої задачі буде три обмеження і три змінні (у1 , у2 і у3).
6. Кожному обмеженню - нерівності прямої задачі
відповідає невід’ємна змінна двоїстої задачі і навпаки. Тобто: в прямої задачі
всі обмеження записані у вигляді нерівностей, тому всі три двоїстих змінних -
невід’ємні (у1 ≥0, у2 ≥0, у3 ≥0)
і навпаки: всі змінні прямої задачі невід’ємні (х1 ≥ 0 ; х2
≥ 0; х3 ≥ 0 ), тому обмеження двоїстої задачі будуть
записані у вигляді нерівностей.
Таким чином одержуємо:
Двоїста задача:

Використаємо теорему двоїстості (перша теорема):
Якщо одна з задач має оптимальний план, то друга також має
оптимальний розв’язок, причому значення їх цільових функцій збігаються, тобто Zmах
= Fmіn .
Якщо цільова функція однієї з задач не обмежена на множині
розв’язків, то друга задача не має розв’язків.
Таким чином необхідно розв’язати одну з задач і по її
розв’язку знайти розв’язок другої задачі. В даному випадку зручніша для
розв’язання задача (1). Запишемо її у канонічному вигляді, ввівши нові додатні
змінні х4 ≥ 0, х5 ≥ 0, х6 ≥
0. Віднімаємо їх від лівої частини нерівностей, якщо знак нерівностей “≥”
і додаємо, якщо знак “≤”:
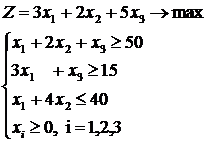 Þ
Þ 
Система обмежень не містить одиничної матриці, тому для побудови початкового
опорного плану використовуємо метод штучного базису (М- метод).
Запишемо розширену задачу.
В перше та друге рівняння вводимо штучні змінні х7 ≥
0, х8 ≥ 0 . Таким чином розширена задача має вигляд:
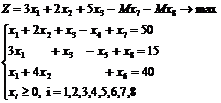
Складемо першу симплекс - таблицю для розширеної задачі.
Умова оптимальності в задачі на mах - це
відсутність в останньому (індексному) рядку від’ємних оцінок.
Таблиця 1
|
і
|
Баз
|
Сбаз
|
А0
|
3
|
2
|
5
|
0
|
0
|
0
|
-M
|
-M
|
|
|
|
|
А1
|
А2
|
А3
|
А4
|
А5
|
А6
|
А7
|
А8
|
|
1
|
А7
|
-М
|
50
|
1
|
2
|
1
|
-1
|
0
|
0
|
1
|
0
|
|
2
|
А8
|
-M
|
15
|
3
|
0
|
1
|
0
|
-1
|
0
|
0
|
1
|
|
3
|
А6
|
0
|
40
|
1
|
4
|
0
|
0
|
0
|
1
|
0
|
0
|
|
4
|
Dj
|
0
|
-3
|
-2
|
-5
|
0
|
0
|
0
|
0
|
|
5
|
|
-65
|
-4
|
-2
|
-2
|
1
|
1
|
0
|
0
|
0
|
X1=(0, 0, 0, 0, 0, 40, 50, 15)
План X1 не є оптимальним. Серед дельт є від'ємні: -4, -2, -2.
За направляючий стовпчик візьмемо А1, оскільки max(|-4|, |-2|, |-2|)=4.
За направляючий візьмемо 2-й рядок, оскільки min(50 / 1, 15 / 3, 40 / 1)=15 /
3. Головний
елемент = 3.
Переходимо до таблиці 2.
Таблиця 2
|
і
|
Баз
|
Сбаз
|
А0
|
3
|
2
|
5
|
0
|
0
|
0
|
-M
|
-M
|
|
|
|
|
А1
|
А2
|
А3
|
А4
|
А5
|
А6
|
А7
|
А8
|
|
1
|
А7
|
-М
|
45
|
0
|
2
|
2/3
|
-1
|
1/3
|
0
|
1
|
-1/3
|
|
2
|
А1
|
3
|
5
|
1
|
0
|
1/3
|
0
|
-1/3
|
0
|
0
|
1/3
|
|
3
|
А6
|
0
|
35
|
0
|
4
|
-1/3
|
0
|
1/3
|
1
|
0
|
-1/3
|
|
4
|
Dj
|
15
|
0
|
-2
|
-4
|
0
|
-1
|
0
|
0
|
1
|
|
5
|
|
-45
|
0
|
-2
|
-2/3
|
1
|
-1/3
|
0
|
0
|
4/3
|
X2=(5, 0, 0, 0, 0, 35, 45)
План X2 не є оптимальним. Серед дельт є від'ємні: -2, -2/3,
-1/3. За направляючий стовпчик візьмемо А2, оскільки
max(|-2|, |-2/3|, |-1/3|)=2. За направляючий візьмемо 3-й рядок, оскільки
min(45 / 2, 35 / 4)=35 / 4
Таблиця 3
|
і
|
Баз
|
Сбаз
|
А0
|
3
|
2
|
5
|
0
|
0
|
0
|
-M
|
-M
|
|
|
|
|
А1
|
А2
|
А3
|
А4
|
А5
|
А6
|
А7
|
А8
|
|
1
|
А7
|
-М
|
55/2
|
0
|
0
|
5/6
|
-1
|
1/6
|
-1/2
|
1
|
-1/6
|
|
2
|
А1
|
3
|
5
|
1
|
0
|
1/3
|
0
|
-1/3
|
0
|
0
|
1/3
|
|
3
|
А2
|
2
|
35/4
|
0
|
1
|
-1/12
|
0
|
1/12
|
1/4
|
0
|
-1/12
|
|
4
|
Dj
|
65/2
|
0
|
0
|
-25/6
|
0
|
-5/6
|
1/2
|
0
|
5/6
|
|
5
|
|
-55/2
|
0
|
0
|
-5/6
|
1
|
-1/6
|
1/2
|
0
|
7/6
|
X3=(5, 35/4, 0, 0, 0, 0, 55/2)
План X3 не є оптимальним. Серед дельт є від'ємні: -5/6, -1/6.
За направляючий стовпчик візьмемо А3, оскільки max(|-5/6|, |-1/6|)=5/6.
За направляючий візьмемо 2-й рядок, оскільки min(55/2 / 5/6, 5 / 1/3)=5 / 1/3
Таблиця 4
|
і
|
Баз
|
Сбаз
|
А0
|
3
|
2
|
5
|
0
|
0
|
0
|
-M
|
-M
|
|
|
|
|
А1
|
А2
|
А3
|
А4
|
А5
|
А6
|
А7
|
А8
|
|
1
|
А7
|
-М
|
15
|
-5/2
|
0
|
0
|
-1
|
1
|
-1/2
|
1
|
-1
|
|
2
|
А3
|
5
|
15
|
3
|
0
|
1
|
0
|
-1
|
0
|
0
|
1
|
|
3
|
А2
|
2
|
10
|
1/4
|
1
|
0
|
0
|
0
|
1/4
|
0
|
0
|
|
4
|
Dj
|
95
|
25/2
|
0
|
0
|
0
|
-5
|
1/2
|
0
|
5
|
|
5
|
|
-15
|
5/2
|
0
|
0
|
1
|
-1
|
1/2
|
0
|
2
|
X4=(0, 10, 15, 0, 0, 0, 15)
План X4 не є оптимальним. Серед дельт є від'ємні: -1. За
направляючий стовпчик візьмемо А5. За направляючий візьмемо 1-й рядок.
Таблиця 5
|
і
|
Баз
|
Сбаз
|
А0
|
3
|
2
|
5
|
0
|
0
|
0
|
-M
|
-M
|
|
|
|
|
А1
|
А2
|
А3
|
А4
|
А5
|
А6
|
А7
|
А8
|
|
1
|
А5
|
0
|
15
|
-5/2
|
0
|
0
|
-1
|
1
|
-1/2
|
1
|
-1
|
|
2
|
А3
|
5
|
30
|
1/2
|
0
|
1
|
-1
|
0
|
-1/2
|
1
|
0
|
|
3
|
А2
|
2
|
10
|
1/4
|
1
|
0
|
0
|
0
|
1/4
|
0
|
0
|
|
4
|
Dj
|
170
|
0
|
0
|
0
|
-5
|
0
|
-2
|
5
|
0
|
|
5
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
X5=(0, 10, 30, 0, 15, 0)
Всі штучні вектори вилучені з базису, тому визначення оптимального плану
продовжимо за передостаннім рядком. План X5 не є оптимальним. Серед
дельт є від'ємні: -5, -2. За направляючий стовпчик візьмемо А4, оскільки max(|-5|, |-2|)=5. Але стовпчик А4 не містить додатніх елементів!
Це означає, що цільова функція задачі не обмежена на множині
розв’язків, тоді двоїста до неї задача не має розв’язку.
Відповідь: задача не має розв’язку.
Задача 5. Розв’язати транспортну задачу
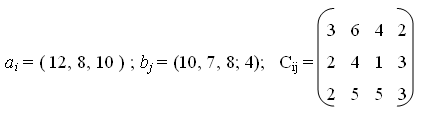
Розв’язання:
Нехай у пунктах постачання А1, А2, А3
є однорідний вантаж в обсязі а1, а2, а3
одиниць відповідно, цей вантаж треба транспортувати у пункти В1, В2,
В3, В4 в обсязі b1, b2, b3
, b4 одиниць відповідно. Потреби замовників (в умовних одиницях),
запаси вантажу на кожному пункті постачання (у тих же одиницях), і тарифи
(вартість перевезення одиниці вантажу з даного пункту постачання данному
замовнику) вказані в умові задачі.
Потрібно спланувати перевезення так, щоб загальна сума
вартості перевезень була найменьшою. Запишемо дані в таблицю:
Таблиця 1
|
Пункти постачання
|
Пункт призначення
|
Запаси
|
|
В1
|
В2
|
В4
|
|
|
А1
|
3
|
6
|
4
|
2
|
12
|
|
А2
|
2
|
4
|
1
|
3
|
8
|
|
А3
|
2
|
5
|
5
|
3
|
10
|
|
Потреби
|
10
|
7
|
8
|
4
|
|
Складемо математичну модель задачі. Нехай:
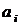 -
кількість вантажів на і-му пункті відправлення Аі (запаси)
-
кількість вантажів на і-му пункті відправлення Аі (запаси)
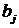 -
кількість вантажів, що потребує j-й пункт призначення Вj (потреби).
-
кількість вантажів, що потребує j-й пункт призначення Вj (потреби).
Сіj - вартість перевезення одиниці вантажу з пункта Аі
в пункт Вj.
хіj - кількість вантажу , що планується перевезти з пункта Аі
в пункт Вj (план перевезень).
Тоді загальна вартість усіх перевезень буде: Z = Σ Σ Cij хij , її необхідно мінімізувати. Кількість
вантажів не може бути від’ємною, тому хіj ≥
0.
Сумарні запаси Σ аі
= 12 + 8 + 10 = 30 од., сумарні потреби Σ bj= 10 + 7 + 8 + 4 = 29 од. Σ аі ≠ Σ bj, запаси не
дорівнюють потребам, тобто це відкрита модель транспортної задачі.
Вводимо фіктивного споживача В5,ф з потребами
b5 = 30 - 29 = 1 од.
З умови задачі випливає, що повинні виконуватись таки умови : Σ хіj
= аі ,і =1,2,3, тобто весь вантаж з пунктів Аі необхідно
вивезти. Крім того потреби Вj повинні бути повністю задоволені, тобто Σ хіj
= bj , j = 1,2,3,4,5. Таким
чином, математична модель задачі має вигляд :
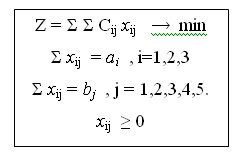
Для пошуку початкового опорного плану використаємо метод “мінімального
елемента”. Складемо транспортну таблицю, в кути клітин запишемо задані тарифи Сіj ,а в середини клітин будемо послідовно заносити
значення хіj за схемою :
З усієї таблиці вартостей обираємо клітину Аі Вj з найменшою вартостю Сіj, тобто шукаємо min Сіj , і заносимо до неї число хіj = min { аі , bj }. Потім викреслюємо і більше не розглядаємо рядок, що відповідає
постачальнику, запаси якого повністю вичерпано, або стовпець, що відповідає
споживачу, потреби якого повністю задоволено.
У частині таблиці , що залишилася після викреслювання, знову шукаємо min Сіj і процес розподілу продовжуємо доти, поки всі
запаси не буде вичерпано, а потреби - задоволено. Вартості Сіj в
фіктивному стовпці В5,ф всі дорівнюють нулю. Ці фіктивні клітини
заповнюємо в останню чергу.
Таблиця 1
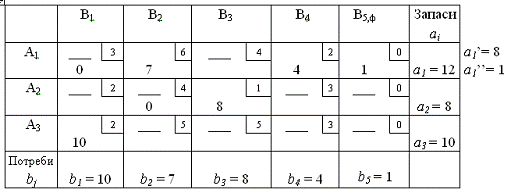
1) min Сіj =C23=1 ; х23 =min { а2 , b3 } = min {8, 8} = 8;
Рядок А2 і стовпець В3 викреслюємо
2) min Сіj = С14 = 2; х14 = min { а1, b4} = min {12, 4} = 4;
Стовпець В4 викреслюємо, а1 ’ = 12 - 4
= 8
3) min Сіj =C31 = 2; х31 = min { а3, b1 } = min {10, 10} = 10;
Рядок А1 і стовпець В3 викреслюємо
4) min Сіj = С12 = 3; х12 = min { а1’, b2} = min {8, 7} = 7;
Стовпець В2 викреслюємо, а1 ’’ = 8 - 7
= 1
5) Залишилася одна фіктивна клітина:
х15 = mіn {1, 1} = 1.
Транспортну таблицю заповнено. Одержано 5 зайнятих клітин.
Початковий опорний план має вигляд :
х12 = 7; х14 = 4; х15 = 1; х23 = 8; х31 = 1; решта хіj = 0
Вартість цього плану :
Z = 7∙6 + 4∙2 + 1∙0 + 8∙1 + 10·2 = 78 у.о.
Тепер потрібно перевірити цей план на оптимальність за
допомогою метода потенціалів.
Опорний план повинен бути невиродженим, тобто в таблиці
повинно бути m + n - 1 = 3 + 5 - 1 = 7 зайнятих клітин, тому в дві не зайняті
клітини, наприклад А1В1 і А2В2,
заносимо нульовв перевозки х11 = 0, х22
= 0 і вважаємо
ці клітини зайнятими.
Числа ui і vj - це потенціали, які знаходимо з умови : ui + vj = Сіj для зайнятих клітин, причому
u1= 0. В таблиці є 7 зайнятих клітин,
тому одержуємо систему з 7 рівнянь, з якої знаходимо потенціали ui і vj :
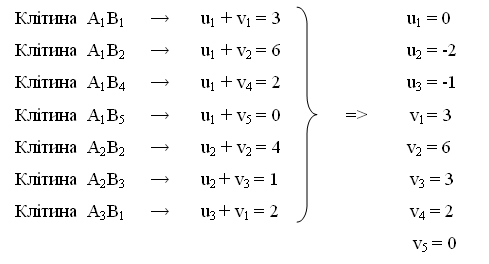
Перекреслимо транспортну таблицю, додав до неї рядок і
стовпець для запису потенціалів, і перевіримо виконання умови оптимальності : ui + vj ≤ Сіj для всіх вільних ( не
зайнятих ) клітин.
Таблиця 2
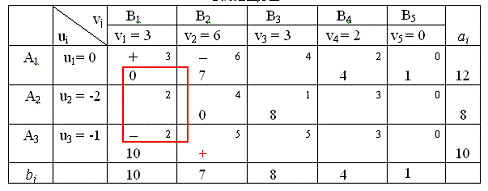
Для вільних клітин : ui + vj ≤ Сіj
u1 + v3 = 0 + 3 = 3 < 42 + v1 = -2 + 3 = 1 < 22 + v4 = -2 + 2 = 0 < 32 + v5 = -2 + 0 = -2 < 0
u3 + v2 = -1 + 6 = 5 = 5
u3 + v3 = -1 + 3 = 2 < 5
u3 + v4 = -1 + 2 = 1 < 3
u3 + v5 = -1 + 0 = -1 < 0
Бачимо, що умову оптимальності виконано в усіх клітинах, отже
початковий опорний план є оптимальним, тобто його вартість мінімальна.
Але цей оптимальний план не є єдиним можливим, тому що в
одній небазисній клітині А3В2 умова ui + vj ≤ Сіj виконується як строга
рівність. Якщо цю клітину ввести до базису, то одержимо ще один оптимальний
план з такою самою вартістю Zmіn = 78.
Для цього треба перерозподілити вантаж по клітинах таблиці.
Будуємо цикл, тобто замкнену прямокутну ламану лінію, одна
вершина якого знаходиться в клітині, в якої умова ui + vj ≤ Сіj виконується як строга
рівність, тобто в клітині А3В2 , а решта вершин - в
зайнятих клітинах. Вершини цикла по черзі помічаємо знаками “+” і “- “ , серед
клітин з “- “ обираємо найменше значення хіj :
θ0 = min { хіj } = min { 7, 10} = 7 - в клітині А1В2
Далі, рухаючись по вершинах цикла, додаємо це значення
θ0 до значень хіj в клітинах з “+” і
віднімаємо від значень хіj в клітинах з “-” . Клітину А1В2
не заповнюємо. Решту клітин переписуємо без змін. Нову таблицю знову
перевіряємо на оптимальність , тобто обчислюємо безпосередньо в таблиці нові
значення потенціалів і перевіряємо виконання умови оптимальності.
Таблиця 3
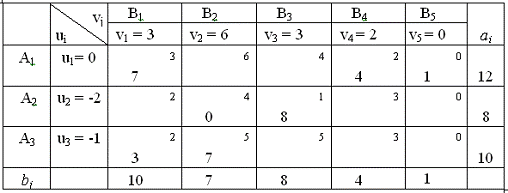
х11 = 7; х14 = 4; х15 = 1; х23 = 8; х31 = 3; х32 = 7; решта хіj = 0
Zmіn = 78
Маємо два оптимальних плани перевезень :
) х12 = 7; х14 = 4; х15 = 1; х23 = 8; х31 = 1; решта хіj = 0;
) х11 = 7; х14 = 4; х15 = 1; х23 = 8; х31 = 3; х32 = 7; решта хіj = 0
Zmin = 78 у.о.
Задача 6. Розв’язати графічно задачу дробово-лінійного
програмування
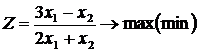 за
умов
за
умов 
Розв’язання:
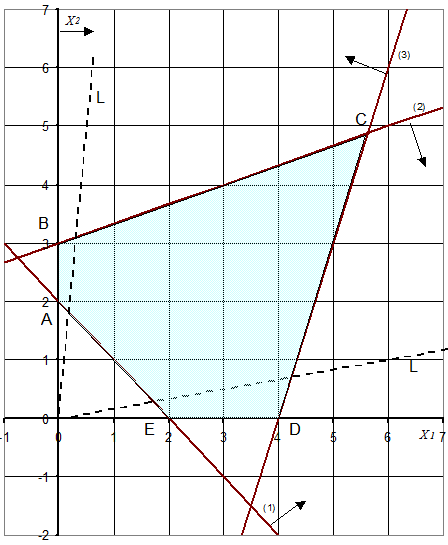
Як і в задачі лінійного програмування, цільова функція задачі дробово -
лінійного програмування досягає свого оптимуму в вершинах многокутника
розв’язків, тому спочатку будуємо множину розв’язків (аналогічно задачі 2). Це
п’ятикутник AВСDЕ.
Далі будуємо пряму Z = const, тобто надаємо значення функції, рівним
деякому числу h так, щоб пряма (L):
 ,
,
яка проходить через початок координат, мала спільні точки з
многокутником розв’язків.
Обертая побудовану пряму навколо початку координат, знаходимо найбільше
і найменше значення функції, або доводимо необмеженість функції Z на множині
планів.
Для зручності можна взяти пряму L,
співпадаючою з віссю Ох1 і обертати її проти годинної стрілки.
Перші зустрінуті точки многокутника розв’язків - це всі точки осі Ох1
між точками Е(2; 0) і D(4; 0), а останні зустрінуті точки - це всі точки осі Ох2
між точками А(0; 2) і В(0; 3).
Для
точок відрізку [ЕD] маємо:
х2
= 0 Þ 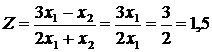 ← mах
← mах
Для
точок відрізку [АВ] маємо:
х1
= 0 Þ 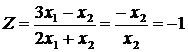 ← mіn
← mіn
Відповідь: Zmіn
= -1 при х1 = 0, х2 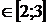 ; Zmах
= 1,5 при х2 = 0; х1
; Zmах
= 1,5 при х2 = 0; х1 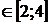 .
.
Задача 7.
Побудувати
економетричну модель залежності між витратами обігу (Y грн), та вантажообігом
(Х грн). Дослідити статистичну значущість моделі та оцінок її параметрів. Дати
загальну характеристику адекватності моделі та її параметрів для рівня
значущості 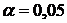 , розрахувати коефіцієнти детермінаціі, кореляції,
еластичності. Спрогнозувати значення Y при
, розрахувати коефіцієнти детермінаціі, кореляції,
еластичності. Спрогнозувати значення Y при
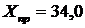 , вказавши надійний інтервал прогнозного значення.
Зробити висновки. Вихідні дані
наведено в таблиці:
, вказавши надійний інтервал прогнозного значення.
Зробити висновки. Вихідні дані
наведено в таблиці:
Таблиця 1
|
Х
|
7,8
|
11,4
|
8,1
|
17,5
|
21,3
|
22,9
|
28,7
|
34,1
|
30,7
|
|
Y
|
2,7
|
3,6
|
4,9
|
6,0
|
6,3
|
7,0
|
7,7
|
8,6
|
9,7
|
Розв’язання:
. Ідентифікуємо змінні:- витрати обігу ( залежна
змінна);
Х - вантажообіг (незалежна змінна).
2. Нехай економетрична модель специфікована у лінійній
формі:
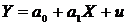 ,
,
де 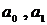 - параметри моделі (оцінки економетричної моделі),
- параметри моделі (оцінки економетричної моделі),
u - стохастична складова (залишки).
Побудуємо
декартову систему координат на площині. Відкладемо на ній точки 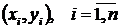 . Обведемо всі відкладені точки замкнутою кривою - це
буде хмара (еліпс) розсіювання
експериментальних даних. Проведемо криву, яка відповідає усередненим значенням.
Це пряма лінія.
. Обведемо всі відкладені точки замкнутою кривою - це
буде хмара (еліпс) розсіювання
експериментальних даних. Проведемо криву, яка відповідає усередненим значенням.
Це пряма лінія.
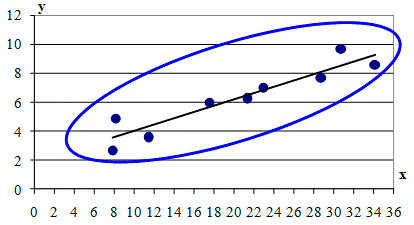
3. Оцінимо параметри моделі за методом 1МНК. Модель
розглядатимемо у вигляді :
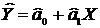 ,
,
де 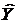 - очікувані витрати обігу ;
- очікувані витрати обігу ; 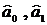 - очікувані параметри.
- очікувані параметри.
Для цього запишемо систему нормальних рівнянь:
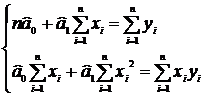 (1)
(1)
і = 1, n = 9 - кількість спостережень.
Для розв’язання системи (1) відносно  складемо
розрахункову таблицю:
складемо
розрахункову таблицю:
Таблиця
2
|
№
|
Y
|
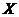 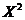 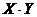 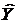 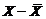 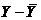 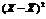 ( (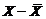 )·( )·(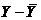 )u =Y- )u =Y-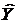 u² u²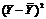
|
|
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|
1
|
2,7
|
7,8
|
60,84
|
21,06
|
3,56
|
-12,48
|
-3,58
|
155,69
|
44,64
|
-0,86
|
0,74
|
12,80
|
|
2
|
3,6
|
11,4
|
129,96
|
41,04
|
4,34
|
-8,88
|
-2,68
|
78,81
|
23,77
|
-0,74
|
0,55
|
7,17
|
|
3
|
4,9
|
8,1
|
65,61
|
39,69
|
3,62
|
-12,18
|
-1,38
|
148,30
|
16,78
|
1,28
|
1,64
|
1,90
|
|
4
|
6,0
|
17,5
|
306,25
|
105,00
|
5,67
|
-2,78
|
-0,28
|
7,72
|
0,77
|
0,33
|
0,11
|
0,08
|
|
5
|
6,3
|
21,3
|
453,69
|
134,19
|
6,50
|
1,02
|
0,02
|
1,04
|
0,02
|
-0,2
|
0,04
|
0,00
|
|
6
|
7,0
|
22,9
|
524,41
|
160,30
|
6,85
|
2,62
|
0,72
|
6,88
|
1,89
|
0,15
|
0,02
|
0,52
|
|
7
|
7,7
|
28,7
|
823,69
|
220,99
|
8,11
|
8,42
|
1,42
|
70,93
|
11,98
|
-0,41
|
0,17
|
2,02
|
|
8
|
8,6
|
34,1
|
1162,81
|
293,26
|
9,29
|
13,82
|
2,32
|
191,05
|
32,10
|
-0,69
|
0,48
|
5,39
|
|
9
|
9,7
|
30,7
|
942,49
|
297,79
|
8,55
|
10,42
|
3,42
|
108,62
|
35,67
|
1,15
|
1,32
|
11,71
|
|
Сума
|
56,5
|
182,5
|
4469,75
|
1313,32
|
|
|
|
769,06
|
167,63
|
|
5,06
|
41,60
|
|
Серед.
|
6,28
|
20,28
|
|
|
|
|
|
|
|
|
|
|
Середні значення:
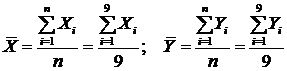
Стовпчики 6 ,11 і 12 заповнюємо після обчислення  .
.
Підставимо в систему (1) значення сум 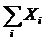 ,
, 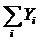 ,
, 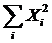 ,
, 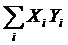
із передостаннього рядка.
Одержуємо систему рівнянь
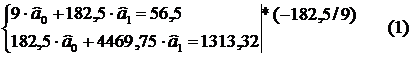

Отже економетрична модель витрат обігу запишеться так:  1,858 + 0,218 · X
1,858 + 0,218 · X
4. На основі отриманих даних розраховуємо 6-й, 11 і 12
стовпчики таблиці 1.2.
. Обчислимо дисперсії залежної змінної та залишків:
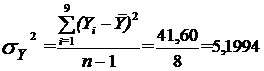
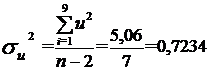
6. Визначимо коефіцієнти детермінації та кореляції:
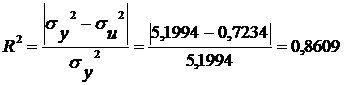
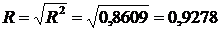
Коефіцієнт детермінації R² = 0,8609 свідчить (визначає) про те, що
варіація витрат обігу на 86,09 % визначається вантажообігом .
Коефіцієнт кореляції R = 0,9278 > 0,9 показує, що існує
дуже тісний зв’язок між цими економічними показниками. Значення R2 і R для парної економетричної
моделі свідчать про статистичну значущість зв'язку, якщо вони наближаються до
одиниці.
Визначимо коефіцієнт еластичності витрат обігу залежно
від вантажообігу:
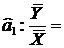 0,70
0,70
Отже, знаючи коефіцієнт еластичності, можна дійти висновку, що зі
збільшенням вантажообігу на 1% витрати
обігу збільшуються на 0,7%.
Знаходимо
F - статистику за формулою:
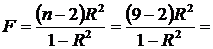 43,31.
43,31.
Обчислене значення F - критерію порівняємо з табличним при
ступенях вільності k1 = 1 і k2 = n - 2 = 9 - 2 = 7 і вибраному рівні значущості α = 0,05.
Якщо F > Fтабл , то гіпотезу Н0 : а1 = 0 про
неістотність зв’язку між залежною та незалежною змінною моделі не приймаємо з
ризиком α, тобто коефіцієнт а1 значущий;
інакше - приймаємо, тобто коефіцієнт а1 = 0 - незначущий. Тут Fтабл = 5,6, тобто F > Fтабл коефіцієнт а1 значущий.
Перевірку на значущість коефіцієнтів регресії можна здійснити також за t - тестом. Обчислимо t - статистику за формулою:
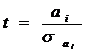 ( і = 0;
1),
( і = 0;
1),
де
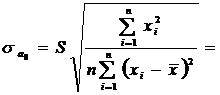 0,68;
0,68; 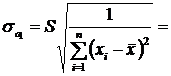 0,03
0,03
За таблицями t - статистики знаходимо критичне значення 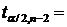 2,36 і порівнюємо її з обчисленою t -
статистикою: якщо
2,36 і порівнюємо її з обчисленою t -
статистикою: якщо 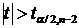 , то приймаємо, що коефіцієнт аі значущій,
тобто гіпотезу Н0 відкидаємо; інакше ця гіпотеза приймається, тобто коефіцієнт
аі незначущій.
, то приймаємо, що коефіцієнт аі значущій,
тобто гіпотезу Н0 відкидаємо; інакше ця гіпотеза приймається, тобто коефіцієнт
аі незначущій.
Тут
для і = 0: 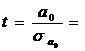 2,72 Þ
2,72 Þ 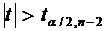 ,
коефіцієнт а0 значущій;
,
коефіцієнт а0 значущій;
для
і = 1:  7,11 Þ
7,11 Þ 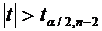 , коефіцієнт а1
значущій.
, коефіцієнт а1
значущій.
7. Знаходимо матрицю С -
матрицю похибок. (Матриця похибок обернена до матриці системи (1) нормальних рівнянь).
8. Визначаємо стандартні похибки оцінок параметрів 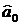 і
і 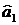 моделі,
враховуючи дисперсію залишків і діагональні елементи матриці С:
моделі,
враховуючи дисперсію залишків і діагональні елементи матриці С:
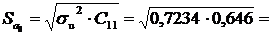 0,6835
0,6835
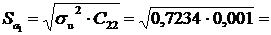 0,0307
0,0307
Порівняємо стандарті похибки оцінок параметрів моделі зі
значеннями цих оцінок.
Стандартна похибка оцінки параметра 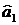 становить:
становить:
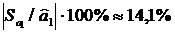 абсолютного
значення цієї оцінки (0,218), що свідчить про деяку зміщеність такої
оцінки параметра, тобто параметр
абсолютного
значення цієї оцінки (0,218), що свідчить про деяку зміщеність такої
оцінки параметра, тобто параметр 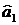 може
мати зміщення, яке зумовлене невеликою сукупністю спостережень (n= 9).
може
мати зміщення, яке зумовлене невеликою сукупністю спостережень (n= 9).
Стандартна похибка оцінки параметра 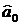 становить:
становить:
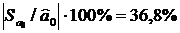 абсолютного
значення цієї оцінки (1,858). Отже параметр
абсолютного
значення цієї оцінки (1,858). Отже параметр 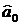 також може мати зміщення, яке зумовлене невеликою
сукупністю спостережень (n= 9).
також може мати зміщення, яке зумовлене невеликою
сукупністю спостережень (n= 9).
9. Обчислення прогнозних значень і знаходження меж надійних
інтервалів індивідуальних прогнозних значень(точковий та інтервальний
прогнози).
Для
визначення прогнозних значень підставляємо у рівняння 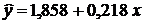 задане значення
задане значення
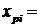 34,0, яке
знаходиться за межами базового періоду (точковий прогноз):
34,0, яке
знаходиться за межами базового періоду (точковий прогноз):
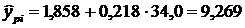
Знаходимо
межі надійних інтервалів індивідуальних прогнозних значень за формулою:
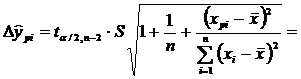 2,342
2,342
Запишемо
межі надійних інтервалів індивідуальних прогнозних значень:
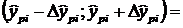
 .
.
Висновок:
Економетрична модель Ŷ = 1,858 + 0,218·Х кількісно описує зв’язок витрат обігу і
вантажообігу.
Параметр 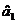 = 0,218 характеризує граничний розмір витрат обігу,
коли вантажообіг збільшується на одиницю, тобто коли вантажообіг збільшиться на
одиницю, то обсяг витрат обігу збільшиться на 0,218 одиниці:
= 0,218 характеризує граничний розмір витрат обігу,
коли вантажообіг збільшується на одиницю, тобто коли вантажообіг збільшиться на
одиницю, то обсяг витрат обігу збільшиться на 0,218 одиниці:
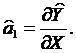
Задача 8.
Нехай на витрати обігу впливають: обсяг вантажообігу, тис.грн.; запаси
з вантажообігу, тис.грн.; трудомісткість одиниці вантажообігу, людино-годин.
Щоб побудувати економетричну модель цієї залежності за методом 1 МНК, необхідно
бути впевненим, що між факторами вантажообігу, запасів та трудомісткості не
існує мультиколінеарності. Треба
дослідити наявність мультиколінеарності між цими чинниками на підставі даних, наведених
у таблиці:
Таблиця 1.
|
№ п/п
|
Обсяг вантажообігу
Х1 (грн.)
|
Запаси з
вантажообігу Х2 (грн.)
|
трудомісткість
одиниці вантажообігу Х3 (людино-годин)
|
|
1
|
2,37
|
10,27
|
|
2
|
4,77
|
11,87
|
7,88
|
|
3
|
6,24
|
13,88
|
8,50
|
|
4
|
8,70
|
14,62
|
8,86
|
|
5
|
10,79
|
15,28
|
10,51
|
|
6
|
13,60
|
17,29
|
10,53
|
|
7
|
16,31
|
19,04
|
11,74
|
|
8
|
18,40
|
20,45
|
13,96
|
|
9
|
21,25
|
21,94
|
13,86
|
|
10
|
22,87
|
22,55
|
14,60
|
|
Сума
|
125,3
|
167,19
|
106,84
|
|
Середнє
|
12,53
|
16,719
|
10,684
|
Крок 1. Нормалізація (стандартизація) змінних.
Нехай Х1, Х2, Х3, - вектори
пояснювальних змінних. Елементи стандартизованих змінних обчислимо за формулою:
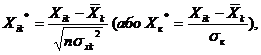
де n - кількість спостережень (n = 10 ), і= 1,...,m (m =3), 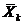 - середнє арифметичне значення Хк,
- середнє арифметичне значення Хк, 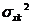 -
дисперсія змінної Хк.
-
дисперсія змінної Хк.
Спочатку обчислимо середні арифметичні для кожної пояснювальної змінної
в останньому рядку таблиці:
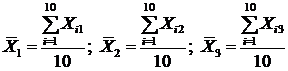
Розрахункові дані для стандартизації змінних Х1, Х2,
Х3 подані в таблиці :
Таблиця 2
|
№
|
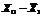 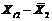 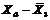 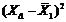 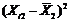 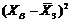 X1*X2*X3* X1*X2*X3*
|
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
-10,16
|
-6,449
|
-4,284
|
103,226
|
41,5896
|
18,3527
|
-0,4771
|
-0,509
|
-0,5062
|
|
2
|
-7,76
|
-4,849
|
-2,804
|
60,2176
|
23,5128
|
7,86242
|
-0,3644
|
-0,3827
|
-0,3313
|
|
3
|
-6,29
|
-2,839
|
-2,184
|
39,5641
|
8,05992
|
4,76986
|
-0,2954
|
-0,2241
|
-0,258
|
|
4
|
-3,83
|
-2,099
|
-1,824
|
14,6689
|
4,4058
|
3,32698
|
-0,1798
|
-0,1657
|
-0,2155
|
|
5
|
-1,74
|
-1,439
|
-0,174
|
3,0276
|
2,07072
|
0,03028
|
-0,0817
|
-0,1136
|
-0,0206
|
|
6
|
1,07
|
0,571
|
-0,154
|
1,1449
|
0,32604
|
0,02372
|
0,05024
|
0,04507
|
-0,0182
|
|
7
|
3,78
|
2,321
|
1,056
|
14,2884
|
5,38704
|
1,11514
|
0,17749
|
0,18319
|
0,12477
|
|
8
|
5,87
|
3,731
|
3,276
|
34,4569
|
13,9204
|
10,7322
|
0,27563
|
0,29447
|
0,38706
|
|
9
|
8,72
|
5,221
|
3,176
|
76,0384
|
27,2588
|
10,087
|
0,40945
|
0,41207
|
0,37525
|
|
10
|
10,34
|
5,831
|
3,916
|
106,916
|
34,0006
|
15,3351
|
0,48552
|
0,46022
|
0,46268
|
|
Σ
|
|
|
|
453,548
|
160,532
|
71,6352
|
|
|
|
Обчислимо дисперсії кожної незалежної змінної:
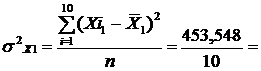 45,3548
45,3548
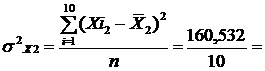 16,0532
16,0532
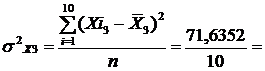 7,16352
7,16352
Розрахуємо знаменники для стандартизації кожної незалежної змінної:
для 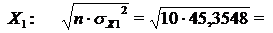 21,2967
21,2967
для 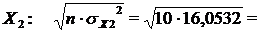 12,6701
12,6701
для 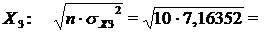 8,46376
8,46376
Далі кожний елемент стовпчика 2 таблиці ділимо на 21,2967 і
заповнюємо стовпчик 8, а кожний елемент стовпчика 3 ділимо на 12,6701 і
заповнюємо стовпчик 9 і нарешті, кожний елемент стовпчика 4 ділимо на 8,46376 і
заповнюємо стовпчик 10.
Елементи стовпчиків 8, 9 і 10 складають матрицю
стандартизованих змінних:

Крок 2. Знаходження кореляційної матриці
r = X*T· X*
де: Х* - матриця стандартизованих (нормалізованих)
змінних,
Х*Т - матриця, транспонована до Х*.
Кожний елемент матриці r характеризує тісноту зв’язку однієї
незалежної змінної з іншою. Діагональні елементи r11, r22 , r33 характеризують тісноту зв’язку
кожної незалежної змінної з цією самою змінною, тому вони дорівнюють одиниці.

Крок 3. Обчислимо детермінант кореляційної матриці r і χ².
Д = |r| = 0,00025
χ² = - [n - 1 - 1/6∙(2m + 5)]ln
Д = -[9 - 1/6∙(6 + 5)]ln 0,00025 = 59,5
При ступенях свободи 1/2m(m-1) = 3 і рівні значущості α
= 0,01 критерій
χ²табл.= 11,34.
59,5 > 11,34 ,
χ²факт
> χ²табл,
отже, в масиві змінних існує мультиколінеарність.
Крок 4. Знаходимо матрицю С, обернену до матриці r.
С = r -1 = (Х*Т ∙ Х*)-1.
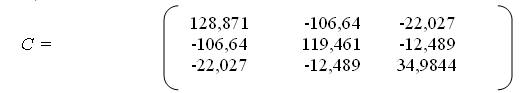
Крок 5. Обчислимо F - критерії, використовуючи діагональні
елементи матриці С.
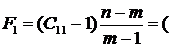 128,871
128,871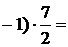 447,55
447,55
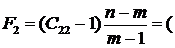 119,461
119,461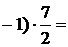 414,615
414,615
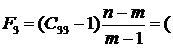 34,9844
34,9844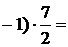 118,945
118,945
Для рівняння α = 0,05 і ступенів свободи чисельника 7, а знаменника 2 дробу 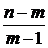 табличне значення Fкр = 19,4.
табличне значення Fкр = 19,4.
1 факт > Fтабл
F2 факт > Fтабл
F3 факт > Fтабл
Отже, кожна з пояснювальних змінних мультиколінеарна з двома іншими.
Щоб визначити наявність попарної мультиколінеарності, продовжимо
дослідження.
Крок 6. Обчислимо частинні коефіцієнти кореляції, скориставшись
елементами матриці С.
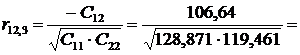 0,85946
0,85946
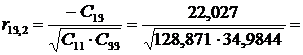 0,32804
0,32804
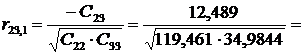 0,19318
0,19318
Частинні коефіцієнти кореляції показують тісноту зв’язку між
двома змінними за умови, що третя не впливає на цей зв’язок.
Крок 7. Визначимо t -
критерій на основі частинних коефіцієнтів кореляції:
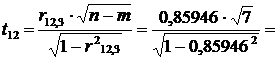 4,44808
4,44808
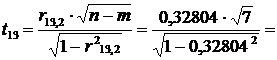 0,91877
0,91877
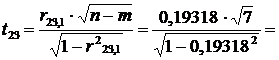 0,52093
0,52093
Табличне значення t - критерію при n - m = 7 ступенях свободи і рівні значущості α = 0,05 дорівнює 2,36.
Значення обчислення t - критеріїв за абсолютним значенням
менші за табличне для другої та третьої пар пар. Отже, ці пари незалежних
змінних не є мультиколінеарними, а перша пара Х1, Х2 є мультиколінеарною.
Висновок.
1. Дослідження вихідних даних показали, що у масиві вихідних даних
існує мультиколінеарність.
2. Для включення факторів у модель потрібно, щоб вони були слабо
пов'язані між собою, та зв'язані з результуючим фактором. Оскільки між
факторами Х1 і Х2 виявлено мультиколінеарний зв'язок, то краще у модель фактори
Х1 та Х2 разом не включати.
оптимальний кореляція симплексний
мультиколінеарніость
Список використаної літератури
1. Акулич И.Л. Математическое программирование в
примерах и задачах.- М.:Высш.шк.,1985
2. Калихман И.С. Сборник задач по математическому
программированию.- М.:Высш.шк.,1975
. Степанюк В.В. Методи математичного
програмування.-К.:Вища школа,1977
4. Кузнецов Ю.Н. , Кузубов В.И. , Волощенко А.Б.
Математическое программирование. - М.:Высш.шк.,1980
. Назаренко О.М. Основи економетрики:
Підручник. - К.: Центр навчальної літератури, 2004.
. Наконечний С.І. Економетрія: Підручник /
С.І. Наконечний, Т.О. Терещенко, Т.П. Романюк - Вид. 2-ге, допов. та перероб.-
К.:КНЕУ, 2000.