Классификация экономико-математических методов и моделей

Содержание

Введение

Раздел 1. Теоретические основы математических методов

Раздел 2. Этапы принятия решений

Раздел 3. Классификация задач оптимизации

.1 Задача линейного программирования.

.2 Задача нелинейного программирования.

.3 Задача выпуклого программирования

.4 Задача квадратичного программирования

.5 Задача целочисленного программирования

.6 Задача параметрического программирования

.7 Задача динамического программирования

.8 Задача стохастического программирования

Раздел 4. Практическое применение MS Excel к решению задачи линейного программирования.

Заключение

Список использованных источников

Введение

Экономическая наука многогранна и интересна. Классификация экономико-математических методов имеет большое значение - этим и обуславливается актуальность курсовой работы.

Целью данной курсовой работы является проведение классификации экономико-математических методов и моделей.

Поставленная цель предполагает решение следующих задач:

˗      изучение теоретических основ математических методов;

˗        определение этапов принятия решений;

˗        проведение классификации задач оптимизации;

˗        решение задачи линейного программирования в MSEXCEL.

Структура курсовой работы представлена четырьмя главами, введением, заключением, списком использованных источников.

В первой главе приведены теоретические основы математических методов.

Вторая глава содержит этапы принятия решений.

В третьей главе классифицируются задачи оптимизации.

Четвертая глава посвящена решению задач линейного программирования в MS EXCEL.

В заключении подведены итоги и сделаны выводы.

В списке использованных источников приведены источники, которые были использованы при написании курсовой работы.

Раздел 1. Теоретические основы математических методов

Разработка моделей всегда играла жизненно важную роль в духовной деятельности человечества с тех пор, как оно стало стремиться к пониманию и изменению окружающей среды. Люди всегда использовали концепцию модели, пытаясь представить и выразить с ее помощью абстрактные идеи и реальные объекты.

Модель - это, прежде всего, упрошенное представление реального объекта или явления, сохраняющее его основные, существенные черты. Обычно считается, что модель - это используемый для предсказания и сравнения инструмент, позволяющий логическим путем спрогнозировать последствия альтернативных действий и достаточно уверенно указать, какому из них отдать предпочтение. Хотя такое использование моделей имеет большое значение, оно ни в коей мере не исчерпывает целей моделирования. В определенных рамках модель может служить также эффективным средством общения и осмысления действительности, обучения и тренажа, средством постановки экспериментов, инструментом прогнозирования и управления.

Модели, отвечающие основным требованиям целей исследования экономических систем, отличаются друг от друга существенными признаками. Разные причины для нахождения этих отличий позволяют отнести модель к тому или иному подмножеству, определенные характеристики элементов которого соответствуют друг другу. Этот процесс называется классификацией экономико-математических моделей. Она позволяет упорядочить элементы множества моделей.

Процессы и объекты управления в экономике столь многообразны, что не существует классификации, претендующей на полноту охвата всего множества социально-экономических задач, описываемых различными моделями. Однако это многообразие вызвано диалектикой познания, а не скудостью математических методов.

Следует четко выделять классификационные признаки и рассматривать экономико-математические модели с различных точек зрения, данная классификация показана на рисунке 1.1. Важно понять, что именно таким образом формируется системный взгляд на любой объект.

В зависимости от моделируемых объектов и назначения моделей используемая в них исходная информация имеет различный характер и происхождение. Она может быть разделена на две категории:

прошлое и настоящее экономических наблюдений и их обработка;

будущее развитие объектов, включающее данные об ожидаемых изменениях их внутренних параметров и внешних условий (прогнозы).

Рисунок 1.1. Основные признаки классификации экономико-математических моделей

экономический математический оптимизация программирование

Вторая категория информации является результатом самостоятельных исследований, которые также могут выполняться посредством моделирования.

Степень применимости модели к теоретическим исследованиям или практическим действиям дает основание для градации экономико-математических моделей по предназначению на теоретико-аналитические, используемые в исследованиях общих свойств и закономерностей экономических процессов, и прикладные, применяемые в решении конкретных экономических задач (модели экономического анализа, прогнозирования, управления). Экономико-математические модели могут предназначаться для исследования разных сторон хозяйственной деятельности (в частности, ее производственно-технологической, социальной, территориальной структур) и ее отдельных частей.

Главная задача экономической науки конструктивна - это разработка научных методов планирования и управления экономикой. Поэтому распространенный тип математических моделей экономики - это модели управляемых и регулируемых экономических процессов, используемые для преобразования экономической действительности. Такие модели называются нормативными. Нормативные модели отвечают на вопрос, как это должно быть, т. е. предполагают целенаправленную деятельность. Типичным примером нормативных моделей являются модели оптимального планирования, формализующие тем или иным способом цели экономического развития, возможности и средства их достижения.

Дескриптивные модели помогают решить вопросы "Как это происходит?" или "Как это вероятнее всего может дальше развиваться?", объясняют наблюдаемые факты или дают вероятный прогноз. Применение дескриптивного подхода в моделировании экономики объясняется необходимостью эмпирического выявления различных зависимостей в экономике, установления статистическими закономерностями экономического поведения социальных групп, изучения вероятных путей развития каких-либо процессов при неизменяющихся условиях или протекающих без внешних воздействий. Примерами дескриптивных моделей являются производственные функции и функции покупательского спроса, построенные на основе обработки статистических данных.

Является ли экономико-математическая модель дескриптивной или нормативной, зависит не только от ее математической структуры, но от характера использования этой модели. Например, модель межотраслевого баланса дескриптивна, если она используется для анализа пропорций прошлого периода. Но эта же математическая модель становится нормативной, когда она применяется для расчетов сбалансированных вариантов развития народного хозяйства, удовлетворяющих конечные потребности общества при плановых нормативах производственных затрат. Многие экономико-математические модели сочетают признаки дескриптивных и нормативных моделей. Типична ситуация, когда нормативная модель сложной структуры объединяет отдельные блоки, которые являются частными дескриптивными моделями. Например, межотраслевая модель может включать функции покупательского спроса, описывающие поведение потребителей при изменении доходов. Подобные примеры характеризуют тенденцию эффективного сочетания дескриптивного и нормативного подходов к моделированию экономических процессов. Дескриптивный подход широко применяется в имитационном моделировании. Если ориентировать нормативные модели только на подтверждение действительности, то они не смогут служить инструментом решения качественно новых социально-экономических задач.

По внутренней структуре модельного описания системы выделяют ряд видов моделей, которые схематически представлены на рисунке 1.2.

В статических моделях все зависимости относятся к одному моменту или периоду времени. Динамические модели характеризуют изменения экономических процессов во времени. Само время в экономико-математических моделях может изменяться либо непрерывно, либо дискретно. По соотношению экзогенных и эндогенных переменных, включаемых в модель, они могут разделяться на открытые и закрытые. Полностью открытых моделей не существует; модель должна содержать хотя бы одну эндогенную переменную.

Рисунок 1.2. Классификация экономико-математических моделей по внутренней структуре

Полностью закрытые экономико-математические модели, т. е. не включающие экзогенных переменных, исключительно редки; их построение требует полного абстрагирования от "среды", т. е. серьезного огрубления реальных экономических систем, всегда имеющих внешние связи. Подавляющее большинство экономико-математических моделей занимает промежуточное положение и различаются по степени открытости (закрытости).

Для моделей народнохозяйственного уровня важно деление на агрегированные и детализированные.

Ответ на вопрос, каким образом модель описывает экономическую систему, является аргументом для классификации экономико-математических моделей по          способу описания, представлен на рисунке 1.3.

К символическим моделям относятся, т.е. в которых для представления процесса или системы используются символы. Обычным примером представления систем в этом случае можно считать системы дифференциальных уравнений.

Поскольку последние представляют собой наиболее абстрактные и, следовательно, наиболее общие модели, то их применение таит в себе весьма реальные опасности и ловушки. Символическая модель является всегда абстрактной идеализацией задачи, и, если хотят, чтобы эта модель позволяла решить задачу, необходимы некоторые упрощающие предположения. Поэтому особое внимание должно быть обращено на то, чтобы модель служила действительным представлением данной задачи.

Рисунок 1.3.  Классификация экономико-математических моделей по способу их описания

Интересны математические модели таких систем, в которых результат взаимодействия компонент не является полностью определенным (детерминированным). Их обычно называют вероятностными, стохастическими или недетерминированными. Все эти термины можно рассматривать как синонимы. Такие модели являются скорее "прогонными", чем "разрешимыми" в том смысле, что в результате разового расчета варианта ("прогона") по модели получается некоторая последовательность изменений состояний системы во времени (траектория системы).

Повторяя этот процесс некоторое число раз с изменяющимися значениями стохастических переменных, можно получить статистические сведения о поведении исследуемой системы при определенных начальных данных и фиксированных значениях управляющих переменных. Изменяя значения управляющих переменных, можно попытаться решить задачу о выборе наилучшего решения в статистическом смысле.

Для этого типа моделей необходимо различать неопределенность, описываемую вероятностными законами, и неопределенность, для описания которой законы теории вероятностей неприменимы. Второй тип неопределенности гораздо более сложен для моделирования.

В настоящее время как мощное средство анализа, прогнозирования и методологии принятия управленческих решений большое значение приобретают эконометрические модели, основу которых составляют достижения теории вероятности и математической статистики.

Развитие этого направления связано с необходимостью построения моделей экономических процессов как сложных систем с огромным числом влияющих факторов. Появление быстродействующей вычислительной техники позволило обобщить этот тип моделей в класс имитационных моделей.

Модели экономических процессов чрезвычайно разнообразны по форме математических зависимостей. Особенно важно выделить класс линейных моделей, наиболее удобных для анализа и вычислений и получивших вследствие этого большое распространение. Различия между линейными и нелинейными моделями существенны не только с математической точки зрения, но и в теоретико-экономическом отношении, поскольку многие зависимости в экономике носят принципиально нелинейный характер: эффективность использования ресурсов при увеличении производства, изменение спроса и потребления населения при увеличении производства, изменение спроса и потребления населения при росте доходов и т. п.

Рисунок 1.4. Классификация экономико-математических моделей по способу отражения действительности

На рисунке 1.4. представлена классификация экономико-математических моделей по способу отражения действительности.

Балансовые модели реализуют равенство суммы наличных объемов (товаров, ресурсов, финансовых потоков и т. п.), полученных из различных источников, сумме объемов, использованных по различным направлениям.

Технологические модели раскрывают и детализируют технологические процессы конкретных экономических систем, а также их производственные возможности на краткосрочную и длительную перспективу.

Поведенческие модели описывают поведение элементов экономической системы, имеющих некоторую свободу выбора решений. Сюда можно отнести функциональные и причинно-следственные отношения. Функциональные модели описывают поведение системы безотносительно к ее внутренней структуре (черный ящик). Они выражают, как правило, прямые зависимости между известными (экзогенными) и неизвестными (эндогенными) величинами.

Аналоговыми моделями являются модели, в которых свойство реального объекта представляется некоторым другим свойством аналогичного по поведению объекта. Примером может служить графический анализ развития различных экономических систем.

Модели, где во взаимодействие вступают люди и машинные компоненты, часто называется играми (управленческими, военными, планировочными). В так называемых управленческих (деловых) играх человек взаимодействует с информацией, поступающей с выхода вычислительной машины (которая моделирует все другие свойства системы), и принимает решения на основе полученной информации. Решения человека затем снова вводятся в машину в качестве входной информации, которая используется системой. Продолжая этот процесс дальше, мы приходим к полностью машинному моделированию, которое обычно и понимается под термином "моделирование".

Информационные модели - совокупность сигналов, несущих информацию об объекте управления и внешней среде, организованная по определенным правилам.

Демографические модели учитывают влияние роста и структуры населения на производство.

Экономико-математическое моделирование охватывает весь спектр реальных систем. Для любого экономического события можно подобрать по приведенным классификационным признакам наиболее подходящую модель.

Раздел 2. Этапы принятия решений

Чтобы принять управленческое решение без компьютера, зачастую ничего не надо. Возникла в производстве ситуация, требующая своего разрешения, т. е. принятия соответствующего решения, он подумал и принял его. Правда, без гарантии оптимальности (т. е. правильности). Компьютер же никаких решений не принимает, а только подготавливает их для принятия менеджером. Что нужно сделать, чтобы найти такие варианты решений (рисунок 2.1)? Разработку любой модели оптимизации можно приблизительно разбить на 5 стадий, частично перекрывающих друг друга и не имеющих четких границ.

. Постановка (формулировка) задачи.

. Разработка математической модели изучаемой системы.

. Отыскание решения с помощью этой модели.

. Проверка данной модели и решения.

. Уточнение решения на практике.

При постановке задачи проводится предпроектное обследование объекта моделирования, формулируется цель решения, ограничения, формы исходной и результатной информации, порядок ее преобразования и использованияи т. д. Порядок принятия решений мы можем проследить по рисунку 2.1.

Рисунок 2.1. Стадии принятия решений

При разработке математической модели формализуется цель решения, с которой увязываются переменные величины и наличные ограничения, оценивается число возможных (допустимых) вариантов решения.

Собственно решению на ЭВМ предшествует разработка алгоритма - формализованной последовательности действий по реализации модели (блок-схем решения задачи), по которой разрабатывается программа решения задачи на ЭВМ или подбирается готовый программный продукт.

Далее сравнивается полученное решение с реальной действительностью, чтобы выяснить, действительно ли решена реальная задача, все ли переменные в модели учтены, все ли ограничения формализованы, все ли изменения объекта внесены в модель и т. д. Особенно важным на этих этапах представляется выбор цели решения. Например, установка зениток на торговых судах в Атлантике во время Второй мировой войны. Из 25 вражеских самолетов сбивали один, что не окупало установку орудий. Но после установки зениток потопляемость судов уменьшилась в 2,5 раза. Так ставить зенитки или нет? А если ставить, то какая при этом должна быть цель - сбивать самолеты или сохранять свои суда? Хорошую модель, достаточно полно отражающую реальный моделируемый объект, составить непросто. По словам Беллмана, «если мы попытаемся включить в нашу математическую модель слишком много черт действительности, то захлебнемся в сложных уравнениях, содержащих неизвестные параметры и неизвестные функции. Определение этих функций приведет к еще более сложным уравнениям с еще большим числом неизвестных параметров и функций и т. д. Если же, наоборот, оробев от столь мрачных перспектив, построим слишком упрощенную модель, то обнаружим, что она не определяет последовательность действий так, чтобы удовлетворять нашим требованиям. Следовательно, ученый, «подобно паломнику, должен идти прямой и узкой тропой между западнями переупрощения и болотом переусложнения». Для обеспечения успеха моделирования надо выполнить три правила, которые, по мнению древних, являются признаками мудрости.

. Отделить главные свойства моделируемого объекта от второстепенных.

. Учесть в модели главные свойства объекта.

. Пренебречь его второстепенными свойствами.

Модель - это условное представление действительности. Степень соответствия может быть различной, и проблема заключается в том, чтобы, выбирая уровень упрощения реальной ситуации, оставить основные влияющие факторы и соотношения между ними. По этому поводу рассказывают, что академик С. А. Чаплыгин, будучи в свое время научным руководителем Центрального аэрогидродинамического института, не утвердил в смете расходы на продувку в аэродинамической трубе петуха. Причина его решения была лаконично проста: «Петух не летает». Для экономических оптимизационных задач можно сформулировать ряд обязательных требований:

˗     Экономические задачи должны ставиться и решаться количественно, путем объективного расчета.

˗        Экономические задачи выбора рассматриваются как экстремальные.

˗        Функционирование экономики в целом, предприятия иего отдельного подразделения должно оцениваться по некому критерию.

˗        Лучший вариант приходится выбирать в условиях ограниченности ресурсов.

Раздел 3. Классификация задач оптимизации

Во всех сферах человеческой деятельности большое место занимает принятие решений. Для постановки задачи принятия решения необходимо выполнение двух условий:

) должно быть много решений;

) вариант должен быть выбран по определенному принципу.

Очевидно, что если нет хотя бы двух возможных вариантов решения, то выбирать нечего и задача принятия решения отсутствует. Так, если предприятию задан план, устанавливающий номенклатуру и количество выпускаемой продукции, то задачи определения плана нет, так как план задан.

Известны два принципа выбора: волевой и критериальный.

Волевой выбор, наиболее часто используемый, применяют при отсутствии формализованных моделей как единственно возможный.

Критериальный выбор заключается в принятии некоторого критерия и сравнении возможных вариантов, соответствующих критерию. Вариант, для которого выбранный критерий принимает наилучшее решение, называют оптимальным (от лат. optimus), а задачу принятия наилучшего решения - задачей оптимизации.

Решение не может быть оптимальным вообще, во всех смыслах, а только в одном, единственном смысле, определяемом выбранным критерием. Критерий оптимизации называют целевой функцией, функцией цели, функционалом и др. Любую задачу, решение которой сводится к нахождению максимума или минимума целевой функции, называют задачей оптимизации. Задачи менеджмента чаще всего связаны с нахождением условного экстремума целевой функции при известных ограничениях, накладываемых на ее переменные.

В качестве целевой функции при решении различных оптимизационных задач принимают количество или стоимость выпускаемой продукции, затраты на производство, сумму прибыли и т. п. Ограничения обычно - ресурсы: людские, материальные, денежные.

Можно показать, что оптимизационные задачи менеджмента, различные по своему содержанию и реализуемые с использованием стандартных программных продуктов, соответствуют тому или иному классу экономико-математических моделей. Классификация задач оптимизации, реализуемых менеджментом на производстве, представлена в таблице 3.1.

Таблица 3.1 Классификация задач оптимизации

Другой важный признак систематизации - классификация моделей по ее элементам: исходным данным, искомым переменным, зависимостям, описывающим цель задачи (моделирования) и ограничения.

В зависимости от исходных данных выделяют 3 типа математического описания задач управления: детерминированные, вероятностные и задачи в условиях неопределенности. Исходные данные, которые заданы определенными величинами, называют детерминированными. Детерминированные задачи формулируются в условиях полной определенности о значениях используемых параметров, составе и виде влияющих ограничивающих условий. Такое описание имеет однозначность при математическом представлении и позволяет получить однозначное решение.

В детерминированной задаче всегда известно, что стратегия действий А приведет к результату A, а стратегия действий В - к результату B. Остается только определить, какой результат имеет большую полезность, чтобы выбрать лучшую из двух стратегий.

Исходные данные, которые зависят от ряда случайных факторов, называют случайными величинами. Например, имеющееся наличие ресурсов зависит от своевременности их поставки, производительность оборудования и т. д. Вероятностные, или, как их еще называют, стохастические задачи, включают в своей постановке задачи параметры, задаваемые в виде случайных величин, для которых известны вероятности достижения возможных значений. Такие задачи называют также задачами с риском, и их решение формулируется как конкретные результаты с вероятностной оценкой каждого из них.

Заметим, что детерминированные задачи можно рассматривать как предельный вариант задач с риском, в которых вероятность появления значений используемых параметров равна единице. Оценки вероятностей бывают объективными и субъективными. Объективные вероятности получаются путем определения отношения числа интересующих нас событий к общему числу наблюдаемых событий. Задачи в условиях неопределенности возникают в ситуациях, когда нет предварительной вероятностной оценки возможных будущих ситуаций или значений параметров, их характеризующих. В подобных задачах используют своеобразный подход для описания оценки предпочтительности управленческих стратегий. Оценка максимин предполагает предпочтительность стратегии действий, у которой достигается максимально полезный результат при наиболее неблагоприятном развитии событий. Оценка минимакс ориентирует на выбор стратегии, требующей наименьших расходов при наиболее неблагоприятном развитии событий. Переменные величины могут быть непрерывными и дискретными. Непрерывные величины могут принимать в заданном интервале любые значения (например, процентное содержание элементов в марке материала). Дискретные или целочисленные, принимают только целые значения (например, нельзя ввести в эксплуатацию 1,5 здания). Зависимости между элементами могут быть линейными и нелинейными. Линейными называют зависимости, в которые входят переменные в первой степени и нет их произведения. Если входят переменные не в первой степени или есть произведение переменных, то зависимости называют нелинейными.

Сочетание различных элементов модели приводит к различным классам задач оптимизации, которые требуют разных методов решения, следовательно, и разных программных средств, представленных в таблице 3.2).

Таблица 3.2 Методы решения

.1 Задача линейного программирования

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

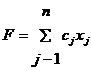                                                         (1)

при условиях:

                                       (2)

                                          (3)

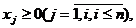                                                (4)

где - заданные постоянные величины и .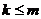

.2 Задача нелинейного программирования

Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции  при выполнении условий

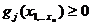                                                (5)

где 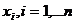 -параметры,  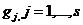- ограничения, n - количество параметров, s - количество ограничений.

В отличие от задачи линейного программирования, в задаче программирования нелинейного оптимум не обязательно лежит на границе.

3.3 Задача выпуклого программирования

Рассмотрим n-мерную задачу выпуклого программирования <javascript:termInfo(%22%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D1%83%20%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%BE%D0%B3%D0%BE%20%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F%22)>

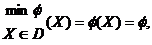                                   (6)

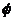(X)- выпуклая функция <javascript:termInfo(%22%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%B0%D1%8F%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%22)>, D - выпуклое не пустое ограниченное и замкнутое множество допустимых значений вектора варьируемых переменных <javascript:termInfo(%22%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE%20%D0%B4%D0%BE%D0%BF%D1%83%D1%81%D1%82%D0%B8%D0%BC%D1%8B%D1%85%20%D0%B7%D0%BD%D0%B0%D1%87%D0%B5%D0%BD%D0%B8%D0%B9%20%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B0%20%D0%B2%D0%B0%D1%80%D1%8C%D0%B8%D1%80%D1%83%D0%B5%D0%BC%D1%8B%D1%85%20%D0%BF%D0%B5%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D1%8B%D1%85%22)>. Напомним, что по определению выпуклая функция является непрерывной.

Во внутренних точках множества допустимых значений D функция 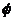(X) достигает минимального значения в точках, которые являются ее либо стационарными точками функции <javascript:termInfo(%22%D1%81%D1%82%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D1%80%D0%BD%D1%8B%D0%BC%D0%B8%20%D1%82%D0%BE%D1%87%D0%BA%D0%B0%D0%BC%D0%B8%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8%22)>, либо критическими точками функции. Однако функция может достигать своего наименьшего значения и в граничных точках области определения D.

Важные свойства задачи выпуклого программирования определяют две следующие теоремы.

Теорема 1. Если внутренняя точка X* множества D является точкой локального минимума в задаче выпуклого программирования <javascript:termInfo(%22%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B5%20%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%BE%D0%B3%D0%BE%20%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F%22)>, то в этой точке функция 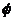(X) достигает глобального минимума.

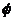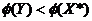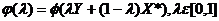Доказательство. Положим, что в точке X* функция (X) не достигает наименьшего во множестве D значения. Тогда существует точка , для которой . Рассмотрим сечение . Функция 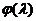достигает в точке 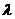=0 наибольшее значение. Действительно, поскольку

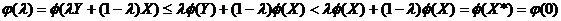
Это значит, что существует окрестность 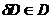 точки X* и некоторое 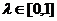 такие, что . Но тогда 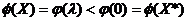, что противоречит условию теоремы.

Из теоремы следует, что во всех точках локального минимума выпуклая функция <javascript:termInfo(%22%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%B0%D1%8F%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%22)> имеет одинаковые значения.

Теорема 2. Функция 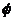(X), строго выпуклая функция <javascript:termInfo(%22%D1%81%D1%82%D1%80%D0%BE%D0%B3%D0%BE%20%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%B0%D1%8F%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%22)> на выпуклом множестве <javascript:termInfo(%22%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%BE%D0%BC%20%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%B5%22)>, имеет в этом множестве не более одной точки минимума (глобального).

Условие существования решения задачи выпуклого программирования <javascript:termInfo(%22%D0%A3%D1%81%D0%BB%D0%BE%D0%B2%D0%B8%D0%B5%20%D1%81%D1%83%D1%89%D0%B5%D1%81%D1%82%D0%B2%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F%20%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F%20%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8%20%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%BE%D0%B3%D0%BE%20%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F%22)> дает следующая теорема.

Теорема 3. Пусть функция 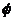(X) выпукла на выпуклом множестве <javascript:termInfo(%22%D0%B2%D1%8B%D0%BF%D1%83%D0%BA%D0%BB%D0%BE%D0%BC%20%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%B5%22)> и дифференцируема в точке 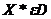 Тогда для того чтобы эта точка была точкой минимума функции 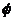(X), необходимо и достаточно, чтобы для любой точки  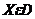выполнялось неравенство

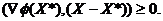     (7)

Необходимость. Рассмотрим сечение 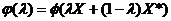 функции 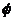(X). Функция 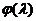определена на отрезке [0,1], имеет в точке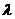=0 локальный минимум и дифференцируема в этой точке. Следовательно 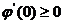 (равенство нулю имеет место в том случае, когда точка X* является внутренней точкой множества D). По правилу дифференцирования сложной функции

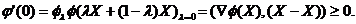
Достаточность. Пусть в точке 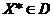 выполнено неравенство. Рассмотрим сечение  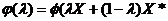функции 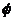(X), где X - произвольная точка из множества D. Поскольку 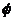(X) выпукла во множестве D, то функция 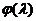также выпукла на отрезке [0,1]. Кроме того, из неравенства следует, что 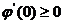. Это означает, что 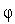(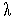) - неубывающая отрезке [0,1] функция, т.е.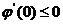(1). Последнее неравенство означает, что  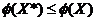и в точке X* функция 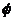(X) принимает наименьшее в области значение.

Теорему 3 иллюстрирует рисунок 3.3.1 линии уровня на котором получены с помощью следующей MATLAB-программы:

x=-2:0.06:-0.1;=x;

[X,Y]=meshgrid(x);=100.*(Y-X.^2).^2+(1-X).^2;=[2,8,32,125,250,500,1000,2000];(X,Y,Z,V);

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

Рисунок 3.3.1. Линии уровня

Точка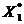 на рисунке 3.3.1. является точкой локального минимума, поскольку не существует такой точки 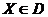, что скалярное произведение 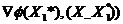 отрицательно. Точка 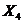, например, не является точкой локального минимума, так как существуют такие точки 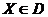, что скалярное произведение  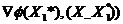отрицательно.

3.4 Задача квадратичного программирования

Частным случаем задачи нелинейного программирования является задача квадратичного программирования, в которой ограничения

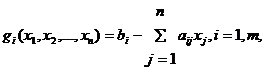                                (8)

являются линейными, а функция 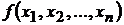 представляет собой сумму линейной и квадратичной функции (квадратичной формы)

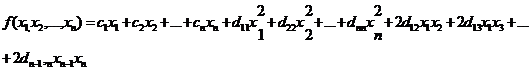
Как и в общем случае решения задач нелинейного программирования, для определения глобального экстремума задачи квадратичного программирования не существует эффективного вычислительного метода, если не известно, что любой локальный экстремум является одновременно и глобальным. Так как в задаче квадратичного программирования множество допустимых решений выпукло, то, если целевая функция вогнута, любой локальный максимум является глобальным; если же целевая функция - выпуклая, то любой локальный минимум также и глобальный.

Функция  представляет собой сумму линейной функции (которая является и выпуклой, и вогнутой) и квадратичной формы. Если последняя является вогнутой (выпуклой), то задачи отыскания максимума (минимума) целевой функции могут быть успешно решены. Вопрос о том, будет ли квадратичная форма вогнутой или выпуклой, зависит от того, является ли она отрицательно-определенной, отрицательно-полуопределенной, положительно-определенной, положительно-полуопределенной или вообще неопределенной.

3.5 Задача целочисленного программирования

Под задачей целочисленного программирования понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограничения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, когда хотя бы одна зависимость будет нелинейной, это будет целочисленной задачей нелинейного программирования.

Задачу целочисленного программирования решают без учета условий целочисленности переменных, а затем округляют полученное решение с избытком или недостатком.

.6 Задача параметрического программирования

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.

Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, чтобы в результате решения иметь наилучшие планы для любого варианта исходных данных.

С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

3.7 Задача динамического программирования

Рассматривается управляемая система, которая под влиянием управления переходит из начального состояния  в конечное состояние .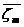

Предположим, что процесс управления системой можно разбить на n шагов. Пусть 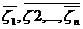 - состояния системы после 1-го, 2-го, …, n-го шагов (рис. 16.1). Состояние 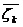 системы после k шага  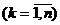характеризуется параметрами 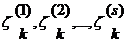, которые называются фазовыми координатами. Состояние можно изобразить точкой s-мерного пространства, называемого фазовым. Последовательное преобразование системы (по шагам) достигается с помощью некоторых мероприятий , которые составляют управление системой 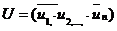, где 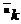 - управление на k-м шаге, переводящее систему из состояния  в состояние 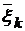. 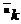Управление  на k-м шаге заключается в выборе значений определенных управляющих переменных 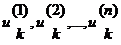 предполагаем, что состояние системы в конце k-го шага зависит только от предшествующего состояния системы 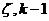 и управления  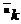на данном шаге. Такое свойство получило название отсутствие последействия. Запишем эту зависимость в виде:

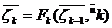                                           (9)

Равенства (9) получили название уравнений состояний представленных на рисунке 3.7.1.

Рисунок 3.7.1Название уравнений состояний

Варьируя управление U, получим различную эффективность процесса, которую будем оценивать количественно целевой функцией

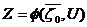.                                               (10)

Показатель эффективности k-го шага процесса управления, который зависит от состояния 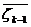 в начале этого шага и управления , выбранного на этом шаге, обозначим через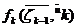. В рассматриваемой задаче пошаговой оптимизации целевая функция полагается аддитивной, т. е.

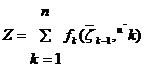                                     (11)

Обычно условиями процесса на управление на каждом шаге 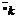 накладываются некоторые ограничения. Управления, удовлетворяющие этим ограничениям, называются допустимыми.

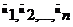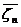Задачу пошаговой оптимизации можно сформулировать следующим образом. Определить совокупность допустимых управлений , переводящих систему из начального состояния  в конечное состояние  и максимизирующих или минимизирующих показатель эффективности. В дальнейшем будем рассматривать задачу на максимум.

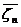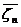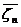
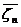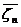
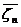Начальное состояние  и конечное состояние  могут быть заданы однозначно или могут быть указаны множество  начальных состояний и множество  конечных состояний так, что , . В последнем случае в задаче пошаговой оптимизации требуется определить совокупность допустимых управлений, переводящих систему из начального состояния  в конечное состояние и максимизирующих целевую функцию (11). Управление, при котором достигается максимум целевой функции (11), называется оптимальным управлением и обозначается через

.                                     (12)

.8 Задача стохастического программирования

В стохастическом программировании рассматриваются проблемы после принятия решений в условиях действия случайных факторов, которые необходимо учитывать в соответствующих математических моделях.

Рассмотрим типичную задачу нелинейного программирования:

найти такой вектор Х, для которого

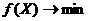
при ограничениях

,

.

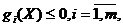Задачи стохастического программирования возникают в случаях, когда функции , 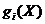зависят также от случайных параметров . При этом предполагается, что является элементом пространства состояний природы (или пространства случайных параметров) . Тогда задачу стохастического программирования можно сформулировать так:

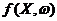
при условиях

,

.

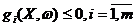Постановка задач стохастического программирования существенно зависит от того, есть ли возможность при выборе решений уточнить состояние природы  путем некоторых наблюдений или нет. В связи с этим различают задачи оперативного и перспективного стохастического программирования.

В задачах оперативного стохастического программирования решение принимается после некоторого эксперимента над состоянием природы , оно зависит от результатов эксперимента и является случайным вектором .

Решение x принимается до проведения каких-либо наблюдений над состоянием природы и поэтому является детерминированным. Такие задачи возникают в перспективном технико-экономическом планировании, в задачах проектирования, когда параметры системы должны быть выбраны конкретными детерминированными величинами, в расчете на определенный диапазон возможных возмущений.

Раздел 4. Практическое применение MS Excel к решению задачи линейного программирования

Задача: Используя поиск решения найти максимальное значение функции.

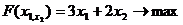
при следующих ограничениях:

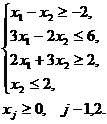
Решение:

1.     Запускаем программу MicrosoftExcel, в верхнем левом углу нажимаем кнопку «Office», внизу находим кнопку «Параметры Excel» (рисунок 4.1).

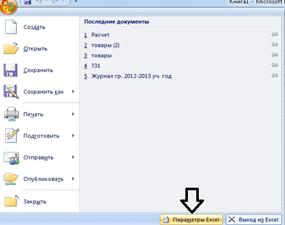
Рисунок 4.1. Кнопка «Параметры Excel»

2.    

3.      В меню «Параметры» переходим на вкладку «Надстройки», после чего кликаем по кнопке «Перейти» (рисунок 4.2).

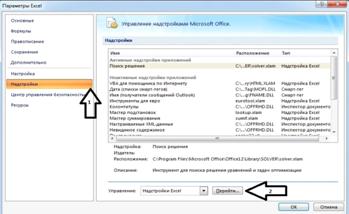
Рисунок 4.2. Кнопки «Надстройки» и «Перейти»

4.     Ставим галочку на пункте «Поиск решения», нажимаем кнопку ОК (рисунок 4.3).

Рисунок 4.3. Галочка на пункте «Поиск решения» в меню «Надстройки»

5.     Указываем переменные в соответствующие ячейки (рисунок 4.4).

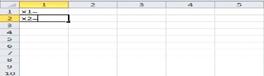
Рисунок 4.4. Указание переменных

6.     Вводим параметры функции, в желтых ячейках вводятся значения переменных, в ячейке зеленого цвета значение самой функции (рисунок 4.5).

Рисунок 4.5. Ввод параметров функции

7.     Кликаем по надстройке «Поиск решений», находящейся на вкладке «Данные» верхней панели Excel (рисунок 4.6).

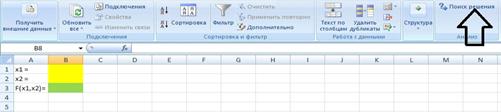
Рисунок 4.6. Кнопка «Поиск решения»

8.     В появившемся окне устанавливаем целевую ячейку, которой является результат функции. В поле «изменяя ячейки» указываем ячейки со значениями переменных (рисунок 4.7).

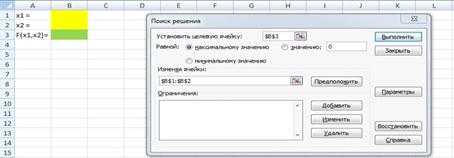
Рисунок 4.7. Установка целевой ячейки

.       Прописываем следующую формулу, по которой будет вычисляться значение самой функции (рисунок 4.8).

Рисунок 4.8. Указание формулы, по которой вычисляется значение функции

10.   Создаем ограничения как показано на рисунке (рисунок 4.9).

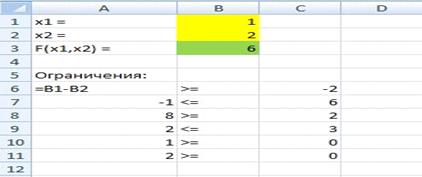
Рисунок 4.9. Создание ограничений

11.   Открываем «Поиск решения», предварительно выделив целевую ячейку, указать изменяемые ячейки (1 - изменяемые ячейки, 2 - целевая ячейка) (рисунок 4.10).

Рисунок 4.10. Открытие «Поиска решений» с предварительным выделением целевой ячейки и указанием изменяемых ячеек

12.   Добавляем ограничения, закрываем окно ограничений (рисунок 4.11).

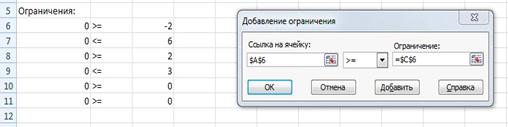
Рисунок 4.11. Добавление ограничений

13.   Кликаем по кнопке «Выполнить» (рисунок 4.12).

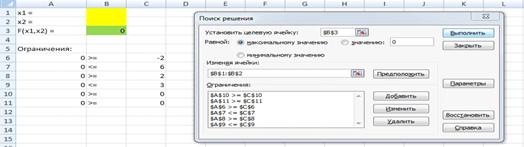
Рисунок 4.12. Кнопка «Выполнить»

14.   Выбираем из списка отчеты, которые необходимо сформировать (рисунок 4.13).

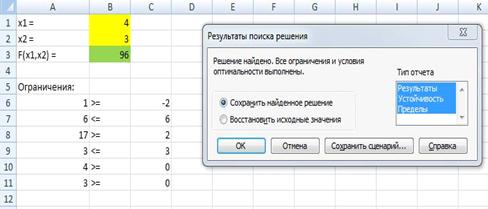
Рисунок 4.13. Окно выбора списка отчетов

.       Формирование отчета по пределам (рисунок 4.14).

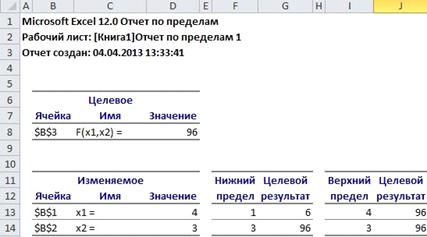
Рисунок 4.14. Отчет по пределам

.        Формирование отчета по результатам (рисунок 4.15).

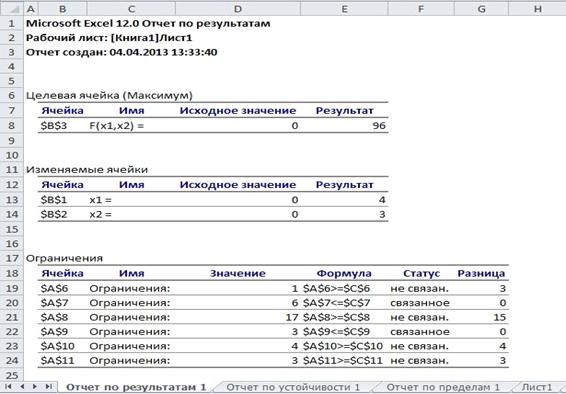
Рисунок 4.15. Отчет по результатам

.       Формирование отчета по устойчивости (рисунок 4.16).

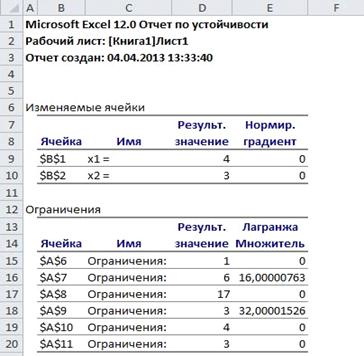
Рисунок 4.16. Отчет по устойчивости

Заключение

В данной курсовой работе были рассмотрены теоретические основы математических методов; этапы принятия решений; проведена классификация задач оптимизации, к которым относятся:

˗      задача линейного программирования,

˗        задача нелинейного программирования,

˗        задача выпуклого программирования,

˗        задача квадратичного программирования,

˗        задача целочисленного программирования,

˗        задача параметрического программирования,

˗        задача динамического программирования,

˗        задача стохастического программирования.

Так же в практической части работы осуществлен расчет, в котором была решена задача линейного программирования.

Список использованных источников

1.        Алексинская Т.В., Сербин В.Д., Учебно-методическое пособие по курсу "Экономико-математические методы и модели. Линейное программирование": Изд-во ТРТУ, 2010.-156с.

2.      Бурков В.Н., Квон О.Ф., Цитович Л.А. Модели и методы мультипроектного управления Издательство ДИС,2009.-267с.

.        Гмурман В.Е. Линейное программирование. Руководство к решению задач. - М.: ФИЗМАТЛИТ, 2008. - 128 с.

.        Замков О.О. Толстопятенко А.В. Математические методы в экономике: Учебник. -М:МГУ им. М.В.Ломоносова, Издательство ДИС, 2010.-238с.

.        Костин В.Н., Тишина Н.А.Статистические методы и модели: Учебное пособие Оренбург: ГОУ ОГУ, 2009.-128с.

.        Макарова С.И. Экономико-математические методы и модели. Учебное пособие. Учебное пособие кол.авторов; под ред. Макарова С.И. КНОРУС,2010.-232с.

.        Макарова С.И., Севастьянова С.А. Экономико-математические методы и модели. Задачник. Учебно- практическое пособие кол. авторов; под ред. Макарова С.И. Севастьянова С.А. -2е изд., перераб. -М. КНОРУС,2009.-208 с.

.        Стариков А. В., Кущева И. С. Экономико-математическое и компьютерное моделирование: учебное пособие ;Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». - Воронеж, 2008.-181с.

.        Федоряк Н.И., Аникьева Э.Н Практикум по использованию MS EXCEL в экономике и финансах., - Мичуринск: Изд. МичГАУ, 2010.-130с.

.        Шапкин А.С. Мазаева Н.П. Математические методы и модели исследования операций: Учебник.-3-е изд.- М.: Издательско-торговая корпорация Дашков и К, 2011.-400с.