|
Наименование детали
|
Тип материала
|
Модуль упругости, Е, кгс/мм2
|
Коэффициент Пуассона
|
|
Лонжерон 333.3950.1100
|
Т25(ВМ)-78, Св. 5-211Б
|
5300
|
0,3
|
|
Бобышка 333.3950.1101
|
ВМС-6-7,2x2,
Св.
5-211Б
|
4468
|
0,3
|
|
Вкладыш 333.3950.1850
|
Т25(ВМ)-78, Св. 5-211Б
|
5300
|
0,3
|
Расчетные схемы.
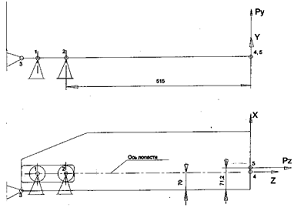
Рис. 1.0
Расчетная схема приведена на рис. 1.0.
Конструкция шарнирно закреплена в центральных точках подшипников 1 и 2, и
закреплена от вращения вокруг оси лопасти в точке 3.
Расчет проводится на случай
нагружения: максимальная нагрузка в плоскости взмаха в полете на режиме висения
(см. таблицу 1.2).
Таблица 1.2
|
(к рис. 1.0)
|
Рх, кгс
|
Ру, кгс
|
Рz,
кгс (в т. 5)
|
|
Величина нагрузки
|
0
|
0
|
6860
|
Построение трехмерной модели осуществлялось по
чертежу 333.3950.1100 СБ.
Схематично на рис. 1 показан лонжерон лопасти.
Длина конструкции 661 см. Конструкция имеет характерные поперечные сечения
(рис. 1.2-1.4)
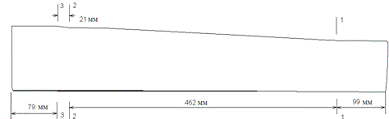
Рис. 1.1

Метод конечных элементов
С точки зрения практики расчета сложных
конструкций матричными методами, МКЭ является естественным распространением
методов расчета стержневых систем на задачи механики сплошной среды. Это объясняется
единством методологии классических методов строительной механики и МКЭ, которая
сводится к расчленению исходной конструкции на отдельные части, как правило
более простой структуры, механическое поведение (процесс деформирования)
которых легко описывается, а затем к объединению их вновь в единую конструкцию
путем выполнения условий равновесия и сплошности. С другой стороны, МКЭ можно
трактовать как специфическую форму метода Ритца приближенного решения задач
механики деформируемого твердого тела, что дает ключ к теоретическому
обоснованию его основных положений. В настоящей работе будем придерживаться
вариационной постановки задач МКЭ: либо как задач минимизации функционала
энергии, либо как решение вариационных уравнений равновесия (движения).
Вариационная постановка задач теории упругости
Для единицы объема упругого тела,
ориентированного вдоль произвольно выбранной декартовой системы координат  ,
, 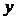 ,
, 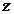 , удельная
потенциальная энергия деформации записывается в виде
, удельная
потенциальная энергия деформации записывается в виде
 (1.1)
(1.1)
Введем вектор деформаций 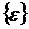 и вектор
напряжений
и вектор
напряжений 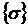
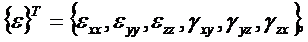
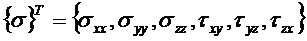 . (1.2)
. (1.2)
Тогда выражение (1.1) можно записать
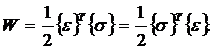 (1.3)
(1.3)
Потенциальная энергия деформации,
накопленная телом, определяется в виде интеграла по всему объему тела 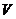
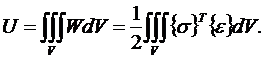 (1.4)
(1.4)
 . (1.5)
. (1.5)
Тогда выражение потенциальной
энергии деформации можем записать
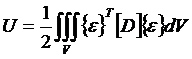 . (1.6)
. (1.6)
Работу внешних сил запишем в
матричном виде. Для этого введем вектор перемещений
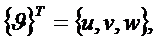 (1.7)
(1.7)
Где 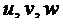 - проекции вектора перемещений
вдоль осей
- проекции вектора перемещений
вдоль осей  ,
, 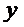 ,
, 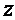 , вектор
массовых сил
, вектор
массовых сил 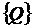
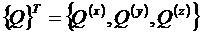 (1.8)
(1.8)
и вектор поверхностных сил 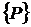 ,
действующий на части поверхности
,
действующий на части поверхности  ,
,
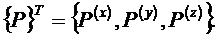 (1.9)
(1.9)
Тогда работа внешних сил может быть
записана в виде
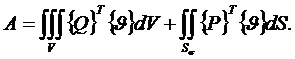 (1.10)
(1.10)
Полная энергия (функционал Лагранжа)
системы определяется как
 (1.11)
(1.11)
Откуда, с учетом (1.6) и (1.10),
получим окончательное выражение
 . (1.12)
. (1.12)
В соответствии с общими теоремами
механики, истинное состояние равновесия тела соответствует минимуму полной
энергии, то есть задача сводится к поиску такого вектора  , и как
следствие
, и как
следствие 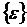 ,
, 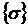 , которые
дают
, которые
дают 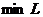 .
Уравнениями Эйлера этой вариационной задачи являются уравнения равновесия и
статические граничные условия.
.
Уравнениями Эйлера этой вариационной задачи являются уравнения равновесия и
статические граничные условия.
МКЭ как метод Ритца.
Одним из главных моментов в методе
Ритца минимизации функционала энергии является построение поля перемещений в
виде разложений по некоторой системе координатных функций
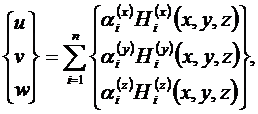 (2.1)
(2.1)
Которые должны удовлетворять
кинематическим граничным условиям. В классическом методе Ритца эти функции  определяются
во всей области и должны обладать свойством полноты. По сути дела (2.1) есть
аппроксимация вектора перемещений
определяются
во всей области и должны обладать свойством полноты. По сути дела (2.1) есть
аппроксимация вектора перемещений  , определенная сразу во всей
области. Здесь выявляется главная трудность поиска решения в виде (2.1), а
именно: сложность построения функций
, определенная сразу во всей
области. Здесь выявляется главная трудность поиска решения в виде (2.1), а
именно: сложность построения функций  для областей неканонической формы.
Чтобы избежать этих осложнений, было предложено разбивать исходную область на
отдельные части, геометрически более простой структуры, внутри которых строить
аппроксимации
для областей неканонической формы.
Чтобы избежать этих осложнений, было предложено разбивать исходную область на
отдельные части, геометрически более простой структуры, внутри которых строить
аппроксимации  значительно
проще. Однако здесь возникает новая трудность, связанная со стыковкой этих
отдельных сегментов в плане выполнения условий непрерывности перемещений
(уравнение равновесия удовлетворяются вариационно). Выходом было предложение
принять в качестве неопределенных коэффициентов разложений
значительно
проще. Однако здесь возникает новая трудность, связанная со стыковкой этих
отдельных сегментов в плане выполнения условий непрерывности перемещений
(уравнение равновесия удовлетворяются вариационно). Выходом было предложение
принять в качестве неопределенных коэффициентов разложений 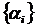 значений
компонент перемещений
значений
компонент перемещений 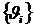 в некоторой
системе точек (узлов), как правило лежащих на границах стыкуемых элементов. В
результате получается такая модификация метода Ритца, которая называется метод
конечных элементов.
в некоторой
системе точек (узлов), как правило лежащих на границах стыкуемых элементов. В
результате получается такая модификация метода Ритца, которая называется метод
конечных элементов.
Таким образом, МКЭ состоит из
следующих основных этапов:
Разбиение исходной области на
отдельные части (элементы) простой геометрической структуры (для двумерных
задач это треугольники и четырехугольники).
На границах между отдельными
элементами, а в случае необходимости и внутри элементов вводятся точки (узлы),
перемещения которых  далее
считаются основными неизвестными.
далее
считаются основными неизвестными.
Для отдельного конечного элемента
строится выражение функционала энергии как функции перемещений узлов,
принадлежащих только этому конечному элементу. Схема здесь следующая.
Рассмотрим некоторый m-ый элемент. Обозначим через вектор  - вектор
узловых перемещений m - ого элемента
- вектор
узловых перемещений m - ого элемента
 . (2.2)
. (2.2)
Введем аппроксимации внутри элемента
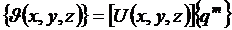 , (2.3)
, (2.3)
Где 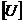 содержит в себе некоторые функции,
ее элементами будут степенные функции, то есть полиномы. По (2.3) можем
вычислить вектор деформации(1.2) в виде
содержит в себе некоторые функции,
ее элементами будут степенные функции, то есть полиномы. По (2.3) можем
вычислить вектор деформации(1.2) в виде
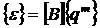 . (2.4)
. (2.4)
Подставляя (2.3), (2.4) в (1.12)
получим выражение энергии на элементе
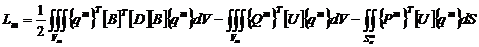 . (2.5)
. (2.5)
Так как параметры 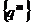 постоянные
на элементе, то (2.5) можем записать в виде
постоянные
на элементе, то (2.5) можем записать в виде
 , (2.6)
, (2.6)
Где 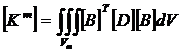 ,
,
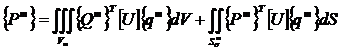 . (2.7)
. (2.7)
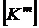 - матрица жесткости элемента,
- матрица жесткости элемента, 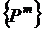 - вектор
узловых сил.
- вектор
узловых сил.
Строится функционал энергии для
всего тела как сумма значений энергии по всем элементам. При этом считается,
что перемещения узлов, принадлежащих разным элементам, одинаковы для всех
прилегающих элементов. Физически это означает выполнение условий неразрывности
поля перемещений во всей области тела. После выполнения операций сборки получим
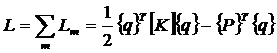 . (2.8)
. (2.8)
Здесь вектор  включает в
себя узловые перемещения всего тела, матрица
включает в
себя узловые перемещения всего тела, матрица 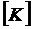 называется матрицей жесткости всего
тела и состоит из суммы матриц
называется матрицей жесткости всего
тела и состоит из суммы матриц 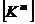 , вектор
, вектор 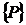 - вектор
внешних сил, состоящий из суммы поэлементных сил
- вектор
внешних сил, состоящий из суммы поэлементных сил 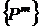 и заданных сосредоточенных
нагрузок.
и заданных сосредоточенных
нагрузок.
В соответствии с методом Ритца
необходимо найти такой вектор 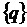 , который дает минимум энергии Э.
Как известно необходимым и достаточным условием минимума полной энергии
является равенство нулю ее первой вариации
, который дает минимум энергии Э.
Как известно необходимым и достаточным условием минимума полной энергии
является равенство нулю ее первой вариации
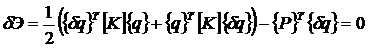 , (2.9)
, (2.9)
Откуда в силу симметрии матрицы  получим
алгебраическую задачу
получим
алгебраическую задачу
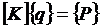 . (2.10)
. (2.10)
Решая эту систему, находим вектор 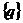 , который
однозначно определяет поле перемещений и позволяет найти распределение
напряжений в теле, что и является конечной целью задач теории упругости.
, который
однозначно определяет поле перемещений и позволяет найти распределение
напряжений в теле, что и является конечной целью задач теории упругости.
Различие МКЭ и метода Ритца состоит
в особенности задания аппроксимации, а именно: в МКЭ она определяется
поэлементно и неизвестными параметрами являются узловые перемещения, тогда как
в классическом методе Ритца неизвестные параметры  не имеют
явного физического смысла.
не имеют
явного физического смысла.
Приведем две квадратичные
аппроксимации: двадцатиузловой параллелепипед и пятнадцати узловая призма. Они
принадлежат классу Сирендиповых аппроксимаций, так как имеют узлы только на
ребрах.
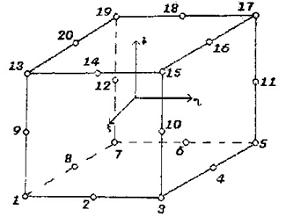
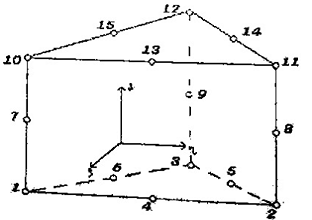
Пробные функции для первого из них имеют вид
неполного триквадратичного полинома, то есть
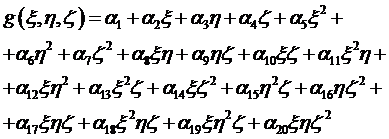 (2.11)
(2.11)
Функции формы для (2.11) получаются
следующими:
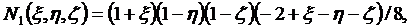
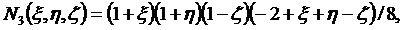
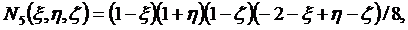
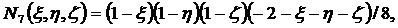
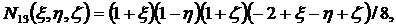
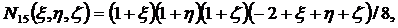
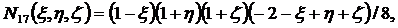
 (2.12)
(2.12)


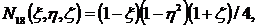
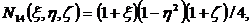
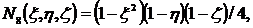
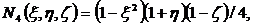
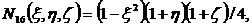
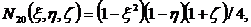

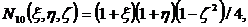
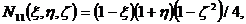
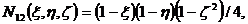
 (2.13)
(2.13)
Функции формы удобнее записать в 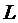 -координатах
плоскости
-координатах
плоскости 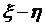 и
и 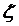 -координаты.
Получим
-координаты.
Получим
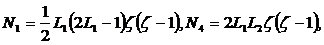
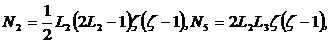
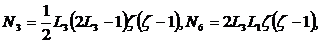
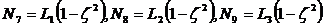 (2.14)
(2.14)
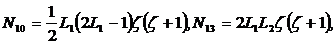

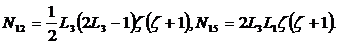
лонжерон энергия
устойчивость тяга
Решение задачи проводилось
в пакете прикладных программ Ansys. Модель построена на основе
данных сечений. Вводились координаты изменения сечений и соединялись прямыми
или сплайнами. Далее строились плоскости, ограниченные этими прямыми и
сплайнами, после чего моделировались конечные объемные
Построение трехмерной модели
осуществлялось по чертежу 333.3950.1100 СБ.
Схематично на рис. 1 показан
лонжерон лопасти. Длина конструкции 661 см. Конструкция имеет характерные
поперечные сечения (рис. 1.2-1.4)
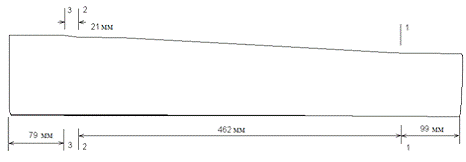
Рис. 1.1
Геометрическое построение модели
производилось по принципу "слева направо". Каждая деталь была разбита
на несколько подконструкций, которые строились по точкам, через которые
проводились линии. Кривые строились с помощью сплайн-линий и дуг окружностей
разных радиусов, дуги окружностей строго соответствовали данным в чертежах. С
помощью замыкающихся линий были образованы площади. Площади, в свою очередь,
образуют контур объемов. На рис.1.2-1.4 изображены базовые поперечные сечения.

Рис. 1.2 Сечение 1-1

Рис. 1.3 Сечение 2-2
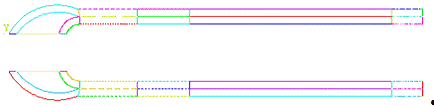
Рис. 1.4 Сечение 3-3
Далее, задавая параметры разбиения
(задаем для каждой линии каждого объема число разбиений), получим
конечноэлементную модель.
При построении сетки конечных
элементов особое внимание уделяется проблеме сопряжения подконструкций между
собой "узел в узел". Это обстоятельство налагает дополнительные
условия на выбор параметров разбиения на отдельные конечные элементы каждой
подконструкции.
Применяли конечный элемент SOLID186 -
двадцатиузловой элемент, который описан подробнее выше в методе конечных
элементов.
Нагрузка прикладывается в виде
распределенной нагрузки, так чтобы равнодействующая сила была в точке,
указанной на рисунках. На рисунках указаны истинные направления приложения
нагрузки.

Численные результаты
На следующих рисунках представлены
результаты расчетов, напряжения измеряются в Н/м2. На рис. 2.1
изображено распределение нормальных напряжений  . В зонах крепления подшипника
появляются максимальные напряжения, которым соответствует голубой цвет. Также в
этих зонах наблюдается максимальные значения нормальных напряжений
. В зонах крепления подшипника
появляются максимальные напряжения, которым соответствует голубой цвет. Также в
этих зонах наблюдается максимальные значения нормальных напряжений  ,
, 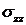 (рис. 2.2 и
2.3, соответственно), касательных напряжений
(рис. 2.2 и
2.3, соответственно), касательных напряжений 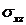 ,
, 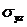 рис. 2.4 и 2.6, соответственно), и
интенсивности напряжений
рис. 2.4 и 2.6, соответственно), и
интенсивности напряжений  (рис. 2.7).
(рис. 2.7).

Рис. 2.1. Распределение нормальных
напряжений 

Рис. 2.2. Распределение нормальных
напряжений 

Рис. 2.3. Распределение нормальных
напряжений 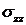
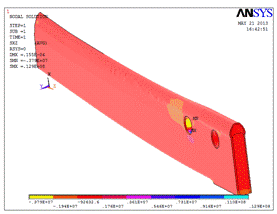
Рис. 2.4. Распределение касательных
напряжений 
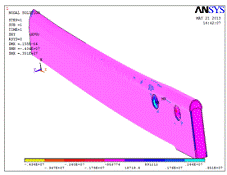
Рис. 2.5. Распределение касательных
напряжений 

Рис. 2.6. Распределение касательных
напряжений 
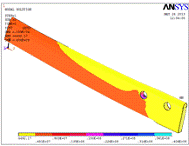
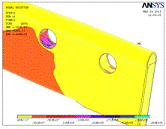
Рис. 2.7. Распределение
интенсивности напряжений 
Значение критической силы
определяется как произведение заданной в статическом анализе нагрузки и
множителя LOAD MULTIPLIER, который вычисляется в результате анализа
устойчивости. Значение множителя LOAD MULTIPLIER выводится в окне ANSYS Output
Window (рис.2.8.) в конце анализа на устойчивость. Для рассчитываемой тяги этот
множитель составляет 52,3236. А поскольку значение сжимающей силы при
статическом анализе было задано равным 6860 кгс, то значение критической силы равно
358939,896 кгс, вызывающей потерю устойчивости лонжерона.
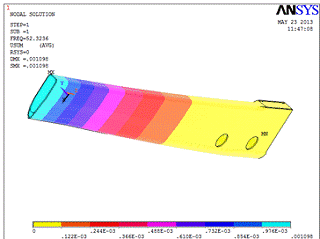
Рис. 2.8. Первая форма потери
устойчивости
Анализируя полученные результаты,
можно говорить, что при выбранной расчетной схеме в зонах подшипника возникают
наибольшие значения напряжения. Распределение нормальных напряжений  варьируется
от -6,2 мПа до 4,67 мПа. Распределение нормальных напряжений
варьируется
от -6,2 мПа до 4,67 мПа. Распределение нормальных напряжений  варьируется
от -3,02 мПа до 5,11 мПа. Распределение нормальных напряжений
варьируется
от -3,02 мПа до 5,11 мПа. Распределение нормальных напряжений 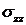 от -7,89
мПа до 15,8 мПа. Распределение касательных напряжений
от -7,89
мПа до 15,8 мПа. Распределение касательных напряжений 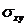 от -4,34
мПа до 3,51 мПа. Распределение касательных напряжений
от -4,34
мПа до 3,51 мПа. Распределение касательных напряжений 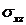 -3,79 мПа
до 12,9 мПа. Распределение касательных напряжений
-3,79 мПа
до 12,9 мПа. Распределение касательных напряжений 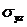 от -3,79
мПа до 12,9 мПа. Распределение касательных напряжений
от -3,79
мПа до 12,9 мПа. Распределение касательных напряжений  от 4492,17
до 40,6 мПа.
от 4492,17
до 40,6 мПа.
Полученные результаты несут
качественную характеристику НДС, для получения более точных количественных
результатов нужно в зонах крепления к подшипникам строить более мелкую сетку и
тогда уже можно будет давать конкретные рекомендации.
Заключение
В настоящей работе представлена методика
построения трехмерной твердотельной неоднородной модели лонжерона на основе
чертежной документации, сформулирована расчетная схема. Данная модель была
использована для конечно элементного анализа. Была изучена постановка метода
конечных элементов, рассмотрен двадцати узловой элемент с квадратичной
аппроксимацией. Построенная модель была использована в пакете прикладных
программ Ansys, с
использованием указанного элемента SOLID186,
получены картины распределения нормальных и касательных напряжений, а также
интенсивности напряжения, проведенных анализ. Для указанной расчетной схемы
решалась задача устойчивости, определена критическая нагрузка.