Проблемы оптимального формирования портфеля ценных бумаг
Содержание
Введение
ГЛАВА 1. Теоретические основы
формирования портфеля ценных бумаг
.1 Понятие портфеля ценных
бумаг, его виды
.2 Основные принципы
формирования портфеля ценных бумаг
.2.1 Диверсификация
.2.2 Структура портфеля
.3 Группы инвестиционных рисков
ГЛАВА 2. Модель
ценообразования на основной капитал: применение парного регрессионного анализа
.1 Основные эконометрические
понятия
.2 Модель Марковица
.3 Вывод линейной зависимости
между риском и прибылью
.4 Дальнейшая интерпритация
линейной зависимости риск-прибыль
.5 Эконометрические аспекты,
используемые в реализации модели ЦОК
ГЛАВА 3. Практическая работа
с моделью ЦОК
.1 Расчет бета - значений
ценных бумаг
.2 Составление оптимального
портфеля
.3 Анализ полученных
результатов
Заключение
Список использованной
литературы
Приложения
Введение
Занимаясь инвестициями, необходимо выработать определенную политику,
тактику и стратегию своих действий, а также состав инвестиционного портфеля,
приемлемое число ценных бумаг, вероятные и неизбежные риски, качество бумаг,
диверсификацию портфеля и т. д.
В наше время, все инвесторы, как индивидуальные, так и институциональные,
покупая те или иные ценные бумаги, стремятся достичь определенных целей. С
точки зрения формирования портфеля эти цели могут быть определены как:
1) безопасность вложений;
2) доходность вложений;
) рост стоимости вложений.
Данная работа посвящена актуальной для современного
инвестора проблеме - проблеме формирования портфеля ценных бумаг. В оптимально
сформированном портфеле риск всего портфеля ниже, чем у каждой отдельной
бумаги, а также в таком портфеле доля собственного (несистематического) риска
будет минимальна. Другими словами владельцы, в разной степени оптимально
сформированных, портфелей имеют возможность получать желаемую прибыль вне
зависимости от собственного риска находящихся в нем ценных бумаг. Прибыль
портфеля будет зависеть практически только от прибыли рынка в целом.
Объектом исследования является портфель ценных бумаг.
Предметом исследования является процесс диверсификации, который способствует
снижению портфельного риска, при сохранении его доходности. Данная работа
посвящена актуальной для нашей экономики проблеме - проблеме формирования и
управления портфелем ценных бумаг.
Достижение поставленной цели предполагает решение ряда
задач:
1) Выявить основные теоретические
предпосылки формирования портфеля ценных бумаг;
2) Применить модель ценообразования на
основной капитал и элементы регрессионного анализа для определения таких
показателей, как бета - значения, показывающие чувствительность актива к
изменениям рыночной доходности рыночная доля общего риска для каждой ценной
бумаги и рынка в целом;
3) Сконструировать портфель ценных
бумаг, и рассчитать его доходность и риск;
4) Проанализировать выводы, полученные
на основе данных парного регрессионного анализа.
В первой части дипломной работы будет рассмотрена методика формирования
портфеля ценных бумаг и освещены основные принципы его формирования, стратегии
инвестирования, модели и риски (по различным классификациям) и некоторые другие
факторы, которые необходимо учитывать при формировании инвестиционного
портфеля. Во второй части описывается эконометрические аспекты формирования
портфеля, приведены основные результаты исследований зарубежных ученых и
специалистов, внесших наиболее заметный вклад в исследование, анализ и решение
данной проблемы, а именно работы Эрнста Берндта, Джэймса Тобина и Тэйлора
Лестора. И наконец, в третьей части представляемой работы -мы построим
оптимальный портфель ценных бумаг на основе данных об основных компаниях
Американской фондовой биржи, представленных Center for Research on Securities Prices (CRSP)
при Чикагском университете, а также продемонстрируем преимущества
диверсификации. Все необходимые вычисления проводились в средах EVeiws6.0 и MathCad15.
ГЛАВА 1. Теоретические основы формирования
портфеля ценных бумаг
.1 Понятие портфеля ценных бумаг, его виды
Под портфелем ценных бумаг понимается совокупность ценных бумаг
принадлежащих физическому или юридическому лицу, выступающая как целостный объект
управления, имеющая своей целью улучшать условия инвестирования, придав данной
совокупности такие инвестиционные характеристики, которые недостижимы с позиции
отдельно взятой ценной бумаги и возможны только при их комбинации. Портфель
ценных бумаг является тем инструментом, с помощью которого инвестору
обеспечивается требуемая устойчивость дохода при минимальном риске.
Главными характеристиками портфеля являются доходность, риск и период
владения.
Доходность портфеля - это относительный доход его держателя за период,
выраженный в процентах годовых.
Риск - это количественное представление неопределенности, в которой
находится инвестор, и связанной с неполнотой информации относительно будущих
доходов (убытков) по ценным бумагам, входящим в портфель.
Еще одной характеристикой портфеля является период владения - это
временной период, в течение которого инвестор держит портфель. Эта
характеристика для конкретного портфеля является постоянной.
Если сопоставить эти три характеристики портфеля, то доходность и риск
портфеля - это объективные, т.е. не зависящие от инвестора характеристики, а
период владения - субъективная характеристика, т.к. полностью определяется
инвестором.
В соответствии с критерием соотношения риска и доходности выделяют три
типа портфелей: портфель роста, портфель дохода и смешанный портфель (портфель
роста и дохода).
Портфель роста - тип портфеля, нацеленный на получение высокого дохода
при высоком риске. Формируется портфель роста преимущественно из акций тех
компаний, курсовая стоимость которых растет. Темпы роста курсовой стоимости
совокупности акций, входящих в портфель, определяют виды портфелей, входящих в
данную группу. Портфель агрессивного роста нацелен на максимальный прирост
капитала. Инвестиции в данный тип портфеля являются достаточно рискованными, но
вместе с тем могут приносить самый высокий доход. Портфель консервативного
роста является наименее рискованным. Состав портфеля остается стабильным в
течение длительного периода времени и нацелен на сохранение капитала. Портфель среднего
(умеренного) роста представляет собой сочетание инвестиционных свойств
портфелей агрессивного и консервативного роста. В данный тип портфеля
включаются наряду с надежными ценными бумагами, приобретаемыми на длительный
срок, рискованные фондовые инструменты, состав которых периодически
обновляется. Данный тип является наиболее распространенной моделью портфеля и
пользуется большой популярностью у инвесторов, не склонных к высокому риску.
Портфель дохода ориентирован на получение высокого текущего дохода -
процентных и дивидендных выплат. В данном типе можно выделить следующие виды
портфелей. Портфель регулярного дохода формируется из высоконадежных ценных
бумаг и приносит средний доход при минимальном уровне риска. Портфель доходных
бумаг состоит из высокодоходных облигаций корпораций, ценных бумаг, приносящих
высокий доход при среднем уровне риска. В зависимости от входящих в портфель
дохода фондовых инструментов можно выделить виды портфелей: конвертируемые,
денежного рынка, облигаций. Конвертируемые портфели состоят из конвертируемых
привилегированных акций и облигаций. Такой портфель может принести
дополнительный доход за счет обмена ценных бумаг, составляющих портфель, на
обыкновенные акции, если этому благоприятствует рыночная конъюнктура. В противном
случае он обеспечивает доход при минимальном риске. Портфели денежного рынка
имеют целью полное сохранение капитала. В их состав включаются денежная
наличность и быстрореализуемые активы. Портфели облигаций формируются за счет
облигаций и приносят средний доход при почти нулевом риске.
Формирование портфеля роста и дохода осуществляется во избежание
возможных потерь на фондовом рынке, как от падения курсовой стоимости, так и
низких дивидендных или процентных выплат. Одна часть финансовых активов, входящих
в состав данного портфеля, дает владельцу рост капитальной стоимости, а другая
- доход. Здесь рассматривают следующие виды портфелей. Портфель двойного
назначения. В состав этого портфеля включаются бумаги, приносящие его владельцу
высокий доход при росте вложенного капитала. В данном случае речь идет о ценных
бумагах инвестиционных фондов двойного назначения. Они выпускают собственные
акции двух типов: первые приносят высокий доход, вторые - прирост капитала.
Сбалансированный портфель предполагает сбалансированность не только
доходов, но и риска, который сопровождает операции с ценными бумагами, и
поэтому в определенной пропорции состоит из ценных бумаг, быстро растущих в
курсовой стоимости, и из высокодоходных ценных бумаг.
Также существуют портфели ценных бумаг, освобожденных от налога, содержат
в основном государственные долговые обязательства, которые обычно сохраняют
капитал и являются высоколиквидными. В частности, ГКО до дефолта в августе 1998
г. были самыми надежными и наиболее привлекательными для инвесторов ценными
бумагами, приносящими относительно высокий доход (см. Приложение 1).
Портфель, содержащий ценные бумаги государственных органов власти, - это
портфель, состоящий из государственных и муниципальных ценных бумаг. Они
надежны и приносят определенный доход, кроме того, имеют налоговые льготы.
1.2 Основные принципы формирования портфеля
ценных бумаг
ценный бумага риск прибыль
Сущность портфельного инвестирования заключается в распределении
инвестиционного потенциала между различными группами активов. Портфельное
инвестирование позволяет планировать и контролировать результаты инвестиционной
деятельности. Обычно портфель представляет собой набор из корпоративных акций,
облигаций с различной степенью риска, ценных бумаг с фиксированным доходом,
гарантированным государством, а значит, с минимальным риском потерь вложенных
средств и получения дохода.
При формировании инвестиционного портфеля придерживаются принципов
безопасности вложений средств, стабильности получения дохода и ликвидности
вложений (возможности быстро и без потерь превратить их в наличные деньги).
Однако ни одна из ценных бумаг не обладает одновременно всеми этими свойствами.
Здесь необходим компромисс, поскольку наиболее перспективные с точки зрения
получения доходов вложения одновременно и наиболее рискованные, а наиболее
безопасные приносят низкие доходы. Главная цель при формировании портфеля -
достижение оптимального соотношения риска и дохода инвестора. Решить эту
проблему позволяет использование принципов диверсификации и достаточной
ликвидности.
1.2.1 Диверсификация
Диверсификация вложений - это основной принцип портфельного
инвестирования, суть которого в том, что нельзя вкладывать все средства только
в одну бумагу, даже самую привлекательную. При диверсификации невысокие доходы
по одним ценным бумагам перекрываются высокими доходами по другим. Снизить риск
можно и за счет включения в портфель ценных бумаг большого круга отраслей, не
связанных между собой, что снижает риск одновременного снижения их деловой
активности.
Упрощенный вариант диверсификации заключается в том, что средства делятся
между несколькими ценными бумагами без серьезного анализа.
Более надежный вариант предполагает использование отраслевой и региональной
диверсификации. Суть отраслевой диверсификации состоит в том, что не следует
приобретать ценные бумаги предприятий только одной отрасли, поскольку
негативные явления могут захватить отрасль в целом. К примеру, падение цен на
нефть на мировом рынке может отразиться на стоимости акций всех предприятий
отрасли.
Подобная ситуация может возникнуть и в отдельном регионе, когда
политическая нестабильность, стихийные бедствия и т.п. приведут к
одновременному снижению цен акций.
Более глубокий анализ возможен с применением экономико-математических
методов. В частности, методы корреляционного анализа дают возможность найти
оптимальный баланс различных ценных бумаг в портфеле.
1.2.2 Структура портфеля
Подход к созданию портфеля формируется с учетом потребностей, целей и
требований выгоды приобретателя портфеля.
При любом портфеле наверняка будет необходимость в некоторой сумме денег
на депозите. Этим преследуются две цели:
если клиенту срочно потребуются средства, управляющему его инвестициями
не понадобится продавать ценные бумаги, особенно если на рынке в данный момент
не очень благоприятная ситуация, и
если управляющий найдет ценную бумагу, которую он особенно хотел бы
приобрести (возможно, новый выпуск), опять же ему не придется продавать другие
бумаги.
Далее, в качестве своего рода защитного механизма, в портфель, скорее
всего, войдут облигации. Это будет часть портфеля с низкой степенью риска,
которая также будет приносить доход, и, возможно, небольшой прирост капитала в
долгосрочном плане.
Если двигаться вверх по шкале риска, следующая часть портфеля, возможно,
будет состоять из долевых ценных бумаг (обыкновенных акций). Здесь может
иметься ряд различных компаний из разных отраслей, что должно обеспечивать
разнообразную сеть из качественных бумаг, приносящих долгосрочный доход, и
более рисковых акций, выпущенных для оздоровления компании, и акций новых
выпусков.
Производные инструменты также нередко используются в портфеле. В
некоторых случаях - для снижения риска, т.е. покупка опционов пут; продажа
опционов колл (для получения дополнительного дохода); или использование
фьючерсов для защиты позиций (вместо того, чтобы продавать акции и платить
налоги) или для переключения с одного класса активов на другой (также
называется распределением средств по классам активов).
В каждую из вышеперечисленных групп могут войти не только национальные,
но также и зарубежные ценные бумаги.
В целом, хотя результат во многом зависит от целей клиента, типичный
портфель может состоять из следующих инвестиций:
Таблица 1
Примерная структура портфеля
|
ДЕНЕЖНЫЕ СРЕДСТВА НА
ДЕПОЗИТЕ
|
4%
|
|
ОБЛИГАЦИИ
|
20%
|
|
АКЦИИ НАЦИОНАЛЬНЫХ КОМПАНИЙ
|
40%
|
|
АКЦИИ ЗАРУБЕЖНЫХ КОМПАНИЙ
|
26%
|
|
ПРОИЗВОДНЫЕ ЦЕННЫЕ БУМАГИ
|
10%
|
|
ИТОГО
|
100%
|
1.3 Группы инвестиционных рисков
Все операции на рынке с ценными бумагами сопряжены с рисками: снижения
доходности, прямых финансовых потерь, упущенной выгоды.
Систематический риск - риск падения ценных бумаг в целом. Представляет
собой общий риск на все вложения в ценные бумаги. Анализ этого риска сводится к
оценке того, стоит ли вкладываться в этот портфель или же лучше обратиться к
альтернативам(прямые денежные инвестиции, недвижимость, валюту).
Несистематический риск - агрегированное понятие, объединяющее все виды
рисков, связанных с конкретной ценной бумагой. Такой риск диверсифицируемый,
понижаемый, может осуществляться выбор той ценной бумаги (по виду, эмитенту,
условиям выпуска и т.д.), которая обеспечивает приемлемые значения этого риска.
Селективный риск - риск неправильного выбора ценных бумаг для
инвестирования.
Временный риск - риск эмиссии, покупки или продажи ценных бумаг в неподходящее
время, что неизбежно влечет за собой потери.
Существуют и более общие закономерности на развитых и наполненных
фондовых рынках, например сезонные колебания (ценные бумаги торговых, с/х и
других сезонных предприятий), циклические колебания (движение курсов ценных
бумаг в различных фазах макроэкономических воспроизводственных циклов).
Риск законодательных изменений - например, необходимость перерегистрации
выпусков, вызывает существенные издержки и потери эмитента и инвестора. Эмиссия
ценных бумаг рискует оказаться недействительной, может неблагоприятно
измениться правовой статус посредников по операциям с ценными бумагами и т.п.
Риск ликвидности - возможность потерь при реализации ценных бумаг из-за
изменения оценки ее качества - один из самых распространенных на рынке рисков.
Кредитный деловой риск - риск того, что эмитент, окажется не в состоянии
выплачивать процент по долговым обязательствам и (или) основную сумму долга.
Инфляционный риск - доходы, получаемые инвесторами, обесцениваются с
точки зрения реальной покупательной способности быстрее, чем растут.
Процентный риск - рост рыночной ставки процента ведет к понижению
курсовой стоимости ценных бумаг, особенно облигаций с фиксированным процентом.
При повышении процентной ставки может начаться также массовый сброс ценных
бумаг, эмитированных под более низкие (фиксированные) проценты и по условиям
выпуска, досрочно принимаемым обратно эмитентом. Процентный риск несет
инвестор, вложивший свои средства в средне - и долгосрочные ценные бумаги с
фиксированным процентом при текущем повышении среднерыночного процента в
сравнении с фиксированным уровнем. Процентный риск несет эмитент, выпускающий
средне - и долгосрочные ценные бумаги с фиксированным процентом при текущем
понижении среднерыночного процента в сравнении с фиксированным уровнем.
Отзывной риск - риск потерь для инвестора в случае, если эмитент отзовет
отзывные облигации в связи с превышением фиксированного уровня процентных
выплат по ним над текущим рыночным процентом.
Политический, социальный, экономический и т.п. риски. В частности,
политический риск - риск финансовых потерь в связи с изменением политической
системы, расстановки политических сил в обществе, политической нестабильностью.
Региональный риск - риск, особенно свойственный моно продуктовым районам.
Отраслевой риск - риск, связанный со спецификой отдельных отраслей. С
позиции этого вида риска все отрасли можно подразделить на подверженные
циклическим колебаниям, на умирающие, стабильно работающие, быстро растущие.
Риск предприятия (финансового и нефинансового) - риск, сходный с
отраслевым и во многом производный от него. Связан с типом поведения
предприятия (стратегии). Валютный риск - риск, связанный с вложениями в
валютные ценные бумаги, обусловленный изменениями курса иностранной валюты.
Капитальный риск - риск существенного ухудшения качества портфеля ценных
бумаг, что приводит к необходимости масштабных списаний потерь и как следствие
- к значительным убыткам и может затронуть капитал банка, вызывая необходимость
его пополнения путем выпуска новых ценных бумаг.
Риск поставки - риск невыполнения продавцом обязательств по своевременной
поставке ценных бумаг.
Операционный риск - неполадки в работе компьютерных систем по обработке
информации, низким качеством работы технического персонала, нарушениями в
технологии операций по ценным бумагам, компьютерным мошенничеством и т.д.
Риск урегулирования расчетов - риск потерь по операциям с ценными
бумагами, связанный с недостатками и нарушениями технологий в платежно -
клиринговой системе.
Для эффективного ведения инвестиционной деятельности необходим капитал,
достаточный для осуществления диверсификации вложений, в противном случае
ведение операций на фондовом рынке лучше поручить специализированным компаниям
(например, фондам), способным аккумулировать средства многих мелких инвесторов
для рационального составления инвестиционного портфеля; степень риска
конкретной ценной бумаги целесообразно определять по отношению к другим ценным
бумагам, а лучше всего - по отношению к степени риска фондового рынка в целом,
т.е. как частное от деления показателя рискованности данного вида ценных бумаг
к показателю рискованности фондового рынка. На практике для этого пользуются
методами оценки степени статистической связи между доходом на единицу капитала,
приносимым данной ценной бумагой и. средним доходом всех ценных бумаг фондового
рынка на единицу вложений. Если относительная цена риска больше единицы,
значит, данный вид ценных бумаг характеризуется большей рискованностью по
сравнению с фондовым рынком в целом и наоборот.
Зная средний доход на единицу вложенного капитала по гарантированным и по
рискованным ценным бумагам, а также зная величину среднего отклонения
фактически полученного дохода по рискованным ценным бумагам от среднего дохода,
можно посчитать «цену риска».
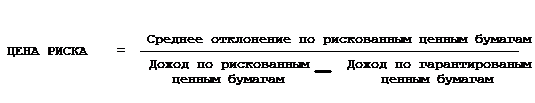
Инвесторов
также можно классифицировать на: консервативных, умеренно-агрессивных,
агрессивных, опытных и изощренных (игроков). Консервативные инвесторы - главная
задача для них: надежность вложений, минимизация возможного риска, пусть даже
ценой скромной отдачи на авансированные средства. Среди всех видов ценных бумаг
этот тип инвесторов предпочитает облигации и преференциальные акции высшего и
высокого качества (активы, имеющие надежную защиту), а среди инвестиционных
институтов - государственные организации и компании с солидной репутацией.
Умеренно-агрессивные
инвесторы - более склонны к риску, хотя также предпочитают его ограничивать. Их
цель защита инвестиций, обеспечение их безопасности, высокая доходность
(проценты, дивиденды) ценных бумаг, которым они владеют. При формировании
инвестиционного портфеля допускается вхождение ценных бумаг более низкого
качества (менее защищенных) и специальных ценных бумаг, предполагающий
дальнейшие операции с ними в зависимости от конъюнктуры рынка (например, с
ордером или конвертируемые в другие виды ценных бумаг).
Агрессивный
тип инвесторов характеризуется лояльным отношением к риску, включением его в
свою инвестиционную стратегию, предполагающую как высокую доходность вложений,
так и перспективный рост курса ценных бумаг, входящих в портфель инвестора.
Этим объясняется ставка на ценные бумаги среднего и низкого качества, а также
на акции роста, высоко рискованные ценные бумаги динамично развивающихся
отраслей. Опытные инвесторы обладают богатой практикой инвестиционной
деятельности, знают и умеют прогнозировать конъюнктуру фондового рынка. Поэтому
вложенные ими средства в ценные бумаги с объективно высоком уровнем риска
обеспечивают им высокий доход, стабильный рост вложенного капитала наряду с
высокой ликвидностью, т.е. возможностью легко реализовать ценные бумаги на
вторичном рынке в случае непредвиденного развития ситуации в нежелательном
направлении.
Изощренные
инвесторы - не боящиеся пожертвовать своим капиталом ради получения
максимальной выгоды. Формируют свой инвестиционный портфель спекулятивными
ценными бумагами низкого качества с колеблющимся курсом, пытаются играть на
изменении курса национальной валюты.
ГЛАВА 2. Модель ценообразования на основной капитал:
применение парного регрессионного анализа
.1 Основные эконометрические понятия
Одним из наиболее ценных приобретений для типичного частного инвестора
или специалиста по анализу рынка ценных бумаг является надежное уравнение для
прогнозирования прибылей по альтернативным ценным бумагам. Первый шаг в
разработке и практическом применении такого уравнения включает понимание
причины получения низкой или высокой нормы прибыли от конфетного капитала. В
этой главе мы сосредоточим свое внимание на модели ЦОК - модели ценообразования
на основной капитал (САРМ, the capital
asset pricing model), которая может оказать значительную помощь в
понимании данных процессов. Как мы увидим далее, примечательной особенностью
модели ЦОК является то, что ее наиболее важные параметры могут быть оценены на
основе простейших эконометрических методов, а именно: на основе модели парной
линейной регрессии, в которой зависимая переменная выражается в виде линейной
функции от единственной независимой переменной. Таким образом, простая структура
модели ЦОК обеспечивает полезное введение в практическую эконометрику.
По этой причине в данной работе по эконометрике первым шагом является
практическое изучение фондовых рынков. В этой главе мы вначале обсудим
финансовую теорию, лежащую в основе модели ЦОК, далее рассмотрим роль
диверсификации, выведем основные уравнения для оценок, интерпретируем их и
затем рассмотрим вопросы, связанные с практической реализацией модели. Наконец,
мы изучим данные ежемесячных прибылей за 10 лет для различных компаний и для
всего рынка в целом; дадим оценку так называемых (3-значений, отражающих
специфику компаний), используя для этого процедуру парной регрессии; определим,
почему золото является специфическим активом; дадим интерпретацию коэффициента
детерминации R2 в терминах доли общего риска,
который является недиверсифицированным, т.е. объясненным; оценим свойства
некоторых портфелей ценных бумаг; проведем исследования событий; дадим оценку
обобщенного варианта модели ЦОК, и затем проверим выполнение допущений, касающихся
стохастической спецификации.
Для определения связи между ценными бумагами используют такие показатели,
как ковариация и коэффициент корреляции.
Ковариация - взаимозависимое совместное изменение двух и более признаков
экономического процесса. Ковариация служит для измерения степени совместной
изменчивости двух ценных бумаг, например акций.
Показатель ковариации определяется по формуле:
Соvij=∑(r доходность i-й
акций - r средняя доходность i-й акции)×(r доходность j-й акции - r средняя доходность j-й акции) / n -
1, (2.1.1)
где n - число периодов, за которые рассчитывалась доходность i-й и j-й
акций.
Проанализируем, какое влияние на риск портфеля оказывают коэффициенты
корреляции (Cor), входящие в портфель ценных бумаг.
Корреляция - это математический термин, обозначающий систематическую и
обусловленную связь между двумя рядами данных.
На рынке акций принято рассматривать корреляцию (взаимозависимость)
разных акций, либо акций и индексов. Считается, что российские акции высоко
коррелированы, то есть в определенный момент времени все акции движутся в одном
направлении. Коэффициент корреляции изменяется в пределах от -1 до +1.
Положительное значение коэффициента говорит о том, что доходности активов
изменяются в одном направлении при изменении конъюнктуры, отрицательное - в
противоположном. При нулевом значении коэффициента корреляция между
доходностями активов отсутствует.
Показатель корреляция определяется по формуле:
Соr = Соvij / (δi × δj), (2.1.2)
где Соvij - ковариация доходности i-й и j-й акции;
δi - стандартное отклонение доходности
i-й акции;
δj - стандартное отклонение доходности
j-й акции.
Дисперсия - это стандартное отклонение в квадрате, рассчитываемое по
формуле:
δ2 = ∑ (r доходность акции - r средняя доходность акции)2 / n - 1. (2.1.3)
Таким образом, стандартное отклонение - это квадратный корень из
дисперсии.
В целом, используя данные корреляции, можно сделать выводы:
) чем меньше коэффициент корреляции акций в портфеле, тем меньше риск
портфеля, поэтому при формировании портфеля следует включить в него акции,
имеющие наименьшую корреляцию;
) если коэффициент корреляции акций в портфеле +1, то риск портфеля
усредняется;
) если коэффициент корреляции акций в портфеле меньше +1, то риск
портфеля уменьшается;
) если коэффициент корреляции акций в портфеле -1, то можно получить
портфель без риска.
Теперь допустим, что когда инвесторы вступают на рынки пенных бумаг, их
поведение является полностью рациональным в той смысле, что их единственной
заботой является оценка прибылей от их собственных капиталовложений. Определим
норму прибыли от капиталовложений следующим образом
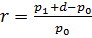
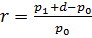 (2.1.4)
(2.1.4)
где
р1 - цена акции в конце временного периода;
d - дивиденды
(если они имеются), выплаченные за данный временной период;
p0 - цена
капитала в начале временного периода.
Хотя
прибыль r может быть легко вычислена по факту (после внесения
капиталовложений), она, разумеется, будет неопределенной до принятия решения о
капиталовложениях. Поэтому мы интерпретируем r как ожидаемую
норму прибыли.
Обычно
инвесторы (за исключением тех, которым нравится действовать на свой страх и
риск) интересуются не только величиной наиболее вероятной (или ожидаемой)
прибыли от капиталовложений; они хотят также знать распределение возможной
прибыли r, где r рассматривается как случайная переменная. Риск,
связанный с возможными капиталовложениями, обычно характеризуется
распределением таких возможных прибылей. Часто предполагается, что прибыли
будут распределены нормально, и в таких случаях распределение может быть
полностью описано двумя параметрами - ожидаемым (средним) значением и
дисперсией σ2
(или квадратным корнем из дисперсии σ, называемым стандартным отклонением). При допущении
нормальности в прикладной литературе, посвященной финансовым вопросам, риск
обычно измеряется стандартным отклонением σ
Хотя
инвесторы фактически единодушны в своем желании получить при прочих равных
условиях более высокие прибыли, а не более низкие, несомненным является тот
факт, что большинство из них не расположены к риску, иными словами, при условии
одинаковой ожидаемой прибыли они предпочитают более низкое стандартное
отклонение более высокому. Это означает, что если риск от капиталовложений или
пакета капиталовложений кажется большим, то инвесторы, вероятно, пойдут на этот
риск только в том случае, если ожидается более высокая прибыль. Аналогичным
образом капиталовложения с низкой ожидаемой прибылью будут приемлемыми, если
только они имеют небольшой риск.
Если
инвесторы должны купить ценные бумаги, имеющие нулевой риск, то они тем не
менее хотели бы получить прибыль в качестве компенсации за отказ от текущего
потребления. Такая прибыль называется свободной от риска нормой прибыли, и мы
обозначим ее как rf. Специалисты по анализу рынка ценных бумаг США часто
используют в качестве измерителя величины rf доходность к
погашению 30-дневных казначейских билетов США. Очевидно, так принято потому,
что инвесторы считают, что вероятность неуплаты по таким ценным бумагам
фактически равна нулю. Мы можем использовать эти положения для определения
компенсации за риск или премии за риск по j-й ценной
бумаге как превышение прибыли над свободной от риска нормой прибыли rf,
т.е.
(Премия
за риск)j = rj - rf (2.1.5)
Запомнив
эти определения, мы теперь вернемся к рассмотрению диверсификации и управления
риском.
2.2 Модель Марковица
Одними из основных базовых моделей формирования портфеля ценных бумаг
являются модель Марковица.
Подход Г. Марковица начинается с предположения, что инвестор в настоящий
момент времени имеет конкретную сумму денег для инвестирования. Эти деньги
будут инвестированы на определенный промежуток времени, который называется
периодом владения. Г. Марковиц предположил, что распределение вероятностей
значения доходности портфеля вокруг ее математического ожидания описывается
симметричной нормальной кривой Гаусса. Введя понятие дисперсии как меры риска,
или неопределенности дохода, Г. Марковиц имел в виду, что распределение этой
кривой вокруг среднего значения отражает изменчивость доходности портфеля -
область возможных результатов и вероятностей отклонений фактической доходности
портфеля от ожидаемой доходности. Согласно портфельной теории Г. Марковица, в
качестве «нормального» ожидания инвестора может рассматриваться среднее
значение наблюдаемой ранее доходности инвестирования в ценные бумаги.
Теория Марковица положена в основу модели оценки стоимости активов
Capital Asset Pricing Model (CAPM). Модель оценки стоимости активов описывает
взаимосвязь между риском и ожидаемой доходностью активов. Взаимосвязь риска с
доходностью согласно модели оценки долгосрочных активов описывается следующим
образом:
r = rб/р + β ×
(rр - rб/р), (2.2.1)
где r - ожидаемая норма доходности;
rб/р -
безрисковая ставка (доход);
rр -
доходность рынка в целом;
β - коэффициент бета.
Основная идея CAPM заключается в том, что инвесторы должны получать 2
вида компенсации: за время (временная стоимость денег) и за риск. Стоимость
денег во времени представлена безрисковой ставкой и является компенсацию
инвестору за то, что он размещает денежные средства в какие-либо инвестиции на
определенный период времени.
Безрисковый доход измеряется, как правило, по ставкам государственных
облигаций, так как те практически без риска. На западе безрисковый доход равен
примерно 4-5 %, у нас же - 7-10 %. Доходность рынка в целом - это норма
доходности индекса данного рынка. В США, например, индекс S&P 500, а в
России - индекс РТС.
Оставшаяся часть формулы представляет собой компенсацию за дополнительный
риск, взятый на себя инвестором. Здесь мерой риска является коэффициент бета,
сравнивающий доходность актива с доходностью рынка за период, а также с
рыночной премией.
Коэффициент бета определяется по формуле:
β = Соrх × δх / δ (2.2.2)
или β = Covx / δ2, (2.2.3)
где Соrх - корреляция между доходностью ценной бумаги х и средним уровнем
доходности ценных бумаг на рынке;- ковариация между доходностью ценной бумаги х
и средним уровнем доходности ценных бумаг на рынке;
δх - стандартное отклонение доходности
по конкретной ценной бумаге;
δ - стандартное отклонение доходности по
рынку ценных бумаг в целом.
Уровень риска отдельных ценных бумаг определяется на основании таких
значений:
β = 1 - средний уровень риска;
β > 1 - высокий уровень риска;
β < 1 - низкий уровень риска.
Акции с большой бетой (β > 1) называют агрессивными, с низкой бетой
(β
< 1) - защитными.
Например, агрессивными являются акции компаний, чьи доходы существенно зависят
от конъюнктуры рынка. Когда экономика на подъеме, агрессивные акции приносят
большие прибыли. Например, акции автомобилестроительных компаний являются
агрессивными. Инвесторы, ожидающие подъема экономики, покупают агрессивные
акции, обеспечивающие больший уровень доходности в условиях растущего рынка,
чем защитные. Акции компаний, чья прибыль в меньшей степени зависит от состояния
рынка, являются защитными (например, акции компаний коммунальной сферы). Доходы
таких компаний сокращаются в меньшей степени в условиях экономического спада.
Поэтому использование защитных акций в периоды кризисов позволяет инвестору
извлечь большую прибыль в сравнении с агрессивными акциями.
По портфелю ценных бумаг β рассчитывается как средневзвешенный β
- коэффициент отдельных
видов входящих в портфель инвестиций, где в качестве веса берется их удельный
вес в портфеле. Таким образом, чем более раскованный портфель, тем больше
показатель β, а следовательно, доход должен быть выше, и наоборот.
Следовательно, модель CAPM демонстрирует прямую связь между риском ценной
бумаги и ее доходностью, что позволяет ей показать справедливую доходность
относительно имеющегося риска и наоборот.
2.3 Вывод линейной зависимости между риском и
прибылью
До сих пор мы устанавливали зависимости между дисперсиями, ковариациями,
предельными дисперсиями и бета - значениями и определили важный принцип
оптимальности портфеля ценных бумаг. Но каким образом можно перейти от этих
понятий к выбору портфеля ценных бумаг и практически применимой зависимости
между риском и прибылью? Далее мы покажем важность модели ЦОК для проведения
достаточно простого эмпирического анализа и продемонстрируем, что зависимость
между риском и прибылью является линейной.
Предположим, инвестор имеет портфель ценных бумаг, называемый а и
состоящий из различных ценных бумаг. Сочетание ценных бумаг дает ожидаемую
прибыль от портфеля ценных бумаг rа и
имеет дисперсию σ2a . Теперь допустим, что существует свободная от риска ценная
бумага, прибыль от которой равняется rf , и пусть инвестор может взять или предоставить ссуду на неопределенный
срок по безрисковой ставке rf .
Одна из возможностей для этого инвестора состоит в объединении портфеля а
ценных бумаг со свободной от риска ценной бумагой в новый портфель. В этом
случае ожидаемая прибыль от нового портфеля ценных бумаг:
rp =
(1 - wa)rf + wara
(2.3.1)
где wa - доля общего капитала,
инвестированного в портфель а. Дисперсия этого портфеля:
σ2p =
w2aσ2a+( 1 -wa)2σ2f +2wa(1-wa)σaf (2.3.2)
где σaf-
ковариация между ожидаемой прибылью от портфеля ценных бумаг а и ожидаемой
прибылью от безрисковой ценной бумаги. Но так как по определению свободная от
риска ценная бумага имеет прибыль с нулевой дисперсией, эта свободная от риска
прибыль также не коррелируется с прибылью от любой другой ценной бумаги, что
означает σ2f =σaf =0. Следовательно, уравнение (2.3.2) сводится к следующему:
σ2p=w2aσ2a или σp=waσa (2.3.3)
Перегруппировав второе выражение в уравнении (2.3.3), получим:
wa=σp/σa и (1-wa) = 1-σp/σa ,
что после подстановки в уравнение (2.3.2) и приведения подобных членов
дает нам
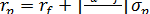
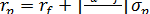 (2.3.3)
(2.3.3)
Уравнение (2.3.3) дает нам простое линейное соотношение между прибылью rр и риском портфеля ценных бумаг σp, которое восхитило бы даже Альберта
Эйнштейна В частности, общая прибыль от портфеля ценных бумаг σр равна сумме двух членов: свободной
от риска норме прибыли rf и (ra- rf)/σa, умноженной на риск σp портфеля ценных бумаг. Эта линейная
зависимость показана на рис. 2.3.1, по оси ординат - ожидаемая прибыль, а риск
- по оси абсцисс; точка пресечения с осью ординат отсекает на ней отрезок, равный
rf(свободный член), а коэффициент
наклона определяется величиной(ra-rf)/σa.
r
ra
коэффициент наклона
(ra- rf)/σa
rf
σa σ
Рис. 2.3.1 Линейная зависимость между риском и прибылью
Следует отметить несколько особенностей рис. 2.3.1. Во-первых, если
инвестор решил инвестировать только в безрисковый актив (т.е. wa = 0), то из уравнения (2.3.1)
следует, что rp = rf, а из уравнения (2.3.2) получаем σр=0. Во-вторых, если вместо этого
инвестор собирается инвестировать только в портфель ценных бумаг а и полностью
откажется от безрисковой ценной бумаги, то wa = 1, rp=ra и σр=σа. В-третьих, коэффициент наклона на
рис. 2.3.1 представляет собой премию инвестору за принятие увеличенного риска,
иными словами, за увеличение пропорции капитала, инвестированного в рисковый
портфель ценных бумаг а.
Разумеется, портфель ценных бумаг а является одним из многочисленных
рисковых портфелей ценных бумаг, которые могут быть составлены нашим
инвестором: ценные бумаги 1 и 2 могли бы быть скомбинированы в многочисленные
альтернативные комбинации. В результате возникает интересная проблема,
связанная с тем, какими должны быть предельные значения риска и прибыли для
инвестора, который рассматривает другие возможности составления портфеля из
этих двух рисковых ценных бумаг.
2.4 Дальнейшая интерпретация линейной
зависимости риск-прибыль
Мы показали, что диверсификация является эффективной мерой уменьшения
риска, поскольку цены различных ценных бумаг коррелированны не идеально.
Рассмотрим теперь более подробно проблему риска. В классическом
экспериментальном исследовании, проведенном в работе В. Вагнера и Ш. Лау, было
показано, что сначала диверсификация очень быстро снижает риск, но через
некоторое время дополнительная диверсификация будет мало влиять на риск или на
изменчивость. В частности, используя портфели разных размеров, выведенные из
исторических выборок ценных бумаг, Вагнер и Лау показали, что в результате
диверсификации вариация прибылей может быть уменьшена наполовину, но большая
часть этих преимуществ может быть достигнута приобретением относительно
небольшого количества ценных бумаг или акций; улучшение будет незначительным,
когда количество ценных бумаг будет больше, скажем, десяти.
Конечно, диверсификация не может полностью исключить риск. Риск, который
потенциально может быть исключен посредством диверсификации, называется
специфическим, уникальным или несистематическим риском. Специфический риск
выводится из факта, что большая часть рисков или их вероятностей, которые
имеются для отдельной компании, являются специфическими для данной компании и,
вероятно, ее непосредственных конкурентов, поэтому специфический риск может
быть исключен за счет владения хорошо диверсифицированным портфелем. Однако
существует также некоторый риск, которого нельзя избежать независимо от
количества диверсификаций. Этот риск обычно известен как рыночный, или
систематический, риск. Рыночный риск выводится из существования других
экономических и глобальных опасностей и вероятностей, имеющихся для всех видов
бизнесов. Тот факт, что ценные бумаги или акции имеют тенденцию «изменяться
вместе», отражает наличие рыночного риска, который не может быть исключен за
счет диверсификации. Отметим, что это тот риск, который остается даже тогда,
когда составляется оптимальный портфель ценных бумаг.
Для дальнейшего исследования этой зависимости прибылей от рыночного риска
отметим, что один из результатов модели ЦОК состоит в том, что риск хорошо
диверсифицированного портфеля зависит только от рыночного риска для ценных
бумаг, включенных в портфель. Поэтому предположим, что вы имели хорошо
диверсифицированный портфель (скажем, микроскопический аналог всего портфеля
ценных бумаг на рынке) и что вы хотели бы дополнительно оценить зависимость
прибылей от ценных бумаг от риска путем вычисления чувствительности ценных
бумаг конкретной компании в вашем портфеле, скажем, чувствительности компании j к изменениям в прибыли всего рынка.
Очевидно, что вы не захотите вычислять это на основе изолированного
рассмотрения прибылей компании j.
Напротив, вы, вероятно, захотите использовать информацию о ковариаций из
уравнений (2.1.4) и (2.1.5) относительно рынка в целом.
В частности, вспомним, что ранее нами было отмечено, что одним из
критериев для относительной предельной дисперсии ценных бумаг, скажем, k-го актива является его бета-значение
относительно портфеля. В уравнении (2.1.5) это было определено как betak = σкр/σ2р
Одна из интерпретаций этого понятия относительной дисперсии состоит в
том, что, если прибыль от портфеля ценных бумаг может увеличиться, скажем, на
1%, то прибыль от k-й ценной бумаги
может увеличиться на величину бетаk, умноженную на 1%. Поэтому бета - капиталовложения являются критерием
чувствительности прибыли от k-й
ценной бумаги к изменениям в прибыли от портфеля ценных бумаг; betak суммирует в себе зависимость от
риска для портфеля ценных бумаг.
Целесообразно будет рассмотреть портфель ценных бумаг как общий рыночный
портфель. Определим бета - капиталовложения, скажем, для компании j относительно общего рыночного
портфеля следующим образом
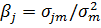
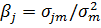 (2.4.1)
(2.4.1)
где σjm - ковариация между прибылью компании j и прибылью рынка в целом;
σ2m - дисперсия прибылей рынка.
Однако существует проблема, связанная с соотношением beta, к структуре модели ЦОК. Члены
ковариаций и дисперсии для betaj
в уравнении (2.4.1) относятся к общим прибылям от ценных бумаг, в то время как
в противоположность этому при разработке модели ЦОК мы имели дело с изменениями
в премии за риск, т.е. с избыточной прибылью сверх безрисковой ставки, rm-rf, где rт
является прибылью от всех ценных бумаг рынка. Возможно ли в уравнении (2.4.1)
вместо премий за риск использовать общие прибыли? Как видим из ранее
изложенного, это возможно, поскольку это изменение не окажет влияния на betaj.
Чтобы показать это, отметим, что поскольку на отношение ковариаций σJm к дисперсии σ2т не влияет вычитание безрисковой
прибыли из общих прибылей, инвестиционный коэффициент beta в уравнении (2.4.1) сохраняется даже тогда, когда он
определяется на основе премий за риск, а не на основе общих прибылей. Это имеет
важное значение в контексте применения модели ЦОК, где мы имеем дело скорее с
премиями за риск, чем с общими прибылями. В частности, поскольку уравнение
(2.4.1) можно представить как в терминах премий за риск, так и в терминах общих
прибылей, значение beta для
конкретной компании равняется ковариаций между премией за риск этой компании и
премией за риск для рыночного портфеля ценных бумаг, деленной на дисперсию
премии за риск рынка. На основании этого можно предположить, что сводный
измеритель зависимости от рыночного риска betaj имеет широкое применение.
Ценные бумаги могут значительно различаться по значению их инвестиционных
коэффициентов beta. Например, некоторые из них имеют
значение 2, что указывает на увеличение (или падение) на 1% стоимости этой
ценной бумаги при однопроцентном увеличении (или падении) на рынке в целом.
Такие ценные бумаги являются относительно рискованными. С другой стороны, акции
«голубых фишек» не так чувствительны к изменениям на рынке и имеют намного
меньшее значение beta, скажем 0,5,
т.е. 0,5-процентное увеличение или падение их стоимости при однопроцентном
увеличении и падении на рынке в целом. Традиционно считается, что покупка
ценных бумаг с бета - значением выше 1 называется «агрессивной позицией», в то
время как сохранение ценных бумаг с бета - значением меньше 1 называется
«защитной позицией». Как мы увидим из упражнения 3 к этой главе, значение beta для некоторых ценных бумаг может
быть даже отрицательным - это относится к так называемым «сверхзащитным» ценным
бумагам!
Инвестиционные коэффициенты beta можно также определить для портфелей ценных бумаг (а не для отдельных
ценных бумаг) по отношению к рынку в целом. Например, рассмотрим портфель q, состоящий из п ценных бумаг, и
определим их бета - значения относительно рынка в целом как
betaqm = σqm/σ2m. Используя определение ковариации, можно переписать betaq следующим образом
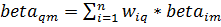
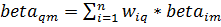 (2.4.2)
(2.4.2)
где wiq - доля портфеля q, инвестированная в ценную бумагу r;
betaiw
- бета - значение i-й ценной бумаги
относительно рыночного портфеля.
Следовательно, бета-значение портфеля является просто взвешенным
усреднением бета - значений, составляющих портфель ценных бумаг (весовые
коэффициенты при этом являются долями капиталовложений в активы).
Вполне очевидно, что для рынка акций или фондовой биржи в целом
ковариация с самой собой будет равна его дисперсии, а это означает, что
соотношение beta для фондовой биржи в целом
составляет 1,0. Более того, поскольку по уравнению (2.4.2) beta для хорошо диверсифицированного
общего рыночного портфеля является средним взвешенным бета-значений ценных
бумаг, включенных в портфель, то в среднем отдельные акции имеют бета-значения,
равные 1,0. Наконец, следует отметить, что, поскольку ковариация безрисковой
ценной бумаги с рыночным портфелем равна нулю, betaim безрисковой ценной бумаги всегда равна нулю.
2.5 Эконометрические аспекты, используемые в
реализации модели ЦОК
Теперь мы хотим перейти к эконометрической реализации структуры модели
ЦОК. Наша первая задача будет состоять в выводе уравнения, допускающего его
статистическое оценивание. Рассмотрим небольшой портфель p, содержащий единственную ценную
бумагу j, и большой, хорошо
диверсифицированный портфель т, который является общим рыночным портфелем.
Подставляя j вместо р и т вместо а в уравнение
(2.3.3), мы можем переписать линейную зависимость для модели ЦОК в уравнении
(2.3.3) следующим образом:
rj-rf=(σj/σm)-(rm-rf),
(2.5.1)
где rj, rf - соответственно, прибыли для ценной бумаги j и безрискового актива;
rт -
прибыль общего рыночного портфеля ценных бумаг;
σj/σm - отношение стандартных отклонений
прибылей ценной бумаги j и
рыночного портфеля т.
Член r} - rf является премией за риск для ценной бумаги j, в то время как rm - rf представляет собой премию за риск для всего рынка. Следует
отметить, что за последние 60 лет в США средняя премия за риск для рынка
составляла примерно 8,4% в год.
В соответствии с уравнением (2.5.1) премия за риск j-й ценной бумаги является
коэффициентом пропорциональности σj/σm , умноженным на премию за рыночный
риск; этот коэффициент пропорциональности выражает зависимость прибыли от
ценной бумаги j от рыночной прибыли - зависимость,
которая была выявлена с помощью модели ЦОК. Такое рассуждение наводит на мысль,
что коэффициент пропорциональности σj/σm должен быть определенным образом
связан с бета - значением капиталовложений, рассмотренным в предыдущем
параграфе.
Для последующего исследования этого отношения обобщим уравнение (2.5.1)
путем добавления к нему постоянного члена αj и случайного возмущения εj и затем определим новый параметр βj , равный коэффициенту
пропорциональности, т.е.β =σj/σm . Это даст нам уравнение оценки,
которое устанавливает зависимость между общей премией за риск от ценной бумаги j и премией за рыночный риск (с учетом
стохастического возмущения εj):
rj - rf = αj + βj (rm - rf ) +εj
(2.5.2)
В уравнении (2.5.2) случайный остаток εj - отражает влияние на rj -rf специфического (несистематического) и диверсифицируемого
риска. Допустим, что величины εj имеют нулевые ожидаемые (средние) значения и дисперсии σ2ε,
и что они, кроме того,
независимо и одинаково нормально распределены.
Оказывается ,оценка по методу наименьших квадратов величины βj в уравнении (2.5.2) на самом деле
совпадает со значением инвестиционного коэффициента beta из уравнения (2.4.2). Для подтверждения этого
рассмотрим модель парной регрессии: y = α + βx. + ε. Оценка по методу наименьших
квадратов для β будет иметь вид: cov(x,y)/var(x).
Теперь в уравнении (2.5.2) положим y = rj-rf, и пусть x = rm-rf. Тогда оценка по методу наименьших квадратов для βj примет вид: βj = cov(rj - rf, rm -rf)/var(rm -rf). Но это
выражение в точности равняется σjm/σ2m , капиталовложениям beta, определенным в уравнении (2.4.2).
Интуитивно понятно, что МНК-оценка коэффициента пропорциональности βj будет отношением стандартных
отклонений премий за риск для ценной бумаги j и для рынка т.
Эти результаты означают, что для любой ценной бумаги j можно дать оценку для βj используя для этого процедуры метода
наименьших квадратов в уравнении парной регрессии (2.5.2). Если это показать
графически, то отношение ковариаций к дисперсии является оценкой по методу
наименьших квадратов наклона линии регрессии, связывающей премию за риск от
конкретной ценной бумаги j на
вертикальной оси с ее премией за рыночный риск на горизонтальной оси;
линейность этой зависимости выводится из уравнения (2.3.3). Хотя можно
использовать процедуры по методу наименьших квадратов в рамках парной
регрессии, оценка βj является тривиальной: если имеются значения для
соответствующих ковариаций и дисперсий все что вам необходимо - это вычислить βj как их отношение.
Для оценки параметра на βj основе данных временных рядов для отдельных компаний
следует, конечно, допустить, что для конкретной компании βj является относительно стабильным в
течение какого-то времени. Довольно часто используются ежемесячные данные,
основанные на данных прибылей от Нью-Йоркской фондовой биржи.
Эконометрические исследования, основанные на этих данных, показали, что в
большинстве случаев (но с некоторыми исключениями) βj сохраняет относительную стабильность
в течение пяти лет (60 месяцев). Однако были зарегистрированы случаи, когда
состояние промышленности или компании резко менялось, что влекло за собой
соответствующее изменение βj. Например, акции нефтяной компании имели бета-значение ниже
единицы до 1973 г., когда ОПЕК было принято эмбарго на нефть, затем ситуация
изменилась, и бета-значения для нефтяных компаний стали в основном возрастать.
Аналогичным образом, когда в 1978 г. с системы авиатранспортных предприятий США
были сняты ограничения, бета-значения для большинства американских авиакомпаний
возросли; аналогичные изменения в бета -значениях произошли для электростанций
общего назначения, особенно после Чернобыльской катастрофы в 1986 г. для тех
электростанций, которые были связаны с производством атомной энергии. Однако
стабильность бета -значений остается проблемой.
Хотя параметр βj представляет особый интерес и важность, в нашем уравнении
оценки (2.5.2) появляется другой параметр, который был добавлен специально, а
именно αj. В связи с этим вспомним, что αj не присутствуют в уравнении (2.5.1),
которое является линейным уравнением, аналогичным уравнению (2.5.2). На
основании финансовой теории, лежащей в основе модели ЦОК и представленной в
уравнении (2.5.1), можно было бы ожидать оценок для αj в среднем близких к нулю (более
подробно это рассматривается далее). Фактически типичный эмпирический результат,
полученный при оценке параметров уравнения (2.5.2), состоит в том, что оценка αj по методу наименьших квадратов
незначительно отличается от нуля. Нулевая гипотеза в отношении того, что αj = 0, может быть проверена
стандартными методами с помощью соответствующих t-статистик при некотором предварительно установленном уровне
значимости. Более того, если вам необходимо включить ограничение в виде αj = 0 в уравнение (2.5.2), большая
часть программ регрессии для ЭВМ обеспечит варианты, которые позволят пользователю
опустить постоянный член из этого уравнения парной регрессии.
Следует отметить, что в некоторых инвестиционных фирмах характеристики
портфельных менеджеров ценных бумаг были случайно оценены посредством
вычисления прогнозов прибылей, которые могли бы получить менеджеры, на
основании бета - значений компаний, участвующих в составе их портфелей, и путем
вычитания этих прогнозных прибылей из реально полученных прибылей. Таким
образом, получили неявную оценку величины a для данного менеджера. Если реальная прибыль больше, чем
прибыль, прогнозируемая с помощью величины для общего портфеля, то считается,
что менеджер портфеля обеспечил положительное значение а, и он получает
соответствующее вознаграждение. Такие простые схемы определения вознаграждения
менеджера сейчас редко используются, но они предлагают интересную интерпретацию
а для менеджеров, занимающихся составлением портфелей.
Предположим, что специалист по анализу рынка ценных бумаг использовал
ежемесячные данные временных рядов частной компании за последние пять лет и
оценил параметры α и β, используя для этого обычные методы
линейной регрессии. Возможно, что этот специалист получил эмпирический
результат, состоявший в том, что для частной компании оценка величины а
оказалась положительной и статистически значимо отличной от нуля. Это могло бы
означать, что даже если ожидается, что рынок в целом ничего не заработает (т.е.
если rm- rf в уравнении (2.5.2) равняется нулю), инвесторы этой копании
ожидают положительный темп роста цены. (Отметим, например, что оценка α,
основанная на
ежемесячных данных и равная 0,67, интерпретируется как годовой темп роста цены,
примерно равный произведению 12*0,67, или около 8% в год.) Для какой-нибудь
другой компании этот специалист может получить оценку а отрицательную и значимо
отличную от нуля. Истинные последователи применения модели ЦОК могут поэтому
утверждать, что в среднем можно ожидать оценок α, равных нулю.
По этой причине возникает важный вопрос о возможности проверки модели
ЦОК. Здесь можно сделать пять замечаний.
Во-первых, финансовая теория, лежащая в основе модели ЦОК, явно
использует ожидаемые прибыли, в то время как мы можем наблюдать лишь
реализованные прибыли. Поэтому процедура строгой проверки модели ЦОК становится
более трудной, но все же выполнимой задачей, использующей более сложные
эконометрические методы.
Во-вторых, в соответствии с моделью ЦОК, рыночный портфель должен
включать все связанные с риском инвестиции, тогда как большинство рыночных
показателей и оценок для rт
строятся на основании только ограниченного числа акций, скажем, тех, которые
продаются на Нью-Йоркской фондовой бирже (тем самым исключаются все остальные
активы, продаваемые в мире и связанные с риском, такие, например, как
человеческий капитал, предпринимательская способность и частное имущество).
Сбор достаточных данных о связанных с риском капиталах для оценки величины rт в действительности мог бы стать
трудной и чрезвычайно дорогостоящей задачей. В этом контексте следует отметить,
что проведенные эмпирические исследования на основе модели ЦОК выявили тот
факт, что оценки величины β в значительной степени зависят от
выбора rт в частности, измерения величин rт основанные на индексе Доу-Джонса («Dow Jones 30 Industrials Index»), давали
результаты, существенно отличающиеся от тех, которые были основаны на индексах
«Standard & Poor 500» и «Wilshire 5000». В настоящее время Научно-исследовательский центр цен
на ценные бумаги (Center for Research on Securities Prices - CRSP)
при Чикагском университете, финансируемый по большей части корпорацией « Lynch, Pierce, Fenner
& Smith, Inc.», познакомил исследователей с оценками величины rт, основанными на операции взвешенной
стоимости всех акций, котирующихся на Нью-Йоркской и Американской фондовых
биржах.
В-третьих, в качестве безрискового актива обычно используются 30-дневные
казначейские векселя США, которые являются действительно безрисковыми только в
том случае, если хранятся в портфеле до момента погашения. Далее, даже если
такая бумага хранится до погашения, она является безрисковой, опять таки только
символически - неопределенность, связанная с инфляцией, делает реальную норму
прибыли неопределенной. Поэтому представляется трудным, даже почти невозможным,
получение хорошего критерия для оценки прибыли безрискового актива. А это, в
свою очередь, еще больше затрудняет процесс проверки модели ЦОК.
В-четвертых, в статистике существует строгая традиция, согласно которой
нельзя проверить конкретную модель, если не существует альтернативная
жизнеспособная модель, с которой ее можно сравнивать. В случае с моделью ЦОК
может быть использована одна альтернативная модель, получившая название простой
модели арбитражного ценообразования, которая была разработана С. Россом. Суть
его разработки состояла в простейшей интерпретации, включающей в основном добавление
переменных, таких, как темпы неожиданной инфляции, в правую часть уравнения
(2.10). Если правильно учтены все указанные выше аспекты, можно сравнить модель
ЦОК с моделью арбитражного ценообразования посредством проверки нулевой
гипотезы о том, что параметры дополнительных переменных в правой части
одновременно равны нулю.
И, наконец, в-пятых, более неформальный метод проверки модели ЦОК
включает проверку соответствия прогнозов, сделанных на ее основе, тому, что
наблюдается в действительности. В этом контексте следующие два аспекта,
касающиеся модели ЦОК, по-видимому, не будут совпадать с наблюдениями на
практике.
Одно из важных положений модели ЦОК состоит в том, что связь между риском
и прибылью является не только линейной, но и положительной. Однако, как было
отмечено Ф. Блэком, М. Йенсеном и М. Шоулсом (Fischer Black, Michael Jensen and Myron Scholes, 1972), имелось несколько случаев, когда эта
зависимость была отрицательной, а не положительной. В частности, ими было
установлено, что в течение девятилетнего периода, с апреля 1957 г. по декабрь
1965 г., ценные бумаги с более высокими значениями β
давали более низкую
прибыль по сравнению с ценными бумагами с меньшим риском (с более низкими
значениями β). Причина этого до сих пор полностью не установлена, что
свидетельствует о некоторой противоречивости структуры модели ЦОК.
Другой вывод модели ЦОК заключается в том, что ценная бумага с нулевым
значением β должна давать прибыль, точно равную безрисковой ставке.
Указанные выше исследователи изучили прибыли от ценных бумаг на Нью-Йоркской
фондовой бирже за 35 летний период и установили, что измеренная норма прибыли с
нулевым β
превысила норму прибыли,
свободную от риска, а это означает, что некоторый несистематический (без β)
риск делает прибыль для
портфеля с нулевым β большей по сравнению с той, что прогнозируется
моделью ЦОК. Более того, фактическая зависимость риск-прибыль, изученная
Блэком, Йенсеном и Шоулсом, оказывается более пологой, чем спрогнозированная с
помощью модели ЦОК. Поэтому неясно, какие факторы, кроме премии за рыночный
риск, необходимо оценивать на рынке. В соответствии с моделью ЦОК имеет
значение только рыночный риск, поскольку несистематический риск может быть
диверсифицирован. В настоящее время проводятся многочисленные исследования, в
которых делается попытка определить, какие еще факторы, кроме rт, влияют на рыночный риск.
В этом контексте следует отметить, что некоторые инвестиционные компании,
такие как «Lynch, Pierce, Fenner and Smith», регулярно публикуют «бета -
справочники», где даются оценки α и β в рамках моделей стандартной
регрессии по методу наименьших квадратов, а также оценки для «регулируемого β», где делается попытка рассмотреть
указанную выше проблему для портфеля с нулевым β, используя для этого более сложные
байесовские статистические процедуры. Хотя байесовские процедуры представляют
большой интерес, они не рассматриваются .мною.
Здесь следует вкратце отметить несколько других эконометрических
аспектов. Компьютерные программы построения регрессии обычно выдают значения
коэффициента детерминации R2,
стандартных ошибок коэффициентов регрессии и t-статистик. Эти и другие стандартные статистические величины
представляют особый интерес с точки зрения интерпретации и использования в
рамках модели ЦОК. Рассмотрим, например, простую корреляцию между премией за
риск от j-й ценной бумаги (rm -rf) и премией за рыночный риск (rm - rf)
как переменные в левой и правой части, соответственно, в уравнении регрессии
для модели (2.10). Выборочный коэффициент корреляции между ними может быть
переписан следующим образом:
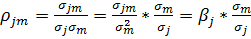
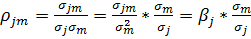 (2.12)
(2.12)
где σjm ,σ2т , σ2 - выборочные ковариации и дисперсии
для rm - rj
rj - rf ; βj - оценка по методу наименьших
квадратов для βj .
Следовательно, выборочная корреляция между премиями за портфельный и
рыночный риск является произведением оценки МНК для βj и отношения выборочных стандартных
отклонений премий за портфельный и рыночный риски.
Стандартная ошибка остатка в уравнении регрессии (2.10) также имеет
полезную интерпретацию. В частности, в то время как левая часть уравнения
(2.10) отражает влияние на портфель как специфического (несистематического),
так и рыночного (систематического) риска для компании j, член βj(rm- rf) в правой части уравнения отражает
только влияние рыночного риска. Отсюда следует, что оцененный остаток в
уравнении (2.10) включает только эффекты специфического (несистематического)
риска. Стандартная ошибка остатка (называемая также стандартной ошибкой
регрессии) вычисляется как квадратный корень из s2, где s2
определяется следующим образом:
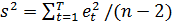
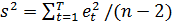 (2.13)
(2.13)
В этом соотношении «невязка» et является остатком по методу наименьших квадратов для t-го наблюдения, поэтому это
обеспечивает оценку среднего квадратического отклонения специфического
(несистематического) риска - риска для портфеля, которое не реагирует на
колебания цен на рынке. Большая относительная стандартная ошибка остатка,
скажем около 15% в месяц, указывает на то, что значительные изменения в премии
за риск для портфеля можно было бы объяснить изменениями в премии за рыночный
риск.
Далее, поскольку значение R2 из
выходных данных регрессии, полученных с помощью ЭВМ, указывает какая часть
изменений зависимой переменной объясняется изменением в правой части
независимой переменной модели (2.10), то R2 измеряет рыночную (систематическую) долю общего риска. С
другой стороны, 1 - R2 определяет долю
общего риска, которая является специфической (несистематической). В работе У.
Шарпа (William F. Sharpe, 1985, )
отмечается, что для отдельной компании типичное значение критерия R2 из уравнения модели ЦОК составляет
примерно 0,30, но по мере осуществления диверсификации ценных бумаг компании в
более крупный портфель значение коэффициента детерминации R2 увеличивается за счет уменьшения специфического
риска при осуществлении диверсификации.
Важно отметить, что, так как в модели парной регрессии R2 = р2тj , большими значения для R2 не обязательно согласуются с большими значениями оценок βj . Чтобы показать это, отметим, что в
соответствии с (2.8)
R2 = ρ2jm =β2j .σ2m/σ2j (2.14)
Отсюда следует, что для некоторых акций с очень большой дисперсией σ2j критерий R2 может быть низким даже при большом значении оценки βj; в таких случаях реакция конкретной
акции (или портфеля) на колебания цен на рынке является весьма резкой, тем не
менее, изменение рынка объясняет лишь небольшую часть большой изменчивости
акции. Уравнение регрессии для других акций может иметь высокое значение R2, но низкую оценку βj ; это может произойти в том случае,
когда изменение в премии за риск для акции (или портфеля ценных бумаг) будет
небольшим по сравнению с изменением в премии за рыночный риск. Иными словами,
отношение выборочных дисперсий в уравнении (2.13) будет большим. Более того,
отметим, что очень низкое значение R2 не означает, что модель ЦОК неверна; наоборот, это просто указывает на
то, что общий риск активов конкретной компании почти полностью относится к
данной компании и не связан с рынком в целом.
Одним из типовых конечных результатов регрессии, который представляет для
нас сейчас особый интерес, является t-статистика. Ранее отмечалось, что t-статистика для оценки коэффициента а может быть использована
для непосредственной проверки нулевой гипотезы, что α
= 0, против
альтернативной гипотезы, что α ≠ 0. Отсутствие оснований для отвержения
этой нулевой гипотезы может рассматриваться как основание в поддержку модели
ЦОК.
Аналогично, t-статистика для
оценки β
может быть использована
для проверки гипотезы β = 0 против альтернативной гипотезы β
≠ 0.
Довольно часто оказывается интересным проверить другие гипотезы, в
частности, гипотезу о соответствии движения цен на акции конкретной компании
движению цен на рынке в целом. Это означает проверку нулевой гипотезы β
= 1 при альтернативной
гипотезе β ≠ 1. Для проверки такой гипотезы можно взять оцененную
стандартную ошибку оценки β (обычно вычисляемую с помощью ЭВМ),
построить доверительный интервал для некоторого приемлемого доверительного
уровня (например, 95 или 99%) и затем определить, попадает ли β
= 1 в этот доверительный
интервал. Если ответ положительный, то нулевая гипотеза не отвергается, а если
ответ отрицательный, то нулевая гипотеза отвергается.
До перехода к выполнению упражнений следует сделать еще одно замечание.
Так как с помощью модели ЦОК знание значения параметра β
позволяет вычислить
значение требуемой прибыли от конкретной акции, она также косвенным образом
позволяет вычислить всю долю стоимости капитала компании. Для компании, которая
рассматривает конкретный инвестиционный проект, комбинация ожидаемой прибыли и
соответствующего значения β оказывает большее влияние на принятие
инвестиционного решения, чем стоимость капитала (если речь идет о компании,
обладающей хорошими управленческими кадрами). Если компания рассматривает новый
проект, который представляет больший риск по сравнению с проектами со средним
риском, то она может рассчитывать на большую ожидаемую прибыль, поскольку такой
проект увеличит средний риск компании, и, в соответствии с моделью ЦОК,
приведет к тому, что инвесторы потребуют большей прибыли. Это означает, что по
аналогии с уравнением (2.8) проекты также имеют свои собственные бета -
коэффициенты, и если β для конкретного проекта будет выше β,
среднего по компаниям,
то требуемая ожидаемая норма прибыли также должна быть выше
На этом завершается обсуждение теории, лежащей в основе модели ЦОК, и наш
краткий обзор эконометрических аспектов, использованных при оценке параметров.
Теперь можно перейти к практической реализации модели ЦОК.
ГЛАВА 3. Практическая работа с моделью ЦОК
В этой главе мы применим теорию, описанную в предыдущих параграфах, для
формирования оптимального портфеля ценных бумаг. Для этого нам потребуются
некоторые реальные данные, на основе которых, мы будем проводить наше
исследование. В настоящее время Научно-исследовательский центр цен на ценные
бумаги (Center for Research on Securities Prices - CRSP)
при Чикагском университете, финансируемый по большей части корпорацией « Lynch, Pierce, Fenner
& Smith, Inc.», познакомил исследователей с оценками величины rт, основанными на операции взвешенной
стоимости всех акций, котирующихся на Нью-Йоркской и Американской фондовых
биржах. К счастью, мы получили доступ к этим рядам данных и в этой главе будем
использовать значения показателя rт. CRSP приводит данные о ежемесячных
доходностях за десятилетний период(с января 1978 по декабрь1987) 17 крупных
компаний Нью-Йоркской фондовой биржи (таб. 2), из акций которых мы будем
формировать оптимальный портфель ценных бумаг. Также имеются данные о
доходностях рынка и бумаг с безрисковой ставкой.
На основании этих определений мы можем теперь представить важный принцип
оптимальности портфеля ценных бумаг, выведенный в финансовой теории. Если две
ценные бумаги в портфеле имеют одинаковое значение β,
но разные ожидаемые
прибыли, то этот портфель не может быть оптимальным в смысле обеспечения
максимальной прибыли для данного риска. Причина того, что такой портфель ценных
бумаг не мог быть оптимальным, заключается в том, что можно было бы получить
более высокую прибыль без увеличения риска, имея больше ценных бумаг с более
высокой прибылью. Поэтому если портфель ценных бумаг является оптимальным, все
ценные бумаги с тем же самым значением β должны иметь идентичные ожидаемые
прибыли.
Другими словами, вычислив значения β и средней ожидаемой прибыли r для каждой ценной бумаги, мы,
возможно, сможем сразу исключить некоторые ценные бумаги, у которых при
одинаковых значениях β будут разные значения r.
Проводить вычисления мы будем в среде EViews и MathCad.
В работе будут приведены самые важные и интересные нам результаты
регрессионного анализа в виде таблиц.
Сформируем таблицу доходности и риска по всем семнадцати бумагам при
помощи EVeiws и представим их в виде следующей
таблицы (таб. 3).
На рисунке 3.1.1 мы видим, как в программе EViews вычисляются среднее значение доходности, ее дисперсия
и стандартное отклонение.
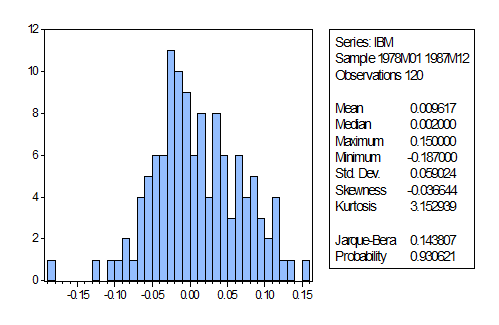
Рис 3.1.1 Основные статистические данные
Таблица 3
Риск-доходность
|
rср
|
rmax
|
rmin
|
σ
|
Сумма
|
|
BOISE
|
0.016675
|
0.379000
|
-0.274000
|
0.0974
|
2.001000
|
|
CITCRP
|
0.011858
|
0.318000
|
-0.282000
|
0.0809
|
1.423000
|
|
CONED
|
0.018508
|
0.151000
|
-0.139000
|
0.0502
|
2.221000
|
|
CONTIL
|
-0.001100
|
0.974000
|
-0.600000
|
0.1506
|
-0.132000
|
|
DATGEN
|
0.007483
|
0.528000
|
-0.342000
|
0.1275
|
0.898000
|
|
DEC
|
0.019750
|
0.385000
|
-0.364000
|
0.0991
|
2.370000
|
|
DELTA
|
0.011692
|
0.289000
|
-0.260000
|
0.0959
|
1.403000
|
|
FREE
|
0.006839
|
0.012550
|
0.002070
|
0.0021
|
0.820630
|
|
GENMIL
|
0.016583
|
0.190000
|
-0.148000
|
0.0650
|
1.990000
|
|
GERBER
|
0.016400
|
0.234000
|
-0.288000
|
0.0877
|
1.968000
|
|
IBM
|
0.009617
|
0.150000
|
-0.187000
|
0.059024
|
1.154000
|
|
MARKET
|
0.013992
|
0.148000
|
-0.260000
|
0.068353
|
1.679000
|
|
MOBIL
|
0.016192
|
0.366000
|
-0.178000
|
0.080308
|
1.943000
|
0.018158
|
0.270000
|
-0.331000
|
0.097987
|
2.179000
|
|
PANAM
|
0.003517
|
0.406000
|
-0.313000
|
0.1318
|
0.422000
|
|
PSNH
|
-0.004217
|
0.318000
|
-0.485000
|
0.1094
|
-0.506000
|
|
TANDY
|
0.025008
|
0.454000
|
-0.246000
|
0.1275
|
3.001000
|
|
TEXACO
|
0.011942
|
0.399000
|
-0.194000
|
0.079704
|
1.433000
|
|
WEYER
|
0.009633
|
0.270000
|
-0.271000
|
0.085066
|
1.156000
|
где
rcр-средняя
доходность бумаги
rmin-
минимальная доходность бумаги
rmax-максимальная
доходность бумаги
σ - собственный риск бумаги
.1 Расчет бета - значений ценных бумаг
Для расчета β-значений снова обратимся к предыдущим параграфам, а
именно, вспомним
rj-rf=(σj/σm)*(rm-rf), (3.2.1)
β=(σj/σm) (3.2.2)
где rj, rf - соответственно, прибыли для ценной бумаги j и безрискового актива;
rт -
прибыль общего рыночного портфеля ценных бумаг;
σj/σm - отношение стандартных отклонений
прибылей ценной бумаги j и
рыночного портфеля m. Член rj - rf является премией за риск для ценной бумаги j, в то время как rm - rf представляет собой премию за риск для всего рынка.
Используя парный регрессионный анализ, составим модель ЦОК для каждой
ценной бумаги в среде EVeiws.
Оценивать бета - значения мы будем относительно премий за риск каждой бумаги rj - rf и премией за риск для всего рынка в целом. Для этого
составим модель ЦОК для каждой ценной бумаги:
rj-rf=α+βj*(rm-rf)+ε, (3.2.3)
где rj, rf - соответственно, прибыли для ценной бумаги j и безрискового актива;
rт -
прибыль общего рыночного портфеля ценных бумаг;
ε- стохастическое возмущение;
В этой модели известны все значения кроме β. Определим эти значения методом
наименьших квадратов. В среде EViews
это делается совсем не сложно. Ниже мы приведем уже результаты вычисления
значений β и R2 для одной
ценной бумаги, а для остальных бумаг проведем расчеты по аналогии .
Представление этих данных в EViews выглядит следующим образом.
|
Dependent Variable:
IBM-FREE
|
|
|
|
|
Method: Least Squares
|
|
|
|
|
Date: 05/23/12 Time: 14:41
|
|
|
|
|
Sample: 1978M01 1987M12
|
|
|
|
|
Included observations: 120
|
|
|
|
|
(IBM-FREE)=C(1)+C(2)*(MARKET-FREE)
|
|
|
|
|
|
|
|
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
C(1)
|
-0.000490
|
0.004640
|
-0.105515
|
0.9161
|
|
C(2)
|
0.456821
|
0.067548
|
6.762932
|
0.0000
|
|
|
|
|
|
|
R-squared
|
0.279333
|
Mean dependent var
|
0.002778
|
|
Adjusted R-squared
|
0.273226
|
S.D. dependent var
|
0.059299
|
|
S.E. of regression
|
0.050553
|
Akaike info criterion
|
-3.115075
|
|
Sum squared resid
|
0.301558
|
Schwarz criterion
|
-3.068617
|
|
Log likelihood
|
188.9045
|
Hannan-Quinn criter.
|
-3.096208
|
|
F-statistic
|
45.73725
|
Durbin-Watson stat
|
1.882688
|
|
Prob(F-statistic)
|
0.000000
|
|
|
|
Рис 3.2.1 Представление данных в EViews
Первое, на что мы обращаем свое внимание на рисунке 3.2.1, это то, какое
значение мы получили для свободного коэффициента α (во всех случаях примерно одинаковые).
Проверив нулевую гипотезу и оценив t-статистику делаем вывод о том, что коэффициент α
не значим и равен
практически нулю.
Посмотрев еще раз на уравнение (3.2.3), очевидно, что при нулевой премии
за риск рынка, премия за риск каждой бумаги будет тоже ровна нулю. Также в этой
таблице мы можем наблюдать значение β и R2 (доля рыночного риска). Доли и рассчитанные количественные
значения несистематического и рыночного рисков продемонстрированы в
Приложении 2.
Далее представим полученные данные в виде таблицы бета-значений и
доходности r по каждой бумаге (таб. 4).
Таблица 4
Бета-значения и доходности
|
Компании
|
β
|
Доходность, r
|
|
BOISE
|
0,941171
|
0.016675
|
|
CITCRP
|
0,635063
|
0.011858
|
|
CONED
|
0,140958
|
0.018508
|
|
DATGEN
|
1,008161
|
0.007483
|
|
DEC
|
0,8661
|
0.019750
|
|
DELTA
|
0,503494
|
0.011692
|
|
GENMIL
|
0,304958
|
0.016583
|
|
CONTIL
|
0,715237
|
-0.001100
|
|
IBM
|
0,462522
|
0.009617
|
|
MOTOR
|
0,826102
|
0.018158
|
|
PANAM
|
0,71073
|
0.003517
|
|
TANDY
|
1,085164
|
0.025008
|
|
TEXACO
|
0,623015
|
0.011942
|
|
WEYER
|
0,811664
|
0.009633
|
|
PSNH
|
0,191795
|
-0.004217
|
|
GERBER
|
0,646995
|
0.016400
|
|
MOBIL
|
0,711504
|
0.016192
|
Далее, следую приведенной выше теории о том, что в оптимальном портфеле
ценных бумаг, активы с одинаковыми коэффициентами β
должны иметь одинаковые
доходности, в противном случае, бумаги с меньшей доходности становятся не
рентабельными для инвестора с точки зрения получения наибольшей прибыли при
заданном уровне риска, и не включаются в портфель ценных бумаг. Следуя этому
принципу исключим некоторые бумаги, после чего у нас останется всего 9 бумаг,
из которых мы и будем составлять оптимальный портфель активов. Наш портфель
будет состоять из следующих бумаг (таб. 5).
Таблица 5
Бета-значения и доходности оставшихся бумаг
|
Компании
|
β
|
r
|
|
BOISE
|
0,941171
|
0.016675
|
|
CONED
|
0,140958
|
0.018508
|
|
DEC
|
0,8661
|
0.019750
|
|
DELTA
|
0,503494
|
0.011692
|
|
GENMIL
|
0,304958
|
0.016583
|
|
GERBER
|
0,646995
|
0.016400
|
|
IBM
|
0,462522
|
0.009617
|
|
MOBIL
|
0,711504
|
0.016192
|
|
TANDY
|
1,085164
|
0.025008
|
3.2 Составление оптимального портфеля
Итак, теперь, когда мы исключили часть бумаг из нашего портфеля, у нас
осталось всего девять разных интересных нам бумаг, тем самым значительно
упростив себе вычисления. Почему так? Об этом речь пойдет ниже. Приведем данные
по оставшимся девяти бумагам (таб. 6).
Таблица 6
Риск-доход портфельных бумаг
|
Компания
|
Риск, σ
|
Доход, r
|
|
1
|
BOISE
|
0,0095
|
0.016675
|
|
2
|
CONED
|
0,0025
|
0.018508
|
|
3
|
DEC
|
0,0098
|
0.019750
|
|
4
|
DELTA
|
0,0091
|
0.011692
|
|
5
|
GENMIL
|
0,0042
|
0.016583
|
|
6
|
GERBER
|
0,0076
|
0.016400
|
|
7
|
IBM
|
0,0034
|
0.009617
|
|
8
|
MOBIL
|
0,0064
|
0.016192
|
|
9
|
TANDY
|
0,0162
|
0.025008
|
Рассмотрим случай, когда инвестор использует диверсификацию, имея п
ценных бумаг, где п может быть больше 2. Как и до этого, ожидаемая прибыль от
всего портфеля ценных бумаг является средним взвешенным числом ожидаемых от
различных ценных бумаг rj,
где весовые коэффициенты wj являются
долями общих ассигнований (общего капитала), вложенных в каждую ценную бумагу,
т.е.
 (3.3.1)
(3.3.1)
И опять при п ценных бумагах общая дисперсия портфеля ценных бумаг
зависит не только от дисперсий п отдельных ценных бумаг, но также от их
ковариаций. В частности, дисперсия портфеля ценных бумаг вычисляется как:
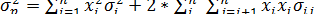
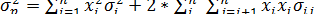 (3.3.2)
(3.3.2)
где-
ковариация между прибылями от ценных бумаг i и j;
σj2 - дисперсия.
Отметим, что дисперсия для всего портфеля ценных бумаг в уравнении
(3.3.2) состоит из п дисперсий и п(п - 1) ковариаций, причем п(п - 1)/2 из них
будут разными. Поэтому чем больше п, при других равных условиях, тем больше относительная
важность ковариаций ценных бумаг для дисперсии всего портфеля. Например, когда
п равно 5, имеется пять дисперсий и 20 ковариаций, когда п увеличивается до 10,
количество дисперсий увеличивается до 10, но количество ковариаций в уравнении
(3.3) увеличивается до 90. По мере того как п становится очень большим,
дисперсия портфеля ценных бумаг приближается к (взвешенному) среднему числу
ковариаций. Следовательно, ковариаций будут чрезвычайно важны в процессе
диверсификации.
Итак, на основе изученной нами теории мы можем составить целевую функцию,
по средствам которой, мы вычислим весовые коэффициенты (доли) ценных бумаг в
портфеле. Для этого нам понадобится составить ковариационную матрицу в EViews (таб 7).
Таблица 7
Ковариационная матрица
|
BOISE
|
CONED
|
DEC
|
DELTA
|
GENMIL
|
GERBER
|
IBM
|
MOBIL
|
TANDY
|
|
BOISE
|
0.0094
|
0.0010
|
0.0052
|
0.0042
|
0.0022
|
0.0025
|
0.0026
|
0.0025
|
0.0062
|
|
CONED
|
0.0010
|
0.0025
|
0.0005
|
0.0004
|
0.0010
|
0.0007
|
0.0003
|
0,0006
|
0.0006
|
|
DEC
|
0.0052
|
0.0005
|
0.0097
|
0.0040
|
0.0013
|
0.0014
|
0.0026
|
0.0032
|
0.0062
|
|
DELTA
|
0.0042
|
0.0004
|
0.0040
|
0.0091
|
0.0023
|
0.0015
|
0.0019
|
0.0010
|
0.0056
|
|
GENMIL
|
0.0021
|
0.0011
|
0.0013
|
0.0023
|
0.0042
|
0.0019
|
0.0006
|
0.0002
|
0.0033
|
|
GERBER
|
0.0025
|
0.0007
|
0.0014
|
0.0016
|
0.0020
|
0.0076
|
0.0015
|
0.0022
|
0.0022
|
|
IBM
|
0.0026
|
0.0003
|
0.0026
|
0.0019
|
0.0006
|
0.0015
|
0.0034
|
0.0015
|
0.0025
|
|
MOBIL
|
0.0025
|
0,0006
|
0.0032
|
0.0010
|
0.0002
|
0.0022
|
0.0015
|
0.0063
|
0.0023
|
|
TANDY
|
0.0062
|
0.0006
|
0.0063
|
0.0056
|
0.0033
|
0.0022
|
0.0025
|
0.0023
|
0.0161
|
Задача по составлению оптимального портфеля ценных бумаг сводится к
нахождению весовых коэффициентов x1,x2,x3…x9 в
уравнении(3.2)
Теперь необходимо решить задачу нелинейного программирования - найдем
доли акций в оптимальном портфеле с заданной доходностью rp и минимальным риском σp. Для этого зададим целевую функцию и
ее ограничения.
Ограничения:
1+x2+x3+…+x9 = 1
сумма всех долей равна единице, и они все должны быть неотрицательными.
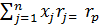
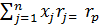
где
rp - желаемая доходность портфеля;
xj -доля j-ой
бумаги в портфеле.
Тогда
целевая функция будет выглядеть так:
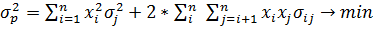
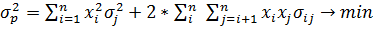 ,
,
Дальнейшие
вычисления будем проводить в MathCad, используя метод неопределенных множителей
<#"660513.files/image013.gif">
Рис.
3.3.1 Представление результатов в MathCad.
Получив
два отрицательных значения x - весового коэффициента ценных бумаг 1 и 4(BOISE
и DELTA), мы исключаем эти бумаги из портфеля. Обратим
внимание на (таб. 6), не трудно заметить, что соотношение показателей
риск-доход у этих бумаг куда хуже, чем у остальных, очевидно, их надо
исключить.
Теперь
снова решаем поставленную выше задачу, исключив из ограничений и целевой
функции все коэффициенты и переменные, связанные с этими бумагами.
Вычисления
проводим в MathCad по аналогии с предыдущими (см. Приложение 4).
3.3 Анализ полученных результатов
Получившиеся
результаты удовлетворяют всем ограничениям, и риск, при получившихся значениях
весовых коэффициентов акций, будет минимальным. Представим их в виде следующей
таблицы (таб. 8).
Таблица
8
Доли
акций в портфеле
|
Компания
|
Риск
|
Доходность
|
%
|
|
11
|
CONED
|
0.050272
|
0.018508
|
55.4%
|
|
22
|
DEC
|
0.099144
|
0.019750
|
5.4%
|
|
23
|
GENMIL
|
0.065040
|
0.016583
|
13.4%
|
|
34
|
GERBER
|
0.087738
|
0.016400
|
4.9%
|
|
35
|
IBM
|
0.059024
|
0.009617
|
6.7%
|
|
36
|
MOBIL
|
0.080308
|
0.016192
|
10.4%
|
|
27
|
TANDY
|
0.127566
|
0.025008
|
3.8%
|
|
1
|
Портфель
|
0.043361
|
0.018034
|
|
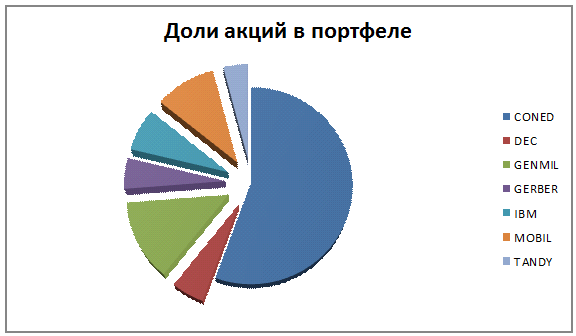
Рис
3.3.2 Доли акций в портфеле.
При
таком составление портфеля риск будет минимальным и равным 0.04, при
достигнутом доходе в 0.018. В этой таблице хорошо видно, что риск портфеля
будет меньше чем у каждой, отдельно взятой, ценной бумаги, а доходность всего
портфеля в свою очередь будет выше средней по всем ценным бумагам. Теперь
построим по аналогии еще четыре портфеля с разными заданными доходностями.
Возьмем доходности равные минимальному, максимальному и среднему значения среди
акций портфеля. Полученные результаты представлены в Приложении 5.
Давайте
понаблюдаем, как будет меняться значение риска, когда мы будем увеличивать или
уменьшать значение желаемой доходности (Рис 3.3.3).
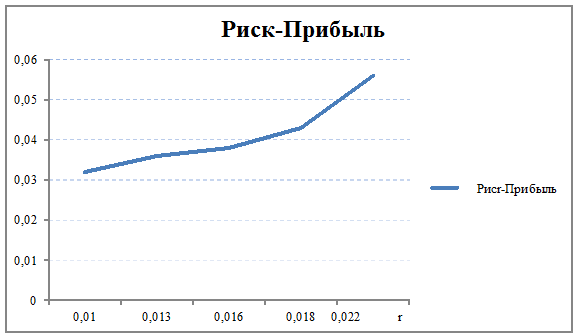
Рис
(3.3.3) Зависимость риск-прибыль.
Таким
образом, мы составили оптимальные портфели ценных бумаг с минимальным, для
заданных доходностей, риском на основе приведенных данных обо всех компаниях и
рынке в целом. Также нам удалось убедиться в эффективности диверсификации, на
конкретных примерах составления портфелей ценных бумаг.
Заключение
В данной дипломной работе была рассмотрена задача диверсификации портфеля
ценных бумаг. Прежде всего, мы ознакомились с финансовой теорией, лежащей в
основе модели ценообразования на основной капитал. Исходными являлись данные о
доходности семнадцати компаний США, представляющих восемь отраслей, среди
которых переработка нефти, вычислительная техника, банки, производство
электроэнергии. С использованием регрессионного анализа для акций каждой
компании были вычислены бета - значения, показывающие чувствительность актива к
изменениям рыночной доходности и рыночная доля общего риска, и на основе
финансовой теории, лежащей в основе модели ЦОК, были исключены те акции компаний,
которые оказались неприемлемыми для оптимального портфеля инвестиций. Из
выбранных акций был составлен оптимальный портфель, который по заданной
доходности позволяет минимизировать специфический (несистематический) риск.
Также были составлены другие пять оптимальных портфелей (с разными показателями
доходности), на примере которых мы смогли пронаблюдать зависимость между риском
и доходностью портфеля ценных бумаг.
В процессе достижения поставленных ранее целей, мы установили зависимость
между риском и прибылью, изучили и продемонстрировали процесс диверсификации,
убедившись в его эффективности.
Все поставленные задачи были раскрыты и выполнены в соответствии с
выбранной темой и поставленной целью.
Список использованной литературы
1. Айвозян
С.А., Методы эконометрики. - М.: Экономист, 2010.-560с.Артюхов С.В., Базюкина
О.А., Королев В.Ю., Кудрявцев А.А. Модель оптимального ценообразования,
основанная на процессах риска со случайными премиями. // Системы и средства
информатики. Специальный выпуск. - М.: ИПИРАН, 2005.-873с.
. Бенинг
В.Е., Королев В.Ю. Асимптотические разложения для вероятности разорения в
классическом процессе риска при малой нагрузке безопасности // Обозрение
прикладной и промышленной математики. Т. 7, вып. 1, 2000.-785с.
. Бенинг
В. Е., Королев В. Ю. Введение в математическую теорию риска. - М.: МАКС-Пресс,
2000.-235с.
. Берндт
Э., Практика эконометрики : классика и современность. -М.: Финансы и
статистика. 2009. - 414 с.
. Бланк
И.А. Стратегия и тактика управления финансами. - Киев: ИТЕМлтд, АДЕФ-Украина,
2008. - 345 с.
. Ван
Хорн Дж.К. Основы управления финансами.- М.: Финансы и статистика, 2009. - 240
с.
. Доугерти
К., Введение в эконометрику. - М.: Дело, 2007. - 310 с.
. Ефимова
О.В. Финансовый анализ. - М.: Бухгалтерский учет. 2008. - 544 с.
. Калашников
В.В., Константинидис Д. Вероятность разорения - Фундаментальная и прикладная
математика. - Т.2, вып. 4, 2006.-401с.
. Ковалев
В.В. Финансовый анализ. Управление капиталом, выбор инвестиций, анализ
отчетности. - М. 1996.-321с.
. Колемаев
В.А. Математическая экономика. - М.: ЮНИТИ, 1998.-326с.
. Королев
В.Ю., Бенинг В.Е., Шоргин С.Я. Математические основы теории риска: Учебн.
Пособ.- М.:ФИЗМАТЛИТ, 2007.-556с.
. Лобанов
А.А., Чугунов А.В. Энциклопедия финансового риск- менеджмента. - М., Альпина
Бизнес Букс, 2005.-322с.
. Мак
Т. Математика рискового страхования. - М.: Олимп-Бизнес, 2005.
. Меньшиков
И.С., Шелагин Д.А. Кооперативное распределение рискового капитала. - М.:
Вычислительный центр РАН, 2001.-232с.
. Фалин
Г.И. Математический анализ рисков в страховании. - М.: Российский юридический
издательский дом, 1994.-544с.
. Шевцова
И. Г. Уточнение структуры оценок скорости сходимости в центральной предельной
теореме для сумм независимых случайных величин. // Дис. канд. физ.-матем. наук.
- МГУ, 2006.-344с.
. Ширяев
А.Н. Теория вероятностей. - М.: Наука, 1989.-184с.
. Ширяев
А.Н. Актуарное и финансовое дело: современное состояние и перспективы развития.
// Обозрение прикладной и промышленной математики.-1994. - Т.1.-570с.
. Ширяев
А.Н. Вероятностно-статистические модели эволюции финансовых индексов. //
Обозрение прикладной и промышленной математики, - 1995.- Т.2,.-414с.
. Ширяев
А.Н. Основы стохастической финансовой математики. Факты. Модели. - М.: Фазис,
1998.-482с.
. Ширяев
А.Н. Основы стохастической финансовой математики. Теория. - М.: Фазис,
1998.-506с.
. Штойян
Д. Качественные свойства и оценки стохастических моделей. - М.: Мир,
1999.-456с.
Приложения
Приложение 1
«Связь между типом инвестора и типом портфеля»
|
Тип инвестора
|
Цель инвестирования
|
Степень риска
|
Тип ценной бумаги
|
Тип портфеля
|
|
Консервативный
|
Защита от инфляции
|
Низкая
|
Государственные ценные
бумаги, акции и облигации крупных стабильных эмитентов
|
Высоконадежный, но низко
доходный
|
|
Умеренно-агрессивный
|
Длительное вложение
капитала и его рост
|
Средняя
|
Малая доля государственных
ценных бумаг, большая доля ценных бумаг крупных и средних, но надежных
эмитентов с тигельной рыночной историей
|
Диверсифицированный
|
|
Агрессивный
|
Спекулятивная игра,
возможность быстрого роста итоженных средств
|
Высокая
|
Высокая доля высокодоходных
ценных бумаг небольших эмитентов, венчурных компаний и т.д.
|
Рискованный, но
высокодоходный
|
|
Нерациональный
|
Нет четких целей
|
Низкая
|
Произвольно подобранные
ценные бумаги
|
Бессистемный
|
Приложение 2
«Основные статистические показатели ценных бумаг»
|
риск
|
доход
|
a
|
b
|
собст.риск
|
рыночн.риск
|
доля рыноч.риска
|
|
BOISE
|
0.097488
|
0.016675
|
0
|
0,941171294
|
0,00547
|
0,00429
|
44
|
|
CITCRP
|
0.080972
|
0.011858
|
0
|
0,67506329
|
0,00447
|
0,0091
|
33,1
|
|
CONED
|
0.050272
|
0.018508
|
0
|
0,140957653
|
0,00277
|
0,000092
|
3
|
|
DATGEN
|
0.127540
|
0.007483
|
0
|
1,008160779
|
0,01137
|
0,00487
|
30
|
|
DEC
|
0.099144
|
0.019750
|
0
|
0,866100411
|
0,00656
|
0,00369
|
35,7
|
|
DELTA
|
0.095932
|
0.011692
|
0
|
0,503493656
|
0,00811
|
0,001285
|
13,2
|
|
GENMIL
|
0.065040
|
0.016583
|
0
|
0,30495842
|
0,00405
|
0,00045
|
10
|
|
CONTIL
|
0.150699
|
-0.001100
|
0
|
0,705236946
|
0,02028
|
0,00225
|
10,6
|
|
IBM
|
0.059024
|
0.009617
|
0
|
0,462522369
|
0,00252
|
0,0011
|
29,1
|
|
MOTOR
|
0.097266
|
0.018158
|
0
|
0,866102137
|
0,00613
|
0,0036
|
37,3
|
|
PANAM
|
0.131805
|
0.003517
|
0
|
0,710729811
|
0,00149
|
0,0024
|
14,1
|
|
TANDY
|
0.127566
|
0.025008
|
0
|
1,085164432
|
0,01116
|
0,0057
|
33,9
|
|
TEXACO
|
0.079704
|
0.011942
|
0
|
0,623014812
|
0,00461
|
0,00187
|
29
|
|
WEYER
|
0.085066
|
0.009633
|
0
|
0,811663581
|
0,00412
|
0,00323
|
42,9
|
|
PSNH
|
0.109471
|
-0.004217
|
0
|
0,191794698
|
0,01182
|
0,00012
|
1,4
|
|
GERBER
|
0.087738
|
0.016400
|
0
|
0,646994973
|
0,00593
|
0,00197
|
25,5
|
|
MOBIL
|
0.080308
|
0.016192
|
0
|
0,731503644
|
0,0041
|
0,00262
|
38,8
|
|
Рынок
|
0.068353
|
0.013992
|
|
|
|
|
|
Приложение 3
«Листинг программы 1 MathCad»
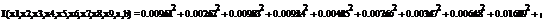
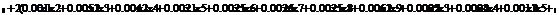
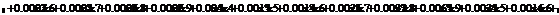
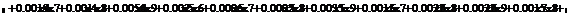
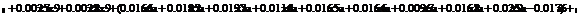
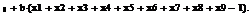
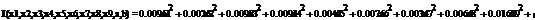
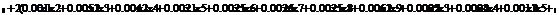
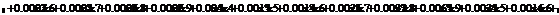
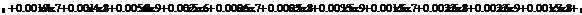
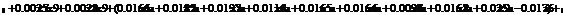
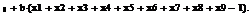
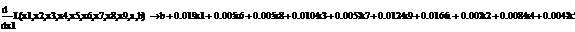

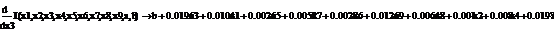
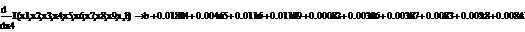
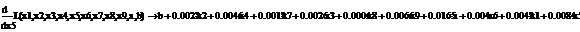
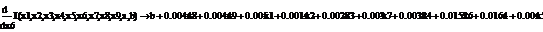
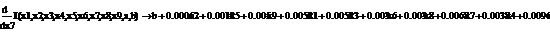
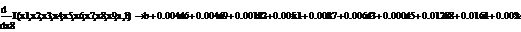
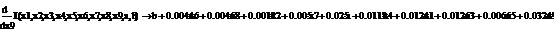
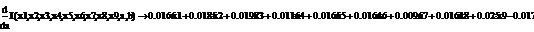
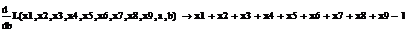
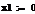
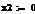
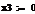
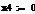
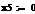
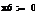
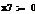
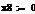
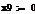
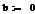
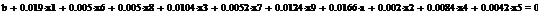
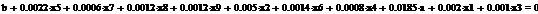
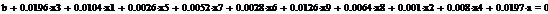
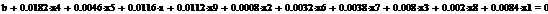
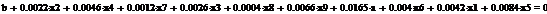
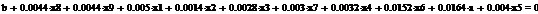
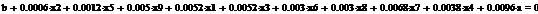
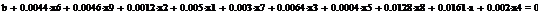
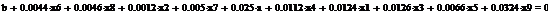
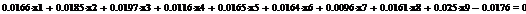
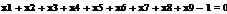

Приложение 4
«Листинг программы 2 в MathCad»
 +
+
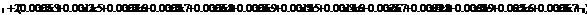
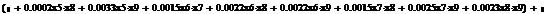
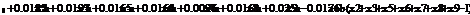
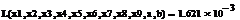
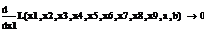
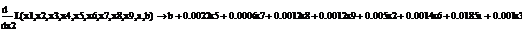
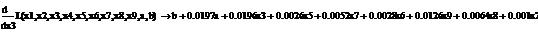
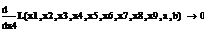
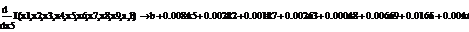
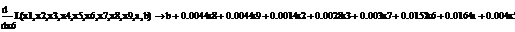
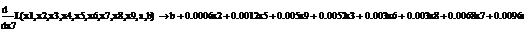
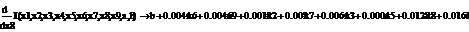
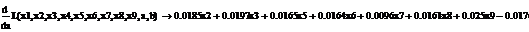
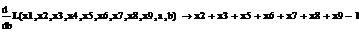
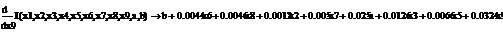
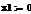
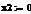
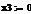
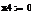
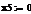
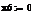
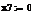
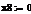
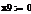
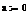
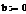
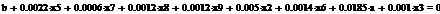
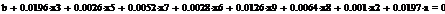
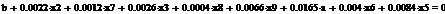
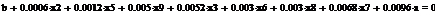
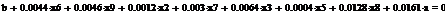
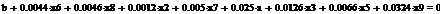
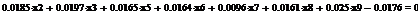
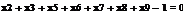
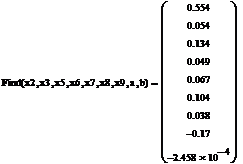
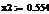
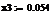
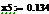
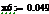
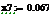
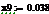
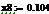
Приложение 5
«Доли акций в портфелях с разными доходностями»
|
CONED
|
DEC
|
GENMIL
|
GERBER
|
IBM
|
MOBIL
|
TANDY
|
|
r = 0,01
|
0,148
|
0
|
0,161
|
0
|
0,54
|
0,16
|
0,05
|
|
r = 0,013
|
0,27
|
0
|
0,25
|
0
|
0,474
|
0,113
|
0
|
|
r = 0,016
|
0,471
|
0,03
|
0,169
|
0,027
|
0,208
|
0,107
|
0
|
|
r = 0,018
|
0,55
|
0,054
|
0,134
|
0,049
|
0,067
|
0,104
|
0, 038
|
|
r = 0,022
|
0,33
|
0,105
|
0,081
|
0,083
|
0
|
0,09
|
0,037
|