Планирование эксперимента и статистическая обработка результатов измерений
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
1. ОСНОВЫ
МАТЕМАТИЧЕСКОГО ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
1.1
История возникновения планирования эксперимента
1.2
Основные понятия и определения
1.3
Представление результатов экспериментов
1.4
Применение математического планирования эксперимента в научных исследованиях
1.5
Требования, предъявляемые к факторам при планировании эксперимента
1.6
Ошибки опыта
2. ПОЛУЧЕНИЕ
СОВОКУПНОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН
2.1 Расчёт
оценок математического ожидания, дисперсии и среднеквадратического отклонения
2.2 Исключение
резко выделяющихся экспериментальных данных
2.3 Расчет
относительных характеристик рассеяния случайной величины
2.4 Определение
ошибки среднего и границ доверительного интервала
2.5 Доверительный
объем испытаний
3. ПОСТРОЕНИЕ
ГИСТОГРАММЫ И ПОЛИГОНА ИМПЕРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
4. ПРОВЕРКА
ОСНОВНОЙ ГИПОТЕЗЫ
5. ТОЧЕЧНАЯ
И ИНТЕРВАЛЬНАЯ ОЦЕНКА. СРАВНЕНИЕ ДВУХ ВЫБОРОК
6. ОДНОФАКТОРНЫЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ
7. ТРЁХФАКТОРНЫЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ
8. КОРРЕЛЯЦИОННЫЙ
И РЕГРЕССИОННЫЙ АНАЛИЗ
9. СПОСОБ
ОБРАБОТКИ ЭМПИРИЧЕСКИХ ДАННЫХ
СПИСОК
ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
При измерении свойств продуктов легкой
промышленности и разработке методов оценки технологических параметров, как
правило, изучается совокупность случайных величин. Которая может быть
определена основными числовыми характеристиками: средним значением, дисперсией,
коэффициентом вариации, квадратической неровнотой и т.д.. Известно, что
числовые характеристики меняются от выборки к выборке и являются также
случайными величинами, которые варьируют с заданной доверительной вероятностью
в определенном интервале. Чем больше ошибка числовой характеристики, тем шире
интервал. Точность каждой числовой характеристики определяется ее ошибкой, а
надежность - доверительной вероятностью. Задаваясь точностью и надежностью при
известной дисперсии случайной величины, можно определить доверительный объем
испытаний для оценки числовой характеристики.
Целью данной курсовой работы является изучение
методов определения основных числовых характеристик и получение начальных
навыков работы с совокупностью случайных величин.
1. ОСНОВЫ
МАТЕМАТИЧЕСКОГО ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
.1 История возникновения планирования
эксперимента
Планирование эксперимента - продукт нашего
времени, однако истоки его теряются в глубине веков.
Истоки планирования эксперимента уходят в
глубокую древность и связаны с числовой мистикой, пророчествами и суевериями.
Это собственно не планирование физического
эксперимента, а планирование числового эксперимента, т.е. расположение чисел
так, чтобы выполнялись некоторые строгие условия, например, на равенство сумм
по строкам, столбцам и диагоналям квадратной таблицы, клеточки которой
заполнены числами натурального ряда.
Такие условия выполняются в магических
квадратах, которым, по-видимому, принадлежит первенство в планировании
эксперимента.
Согласно одной легенде примерно в 2200 г. до
н.э. китайский император Ю выполнял мистические вычисления с помощью
магического квадрата, который был изображен на панцире божественной черепахи.
Квадрат императора Ю
9 2
5 7
1 6
Клетки этого квадрата заполнены числами от 1 до
9, и суммы чисел по строкам, столбцам и главным диагоналям равны 15.
В 1514 г. немецкий художник Альбрехт Дюрер
изобразил магический квадрат в правом углу своей знаменитой гравюры-аллегории
«Меланхолия». Два числа в нижнем горизонтальном ряду A5 и 14) составляют год
создания гравюры. В этом состояло своеобразное «приложение» магического
квадрата.
Квадрат Дюрера
3 2 13
10 11 8
6 7 12
15 14 1
В течение нескольких веков построение магических
квадратов занимало умы индийских, арабских, немецких, французских математиков.
В настоящее время магические квадраты
используются при планировании эксперимента в условиях линейного дрейфа, при
планировании экономических расчетов и составлении рационов питания, в теории
кодирования и т.д.
Построение магических квадратов является задачей
комбинаторного анализа, основы которого в его современном понимании заложены Г.
Лейбницем. Он не только рассмотрел и решил основные комбинаторные задачи, но и
указал на большое практическое применение комбинаторного анализа: к кодированию
и декодированию, к играм и статистике, к логике изобретений и логике геометрии,
к военному искусству, грамматике, медицине, юриспруденции, технологии и к
комбинации наблюдений. Последняя область применения наиболее близка к
планированию эксперимента.
Одной из комбинаторных задач, имеющей прямое
отношение к планированию эксперимента, занимался известный петербургский
математик Л. Эйлер. В 1779 г. он предложил задачу о 36 офицерах как некоторый
математический курьез.
Он поставил вопрос, можно ли выбрать 36 офицеров
6 рангов из 6 полков по одному офицеру каждого ранга от каждого полка и
расположить их в каре так, чтобы в каждом ряду и в каждой шеренге было бы по
одному офицеру каждого ранга и по одному от каждого полка. Задача эквивалентна
построению парных ортогональных 6x6 квадратов. Оказалось, что эту задачу решить
невозможно. Эйлер высказал предположение, что не существует пары ортогональных
квадратов порядка п=1 (mod 4).
Задачей Эйлера, в частности, и латинскими квадратами
вообще занимались впоследствии многие математики, однако почти никто из них не
задумывался над практическим применением латинских квадратов.
В настоящее время латинские квадраты являются
одним из наиболее популярных способов ограничения на рандомизацию при наличии
источников неоднородностей дискретного типа в планировании эксперимента.
Группировка элементов латинского квадрата, благодаря своим свойствам (каждый
элемент появляется один и только один раз в каждой строке и в каждом столбце
квадрата), позволяет защитить главные эффекты от влияния источника
неоднородностей. Широко используются латинские квадраты и как средство
сокращения перебора в комбинаторных задачах.
Возникновение современных статистических методов
планирования эксперимента связано с именем Р. Фишера.
С 1918 г. он начал свою известную серию работ на
Рочемстедской агробиологической станции в Англии. В 1935 г. появилась его
монография «Design of Experiments», давшая название всему направлению.
Дальнейшие развития этих идеи было планирование,
ортогональное к неконтролируемому временному дрейфу, которое следует
рассматривать как важное открытие в экспериментальной технике - значительное
увеличение возможностей экспериментатора.
.2 Основные понятия и определения
Под экспериментом будем понимать совокупность
операций совершаемых над объектом исследования с целью получения информации о
его свойствах. Эксперимент, в котором исследователь по своему усмотрению может
изменять условия его проведения, называется активным экспериментом. Если исследователь
не может самостоятельно изменять условия его проведения, а лишь регистрирует
их, то это пассивный эксперимент.
Важнейшей задачей методов обработки полученной в
ходе эксперимента информации является задача построения математической модели
изучаемого явления, процесса, объекта. Ее можно использовать и при анализе
процессов и при проектировании объектов. Можно получить хорошо аппроксимирующую
математическую модель, если целенаправленно применяется активный эксперимент.
Другой задачей обработки полученной в ходе эксперимента информации является
задача оптимизации, т.е. нахождения такой комбинации влияющих независимых
переменных, при которой выбранный показатель оптимальности принимает
экстремальное значение.
Опыт - это отдельная экспериментальная часть.
План эксперимента - совокупность данных
определяющих число, условия и порядок проведения опытов.
Планирование эксперимента - выбор плана
эксперимента, удовлетворяющего заданным требованиям, совокупность действий
направленных на разработку стратегии экспериментирования (от получения
априорной информации до получения работоспособной математической модели или
определения оптимальных условий). Это целенаправленное управление
экспериментом, реализуемое в условиях неполного знания механизма изучаемого
явления.
В процессе измерений, последующей обработки
данных, а также формализации результатов в виде математической модели,
возникают погрешности и теряется часть информации, содержащейся в исходных
данных. Применение методов планирования эксперимента позволяет определить
погрешность математической модели и судить о ее адекватности. Если точность
модели оказывается недостаточной, то применение методов планирования
эксперимента позволяет модернизировать математическую модель с проведением
дополнительных опытов без потери предыдущей информации и с минимальными
затратами.
Цель планирования эксперимента - нахождение
таких условий и правил проведения опытов при которых удается получить надежную
и достоверную информацию об объекте с наименьшей затратой труда, а также представить
эту информацию в компактной и удобной форме с количественной оценкой точности.
Пусть интересующее нас свойство (Y) объекта
зависит от нескольких (n) независимых переменных (Х1, Х2, …, Хn) и мы хотим
выяснить характер этой зависимости - Y=F(Х1, Х2, …, Хn), о которой мы имеем
лишь общее представление. Величина Y - называется «отклик», а сама зависимость
Y=F(Х1, Х2, …, Хn) - «функция отклика».
Отклик должен быть определен количественно.
Однако могут встречаться и качественные признаки Y. В этом случае возможно
применение рангового подхода. Пример рангового подхода - оценка на экзамене,
когда одним числом оценивается сложный комплекс полученных сведений о знаниях
студента.
Независимые переменные Х1, Х2, …, Хn - иначе
факторы, также должны иметь количественную оценку. Если используются
качественные факторы, то каждому их уровню должно быть присвоено какое-либо
число. Важно выбирать в качестве факторов лишь независимые переменные, т.е.
только те которые можно изменять, не затрагивая другие факторы. Факторы должны
быть однозначными. Для построения эффективной математической модели
целесообразно провести предварительный анализ значимости факторов (степени
влияния на функцию), их ранжирование и исключить малозначащие факторы.
Диапазоны изменения факторов задают область
определения Y. Если принять, что каждому фактору соответствует координатная
ось, то полученное пространство называется факторным пространством. При n=2
область определения Y представляется собой прямоугольник, при n=3 - куб, при n
>3 - гиперкуб.
При выборе диапазонов изменения факторов нужно
учитывать их совместимость, т.е. контролировать, чтобы в этих диапазонах любые
сочетания факторов были бы реализуемы в опытах и не приводили бы к абсурду. Для
каждого из факторов указывают граничные значения
 , i=1,… n.
, i=1,… n.
Регрессионный анализ функции отклика
предназначен для получения ее математической модели в виде уравнения регрессии
Y=F(X1,X2,...,Xn;B1,B2,...,Bm)+e
где В1, …, Вm - некоторые коэффициенты; е -
погрешность.
Среди основных методов планирования, применяемых
на разных этапах исследования, используют:
планирование отсеивающего эксперимента, основное
значение которого выделение из всей совокупности факторов группы существенных
факторов, подлежащих дальнейшему детальному изучению;
планирование эксперимента для дисперсионного
анализа, т.е. составление планов для объектов с качественными факторами;
планирование регрессионного эксперимента,
позволяющего получать регрессионные модели (полиномиальные и иные);
планирование экстремального эксперимента, в
котором главная задача - экспериментальная оптимизация объекта исследования;
планирование при изучении динамических процессов
и т.д.
Инициатором применения планирования эксперимента
является Рональд А. Фишер, другой автор известных первых работ - Френк Йетс.
Далее идеи планирования эксперимента формировались в трудах Дж. Бокса, Дж.
Кифера. В нашей стране - в трудах Г.К. Круга, Е.В. Маркова и др.
В настоящее время методы планирования
эксперимента заложены в специализированных пакетах, широко представленных на
рынке программных продуктов, например: StatGrapfics, Statistica, SPSS, SYSTAT и
др.
1.3 Представление результатов экспериментов
При использовании методов планирования
эксперимента необходимо найти ответы на 4 вопроса:
Какие сочетания факторов и сколько таких
сочетаний необходимо взять для определения функции отклика?
Как найти коэффициенты В0, В1, …, Bm?
Как оценить точность представления функции
отклика?
Как использовать полученное представление для
поиска оптимальных значений Y?
Геометрическое представление функции отклика в
факторном пространстве Х1, Х2, …, Хn называется поверхностью отклика (рис. 1).
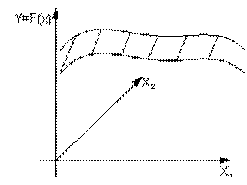
Рис. 1. Поверхность отклика
Если исследуется влияние на Y лишь одного
фактора Х1, то нахождение функции отклика - достаточно простая задача.
Задавшись несколькими значениями этого фактора, в результате опытов получаем
соответствующие значения Y и график Y =F(X) (рис. 2).

Рис. 2. Построение функции отклика одной
переменной по опытным данным
По его виду можно подобрать математическое
выражение функции отклика. Если мы не уверены, что опыты хорошо
воспроизводятся, то обычно опыты повторяют несколько раз и получают зависимость
с учетом разброса опытных данных.
Если факторов два, то необходимо провести опыты
при разных соотношениях этих факторов. Полученную функцию отклика в 3х-мерном
пространстве (рис. 1) можно анализировать, проводя ряд сечений с фиксированными
значениями одного из факторов (рис. 3). Вычлененные графики сечений можно
аппроксимировать совокупностью математических выражений.
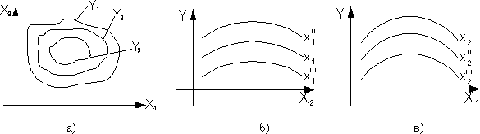
Рис. 3. Сечения поверхности отклика при
фиксированных откликах (а) и переменных (б, в)
При трех и более факторах задача становится практически
неразрешимой. Если и будут найдены решения, то использовать совокупность
выражений достаточно трудно, а часто и не реально.
.4 Применение математического планирования
эксперимента в научных исследованиях
В современной математической теории оптимального
планирования эксперимента существует 2 основных раздела:
планирование эксперимента для изучения
механизмов сложных процессов и свойств многокомпонентных систем.
планирование эксперимента для оптимизации
технологических процессов и свойств многокомпонентных систем.
Планирование эксперимента - это выбор числа
опытов и условий их проведения необходимых и достаточных для решения
поставленной задачи с требуемой точностью.
Эксперимент, который ставится для решений задач
оптимизации, называется экстремальным. Примерами задач оптимизации являются
выбор оптимального состава многокомпонентных смесей, повышение
производительности действующей установки, повышение качества продукции и
снижение затрат на её получение. Прежде чем планировать эксперимент необходимо
сформулировать цель исследования. От точной формулировки цели зависит успех
исследования. Необходимо также удостовериться, что объект исследования
соответствует предъявляемым ему требованиям. В технологическом исследовании
целью исследования при оптимизации процесса чаще всего является повышение
выхода продукта, улучшение качества, снижение себестоимости.
Эксперимент может проводиться непосредственно на
объекте или на его модели. Модель отличается от объекта не только масштабом, а
иногда природой. Если модель достаточно точно описывает объект, то эксперимент
на объекте может быть перенесён на модель. Для описания понятия «объект
исследования» можно использовать представление о кибернетической системе,
которая носит название чёрный ящик.
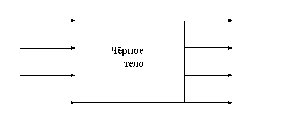
Стрелки справа изображают численные
характеристики целей исследования и называются выходными параметрами (y) или
параметрами оптимизации.
Для проведения эксперимента необходимо
воздействовать на поведение чёрного ящика. Все способы воздействия обозначаются
через «x» и называются входными параметрами или факторами. Каждый фактор может
принимать в опыте одно из нескольких значений, и такие значения называются
уровнями. Фиксированный набор уровней и факторов определяет одно из возможных состояний
чёрного ящика, одновременно они являются условиями проведения одного из
возможных опытов. Результаты эксперимента используются для получения
математической модели объекта исследования. Использование для объекта всех
возможных опытов приводит к абсурдно большим экспериментам. В связи с этим
эксперименты необходимо планировать.
Задачей планирования является выбор необходимых
для эксперимента опытов, методов математической обработки их результатов и
принятия решений. Частный случай этой задачи - планирование экстремального
эксперимента. То есть эксперимента поставленного с целью поиска оптимальных
условий функционирования объекта. Таким образом, планирование экстремального
эксперимента - это выбор количества и условий проведения опытов, минимально необходимых
для отыскания оптимальных условий. При планировании эксперимента объект
исследования должен обладать обязательными свойствами:
. управляемым
. результаты эксперимента должны быть
воспроизводимыми.
Эксперимент называется воспроизводимым, если при
фиксированных условиях опыта получается один и тот же выход в пределах заданной
относительно небольшой ошибки эксперимента (2%-5%). Эксперимент проводят при
выборе некоторых уровней для всех факторов, затем он повторяется через неравные
промежутки времени. И значения параметров оптимизации сравниваются. Разброс
этих параметров характеризует воспроизводимость результатов. Если он не
превышает заранее заданной величины, то объект удовлетворяет требованию
воспроизводимости результатов.
При планировании эксперимента активное
вмешательство предполагает процесс и возможность выбора в каждом опыте тех
факторов, которые представляют интерес. Экспериментальное исследование влияния
входных параметров (факторов) на выходные может производиться методом
пассивного или активного эксперимента. Если эксперимент сводится к получению
результатов наблюдения за поведение системы при случайных изменениях входных
параметров, то он называется пассивным. Если же при проведении эксперимента
входные параметры изменяются по заранее заданному плану, то такой эксперимент
называется активным. Объект, на котором возможен активный эксперимент,
называется управляемым. На практике не существует абсолютно управляемых
объектов. На реальный объект обычно действуют как управляемый, так и неуправляемый
факторы. Неуправляемые факторы действуют на воспроизводимость эксперимента.
Если все факторы неуправляемы, возникает задача установления связи между
параметром оптимизации и факторами по результатам наблюдений или по результатам
пассивного эксперимента. Возможна также плохая воспроизводимость изменения
факторов во времени.
1.5 Требования, предъявляемые к факторам при
планировании эксперимента
При планировании эксперимента факторы должны
быть управляемыми. Это значит, что экспериментатор, выбрав нужное значение
фактора, может его поддерживать постоянным в течение всего опыта, т.е. может
управлять фактором. Планировать эксперимент можно только в том случае, если
уровни факторов подчиняются воле экспериментатора.
Пример: Вы изучаете процесс синтеза аммиака. Колонна
синтеза установлена на открытой площадке. Является ли температура воздуха
фактором, который можно включить в планирование эксперимента?
Температура воздуха - фактор неуправляемый. Мы
еще не научились делать погоду по заказу. А в планировании могут участвовать
только те факторы, которыми можно управлять, - устанавливать и поддерживать на
выбранном уровне в течение опыта или менять по заданной программе. Температурой
окружающей среды в данном случае управлять невозможно. Ее можно только
контролировать.
Чтобы точно определить фактор, нужно указать
последовательность действий (операций), с помощью которых устанавливаются его
конкретные значения (уровни). Такое определение фактора будем называть
операциональным. Так, если фактором является давление в некотором аппарате, то
совершенно необходимо указать, в какой точке и с помощью какого прибора оно
измеряется и как оно устанавливается. Введение операционального определения
обеспечивает однозначное понимание фактора.
С операциональным определением связаны выбор
размерности фактора и точность его фиксирования.
Точность замера факторов должна быть возможно
более высокой. Степень точности определяется диапазоном изменения факторов. При
изучении процесса, который длится десятки часов, нет необходимости учитывать доли
минуты, а в быстрых процессах необходимо учитывать, быть может, доли секунды.
Факторы должны быть непосредственными
воздействиями на объект. Факторы должны быть однозначны. Трудно управлять
фактором, который, является функцией других факторов. Но в планировании могут
участвовать сложные факторы, такие, как соотношения между компонентами, их
логарифмы и т.п.
При планировании эксперимента обычно
одновременно изменяется несколько факторов. Поэтому очень важно сформулировать
требования, которые предъявляются к совокупности факторов. Прежде всего
выдвигается требование совместимости. Совместимость факторов означает, что все
их комбинации осуществимы и безопасны. Это очень важное требование.
При планировании эксперимента важна
независимость факторов, т.е. возможность установления фактора на любом уровне
вне зависимости от уровней других факторов. Если это условие невыполнимо, то
невозможно планировать эксперимент.
Таким образом, установили, что факторы - это
переменные величины, соответствующие способам воздействия внешней среды на
объект.
Они определяют как сам объект, так и его
состояние. Требования к факторам: управляемость и однозначность.
Управлять фактором - это значит установить
нужное значение и поддерживать его постоянным в течение опыта или менять по заданной
программе. В этом состоит особенность «активного» эксперимента. Планировать
эксперимент можно только в том случае, если уровни факторов подчиняются воле
экспериментатора.
Факторы должны непосредственно воздействовать на
объект исследования.
Требования к совокупности факторов:
совместимость и отсутствие линейной корреляции. Выбранное множество факторов
должно быть достаточно полным. Если какой-либо существенный фактор пропущен,
это приведет к неправильному определению оптимальных условий или к большой
ошибке опыта. Факторы могут быть количественными и качественными.
.6 Ошибки опыта
Изучение всех влияющих на исследуемый объект
факторов одновременно провести невозможно, поэтому в эксперименте
рассматривается их ограниченное число. Остальные активные факторы
стабилизируются, т.е. устанавливаются на каких-то одинаковых для всех опытов
уровнях.
Некоторые факторы не могут быть обеспечены
системами стабилизации (например, погодные условия, самочувствие оператора и
т.д.), другие же стабилизируются с какой-то погрешностью (например, содержание
какого-либо компонента в среде зависит от ошибки при взятии навески и
приготовления раствора). Учитывая также, что измерение параметра у
осуществляется прибором, обладающим какой-то погрешностью, зависящей от класса
точности прибора, можно прийти к выводу, что результаты повторностей одного и
того же опыта ук будут приближенными и должны отличаться один от другого и от
истинного значения выхода процесса. Неконтролируемое, случайное изменение и
множества других влияющих на процесс факторов вызывает случайные отклонения
измеряемой величины ук от ее истинного значения - ошибку опыта.
Каждый эксперимент содержит элемент
неопределенности вследствие ограниченности экспериментального материала.
Постановка повторных (или параллельных) опытов не дает полностью совпадающих
результатов, потому что всегда существует ошибка опыта (ошибка
воспроизводимости). Эту ошибку и нужно оценить по параллельным опытам. Для
этого опыт воспроизводится по возможности в одинаковых условиях несколько раз и
затем берется среднее арифметическое всех результатов. Среднее арифметическое у
равно сумме всех n отдельных результатов, деленной на количество параллельных
опытов n:

Отклонение результата любого опыта от среднего
арифметического можно представить как разность y2-  ,
где y2 - результат отдельного опыта. Наличие отклонения свидетельствует об
изменчивости, вариации значений повторных опытов. Для измерения этой
изменчивости чаще всего используют дисперсию.
,
где y2 - результат отдельного опыта. Наличие отклонения свидетельствует об
изменчивости, вариации значений повторных опытов. Для измерения этой
изменчивости чаще всего используют дисперсию.
Дисперсией называется среднее значение квадрата
отклонений величины от ее среднего значения. Дисперсия обозначается s2 и
выражается формулой:
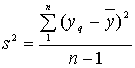
где (n-1) - число степеней свободы, равное
количеству опытов минус единица. Одна степень свободы использована для
вычисления среднего.
Корень квадратный из дисперсии, взятый с
положительным знаком, называется средним квадратическим отклонением, стандартом
или квадратичной ошибкой:

Ошибка опыта является суммарной величиной,
результатом многих ошибок: ошибок измерений факторов, ошибок измерений
параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь,
разделить на составляющие.
Все ошибки принято разделять на два класса:
систематические и случайные (рисунок 1).
Систематические ошибки порождаются причинами,
действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно
изучить и определить количественно. Систематическая ошибка - это ошибка,
которая остаётся постоянно или закономерно изменяется при повторных измерениях
одной и той же величины. Эти ошибки появляются вследствие неисправности
приборов, неточности метода измерения, какого либо упущения экспериментатора,
либо использования для вычисления неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка всех измерительных приборов и
безусловное выполнение выработанных практикой правил экспериментальных работ.
Если систематические ошибки вызваны известными причинами, то их можно
определить. Подобные погрешности можно устранить введением поправок.
Систематические ошибки находят, калибруя
измерительные приборы и сопоставляя опытные данные с изменяющимися внешними
условиями (например, при градуировке термопары по реперным точкам, при
сравнении с эталонным прибором). Если систематические ошибки вызываются внешними
условиями (переменной температуры, сырья и т.д.), следует компенсировать их
влияние.
Случайными ошибками называются те, которые
появляются нерегулярно, причины, возникновения которых неизвестны и которые
невозможно учесть заранее. Случайные ошибки вызываются и объективными причинами
и субъективными. Например, несовершенством приборов, их освещением,
расположением, изменением температуры в процессе измерений, загрязнением
реактивов, изменением электрического тока в цепи. Когда случайная ошибка больше
величины погрешности прибора, необходимо многократно повторить одно и тоже
измерение. Это позволяет сделать случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше погрешности прибора, то уменьшать её нет
смысла. Такие ошибки имеют значение, которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми для измерений сделанных даже в
одинаковых условиях. Поскольку причины, приводящие к случайным ошибкам
неодинаковы в каждом эксперименте, и не могут быть учтены, поэтому исключить
случайные ошибки нельзя, можно лишь оценить их значения. При многократном
определении какого-либо показателя могут встречаться результаты, которые
значительно отличаются от других результатов той же серии. Они могут быть
следствием грубой ошибки, которая вызвана невнимательностью экспериментатора.
Систематические и случайные ошибки состоят из
множества элементарных ошибок. Для того чтобы исключать инструментальные
ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно
после опыта. Ошибки при проведении самого опыта возникают вследствие
неравномерного нагрева реакционной среды, разного способа перемешивания и т.п.
При повторении опытов такие ошибки могут вызвать
большой разброс экспериментальных результатов.
Очень важно исключить из экспериментальных
данных грубые ошибки, так называемый брак при повторных опытах. Грубые ошибки
легко обнаружить. Для выявления ошибок необходимо произвести измерения в других
условиях или повторить измерения через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность в записях, тщательность в работе и
записи результатов эксперимента. Грубая ошибка должна быть исключена из
экспериментальных данных. Для отброса ошибочных данных существуют определённые
правила.
Например, используют критерий Стьюдента t (Р;
f): Опыт считается бракованным, если экспериментальное значение критерия t по
модулю больше табличного значения t (Р; f).
2. ПОЛУЧЕНИЕ
СОВОКУПНОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН.
Для ознакомления с методикой определения основных
числовых характеристик совокупности случайных величин необходимо получить
данную совокупность. Она может быть получена на разрывной машине (прочность,
удлинение), весах (масса отрезков пряжи, полосок ткани или трикотажа),
круткомере (крутка пряжи) и других приборах. Рассчитаем работу по данным из
приложения А. Исходные данные представлены в таблице 1. Где 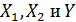 -
соответственно удлинение, масса и прочность образца;
-
соответственно удлинение, масса и прочность образца; 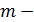 количество
испытаний.
количество
испытаний.
Таблица 1 - исходные данные для обработки
результатов.
|
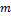
|

|
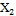
|
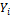
|
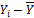
|
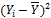
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
835
|
9,8
|
101
|
3
|
9
|
|
2
|
1075
|
14,8
|
107
|
-3
|
9
|
|
3
|
1195
|
13,7
|
101
|
3
|
9
|
|
4
|
1015
|
13,0
|
107
|
-3
|
9
|
|
5
|
1025
|
13,9
|
113
|
-9
|
81
|
|
6
|
1035
|
15,6
|
101
|
3
|
9
|
|
7
|
995
|
13,9
|
107
|
-3
|
9
|
|
8
|
885
|
12,2
|
95
|
9
|
81
|
|
9
|
965
|
11,6
|
88
|
16
|
256
|
|
10
|
1175
|
15,2
|
120
|
-16
|
256
|
|
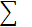
|
10200
|
133,7
|
1040
|
0
|
728
|
|
Среднее
значение
|
1020
|
13,2
|
104
|
-
|
132,4
|
2.1 Расчёт
оценок математического ожидания, дисперсии и среднеквадратического отклонения
Математическое ожидание Ỹ (среднее
значение) определяет центр распределения случайных величин, около которого
группируется большая их часть. Абсолютными характеристиками рассеяния случайной
величины Y около центра распределения Ỹ является дисперсия S2 {Y} и
среднее квадратическое отклонение S{Y}.
Расчет оценок математического ожидания,
дисперсии и среднего квадратического отклонения для анализируемой выборки
осуществляется по следующим формулам:
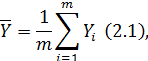

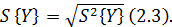
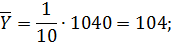
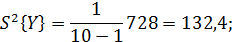
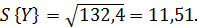
2.2 Исключение
резко выделяющихся экспериментальных даннях
Совокупность полученных экспериментальных данных
часто имеет значения, резко выделяющиеся относительно других, что приводит к
постановке вопроса об их исключении из дальнейшей обработки. Причиной появления
таких данных может быть изменение условий проведения опыта в момент наблюдения,
ошибочная регистрация параметра (по вине оператора) и т.п. Независимо от причин
получения резко выделяющихся данных они могут существенно исказить числовые
характеристики. С другой стороны, при необоснованном исключении таких данных
числовые характеристики также будут искажены.
Самый надежный метод определения возможности
исключения резко выделяющихся данных - это анализ условий, при которых они были
получены. Если условия существенно отличаются от стандартных (или установленных
по плану эксперимента), то данные необходимо исключить из дальнейшей обработки
независимо от их величины. Если определение существенности изменения условий
эксперимента невозможно или представляет большие трудности, то используют
статистический метод исключения данных, сущность которого заключается в
следующем:
находят в совокупности максимальную и
минимальную величины и определяют расчетные значения критерия Смирнова-Граббса:
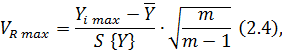



сравниваем полученные значения с табличным VТ ,
если VR max или VR min больше VТ, то соответствующее значение Yi необходимо
исключить из совокупности 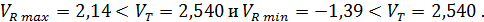 Таким образом
полученные значения не исключаем.
Таким образом
полученные значения не исключаем.
2.2 Расчет
относительных характеристик рассеяния случайной величины
Относительной характеристикой рассеяния
случайной величины является коэффициент вариации СV{Y}:
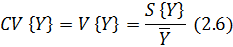
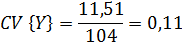
Если данная величина выражается в процентах, то
она называется квадратической неровнотой C{Y}:


2.4 Определение
ошибки среднего и границ доверительного интервала
В результате измерений исследуемого параметра
возникают ошибки (погрешности измерения), для описания которых введена оценка
абсолютной εi, погрешности.
Абсолютная и относительная доверительные ошибки, допущенные при оценке
математического ожидания, определяются по формулам:
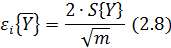

где 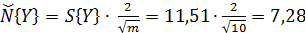


Двусторонним доверительным интервалом называется
интервал, который покрывает неизвестный параметр распределения с заданной
доверительной вероятностью РD:
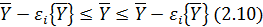
В практике текстильных исследований при
статистической обработке обычно принимают РD = 0,95 . Величина, равная α
= 1−РD, называется уровнем значимости и иногда
выражается в процентах.
.5 Доверительный
объем испытаний
Анализируя точность оценки среднего значения,
можно решить, является ли она достаточной или требуется увеличение объема
измерений. Задаваясь требуемой величиной относительной ошибки (например, δ
= 3%) и
приняв квадратическую неровноту по данным предыдущих опытов или другой
априорной информации, можно рассчитать доверительный объем выборки:
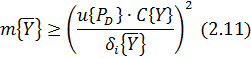
где u{PD} − квантиль нормального
распределения случайной величины (при РD = 0,954 и u{РD} = 2).

3. ПОСТРОЕНИЕ
ГИСТОГРАММЫ И ПОЛИГОНА ИМПЕРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ.
Исходные данные представлены в таблице 1.
Таблица 1 - Исходные данные для расчёта на
примере измерений высоты початка кукурузы от земли.
|
№
п/п
|
Значение
|
№
п/п
|
Значение
|
№
п/п
|
Значение
|
№
п/п
|
Значение
|
№
п/п
|
Значение
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
67
|
21
|
55
|
41
|
74
|
61
|
79
|
81
|
59
|
|
2
|
80
|
22
|
54
|
42
|
77
|
62
|
72
|
82
|
81
|
|
3
|
80
|
23
|
60
|
43
|
100
|
63
|
88
|
83
|
93
|
|
4
|
68
|
24
|
63
|
44
|
103
|
64
|
89
|
84
|
90
|
|
5
|
69
|
25
|
78
|
45
|
69
|
65
|
94
|
85
|
79
|
|
6
|
74
|
26
|
87
|
72
|
66
|
82
|
86
|
83
|
|
7
|
72
|
27
|
94
|
47
|
74
|
67
|
80
|
87
|
91
|
|
8
|
69
|
28
|
91
|
48
|
66
|
68
|
81
|
88
|
87
|
|
9
|
80
|
29
|
88
|
49
|
67
|
69
|
77
|
89
|
89
|
|
10
|
79
|
30
|
90
|
50
|
72
|
70
|
80
|
90
|
94
|
|
11
|
90
|
31
|
79
|
51
|
72
|
71
|
79
|
91
|
92
|
|
12
|
109
|
32
|
84
|
52
|
68
|
72
|
78
|
92
|
91
|
|
13
|
99
|
33
|
84
|
53
|
80
|
73
|
83
|
93
|
76
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
14
|
100
|
34
|
108
|
54
|
81
|
74
|
92
|
94
|
79
|
|
15
|
115
|
35
|
83
|
55
|
84
|
75
|
93
|
95
|
73
|
|
16
|
68
|
36
|
84
|
56
|
77
|
76
|
81
|
96
|
84
|
|
17
|
70
|
37
|
99
|
57
|
79
|
77
|
82
|
97
|
79
|
|
18
|
72
|
38
|
98
|
58
|
81
|
78
|
86
|
98
|
84
|
|
19
|
73
|
39
|
102
|
59
|
84
|
79
|
89
|
99
|
79
|
|
20
|
70
|
40
|
101
|
60
|
76
|
80
|
93
|
100
|
84
|
Определим размах варьирования результатов
измерения по следующему выражению:
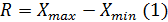
где R-размах варьирования в , см.
Хmax,min-максимальное и минимальное значение
высоты прикреплённого початка.
R= 115-54=61 см.
Определяем интервал групп из значения:

Где K- число групп ( К )
)
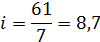
Далее построим таблицу 2 и в ней произведём
дальнейший расчёт.
Таблица 2 -Расчёт квадратов суммы отклонений.
|
Интервал
|
Частота
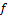
|
Среднее
значение по группе 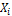
|
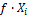
|

|
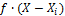
|
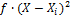
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
54-61,7
|
4
|
57,85
|
231,4
|
24,44
|
97,76
|
2389,25
|
|
62,7-70,4
|
12
|
66,55
|
798,6
|
15,71
|
189
|
2961,65
|
|
71,4-79,1
|
27
|
75,25
|
2031,75
|
7,01
|
189,27
|
1326,78
|
|
80,1-87,8
|
29
|
83,95
|
2434,55
|
-1,69
|
-49,01
|
82,82
|
|
88,8-96,5
|
16
|
92,65
|
1482,4
|
-10,39
|
-166,24
|
1727,23
|
|
97,5-105,2
|
9
|
101,35
|
912,15
|
-19,09
|
-171,81
|
3279,85
|
|
106,2-113,9
|
2
|
110,05
|
220,1
|
-27,79
|
-55,58
|
1544,57
|
|
114,9-115
|
1
|
114,95
|
114,95
|
-32,69
|
-32,69
|
1068,63
|
|
Итог
|
100
|
|
8225,9
|
|
0,7
|
14380,78
|
Находим текущее значение высоты прикрепления
початка, в см.
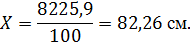
Определяем среднеквадратическое отклонение из
выражения:
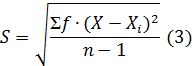
где S- стандартное отклонение, X и Xi- текущее и
среднее значение высоты прикрепления початка, см, n-объём выборки.
Подставив данные из таблицы 2 в выражение (3)
получим:
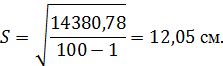
Определяем ошибку выборочной средней из
выражения:

Из выражения (4) находим:
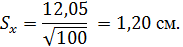
Определяем коэффициент вариации:
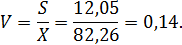
Находим относительную ошибку по формуле:

Построение гистограммы и полигона и
эмпирического распределения.
Гистограмма представлена на рисунке 1.
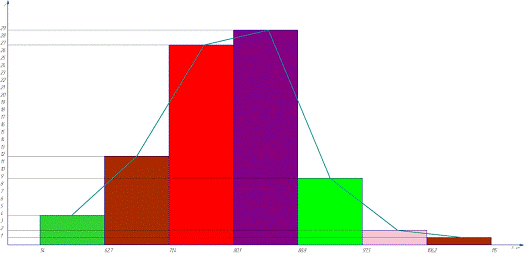
Рисунок 1- Гистограмма и полигон эмпирического
распределения.
4. ПРОВЕРКА ОСНОВНОЙ
ГИПОТЕЗЫ
Исходные данные для расчёта представлены в
таблице 3.
Таблица 3 - Исходные данные к расчёту критерий
Пирсона
|
Интервал
группировки
|
Фактическая
частота
|
Теоретические
значения fpi попадающий в соответствующий интервал
|
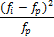
|
|
1
|
2
|
3
|
4
|
|
54-61,7
|
4
|
3,5
|
0,28
|
|
62,7-70,4
|
12
|
11,09
|
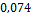
|
|
71,4-79,1
|
27
|
21,33
|
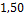
|
|
80,1-87,8
|
29
|
24,47
|
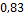
|
|
88,8-96,5
|
16
|
13,56
|
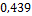
|
|
97,5-105,2
|
9
|
7,51
|
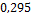
|
|
106,2-113,9
|
2
|
1,95
|
0,28
|
|
114,9-115
|
1
|
0,01
|
|
|
Итог
|
100
|
|
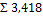
|
Основной называют гипотезу об отсутствии
реального различия между двумя сравниваемыми вариационными рядами: эмпирическим
и теоретическим или двумя эмпирическими.
Для оценки соответствия эмпирического
распределения теоретическому используют критерий согласия (подобия) 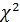 ,
закон распределения которого открыл К. Пирсон. Кривая распределения, полученная
из функции
,
закон распределения которого открыл К. Пирсон. Кривая распределения, полученная
из функции 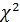 имеет вид:
имеет вид: 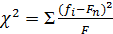 ,
где -фактическая частота численности объектов выборки; F- гипотетическая
(теоретическая) частота объектов выборки).
,
где -фактическая частота численности объектов выборки; F- гипотетическая
(теоретическая) частота объектов выборки).
Гипотеза опровергается, если  и
не опровергается, если
и
не опровергается, если 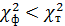 .
.
Фактическая частота численности объектов в
определённой части известна из эмпирического распределения. Гипотеза о
нормальном характере распределения частот позволяет вычислить теоретические их
значения для вероятности Pi попасть в i-интервал.
Для этого используют следующие выражение
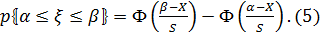
где 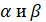 -
концы рассматриваемого интервала; и S- параметры распределения, среднее и
стандартное отклонение соответственно.
-
концы рассматриваемого интервала; и S- параметры распределения, среднее и
стандартное отклонение соответственно.
В третьей графе приведены теоретические значения
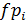 ,
попадающие в соответствующий интервал. Вероятности вычислим в предложении что
генеральная совокупность имеет нормальное распределение с параметрами X=82,26
см и S= 12,05 см. Вероятность
,
попадающие в соответствующий интервал. Вероятности вычислим в предложении что
генеральная совокупность имеет нормальное распределение с параметрами X=82,26
см и S= 12,05 см. Вероятность  определяем по
формуле (5). Значение функции Лапласа Ф(Хi) принимаем по таблице 4 из
приложения.
определяем по
формуле (5). Значение функции Лапласа Ф(Хi) принимаем по таблице 4 из
приложения.
Тогда
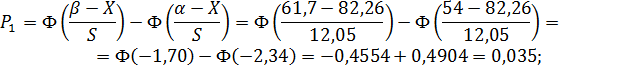
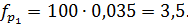
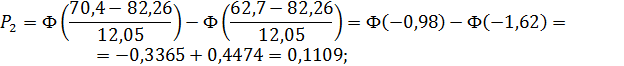
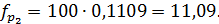
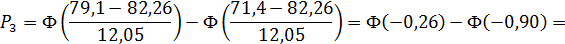
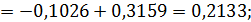
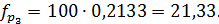
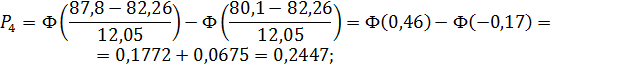
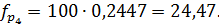
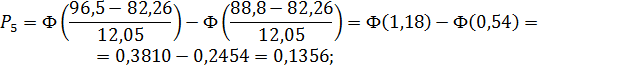
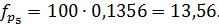
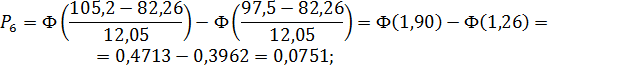

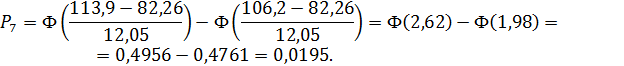
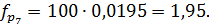
Для того чтобы соблюсти условие  ,
объединим в один 1,7,8 интервалы.
,
объединим в один 1,7,8 интервалы.
В этом случае после подстановки конкретных
значений в выражение
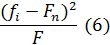
Получим,
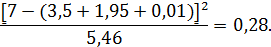
Для второго интервала:
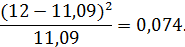
Для третьего интервала:
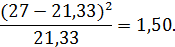
Для четвёртого интервала:
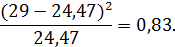
Для пятого интервала:
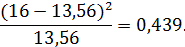
Для шестого интервала:
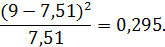
Суммируем все значения и определяем 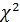
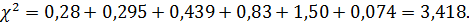
При числе степеней свободы  ,
имеем
,
имеем  и
табличное значение критерия Пирсона
и
табличное значение критерия Пирсона  (см.
таблицу 3 приложения).
(см.
таблицу 3 приложения).
Отсюда
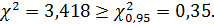
Следовательно, по критерию Пирсона следует
отклонить основную гипотезу.
Статические характеристики выборочной
совокупности являются приближёнными оценками независимых параметров генеральной
совокупности. Оценка может быть представлена одним числом, точкой (точечная оценка)
или некоторым интервалом (интервальная оценка), в которой с определённой
вероятностью может находиться искомый параметр.
Обозначив ошибку выборочной средней как S,
точечную оценку генеральной средней можно записать в виде 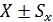 .
.
Интервальной называют оценку, которая
характеризуется двумя числами - концами интервала, покрывающего оцениваемый
параметр. Доверительным называют такой интервал, который с заданной
вероятностью покрывает оцениваемый параметр. Центр такого интервала -
выборочная оценка точки, а пределы, или доверительные границы интервала
определяются средней ошибкой и уровнем вероятности. Интервальная оценка
является дальнейшим развитием точечной оценки.
В общем виде доверительный интервал для
генеральной средней записывается как
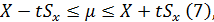
или в более краткой форме
 .
.
Здесь 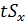 -
предельная ошибка выборочной средней при данном числе степеней свободы и
принятом уровнем значимости, а
-
предельная ошибка выборочной средней при данном числе степеней свободы и
принятом уровнем значимости, а 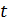 - критерий
Стьюдента при выбранном уровне зависимости и числе степеней свободы.
- критерий
Стьюдента при выбранном уровне зависимости и числе степеней свободы.
Исходные данные для расчёта представлены в
таблице 4.
Таблица 4 - исходные данные
|
n
|
X
|
Sx
|
n1;2
|
X1
|
Sx1
|
X2
|
Sx2
|
|
6
|
11,8%
|
0,40%
|
13
|
17
|
0,6
|
19
|
0,8
|
Пример №1: при числе степеней свободы равном
n-1=3-1=2 имеем t05=4,30 и t01=9,93.
Найдём доверительные интервалы 95%-ный и 99%-ный
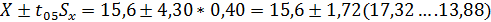
 .
.
Такая запись говорит о том, что с вероятностью
95% генеральная средняя содержания белка в зерне заключена в интервале 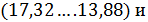 с
вероятностью 99% она находиться в интервале
с
вероятностью 99% она находиться в интервале 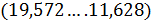 .
Вероятность выйти за эти интервалы в первом случае составляет 5%, а во втором
-1%(уровень значимости).
.
Вероятность выйти за эти интервалы в первом случае составляет 5%, а во втором
-1%(уровень значимости).
Крайние точки начало и конец называют
доверительными границами.
Интервальную оценку параметров распределения
можно использовать для статической проверки гипотез при сравнении выборочных
средних.
Пример №2: пусть, например, при числе
повторностей 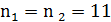
полученные средние их ошибки 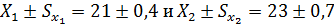 .
.
Необходимо определить, существенно ли
различаются эти выборочные средние при 95%-ном уровне вероятности или 5%-ном
уровне значимости т.е проверить нулевую гипотезу Н0: 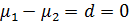 .
Для 11-1=10 степеней свободы имеем
.
Для 11-1=10 степеней свободы имеем  и
95%-ные доверительные интервалы равны:
и
95%-ные доверительные интервалы равны:
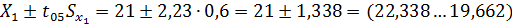
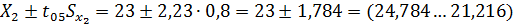
Доверительные интервалы для генеральных средних
перекрывают друг друга и следовательно, разность между выборочными средними  нельзя
переносить на генеральные средние
нельзя
переносить на генеральные средние  ,
так как она может быть равна нулю. Поэтому нулевая гипотеза не отвергается.
,
так как она может быть равна нулю. Поэтому нулевая гипотеза не отвергается.
Величину, указывающую границу случайным
предельным отклонением называют наименьшей существенной разностью. Её
сокращённо обозначают НСР и определяют по отношению

Здесь t определяется при 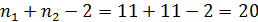 степеней
свободы.
степеней
свободы.
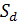 - ошибка разности
средних. В теории статически доказывается, что ошибка разности или суммы
независимых средних арифметических выборок при одинаковом числе наблюдений
- ошибка разности
средних. В теории статически доказывается, что ошибка разности или суммы
независимых средних арифметических выборок при одинаковом числе наблюдений 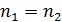 определяется
соотношением
определяется
соотношением

Если фактическая разность между выборочными
средними больше НСР
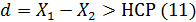 ,
,
то гипотеза об отсутствии разницы отвергается и
доказывается существенность разности.
Если выполняется условие
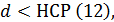
То нулевая гипотеза не отвергается и разность
между выборочными средними статически не доказывается.
Для рассмотренного выше примера имеем:
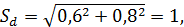
При  степеней
свободы критерий Стьюдента при 5% ном и 1% ном уровнях значимости
соответственно равны
степеней
свободы критерий Стьюдента при 5% ном и 1% ном уровнях значимости
соответственно равны
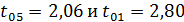
Отсюда 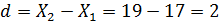
Величину НСР определяем из выражения (9)

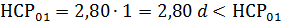
Следовательно, разность между средними при 5%ном
уровне значимости по условию (11) гипотеза об отсутствии разницы отвергается, а
при 1%ном уровне значимости не существенна.
Другим способом оценки существенности различий
между Х1 и Х2 служит отношение разности к её ошибке. Это отношение получило
название критерия существенности разности.

Если  ,
то различия находятся в пределах случайных колебаний(различия между средними не
доказывается), а если
,
то различия находятся в пределах случайных колебаний(различия между средними не
доказывается), а если 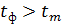 - нулевая гипотеза
опровергается.
- нулевая гипотеза
опровергается.
В нашем случае
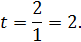
Таким образом имеем 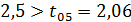 и
и

Следовательно, разность между Х1 и Х2 находится
в пределах случайных колебаний для 5%ного уровня значимости, а для 1%ного уровня
значимости она не существенна.
6. ОДНОФАКТОРНЫЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ.
Исходные данные представлены в таблице 5.
Таблица 5 - исходные данные для расчёта.
|
№
варианта
|
Марка
комбайна
|
Дробление
зерна в % повторностей
|
|
2
|
СК-5М1
|
7
|
11
|
9
|
9
|
|
ДОН
1500
|
5
|
7
|
3
|
5
|
Сущность дисперсного анализа является
расчленение общей суммы квадратов отклонений и общего числа степеней свободы на
части - компоненты, соответствующая структуре эксперимента и оценка значимости
действия и взаимодействия изучаемых факторов по F - критерию.
Дисперсия - это частное от деления суммы
квадратов отклонений текущих значений от среднего 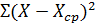 на
число степеней свободы. Число степеней свободы каждой дисперсии равно
количеству всех измерений без единицы ( на каждую дисперсию наложена одна
связь).
на
число степеней свободы. Число степеней свободы каждой дисперсии равно
количеству всех измерений без единицы ( на каждую дисперсию наложена одна
связь).
Для определения суммы квадратов отклонений
используется следующие выражение
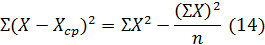
Вторая часть этой формулы сильно облегчает
работу по вычислению дисперсии с многозначными членами.
Расчёт проведём для однофакторного опыта, в
котором сравниваются два варианта. Общее число которых равно восьми - по четыре
в каждом варианте.
Пример 1. Было определенно дробление зерна
кукурузы при уборке её комбайнами СК-5М1 «Нива» и ДОН-1500, соответственно с
кукурузоуборочными приставками ППК-4 и КДМ-8. Независимость выборок
обеспечивалась отбором проб в случайном порядке.
Полученные опытные данные представлены в таблице
6.
Таблица 6 - Дробление зерна кукурузы.
|
Варианты
|
Дробление,
%
|
Сумма
по вариантам, V
|
Среднее
по вариантам
|
|
СК-5М1
|
7,11,9,9
|
36
|
9
|
|
ДОН
1500
|
5,7,3,5
|
20
|
5
|
|
Общая
сумма 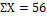
|
Общие
среднее Х=7
|
В этом эксперименте возможна лишь одна
группировка исходных дат- по вариантам. Находим суммы и средние по вариантам,
общую сумму и общую среднюю по опыту. Варьирование дробления, то есть
отклонение его общей средней 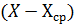 обусловлена здесь
двумя компонентами - эффектами вариантов и случайным варьированием. Других
источников вариации дробления зерна в опыте нет.
обусловлена здесь
двумя компонентами - эффектами вариантов и случайным варьированием. Других
источников вариации дробления зерна в опыте нет.
Следовательно, общие варьирование CY, которое
измеряется суммой квадратов отклонений дробления от общей средней  состоит
из варьирования вариантов Сv и случайного варьирования Сz.
состоит
из варьирования вариантов Сv и случайного варьирования Сz.
Модель дисперсионного анализа данных этого опыта
имеет вид
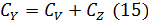
Определяем общую сумму квадратов отклонений
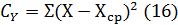
По формуле (16) определим
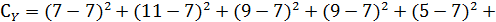
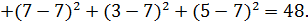
Эту же величину мы получим, если воспользуемся
правой частью выражения (14)

Второй член этого выражения носит название
корректирующего фактора С.
Следовательно выражение (17) примет вид

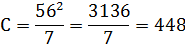
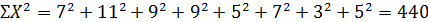
Подставим полученные данные в выражение (18)
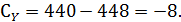
Общие число степеней свободы для этой
группировки составляет
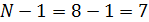
Для определения суммы квадратов отклонений по
вариантов вместо каждой даты Х в таблицу 6 подставим среднее соответствующие
вариантов.
Таблица 7 - Дробление зерна кукурузы.
|
Варианты
|
Дробление,
%
|
Сумма
по вариантам, V
|
Среднее
по вариантам
|
|
СК-5М1
|
9,9,9,9
|
36
|
9
|
|
ДОН
1500
|
5,5,5,5.
|
20
|
5
|
|
Общая
сумма 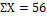
|
Общие
среднее Х=7
|
Подставляя вместо фактических данных Х средние
по вариантам ХV, мы тем самым устраняем случайную вариацию внутри вариантов
выборки.
Сумму квадратов отклонений для вариантов находим
по соотношению
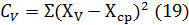
Подставим и получим
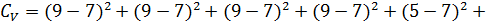
 .
.
Это же самое можно найти и менее громоздким
способом, минуя вычисления средних. Для этого достаточно использовать выражение
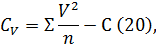
Отсюда

Разность между общим варьированием и
варьированием вариантов даёт сумму квадратов отклонений для ошибки
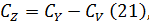

Общие число степеней свободы 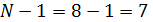 также
расчленяется на две части:
также
расчленяется на две части:
Степени свободы для вариантов
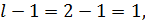
Степени свободы для ошибки
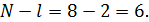
Для вычисления фактического критерия
существенности находим два средних квадрата (дисперсии).
Для вариантов
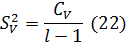

Для ошибки
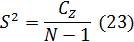

Определяем критерий существенности
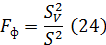
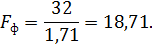
Сравним полученное значение с табличным при
5%ном уровне значимости для одной степени свободы вариантов (числитель) и шести
степеней свободы ошибки (знаменатель)
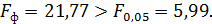
Следовательно, варианты в опыте различаются
существенно, и таким образом, нулевая гипотеза отвергается.
Определяем наименьшую существенную разность для
5%-ного уровня значимости.

Теоретическое значение критерия Стьюдента 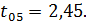
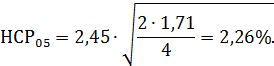
Следовательно
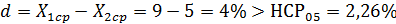
Таким образом, комбайн ДОН-1500 дробит зерно
существенно меньше, чем комбайн СК-5М-1.
7.
ТРЁХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
Исходные данные приведены в таблице 8.
Таблица 8 - Степень очистки початков и их
листьев.
|
Факторы
|
Степень
очистки початков, %
|
|
А
|
В
|
С
|
Вариант
№2
|
|
3
км/ч
|
230
|
700
мин-1
|
39,1
|
45,5
|
31,4
|
|
|
900
мин-1
|
52,6
|
55,5
|
51,1
|
|
430
|
700
мин-1
|
51,6
|
56,8
|
55,9
|
|
|
900
мин-1
|
46,9
|
48,0
|
48,7
|
|
9
км/ч
|
230
|
700
мин-1
|
33,2
|
31,2
|
31,3
|
|
|
900
мин-1
|
58,4
|
53,0
|
56,1
|
|
430
|
700
мин-1
|
42,8
|
47,1
|
43,4
|
|
|
900
мин-1
|
60,1
|
54,5
|
60,0
|
Многофакторный дисперсионный комплекс - это
совокупность исходных наблюдений (дат), позволяющих статически оценить действие
и взаимодействие нескольких изучаемых факторов на изменчивость результативного
признака.
Статическую обработку данных в этом случае
проводят в следующей последовательности:
Заносят исходные данные в таблицу, определяют
сумму и средние.
Вычисляют суммы квадратов для общего
варьирования CY, варьирование повторений Cp, вариантов Cv, и остатка Cz, т.е
обрабатывают данные, так же как и результаты однофакторного опыта.
Общие варьирование вариантов Cv, разлагают на компоненты
- главные эффекты изучаемых факторов и их взаимодействия.
Составляют таблицу дисперсионного анализа и
проверяют нулевую гипотезу о существенности действий и взаимодействия факторов
по F- критерию.
В таблице 9 определяем суммы и средние.
Таблица 9 - Влияние изучаемых факторов на
степень очистки початков и обёрточных листьев, %
|
Факторы
|
Степень
очистки початков, %
|
Суммы
V
|
Средние
|
|
А
|
В
|
С
|
Повторения
|
|
|
|
3
км/ч
|
230
|
700
мин-1
|
39,1
|
45,5
|
31,4
|
116
|
38,7
|
|
|
900
мин-1
|
52,6
|
55,5
|
51,1
|
159,2
|
53,1
|
|
430
|
700
мин-1
|
51,6
|
56,8
|
55,9
|
164,3
|
54,8
|
|
|
900
мин-1
|
46,9
|
48,0
|
48,7
|
143,6
|
47,9
|
|
9
км/ч
|
230
|
700
мин-1
|
33,2
|
31,2
|
31,3
|
95,7
|
31,9
|
|
|
900
мин-1
|
58,4
|
53,0
|
56,1
|
167,5
|
55,8
|
|
430
|
700
мин-1
|
42,8
|
47,1
|
43,4
|
133,3
|
44,4
|
|
|
900
мин-1
|
60,1
|
54,5
|
60,0
|
174,6
|
58,2
|
|
Суммы
P
|
384,7
|
391,6
|
377,9
|
1154,2
|
X=48,1
|
Правильность вычисления проверим по соотношению
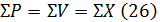
Далее рассчитываем суммы квадратов отклонений
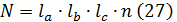

Число степеней свободы

Корректирующий фактор

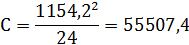
Общая сумма квадратов
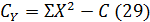

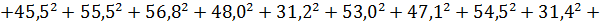

Число степеней свободы 
Сумма квадратов для повторений
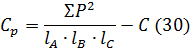

Число степеней свободы 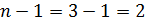 .
.
Суммы квадратов для вариантов


Число степеней свободы 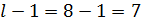
Сумма квадратов отклонений для остатка
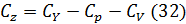
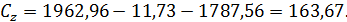
Число степеней свободы 23-(2+3)=14.
Следующий этап - определение сумм квадратов АВ,
АС, ВС, АВС. Для этого на основании таблицы 10 составим вспомогательную таблицу
11, в которую из таблицы 9 выпишем суммы по вариантам и определим суммы сумм
для главных эффектов и взаимодействий, исключая действия разных факторов.
|
Суммы
по вариантам
|
Суммы
сумм по факторам и взаимодействиям
|
|
А
|
В
|
С
|
А
|
В
|
АВ
|
АС
|
ВС
|
|
|
0
|
1
|
|
|
|
|
|
|
0
|
0
|
Х1
|
Х2
|
А0
Х1+Х2+ +Х3+Х4
|
В0
Х1+Х2+ +Х5+Х6
|
А0С0
Х1+Х3
|
В0С0
Х1+Х5
|
|
1
|
Х3
|
Х4
|
|
|
А0В1
Х3+Х4
|
А0С1
Х2+Х4
|
В0С0
Х2+Х6
|
|
1
|
0
|
Х5
|
Х6
|
А1
Х5+Х6+ +Х7+Х8
|
В1
Х3+Х4+ +Х7+Х8
|
А1В0
Х5+Х6
|
А1С0
Х5+Х7
|
В1С0
Х3+Х7
|
|
1
|
Х7
|
Х8
|
|
|
А1В1
Х7+Х8
|
А1С1
Х6+Х8
|
В1С1
Х4+Х8
|
|
Суммы
сумм С
|
С0
Х1+Х3 +Х5+Х7
|
С1
Х2+Х4 +Х6+Х8
|
-
|
-
|
-
|
-
|
-
|
|
 (проверка) (проверка)
|
|
С0+С1
|
А0+А1
|
В0+В1
|
А0В0+А0В1
+А1В0+А1В1
|
А0С0+А0С1
+А1С0+А1С1
|
А0В0+А0В1
+А1В0+А1В1
|
|
|

|
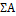
|

|
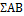
|
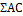
|
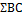
|
Таблица 9 - расчётные формулы для определения
главных эффектов и взаимодействий
Таблица 10 - Определение главных эффектов и
взаимодействий
|
Суммы
по вариантам
|
Суммы
сумм по факторам и взаимодействиям
|
|
А
|
В
|
С
|
А
|
В
|
АВ
|
АС
|
ВС
|
|
|
0
|
1
|
|
|
|
|
|
|
0
|
0
|
103,2
|
162,1
|
А0
587,9
|
В0
539,6
|
А0В0
265,3
|
А0С0
275
|
В0С0
202,6
|
|
1
|
171,8
|
150,8
|
|
|
А0В1
322,6
|
А0С1
312,9
|
В0С0
337
|
|
1
|
0
|
99,4
|
174,9
|
А1
592,3
|
В1
640,6
|
А1В0
274,3
|
А1С0
239
|
В1С0
311,4
|
|
1
|
139,6
|
178,4
|
|
|
А1В1
318
|
А1С1
353,3
|
В1С1
329,2
|
|
Суммы
сумм С
|
С0
514
|
С1
666,2
|
-
|
-
|
-
|
-
|
-
|
|
 (проверка) (проверка)
|
|
С0+С1
1180,2
|
А0+А1
1180,2
|
В0+В1
1180,2
|
1180,2
|
1180,2
|
1180,2
|
|
|

|
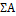
|

|
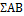
|
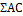
|
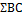
|
Вычисляем суммы квадратов отклонений для
факторов А, В, С (главных эффектов) и парных взаимодействий АВ, АС, ВС.

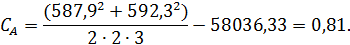
при  степеней
свободы.
степеней
свободы.
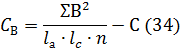
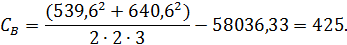
при  степеней
свободы.
степеней
свободы.
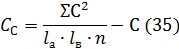
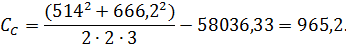
при  степеней
свободы.
степеней
свободы.
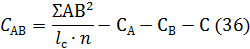
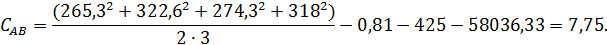
при  степеней
свободы.
степеней
свободы.
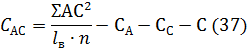

при 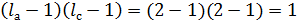 степеней
свободы.
степеней
свободы.
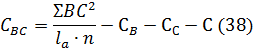
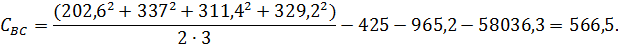
при  степеней
свободы.
степеней
свободы.
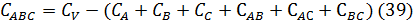
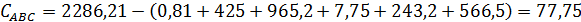
при одной степени свободы.
Теоретическое значение F-критерия при 5%-ном
уровне значимости, одной степени свободы для главных эффектов и взаимодействий,
14 степеней свободы для остатка (ошибки) равно 4,60.
Результаты расчётов сводим в таблицу 11.
Таблица 11 Результаты дисперсионного анализа
|
Дисперсия
|
Сумма
квадратов
|
Степени
свободы
|
Средний
квадрат
|
FФ
|
F05
|
|
Общая
|

|
23
|
-
|
-
|
-
|
|
Повторений
|
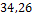
|
2
|
-
|
-
|
-
|
|
Скорости
А
|
0,81
|
1
|
0,81
|
|
4,60
|
|
Угла
В
|
425
|
1
|
425
|
|
4,60
|
|
Частоты
вращения С
|
965,2
|
1
|
965,2
|
|
4,60
|
|
Взаимодействие
АВ
|
7,75
|
1
|
7,75
|
|
4,60
|
|
Взаимодействие
АС
|
243,2
|
1
|
243,2
|
|
4,60
|
|
Взаимодействие
ВС
|
566,5
|
1
|
566,5
|
|
4,60
|
|
Взаимодействие
АВС
|
77,75
|
1
|
77,75
|
|
4,60
|
|
Остаток
(ошибка)
|
91,92
|
14
|
6,5
|
-
|
-
|
Определим наименьшую существенную разность.
Значений t-критерия при 5%-ном уровне значимости и 14 степенях свободы ошибки
составит 2,15 (таблица 1 приложения)
Для частных различий
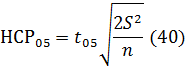

Для главных эффектов
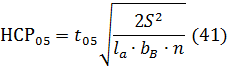
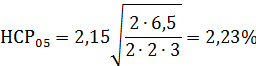
Для парных взаимодействий


Из сравнения дисперсий следует (по таблице 4 при
условии  ,
что существенно влияют на степень очистки початков: угол наклона русел; частота
вращения вальцов; взаимодействие скорости и частоты, угла и частоты.
,
что существенно влияют на степень очистки початков: угол наклона русел; частота
вращения вальцов; взаимодействие скорости и частоты, угла и частоты.
Влияние факторов
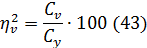
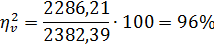
Влияние повторений
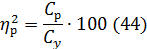
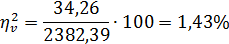
Влияние случайных факторов
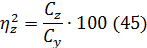

8.
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
Под линейной (прямолинейной) корреляционной
зависимостью между двумя признаками X и Y понимают такую зависимость, которая
носит линейный характер и выражается уравнением прямой линии Y=a+bX.
Это уравнение называется уравнением регрессии X
и Y, а соответствующая ему прямая линия - выборочной линией регрессии X на Y.
Исходные данные представлены в таблице 12.
Таблица 12 - Исходные данные
|
№
пары
|
Пример
№1
|
Пример
№2
|
|
Относительная
Влажность почвы Х, %
|
Липкость
почвы Y, г/см3
|
Концентрация
Аммиака Х, кг На 100 м3
|
Потери
Y, %
|
|
1
|
14,8
|
1
|
4
5
|
26
24
|
|
2
|
15,7
|
1,6
|
|
|
|
3
|
21,1
|
2,1
|
7
7
|
16
15
|
|
4
|
24,4
|
2,2
|
|
|
|
5
|
25,5
|
2,7
|
9
10
|
13
12
|
|
6
|
35,3
|
2,7
|
|
|
|
7
|
39,8
|
3,6
|
18
19 18
|
6
8 8
|
|
8
|
42,7
|
4,4
|
|
|
|
9
|
50,6
|
5,2
|
|
|
|
10
|
53,3
|
6,8
|
26
28 41
|
6
4 3
|
|
11
|
59,2
|
7,3
|
|
|
|
12
|
71,6
|
8,3
|
|
|
Коэффициент корреляции определяется по выражению
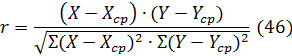
Вычислим вспомогательные величины. При расчёте
учтём, что число пар наблюдений n=12.
Для удобства расчётов занесём в таблицу 13
значение Х2.
Таблица 13 - К расчёту корреляции и регрессии Y
по X
|
Номер
пары
|
Значение
признаков
|
Х2.
|
Y2
|
XY
|
|
Х,%
|
Y,%
|
|
|
|
|
1
|
14,8
|
1
|
219,04
|
1
|
14,8
|
|
2
|
15,7
|
1,6
|
246,49
|
2,56
|
25,12
|
|
3
|
21,1
|
2,1
|
445,21
|
4,41
|
44,31
|
|
4
|
24,4
|
2,2
|
595,36
|
4,84
|
53,68
|
|
5
|
25,5
|
2,7
|
650,25
|
7,29
|
68,85
|
|
6
|
35,3
|
2,7
|
1246,09
|
7,29
|
95,31
|
|
7
|
39,8
|
3,6
|
1584,04
|
12,96
|
143,28
|
|
8
|
42,7
|
4,4
|
1823,29
|
19,36
|
187,88
|
|
9
|
50,6
|
5,2
|
2560,36
|
27,04
|
263,12
|
|
10
|
53,3
|
6,8
|
2840,89
|
46,24
|
362,44
|
|
11
|
59,2
|
7,3
|
3504,64
|
53,29
|
432,16
|
|
12
|
8,3
|
5126,56
|
68,89
|
594,28
|
|
Сумма
|
454
|
47,9
|
20842,22
|
255,17
|
2285,23
|
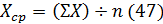
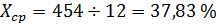
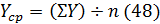

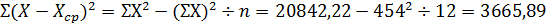
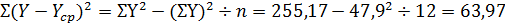
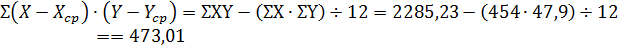
Подставим полученные данные в выражение (46) и
получим

Коэффициент регрессии определим по выражению

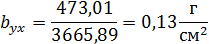
Уравнение регрессии в каноническом виде имеет
вид

Отсюда
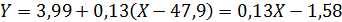
Стандартную ошибку коэффициента корреляции
определяем по формуле:
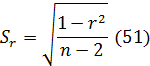
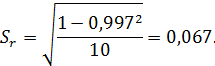
Ошибку коэффициента регрессии найдём по
выражению

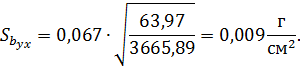
Ошибка отклонения регрессии определяется по
формуле
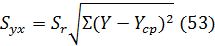
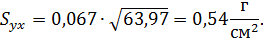
Критерий значимости рассчитывается по выражению
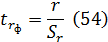

Количество степеней свободы составит
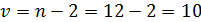
Критерий Стьюдента при 5 % -ном уровне
значимости в этом случае составит t05=2,23.
Доверительный интервал для коэффициента
корреляции

Доверительный интервал для коэффициента
регрессии
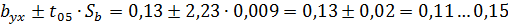
Так как  ,
то корреляционная связь существенна.
,
то корреляционная связь существенна.
По уравнению регрессии (50) рассчитываем
усреднённые теоретические значения (минимум и максимум), подставляя в уравнение
координаты X=19,9 и Х=76,6.

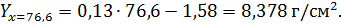
График регрессии показывает, что увеличение
влажности почвы на 1 % соответствует увеличению липкости в среднем на 0,13
г/см2 .
Коэффициент детерминации, равен квадрату
коэффициента корреляции
 .
.
Судя по коэффициенту детерминации, примерно 95 %
изменений липкости обусловлено изменениями по влажности почвы и только 5%
связано с другими факторами.
Чтобы ограничить доверительную зону необходимо
вверх и вниз от теоретической линии регрессии отклонить величину одной (68%-ая
зона) или (98%-ая зона) ошибок отклонений от регрессии Syx , то есть ± Syx или
2Syx и провести пунктирные линии.
Есть связь изучаемыми явлениями существенно
отклоняется от линейной, что легко установить по виду корреляционной решётки
или по точечному графику, то коэффициент корреляции непригоден в качестве меры
связи. Он может указать на отсутствие сопряженности там, где на лицо сильная
криволинейная зависимость. Поэтому необходим такой показатель, который измерял
бы степень криволинейной зависимости. Таким показателем является корреляционное
отношение, обозначенное греческой буквой 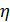 (эта).
(эта).
В таблице 14 приведены исходные данные для
расчета разобьём на группы, чтобы в каждой группе независимого признака Х было
не менее двух наблюдений. Также составим вспомогательную таблицу 15 и вычислим
суммы квадратов отклонений и средние.
Таблица 14 - Потери аммиака от испарения в
зависимости от концентрации его в поливной воде
|
Номер
пары
|
Концентрация
аммиака в поливной воде Х, кг на 100 м3
|
Потери
Y, %
|
Группа
|
|
1
2
|
4
5
|
26
24
|
1
|
|
3
4
|
7
7
|
16
15
|
2
|
|
5
6
|
9
10
|
13
12
|
3
|
|
7
8 9
|
18
19 18
|
6
8 8
|
4
|
|
10
11 12
|
26
28 41
|
6
4 3
|
5
|
Построим вспомогательную таблицу 15
Таблица 15 - Вспомогательная таблица к расчёту
корреляционного отношения.
|
№
пары
|
Х
|
Групповая
Средняя Хf
|
nx
|
Y
|
Групповая
Средняя Yx
|
Y-Yx
|
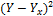
|
Y-Ycp
|
(Y-Ycp)2
|
|
1
2
|
4
5
|
4,5
|
2
|
26
24
|
25
|
1
-1
|
1
1
|
14,25
12,25
|
203,06
150,06
|
|
3
4
|
7
7
|
7
|
2
|
16
15
|
15,5
|
0,5
-0,5
|
0,25
0,25
|
4,25
3,25
|
18,06
10,56
|
|
5
6
|
9
10
|
9,5
|
2
|
13
12
|
12,5
|
0,5
-0,5
|
0,25
0,25
|
1,25
0,25
|
1,56
0,06
|
|
7
8 9
|
18
19 18
|
18,67
|
3
|
6
8 8
|
7,33
|
-1,33
0,67 0,67
|
1,76
0,44 0,44
|
-5,75
-3,75 -3,75
|
33,06
14,06 14,06
|
|
10
11 12
|
26
28 41
|
31,67
|
3
|
6
4 3
|
4,33
|
1,67
-0,33 -1,33
|
2,78
0,10 1,76
|
-5,75
-7,75 -8,75
|
33,06
60,06 76,56
|
|
-
|
192
|
14,27
|
12
|
141
|
11,75
|
0,02
|
10,28
|
0
|
614,22
|
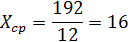

Определим квадрат корреляционного отношения
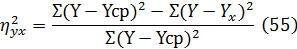

Корреляционное отношение найдём по выражению

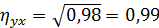
Ошибку корреляционного отношения определим по
формуле
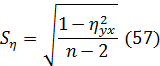

Определяем критерий существенности
корреляционного отношения
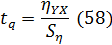
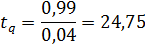
При числе степеней свободы 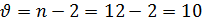 табличное
значение критерия Стьюдента составит 2,23
табличное
значение критерия Стьюдента составит 2,23
Так как 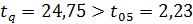 ,
то нулевая гипотеза отклоняется и считается доказанным наличие криволинейной
зависимости.
,
то нулевая гипотеза отклоняется и считается доказанным наличие криволинейной
зависимости.
Доверительный интервал для корреляционного
отношения
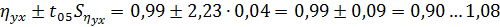
9. СПОСОБ
ОБРАБОТКИ ЭМПИРИЧЕСКИХ ДАННЫХ
Первоначально данные исследований представляют в
виде таблиц. Однако табличные данные не имеют наглядности и не могут быть
использованы в математических моделях, описывающих тот или иной процесс.
Указанных недостатков лишены эмпирические формулы, отражающие с определённым
уровнем достоверности зависимость между изучаемыми величинами. Этот процесс
называется аппроксимацией. При аппроксимации опытных данных, прежде всего, наносят
на координатную сетку опытные данные и затем через полученные точки проводят
кривую таким образом, чтобы она по возможности близко проходила от всех
экспериментальных точек. Таким образом, первый этап математической обработки
данных состоит в выборе формулы, графическое изображение которой согласуется в
общих чертах с размещением экспериментальных точек на координатной сетке.
Задачей дальнейшей математической обработки является определение числовых
значений, входящих в формулу параметров. В большинстве случаев зависимость
между переменными можно задать множеством эмпирических формул, и только
глубокое значение физической сущности изучаемого процесса позволяет
остановиться на одной из них.
Метод подбора числовых значений, входящих в
формулу параметров основан на принципе наименьших квадратов, суть которого
состоит в том, что из множества возможных эмпирических зависимостей 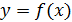 выбирается
та, для которой сумма квадратов отклонений, замеряется по оси
выбирается
та, для которой сумма квадратов отклонений, замеряется по оси  является
наименьшей.
является
наименьшей.
Впервые этот метод предложил Гаусс. Рассмотрим
применение этого метода для эмпирических формул, описывающие различные формы
зависимостей.
Исходные данные для расчётов приведены в таблице
16
Таблица 16 - исходные данные для исследования
|
№
Вар
|
Наработка
Хi тыс. мото часов
|
Износ
Yj, мм
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
8
|
0,3
|
0,9
|
1,5
|
2,1
|
2,7
|
3,3
|
3,9
|
4,5
|
0,05
|
0,08
|
0,17
|
0,21
|
0,27
|
0,37
|
0,4
|
0,42
|
Линейная функция.
Пусть дано n точек с координатами представляющих
данные эксперимента - таблица 17.
Очевидно, что эмпирическую формулу нужно искать
в виде линейной функции. 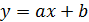
Причём коэффициенты a и b нужно подбирать так,
чтобы суммарное отклонение  принимало
минимальное значение.
принимало
минимальное значение.
Таблица 17 - Износ коренных шеек коленчатого
вала двигатель Д 240 от наработки.
|
i
|
Наработка
хi тыс. мото - час
|
Износ
yi мм
|
Хi2
|
Хi*
yi
|
|
1
|
0,3
|
0,05
|
0,09
|
0,015
|
|
2
|
0,9
|
0,08
|
0,81
|
0,072
|
|
3
|
1,5
|
0,17
|
2,25
|
0,255
|
|
4
|
2,1
|
0,21
|
4,41
|
0,441
|
|
5
|
2,7
|
0,27
|
7,29
|
0,729
|
|
6
|
3,3
|
0,37
|
10,89
|
1,221
|
|
7
|
3,9
|
0,40
|
15,21
|
1,56
|
|
8
|
4,5
|
0,42
|
20,25
|
1,89
|
|
|
19,2
|
1,97
|
61,17
|
6,183
|
Составим систему уравнений и найдём значения.
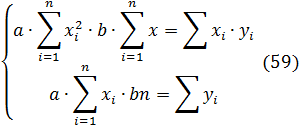
В формулу (59) подставим значения из таблицы 17
и получим
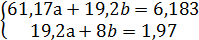
В результате расчётов имеем

Таким образом, эмпирическое уравнение линейной
функции имеет вид
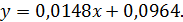
Квадратичная функция.
Эмпирическую формулу нужно искать в виде
квадратичной функции
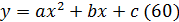
Составим таблицу 18 для упрощения расчётов.
Таблица 18 - Экспериментальные данные в общем
виде
|
i
|
Xi
|
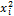
|

|
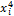
|

|
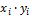
|
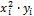
|
|
1
|
0,3
|
0,09
|
0,027
|
0,0081
|
0,05
|
0,015
|
0,0045
|
|
2
|
0,9
|
0,81
|
0,729
|
0,6561
|
0,08
|
0,072
|
0,0648
|
|
3
|
1,5
|
2,25
|
3,375
|
5,0625
|
0,17
|
0,255
|
0,3825
|
|
4
|
2,1
|
4,41
|
9,261
|
19,4481
|
0,21
|
0,441
|
0,9261
|
|
5
|
2,7
|
7,29
|
19,683
|
53,1442
|
0,27
|
0,729
|
1,9683
|
|
6
|
3,3
|
10,89
|
35,937
|
118,5921
|
0,37
|
1,221
|
4,0293
|
|
7
|
3,9
|
15,21
|
59,319
|
231,3441
|
0,40
|
1,56
|
6,084
|
|
8
|
4,5
|
20,25
|
91,125
|
410,0625
|
1,89
|
8,505
|
|
|
19,2
|
61,17
|
219,456
|
838,3177
|
1,97
|
6,183
|
21,9645
|
Составим систему уравнений

В систему (61) подставим, значения из таблицы 18
получим,

В результате решения данной системы найдём
значения a,b,c.

Гиперболическая функция
Уравнение гиперболы функции выглядит так
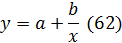
Составим систему уравнений
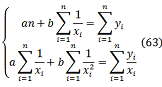
При вычислении коэффициента данные удобно свести
в таблицу 19.
Таблица 19 - Экспериментальные данные для
обработки.
|
i
|
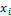
|

|
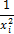
|

|
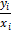
|
|
1
|
0,3
|
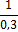
|
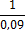
|
0,05
|
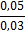
|
|
2
|
0,9
|
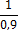
|
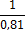
|
0,08
|
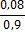
|
|
3
|
1,5
|
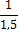
|
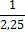
|
0,17
|
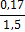
|
|
4
|
2,1
|
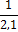
|
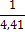
|
0,21
|

|
|
5
|
2,7
|
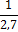
|

|
0,27
|
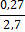
|
|
6
|
3,3
|
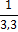
|
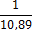
|
0,37
|
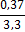
|
|
7
|
3,9
|
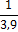
|
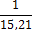
|
0,40
|
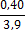
|
|
8
|
4,5
|
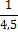
|
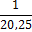
|
0,42
|
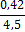
|
|
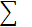
|
19,2
|
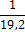
|
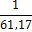
|
1,97
|

|
Подставим значения из таблицы 19, в формулу 63
получим

Численные значения параметров а и b найдём путём
решения системы уравнения (64).
В результате решения системы получили 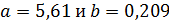
Подставив эти значения, в уравнение гиперболы
получим

Показательная функция
Данные опыта могут быть апроксимированы
показательной кривой
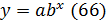
Для получения параметров 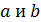 прологарифмируем
обе части функции. При этом учтём, что логарифм произведения равен сумме
логарифмов сомножителей, а логарифм её степени равен произведению показателя на
логарифм её основания. Затем следует найти величины
прологарифмируем
обе части функции. При этом учтём, что логарифм произведения равен сумме
логарифмов сомножителей, а логарифм её степени равен произведению показателя на
логарифм её основания. Затем следует найти величины 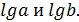
Получим систему логарифмических уравнений
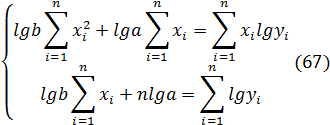
Для решения системы удобно составить таблицу 20.
|
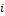 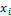 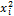  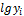 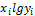
|
|
|
|
|
|
|
1
|
0,3
|
0,09
|
0,05
|
-2,99
|
-0,897
|
|
2
|
0,9
|
0,81
|
0,08
|
-2,52
|
-2,268
|
|
3
|
1,5
|
2,25
|
0,17
|
-1,77
|
-2,655
|
|
4
|
2,1
|
4,41
|
0,21
|
-1,56
|
-3,276
|
|
5
|
2,7
|
7,29
|
0,27
|
-1,30
|
-3,51
|
|
6
|
3,3
|
10,89
|
0,37
|
-0,99
|
-3,267
|
|
7
|
3,9
|
15,21
|
0,40
|
-0,91
|
-3,549
|
|
8
|
4,5
|
20,25
|
0,42
|
-0,86
|
-3,87
|
|
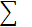
|
19,2
|
61,17
|
1,97
|
-12,6
|
-23,292
|
математическое
планирование эксперимент дисперсия
В результате решения этой системы получили 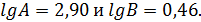
СПИСОК ЛИТЕРАТУРЫ
1. Подобие
и моделирование
Седов
Л.И. Методы подобия и размерности в механике.-М.:Наука, 1981.-448 с.
Веников
В.А., Веников Г.В. Теория подобия и моделирование/применительно к задачам
электроэнергетики/.-М.:Наука,1984.-439 с.
. Планирование
эксперимента
Планированиеэксперимента
в технике / В.И.Барабащук, Б.П.Креденцер, В.И.Мирошниченко; под. ред..
Б.П.Креденцера.-К.:Техніка 1984.-200с.
Адлер
Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске
оптимальных условий.-М.:Наука,1971.-283с.
Ахназарова
С.Л., Кафаров В.В. Методы оптимизации в химической технологии .-М.Высшая школа,
1985.-325 с.
. Статистическая
обработка результатов эксперимента
Вентцель
Е.С. Теория вероятностей,-М.Наука,1969.-576 с.
Вентцель
Е.С., Овчаров Л.А. Теория вероятностей и ее инженерные
приложения.-М.:Наука.-1988.- 480 с.
Коваленко
И.Н., Филиппова А.А. Теория вероятностей и математическая статистика.-М.,
Высшая школа, 1973.-368 с.
Базара
М.,Шетти К. Нелинейное программирование. Теория и алгоритмы.-М.,Мир.-1982.-583
с.
Колкер
Я.Д. Математический анализ точности механической обработки деталей.-Киев,
Техника.-1976.-200с.