Целевая функция задачи нелинейного программирования
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ,
МОЛОДЕЖИ И
СПОРТА УКРАИНЫ
ДОНЕЦКИЙ
НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ
МАТЕМАТИКИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Задача
по
курсу «Методы оптимизации»
Донецк
2013г.
Задача
В приведенной далее таблице 1 указаны
значения параметров целевой функции задачи нелинейного программирования (ЗНП) и
координаты вершин 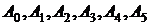 выпуклого
многоугольника, задающего множество допустимых точек ЗНП, причем целевая
функция задана в виде
выпуклого
многоугольника, задающего множество допустимых точек ЗНП, причем целевая
функция задана в виде
 ,
, 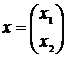
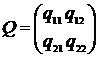 ,
,  ,
,  ,
,
а ЗНП поставлена на максимум.
Выполнить следующие задания:
восстановить математическую модель
ЗНП, воспользовавшись данными Таблицы 4;
выполнить две итерации методом
линеаризации, взяв в качестве начальной точку 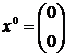 .
.
Таблица 1
|
Вариант
|
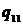 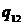 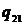  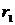 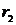   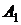 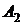 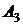 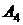 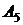
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53
|
-9
|
6
|
6
|
-12
|
2
|
2
|
6
|
0
|
0
|
0
|
3
|
15
|
8
|
10
|
13
|
6
|
12
|
15
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
Восстановить математическую модель ЗНП,
воспользовавшись данными таблицы 1.
Поставим задачу нелинейного программирования
max(f(x)), воспользовавшись данными таблицы.
Восстановим заданную квадратичную функцию по
формуле:
 , где Q=
, где Q=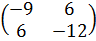 , r =
, r = , p = 6.=
, p = 6.= 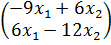 ;
;
(Qx,x) =  ;
;
(r,x) = 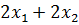 .
.
Значит, f(x) = 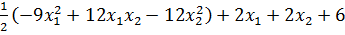 ;(x) -
непрерывная, нелинейная, по крайней мере один раз непрерывно дифференцируема.
;(x) -
непрерывная, нелинейная, по крайней мере один раз непрерывно дифференцируема.
Наша задача будет выглядеть так:
max(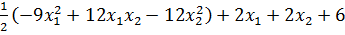 );
); E2
E2
Соединим данные точки на
координатной плоскости так, чтобы получился выпуклый многоугольник.
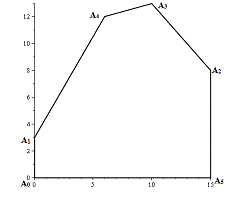
Рис. 1
Для того, чтобы восстановить математическую
модель ЗНП:
а) Найдем уравнения прямых:
А0А1 : x1 = 0;
А0А5 : x2 = 0;
А1А4 :  ;
9
;
9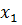 =
6
=
6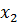 - 18;
- 18;
А4А3 : 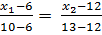 ;
;
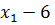 =
4
=
4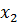 - 48;
- 48;
А3А2 :  ;
;
 =
5
=
5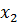 - 65;
- 65;
А2А5 : 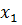 =
15.
=
15.
Исходя из положения полученного многоугольника
относительно выше описанных прямых на координатной плоскости, выпишем
ограничения ЗНП:
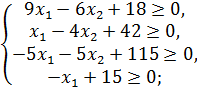
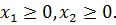
Так как известно, что задача поставлена на max,
а также известны ограничения и целевая функция, можем поставить ЗНП. Она будет
иметь вид:
(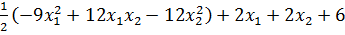 );
);
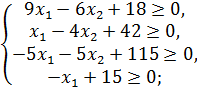
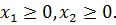
Выполнить две итерации методом
линеаризации, взяв в качестве начальной точку 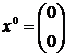 .
.
Будем решать поставленную ЗНП
методом линеаризации. Проверим условия сходимости метода: очевидно, что f(x)
непрерывна, имеет непрерывные частные производные по всем своим переменным
первого порядка, а множество допустимых точек замкнуто и ограничено (обозначим
его D).
Множество подходящих точек имеет
вид:
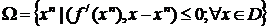
В качестве начальной точки взяли  .
.
 ;
;
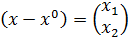 ;
;
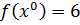 ;
;
(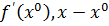 ) =
) = 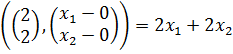 ;
;
 : (
: (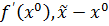 ) = 4 > 0
) = 4 > 0 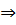
 Ω ⇒ можем найти
точку
Ω ⇒ можем найти
точку
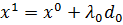 ,
, 
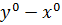 ,
, 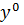 - оптимальный план.
- оптимальный план.
Следуя методу линеаризации, поставим
вспомогательную задачу и решим её графическим методом.
max(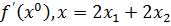 )
)
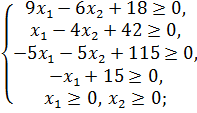
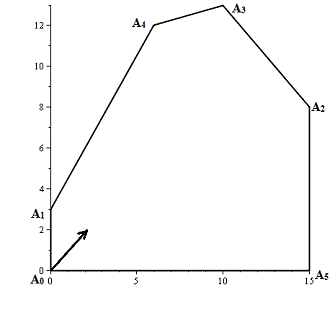
Рис. 2
Решением этой задачи является точка 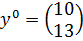 .
.
Тогда 
 .
.
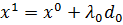 , где
, где 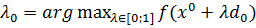
Для определения  формируем
выражение:
формируем
выражение:

 ;
;
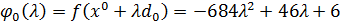 ;
;
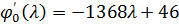 ;
;
λ= ;
;

Рис. 3
⇒ λ = 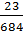 -
точка максимума функции
-
точка максимума функции 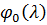 .
.
λ = 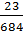 ∈
[0;1] ⇒
∈
[0;1] ⇒
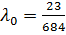 ;
;
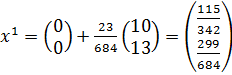 ;
;
Проверим,  Ω?
Ω?
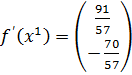 ;
;
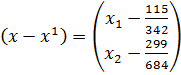 ;
;
(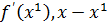 ) =
) = 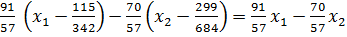 ;
;
 : (
: ( )
=
)
= 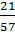 >
0
>
0 
 Ω
Ω
Можем найти точку  .
.
Поставим вспомогательную задачу:
(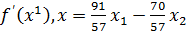 )
)
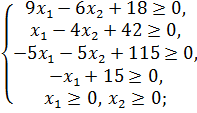
линейный программирование задача
уравнение
Решим её графическим методом:

Рис. 4
Решением этой задачи является точка  .
.
Тогда 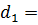
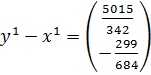 .
.
Найдем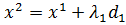 ,
где
,
где 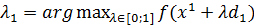
Для определения  формируем
выражение:
формируем
выражение:
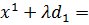
 ;
;
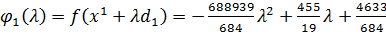 ;
;
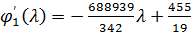 ;
;
λ=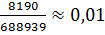 ;
;
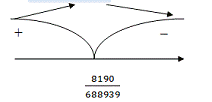
Рис. 5
⇒ λ = 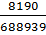 -
точка максимума функции
-
точка максимума функции 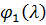 .
.
λ = 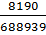 ∈
[0;1] ⇒
∈
[0;1] ⇒
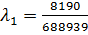 ;
;
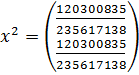 ;
;
Проверим,  Ω?
Ω?
 ;
;
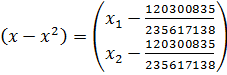 ;
;
(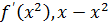 )
) 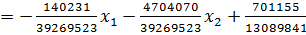 ;
;
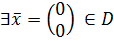 : (
: (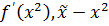 )
=
)
= 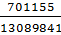 >
0
>
0 
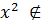 Ω.
Ω.