Решение задач линейного программирования

Решение задач линейного программирования

Лабораторная работа №1 «Решение ЗЛП в среде ЭТ Excel»

Задание

Решить задачу об оптимальном использовании сырья

Цель работы: овладеть навыками решения ЗЛП c помощью надстройки Поиск решения в среде ЭТ Excel.

Выполнил студент ЗФО МН-06 Еременко С.Г.

Проверил к.т.н., доц. Растеряев Н.В.

Вариант №4

Решение

) Создадим таблицу для ввода условий задачи и введем исходные данные.

Нахождение оптимального решения

. Укажем адреса ячеек D14:G14, в которые помещены нулевые начальные значения искомых переменных х.

. В ячейку G18 введем формулу целевой функции.

F=D8*D14+E8*E14+F8*F14+G8*G14

. Введем формулу = D3*$D$14+E3*$E$14+F3*$F$14+G3*$G$14 для ограничения по сырью S₁ в ячейку С3. Завершив ввод нажатием клавиши Enter, получим в ячейке С3 нулевое значение, т.к. пока равны нулю переменные х₁ и х₂. Скопируем эту формулу, автозаполнением, в ячейки С4-С7, предварительно заменив относительную ссылку на ячейки D14-G14 на абсолютную при помощи клавиши F4.

. Наберем команду Сервис→ Поиск решения. В появившемся диалоговом окне Поиск решения необходимо выполнить три основные установки:

.1. Заполним поле «Установить целевую ячейку». Для рассматриваемой задачи выполним ссылку на ячейку G18, где записана формула целевой функции, и установите радиокнопку «Равной максимальному значению».

5.2. Изменяемые ячейки - это те ячейки, значения в которых будут подбираться так, чтобы оптимизировать результат в целевой ячейке.

.3. Введем ограничения по запасам сырья и естественные условия неотрицательности переменных х₁ и х₂, для этого:

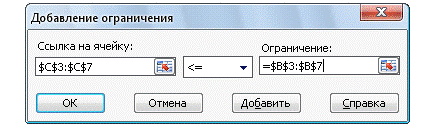
а) щелкнем по кнопке «Добавить» диалогового окна и в появившемся окне «Изменение ограничения» выполните следующие установки:

б) ещё раз щелкнем по кнопке «Добавить» диалогового окна Поиск решения и в появившемся окне «Добавление ограничения» выполните следующие установки:

Задание таких условий обеспечивает неотрицательность переменных. Щелкнем по кнопке ОК - все ограничения занесены и диалоговое окно Поиск решения примет вид

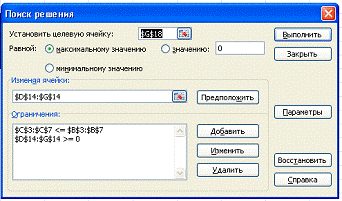
. Щелкнем по кнопке «Выполнить». Если решение найдено, то появится диалоговое окно

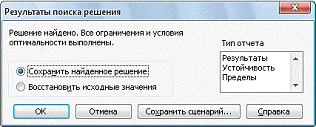
щелчок по кнопке ОК которого позволяет сохранить найденное решение, имеющее следующий вид

7) Делая вывод о проделанной работе, можно сказать следующее: по имеющимся данным, чтобы максимизировать прибыль нам необходимо выпускать 37 единиц продукта И1, 5 единиц продукта И2 и 54 единицы продукта И4 а оставшееся изделие И3 не выпускать. Получим при этом прибыль в размере 2059,66 р.

Лабораторная работа №2 «Решение ЗЛП в среде пакета Mathcad»

Задание

Найти план выпуска продукции, при котором предприятие получает максимальную прибыль при ограничениях на запасы сырья и учёте естественных условий неотрицательности переменных х₁ и х₂

Цель работы: овладеть навыками решения ЗЛП c помощью блока Given. Maximize (Given. Minimize) в среде пакета Mathcad.

Выполнил студент ЗФО МН-06 Еременко С.Г.

Вариант №4

Решение

1. Зададим запасы сырья и рецептуру выпускаемых изделий в условных единицах.

. Зададим прибыль, получаемую предприятием от реализации единицы изделия каждого вида, и определите целевую функцию - суммарную прибыль предприятия.

. Присвоим переменным x начальные нулевые значения.

. Введем служебное слово Given и, после него, систему ограничений.

. Найдем оптимальное решение с помощью функции Maximize.

. Вычислим значение максимальной прибыли.

. Найдем фактический расход и остаток каждого вида сырья после выполнения оптимального плана выпуска продукции.

Полученные результаты имеют следующий вид:

Вывод: согласно полученному решению, можно сделать вывод, что выпуская изделия 2 и 4 в количестве 28 и 83 штук, мы получим максимальную прибыль, которая составляет 2342 руб.

Лабораторная работа №3 «Решение задачи о назначении в среде электронных таблиц Excel»

Задание

Решить задачу о назначении - распределить машины по строящимся объектам так, чтобы обеспечить возведение всех объектов с минимальными суммарными затратами. Математическая модель задачи представлена целевой функцией и системами ограничений и граничных условий.

Цель работы: овладеть навыками составления математических моделей задачи о назначении и решения их в среде ЭТ Excel с помощью надстройки «Поиск решения».

Выполнил студент ЗФО МН-06 Медведева С.П.

Проверил к.т.н., доц. Растеряев Н.В.

Вариант 8. Для реализации производственного процесса необходимо выполнить n операций. Имеется n рабочих, которые способны осуществить их, и время t_ij (в часах) выполнения каждым рабочим любой из n операций. Требуется определить: какой рабочий и какую операцию должен выполнять, чтобы суммарное время выполнения всего производственного процесса было минимально.

Решение

1. В ячейки диапазона B5:F9 занесем матрицу времени строительства объектов каждым рабочим.

. В ячейках диапазона B14:F18 разместим, пока нулевые, значения матрицы Х - элементы x_ij, которые будут равны 1, если i-й рабочий работает нa j-ой операции и 0, если он не работает там.

. В ячейки диапазонов G14:G18 и B19:F19 занесем суммы элементов матрицы Х по столбцам и строкам соответственно. Для этого необходимо щелкнуть на кнопке «Автосумма» на стандартной панели инструментов и, если необходимо, выделить нужный диапазон.

. В ячейку D21 занесем формулу, по которой вычисляется суммарный диапазон времени выполнения всех работ. Набор формулы в Excel начинается символом «=» и заканчивается нажатием клавиши Enter. Для нашей задачи формула имеет вид:

=B5*B14+C5*C14+D5*D14+E5*E14+F5*F14+B15*B6+C6*C15+D6*D15+E6*E15+F6*F15+B7*B16+C7*C16+D7*D16+E7*E16+F7*F16+B8*B17+C8*C17+D8*D17+E8*E17+F8*F17+B9*B18+C9*C18+D9*D18+E9*E18+F9*F18 После нажатия клавиши Enter в ячейке D21 появится ноль, так как пока все значения x_ij = 0.

. Наберем команду Сервис®Поиск решения, открыв диалоговое окно Поиск решения. Выполним в нем необходимые установки.

o   В поле «Установить целевую» диалогового окна Поиск решения укажем ячейку, содержащую пока нулевое значение целевой функции F(X). Установим переключатель «Равной минимальному значению», т.к. требуется найти минимум выполнения всех работ.

o   В поле «Изменяя ячейки» задать диапазон подбираемых параметров - B14:F18

o   Чтобы определить ограничения щелкнем на кнопке «Добавить». В диалоговом окне «Добавление ограничения» в поле «Ссылка на ячейку» укажем диапазон G14:G18. В качестве условия - символ равно (=). В поле «Ограничение» зададим число - единица и щелкнем по кнопке ОК. Это условие указывает, что каждый объект может возводиться только одним краном. Повторим те же действия для диапазона ячеек B19:F19.

o   Снова щелкнем на кнопке «Добавить» диалогового окна Поиск решения. Повторим те же действия для диапазона изменяемых ячеек B14:F18, указав в качестве условия отношение 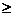, а в поле «Ограничение» - число 0. Это указывает, что все элементы x_ij матрицы Х неотрицательны.

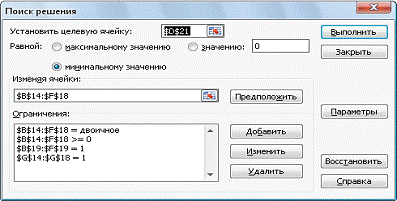
o   Далее необходимо указать, что элементы x_ij матрицы Х могут принимать только два значения 1 или 0. Для этого в соответствующем поле окна «Добавление ограничения» в качестве условия выбираем пункт «двоич» и щелкаем ОК.

Диалоговое окно примет следующий вид:

7. Запустим надстройку на выполнение щелчком по кнопке выполнить и сохраните полученное решение.

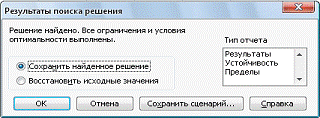
Полученное решение имеет вид:

Вывод: Исходя из полученного результата, можно сделать вывод, что для того чтобы минимизировать затраты, необходимо, чтобы Рабочий А выполнял операцию 4, Рабочий Б - операцию 1, рабочий В - операцию2, рабочий Г - операцию 5, рабочий Д - операцию 3. Суммарное время выполнения всех операций составит, в этом случае, 7.60 часов.

Лабораторная работа №4

Обработка выборки в ЭТ MS Excel: описательная статистика и гистограмма

Цель работы: овладеть практическими навыками обработки выборки в приложении Microsoft Excel - построения гистограмм и определения числовых характеристик.

Исходные данные

Выполнил студент ЗФО МН-06 Медведева С.П.

Проверил к.т.н., доц. Растеряев Н.В.

Решение

1.      Наберем столбец исходных данных и скопируем его на Лист 3 в Excel.

2.      Вычислим величины U_max, U_min, R, n, N, N_{округл.}, Д и Д_{округл.}, используя встроенные функции Excel МАКС, МИН, СЧЕТ, КОРЕНЬ и ОКРУГЛ.

.        Сформируем столбец интервалов группировки (карманов). Если диапазон карманов не введен, то набор отрезков, равномерно распределенных между максимальным и минимальным значениями исходных данных, будут созданы Excel автоматически.

.        Наберем команду Сервис → Анализ данных → Гистограмма и в появившемся диалоговом окне выполните нужные установки.

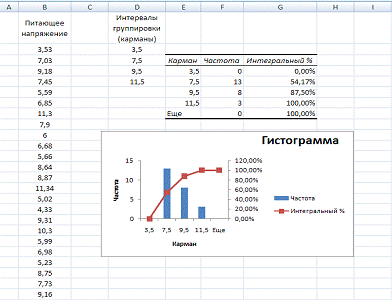
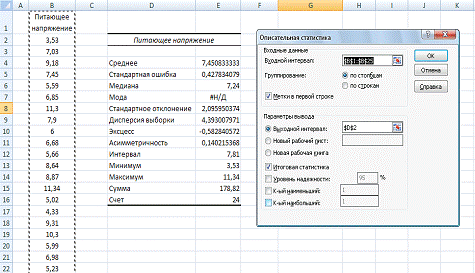
5.      Для получения числовых характеристик выборки наберем команду Сервис → Анализ данных → Описательная статистика и в появившемся диалоговом окне выполним нужные установки.

Лабораторная работа №5

Анализ экономических данных с помощью диаграмм Парето

Цель работы: овладеть практическими навыками анализа экономических данных с помощью диаграмм Парето в среде электронных таблиц Microsoft Excel

Данные распределения домашних хозяйств по размеру занимаемого жилья по России в 1998 г. представлены в таблице 9.

линейный программирование парето excel

Таблица 9 Исходные данные для варианта 8

Выполнил студент ЗФО МН-06 Медведева С.П.

Проверил к.т.н., доц. Растеряев Н.В.

Решение:

В среде Excel составим таблицу исходных и расчетных данных задачи. Вклады факторов в общий результат во втором столбце необходимо расположить в порядке их убывания с помощью команды Данные → Сортировка → По убыванию или с помощью кнопки  В первом столбце указываем наименование соответствующего фактора. Для построения диаграммы Парето необходимо рассчитать в процентах долю вклада каждого фактора от общей суммы вкладов (столбец 3) и данные Парето (столбец 4). Доля вклада факторов даны в условии задачи. Данные Парето получены постепенным накапливанием долей каждого фактора. Первая строка столбца 4 совпадает со значением первой строки столбца 3 (формула =D4). Вторая строка столбца 4 получена суммированием значения первой строки столбца 4 и значения второй строки столбца 3. Остальные строки столбца 4 получены копированием формулы второй строки столбца 4. О корректности вычислений свидетельствует число 100 в строке последнего фактора, соответствующее 100% результата.

Для построения диаграммы Парето выделим данные первого, второго и четвертого столбцов. В режиме Мастера диаграмм выбираем тип диаграммы Нестандартные → График гистограмма 2, позволяющей отобразить трехосевую диаграмму.

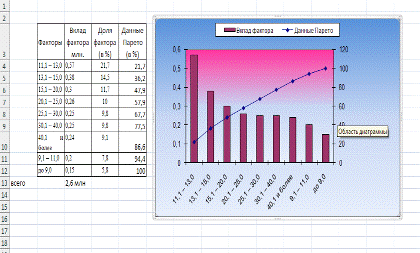
Проведем горизонтальную прямую, соответствующую 80% вкладов факторов до пересечения с графиком вкладов.

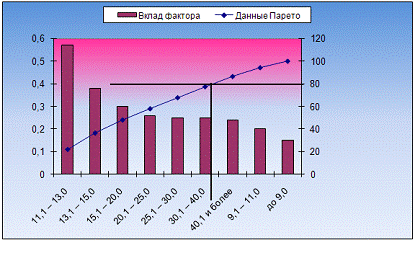
Вывод: Слева от точки пересечения размещены факторы, обеспечивающие 80% результата.