Разработка и исследование метода грамматической эволюции для структурно-параметрического синтеза системы управления динамическим объектом
Содержание
Введение
Основные сокращения и обозначения
. Постановка задачи синтеза системы управления
. Методы поиска оптимального управления
.1 Принцип Максимума Понтрягина
.2 Метод аналитического конструирования оптимальных
регуляторов (АКОР)
.3 Метод аналитического конструирования нелинейных
агрегированных регуляторов (АКАР)
.4 Метод динамического программирования Беллмана
. Символьная регрессия
.1 Генетическое программирование (ГП)
.2 Грамматическая эволюция (ГЭ)
.3 Аналитическое Программирование (АП)
.4 Сетевой оператор
.1 Генетический алгоритм
.2 Грамматическая эволюция
. Вычислительный эксперимент
Список литературы
Приложение 1
Введение
Одной из самых обсуждаемых и актуальных проблем в науке управления в
нашем мире является поиск решения синтеза управления. Большое значение на
сегодняшний день имеет развитие методов интеллектуального управления, которые
используют различные подходы искусственного интеллекта, такие как искусственные
нейронные сети, нечеткая логика, машинное обучение, эволюционные вычисления и
генетические алгоритмы.
Суть задачи синтеза системы управления заключается в нахождении
синтезирующей функции, которая описывает зависимость управления от состояния
объекта. Объект может находиться в разных состояниях и можно получить
синтезирующей функции, решая задачу оптимального управления для текущего
состояния объекта (считая его начальным состоянием).
Цель синтеза управления заключается в том, чтобы найти такое управление,
при котором поведение объекта управления удовлетворяло бы заданным критериям.
Данная задача до сих пор не решена аналитически в общем виде.
Одним из методов, позволяющих решить эту проблему, является генетическое
программирование, созданное Дж. Козой. Принцип работы генетического
программирования базируется на представлении математических выражений в виде
бинарных векторов и на генетическом алгоритме.
Идея генетических алгоритмов заимствована у живой природы и состоит в
организации эволюционного процесса, конечной целью которого является получение
оптимального решения в сложной комбинаторной задаче. Разработчик генетических
алгоритмов выступает в данном случае как «создатель», который должен правильно
установить законы эволюции, чтобы достичь желаемой цели как можно быстрее.
Впервые эти нестандартные идеи были применены к решению оптимизационных задач в
середине 70-х годов.
В данной дипломной работе будет разработан программный комплекс,
позволяющий решать задачу синтеза управления заданным динамическим объектом на
основе грамматической эволюции.
Основные
сокращения и обозначения
ГЭ - Грамматическая эволюция
ГА - Генетический алгоритм
ГП - Генетическое программирование
АП - Аналитическое программирование
АКОР - Аналитического конструирования оптимальных регуляторов
БНФ - Бэкуса-Наура Форма
1.
Постановка задачи синтеза системы управления
Объект управления задан системой обыкновенных дифференциальных уравнений:
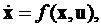 (1)
(1)
где
в общем случае 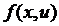 - нелинейная функция векторных аргументов
- нелинейная функция векторных аргументов 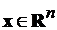 ,
,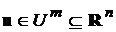 , где множество
, где множество 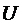 замкнуто
и ограничено,
замкнуто
и ограничено, 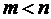 .
.
Пусть
начальным условием для данной системы будет точка
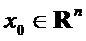 . (2)
. (2)
Целевое значение
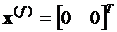 . (3)
. (3)
Функционалы качества для заданной системы определяется как
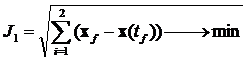 , (4)
, (4)
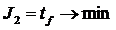 , (5)
, (5)
Где
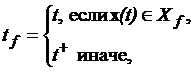 (6)
(6)
и
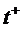 - заданная верхняя границ приемлемого времени
управления.
- заданная верхняя границ приемлемого времени
управления.
Требуется
найти функцию управления
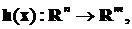 (7)
(7)
обеспечивающую минимум функционалов и удовлетворяющую терминальным
условиям
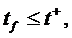 (8)
(8)
и ограничениям, наложенным на управление
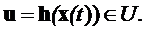 (9)
(9)
В общем случае искомая функция управления нелинейная и может иметь
разрывы, следовательно, её сложно найти аналитическими методами.
2.
Методы поиска оптимального управления
.1 Принцип
Максимума Понтрягина
Принцип максимума был получен советским академиком Понтрягин Л.С. в 1951
году [1], и, несмотря на то, что прошло уже полвека с момента изобретения, этот
принцип работает и используется в наше время.
В принципе максимума может быть применено уравнение Эйлера-Лагранжа для
особых случаев. Чтобы найти оптимальное управление необходимо максимизировать
функцию гамильтониана.
Если
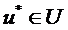 является оптимальной управление, то гамильтониан
будет выглядеть следующим образом:
является оптимальной управление, то гамильтониан
будет выглядеть следующим образом:
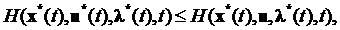
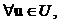
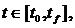 (10)
(10)
где
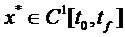 - оптимальная фазовая траектория;
- оптимальная фазовая траектория;  -оптимальная сопряженная траектория. Результат этого
принципа впервые был применён в проблеме с минимальным временем, где
управляющее воздействие было ограничено. Также принцип максимума хорошо
работает в решении задач с фазовыми ограничениями.
-оптимальная сопряженная траектория. Результат этого
принципа впервые был применён в проблеме с минимальным временем, где
управляющее воздействие было ограничено. Также принцип максимума хорошо
работает в решении задач с фазовыми ограничениями.
Принцип
максимума часто применяется в системах управления, где нужно добиться
максимального быстродействия и минимального расхода энергии, где применяются
управления релейного типа, принимающие крайние значения на допустимом интервале
управления.
Недостатком
принцип максимума можно назвать то, что его невозможно применять в задачах, где
отсутствуют выпуклые свойства.
2.2
Метод аналитического конструирования оптимальных регуляторов (АКОР)
АКОР в России впервые был разработан профессором Летовым. Заслуга
профессора Летова состоит в том, что он процесс синтеза оптимального управления
поставил на математическую основу, выраженную в аналитической форме. Для этого
профессор Летов в своем методе делал следующие шаги:
) выбирал критерий оптимальности на основании математической модели
объекта управления;
) по выбранному критерию оптимальности аналитически находил выражение для
оптимального регулятора.
Этот метод может помочь при решении задач оптимальной стабилизации с
очень высокой точностью.
Метод аналитического конструирования оптимальных регуляторов для
нелинейных систем, основанный на задании инвариантных притягивающих
многообразий в замкнутой системе управления и конструирования связанного с ними
минимизируемого функционала, является очень простым и эффективным, позволяющим
точно вычислять решение задачи оптимальной стабилизации.
По принципу метода аналитического конструирования оптимальных регуляторов
(АКОР) была сформулирована задача, которая представляла собой сложную
вариационную проблему. При использовании многих известных методов не удалось
найти решение этой задачи. Причиной этого было наличие нелинейной функции и
ограничение фазовых координат системы.
Такая
задача называется задачей синтеза, а функцию 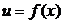 называют
оптимальным алгоритмом управления.
называют
оптимальным алгоритмом управления.
Одновременно
с профессором Летовым, математиком Калманом [2] был разработан метод подобный
АКОРу, который назывался Метод пространства состояния. Этот метод явился
основой современной теории управления. Заслуга Калмана состоит в том, что он
разработал методы синтеза алгоритма оптимального управления не только для
детерминированной динамической системы, но и для стохастических динамических
систем (со случайным переходным процессом).
В
постановке задачи АКОР очень важное место занимает выбор критерия оптимальности
или выбор функционала качества [3].
Этот
метод получил развитие в работах учёных А.А. Красовского, М.М. Атанса и П.
Фалба, В.Н. Афанасьева и других.
Недостаток этого метода в том, что он решает задачу синтеза для одного
конкретного начального условия и то, что он применим только для линеаризованных
систем.
2.3 Метод
аналитического конструирования нелинейных агрегированных регуляторов (АКАР)
Этот метод играет очень важную роль в проблеме синтеза систем управления
нелинейными динамическими объектами.
Метод
АКАР опирается на идею введения притягивающих инвариантных многообразий (ИМ)  с которыми наилучшим образом согласуются естественные
(энергетические, механические, тепловые и т.д.) свойства объекта и требования
задач управления.
с которыми наилучшим образом согласуются естественные
(энергетические, механические, тепловые и т.д.) свойства объекта и требования
задач управления.
С
математической точки зрения отличительная особенность постановки проблемы
синергетического синтеза состоит в способе генерации такой совокупности
обратных связей - законов управления 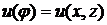 , которые
переводят систему из произвольного исходного состояния сначала в окрестность ИМ
, которые
переводят систему из произвольного исходного состояния сначала в окрестность ИМ
 , а затем обеспечивают асимптотически устойчивое
движение вдоль этих ИМ вплоть до попадания на целевые аттракторы. На этих
аттракторах гарантируется выполнение заданных инвариантов - технологических,
механических, энергетических и др.
, а затем обеспечивают асимптотически устойчивое
движение вдоль этих ИМ вплоть до попадания на целевые аттракторы. На этих
аттракторах гарантируется выполнение заданных инвариантов - технологических,
механических, энергетических и др.
В
методе АКАР, основанном на процедуре агрегирования (декомпозиции), для
обеспечения асимптотической устойчивости синтезируемых нелинейных систем
высокой размерности используется параллельно-последовательная совокупность
функций Ляпунова. При этом сначала вводятся простейшие функции Ляпунова вида 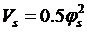 , относительно макропеременных
, относительно макропеременных 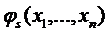 , а затем на конечном многообразии
, а затем на конечном многообразии 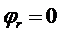 исследуется устойчивость движения только по отношению
к части координат
исследуется устойчивость движения только по отношению
к части координат 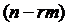 , которые описывают поведение изображающей точки
декомпозированной системы на заключительном этапе движения. Указанная
совокупность функций Ляпунова представляет собой своего рода аналог метода
векторных функций Ляпунова (ВФЛ), развитый в работах академика РАН В.Ф.
Матросова [4], в применении к синергетической теории синтеза нелинейных систем.
В теории АКАР метод ВФЛ отличается асимптотически точной динамической
декомпозицией исходной системы. Кроме того, не требуется поиск соответствующих
систем и теорем сравнения для оценки асимптотической устойчивости движения
системы. Эта важная особенность связана с тем, что в методе АКАР
рассматриваются задачи устойчивости управляемых динамических систем. Иначе
говоря, в синергетическом подходе метод ВФЛ естественным образом связан с
процедурой АКАР. Именно возможность структурного синтеза управлений,
переводящих изображающие точки от одного многообразия к другому, пониженной
размерности, позволяет в методе АКАР осуществить строгую процедуру
аналитического построения ВФЛ для текущего анализа асимптотической устойчивости
синтезируемых нелинейных систем.
, которые описывают поведение изображающей точки
декомпозированной системы на заключительном этапе движения. Указанная
совокупность функций Ляпунова представляет собой своего рода аналог метода
векторных функций Ляпунова (ВФЛ), развитый в работах академика РАН В.Ф.
Матросова [4], в применении к синергетической теории синтеза нелинейных систем.
В теории АКАР метод ВФЛ отличается асимптотически точной динамической
декомпозицией исходной системы. Кроме того, не требуется поиск соответствующих
систем и теорем сравнения для оценки асимптотической устойчивости движения
системы. Эта важная особенность связана с тем, что в методе АКАР
рассматриваются задачи устойчивости управляемых динамических систем. Иначе
говоря, в синергетическом подходе метод ВФЛ естественным образом связан с
процедурой АКАР. Именно возможность структурного синтеза управлений,
переводящих изображающие точки от одного многообразия к другому, пониженной
размерности, позволяет в методе АКАР осуществить строгую процедуру
аналитического построения ВФЛ для текущего анализа асимптотической устойчивости
синтезируемых нелинейных систем.
Эти
особенности метода АКАР позволяют наделить синтезируемые системы замечательным
свойством грубости (робастности) переходных процессов к структурным вариациям и
параметрическим возмущениям. Известно, что асимптотическая устойчивость систем
в определенной области фазового пространства является грубым свойством, которое
усиливается в случае экспоненциальной устойчивости систем. Системы управления,
синтезируемые по синергетическим принципам, являются как асимптотически
устойчивыми в целом (т.е. во всей области фазового пространства), так и
экспоненциально устойчивыми относительно вводимых инвариантных многообразий 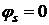 . Это означает, что такие системы обладают
отличительным свойством грубости (робастности) переходных процессов.
. Это означает, что такие системы обладают
отличительным свойством грубости (робастности) переходных процессов.
Задача
АКАР с ограничением на управление выглядит следующим образом:
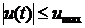 , (11)
, (11)
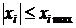 . (12)
. (12)
С такими ограничениями задачу можно считать сложной и нерешаемой как в
системе АКОР, так и в других методах. Прямая причина этой сложности можно
сказать в том, что указанные ограничения на управления и координаты могут
привести к появлению нелинейности синтезируемого закона управления.
Одним
из очевидных способов учета ограничения 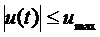 является
введение в канал управления статического звена, имеющего характеристику типа
«насыщение», т.е. обладающего свойствами релейного элемента в режиме больших
отклонений. Отличительной особенностью такого способа является необходимость
установки на выходе этого звена некоторого дополнительного динамического звена,
например интегратора. Тогда за новое условное (неограниченное) управление
следует выбрать управление
является
введение в канал управления статического звена, имеющего характеристику типа
«насыщение», т.е. обладающего свойствами релейного элемента в режиме больших
отклонений. Отличительной особенностью такого способа является необходимость
установки на выходе этого звена некоторого дополнительного динамического звена,
например интегратора. Тогда за новое условное (неограниченное) управление
следует выбрать управление 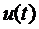 на входе
введенного интегратора. Следовательно, размерность неизменяемой части
синтезируемой системы увеличивается на единицу по сравнению с размерностью
сходного объекта.
на входе
введенного интегратора. Следовательно, размерность неизменяемой части
синтезируемой системы увеличивается на единицу по сравнению с размерностью
сходного объекта.

Рис.1.
Структурная схема
На
рис. 1 изображена структурная схема, отражающая предложенный способ учета
ограничения на управление.
Недостаток
этого метода тот же что и в АКОР, но преимущество его заключается в том, что он
лучше работает с нелинейными системами.
2.4 Метод
динамического программирования Беллмана
Уравнение Беллмана названо в честь его открывателя Ричарда Беллмана [5].
Оно является необходимым условием оптимальности связанным с методом
математической оптимизации, который так же известен, как динамическое
программирование.
Чтобы понять уравнение Беллмана нужно понять несколько правил, любая
проблема оптимизации включает в себя некую задачу (например, минимизация
времени полёта, минимизация цен, максимизация прибыли и т.д.), а каждая
математическая функция описывающая эту задачу, называется «целевая функция».
Ричард Беллман показал, что проблему динамической оптимизации в
дискретном времени можно решить в рекурсивном виде или в итеративно через
описание соотношения между значением функции в один период и значением функции
в следующем периоде. Соотношение между этими двумя значениями называется
уравнением Беллмана.
Вывод уравнения Беллмана:
) Решение динамической задачи
Пусть
 будет состоянием системы в момент
будет состоянием системы в момент 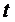 . В момент времени
. В момент времени  пусть
будет начальное состояние
пусть
будет начальное состояние 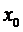 , в любой момент времени набор возможных решении
зависит от текущего состояния, этого можно описать в следующем виде:
, в любой момент времени набор возможных решении
зависит от текущего состояния, этого можно описать в следующем виде:
 , (13)
, (13)
где
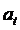 представляет одну или больше перемен управления. Надо
еще учитывать, что изменение происходит из состояния
представляет одну или больше перемен управления. Надо
еще учитывать, что изменение происходит из состояния 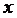 в новое состояние
в новое состояние 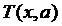 , где
, где 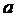 заданная переменная и текущее изменение от этой
переменной
заданная переменная и текущее изменение от этой
переменной 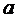 в состояние
в состояние 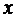 будет
будет 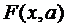 .
.
В
этом случае, в бесконечном пространстве решений задачи имеет следующий вид:
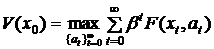 , (14)
, (14)
где
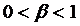 ,
, 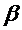 -
коэффициент дисконтирования, с учетом ограничений,
-
коэффициент дисконтирования, с учетом ограничений,
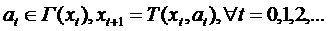 . (15)
. (15)
Обратите
внимание, что мы обозначили 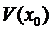 чтобы
представить оптимальное значение, которое можно получить через максимизацию
целевой функции с учётом ограничения.
чтобы
представить оптимальное значение, которое можно получить через максимизацию
целевой функции с учётом ограничения.
2) Принцип оптимальности Беллмана
Принцип оптимальности Беллмана для решения задачи оптимального управления
заключается в следующем.
Оптимальное
поведение системы обладает тем свойством, что какой бы ни был момент времени 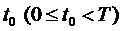 , оно остается оптимальным относительно состояния
системы в этот момент времени на всем оставшемся отрезке времени
, оно остается оптимальным относительно состояния
системы в этот момент времени на всем оставшемся отрезке времени 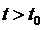 , независимо от того, каким образом система достигла
состояния в момент времени
, независимо от того, каким образом система достигла
состояния в момент времени 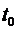 .
.
Метод
динамического программирования разделяет решение проблемы на ряд маленьких
подпроблем. Принцип Оптимальности Беллмана описывает как это сделать:
Политика
оптимальности имеет такое свойство, при котором каким бы ни было начальное
состояние и начальное решение, остальные решения должны составлять оптимальную
политику с учетом состояния в результате первого решения [6].
В
области компьютерных наук, проблема, которая может быть разделена на части
имеет оптимальную подструктуру.
Как
следует из принципа оптимальности, мы будем рассматривать отдельно первое
решение, отменяя все будущие решения (начнём заново время от 1 с новым
состоянием 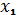
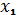 ).
).
После
сбора всех будущих решении, предыдущая проблема будет равна:
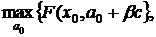 (16)
(16)
где
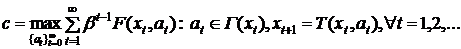 ,
,
с учетом ограничений,
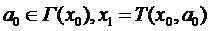 , (17)
, (17)
здесь
мы выбираем 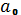
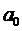 , зная
что наш выбор в момент времени 1 сделает состояние
, зная
что наш выбор в момент времени 1 сделает состояние 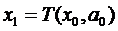
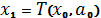 . Далее
новое состояние будет влиять на решение проблемы с момента времени 1.
. Далее
новое состояние будет влиять на решение проблемы с момента времени 1.
Кроме
описанных выше методов задача синтеза может быть решена методами символьной
регрессии. В нашем случае для поиска оптимального решения синтеза управления
используется метод грамматической эволюции.
3. Символьная
регрессия
Символьная регрессия - это процесс, во время которого полученные данные
аппроксимируются подходящей математической формулой.
Символьная регрессия как процесс входит в область работы не только людей,
но и компьютеров в последние десятилетия и первый, кто представил идею решения
различных проблем с помощью этого процесса являлся Джон Коза.
Джон Коза - ученый в области компьютерных наук и программирования, бывший
профессор в Стэнфордском университете, наиболее известный введением
использования генетического программирования для поиска оптимальных решений
сложных проблем [7].
Коза использовал генетический алгоритм (ГА) в генетическом
программировании (ГП) [8], которое принадлежит к классу методов символьной
регрессии, которая выполняется эволюционными алгоритмами вместо обычных
расчётных процессов, выполняемых людьми.
Важно отметить, что символьная регрессия становится всё важнее и важнее в
областях науки из-за того, что сложность задач в мире вокруг нас со временем
увеличивается.
В символьной регрессии можно отметить очень важный признак - это то, что
она выполняется эволюционными алгоритмами, а эволюционный алгоритм в целом
работает с функциональным и терминальным набором.
Функциональное множество - это множество функций, определенных
пользователем.
Терминальное множество - это множество всех констант и переменных.
Далее рассмотрим четыре метода символьной регрессии:
) генетическое программирование (ГП)
) грамматическая эволюция (ГЭ)
) аналитическое программирование (АП)
) сетевой оператор (СО)
В данной работе был применён метод грамматической эволюции со специальным
функциональным и терминальным наборами, которые были реализованы и разработаны
на одном из новейших языков программирования (Python). Это привело к получению хороших результатов,
которые будут приведены далее.
Важно отметить, что класс эволюционных алгоритмов основан на дарвинистской
теории эволюции и один из главных признаков этого класса алгоритмов то, что он
обрабатывает группу возможных решений (популяций). Члены этой популяции
называются «хромосомы».
В математическом виде они представляют собой возможные решения, которые
можно применить в текущей задачи, но главная цель эволюционных алгоритмов - это
найти оптимальное решение из всех найденных решений.
Эволюционные алгоритмы отличаются между собой по
многим параметрам. Например, представление особи (двоичное, десятичное) или создание
потомков (стандартный кроссовер, арифметические операции, векторные операции, и
т.д.). Они также отличаются по философскому фону, на котором они были развиты,
и обычно им дают название согласно данной точке зрения.
Символьная регрессия основана на эволюционных
алгоритмах, и её главная цель - «синтезировать» эволюционным способом такую
"программу" (математические формулы, компьютерные программы,
логические выражения, и т.д.), которая решит определенную задачу пользователя
по возможности наилучшим образом. В то время, как область ЭА имеет числовую
природу (вещественные, комплексные, целые, дискретные), область символьной
регрессии имеет функциональную природу, т.е. она состоит из множества функций,
например, (sin(), cos(), sqr(),
func1(), ...) и так называемого
терминального набора, например, (t, x, p, q, ...). Путем комбинации элементов этих множеств, формируется
окончательная программа, которая может быть весьма сложна с точки зрения её
структуры.
В настоящее время есть четыре метода, позволяющие сделать это:
генетическое программирование, грамматическая эволюция, аналитическое
программирование и сетевой оператор.
3.1 Генетическое программирование (ГП)
Если обратить внимание на возраст метода, то ГП является самым старым
методом автоматического создания программы для решения задач высокого уровня
сложности через генетический алгоритм, который был развит Дж. Козой [7] [8].
ГП начинается с формулировки «какую задачу нужно решить?» и автоматически
создает компьютерную программу для решения данной задачи.
На данный момент существует не менее 36 случаев, где ГП автоматически
выработал результат, который имеет возможность конкурировать с продуктом
человеческого интеллекта.
ГП заставляет эволюционировать решения, которые конкурентоспособны с
человеческими решениями и это привело к тому, что ГП был применен в
изобретающих вычислительных машинах, чтобы создать новые продвинутые программы.
ГП имеет множество важных атрибутов, которые создают хорошее впечатление о
генерируемой системе синтеза программы.
Генетическое программирование имеет семь важных отличий [9] от
общепринятых подходов к искусственному интеллекту, таких как нейронные сети,
адаптивные системы или автоматизированная логика:
) Представление: ГП открыто проводит свой поиск решение данной
задачи в программном пространстве;
) Принцип преобразования в виде точка-точка в поиске: ГП не
проводит свой поиск решения через преобразование одной точки в пространстве
поиска в другую. Вместо этого ГП преобразует множество точек в другое
множество;
) Принцип преодоления подъема в поиске: ГП не полагается
исключительно на огромные шаги при восхождении на холм, а выделяет определенное
количество попыток в подмножество неудачных попыток;
) Принцип детерминизма в поиске: ГП ведёт свой поиск случайно;
) Принцип абсолютного знания базы: отсутствует;
) Принцип формальной логистики в поиске: отсутствует;
) Принцип поиска: биологический.
Принцип работы ГП
Генетическое программирование начинается с множества случайно
генерируемых программ. Популяция этих программ эволюционирует через несколько
поколений. Эволюционный поиск использует дарвиновский принцип естественного
отбора (выживание приспособленного) и аналогичные другие операции как
кроссовер, мутация, генетическая дубликация, генетическое удаление и т.д.
Блок-схема работы ГП Изображена на рис. 2.:
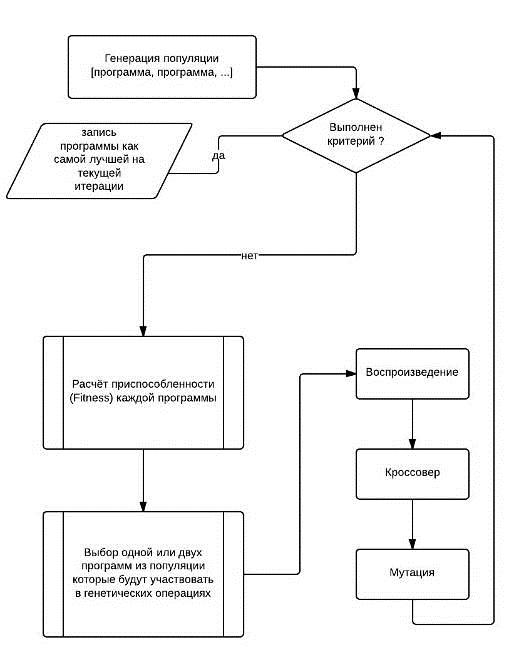
Рис. 2. Главный цикл ГП
С помощью этих операций ГП на каждой итерации преобразует старую
популяцию компьютерных программ в новую. Эти операции применяются над
отдельными хромосомами, выбранными из популяции, путём наиболее жизнеспособным,
чтобы они участвовали в последующих генетических операциях. Итерационное
преобразование популяции выполняется внутри главного цикла ГП.
Техника работы ГП построена на принципах генетики и эволюционных вычислениях,
которые в свою очередь содержат такие методы как генетический алгоритм (ГА),
эволюционное программирование (ЭП), Грамматическая Эволюция (ГЭ) и другие.
Недостатки ГП:
) Если представить принцип работы ГП в виде дерева, то число
входящих переменных должно равняться числу листьев на этом дереве;
) Во время выполнения операции скрещивания, необходимо определить
подстрок символов;
) Некоторые операции, такие как скрещивание, могут изменять
формулу;
) Сложно задать структуру математического выражения.
) На стадиях преобразования, для расшифровки символов при
выполнении вычисления требуется анализатор.
3.2 Грамматическая
эволюция (ГЭ)
Грамматическая эволюция - второй метод для выполнения символьной
регрессии, который во многом происходит от ГП и использует грамматику для
эволюционирования структур.
Конор Райан и Майкел О’Нейл являются одними из первых, кто ввёл понятие
ГЭ и вместе они написали первую книгу о грамматической эволюции [10], а также
открыли первую лабораторию для исследования и развития ГЭ.
Конор Райан занимается биовычислениями и развивающимися системами в
университете Лимерика и совместно с О’Нейлом написал книгу по ГЭ [10].
Согласно автору, ГЭ является символьной регрессией, которая может быть
осуществлена посредством произвольного языка программирования, например: Lisp,
C ++, Java, XML, Perl, Fortran, Python
(в данной работе) и т.д. В отличие от ГП грамматическая эволюция в основном
является его расширением, которое не использует прямое символьное представление
в Lisp, но использует так называемую форму записи Бэкуса - Наура (BNF).
Основанная на BNF ГЭ способна выполнить символьную регрессию вне зависимости от
компьютерного языка.
Форма Бэкуса - Наура
В формальной системе описания синтаксиса одни синтаксические категории
последовательно определяются через другие категории. БНФ используется для
описания контекстно-свободных формальных грамматик. Существует расширенная
форма Бэкуса Наура, которая отличается лишь более емкими конструкциями.
БНФ-конструкция определяет конечное число символов (нетерминалов). Кроме
того, она определяет правила замены символа на какую-то последовательность букв
(терминалов) и символов. Процесс получения цепочки букв можно определить
поэтапно: изначально имеется один символ (символы обычно заключаются в угловые
скобки, а их название не несет никакой информации). Затем этот символ
заменяется на некоторую последовательность букв и символов, согласно одному из
правил. После этого процесс повторяется (на каждом шаге один из символов
заменяется на последовательность, согласно правилу). В конце концов, получается
цепочка, состоящая из букв и не содержащая символов. Это означает, что
полученная цепочка может быть выведена из начального символа.
Принцип работы ГЭ
В приведенном рисунке 3 упрощенно показан способ нахождения результатов,
а также с какими методами работает ГЭ.
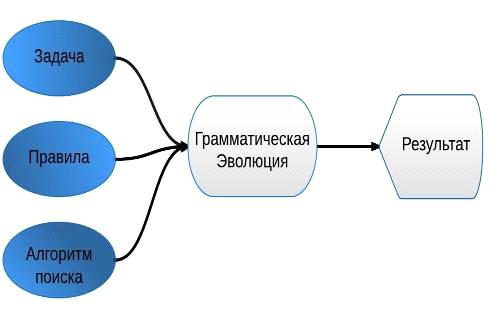
Рис. 3. Способ работы ГЭ
Пока ГП манипулирует с символическими выражениями языка Lisp, ГЭ использует индивидуальные
структуры, основанные на двоичных строках. Они преобразуются в
последовательности целых чисел, а затем передаются в финальную часть программы,
а именно в форму записи Бэкуса - Наура (BNF).
Для наглядности приведен следующий пример.
Пусть T = {+,−,×, /, x, y} - набор операторов и
терминалов, а множество F =
{eхpr, op, var} содержит нетерминальные символы.
В этом случае, грамматика используема для синтеза финальной программы
приведенной в таблице 1.
Правило, используемое для преобразования индивидуальных структур в
программе, основано на уравнении (18).
ГЭ основана на двоичных хромосомах с переменной длиной, разделенных на
так называемые кодоны (диапазон целых значений, 0-255), которые затем
превращаются в целое число (в соответствии с таблицей 2).
Таблица 1. Продукционные правила для грамматики алгебраического выражения
на рис. 4
|
Нетерминалы
|
Правила
|
Индекс
|
|
expr
|
op expr
expr var
|
0 1
|
|
op
|
+ - * /
|
0’ 1’ 2’ 3’
|
|
var
|
X Y
|
0’’ 1’’
|
Таблица. 2. Примеры кодонов для грамматики алгебраического выражения.
|
хромосом
|
бинарный
|
Целое число
|
Индекс
|
|
Codon 1 Codon 2
Codon 3 Codon 4 Codon 5 Codon 6 Codon 7 Codon 8
|
101000 10100010
1000011 1100 11111101 11100111 10010010 10001011
|
40 162 67 12 125 231 146
139
|
0 2’ 1 0’’ 1 1’’ Не
использ. Не использ.
|
Unfolding = codon mod rules, (18)
где «unfolding» - раскладывание,
«Rules» - количество правил для данного
нетерминала.
Синтез актуальной программы может быть описан следующим образом.
1) Программа
начинает преобразование с нетерминального объекта «expr». Так как целое число Codon 1 равно 40 (смотрите табл. 2), согласно уравнению
(18), раскладывание нетерминала «expr»
будет выглядеть так - «op expr expr» (40 mod 2,
2 правило для expr, т.е. 0 и 1).
2) Используя
«Codon 2» программа раскладывает «op» на «*» (т.е. 162 mod 4). Оператор «*» является терминалом
и поэтому раскладывание этой части программы завершается. Затем, продолжается
раскладывание оставшихся нетерминалов (expr expr) до тех пор пока программа полностью не будет
заполнена терминалами.
Если программа будет заполнена до того как конец хромосомы будет
достигнут, то остальные кодоны игнорируются. В противном случае, программа
продолжит снова с начала хромосомы.
Концом программы в данном примере будет уравнение в виде «X*Y» (Рисунок 4).
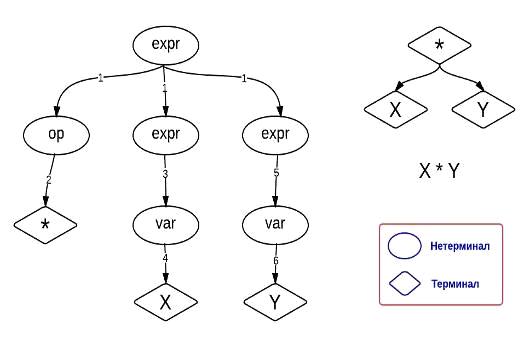
Рис. 4. Пример раскрывания хромосом
Преимущества ГЭ
) Совершенная развязка множества решений (грамматика) с
эволюционным механизмом.
) Простое представление, которое позволяет использовать любой
алгоритм поиска, работающий с двоичными строками.
) Структуры представлены очень эффективно, на высоком уровне они
автоматически сжимаются в двоичные строки.
) Поведение системы можно изменить путём изменения и улучшения
грамматики, при этом основные ГЭ системы никогда не должны изменяться.
Недостатки метода
Несмотря на свои успехи, ГЭ была предметом некоторой критики. Одной из
проблем является то, что в результате операции отображения, генетические
операторы ГЭ не достигают высокой локальности свойства, которая очень актуальна
в эволюционных алгоритмах.
3.3 Аналитическое
Программирование (АП)
Основатель АП является чешский учёный Зелинка Иван, профессор информатики
в техническом университете в Остраве, его исследования проходят в разных
областях, например, искусственного интеллекта, управления и синтеза хаотических
детерминированных систем, биоинформатики и компьютерных вирусов и компьютерной
безопасности.
Базовые принципы АП были разработаны в 2001 году. В то время существовали
только ГП и ГЭ. Грамматическое программирование использовало генетический
алгоритм, в то время как АП мог быть применён с любым эволюционным алгоритмом.
Название «Аналитическое Программирование» было выбрано потому, что АП
представлял синтез аналитического решения, основываясь на эволюционном
алгоритме.
АП был основан на специальном наборе математических объектов и операций.
Набор операций представлял собой функции, операторы и терминалы (также как в
ГП), которые обычно являлись константами или независимыми переменными.
Этот набор переменных обычно раскладывается на группы и описывается в
таком виде:
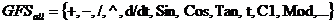
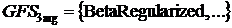
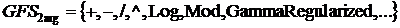
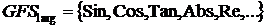
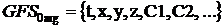
Структура
общего набора функций (GFS) делится на подгруппы в зависимости от количество
аргументов принятых функцией, например 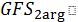
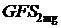 - это
подгруппа функций, которые принимают два аргумента, а
- это
подгруппа функций, которые принимают два аргумента, а 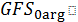
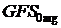 - это
подгруппа терминалов.
- это
подгруппа терминалов.
Такое
деление на подгруппы очень важно для АП чтобы избежать синтеза патологических
программ. Это программы которые содержать функции без аргументов и т.д.
Содержание
общего набора функций (GFS) зависит только от пользователя.
Много
функций и терминалов могут быть использованы вместе в этом наборе [11] [12].
Вторая
часть Аналитического программирования - это ряд математических операций,
которые используются в синтезе программы. Эти операции используются для
преобразования одной части популяции в рабочую программу.
Если
выразиться математическим языком, то эта операция является отображением
отдельного домена в программный домен. Такое отображение состоит из двух
основных частей. Первая часть называется «Обработка дискретного
множества» [13]. Вторая часть отвечает за процедуры безопасности, которые запрещают
синтезирование патологических программ.
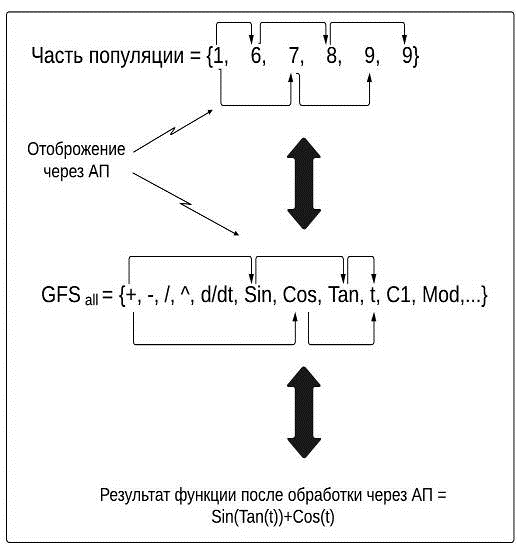
Рис.
5. Принцип работы АП
Создание
программы может быть реализовано с помощью предыдущего рисунка 5, где часть
популяции имеет номера, которые являются индексами множеств GFS.
3.4 Сетевой
оператор
Основная задача сетевого оператора состоит в поиске необходимого
математического выражения. К таким задачам можно отнести
структурно-параметрический синтез системы автоматического управления,
аппроксимацию, идентификацию и другие.
Автором метода сетевого оператора является профессор, доктор технических
наук А.И. Дивеев [14].
Метод сетевого оператора осуществляет поиск математического выражения в
полуавтоматическом режиме.
Значение математического выражения вычисляют с помощью несложного
алгоритма по символьной префиксной записи математического выражения. В
генетическом программировании для поиска решения в виде символьной записи
используют генетический алгоритм.
Принцип работы сетевого оператора
Согласно правилам работы генетического алгоритма первоначально генерируют
множество возможных решений или хромосом в виде строк символов, каждая из
которых представляет собой математическое выражение. Затем оценивают каждое
возможное решение с помощью функции приспособленности, которую для оптимизационных
задач строят на основе целевой функции с учетом ограничений. На следующем этапе
на основе отобранных возможных решений, которые называют родителями, с учетом
их оценок по значениям функции приспособленности воспроизводят новые возможные
решения, которые называют потомками, с помощью специальных операций
генетического алгоритма скрещивания и мутации. Вероятность какого-либо
возможного решения быть использованным для создания нового решения зависит от
его оценки на основе функции приспособленности. Чем лучше возможное решение по
значению целевой функции с учетом ограничений, тем больше вероятность того, что
на его основе будет построено новое, возможно лучшее, решение.
Сетевой оператор - это ориентированный граф, обладающий следующими
свойствами:
) в графе отсутствуют циклы;
) к любому узлу, который не является источником, имеется хотя бы
один путь от узла-источника;
) от любого узла, который не является стоком, имеется хотя бы один
путь до узла-стока;
4) каждому
узлу-источнику соответствует элемент из множества переменных 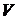 или из множества констант
или из множества констант 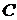 ;
;
) каждому
узлу соответствует бинарная операция из множества  бинарных операций;
бинарных операций;
) каждой
дуге графа соответствует унарная операция из множества 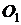 унарных операций.
унарных операций.
Правила вычисления по сетевому оператору:
1) вычисления начинаются с дуги, выходящей из узла, в который не
входит никакая другая дуга;
2) выполняется
унарная, которая соответствует дуге, выходящей из найденного узла и бинарная
операция, соответствующая узлу, в который дуга
<#"656515.files/image081.gif">.
Программная
запись
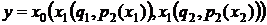 .
.
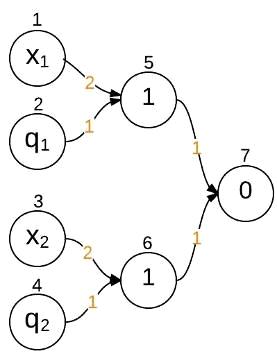
Рис.
6. Древовидная форма сетевого оператора
Графическая
запись
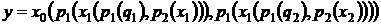
Матрица
сетевого оператора


Сетевой
оператор [14, 15] представляет собой ориентированный граф без циклов, поэтому
его структуру можно описать с помощью матрицы смежности верхнего треугольного
вида.
Матрица
смежности любого ориентированного графа без циклов с помощью изменения номеров
узлов всегда может быть представлена в верхнем треугольном виде.
Матрица
<#"656515.files/image087.gif">, а остальные элементы либо нули, либо номера унарных
операций 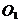 , причем при замене диагональных элементов на нули, а
ненулевых недиагональных элементов на единицы получаем матрицу смежности графа
сети.
, причем при замене диагональных элементов на нули, а
ненулевых недиагональных элементов на единицы получаем матрицу смежности графа
сети.
Чтобы
представить граф в памяти компьютера используется матрица смежности (показывает
какой узел, с каким узлом соединяется), которая состоит из 1 и 0, имеет
размерность 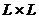 , где
, где 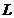 - число
узлов в графе. 1 находится на пересечении
- число
узлов в графе. 1 находится на пересечении 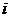 строки и
строки и
 столбца, где
столбца, где 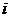 - номер
узла, откуда выходит дуга, а
- номер
узла, откуда выходит дуга, а  - номер
узла, куда входит дуга. Для графической записи желательно пронумеровать узлы
так, чтобы номер узла, из которого дуга выходит, был меньше, чем номер узла, в
который дуга входит. Для ориентированного графа без циклов это всегда можно
сделать. Матрица сетевого оператора имеет ту же структуру, что и матрица
смежности, только вместо единиц стоят номера унарных операций
- номер
узла, куда входит дуга. Для графической записи желательно пронумеровать узлы
так, чтобы номер узла, из которого дуга выходит, был меньше, чем номер узла, в
который дуга входит. Для ориентированного графа без циклов это всегда можно
сделать. Матрица сетевого оператора имеет ту же структуру, что и матрица
смежности, только вместо единиц стоят номера унарных операций 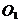 , а на диагоналях стоят номера бинарных операций
, а на диагоналях стоят номера бинарных операций 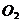 .
.
4. Разработка
алгоритма решения задачи
4.1 Генетический алгоритм
Генетический алгоритм - адаптивный метод поиска, который в последнее
время часто используется для решения задач функциональной оптимизации. Он
основан на генетических процессах биологических организмов: биологические
популяции развиваются в течение нескольких поколений, подчиняясь законам
естественного отбора и по принципу «выживает наиболее приспособленный» [15].
Подражая этому процессу генетический алгоритм способен “развивать” решения
реальных задач, если те соответствующим образом закодированы. Генетический
алгоритм может использоваться для проектирования структуры моста, поиска
максимального отношения прочности, для использования интерактивного управления
процессом или балансировании загрузки на многопроцессорном компьютере. Основные
принципы генетического алгоритма были сформулированы Голландом (Holland, 1975)
[15]. Алгоритм моделирует те процессы в популяциях, которые являются
существенными для развития. Генетический алгоритм работает с совокупностью
“особей” - популяцией, каждая из которых представляет возможное решение данной
проблемы. Каждая особь оценивается мерой ее “приспособленности” согласно тому,
насколько “хорошо” соответствующее ей решение задачи. Воспроизводится вся новая
популяция допустимых решений, выбирая лучших представителей предыдущего
поколения, скрещивая их и получая множество новых особей. Это новое поколение
содержит более высокое соотношение характеристик, которыми обладают хорошие
члены предыдущего поколения. Таким образом, из поколения в поколение, хорошие
характеристики распространяются по всей популяции. Скрещивание наиболее
приспособленных особей приводит к тому, что исследуются наиболее перспективные
участки пространства поиска. В конечном итоге, популяция будет сходиться к
оптимальному решению задачи.

Рис. 7. Принцип работы генетического алгоритма
Преимущество генетического алгоритма:
) Поиск оптимального решения осуществляется в кодовом пространстве;
) С каждым разом после операции селекции мы получаем две новые
пары, которые являются возможным решением.
) Благодаря множеству операций (селекция, мутация, скрещивания)
можно получить разнообразный набор возможных решений.
) ГА имеет множество способов завершения вычислений. Например, он
может ограничить по числу циклов воспроизводство популяций возможных решений
или завершить вычисление после достижения удовлетворительного решения функции
приспособленности.
Генетический алгоритм [15] является достаточно мощным средством и может с
успехом применяться для широкого класса прикладных задач, включая те, которые
трудно, а иногда и вовсе невозможно, решить другими методам. Однако,
генетический алгоритм, как и другие методы эволюционных вычислений, не гарантирует
обнаружения глобального решения за полиномиальное время, не гарантирует и того,
что глобальное решение будет найдено, но они хороши для поиска «достаточно
хорошего» решения задачи «достаточно быстро». Главным же преимуществом
генетического алгоритма является то, что они могут применяться даже на сложных
задачах, там, где не существует никаких специальных методов.
4.2 Грамматическая
эволюция
В данной дипломной работе был применён метод грамматической эволюции для
решения задачи синтеза, и для реализации этого использовался язык
программирования Python [16] в
среде Eclipse [17].
Python
- является высокоуровневым языком программирования общего назначения,
ориентированным на повышение производительности разработчика и читаемости кода.
Синтаксис ядра Python минималистичен.
Python
был выбран специально для этой задачи благодаря его лёгкости обращения со
структурами.
Важно отметить, что неявное преобразование типов в Python очень помогла в поставленной задаче,
а именно в реализации метода грамматической эволюции, где множества правил в
виде строк (String) преобразуются в решение в виде
функции.
eval -
одна из важнейших функций языка Python,
которая в качестве аргумента принимает строку и воспроизводит её как выражение
Python. еval может возвращать число, строку, список,
кортеж и т.д.
Эклипс (Eclipse) - это свободная интегрированная
среда разработки модульных кроссплатформенных приложений, которая поддерживает
язык Python.
Метод ГЭ, который был описан ранее, был выбран для решения поставленной
задачи с продукционными правилами, подходящими для задачи синтеза управления. В
следующей таблице представлено множество правил использованных в ГЭ в данной
дипломной работе.
Таблица. 3. Продукционные правила для синтеза системы управления
|
нетерминалаы
|
раскладывания
|
Индекс
|
|
expr
|
expr op expr
fun1(expr) fun2(expr,expr)
var
|
0 1 2 3
|
op +
-  0’
0’
’
|
var
|
Xk[0] Xk[1] q1
q2
|
0’’ 1’’ 2’’ 3’’
|
|
fun1
|
sqr sign atan
minus sqrtX sin step plfun1 plfun2
|
0’’’ 1’’’ 2’’’
3’’’ 4’’’ 5’’’ 6’’’ 7’’’ 8’’’
|
|
fun2
|
divX
|
0’’’’
|
В Таблице 3 представлено множество продукционных правил в форме БНФ для
реализации генетического алгоритма в данной работе.
Множество состоит из пяти нетерминалов, где expr - это выражение, которое можно разложить на 4 вида:
1) expr op expr - операция из множества op, которая находится между двумя
выражениями.
2) fun1(expr) - функции принимающие один
аргумент.
3) fun2(expr,expr) - функции принимающие два аргумента.
4) var - множество терминалов, которое состоит из переменных.
Множество op состоит из
любых возможных математических операторов.
Множество
var состоит из переменных xk[0], xk[1]
и параметров q1 и q2, где xk[0] - это 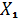
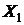 , xk[1]
- это
, xk[1]
- это 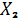
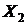
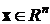 , (19)
, (19)
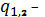
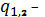 коэффициенты
функции управления.
коэффициенты
функции управления.
Множество
fun1 и fun2 состоят из следующих функций:
) sqr
соответствует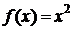 ;
;
) sign
соответствует 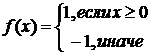 ;
;
) atan
соответствует 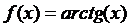 ;
;
) minus
соответствует 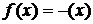 ;
;
) sqrtX
соответствует 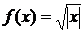 ;
;
) sin
соответствует 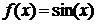 ;
;
) step
соответствует  ;
;
) plfun1
соответствует 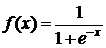
) plfun2
соответствует 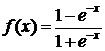
10) divX
соответствует делению с некоторыми ограничениями.
Пример работы ГЭ в проекте:
Вектор чисел = [17,14,40,55,23,32,45,57,11,8]
С помощью продукционных правил в таблице 3 можно получить функцию по
следующей схеме:
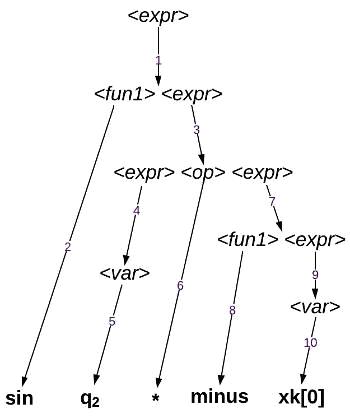
Рис. 8.
После получения функции sin(q2 * minus(xk[0]))
и замены параметров и значений переменных, функция ограничивается множеством
допустимых решений.
При решении многокритериальных задач, для определения оптимального
результата используется множество Парето.
Эффективность по Парето
Оптимальность по Парето - такое состояние системы, при
котором значение каждого частного показателя, характеризующего систему, не
может быть улучшено без ухудшения других.
Таким образом, по словам самого Парето: «Всякое
изменение, которое никому не приносит убытков, а некоторым людям приносит
пользу (по их собственной оценке), является улучшением». Значит, признаётся
право на все изменения, которые не приносят никому дополнительного вреда.
Множество решений, оптимальных по Парето, называют
«множеством Парето».
Эффективность по Парето [18] является одним из центральных понятий для
современной экономической науки, а также применяется в задачах оптимального
управления. В случаях, когда задан набор возможных решений и из этих решений
нужно выбрать самое оптимальное, построение их на Парето-плоскости может
повысить эффективность поиска оптимальной точки по каким-либо параметрам.
График границы Парето, выглядеть следующим образом.
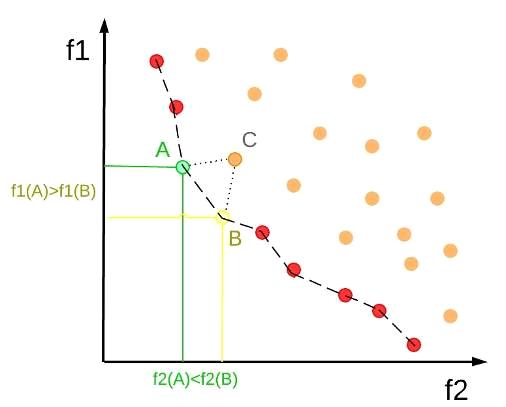
Рис. 9.
Круглые точки на графике показывают возможные решения (лучшие решения те,
которые меньшие по значению).
Точка С не находится на границе Парето потому, что точки А и В являются
ближе к оптимальности и доминируют над точкой С.
Точки А и В находятся на границе и ни одна из них не доминирует над
другой.
Оптимальное решение в задачах поиска в большинстве случаев требует
минимизировать значение функции. В нашей задаче нужно построить систему
управления, соответствующую двум критериям: времени и точности попадания в
заданную точку.
5.
Вычислительный эксперимент
Поставленная задача синтеза управления была рассмотрена на примере
системы уравнений осциллятора Дуффинга [19]. Из заданных начальных условий
система должна прийти в терминальную точку (0,0) за минимальное время.
Осциллятор Дуффинга
Осциллятор Дуффинга представляет собой механическую систему, которая
состоит из тонкой металлической стрелки и двух магнитов внутри стабильной
рамки. Стрелка является достаточно тонкой, поэтому стрелка прилипает к одному
магниту и останется в той же положений пока на систему не подействует другая
сила. Существует сила, которая периодически воздействует на рамку и не даёт
стрелке остаться в одном положении. Чем большая сила влияет на рамку, тем
больше стрелка будет колебаться между двумя магнитами, а в случае уменьшения
этой силы, стрелка будет стремиться к одному магниту.

Рис. 10. Осциллятор Дуффинга
Осциллятор Дуффинга можно представить следующими уравнениями [20]:
 , (20)
, (20)
Где,
 - точка фиксации конца стрелки;
- точка фиксации конца стрелки;
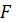
 -
магнитуда периодической силы, которая действует на рамку;
-
магнитуда периодической силы, которая действует на рамку;
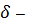
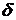 -
коэффициент затухания (всегда больше или равен нулю);
-
коэффициент затухания (всегда больше или равен нулю);
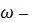
 -
частота силы.
-
частота силы.
Следующее
уравнение описывает силу, которая возвращает стрелку к точке её равновесия:
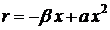 , (21)
, (21)
Нефорсированный осциллятор Дуффинга
Обычный вид системы Дуффинга - нефорсированный (стабильный).
Это происходит, когда F = 0.
Уравнение системы будет выглядеть следующим образом:
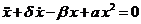 , (22)
, (22)
Представляем
уравнение (22) в виде дифференциальных уравнений первого порядка. Пусть 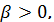
 тогда:
тогда:
Отсюда
можно найти 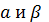
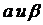 полагая,
что
полагая,
что 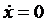
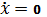 и
и 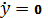
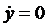 ,
,
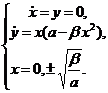 (24)
(24)
После
проведения ряда экспериментов над системой Дуффинга с разными коэффициентами
затухания, с разными значениями 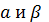
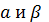 и
разными начальными условиями, были получены следующие результаты:
и
разными начальными условиями, были получены следующие результаты:
В
таблице 4 представлены параметры генетического алгоритма использованного в
программе:
Таблица. 4. Параметры генетического алгоритма данной программе
|
Параметр
|
Значение
|
|
Размер популяции (Lenppl)
|
72
|
|
Число поколений (Niter)
|
32
|
|
Число пар в одном поколении
|
36
|
|
Число функционалов
|
2
|
Исследование 1:
Условия запуска:
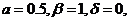
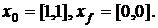
Таблица.
5. Результаты исследования № 1
|
№ запуск
|
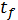 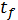 (с) (с)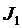 Время работы программы (с) Время работы программы (с)
|
|
|
|
1
|
2.77
|
0.009
|
654
|
|
2
|
2.54
|
0.004
|
588
|
|
3
|
2.26
|
2.5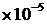 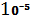 528 528
|
|
|
4
|
6.67
|
5.78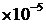 424 424
|
|
|
5
|
8.15
|
0.0001
|
623
|
|
6
|
6.6
|
6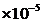 523 523
|
|
|
7
|
6.85
|
2.59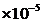 725 725
|
|
|
8
|
4.51
|
4.16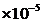 640 640
|
|
|
9
|
10
|
0.0013
|
835
|
|
10
|
4.03
|
7.12 709 709
|
|
После проведения 10 запусков с одинаковыми параметрами, были получены
результаты в Таблице 5. Далее представлены графики управления и фазовой
траектории самого лучшего результата:
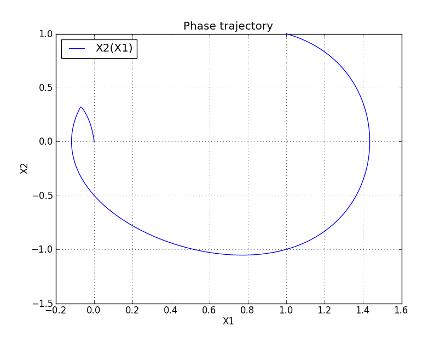
Рис. 11. Фазовая траектория Запуска № 10
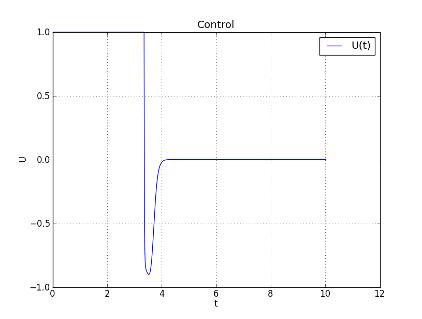
Рис. 12. Управление u(t) запуска № 10
Функция управления № 10 имеет следующий вид:
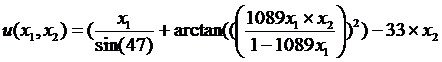 .
.
Исследование 2:
Условия запуска:
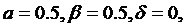
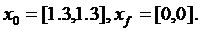
Таблица.
6. Результаты исследования № 2
|
№ запуск
|
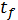 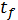 (с) (с)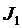 Время работы программы(с) Время работы программы(с)
|
|
|
|
1
|
10
|
0.0015
|
682
|
|
2
|
10
|
0.0013
|
662
|
|
3
|
8.62
|
0.00027
|
790
|
|
4
|
7.15
|
0.00036
|
623
|
|
5
|
8.69
|
0.00044
|
786
|
|
6
|
9.96
|
0.00061
|
633
|
|
7
|
10
|
0.0005
|
711
|
|
8
|
3.02
|
2.257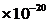 600 600
|
|
|
9
|
9.35
|
0.0008
|
691
|
|
10
|
6.55
|
3.36 874 874
|
|
После проведения 10 запусков с одинаковыми параметрами, были получены
результаты в Таблице 6. Далее представлены графики управления и фазовой
траектории самого лучшего результата:
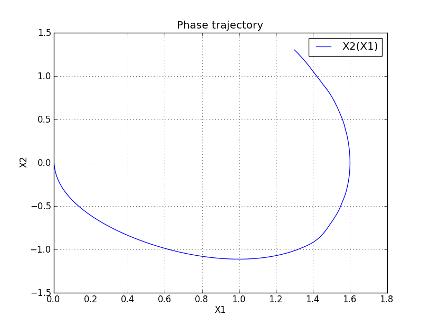
Рис. 13. Фазовая траектория Запуска № 8
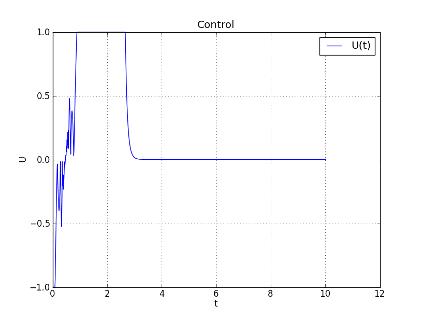
Рис. 14. Управление u(t) запуска № 8
Функция управления № 8 имеет следующий вид:
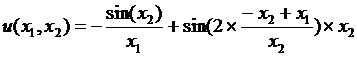 .
.
Исследование
3:
Условия
запуска:
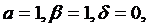
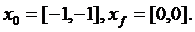
Таблица.
7. Результаты исследования № 3
|
№ запуск
|
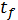 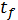 (с) (с)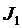 Время работы программы(с) Время работы программы(с)
|
|
|
|
1
|
8.83
|
0.0001
|
685
|
|
2
|
3.83
|
0.0004
|
628
|
|
3
|
9.94
|
0.0009
|
338
|
|
4
|
3.94
|
2.3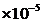 621 621
|
|
|
5
|
3.51
|
1.26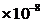 589 589
|
|
|
6
|
3.64
|
1.66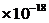 906 906
|
|
|
7
|
10
|
0.0017
|
396
|
|
8
|
5
|
9.57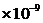 768 768
|
|
|
9
|
8.69
|
0.0007
|
482
|
|
10
|
3.19
|
2.77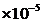 704 704
|
|
После проведения 10 запусков с одинаковыми параметрами, были получены
результаты в Таблице 7. Далее представлены графики управления и фазовой траектории
самого лучшего результата:
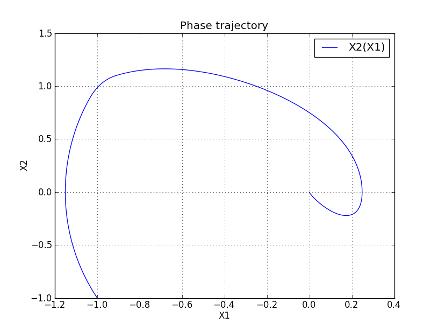
Рис. 15. Фазовая траектория Запуска № 8
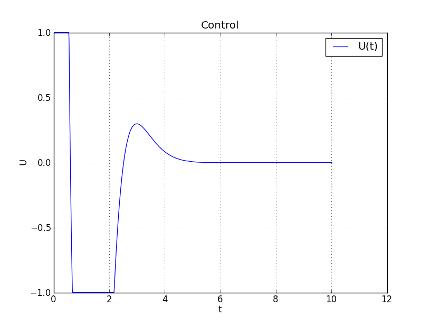
Рис. 16. Управление u(t) запуска № 8
Функция управления № 8 имеет следующий вид:
 .
.
Исследование
4:
В
исследование № 4 были зафиксированы 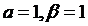 , а
начальные точки поиска изменены. Было проведено 4 запуска, представленные в
таблице:
, а
начальные точки поиска изменены. Было проведено 4 запуска, представленные в
таблице:
Таблица.
8. Результаты исследования № 4
|
№ запуск
|
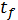 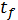 (с) (с)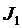 Время работы программы(с) Время работы программы(с)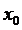
|
|
|
|
|
1
|
10
|
0,009
|
617
|

|
|
2
|
9
|
9,4*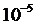 481 481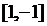
|
|
|
|
3
|
10
|
0,0019
|
546
|
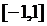
|
|
4
|
10
|
0,0013
|
509
|
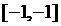
|
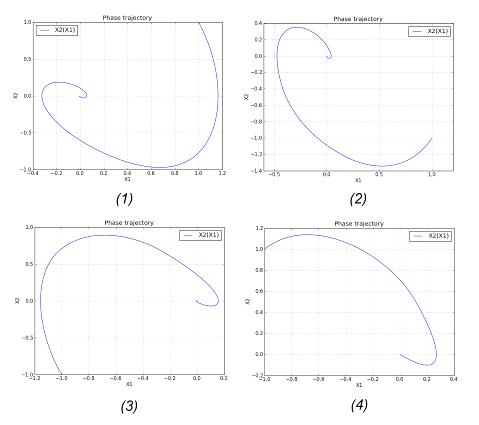
Рис. 17. ФТ для всех запусков в исследование № 4

Рис. 18. Управление u(t) запуска № 2
На рис. 18 представлен график функции управления №2, которая имеет
наилучшие значение функционала в эксперименте № 4.
 .
.
Заключение
В данной дипломной работе было осуществлено решение следующих задач:
) Разработан и исследован метод грамматической эволюции для
решения задачи синтеза системы управления, который является методом символьной
регрессии. Определены его свойства и преимущества.
) Рассмотрена БНФ-форма записи, с помощью которой была построена
функция из набора правил и вектора чисел.
) Программа, реализующая алгоритм для решения задачи оптимального
управления и синтеза системы управления на основе генетического
программирования с применением грамматической эволюции разработана в среде Eclipse Indigo. Несмотря на всю представленную сложность, алгоритм
управления можно реализовать на ЭВМ.
) На основе метода грамматической эволюции и генетического
алгоритма разработан алгоритм для решения задачи синтеза системы управления и
получено управление объектом (осциллятор Дуффинга).
) Исследован объект осциллятор Дуффинга и в виде системы
дифференциальных уравнений был реализован в программе. Сделано множество
запусков программы и были получены результаты, которые представлены в виде
таблиц и графиков.
Список литературы
1. Алексеев
В. М., Тихомиров В. М., Фомин С. В. Оптимальное управление. - М.: Наука, УДК
519.6, - 223 c., 1979, 406 с.
. Колесников
А.А. Аналитическое конструирование нелинейных оптимальных систем.Таганрог:
Изд-во ТРТУ, 1984, 72 с.
. Рафиков
Г.Ш. Цифровые системы управления. Конспект лекций. - Донецк, 1999, 102 с.
4. Tsinias
J. Sufficient Lyapunov-like conditions for stabilization Mat. Contr. Signals Syst. 1989. Vol. 2.
#12. Pр 343 - 357.
. Егоров
А. И. Оптимальное управление тепловыми и диффузионными процессами. М.: Наука,
1978, 468 с.
6. Bellman,
R.E. 1957. Dynamic Programming. Princeton University Press, Princeton, NJ. Republished 2003: Dover, 339 p.
7. Koza,
J.R. Genetic Programming: On the Programming of Computers by Means of Natural
Selection (Complex Adaptive Systems). 1992, 840 pages.
. Koza
J.R., Bennet F.H., Andre D., Keane M., Genetic Programming III, Morgan Kaufnamm
pub., 2002, 393 p.
. Genetic
Programming III: Darwinian Invention and Problem Solving by John R. Koza
(Stanford University), Forrest H Bennett III (Genetic Programming Inc.), David
Andre (University of California at Berkeley), Martin A. Keane (Econometrics
Inc.), 1999, 1154 p.
. Ryan
C., Collins J.J., O'Neill M. Grammatical Evolution: Evolving Programs for an
Arbitrary Language. Lecture Notes in Computer Science 1391. First European
Workshop on Genetic Programming 1998, 160 p.
. Zelinka
I., 2002: Analytic programming by Means of Soma Algorithm. Mendel ’02, In:
Proc. 8th International Conference on Soft Computing Mendel’02, Brno, Czech
Republic, 2002, pр 93-101.
. Zelinka
I., Oplatkova Z.: 2003: Analytic programming - Comparative Study. CIRAS’03, The
second International Conference on Computational Intelligence, Robotics, and
Autonomous Systems, Singapore, 2003, 560 p.
. Lampinen
J., Zelinka I.,1999,New Ideas in Optimization - Mechanical Engineering Design
Optimization by Differential Devolution, Volume 1. London: McGraw-hill, 1999,
20 p.
14. Дивеев
А.И., Сафронова Е.А. Метод сетевого оператора и его применение в задачах
управления. - М.: РУДН, 2012. - 182 с.
. Дивеев
А. И., Софронова Е. А. Основы генетического программирования
Учебно-методическое пособие - М.: Изд-во РУДН, 2006, 180 с.
. Марк
Лутц. Программирование на Python / Пер. с англ. - 4-е изд. - СПб.: Символ-Плюс,
2011. - Т. II. 992 с.
. Официальный
сайт проекта Eclipse, 2003-2013. URL: http://www.eclipse.org (Дата обращения: 28.05.2013).
18. Godfrey,
Parke; Shipley, Ryan; Gryz, Jarek (2006). Algorithms and Analyses for Maximal
Vector Computation, 2006, VLDB Journal 16: p 5-28.
. Chua
V., Cubic-Quintic Duffing Oscillators, Atlanta, 2003, 19 pages. Retrieved from
http://www.its.caltech.edu/ mason/research/duf.pdf.
. Wolfram
MathWorld. (n.d.). Dung Deferential Equation, 1999-2013. URL:
http://mathworld.wolfram.com (Дата обращения: 29.05.2013).
Приложение 1
Листинг модуля MainProg:GenetikAlg import
InitialPop, gaproblem import Criterion, ForGraphic, PhaseTrajectory,
GraphicUcProfiletime
#############################################################main():=6=40=72=32_t=time.time()=InitialPop(LenP,
LenPPL, n),func=ga(PPL, Criterion, NIter, n, LenP,
LenPPL)_t=time.time()-start_tp, funcstop_t,x2,u,t=ForGraphic(p[:-2], p[-2],
p[-1])(x1,x2)(u,t)__name__=="__main__":
#cProfile.run('main()')()
Листинг модуля GenetikAlg:ParetoDomination import
Paretorandom import random,randintmath import ceil, sqrt
###########################################
def bin2dec(b): # переводит двоичный код в десятичное число
s=''i in b: s+=str(i)int(s,2)merger(ppl,lenp,lenppl): # объединяет подмножества в хромосомеi in xrange(lenppl):=[]j in xrange(lenp+2): x+=ppl[i][j][i]=xppldem(ch,n,lenp):
# разделяет хромосому на подмножества=0=[0]*(lenp+2)(ii+n)<=len(ch):i in
xrange(lenp+2):=ch[ii:ii+n]+=n[i]=bchiInitialPop(lenp,lenppl,n): # гнерирует начальную популяцию=[[[randint(0,1) for ii in
xrange(n)]j in xrange(lenp+2)] for i in
xrange(lenppl)]pplTournament(ppl,fit,lenppl): # турнирный отбор=[0]*lenppli in
xrange(lenppl):=randint(0,lenppl-1)=randint(0,lenppl-1)i1==i2:i1==i2:
i2=randint(0,lenppl-1)=max(fit[i1],fit[i2])[i]=ppl[fit.index(win)]parentsSelection(ppl,fit,lenppl):
# отбор родителей со случайной вероятностью=[0]*lenppli in
xrange(0,lenppl-1,2):= random()= randint(0,lenppl-1)=
randint(0,lenppl-1)fit[i1]<p: i1 = randint(0,lenppl-1)fit[i2]<p: i2 =
randint(0,lenppl-1)[i]=ppl[i1][i+1]=ppl[i2]parentsCrossover(parent,lenppl,ch,m,CrossType):
# скрещивание=ch=ch+1CrossType=='Single-point':=randint(1,len(parent[i1])-(2+2*m))=parent[i1][:n]+parent[i2][n:-2*m]+parent[i1][-2*m:]=parent[i2][:n]+parent[i1][n:-2*m]+parent[i2][-2*m:]CrossType=='Two-points':=len(parent[i1])=randint(1,lenpar1-2)=randint(1,lenpar1-2)n==n1:n==n1:
n1=randint(1,lenppl-2)n<n1:=parent[i1][:n]+parent[i2][n:n1]+parent[i1][n1:]=parent[i2][:n]+parent[i1][n:n1]+parent[i2][n1:]n1<n:=parent[i1][:n1]+parent[i2][n1:n]+parent[i1][n:]=parent[i2][:n1]+parent[i1][n1:n]+parent[i2][n:]child1,child2Mutation(genom):
# мутацияi in
xrange(len(genom)):=random()P<=1.0/(3.0+i):genom[i]==1: genom[i]=0:
genom[i]=1genomga(P,fun,Nitr,n,lenp,lenppl): # генетический алгоритм=0=Pareto()=[fun([bin2dec(P[j][i])
for i in xrange(lenp)],dec(P[j][-2]) , bin2dec(P[j][-1]) ) for j in
xrange(lenppl)]=obj.assign_ranks(func)=obj.set_fitness_from_ranks(rank,lenppl)itr<Nitr:+=1itr=Selection(P,fit,lenppl)=merger(par,lenp,lenppl)=[]i
in xrange(lenppl/2):,ch2=Crossover(par,lenppl,i*2,n,CrossType='Single-point')=Mutation(ch1)=Mutation(ch2).append(dem(ch1,n,lenp)).append(dem(ch2,n,lenp))=P+Q=[fun([bin2dec(PQ[j][i])
for i in xrange(lenp)],dec(PQ[j][-2]), bin2dec(PQ[j][-1])) for j in
xrange(2*lenppl)]=obj.assign_ranks(f2)=obj.set_fitness_from_ranks(rank2,2*lenppl)=zip(fit,range(2*lenppl)).sort()=[fitz[i][0]
for i in xrange(2*lenppl)]=[PQ[fitz[i][1]] for i in
xrange(2*lenppl)]=fit[lenppl:]=P[lenppl:]=[bin2dec(i) for i in
P[-1]]=f2[fitz[-1][1]][:]best,q
Листинг модуля grammer_evolution:math import
*gramevo(p):=['(<expr>)<op>(<expr>)','<fun1>(<expr>)',
'<fun2>(<expr>,<expr>)','<var>']=['sqr','sign','atan','minus','sqrtX','sin','step','plfun1','plfun2']=['divX']=['+','-','*']=['xk[0]','xk[1]','q1','q2']='<expr>'=1=0v!=-1:i
in range(len(p)):=fun.find('<')fun[v+1:v+5]=='expr':bool1==1:=p[i] %
len(expr)= fun[:v] + expr[m] + fun[v+6:]:= fun[:v] + '<var>' +
fun[v+6:]fun[v+1]=='f' and fun[v+4]=='1':=p[i] % len(fun1)= fun[:v] + fun1[m] +
fun[v+6:]fun[v+1]=='f' and fun[v+4]=='2':=p[i] % len(fun2)= fun[:v] + fun2[m] +
fun[v+6:]fun[v+1]=='o':=p[i] % len(op)= fun[:v] + op[m] +
fun[v+4:]fun[v+1]=='v':=p[i] % len(var)= fun[:v] + var[m] +
fun[v+5:]v==-1:=0fun
Листинг модуля Prod_laws:math import sqrt,
expminus(x):-(x)sqrtX(x):sign(x)*sqrt(abs(x))sqr(x):x**2sign(x):x>0 or x==0:
result=1: result=-1resultstep(x):x>0 or x==0: y=1:
y=0yplfun1(x)::=round(1/(1+exp(-x)),6):sign(x)==-1:=0sign(x)==1:=1resultplfun2(x)::=round((1-exp(-x))/(1+exp(-x)),6):sign(x)==-1:=0sign(x)==1:=1resultdivX(x,
y)::= x / y:= sign(x) * sign(y) * 10e+8
return z
Листинг модуля RK4:
def rk4(func,dt,time,x,u):
#time=0
#x = x1[:]=len(x[0])=func(time,x[-1],u)[-1]=[dt*f[i] for i in
xrange(n)]=func(time+(dt/2),[x[-1][i]+(k1[i]/2) for i in xrange(n)],u)=[dt*f[i]
for i in xrange(n)]=func(time+(dt/2),[x[-1][i]+(k2[i]/2) for i in
xrange(n)],u)=[dt*f[i] for i in xrange(n)]=func(time+dt,[x[-1][i]+k3[i] for i
in xrange(n)],u)=[dt*f[i] for i in xrange(n)]
return [x[-1][i]+(1.0/6.0)*(k1[i]+2*k2[i]+2*k3[i]+k4[i]) for
i in xrange(n)]
Листинг модуля ParetoDomination:
class Pareto:dominate(self,
F1, F2):= Falsei in range(len(F1[1])):F1[1][i] > F2[1][i]:= TrueF2[1][i]
> F1[1][i]:Falsednon_dominated_front(self, Group):= []G in Group:.append(G)=
Front[:]C in Front:G != C:self.dominate(G, C):.remove(G)self.dominate(C,
G):.remove(C)= tmpFront[:]Frontassign_ranks(self, functionals):_functionals =
[(i, functionals[i]) for i in range(len(functionals))]= []= 0tmp_functionals !=
[]:.append(self.non_dominated_front(tmp_functionals))R in
ranks[i]:_functionals.remove(R)+= 1
# print
ranksranksset_fitness_from_ranks(self, ranks, pop_size):= [0.0 for i in
range(pop_size)]= 0.0R in ranks:e in R:[e[0]] = 1.0 / (1.0 + cr)+= 1
return Fitness
Листинг модуля ParetoDomination:
from grammar_evolution import gramevoprod_laws import *RK4
import rk4Euler2method import Euler2math import *matplotlib.pyplot as
pltoperator import *
#############################################=2=[1,1]=[0.0,0.0]=10.0=0.01
#############################################Sys1(time,x,u):=
[x[1], u]i in xrange(2):y[i]>=1e8: y[i]=sign(y[i])*1e8yDuffing(time,x,u):=1=1=[x[1],u-B*x[0]-(a*(x[0]**3))]i
in xrange(2):y[i]>=1e8: y[i]=sign(y[i])*1e8ynorma(x,xf):=0.0i in
xrange(len(xf)): s+=(xf[i]-x[i])**2sqrt(s)Criterion(p, qx1,
qx2):=qx1=qx2=[[x0[i] for i in xrange(LenSys)]]=0_err=0=False= tf= 1e+8(t<=tf):=
x[-1][:]:=eval(gramevo(p))u>1.0: u=1.0u<-1.0: u=-1.0:_err=1e+8xk, q1,
q2gramevo(p)eval(gramevo(p))=
1.0+=dt.append(rk4(Duffing,dt,t,x,u))=norma(x[-1],xf)s<=1e-3:flag == False:=
t= True:= t= False= s[Ft, Fm+miss_err]ForGraphic(p, qx1, qx2):=qx1=qx2=[]=[]=[]=[]=[[x0[i]
for i in xrange(LenSys)]]=0(t<=tf):= x[-1][:]=eval(gramevo(p))u>1.0:
u=1.0u<-1.0: u=-1.0+=dt.append(rk4(Duffing,dt,t,x,u))
# s=norma(x[-1],xf)+=[u]+=[t]e in
x:.append(e[0]).append(e[1])x1,x2,ug,tgPhaseTrajectory(x1,x2):.plot(x1,x2,label='X2(X1)').title('Phase
trajectory').xlabel('X1').ylabel('X2').legend(loc='best').grid(True).show()GraphicU(u,t):.plot(t,u,label='U(t)').title('Control').xlabel('t').ylabel('U').legend(loc='best').grid(True).show()GraphicX1(x1,t):.plot(t,x1,label='X1(t)').title('Graphic
X1').xlabel('t').ylabel('X1').legend(loc='best').grid(True).show()GraphicX2(x2,t):.plot(t,x2,label='X2(t)').title('Graphic
X2').xlabel('t').ylabel('X2').legend(loc='best').grid(True)
plt.show()