Програма обчислення другої похідної за інтерполяційною формулою Стірлінга
Анотація
Об’єктом
дослідження є інтерполяційний многочлен Стірлінга для чисельного
диференціювання функцій. Розроблено оптимальний алгоритм та програму в
середовищі системи Turbo
Pascal як за
розміром пам'яті, необхідної для збереження даних, котрі обчислюються в ході
виконаного алгоритму, так і за кількістю арифметичних операцій для обчислення
за основною формулою. Програма має зручний та наочний інтерфейс, котрий
максимально спрощує роботу з нею.
Зміст
Вступ
. Аналіз теоретичної бази
методів чисельного диференціювання функції
.1 Формули наближеного
диференціювання, основані на першій інтерполяційній формулі Ньютона
.2 Формули наближеного
диференціювання, основані на першій інтерполяційній формулі Гауса
.3 Формули наближеного
диференціювання, основані на інтерполяційній формулі Бесселя
.4 Формули наближеного
диференціювання, основані на інтерполяційній формулі Стірлінга
.5 Приклад чисельного
диференціювання методом Стірлінга
. Розробка алгоритмів та вибір
оптимального алгоритму
. Алгоритм та програма обчислення
другої похідної за інтерполяційною формулою Стірлінга
.1 Інструкція користувача
.2 Лістинг програми
.3 Опис програми
.4 Тестування програми
Висновки
Перелік посилань
Вступ
Актуальність теми.
При рішенні інженерно-технічних і
інших прикладних завдань часто буває необхідно знайти похідну певного порядку
від функції, заданої таблично. Крім того, іноді через складність аналітичного
вираження функції її безпосереднє диференціювання занадто складне. У цих
випадках зазвичай використовують чисельне диференціювання. Тут існує безліч
різних прийомів і способів. Однією з найпростіших формул для обчислення
похідної функції є формула обчислення похідної через рівновіддалені вузли.
Найточнішими серед них є симетричні методи диференціювання, один серед них оснований
на формулі чисельного інтерполювання Стірлінга.
Мета дослідження.
Метою роботи є дослідження
можливості використанням інтерполяційного многочлена Стірлінга при обчислені
похідних для таблично заданих функцій, а також функцій заданих графічно та
аналітично.
Задачі дослідження:
· проаналізувати
існуючі методи знаходження значення похідних для випадків рівновіддалених та
нерівновіддалених значень аргументу, та обґрунтувати переваги використання
інтерполяційного многочлена Стірлінга по відношенню до існуючих;
· розробити алгоритми
обчислення значення похідної та здійснити вибір оптимального з них;
· розробити
програму розв’язку чисельного диференціювання з використанням інтерполяційного
многочлена Стірлінга та провести її тестування.
Об’єкт дослідження.
Об’єктом дослідження є многочлен Стірлінга для
чисельного диференціювання.
Структура курсової
роботи.
Курсова робота
складається з трьох основних розділів. В першому розділі наведено аналіз
теоретичної бази методів чисельного диференціювання функцій та приклад
застосування за формулою Стірлінга. У другому розділі розроблено оптимальний
алгоритм за критерієм комплексної ефективності, що враховує затрати часу та
пам'яті для його виконання, за даним методом. Третій розділ містить інструкцію
користувача, лістинг програми, опис програми та результати тестування.
1.
Аналіз теоретичної бази методів чисельного диференціювання функції
При розв’язуванні практичних
задач часто потрібно знайти похідну вказаних порядків від функції  , заданої
таблично. Також можливо, що в силу складності аналітичного виразу функції
, заданої
таблично. Також можливо, що в силу складності аналітичного виразу функції 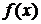 неопосередковане
диференціювання її викликає труднощі. В цих випадках звичайно звертаються до
наближеного диференціювання.
неопосередковане
диференціювання її викликає труднощі. В цих випадках звичайно звертаються до
наближеного диференціювання.
Для виведення формул
наближеного диференціювання замінюють дану функцію 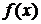 на
потрібному відрізку
на
потрібному відрізку  інтерполяційної
функцією
інтерполяційної
функцією 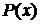 (частіше
всього поліномом), а потім покладають:
(частіше
всього поліномом), а потім покладають:
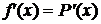 (1)
(1)
при  .
.
Аналогічно роблять при
знаходженні похідних вищих порядків функції 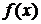 .
.
Якщо для інтерполяційної
функції 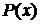 відома
похибка
відома
похибка 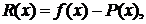 то похибка
похідної
то похибка
похідної 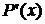 виражається
формулою
виражається
формулою
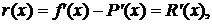 (2)
(2)
Тобто похибка похідної
інтерполяційної функції рівна похідній від похибки цієї функції. Це також
вірно і для похідних вищих порядків.
Слід відмітити, що взагалі
наближене диференціювання являє собою операцію менш точну, ніж інтерполювання.
Дійсно близькість одна до одної ординат двох кривих  і
і  на відрізку
на відрізку
 ще не
гарантує знаходження близько друг до другу їх похідних
ще не
гарантує знаходження близько друг до другу їх похідних  і
і 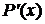 , тобто
малого розходження кутових коефіцієнтів дотичних до даних кривих при однакових
значеннях аргументу (рис. 1.1).
, тобто
малого розходження кутових коефіцієнтів дотичних до даних кривих при однакових
значеннях аргументу (рис. 1.1).

Рисунок 1.1 Процес чисельного
диференціювання
1.1 Формули наближеного
диференціювання, основані на першій інтерполяційній формулі Ньютона
Нехай маємо функцію 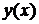 , задану в
рівностоячих точках
, задану в
рівностоячих точках 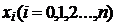 відрізка
відрізка  за
допомогою значень
за
допомогою значень  . Для
знаходження на
. Для
знаходження на  похідних
похідних 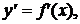
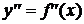 і т.д.
функцію
і т.д.
функцію  наближено
замінимо інтерполяційним поліномом Ньютона, побудованим для системи вузлів
наближено
замінимо інтерполяційним поліномом Ньютона, побудованим для системи вузлів  .
.
Маємо:
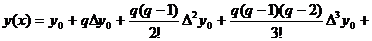
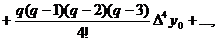 (3)
(3)
де 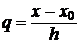 і
і 
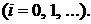
Перемноживши біноми,
отримаємо:

 (3¢)
(3¢)
Так як 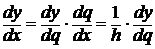 , то
, то
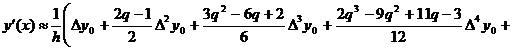
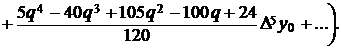 (4)
(4)
Аналогічно, так як
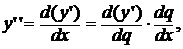 то
то
 .(5)
.(5)
Таким же способом, якщо
потрібно, можна визначити і похідні функції 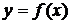 будь-якого порядку.
будь-якого порядку.
Помітимо, що при знаходженні
похідних 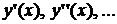 у
фіксованій точці
у
фіксованій точці 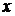 в якості
в якості  слідує
вибирати близьке табличне значення аргументу.
слідує
вибирати близьке табличне значення аргументу.
Іноді вимагається знаходити
похідні функції  в основних
табличних точках
в основних
табличних точках 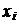 . В цьому
випадку формули чисельного диференціювання спрощуються. Так як кожне табличне
значення можна вважати за початкове, то покладемо
. В цьому
випадку формули чисельного диференціювання спрощуються. Так як кожне табличне
значення можна вважати за початкове, то покладемо  ,
,  ; тоді
матимемо:
; тоді
матимемо:
 (6)
(6)
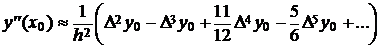 . (7)
. (7)
Якщо 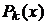 -
інтерполяційний поліном Ньютона, який має різниці
-
інтерполяційний поліном Ньютона, який має різниці 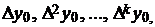 і
і
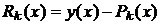 - відповідна похибка, то похибка в
означенні похідної є
- відповідна похибка, то похибка в
означенні похідної є 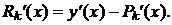
Як відомо,
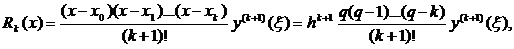 (8)
(8)
де 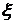 - деяке
проміжне число між значеннями
- деяке
проміжне число між значеннями 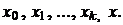
Тому, припустивши, що 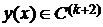 , отримаємо:
, отримаємо:
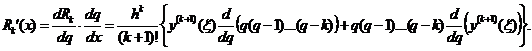 (9)
(9)
Звідси при  і, отже,
при
і, отже,
при  і враховуючи,
що
і враховуючи,
що  будемо
мати:
будемо
мати:
Так як 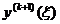 в багатьох
випадках важко оцінити, то при
в багатьох
випадках важко оцінити, то при 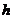 малим наближено покладають:
малим наближено покладають:
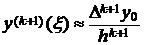
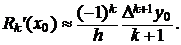 (11)
(11)
Аналогічно може бути знайдена
похибка 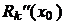 для другої
похідної
для другої
похідної 
При побудові інтерполяційних формул
Ньютона використовуються лише значення функції, що лежать з однієї сторони
початкового наближення, тобто, ці формули носять односторонній характер [3].
В багатьох випадках
виявляються корисними інтерполяційні формули, що містять як наступні, так і
попередні значення функції по відношенню до її початкового наближеного
значення. Найбільш вживаними серед них являються ті, що містять різниці,
розміщені у горизонтальному рядку діагональної таблиці різниць даної функції,
що відповідає початковим значенням 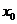 і
і  , або в рядках, що безпосередньо
примикають до неї. Ці різниці
, або в рядках, що безпосередньо
примикають до неї. Ці різниці 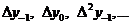 називаються центральними різницями,
причому
називаються центральними різницями,
причому  і т. д.
і т. д.
Відповідні їм формули
називають інтерполяційними формулами із центральними різницями. До їх числа
відносяться формули Гауса, Стірлінга і Бесселя.
1.2 Формули наближеного
диференціювання, основані на першій інтерполяційній формулі Гауса
Формули Гауса застосовуються
для інтерполювання в середині таблиці поблизу 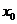 . При цьому перша формула Гауса
застосовується при
. При цьому перша формула Гауса
застосовується при 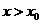 , а друга -
при
, а друга -
при  .
.
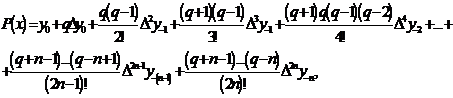 (12)
(12)
Перша інтерполяційна формула Гауса
містить центральні різниці
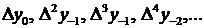 .
.
Формули наближеного диференціювання,
основані на першій інтерполяційній формулі Гауса:
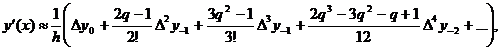
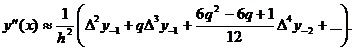 (13)
(13)
Друга інтерполяційна формула Гауса
має вигляд:
 (14)
(14)
Перша інтерполяційна формула Гауса
містить центральні різниці
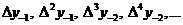
Формули наближеного
диференціювання, основана на другій інтерполяційній формулі Гауса:
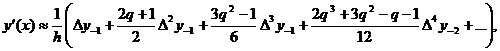
 (15)
(15)
1.3 Формули наближеного
диференціювання, основані на інтерполяційній формулі Бесселя
Формула Бесселя
використовується для інтерполювання всередині таблиці при значеннях q, близьких
до 0.5. Практично вона використовується при  .
.
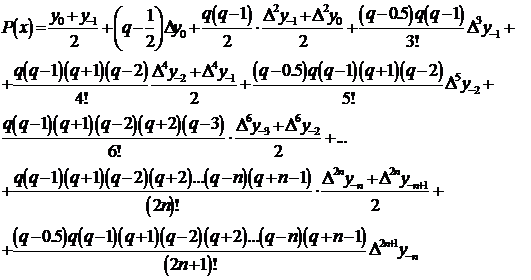 (16)
(16)
де  .
.
Формули наближеного диференціювання,
основані на інтерполяційній формулі Бесселя:
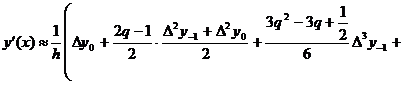
 (17)
(17)
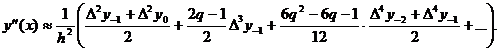 (18)
(18)
1.4 Формули наближеного
диференціювання, основані на інтерполяційній формулі Стірлінга
Виведені в попередньому
пункті формули численного диференціювання для функції  в точці
в точці  володіють
тим дефектом, що вони використовують лише односторонні значення функції при
володіють
тим дефектом, що вони використовують лише односторонні значення функції при  . Відносно
велику точність мають симетричні формули диференціювання, враховуючи значення
даної функції
. Відносно
велику точність мають симетричні формули диференціювання, враховуючи значення
даної функції  як при
як при  , так і при
, так і при 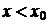 . Ці формули
звичайно називаються центральними формулами диференціювання. Виведемо
одну з них, взяв за основу інтерполяційну формулу Стірлінга.
. Ці формули
звичайно називаються центральними формулами диференціювання. Виведемо
одну з них, взяв за основу інтерполяційну формулу Стірлінга.
Нехай 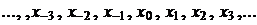 - система
рівностоячих точок з кроком
- система
рівностоячих точок з кроком 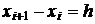 і
і 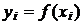 - відповідні значення даної функції
- відповідні значення даної функції
 Покладаючи
Покладаючи 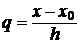 і замінюючи
наближено функцію
і замінюючи
наближено функцію  інтерполяційним
поліномом Стірлінга, будемо мати:
інтерполяційним
поліномом Стірлінга, будемо мати:

 (19)
(19)
де для стислості введені
позначення

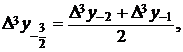 (20)
(20)
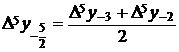
і т. д.
Із формули (1), враховуючи,
що 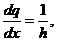 отримуємо:
отримуємо:

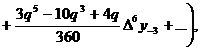 (21)
(21)
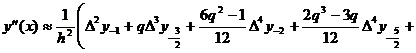
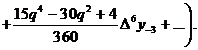 (21¢)
(21¢)
Зокрема, покладаючи  , будемо
мати:
, будемо
мати:
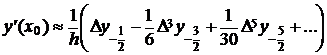 (22)
(22)
і 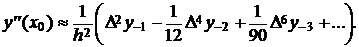 (22¢)
(22¢)
.5 Приклад чисельного
диференціювання методом Стірлінга
Знайти значення першої та
другої похідних даних функцій 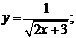 при:
при: 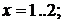 h=0,1 для
h=0,1 для 
Розв’язування.
Складемо діагональну таблицю кінцевих різниць даної функції:
Таблиця 1. Знаходження
кінцевих різниць
|
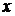 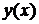 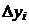 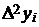 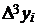 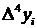 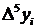
|
|
|
|
|
|
|
|
1,000000
|
0,447214
|
|
|
|
|
|
|
|
-0,008685
|
|
|
|
|
|
1,100000
|
0,438529
|
|
0,000487
|
|
|
|
|
|
-0,008198
|
|
-0,000044
|
|
|
|
1,200000
|
0,430331
|
|
0,000443
|
|
0,000005
|
|
|
|
-0,007754
|
|
-0,000039
|
|
-0,000001
|
|
1,300000
|
0,422577
|
|
0,000005
|
|
|
|
-0,007350
|
|
-0,000034
|
|
-0,000001
|
|
1,400000
|
0,415227
|
|
0,000371
|
|
0,000004
|
|
|
|
-0,006979
|
|
-0,000030
|
|
-0,000001
|
|
1,500000
|
0,408248
|
|
0,000340
|
|
0,000003
|
|
|
|
-0,006639
|
|
-0,000027
|
|
0,000000
|
|
1,600000
|
0,401610
|
|
0,000314
|
|
0,000003
|
|
|
|
-0,006325
|
|
-0,000024
|
|
0,000000
|
|
1,700000
|
0,395285
|
|
0,000290
|
|
0,000002
|
|
|
|
-0,006035
|
|
-0,000021
|
|
0,000000
|
|
1,800000
|
0,389249
|
|
0,000268
|
|
0,000002
|
|
|
|
-0,005767
|
|
-0,000019
|
|
|
|
1,900000
|
0,383482
|
|
0,000249
|
|
|
|
|
|
-0,005518
|
|
|
|
|
|
2,000000
|
0,377964
|
|
|
|
|
|
Нехай 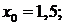 тоді
тоді 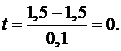
Скористуємося формулами


Які отримують із формули
Стірлінга.
Знаходимо

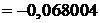 .
.
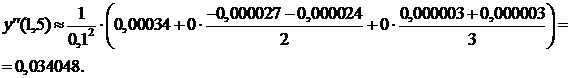
2.
Розробка алгоритмів та вибір оптимального алгоритму
При розробці
алгоритму обчислення значення аргументу, яке відповідає заданому значенню
функції, якого в табл. 2 немає будемо використовувати формулу (13), що наведена
в розділі 1.
Аналіз формули (13)
та прикладу наведеного в першому розділі дозволив розробити алгоритм,
особливість якого полягає в тому, що для знаходження значення похідної
використовується попереднє обчислення скінчених різниць (рис. 2.1). При цьому
перед основним обчисленням складається повна таблиця скінченних різниць.
Перевагою такого підходу є те, що при обчислення проміжних значень таблиці
скінченних різниць виконується лише один раз. До недоліків слід віднести
необхідність обчислення всіх різниць на всьому проміжку, займає багато комірок
пам’яті.
Розрахунки
показують, що для обчислення значення аргументу необхідно 16 операцій
додавання, 204 операцій віднімання, 236 операцій множення та 10 операцій ділення.
З врахуванням того,
що час виконання операцій множення та ділення відповідно в 1,14 та 2,33 рази
більший за час виконання операцій додавання (віднімання) при використанні
арифметичного співпроцесора, загальна кількість операцій обчислення значення
похідної складає

Алгоритм можна побудувати
таким чином, щоб спочатку перевірити умову, чи не збігається значення функції  з будь-яким
із вузлів
з будь-яким
із вузлів 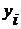
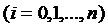 . Якщо ця
умова не підтвердилась, то проводяться відповідні обчислення що передбачені у
блоках 7-12. В цьому випадку для збереження значень аргументу та функції
необхідно 2 комірки пам’яті.
Блок-схема першого алгоритму подана на рис. 2.1.
. Якщо ця
умова не підтвердилась, то проводяться відповідні обчислення що передбачені у
блоках 7-12. В цьому випадку для збереження значень аргументу та функції
необхідно 2 комірки пам’яті.
Блок-схема першого алгоритму подана на рис. 2.1.
Інший спосіб побудови
алгоритму полягає в тому, що для знаходження значення похідної використовується
одночасне обчислення скінчених різниць (рис. 2.2). Даний метод полягає в тому,
що обчислюються лише ті значення, які потрібні. Основним недоліком такого
методу є те, що проміжні значення таблиці скінченних різниць обчислюються
багаторазово, що в свою чергу вимагає більшу кількість арифметичних операцій.
Аналіз формули показує, що
для обчислення необхідно 264 операцій віднімання, 198 операцій множення та 66
операцій ділення

В даному випадку для
збереження результатів обчислення необхідно також 2 комірки пам’яті.
Комплексний коефіцієнт
ефективності 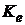 одного
алгоритму в порівнянні з іншим можна обчислити за формулою
одного
алгоритму в порівнянні з іншим можна обчислити за формулою
 ,
,
де 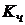 -
коефіцієнт ефективності за часом виконання алгоритму;
-
коефіцієнт ефективності за часом виконання алгоритму;
 - коефіцієнт ефективності за
затратами пам’яті
алгоритму.
- коефіцієнт ефективності за
затратами пам’яті
алгоритму.
Оскільки коефіцієнт
ефективності за часом виконання алгоритму можна приблизно оцінити за кількістю
арифметичних операцій алгоритму, то комплексний коефіцієнт ефективності
описаних вище алгоритмів складає

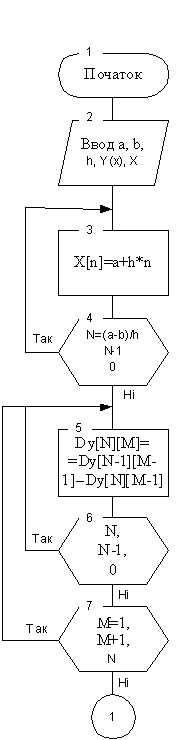
Рисунок 2.1 - Блок-схема першого
алгоритму чисельного диференціювання з використанням інтерполяційного
многочлена Стірлінга з попереднім обчисленням скінченних різниць

Рисунок 2.2 - Блок-схема першого
алгоритму чисельного диференціювання з використанням інтерполяційного
многочлена Стірлінга з попереднім обчисленням скінченних різниць, продовження

Рисунок 2.3 - Блок-схема першого
алгоритму чисельного диференціювання з використанням інтерполяційного
многочлена Стірлінга з поточним обчисленням скінченних різниць
3.
Алгоритм та програма обчислення другої похідної за інтерполяційною формулою
Стірлінга
3.1 Інструкція користувача
інтерполяційний формула
стірлінг похідна
Програму можна запустити в
будь-якому компіляторі або інтерпретаторі для мови програмування Pascal.
Наведемо приклад найпоширенішого з них - Turbo
Pascal.
. Файл з текстом програми simson.pas
слід розмістити в папці BIN вищенаведеного компілятора.
. Після виклику компілятора
з’являється діалогове вікно. Для відкриття програми потрібно вибрати у меню
File команду Open (Відкрити), що відкриває діалогове вікно з переліком файлів
поточної папки.
. Вибір необхідного файлу з цього
списку і наступне натискання кнопки OK приводить до появи вікна з текстом
програми, що дає змогу не тільки коректувати програму, але і проводити її
налагодження. Запуск програми здійснюється вибором в меню RUN команди RUN або
за допомогою комбінації клавіш Ctrl+F9.
. В результаті запуску програми
з’явиться командне вікно, в якому необхідно ввести значення. Після введення
значень слід натиснути клавішу Enter.
. Програму можна компілювати
натисненням комбінації клавіш Alt+F9 або за допомогою головного меню
компілятора. Отриманий файл simson.exe може бути запущений за його викликом. В
такому випадку компілятор не потрібен.
3.2 Лістинг програми
Program stirling;rray=array [1..20]
of real;xo,r,xn,x,krok,it,t,vud,y,h,nq,i,j:integer;,m,s,n,s1,tr,xWykane,t1:real;:rray;;
Writeln('Vvedit
A, B');
read(xo,xn);(' Vvedit krok h);(h);('
Vvedit znachennya Y');(y);('y=',y);
Writeln('Vvedit X');
read(X);
read;:=0;:=0;:=1;:=(xn-xo)+1;i:=0 to
krok do:=(2*sqr(x))+(17*x);:=sqrt(r);[t]:=yform;:=t+1;:=0;:=0;:=x+h;;:=0;:=0;:=krok-1;it:=0
to krok do:=1;:=1;:=0;:=0;:=1;:=r+1;j:=1 to krok dot=vud then
t:=t+1;:=y-mas[t];:=n*s;:=mas[vud]-mas[t];:=m*s1;:=t+1;;:=(n/m)*r;:=xWykane+tr;:=r+1;:=0;;('
Percha pohidna',xWykane);
Writeln(' Druga pohidna',xWykane);(x);.
3.3 Опис програми
В даному файлі описані всі змінні та
присвоєні їм певні значення, необхідні для обчислення чисельного
диференціювання з використанням інтерполяційного многочленна Стірлінга, а також
власний процес обчислення методу. З метою ефективного використання пам’яті для
збереження початкових значень системи, вони зберігаються в динамічній пам’яті,
що дозволяє відводити під них місце динамічного розміру в залежності від
кількості заданих даних.
Файл Stirling.PAS.
містить описи структури методу та функцій, що використовуються основною
програмою, та описи внутрішніх операторів. Нижче наведено список загальних
операторів, їх призначення та основні властивості.
Команда type
описує тип масиву і записується так:
type
< назва типу >=array
[< розмір >] of
< назва базового типу >.
Команда Var
оголошує
тип змінних, що використовуються у подальших розрахунках.
Команда integer
описує
цілий тип змінних.
Команда real
описує дійсний тип змінних.
Команда begin
належить
до службових слів і означає початок програми.
Команда Writeln
призначена
для виведення значень на екран і має такий загальний вигляд:
Writeln
< список >.
Команда read
призначена
для введення даних і має такий загальний вигляд:
read (< список
змінних >).
Оператор циклу for
призначений для повторного виконання операцій, число яких заздалегідь відоме.
Оператор циклу for
ще називають оператор циклу з параметром. Загальний вигляд оператор циклу for:
for <
параметр і > := а to
b do
<команда>.
Оператор умови if
використовується
для виразів результат яких має стандартний булевський тип. Неповне розгалуження
реалізується за допомогою оператора if
і має такий загальний вигляд:
if
<
логічний вираз > then
< команда >.
Команда end
належить
до службових слів і означає закінчення програми [12].
3.4 Тестування програми
На рис.3.1 подано екранне зображення
результатів обчислення програми, розробленої в середовищі системи Turbo
Pascal.
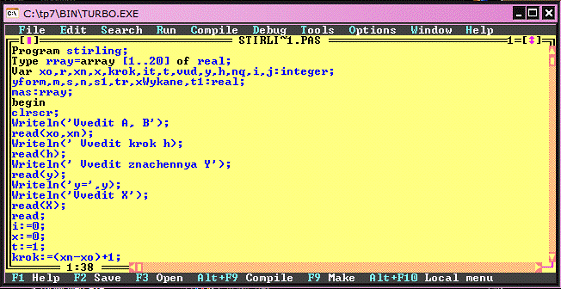
Рисунок 3.1 ─ Середовище
програмування системи Turbo
Pascal

Рисунок 3.2 ─ Результати
обчислення програми, розробленої в середовищі системи Turbo
Pascal
Висновки
. Проаналізовано існуючі методи
чисельного диференціювання та обґрунтовано переваги чисельного диференціювання
з використанням інтерполяційного многочленна Стірлінга по відношенню до
існуючих, які полягають у тому, що даний метод досить простий для розуміння та
точний, що і було підтверджено математично.
2. Запропоновано
два алгоритми чисельного диференціювання. Проведено аналіз ефективності
розроблених алгоритмів за комплексним критерієм ефективності, що враховує час
виконання та розмір алгоритму. Комплексний коефіцієнт ефективності описаних
вище алгоритмів складає 0,796177.
. Розроблено
програму чисельного диференціювання з використанням інтерполяційного
многочленна Стірлінга та проведено її тестування, яке підтвердило її правильну
та коректну роботу.
Перелік посилань
1. Березин И.С., Житков Н.П. Методы
вычислений. - М.: Наука, 1966. - т.1- 633 с.
2. Лященко М.Я.,
Головань М.С. Чисельні методи. - К.: Либідь, 1996.
- 276 с.
3. Бахвалов Н.С., Житков Н.П., Кобельков
Г.М. Численные методы. - М.: Наука, 1987. - 599 с.
4. Демидович
Б.П., Марон И.А. Основы вычислительной математики. - М.: Наука, 1970. - 664 с.
. Калиткин
Н.Н. Численные методы. - М.: Наука, 1978.- 512 с.
6. Бахвалов Н.С. Численные методы. - М.:
Наука, 1975. - 632 с.
7. Турчак Л.И. Основы численных методов. -
М.: Наука, 1987. - 318 с.
. Самарский А.А., Гумен А.В. Численные
методы. - М.: Наука, 1989. - 430 с.
. Вержбицький В.М. Основы численных
методов. - М.: Высшая школа, 2002. - 847 с.
. Григоренко Я.М., Панкратова Н.Д. Обчислювані
методи. - К.: Либідь, 1995. - 227 с.
. Глинський Я.М.
Алгоритмізація і програмування. - Львів, 2003. - 200 с.