Объектно-ориентированное программирование на примере численных методов

Объектно-ориентированное программирование на примере численных методов

ВВЕДЕНИЕ

Студентам, а также инженерам часто требуется решать задачи, которые связаны с численными методами: интегрирование функций, нахождение корня алгебраического уравнения, нахождение решения системы линейных уравнения.

Подобные задачи решаются с помощью численных методов, разработанных для решения математических задач при помощи вычислительной техники на таких языках программирования, как: QBASIC, TURBO PASCAL, C++, DELPHI, VISUAL BASIC и д.р. пакеты программ. В частности, математические пакеты MathCAD, Maple, MathLab также дают возможность решения подобных задач, а так же оптимизации технологического процесса.

Необходимо учитывать, что вычислительная техника не способна без погрешности записывать такие величины как  и т.д., погрешность может появляться и при вычислении, округлении и других операциях.

В некоторых случаях при вычислении необходимо предварительно математически преобразовать или переписать в другом виде функции, это может существенно снизить погрешность или в ряде случаев без преобразования не сходятся решения.

С помощью вычислительной техники можно решить и иные инженерные задачи, но с определенной погрешностью.

Цель данного курсового проекта - научиться с помощью информационных технологий использовать методы структурного программирования на примере численных методов, в частности написание нескольких модулей и связь их в одну общую программу.

Составить программу приближенного вычисления методом половинного деления следующего уравнения:

и описать выше указанный метод, составить блок-схему программы, описать стандартные и нестандартные функции, применяемые в задаче, описать интерфейс и привести пример.

Составить программу для вычисления системы уравнений методом Крамера.

Описать выше указанный метод, составить блок-схему, описать стандартные и нестандартные функции, а так же интерфейс задачи.

Составить программу для работы с матрицами (умножение матрицы на матрицу) и описать выше указанный метод, составить блок-схему программы, описать стандартные и нестандартные функции, применяемые в задаче, описать интерфейс и привести пример.

1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ

.1 Метод половинного деления при приближенном вычислении алгебраических и трансцендентных уравнений

Пусть данное уравнение приведено к виду 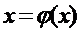[1]:

 (1)

где  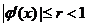(r-постоянная) при 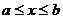. Исходя из начального значения 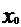, принадлежащего отрезку  построим последовательность чисел …. по следующему закону:

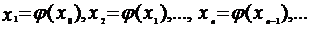 (2)

Если 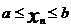 (n=1,2,3,….) то предел

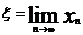
является единственным корнем уравнения (1.1) на отрезке , т.е.  суть последовательные приближения корня .

Оценка абсолютной погрешности n-го приближения  дается формулой

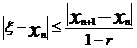
Поэтому, если  и  совпадают с точностью до 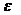, то предельная абсолютная погрешность для  будет

.

Для преобразования уравнения 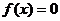 к виду (1.1) заменяем последнее эквивалентным уравнением

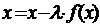 (3)

где число 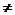0 выбирается так, чтобы функция

=1-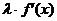

была малой по абсолютной величине в окрестности точки 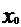 (например, можно положить, что

-)

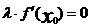Учитывая, все выше изложенное для решения алгебраического уравнения будем использовать формулу (3) приведя ее к следующему виду

 (4)

где

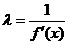
и принимая за 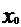 половину выбранного отрезка

при этом необходимо учитывать, что значения 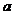 и  выбираются так, чтобы функция 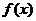меняла знак.

Вычисления по формуле (4) проводится до тех пор, пока выполняется неравенство 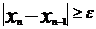, где - заданная точность вычисления. Как только будет выполняться неравенство 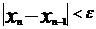, вычисления прекращаются. При этом и будет решением заданного уравнения с точностью .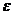

1.2 Решение системы уравнений правилом Крамера

Пусть задана система n линейных уравнений с n неизвестными вида [3]

++…+=

++…+=

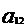
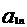
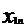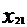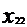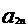
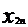………………………………... (1)

++…+=

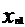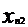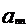
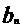
или, в матричной форме, АХ=В, где

А=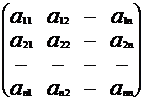, Х=, В=.

Если в системе (1.2) 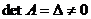, т.е. матрица  имеет обратную матрицу 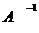, то система (1.2) имеет, и притом единственное, решение

,

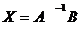или в компонентной записи,

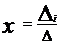, i= 1,2,…,n. (2)

где 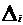 - определитель, получаемый из определителя  заменой i-го столбца на столбец свободных членов.

При этом для вычисления определителя используем основное свойство определителя: Если какую-либо строку или столбец умножить на число и результат прибавить к другой строке или столбцу, то определитель не измениться. Определитель

= при  представим в виде матрицы

 постепенно приводя к треугольному виду

 то есть определитель будет равен произведению членов главной оси матрицы.

В дальнейшем, заменяя i-столбец на столбец свободных членов по формуле (2) находим значения неизвестных.

1.3 Умножение матрицы на матрицу

Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц-сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A на матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой - 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

2. БЛОК-СХЕМА ПРОГРАММЫ GLAV

Рис. 1

2.1 Блок-схема POLdel

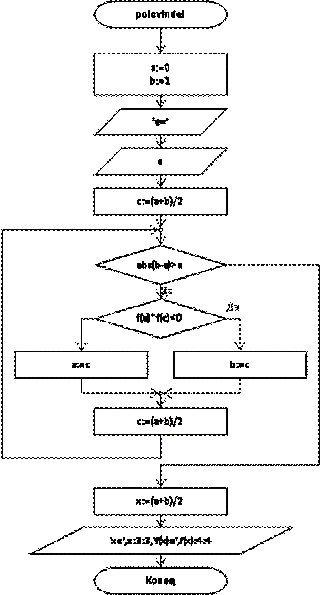
2.2 Блок-схема krame

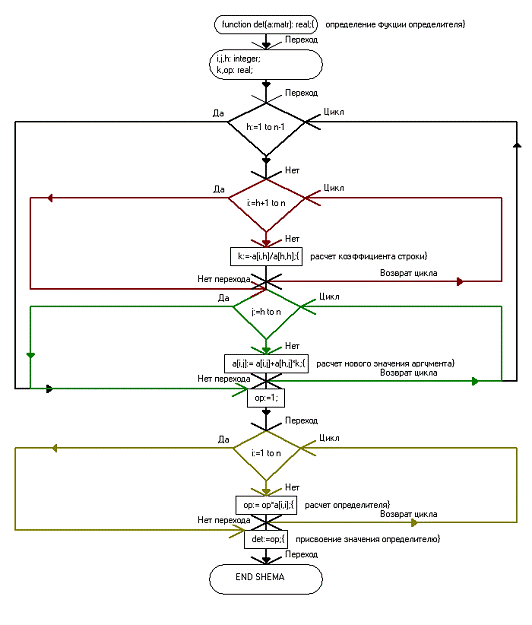
Рис. 3

2.3 Блок-схема matrica

Рис. 4

Рис. 5

3. ОПИСАНИЕ СТАНДАРТНЫХ ФУНКЦИЙ

- очищает экран.- вывод значений на стандартное устройство (консоль) и в файл.- вывод значений на стандартное устройство (консоль) и в файл + перевод каретки.- считать один или несколько символов после нажатия Enter.- считать один или несколько символов после нажатия Enter + перевод каретки.- считать один символ без нажатия Enter.

4. ОПИСАНИЕ НЕСТАНДАРТНЫХ ПРОЦЕДУР И ФУНКЦИЙ

Программа GLAVN сама по себе использует не стандартные модули (POldel, Kramer, matrica), которые в свою очередь содержат не стандартные процедуры и функции, выполнение которых приводит к выполнению программы. Поэтому описание не стандартных процедур и функций, по сути, сводится к описанию процедур и функций, содержащихся в выше перечисленных модулях.- метод половинного деления.- метод Крамера.- умножение матрицы на матрицу.

5. ОПИСАНИЕ ИНТЕРФЕЙСА

После запуска программы GLAVN.exe на экране появляется меню,

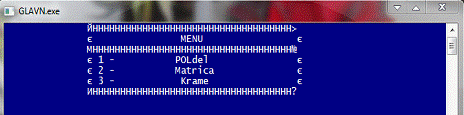
Рис. 6

в котором указаны пункты: 1, 2, 3, они соответственно вызывают методы. При нажатии кнопки 1, 2, 3 вызывается метод. После выполнения выбранного метода выводится меню повторить (y) или нет (n).

Повтор (y/n) при нажатии «y» программа повторяется, а при нажатии «n» программа завершается.

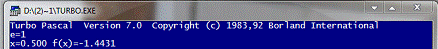
Рис. 7 - Результат процедуры POLdel

Рис. 8 - Результат процедуры Matrica

Рис. 9 - Результат процедуры krame

6. ЧИСЛЕННЫЕ ПРИМЕРЫ

Все выше перечисленное в данной курсовой работе проиллюстрировано на конкретных примерах.

При проверке правильности программы использовалось приложение Microsoft Excel. В приложении вводим данные в виде таблицы и далее строим график используя данные.

Решение уравнения методом половинного деления: 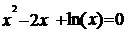. Проверка решения в Microsoft Exсel.

крамер метод деление интерфейс

По данным таблицы построим график зависимости из которого видно, что корень уравнения находится на интервале от 1.6 до 1.7.

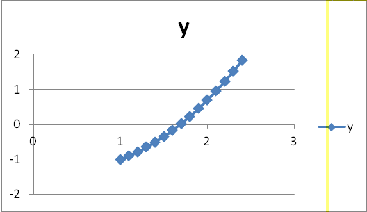
Рисунок 10 - График зависимости у от х

b

(a+b)/2

f(a)

f(b)

f((a+b)/2)

|a-b|

1,6

1,7

1,65

-0,17

0,020628

-0,07672

0,1

1,65

1,7

1,675

-0,07672

0,020628

-0,02856

0,05

1,675

1,7

1,6875

-0,02856

0,020628

-0,0041

0,025

1,6875

1,7

1,69375

-0,0041

0,020628

0,008234

0,0125

1,6875

1,7

1,690625

-0,0041

0,008234

0,002061

0,00625

1,6875

1,690625

1,689063

-0,0041

0,002061

-0,00102

0,003125

1,689063

1,690625

1,689844

-0,00102

0,002061

0,00052

0,001563

1,689063

1,689844

1,689453

-0,00102

0,00052

-0,00025

0,000781

1,689453

1,689844

1,689648

-0,00025

0,00052

0,000135

0,000391

1,689453

1,689551

-0,00025

0,000135

-5,7E-05

0,000195

1,689551

1,689648

1,6896

-5,7E-05

0,000135

3,92E-05

9,77E-05

Примем a = 1,6 и b = 1,7 и по этим данным составим таблицу 5 в Microsoft Exсel, в которой просчитываем решение до момента пока погрешность вычисления не станет равной 0,001

Решение уравнения методом Крамера

При заданной системе уравнений

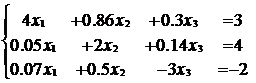
решение методом Крамера имеем следующие значения неизвестных , ,

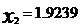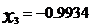
•0.2619+0.86•1.9239+0.3•0.9934 = 3

.05•0.2619+2•1.9239+0.14•0.9934 = 4

.07•0.2619+0.5•1.9239+-3•0.9934 = -2

проверка равенств на интеренет-сайте дает абсолютно точный результат.

Умножение матрицы на матрицу

Умножаем матрицу

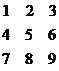 на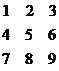

Получаем результат:

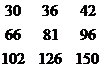
Численный пример проверен на интернет-сайте

Диаграмма взаимодействия

Рис. 11

Диаграмма классов

ЗАКЛЮЧЕНИЕ

В заключение хотелось бы отметить, что методы объектно-ориентированного программирования позволяют более мобильно и качественно проводить работу по модернизации программного обеспечения. В этой курсовой работе был использован метод инкапсуляции.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1.   Воробьев Г.Н., Бахвалов Н.С. «Численные методы». М., 2008. 231 с.

2.      Ефимов А.В., Демидович Б.П. «Линейная алгебра и основы математического анализа». М.: Наука, 2008. 386 с.

.        Бараненков Г.С., Демидович Б.П. «Задачи и упражнения по математическому анализу для ВТУЗОВ». М.: Наука, 2008. 184 с.

.        Абрамов С.А., Зима Е.В. «Начало программирования на языке Паскаль». М.: Наука, 2008. 8 с.

.        Епанешников А.Е., Красильников Ю.И. «Программирование в среде турбо Паскаль». М.: Центр МИФИ СП Диалог, 2008. 3-6 с.

6.      http://window.edu.ru/library/pdf2txt/746/59746/29792/page

ПРИЛОЖЕНИЕ

glavn;crt,POLdel,Matrica,Krame;e1:POLdel;:eiler;: Matrica;:integral;: Krame;:poldel;:real;,flag:integer;Menu;;(' ЙННННННННННННННННННННННННННННННННН»');(' є MENU є');(' МННННННННННННННННННННННННННННННННН№');(' є 1 - POLdel є');(' є 2 - Matrica є');(' є 3- Krame є');('

ИНННННННННННННННННННННННННННННННННј');;;:=1;(flag=1) do;;('Wibirite punkt menu:');(i);i of

: begin;.init;(c.poisk);;;

: begin;.init;(s.poisk);;;

: begin;.init;(y.poisk);;;;.poldel;;crt;Poldel=object;,b,e,c,x:real;.init;shag;poisk:real;;funct(x:real):real;funct(x:real):real;:x*x-2*x+ln(x);Poldel.init;;:=1,2;:=1,3;(‘e= ‘);(e);:=(a+b)/2;;TPoldel.shag;abs(b-a)>e dofunct(a)*func(c)<0:=c;:=c;:=(a+b)/2;;;TPoldel.poisk:real;y:Poldel;:real;.init;.poisk;;.Krame;crt;=array[1..20] of real;=array[1..20] of Tmass;Per(k,n:integer;var a:Tmatrix;var p:integer);z:Real;j,i:integer;:=abs(a[k,k]);:=k;:=0;j:=k+1 to n doabs(a[j,k])>z then:=abs(a[j,k]);:=j;:=p+1;;;i>k thenj:=k to n do:=a[i,j];[i,j]:=a[k,j];[k,j]:=z;;;Znak(p:integer):integer;p mod 2=0 then:=1 else Znak:=-1;;Opr(n:integer;a:tmatrix;var det:real);k,i,j,p:integer;r:real;:=1.0;k:=1 to n doa[k,k]=0 then Per(k,n,a,p);:=znak(p)*det*a[k,k];j:=k+1 to n do:=a[j,k]/a[k,k];i:=k to n do[j,i]:=a[j,i]-r*a[k,i];;;;;a:Tmatrix;:array[1..20] of Tmatrix;,x:Tmass;,det1:real;,k,j,i:integer;;('Порядок системы n=');(n);

writeln('Введите коэффициенты системы:');

for i:=1 to n doj:=1 to n do(a[i,j]);;

writeln('Введите свободные члены:');

for i:=1 to n do(b[i]);

readln;;('Расширенная матрица системы:');

for i:=1 to n doj:=1 to n do(a[i,j]:7:2);(b[i]:9:2);;;

Opr(n,a,det);{определитель системы исходной}

for i:=1 to n dok:=1 to n doj:=1 to n do[i][k,j]:=a[k,j];[i][k,i]:=b[k];;(n,c[i],det1);(det=0)and(det1=0) then

writeln('Система не определена!');

readln;;;(det=0)and(det1<>0) then

begin('Система не имеет решений!');

readln;;;[i]:=det1/det;{корень};('Корни сиcтемы:');i:=1 to n do('x',i,'=',x[i]:7:3);.Max=50;= object,nn,mm: integer;: double;,BB,CC: array [1..Max,1..Max] of Double;input;calculations;output;;Matrix.input;ii,jj:integer;('Vvedite chislo strok 1-y matricy - A (<=50)--> '); readln(NN);('Vvedite chislo stolbcov 2-y matricy - A (<=50)--> '); readln(KK);('Vvedite chislo stolbcov 2-y matricy - B (<=50)--> '); readln(MM);('Vvedite 1-yu matricu (A):');ii:=1 to nn dojj:=1 to kk do('Vvedite A[',ii,',',jj,'] --> ');(AA[ii,jj]);;('Vvedite 2-yu matricu (B):');ii:=1 to kk dojj:=1 to mm do('Vvedite B[',ii,',',jj,'] --> ');(BB[ii,jj]);;;Matrix.calculations;ii,jj,ll:integer;;ii:=1 to nn dojj:=1 to mm do:= 0;ll:= 1 to kk do:= Summa + AA[ii,ll]*BB[ll,jj];[ii,jj] := Summa;;;Matrix.output;ii,jj:integer;('---- rezul''tat: -----');ii:=1 to nn dojj:=1 to mm do(CC[ii,jj]:8:2);;;;MyMatrix:Matrix;.input;.calculations;.output;

readln;.