Написание программы для рисования фигуры и для вычисления функции f(x)

Написание программы для рисования фигуры и для вычисления функции f(x)

Федеральное бюджетное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)»

Кафедра ЭУТ

Контрольная работа

по курсу «Информатика»

Студент: Селин Н.Н.

Преподаватель: Коновалов.Р.С

Санкт-Петербург 2012

Содержание

1. Задание

. Решение

Вывод

Список использованной литературы

1. Задание

. Используя оператор if, написать программу для вычисления функции f(x), изображенной на графике. Функция состоит из дуги окружности и отрезков прямых

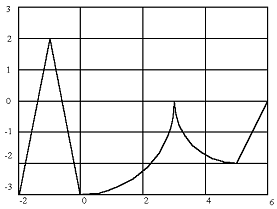
. Составить программу для рисования фигуры, показанной на рисунке, описав ее совокупностью функций. Фигура состоит из дуг окружностей

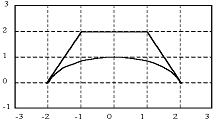
. Используя оператор if, написать программу, которая по заданной ранее функции f(x) строит график функции g(x)

4. Написать программу для нахождения параметров a, b, c функции f(x) вида 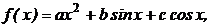проходящей через точки (1;7.3065), (2; 3.8149), (4; 9.1541)

. Написать программу, вычисляющую сумму 101 последовательно расположенных нечетных числа, начиная с числа 3

. Написать программу для построения в интервале [1; 1.5] графика функции f(x) вида 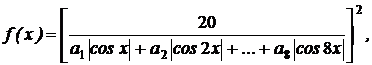 если известна следующая таблица значений функции f(x)

. Решение

1. Используя оператор if, написать программу для вычисления функции f(x), изображенной на графике. Функция состоит из дуги окружности и отрезков прямых

Для решения этой задачи необходимо разбить данную кривую f(x) на отрезки, являющиеся частями некоторых функций, установить аналитические зависимости, описывающие эти функции и, используя оператор if, построить f(x).

Разобьем f(x) на отрезки:

. На отрезке [-2;-1] графиком является часть прямой. Для определения уравнения этой прямой возьмем две точки (-2;-3) и (-1;2) и воспользуемся уравнением прямой с угловым коэффициентом

y = kx + b,

где k - угловой коэффициент, b - сдвиг по оси ординат.

Получим систему уравнений и используем вычислительный блок Given/Find, позволяющий находить корни системы уравнений:

[Given/Find (Дано/найти), вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом: Given - ключевое слово; система, записанная логическими операторами в виде равенств и, возможно, неравенств; Find(x₁, . .. ,х_м) - встроенная функция для решения системы уравнений относительно переменных x₁, ..., х_M.]

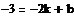
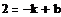
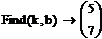
Следовательно:

k=5

b=7

f(x)=5x+7

2. На отрезке [-1;0] графиком является часть прямой. Для определения уравнения этой прямой возьмем две точки (-1;2) и (0;-3) и воспользуемся уравнением прямой с угловым коэффициентом y = kx + b, где k - угловой коэффициент, b - сдвиг по оси ординат.

Получим систему уравнений и используем вычислительный блок Given/Find, позволяющий находить корни системы уравнений:

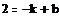
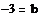
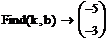
Следовательно:

k=-5

b=-3

f(x)=-5x-3

3. На отрезке [0;3] графиком является часть окружности радиусом r = 3 и, как видно, с центром в точке (0;0).

Выражаем «y» и получается:

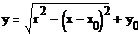
Подставляя в это уравнение данные значения, получается такое выражение: y=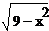

Это уравнение задает нам всю окружность, то есть и верхнюю и нижнюю ее полуокружности. Согласно графику, нам нужно лишь уравнение нижней полуокружности, следовательно, на данном промежутке f(x) =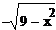

. На отрезке [3;5] графиком является часть окружности радиусом r = 2 и, как видно, с центром в точке (5;0).

Общее уравнение окружности: (x - x₀)² + (y - y₀)² = r²

Выражаем «y» и получается:

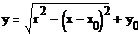
Подставляя в это уравнение данные значения, получается такое выражение:

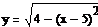
Это уравнение задает нам всю окружность, то есть и верхнюю и нижнюю ее полуокружности. Согласно графику, нам нужно лишь уравнение нижней полуокружности, следовательно, на данном промежутке

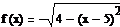
. На отрезке [5;6] графиком является часть прямой. Для определения уравнения этой прямой возьмем две точки (5;-2) и (6;0) и воспользуемся уравнением прямой с угловым коэффициентом

y = kx + b,

где k - угловой коэффициент, b - сдвиг по оси ординат.

Получим систему уравнений и используем вычислительный блок Given/Find, позволяющий находить корни системы уравнений:

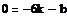
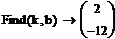
Следовательно:

k=2

b=-12

f(x)=2x-12

Таким образом, мы получили систему из пяти уравнений, которая будет описывать нашу функцию. Воспользуемся операторами Add line и if для задания уравнения и построим график функции f(x):

(Оператор добавления линии Add Line выполняет функции расширения программного блока. Расширение фиксируется удлинением вертикальной черты программных блоков или их древовидным расширением. Условный оператор if является оператором для создания условных выражений, задающийся в виде выражение if условие. Если условие выполняется, то возвращается значение выражения)

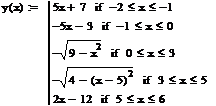
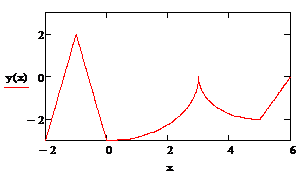
Получившийся график совпадает с исходным, следовательно, он является искомым.

. Составить программу для рисования фигуры, показанной на рисунке, описав ее совокупностью функций. Фигура состоит из дуг окружностей

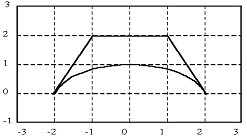
Разобьем имеющийся график на 2 составляющие и обозначим их за f(x), g(x) Пусть f(x) - это часть функции, лежащая снизу, а g(x) - сверху.

. На отрезке [-2;2] графиком является часть окружности радиусом r = 2.5, как видно, с центром в точке (0;-1.5)

Общее уравнение окружности: (x - x₀)² + (y - y₀)² = r²

Выражаем «y» и получается:

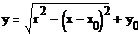
Подставляя в это уравнение данные значения, получается такое выражение:

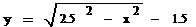
. На второй половине графика (g(x)) расположено три отрезка, которые можно выразить так же, как и мы выражали в 1 пункте первого задания и запишем все это через Add line:

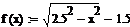
Тем самым, если все объединить, то получается:

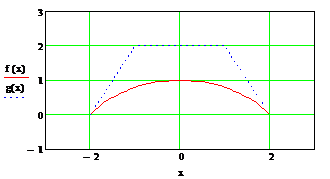
Этот график совпадает с исходным, следовательно, является искомым.

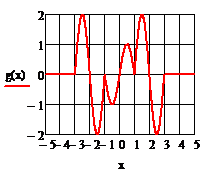
. Используя оператор if, написать программу, которая по заданной ранее функции f(x) строит график функции g(x)

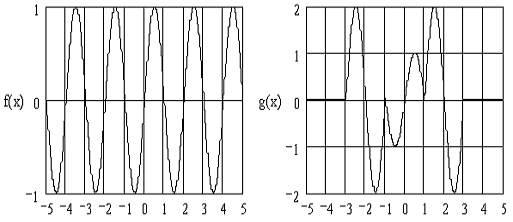
а) Данный график f(x) представляет собой синусоиду f(x) = sinβx. Определим аргумент этой функции. Возьмем точку (0.5;1).

sin (β*0.5) = 1 à β = π.

Следовательно, f(x) имеет вид: f(x) = sin(πx). Построим график этой функции и убедимся, что он идентичен исходному

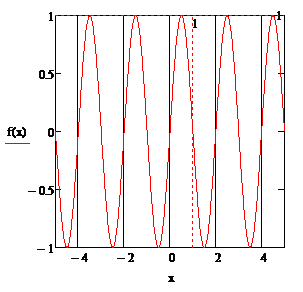
б) 1. На отрезках [-5;-3] и [3;5], очевидно, g(x) = 0. Можно проверить это, взяв любые очевидные точки из промежутков и воспользовавшись Given/Find для определения k и b.

. На отрезке [-3;-1] и [1;3] функцию g(x) можно представить в виде g(x) = a*f(x), где а - коэффициент, определяющий изменение вида кривой f(x).

Возьмем точку (-2.5;2), входящую в исследуемый промежуток и воспользуемся

Given/Find для нахождения коэффициента a:

Следовательно, на данном промежутке g(x) = -2f(x) = -2sin (πx).

. На отрезке [-1;1] аналогично с пунктом 2 функцию g(x) можно представить в виде

g(x) = a*f(x).

Возьмём точку (-0.5;1) , входящую в исследуемый промежуток и воспользуемся

Given/Find для нахождения коэффициента a:

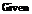
Следовательно, на данном промежутке g(x) = f(x) = sin (πx).

Таким образом, мы имеем систему из пяти уравнений описывающих график функции g(x). Построим этот график с помощью оператора if:

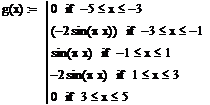
. Написать программу для нахождения параметров a, b, c функции f(x) вида 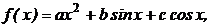проходящей через точки (1;7.3065), (2; 3.8149), (4; 9.1541)

Для решения данной задачи воспользуемся вычислительным блоком Given/Find, позволяющим решать заданную систему уравнений. Given/Find (Дано/найти), вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом: Given - ключевое слово ;система, записанная логическими операторами в виде равенств и, возможно, неравенств; Find(x₁, . .. ,х_м) - встроенная функция для решения системы уравнений относительно переменных x₁, ..., х_M.

Т.к. функция проходит через данные точки (1;7.3065), (2; 3.8149), (4; 9.1541), то мы можем составить систему из трех уравнений, содержащих три переменные a, b и с и решить ее с помощью вычислительного блока Given/Find:

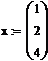
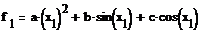
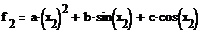
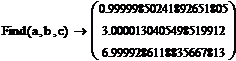
Таким образом, мы получили матрицу, элементы которой являются числа a, b и с соответственно. Если записывать ответ в целых числах, то он будет следующий:

a = 1; b = 3; с = 7.

. Написать программу, вычисляющую сумму 101 последовательно расположенных нечетных числа, начиная с числа 3

. Зададим переменную i, отвечающую за количество чисел в нашей последовательности. Т.к. чисел 101, следовательно i=[0;100]

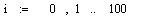
2. Укажем последовательность чисел. Последовательность будет выглядеть так, потому что она начинается с 3, и числа в ней отличаются на 2, так как они последовательные нечётные числа:

3. Вычислим сумму наших последовательно расположенных чисел:

Таким образом, ответ в данной задаче: 10400

6. Написать программу для построения в интервале [1; 1.5] графика функции f(x) вида 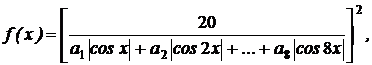 если известна следующая таблица значений функции f(x)

. Зададим количество строк и столбцов в матрице. Оно начинается с 1 и заканчивается 8, т.е. равно 8.

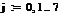
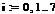
. Зададим матрицы известных значений функции и аргумента:

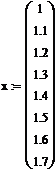
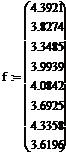
. Матрица А выражает последовательность косинусов

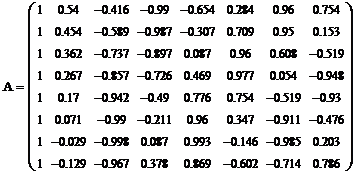
. Матрица С определяет остальную часть выражения, не считая коэффициентов a_1, a₂ ... a₈

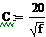
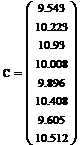
. Матрица B определяет коэффициенты, стоящие перед косинусом a₁,a₂…a₈

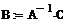
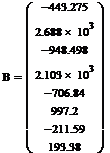
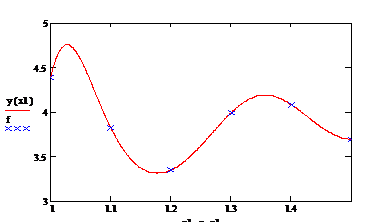
6. Зададим функцию независимой переменной x1.

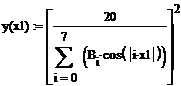
Cтроим график. Так как точки, являющиеся значениями исходной функции, ложатся на график независимой переменной, следовательно, задание выполнено верно и построен искомый график.

Также приравниваем знаменатель нашей функции к нулю и строим еще один график g(x1), сравнивая его с получившимся.

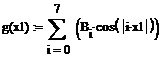
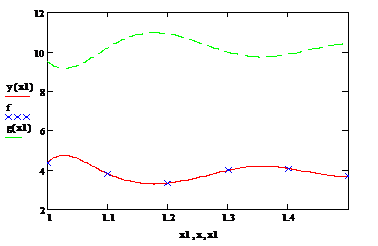
Графики не пересекают друг друга, следовательно, при знаменателе равным нулю, функция не будет существовать, значит задание решено верно.

Вывод

вычисление функция оператор нечетный

При выполнении работы студент группы 2583 Селин Никита научился применять персональный компьютер и математические пакеты прикладных программ в инженерной деятельности на примере вышеизложенных задач, а также сделал следующий вывод: «MathCAD» - универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Mathcad имеет простой для использования интерфейс пользователя. Для ввода формул и данных можно использовать как клавиатуру, так и специальные панели инструментов. Работа осуществляется в пределах рабочего листа, на котором уравнения и выражения отображаются графически. Mathcad содержит сотни операторов и встроенных функций для решения различных технических задач. Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие. Данный набор функций позволяет решать задачи практически из любой области. Пакет обладает широкими графическими возможностями. Программа проста и удобна в использовании, поэтому можно довольно легко ее освоить.

Список использованной литературы

Самоучитель Mathcad. Макаров Е.Г.14 для студентов, инженеров и конструкторов. Очков В.