Диагностирование характеристик лопаток турбины с бандажом
Введение
лопатка турбина бандаж
математический
Хорошо известно, что только на основе теории
колебаний могут быть полностью выяснены такие практически важные проблемы, как
уравновешивание машин, крутильные колебания валов и зубчатых передач, колебания
турбинных лопаток и турбинных дисков, процессы вращающихся валов, колебания
рельсового пути и мостов под действием движущихся грузов, колебания
фундаментов. Лишь при помощи этой теории можно установить наиболее удачные
пропорции конструкций, отодвигающие эксплуатационные условия работы машин
возможно дальше от условий возникновений больших колебаний.
Исследования в области диагностирования
характеристик лопаток турбины, связанных бандажом относятся к задачам
виброакустической диагностики механических систем и технических конструкций.
Возникновение непрогнозируемых колебательных процессов в турбинных лопатках
может привести к функциональным отказам ее составляющих вплоть до разрушения
установки. Поэтому возникает задача определения таких характеристик системы, которые
сохраняли бы безопасные частоты ее колебаний.
Об изменениях характеристик лопаток турбины,
связанных бандажом чаще всего можно судить после разборки механической системы
или ее частей, но этот процесс может быть опасным, трудоемким, дорогостоящим и
может привести к нарушению дальнейшей работы как лопаток, так и турбины в
целом. В настоящее время получило широкое развитие направление, возникшее на
стыке теории механизмов с акустикой, решающее задачи безразборной диагностики
технических конструкций. Поставленная здесь задача призвана решить подобную
проблему виброзащиты для лопаток турбины, связанных бандажом.
Прямая задача по свободным колебаниям лопаток
турбины, связанных с бандажом встречается в традиционных книгах по теории
колебаний, а именно в работах И.М. Бабакова, С.П. Тимошенко, И.А. Биргера. В
них излагаются основы общей теории колебаний, причем ее приложения к решению
технических задач иллюстрированы различными примерами, взятыми во многих
случаях из практики наблюдений над колебаниями машин и сооружений в
эксплуатации.
Нестационарные колебания возникают в
механических системах под действием сил, изменяющихся нагрузок и параметров.
Под изменением параметров конкретных установок подразумевается изменение масс,
геометрических размеров отдельных элементов, жесткостей и пр.
Согласно И.А. Биргеру любая реальная
механическая система состоит из бесконечного числа материальных точек, так как
связи между ними не являются абсолютно жесткими, то число степеней свободы
такой системы бесконечно велико. Основной особенностью процесса колебаний
упругих систем с распределенными параметрами является наличие бесконечного
числа форм и частот их собственных колебаний. Такие системы описываются
дифференциальными уравнениями в частных производных, при решении которых необходимо
учитывать начальные и граничные условия. Начальные условия определяют начальные
смещения и скорости, а граничные - характеризуют концевые закрепления.
По С.П. Стрелкову различают продольные,
поперечные, изгибные и крутильные колебания. Вследствие сходства уравнений
крутильных и продольных колебаний, их можно решать одними и теми же методами по
единому алгоритму. При этом различают стержни постоянного и переменного
сечения, однородные и неоднородные.
Прямая задача по колебаниям лопаток турбины,
связанных бандажом была взята непосредственно из учебника С.П. Тимошенко. В
данной книге содержатся традиционные разделы теории колебаний: колебания систем
с конечным числом степеней свободы, колебания распределенных систем стержней и
пластин, колебания нелинейных систем. Изложены основы теории устойчивости
движения. Для описания колебаний используются преимущественно классические
методы, развитые Дж. Рэлеем и А. Н. Крыловым. Приводится большое число
пояснительных примеров, имеющих самостоятельную прикладную ценность и служащих
справочным материалом. Даны сведения из аналитической механики, матричного и
операционного исчисления, не входящие в обычные вузовские программы. В
приложениях приводятся данные, позволяющие получать численные решения.
В книге А.В. Левина изложены основы теории
колебаний линейных н нелинейных механических систем, а также применение общих
методов к динамическому расчету машиностроительных конструкций, таких, как
роторы турбомашин, системы виброизоляции и др. Рассмотрены колебания, вызываемые
детерминированными и случайными переменными нагрузками, а также ударом или
периодическим изменением параметров системы. Значительное внимание уделено
численным методам.
Но во всех трудах, описывающих колебания
турбины, лопаток турбины исследуются только прямые задачи по определению частот
свободных колебаний системы. В отличие от них в дипломной работе проведены
исследования зависимостей собственных частот лопаток турбины, связанных
бандажом от характеристик системы. Впервые поставлены и решены задачи диагностирования
характеристик лопаток турбины, связанных бандажом по известным частотам
свободных колебаний. Исследована также задача сохранения безопасных частот
колебаний лопаток турбины.
Целью дипломной
работы является исследование влияния характеристик лопаток турбины с бандажом
на частоты свободных колебаний и диагностирование по частотам колебаний
характеристик системы.
В соответствие с целью поставлены следующие
задачи:
– вывод
частотного уравнения для свободных колебаний лопаток турбины, связанных бандажом;
– исследование
влияния на собственные частоты колебаний системы жесткостных и массовых
параметров лопаток турбины с бандажом;
– постановка
и решение обратных задач диагностирования жесткостей и масс лопатки и бандажа
по собственным частотам колебаний системы;
– доказательства
единственности решений задач диагностирования;
– определение
метода решений задач диагностирования;
– исследование
задачи сохранения заданных частот колебаний системы;
– программные
реализации решений прямой и обратной задач.
Поставленные задачи решались аналитически на
основе спектральной теории дифференциальных уравнений, обратных задач
математической физики с применением вычислений на ЭВМ.
Научная новизна полученных результатов состоит в
следующем:
− получено частотное уравнение
свободных колебаний лопаток турбины, связанных бандажом;
− исследовано влияние жесткостных и
массовых характеристик лопаток турбины и бандажа на собственные частоты
свободных колебаний системы;
− впервые поставлены и решены
обратные задачи диагностирования жесткостных и массовых параметров лопаток и
бандажа по частотам их колебаний;
− найден алгоритм диагностирования
параметров лопаток, позволяющий сохранять безопасные частоты колебаний при
изменениях параметров системы;
− решена задача сохранения безопасных
частот колебаний турбины с бандажом при изменениях ее характеристик;
− приведены программные реализации
решений поставленных задач.
Практическая значимость работы состоит в том,
что разработанные методы решения задачи позволяют диагностировать такие характеристики,
как жесткость лопатки и масса лопатки, жесткость бандажа и масса шага бандажа.
Найденные методы решения обратных задач дают возможность идентификации
характеристик по звучанию колебаний лопаток турбины с бандажом. Полученные
алгоритмы позволяют однозначно диагностировать жесткостные и массовые параметры
рассматриваемой системы по первым трем значениям собственных частот ее
свободных колебаний.
Найденный алгоритм позволяет также сохранять
безопасные частоты колебаний лопаток турбины (при изменениях ее физических
параметров) с помощью соответствующих изменений в жесткостях и массах лопаток
турбины и бандажа.
Во введении рассмотрены актуальность темы
исследования, основные цели, задачи исследования. Проведен обзор литературы по
данной тематике. Указана степень разработанности темы исследования.
Первая глава работы посвящена прямой задаче
определения собственных частот свободных колебаний лопаток турбины, связанных
бандажом. Получено и проанализировано частотное уравнение свободных колебаний
лопаток турбины. Приведены конкретные примеры на опреденение частот колебаний
рассматриваемой системы. Составлены программы в математическом пакете Maple для
решения прямой задачи.
Вторая глава посвящена исследованию влияния
жесткостных и массовых характеристиктаких лопаток турбины с бандажом на
собственные частоты свободных колебаний системы. По решению прямой спектральной
задачи показано, что при увеличении жесткостей лопатки и бандажа собственные
частоты колебаний системы увеличиваются, а при увеличение массы лопатки и массы
шага бандажа собственные частоты, наоборот, уменьшаются. Приведены также
графики и таблицы указанных зависимостей.
В третьей главе впервые приводится постановка
обратных спектральных задач - задач диагностирования характеристик лопаток турбины
с бандажом по известныи частотам их свободных колебаний. Исследованы и решены
обратные задачи диагностирования жесткости и массы лопатки, а также жесткости и
массы шага бандажа. Доказаны теоремы о единственности решений поставленных
задач диагностирования. Найдены методы решений задач, которые сведятся к
решениям систем алгебраических нелинейных уравнений.
По решениям обратных задач диагностирования
исследована проблема сохранения частот свободных колебаний лопаток турбины,
связанных бандажом при изменениях параметров системы. Показано, что для
сохранения безопасных частот колебаний лопаток турбины достаточно произвести
соответствующие изменения в жесткостях или массах лопаток или бандажа.
Приведены примеры, подтверждающие выводы и совпадающие с результатами
доказанных теорем. Составлены программы в математическом пакете Maple для
решения обратных задач.
В заключении работы подведены итоги
исследований, сделаны основные выводы.
1.Определение собственных частот
колебаний лопаток турбины
.1 Колебания лопаток турбины,
связанных бандажом
Свободная лопатка с жестко
заделанными в ободе диска хвостом колеблется, поворачиваясь каждым сечением
вокруг главной оси АВ сечения, соответствующей минимальному поперечному моменту
(рисунок 1). Предположим, что лопатка не закручена и что площадь поперечного
сечения и погонная масса по всей ее длине одинаковы. В таком случае ось лопатки
О при колебаниях будет изгибаться в одной плоскости, именно в плоскости MN, образующей
некоторый угол 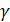
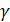 с срединной плоскостью диска KL.
с срединной плоскостью диска KL.
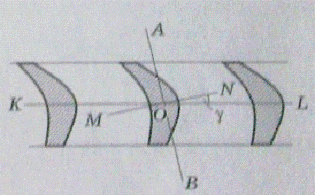
Рисунок 1 − Лопатки турбины,
связанные бандажом
Предположим далее, что лента
бандажа, скрепляющего головки лопаток, не имеет разрывов и все лопатки находятся
в одинаковых условиях закрепления. Каждую лопатку мы рассматриваем как
однородный стержень, жестко закрепленный одним концом 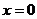 и связанный
на другом конце
и связанный
на другом конце 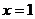 бандажом.
Эта последняя связь приводит к особым условиям на конце лопатки
бандажом.
Эта последняя связь приводит к особым условиям на конце лопатки 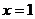 , которыми и
учитывается влияние бандажа на колебания лопатки. Для свободного конца
изгибающий момент и поперечная сила равны нулю. Для конца, закрепленного в
бандаже, изгибающий момент и поперечная сила отличны от нуля. Их значения
найдем, сделав некоторые простейшие предположения относительно характера
деформации бандажа в месте закрепления. В случае, когда все лопатки отклоняются
в одну сторону, в серединах свободных участков бандажа в максимальном
отклонении лопаток образуются точки перегиба (рисунок 2).
, которыми и
учитывается влияние бандажа на колебания лопатки. Для свободного конца
изгибающий момент и поперечная сила равны нулю. Для конца, закрепленного в
бандаже, изгибающий момент и поперечная сила отличны от нуля. Их значения
найдем, сделав некоторые простейшие предположения относительно характера
деформации бандажа в месте закрепления. В случае, когда все лопатки отклоняются
в одну сторону, в серединах свободных участков бандажа в максимальном
отклонении лопаток образуются точки перегиба (рисунок 2).

Рисунок 2 − Отклонения лопаток
турбины
Если в этих точках разрезать бандаж,
выделив отрезок 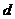 («шаг
бандажа»), прилегающий к рассматриваемой лопатке, то действие на вырезанный шаг
со стороны других частей бандажа сведется только к силам
(«шаг
бандажа»), прилегающий к рассматриваемой лопатке, то действие на вырезанный шаг
со стороны других частей бандажа сведется только к силам  ,
, 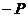 ,
приложенным к концам вырезанного шага, равным по величине направленным в
противоположные стороны, т. е. образующим пару (рисунок 3).
,
приложенным к концам вырезанного шага, равным по величине направленным в
противоположные стороны, т. е. образующим пару (рисунок 3).
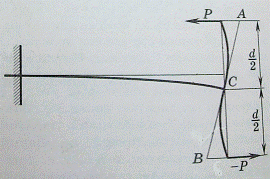
Рисунок 3 − Отрезок бандажа,
прилегающий к лопатке
1.2 Дифференциальное уравнение
свободных колебаний лопаток турбины с бандажом
Дифференциальное уравнение свободных
колебаний лопаток турбины, связанных с бандажом сводится к рассмотрению
свободных колебаний стержня. Поэтому приведем некоторые известные факты по
колебаниям стержня, необходимые для дальнейшего изложения.
При выводе уравнения колебаний
стержня (или балки) будем предполагать, что в недеформированном состоянии
упругая ось стержня прямолинейна и совпадает с линией центров тяжести
поперечных сечений стержня. Эту прямолинейную ось примем за координатную ось x и от нее
будем отсчитывать отклонения элементов стержня при поперечных колебаниях. При
этом будем считать, что отклонения отдельных точек оси стержня происходят
перпендикулярно прямолинейному, недеформированному ее направлению, пренебрегая
смещениями этих точек, параллельными оси.
Далее предполагаем, что отклонения
точек оси стержня при поперечных колебаниях происходят в одной плоскости и
являются малыми отклонениями в том смысле, что возникающие при этом
восстанавливающие силы остаются в пределах пропорциональности.
При таких предположениях отклонения
точек оси стержня при поперечных колебаниях однозначно определяются одной
функцией двух переменных - координаты x и времени t:
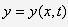
Эта функция удовлетворяет линейному
дифференциальному уравнению в частных производных четвертого порядка, которое
может быть построено следующим образом.
Обозначим через 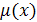
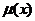
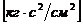 массу единицы длины стержня, через
массу единицы длины стержня, через  - жесткость
на прогиб (
- жесткость
на прогиб (
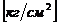 - модуль
упругости,
- модуль
упругости, 
 - момент инерции поперечного
сечения стержня относительно нейтральной оси сечения, перпендикулярной
плоскости колебаний),
- момент инерции поперечного
сечения стержня относительно нейтральной оси сечения, перпендикулярной
плоскости колебаний),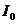
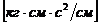 - момент
инерции единицы длины стержня относительно центральной оси, перпендикулярной
плоскости колебаний. На стержень действует распределенная поперечная нагрузка,
интенсивность которой обозначим через
- момент
инерции единицы длины стержня относительно центральной оси, перпендикулярной
плоскости колебаний. На стержень действует распределенная поперечная нагрузка,
интенсивность которой обозначим через 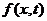 , а также продольная сила
(растягивающая или сжимающая), направленная по оси стержня с интенсивностью
, а также продольная сила
(растягивающая или сжимающая), направленная по оси стержня с интенсивностью 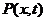 . Эти
нагрузки могут зависеть не только от положения элементов стержня, но и от
времени.
. Эти
нагрузки могут зависеть не только от положения элементов стержня, но и от
времени.
Кинетическая энергия колеблющегося
стержня складывается из кинетической энергии поперечных смещений элементов
стержня

и кинетической энергии вращений
элементов стержня вокруг осей, перпендикулярных плоскости колебаний
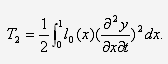
Потенциальная энергия равна сумме
трех слагаемых:
– потенциальной
энергии упругой деформации (работа восстанавливающих упругих сил)
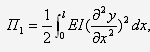
потенциальной энергии прогиба от
поперечной нагрузки 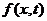
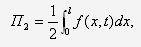
– потенциальной
энергии растяжения от продольной силы 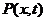
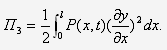
Функционал Остроградского-Гамильтона S
имеет здесь вид
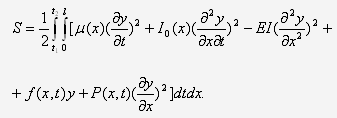
Уравнение поперечных колебаний стержня получим,
составив для функционала S
уравнение Эйлера

Это линейное уравнение четвертого порядка,
составленное при самых общих предположениях относительно действующих на
стержень сил, жесткости и распределения массы.
В стержнях, длина которых значительно
превосходит поперечные размеры, можно пренебречь инерцией вращения и опустить в
левой части уравнения (8) последний член.
Положив 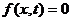 и
и  , мы
рассмотрим сначала свободные колебания однородного стержня с постоянными
жесткостью
, мы
рассмотрим сначала свободные колебания однородного стержня с постоянными
жесткостью  и погонной
массой
и погонной
массой 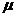 . Обозначим
. Обозначим  . Тогда для
таких колебаний уравнение (8) примет вид
. Тогда для
таких колебаний уравнение (8) примет вид
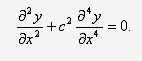
1.3 Вывод частотного уравнения
свободных колебаний турбинных лопаток
Предполагая, что соединения головки
лопатки с бандажом абсолютно жесткое, можно написать для отклонения 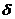 концов шага
от прямолинейного расположения по АВ:
концов шага
от прямолинейного расположения по АВ:

где 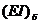 - жесткость на изгиб бандажа. С
другой стороны, из чертежа, в предположении, что углы отклонения касательных к
бандажу и лопатке в точке С
- жесткость на изгиб бандажа. С
другой стороны, из чертежа, в предположении, что углы отклонения касательных к
бандажу и лопатке в точке С 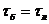 малы, имеем
малы, имеем
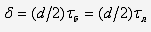
Следовательно,
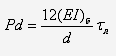
или

Но изгибающий момент лопатки в
сечении 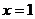 равен
равен

Сравнивая полученные выражения (13)
и (14), получим первое краевое условие на головке лопатки

Второе условие получим, составив
выражение для поперечной силы в месте крепления лопатки в бандаже. Для
свободных колебаний эта сила принимается равной силе инерции массы шага бандажа
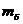 в
предположении, что эта масса сосредоточена в головке лопатки. Для главных
колебаний с частотой
в
предположении, что эта масса сосредоточена в головке лопатки. Для главных
колебаний с частотой 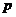 эта сила
равна
эта сила
равна
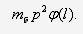
Так как, с другой стороны,
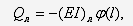
то
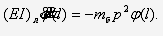
Простейшим периодическим решением
уравнения свободных колебаний стержня (9) является главное колебание, в котором
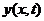 изменяется
с течением времени по гармоническому закону
изменяется
с течением времени по гармоническому закону
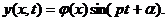
Функция  устанавливающая
закон распределения максимальных (амплитудных) отклонений точек оси стержня от
равновесного расположения, называется формой главного колебания или собственной
формой. Собственных форм колебаний прямого стержня бесконечное множество.
Каждой собственной форме соответствует определенное значение частоты
устанавливающая
закон распределения максимальных (амплитудных) отклонений точек оси стержня от
равновесного расположения, называется формой главного колебания или собственной
формой. Собственных форм колебаний прямого стержня бесконечное множество.
Каждой собственной форме соответствует определенное значение частоты 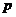 -
собственная частота. Отбор собственных частот и соответствующих им собственных
форм осуществляется с помощью уравнения собственных форм и краевых условий
задачи.
-
собственная частота. Отбор собственных частот и соответствующих им собственных
форм осуществляется с помощью уравнения собственных форм и краевых условий
задачи.
Чтобы получить уравнение собственных
форм однородной задачи, подставим (19) в (9). После сокращения на 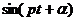
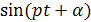 будем иметь
будем иметь
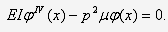
Таким образом, приходим к задаче
интегрирования уравнения
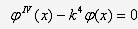
где

при краевых условиях
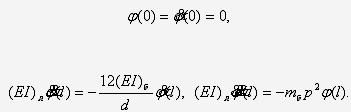
Уравнение (21) имеет следующие четыре
независимых частных решения:
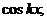

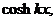
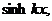
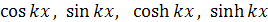 его общий интеграл
его общий интеграл
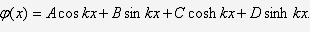
В формуле (25) четыре произвольные
постоянные 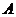 ,
, 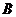 ,
, 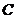 ,
, 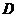 , которые
должны быть подобраны так, чтобы для функции
, которые
должны быть подобраны так, чтобы для функции  выполнялись краевые условия, т.е.
условия закрепления концов стержня.
выполнялись краевые условия, т.е.
условия закрепления концов стержня.
Решение уравнения (21) можно найти
стандартным способом в виде (26):
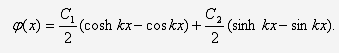
Подставляя решение (26) в краевые
условия (24) получаем систему уравнений (27):
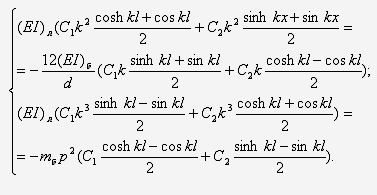
Упрощая систему (27) и делая замены
приходим к системе:
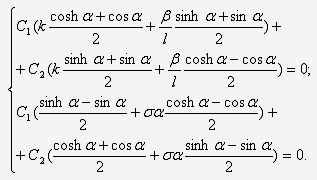
где
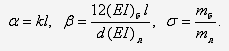
Разрешая систему относительно
постоянных 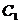
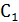 и
и 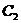 получаем характеристический
определитель вида:
получаем характеристический
определитель вида:
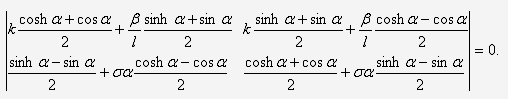
Раскрывая его, получаем частотное
уравнение лопаток турбины:
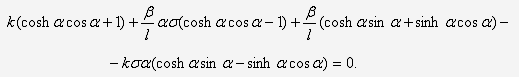
Подставляя физические параметры
механической системы в (31) можно получить частоты ее колебаний.
2.Влияние характеристик лопаток
турбины на собственные частоты ее колебаний
.1 Влияние жесткости на изгиб
бандажа на собственные частоты колебаний
По решению прямой задачи (21), (23),
(24) колебаний лопаток турбины, связанных бандажом исследуем влияние
характеристик лопаток турбины на собственные частоты ее колебаний, а именно
рассмотрим влияние жесткости на изгиб бандажа на собственные частоты.
В ходе решения поставленной задачи
будем изменять значения жесткости на изгиб бандажа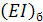 , при этом оставляя
неизменными остальные параметры системы
, при этом оставляя
неизменными остальные параметры системы 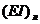
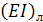 , и вычислять соответствующие этим
жесткостям собственные частоты
, и вычислять соответствующие этим
жесткостям собственные частоты  колебаний.
колебаний.
Рассмотрим, например, следующее
параметры механической системы:
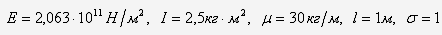
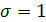 По решению частотного уравнения (31)
получаем, что при увеличении значений жесткости
По решению частотного уравнения (31)
получаем, что при увеличении значений жесткости 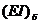 на изгиб бандажа
на изгиб бандажа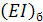 собственные
частоты
собственные
частоты 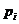
 также увеличиваются.
также увеличиваются.
Зависимость собственных частот
колебаний турбинных лопаток от изменения жесткости на изгиб бандажа показана в
таблице 1.
Таблица1 - Зависимость собственных
частот 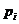 от
жесткости
от
жесткости 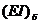 на изгиб
бандажа при параметрах (32) системы
на изгиб
бандажа при параметрах (32) системы
|
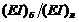 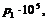 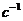 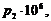 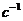 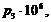 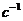 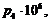 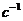 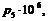 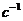  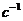
|
|
|
|
|
|
|
|
1
|
2,5576
|
2,2719
|
6,8093
|
1,3928
|
2,3635
|
3,5929
|
|
1,2
|
2,6262
|
2,2956
|
6,8341
|
1,3954
|
2,3660
|
3,5955
|
|
1,4
|
2,6879
|
2,3181
|
6,8582
|
1,3979
|
2,3686
|
3,5980
|
|
1,6
|
2,7435
|
2,3394
|
6,8816
|
1,4003
|
2,3711
|
3,6005
|
|
1,8
|
2,7940
|
2,3597
|
6,9044
|
1,4027
|
2,3755
|
3,6030
|
|
2
|
2,8401
|
2,3790
|
6,9265
|
1,4051
|
2,3760
|
3,6055
|
Графики зависимостей собственных
частот 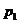 ,
, 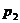
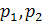 от жесткости
от жесткости 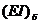 на изгиб
бандажа
на изгиб
бандажа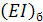 показаны на
рисунках 4, 5.
показаны на
рисунках 4, 5.
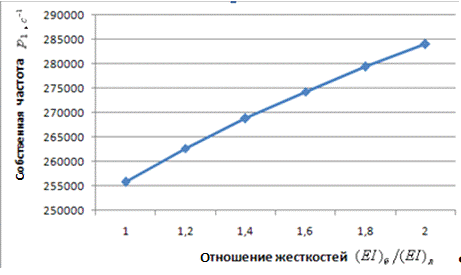
Рисунок 4 - Зависимость собственной
частоты  от жесткости
от жесткости 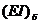 на изгиб
бандажи при параметрах (32) системы
на изгиб
бандажи при параметрах (32) системы
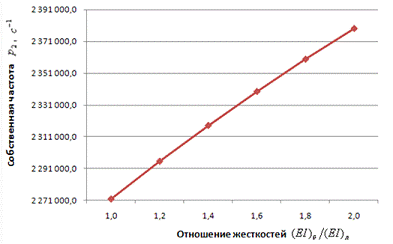
Рисунок 5 - Зависимость собственной
частоты 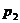 от
жесткости
от
жесткости 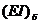 бандажа при
параметрах (32) системы
бандажа при
параметрах (32) системы
Отметим, что такая же прямая зависимость
собственных частот от жесткости на изгиб бандажа справедлива и при других
физических параметрах механической системы.
Таким образом, решения прямой спектральной
задачи по колебаниям лопаток турбины, связанных бандажом показывают, что
увеличение жесткости на изгиб бандажа ведет к увеличению собственных частот
колебаний.
2.2 Влияние массы шага бандажа на
собственные частоты колебаний
Теперь рассмотрим влияние массы шага бандажа на
собственные частоты колебаний лопаток турбины, связанных бандажом.
В ходе решения поставленной задачи
будем изменять значения массы шага бандажа 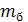 и вычислять соответствующие этим
значениям собственные частоты колебаний
и вычислять соответствующие этим
значениям собственные частоты колебаний .
.
Рассмотрим, например, следующие
параметры механической системы:
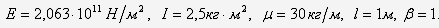
По решению уравнения (31) получаем,
что при увеличении значений массы шага бандажа  при постоянной массе лопаток
собственные частоты
при постоянной массе лопаток
собственные частоты 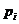
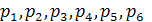 уменьшаются.
уменьшаются.
Зависимость собственных частот
колебаний лопаток турбины, связанных бандажом от изменения массы бандажа
показана в таблице 2.
Таблица 2 - Зависимость собственных
частот 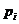 от массы
от массы 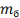 шага
бандажа при параметрах (33) системы
шага
бандажа при параметрах (33) системы
|
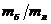 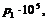 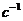 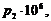 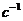 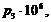 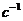 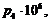 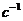 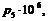 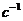  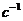
|
|
|
|
|
|
|
|
1
|
2,5576
|
2,2719
|
6,8093
|
1,3928
|
2,3635
|
3,5929
|
|
1,2
|
2,3764
|
2,2526
|
6,7879
|
1,3907
|
2,3613
|
3,5907
|
|
1,4
|
2,2289
|
2,2383
|
6,7724
|
1,3891
|
2,3598
|
3,5892
|
|
1,6
|
2,1058
|
2,2273
|
6,7605
|
1,3879
|
2,3585
|
3,5879
|
|
1,8
|
2,0011
|
2,2185
|
6,7512
|
1,3870
|
2,3576
|
3,5871
|
|
2
|
1,9106
|
2,2113
|
6,7436
|
1,3862
|
2,3569
|
3,5863
|
Графики зависимостей собственных
частот от изменения массы 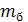
 шага бандажа показаны на рисунках 6,
7.
шага бандажа показаны на рисунках 6,
7.

Рисунок 6 - Зависимость собственной
частоты 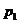 от массы
от массы 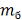 шага
бандажа при параметрах (33) системы
шага
бандажа при параметрах (33) системы

Рисунок 7 - Зависимость собственной
частоты 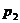 от массы
от массы 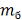 шага
бандажа при параметрах (33) системы
шага
бандажа при параметрах (33) системы
Таким образом, решения прямой спектральной
задачи по колебаниям лопаток турбины, связанных бандажом показывают, что
увеличение массы бандажа ведет к уменьшению собственных частот колебаний.
Проведенные исследования по влиянию физических
параметров лопаток турбины с бандажом на собственные частоты колебаний механической
системы необходимы для решения проблемы сохранения безопасных частот ее
колебаний.
2.3 Применение метода решения прямой
задачи
Рассмотрим применение метода решения
прямой задачи на конкретных примерах. Даны физические параметры лопаток турбины
и бандажа. Необходимо определить соответствующие собственные частоты колебаний
механической системы . По
частотному уравнению (31) можно определить соответствующие заданным физическим
параметрам системы собственные значения
. По
частотному уравнению (31) можно определить соответствующие заданным физическим
параметрам системы собственные значения 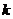 краевой задачи. Затем, используя
зависимость между собственными значениями и собственными частотами (34),
определить соответствующие частоты колебаний системы.
краевой задачи. Затем, используя
зависимость между собственными значениями и собственными частотами (34),
определить соответствующие частоты колебаний системы.
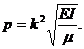
Пример 1. Найти собственные частоты
колебаний лопаток турбины, связанных бандажом, для которой известны следующие
физические параметры:
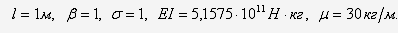
Частотное уравнение (31) после
подстановки в него заданных параметров принимает вид:
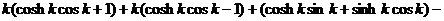

Собственные
значения, найденные с помощью ЭВМ, имеют вид:
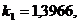
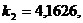
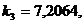
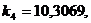

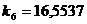 и т. д.
и т. д.
По формуле (34) определяем соответствующие
собственные частоты:
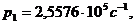
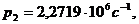
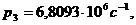


 и т. д.
и т. д.
2.4 Программная реализация прямой
задачи
Для решения прямой задачи составлена
программная реализация с использованием математического пакета Maple 13.
Программа позволяет по заданным характеристикам турбинных лопаток определять
собственные частоты колебаний.
Были использованы следующие команды Maple 13:
With (LinearAlgebra) - вызов
всех программ пакета LinearAlgebra
(усовершенствованные команды линейной алгебры для работы со специальным видом
числовых матриц);
Restart -
используется для отмены всех сделанных назначений и начала нового сеанса без
выхода из Maple ;
Matrix -
используется для определения матрицы, достаточно перечислить элементы матрицы
построчно в квадратных скобках через запятую;
Determinant - вычисляет
определитель матрицы;ollect - приводит подобные члены в
обобщенных полиномах нескольких переменных, в которых в качестве неизвестных
могут выступать функции с аргументами, являющимися неизвестными величинами;
Fsolve -
используется для решения линейных и нелинейных уравнений в аналитическом виде.
Листинг программы:
> restart; with(LinearAlgebra):
> M :=
Matrix(2,[[k*(1/2)*((exp(k*l)+exp(-k*l))/2+cos(k*l))+b*((exp(k*l)-exp(-k))/2+sin(k*l))/2/l,k*((exp(k*l)-exp(-k*l))/2+sin(k*l))/2+b*((exp(k*l)+exp(-k*l))/2-cos(k*l))/2/l],[((exp(k*l)-exp(-k*l))/2-sin(k*l))/2+q*k*l*((exp(k*l)+exp(-k*l))/2-cos(k*l))/2,(1/2)*((exp(k*l)+exp(-k*l))/2+cos(k*l))+q*k*l*((exp(k*l)-exp(-k*l))/2-sin(k*l))/2]]);
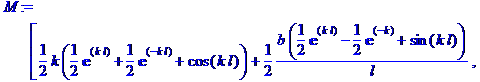
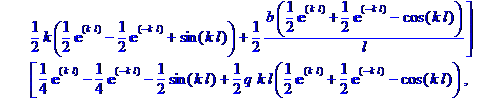
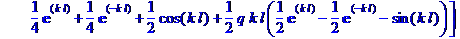
> y:=Determinant(M):
> +
> eg:=collect(y,{k},distributed):
> l:=1; b:=1; q:=1;
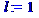


> d:=eg;
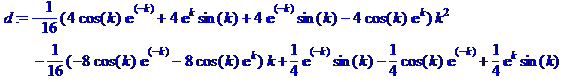

>
k1:=fsolve(d=0,k,0..3);k2:=fsolve(d=0,k,3..5);k3:=fsolve(d=0,k,5..8);k4:=fsolve(d=0,k,10..11);k5:=fsolve(d=0,k,12..14);k6:=fsolve(d=0,k,14..20);


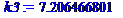
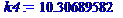
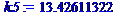

>
>
> EI:=5.1575*10^11;m:=30;

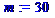
>
p1:=k1^2*sqrt((EI)/(m));p2:=k2^2*sqrt((EI)/(m));p3:=k3^2*sqrt((EI)/(m));p4:=k4^2*sqrt((EI)/(m));p5:=k5^2*sqrt((EI)/(m));p6:=k6^2*sqrt((EI)/(m));
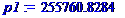
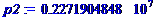


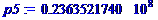
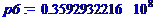
3. Обратная задача по
диагностированию характеристик лопаток турбины с бандажом
.1 Постановка обратной задачи
Поставим теперь к задаче определения частот
колебаний лопаток турбины с бандажом обратную задачу, которая состоит в
диагностировании характеристик лопаток турбины с бандажом по собственным
частотам колебаний. Так как возникновение непрогнозируемых колебательных
процессов в турбинных лопатках может привести к функциональным отказам
составляющих механической системы вплоть до ее разрушения, то возникает задача
определения таких характеристик системы, при которых сохранялись бы безопасные
частоты её колебаний.
А такую проблему сохранения безопасных частот
можно решить с помощью метода решения обратной спектральной задачи.
Итак, известны собственные частоты 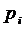 колебаний
лопаток турбины. Необходимо определить физические характеристики лопаток
турбины с бандажом по известным частотам их колебаний. К диагностируемым
характеристикам отнесем коэффициенты жесткостей
колебаний
лопаток турбины. Необходимо определить физические характеристики лопаток
турбины с бандажом по известным частотам их колебаний. К диагностируемым
характеристикам отнесем коэффициенты жесткостей 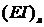 лопатки и
лопатки и 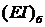 бандажа,
массу
бандажа,
массу 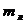 лопатки и
массу
лопатки и
массу 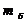 шага
бандажа.
шага
бандажа.
Остановимся на диагностировании этих
характеристик подробнее.
3.2 Диагностирование характеристик
лопаток
Обратная задача: известны
собственные частоты  из
частотного уравнения (31), а также физические характеристики лопаток турбины с
бандажом. Требуется найти коэффициент жесткости лопаток
из
частотного уравнения (31), а также физические характеристики лопаток турбины с
бандажом. Требуется найти коэффициент жесткости лопаток 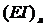 и массу
лопаток
и массу
лопаток 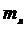 .
.
При исследовании задачи о колебаниях
лопаток турбины с бандажом получено уравнение частот свободных колебаний
системы:
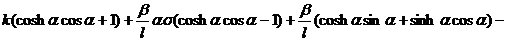
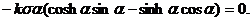
Так как все физические параметры
лопаток турбины с бандажом включены в безразмерные параметры 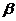 и
и 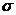 частотного
уравнения (31), то рассмотрим сначала задачу определения указанных параметров
по известным частотам колебаний механической системы.
частотного
уравнения (31), то рассмотрим сначала задачу определения указанных параметров
по известным частотам колебаний механической системы.
Исследуем вопрос о единственности
решения поставленной задачи отыскания безразмерных параметров 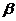 и
и 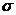 . Для этого
задачу с частотным уравнением (31) обозначим через
. Для этого
задачу с частотным уравнением (31) обозначим через 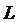 , а задачу с
таким же частотным уравнением и физическими параметрами, но с другими
безразмерными параметрами
, а задачу с
таким же частотным уравнением и физическими параметрами, но с другими
безразмерными параметрами 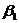 и
и 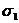 обозначим
через
обозначим
через 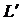 .
.
Теорема 1 (о единственности
решения):
Если собственные частоты задач  и
и 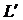 с
характеристическими определителями
с
характеристическими определителями 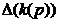 и
и 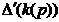 совпадают с учетом их кратностей,
то
совпадают с учетом их кратностей,
то 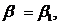
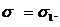
Доказательство.
Собственные частоты задачи 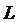 совпадают с
корнями уравнения (31). Преобразуем уравнение (31) к виду:
совпадают с
корнями уравнения (31). Преобразуем уравнение (31) к виду:
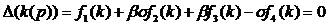
где 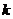 - собственное значение спектральной
задачи, а функции
- собственное значение спектральной
задачи, а функции 

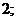
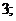
 , зависящие
от собственного значения (а значит от собственной частоты колебаний)
определяются следующим образом:
, зависящие
от собственного значения (а значит от собственной частоты колебаний)
определяются следующим образом:
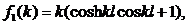

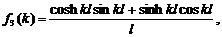

Уравнение (35) является целой
функцией от 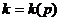 . Функции
. Функции 
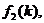
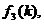
 не
зависят от коэффициентов
не
зависят от коэффициентов 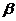 и
и 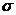 и образуют
систему линейно независимых функций.
и образуют
систему линейно независимых функций.
Для частотного уравнения задачи 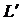 имеем
аналогичное представление:
имеем
аналогичное представление:
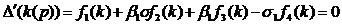 .
.
Поскольку  и
и  являются
целыми функциями от
являются
целыми функциями от 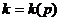 и не равны
тождественно нулю, то из теоремы Адамара получаем, что функции
и не равны
тождественно нулю, то из теоремы Адамара получаем, что функции  и
и 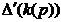 восстанавливаются
по своим нулям с точностью до постоянного множителя
восстанавливаются
по своим нулям с точностью до постоянного множителя  . Значит,
. Значит,
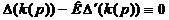 .
.
Из последнего равенства и линейной
независимости функций 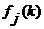

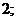
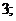
 получаем,
что
получаем,
что 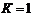 , отсюда
, отсюда 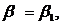
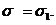 Теорема
доказана.
Теорема
доказана.
Из теоремы 1 следует, что
безразмерные параметры 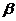 и
и 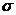 частотного
уравнения можно определить по известным собственным частотам колебаний
единственным образом.
частотного
уравнения можно определить по известным собственным частотам колебаний
единственным образом.
Построим теперь метод нахождения
характеристик лопаток.
Пусть известны две собственные
частоты 
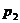 задачи
задачи  и
физические параметры бандажа, такие как масса и жесткость. Поскольку
собственные частоты являются нулями функции
и
физические параметры бандажа, такие как масса и жесткость. Поскольку
собственные частоты являются нулями функции 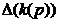 , то из представления (35) получаем
алгебраические уравнения от неизвестных параметров
, то из представления (35) получаем
алгебраические уравнения от неизвестных параметров 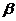 и
и 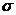 для каждой
из частот.
для каждой
из частот.
Рассмотрим следующую систему
уравнений, полученную из (35) при известных собственных частотах  и
и
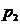 (а
следовательно и собственных значениях, соответственно,
(а
следовательно и собственных значениях, соответственно, 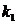 и
и
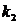 ):
):

Выразим из первого уравнения системы (36)
параметр β:

Подставим выражение (37) во второе
уравнение системы (36) и получим следующее квадратное уравнение:
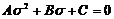
в котором:
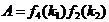 ,
,
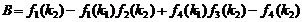 ,
,
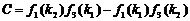 .
.
Решая уравнение (38) относительно 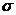 имеем:
имеем:

где
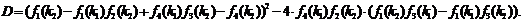
По ходу вывода формул была доказана
следующая теорема.
Теорема 2
Если известны две собственные
частоты  и
и 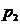 (а
следовательно собственные значения
(а
следовательно собственные значения 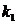 и
и 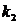 ), ранг
матрицы системы уравнений (36) равен двум, то коэффициенты β и σ однозначно
определяются по формулам (37),(39).
), ранг
матрицы системы уравнений (36) равен двум, то коэффициенты β и σ однозначно
определяются по формулам (37),(39).
Из теоремы 2 следует, что жесткость
и массу лопаток турбины можно определить по известным собственным частотам
колебаний единственным образом.
Таким образом, найденный метод
решения обратной задачи позволяет диагностировать безразмерные параметры β и σ (а значит,
и необходимые физические параметры) по известным частотам колебаний
механической системы.
Рассмотрим также следующий метод
нахождения жесткости и массы лопатки по известным трем частотам колебаний механической
системы.
Пусть известны собственные частоты  ,
, 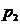 ,
,  (соответственно,
собственные значения
(соответственно,
собственные значения 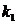 ,
, 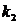 ,
,  ) колебаний
лопаток турбины и характеристики бандажа (масса и жесткость бандажа, а также
длина, погонная масса однородного стержня). Метод основан на решении двух
систем алгебраических уравнений с неизвестными параметрами β и σ.
) колебаний
лопаток турбины и характеристики бандажа (масса и жесткость бандажа, а также
длина, погонная масса однородного стержня). Метод основан на решении двух
систем алгебраических уравнений с неизвестными параметрами β и σ.
Сначала решается система (36) из
двух уравнений при известных собственных значениях 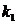 и
и 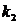 :
:

В результате получим две пары
решений 
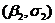 .
.
Аналогично решается система из двух
уравнений при известных собственных значениях 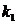 и
и  :
:

которая также имеет две пары решений
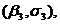
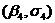 .
.
Зная значения безразмерных
параметров 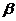 и
и 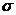 , можно
найти массу лопатки и жесткость лопатки по следующим формулам:
, можно
найти массу лопатки и жесткость лопатки по следующим формулам:


Пример 2. Определить жесткость 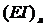 и массу
и массу 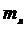 лопаток
турбины, для которой известны физические параметры бандажа и частоты колебаний
системы:
лопаток
турбины, для которой известны физические параметры бандажа и частоты колебаний
системы:
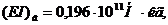
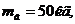

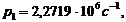
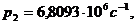
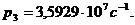
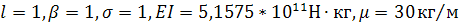 Решая систему уравнений (36) при
данных физических параметрах и известных частотах
Решая систему уравнений (36) при
данных физических параметрах и известных частотах  и
и
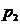 получим:
получим:
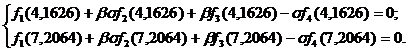

Решение последней системы, найденное
с помощью ЭВМ, имеет вид:
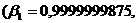



Подставляя теперь в систему
уравнений (36) частоты  и
и
 колебаний
механической системы, получим:
колебаний
механической системы, получим:
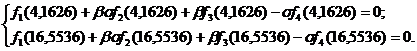

Последняя система имеет решение:
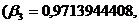
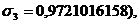
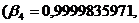
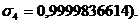
Сравнивая полученные решения двух
систем, видим, что общим для них является лишь один набор переменных 
 который и
является искомым. Таким образом, безразмерные параметры:
который и
является искомым. Таким образом, безразмерные параметры: 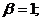
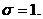 Пользуясь
формулами (40), (41) определяем массу и жесткость лопатки:
Пользуясь
формулами (40), (41) определяем массу и жесткость лопатки:
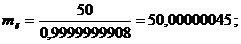
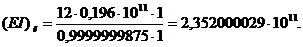
Значит, масса лопатки и жесткость
лопатки, соответственно, равны 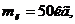

Покажем, что аналогичные значения
массы лопатки и жесткости лопатки получаются, если использовать при решении
обратной задачи аналитические формулы (37)-(39) для параметров 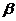 и
и 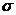 и формулы
(40) и (41) для определения искомых характеристик лопатки.
и формулы
(40) и (41) для определения искомых характеристик лопатки.
Действительно:


Тогда
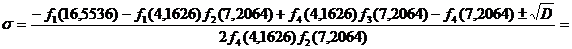
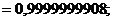

То есть, получаем снова, что 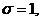
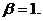
Заметим также, что характеристики
лопатки определены верно, так как именно указанным физическим параметрам
лопаток турбины с бандажом соответствуют заданные частоты колебаний
механической системы.
3.3 Диагностирование характеристик
бандажа
Рассмотрим теперь задачу
диагностирования характеристик бандажа. Обратная задача: известны собственные
частоты  из
частотного уравнения (31), а также физические характеристики лопаток турбины.
Требуется найти коэффициент жесткости
из
частотного уравнения (31), а также физические характеристики лопаток турбины.
Требуется найти коэффициент жесткости 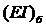 бандажа и
массу
бандажа и
массу  бандажа.
бандажа.
При исследовании задачи о колебаниях
лопаток турбины с бандажом получено уравнение частот свободных колебаний
системы, записанное в форме (35). Проводя аналогичные рассуждения, как в п.3.2,
можно показать, что при решении поставленной обратной задачи для диагностирования
характеристик бандажа также будут справедливы доказанные теоремы 1 и 2.
Следовательно, справедливы формулы (37), (39) для однозначного определения
безразмерных коэффициентов 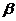 и
и 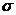 частотного уравнения.
частотного уравнения.
Рассмотрим метод нахождения
жесткости и массы бандажа, основанный на использовании трех известных
собственных частот колебаний системы. Снова известны собственные частоты  ,
, 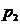 ,
,  (соответственно,
собственные значения
(соответственно,
собственные значения 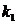 ,
, 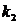 ,
,  ) задачи и
характеристики лопатки (масса и жесткость лопатки, а также длина, погонная
масса однородного стержня). Решая две системы вида (36) из двух уравнений при
известных собственных значениях
) задачи и
характеристики лопатки (масса и жесткость лопатки, а также длина, погонная
масса однородного стержня). Решая две системы вида (36) из двух уравнений при
известных собственных значениях 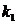 и
и 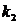
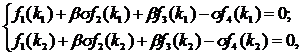
и известных собственных значениях 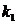 и
и  :
:
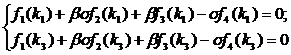
в результате получим по две пары
решений 
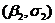 и
и 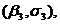
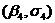 .
.
Общим решением этих двух систем
является лишь один набор значений (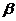 ,
, 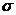 ), который и будет искомым.
), который и будет искомым.
Определив значения безразмерных
параметров 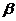 и
и 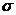 , можно
найти при известных характеристиках лопаток жесткость и массу бандажа по
следующим формулам:
, можно
найти при известных характеристиках лопаток жесткость и массу бандажа по
следующим формулам:


Пример 3. Определить жесткость 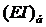 на изгиб
бандажа и массу
на изгиб
бандажа и массу  шага
бандажа турбины, для которой известны физические параметры лопаток и частоты
колебаний системы:
шага
бандажа турбины, для которой известны физические параметры лопаток и частоты
колебаний системы:
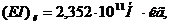
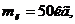

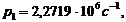
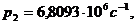
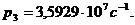
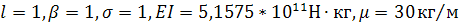
Решая систему уравнений (36) при
данных физических параметрах и известных частотах  и
и
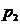 получим:
получим:
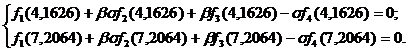

Решение этой системы, найденное с
помощью ЭВМ, имеет вид:
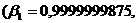



Подставляя теперь в систему
уравнений (36) частоты  и
и
 колебаний
системы, получим:
колебаний
системы, получим:
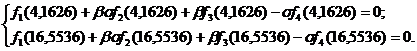

Последняя система имеет решение:
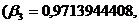
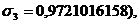
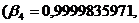
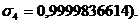
Сравнивая полученные решения двух
систем, видим, что общим для них является лишь один набор переменных 
 который и
является искомым. Таким образом, безразмерные параметры:
который и
является искомым. Таким образом, безразмерные параметры: 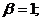
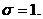 Пользуясь
формулами (42), (43) определяем массу и жесткость лопатки:
Пользуясь
формулами (42), (43) определяем массу и жесткость лопатки:
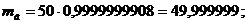
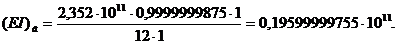
Значит, масса лопатки и жесткость
лопатки, соответственно, равны 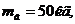
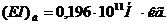 Покажем, что аналогичные значения
массы лопатки и жесткости лопатки получаются, если использовать при решении
обратной задачи аналитические формулы (37) - (39) для параметров
Покажем, что аналогичные значения
массы лопатки и жесткости лопатки получаются, если использовать при решении
обратной задачи аналитические формулы (37) - (39) для параметров 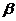 и
и 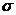 и формулы
(42) и (43) для определения искомых характеристик лопатки.
и формулы
(42) и (43) для определения искомых характеристик лопатки.


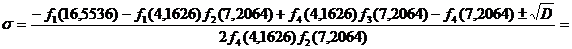
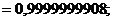

Получаем снова, что 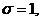
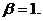 Заметим
также, что характеристики бандажа определены верно, так как именно указанным
физическим параметрам бандажа соответствую заданные частоты колебаний
механической системы.
Заметим
также, что характеристики бандажа определены верно, так как именно указанным
физическим параметрам бандажа соответствую заданные частоты колебаний
механической системы.
3.4 Программная реализация решения
обратной задачи
> 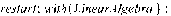
> 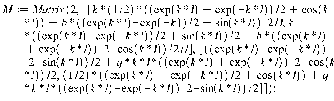

> 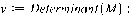
> 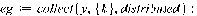
> 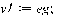

> 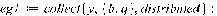
> 

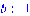
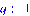
> 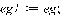

> 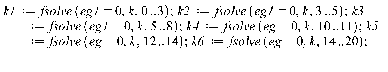
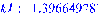
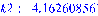
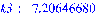
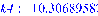
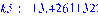

> 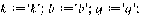
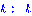

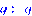
> 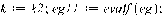
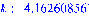
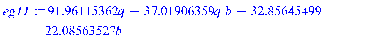
> 
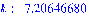
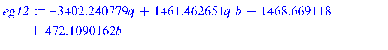
> 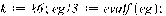
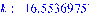
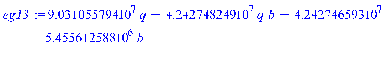
> 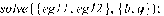
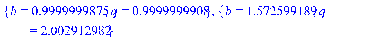
> 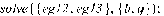
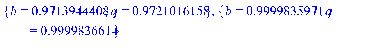
> 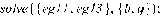
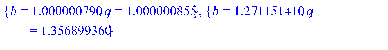
> 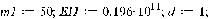

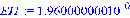
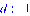
> 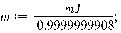
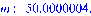
> 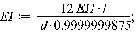
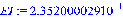
3.5 Исследование проблемы сохранения
собственных частот
Рассмотрим задачу сохранения собственных частот
колебаний лопаток турбины с бандажом при изменениях физических параметров
механической системы, например, масс.
По практической надобности возникают
ситуации, когда необходимо увеличить массу шага бандажа, или же, наоборот,
уменьшить массу. Проведенные исследования по влиянию массы шага бандажа (или
массы лопатки) на значения собственных частот колебаний лопаток турбины
показывают, что при изменении масс 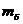 ,
,  собственные частоты изменяются. А
именно, при увеличении массы шага бандажа, собственные частоты уменьшаются.
собственные частоты изменяются. А
именно, при увеличении массы шага бандажа, собственные частоты уменьшаются.
Возникает вопрос: как сохранить
частоты прежними, безопасными? На этот вопрос мы предлагаем ответить с помощью
метода решения обратной задачи диагностирования масс.
Пусть известны следующие физические
параметры: 
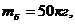

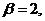

Решая прямую задачу при заданных
физических параметрах, получим соответствующие частоты колебаний:
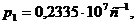
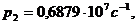

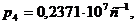
 и т. д.
и т. д.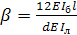
Пусть масса шага бандажа 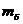 увеличивается
с
увеличивается
с  до
до 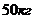 . Известно,
что при этом частоты колебаний турбинных лопаток уменьшаются. А нам нужно
сохранить прежние частоты. Тогда исходя из формулы, полученной ранее:
. Известно,
что при этом частоты колебаний турбинных лопаток уменьшаются. А нам нужно
сохранить прежние частоты. Тогда исходя из формулы, полученной ранее:
 ,
,
можем определить соответствующее для
этого значение массы лопатки  . При этом в формулу для
. При этом в формулу для  подставим
новое значение
подставим
новое значение 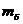 и прежнее
значение безразмерного параметра
и прежнее
значение безразмерного параметра  В нашем случае получим:
В нашем случае получим:
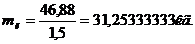
Таким образом, для сохранения
прежних частот при изменении массы шага бандажа с  до
до 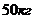 необходимо
увеличить массу лопатки с
необходимо
увеличить массу лопатки с 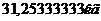 до
до 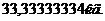 Для
рассмотренной задачи ниже приведены значения масс лопатки и бандажа
Для
рассмотренной задачи ниже приведены значения масс лопатки и бандажа  и
и 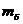 ,
сохраняющие заданные частоты колебаний турбинной лопатки с бандажом (таблица
3).
,
сохраняющие заданные частоты колебаний турбинной лопатки с бандажом (таблица
3).
Таблица 3 - Значения масс лопатки и бандажа,
необходимые для сохранения частот колебаний (44)
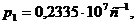
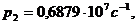

|
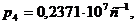  и т. д. и т. д.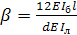  , , 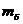 , ,
|
|
|
|
33,33
|
50
|
|
31,25
|
46,88
|
|
30,15
|
45,22
|
|
28,67
|
43
|
|
26,60
|
39,99
|
Таким образом, для сохранения заданных частот
колебаний турбинных лопаток с бандажом при увеличении массы шага бандажа
необходимо соответствующим образом увеличить и массу лопатки.
Подобную задачу сохранения прежних частот
колебаний лопаток турбины с бандажом можно решить и в случае изменения
жесткостных параметров механической системы.
По практической надобности может
возникнуть задача усиления, например, жесткости на изгиб бандажа. Рассмотрим
эту задачу на конкретном примере. Известны следующие физические параметры
механической системы: 

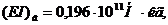
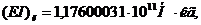
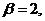
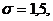 а также
собственные частоты колебаний (44).
а также
собственные частоты колебаний (44).
Пусть коэффициент жесткости на изгиб
бандажа 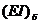 увеличивается
с
увеличивается
с 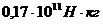 до
до 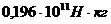 . Известно,
что при увеличение коэффициента жесткости на изгиб бандажа
. Известно,
что при увеличение коэффициента жесткости на изгиб бандажа 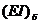 собственные
частоты колебаний лопаток турбины с бандажом также увеличиваются. Для
сохранения частот прежними, следуя формуле, доказанной ранее
собственные
частоты колебаний лопаток турбины с бандажом также увеличиваются. Для
сохранения частот прежними, следуя формуле, доказанной ранее
 ,
,
достаточно изменить соответствующим
образом коэффициент жесткости лопатки 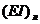 . Подставим в формулу для
. Подставим в формулу для 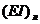 новое
значение
новое
значение 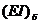 и прежнее
значение безразмерного параметра
и прежнее
значение безразмерного параметра 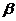 . Тогда получим:
. Тогда получим:
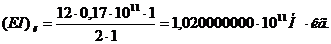
Таким образом, для сохранения
прежних собственных частот колебаний турбинной лопатки с бандажом при изменении
коэффициента жесткости на изгиб бандажа с 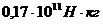 до
до 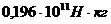 необходимо увеличить коэффициент
жесткости лопатки с
необходимо увеличить коэффициент
жесткости лопатки с 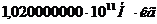 до
до 
Для рассмотренной задачи в таблице 4
приведены значения коэффициентов жесткостей лопатки и бандажа 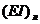 и
и 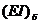 ,
сохраняющие заданные частоты колебаний турбинной лопатки с бандажом.
,
сохраняющие заданные частоты колебаний турбинной лопатки с бандажом.
Таблица 4 - Значения коэффициентов жесткости
лопатки и бандажа, необходимые для сохранения частот колебаний (44)

Таким образом, для сохранения заданных частот
колебаний турбинных лопаток с бандажом при увеличении коэффициента жесткости
бандажа необходимо соответствующим образом увеличить и коэффициент жесткости
лопатки.
Заключение
В работе исследована
и решена задача определения собственных частот колебания лопаток турбины,
связанных бандажом. Частотное уравнение получено с помощью характеристического
определителя. Для нахождения собственных частот колебаний турбинных лопаток
были использованы средства Maple 13. Для построения графиков зависимости
собственных частот колебаний турбинных лопаток от изменения жесткости бандажа и
массы бандажа использована программа пакета Microsoft Office Excel 2010.
Приведены конкретные примеры.
По решению прямой
спектральной задачи исследовано влияние на собственные частоты колебаний
лопаток турбины изменений жесткости бандажа и массы бандажа. Получено, что
увеличение жесткости бандажа ведет к увеличению значений, а увеличение массы
бандажа ведет к уменьшению значений собственных частот колебаний лопаток
турбины. Зависимости рассмотрены при различных физических параметрах
механической системы. Приведены графики и таблицы рассмотренных зависимостей.
Впервые поставлена
и решена обратная спектральная задача - задача диагностирования характеристик
лопаток турбины с бандажом по известным частотам их свободных колебаний.
Исследованы и решены обратные задачи диагностирования жесткости и массы
лопатки, а также жесткости и массы шага бандажа. Доказаны теоремы о единственности
решений поставленных задач диагностирования. Найдены методы решений задач,
которые сводятся к решениям систем алгебраических нелинейных уравнений.
В работе показано,
что для сохранения безопасных частот колебаний лопаток турбины достаточно
произвести соответствующие изменения в жесткостях или массах лопаток, или
бандажа. Приведены примеры, подтверждающие выводы и совпадающие с результатами
доказанных теорем. Составлены программы в математическом пакете Maple для
решения обратных задач.