Структурный анализ плоского рычажного механизма
1. Структурный анализ плоского рычажного
механизма
.1 Структурная схема механизма

Рисунок 1.1 - Структурная схема механизма
Таблица 1 - Звенья механизма
|
№
звена-название звена
|
Схема
звена
|
Вид
движения
|
|
1-
кривошип
|
 вращательное вращательное
|
|
|
2-
шатун
|
 сложное сложное
|
|
|
3-
ползун
|
 поступательное поступательное
|
|
|
4-
шатун
|
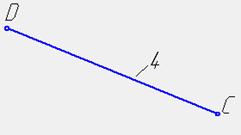 сложенное сложенное
|
|
|
5-
ползун
|
 поступательное поступательное
|
|
|
0-
стойка
|
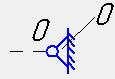 неподвижное неподвижное
|
|
Структурная схема механизма состоит из пяти
подвижных звеньев и неподвижной стойки, представленной шарнирно-неподвижной
опорой и двумя направляющими ползунов 3 и 5.
.2 Подвижность механизма
Подвижность механизма определяем по формуле
Чебышева:
 (1)
(1)
где W -
подвижность механизма;
n - число
подвижных звеньев;
p5 и p4 -
соответственно число пар пятого и четвертого класса.
Для определения значений p4 и p5 найдем все
кинематические пары, входящие в состав рассматриваемой кинематической цепи.
Результаты исследования заносим в таблицу 1.
Таблица 2 - Кинематические пары
|
Кинематическая
пара
|
Схема
|
Подвижность
|
Класс
|
|
0-1
|
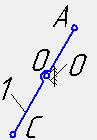 1В5 1В5
|
|
|
|
1-2
|
 1В5 1В5
|
|
|
|
2-3
|
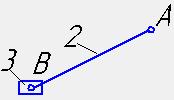 1В5 1В5
|
|
|
|
1-4
|
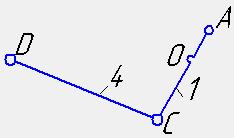 1В5 1В5
|
|
|
|
4-5
|
 1В5 1В5
|
|
|
|
0-3
|
 1П5 1П5
|
|
|
|
0-5
|
 1П5 1П5
|
|
|
Из анализа данных (таблица 2) следует, что
исследуемая схема кривошипно-ползунного механизма представляет собой замкнутую кинематическую
цепь и состоит из семи пар пятого класса, пар четвертого класса в составе
структуры нет. Следовательно, p5=7,
а p4=0.
Подставив найденные значения n,
p4
и p5
в формулу (1), получим:

Полученный результат означает, что
для однозначного описания положения всех звеньев механизма в рассматриваемой
плоскости достаточно знать одну обобщенную координату φ1.
.3 Анализ состава структуры
механизма
Для решения данной задачи
используется структурная классификация механизмов, предложенная профессором
Ассуром, согласно которой плоские рычажные механизмы состоят из структурных
групп звеньев и первичных (элементарных) механизмов.
Начиная с выходных звеньев - ползунов 3 и 5,
разбиваем рассматриваемую схему кривошипно-ползунного механизма на группы
звеньев. При этом руководствуемся следующим правилом: если выделенная группа
звеньев обладает совместно нулевой подвижностью, то эта группа звеньев является
структурой группой Ассура (СГА).
Количество подвижных звеньев определяет класс
СГА.
Поводок - это конечное звено СГА, входящее в
состав кинематической пары и имеющее свободный элемент звена.
Количество поводков определяет порядок группы, а
вид СГА определяется ее структурной схемой.
Рассмотрим группу звеньев 2-3 (рисунок 1.2).
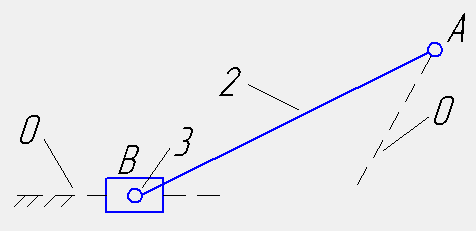
Рисунок 1.2 - Группа звеньев 2-3
Данная группа состоит из двух подвижных звеньев:
шатун 2 и ползун 3, и трех кинематических пар:
-2 вращательная пара пятого класса;
-3 вращательная пара пятого класса;
-0 поступательная пара пятого класса.
Следовательно, структурная формула - ВВП,
являющаяся вторым видом.
Поводки представлены звеном 1 и направляющей
ползуна.
Таким образом, n=2,
p5=3,
а p4=0.
Подставив выявленные значения в формулу (1),
получим:
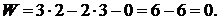
Следовательно, группа звеньев 2-3 является
структурной группой Ассура второго класса, второго порядка, второго вида.
Рассмотрим группу звеньев 4-5 (рисунок 1.3).

Рисунок 1.3 - Группа звеньев 4-5
Данная группа состоит из двух подвижных звеньев:
шатун 4 и ползун 5, и трех кинематических пар:
-4 вращательная пара пятого класса;
-5 вращательная пара пятого класса;
-0 поступательная пара пятого класса.
Следовательно, структурная формула - ВВП,
являющаяся вторым видом.
Поводки представлены звеном 1 и направляющей
ползуна.
Таким образом, n=2,
p5=3,
а p4=0.
Подставив выявленные значения в формулу (1),
получим:
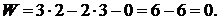
Следовательно, группа звеньев 4-5 является
структурной группой Ассура второго класса, второго порядка, второго вида.
Рассмотрим группу звеньев 0-1 (рисунок 1.3).

Рисунок 1.3 - Группа звеньев 0-1
Данная группа состоит из подвижного звена
кривошипа 1, стойки 0 и одной кинематической пары (вращательная 0-1)
Тогда n=1,
p5=1,
а p4=0.
Подставив найденные значения в формулу (1),
получим:

Следовательно, группа звеньев 0-1 не
является структурной группой Ассура, а представляет собой первичный механизм,
подвижность которого равна единице, т.е. существует одна обобщенная координата.
Из проведенного анализа следует, что число
степеней свободы механизма равно единице; механизм имеет следующий структурный
состав (рисунок 1.4): первичный механизм с подвижностью равной единице и две
структурные группы Ассура второго класса, второго порядка, второго вида.

Рисунок 1.4 - Структурный состав
кривошипно-ползунного механизма
Вывод: подвижность механизма определяется
подвижностью первичного механизма, входящего в его состав. Класс механизма
определяется классом наиболее сложной структурной группы. Рассмотренный
механизм является механизмом второго класса.
. Синтез кинематической схемы плоского рычажного
механизма
Для построения кинематической схемы плоского
рычажного механизма выберем масштабный коэффициент.
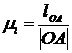
 , (2.1)
, (2.1)
где µl
- масштабный коэффициент длин, м/мм;
 - действительная длина кривошипа,
м;
- действительная длина кривошипа,
м;
 - произвольно выбранная длина
кривошипа на чертеже, мм.
- произвольно выбранная длина
кривошипа на чертеже, мм.
Отрезок |OA| принимаем
равным 19,5 мм.
В этом случае масштабный коэффициент
будет равен:
 .
.
Размеры остальных звеньев
высчитываем по формуле:
 , (2.2)
, (2.2)
где i
- номер звена, для которого вычисляется длина на кинематической схеме.
Длины звеньев с учетом масштабного коэффициента:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Построим по заданным геометрическим
параметрам кинематическую схему механизма в масштабном коэффициенте  .
.
. Кинематический анализ плоского
рычажного механизма
.1 Построение плана положений
механизма
План положений - графическое
изображение взаимного расположения звеньев в данный момент времени, выполненный
в определенном масштабном коэффициенте.
Построим положения механизма через
каждые 30 градусов вращения кривошипа, начиная от одного из крайних положений.
Каждое положение строится тем же методом, что и кинематическая схема механизма.
Пронумеруем положения от 0 до 12.
.2 Построение планов скоростей
относительно 12-ти положений ведущего звена
Для построения планов скоростей
необходимо составить векторные уравнения скоростей.
Проанализируем полученную схему
кривошипно-ползунного механизма: точка  является неподвижной точкой,
следовательно, модуль скорости этой точки равен нулю
является неподвижной точкой,
следовательно, модуль скорости этой точки равен нулю  .
.
Вектор скорости точки  представляет
собой геометрическую сумму вектора скорости точки
представляет
собой геометрическую сумму вектора скорости точки  и скорости
относительного вращательного движения точки
и скорости
относительного вращательного движения точки  вокруг точки
вокруг точки  :
:

Линия действия вектора скорости  является
перпендикуляром к оси кривошипа 1, а направление действия этого вектора
является
перпендикуляром к оси кривошипа 1, а направление действия этого вектора  совпадает с
направлением вращения кривошипа 1.
совпадает с
направлением вращения кривошипа 1.
Модуль скорости звена 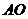 :
:
 (3.1)
(3.1)
где VAO
- модуль скорости звена ОА, м/с;
ω1 - угловая
скорость звена  , с-1;
, с-1;
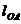 - длина кривошипа
- длина кривошипа  , м.
, м.
Для вычисления величины модуля
скорости звена  , нужно
определить угловое ускорение данного звена по формуле:
, нужно
определить угловое ускорение данного звена по формуле:
 (3.2)
(3.2)
где ω1 - угловая
скорость звена, с-1;
π - 3,14;
n -
количество оборотов в минуту, об/мин.
Подставив заданные значения в
выражение (3.2), получим:

Подставив найденное значение угловой
скорости в выражение (3.1), получим:

Вектор скорости точки 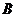 ,
принадлежащей шатуну 2, представляет собой геометрическую сумму вектора
скорости точки
,
принадлежащей шатуну 2, представляет собой геометрическую сумму вектора
скорости точки  и вектора
скорости относительного вращательного движения точки
и вектора
скорости относительного вращательного движения точки 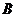 вокруг точки
вокруг точки
 (
( ):
):

В то же время точка 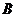 принадлежит
и ползуну 3. Ползун 3 совершает прямолинейные возвратно-поступательное движение
вдоль направляющей (прямой
принадлежит
и ползуну 3. Ползун 3 совершает прямолинейные возвратно-поступательное движение
вдоль направляющей (прямой  ), следовательно, линия действия
вектора скорости точки
), следовательно, линия действия
вектора скорости точки 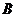 проходит
параллельно прямой
проходит
параллельно прямой  :
:

Совместное решение последних двух
выражений позволит определить модуль и направление действия вектора скорости
точки 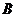 .
.
Вектор скорости точки  представляет
собой геометрическую сумму вектора скорости точки
представляет
собой геометрическую сумму вектора скорости точки  и скорости
относительного вращательного движения точки
и скорости
относительного вращательного движения точки  вокруг точки
вокруг точки  :
:

Линия действия вектора скорости  является
перпендикуляром к оси кривошипа 1, а направление действия этого вектора
совпадает с направлением вращения кривошипа 1.
является
перпендикуляром к оси кривошипа 1, а направление действия этого вектора
совпадает с направлением вращения кривошипа 1.
Модуль скорости звена  :
:

Вектор скорости точки 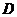 ,
принадлежащей шатуну 4, представляет собой геометрическую сумму вектора
скорости точки
,
принадлежащей шатуну 4, представляет собой геометрическую сумму вектора
скорости точки  и вектора
скорости относительного вращательного движения точки
и вектора
скорости относительного вращательного движения точки 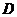 вокруг
точки
вокруг
точки  (
(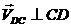 ):
):
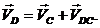
В то же время точка 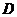 принадлежит
и ползуну 5. Ползун 5 совершает прямолинейные возвратно-поступательное движение
вдоль направляющей (прямой
принадлежит
и ползуну 5. Ползун 5 совершает прямолинейные возвратно-поступательное движение
вдоль направляющей (прямой 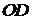 ), следовательно, линия действия
вектора скорости точки
), следовательно, линия действия
вектора скорости точки 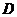 проходит
параллельно прямой
проходит
параллельно прямой 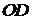 :
:

Совместное решение последних двух
выражений позволит определить модуль и направление действия вектора скорости
точки 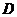 .
.
Найдем масштабный коэффициент
скорости µV по формуле:
 (3.3)
(3.3)
где µV -
масштабный коэффициент скорости, (м/с)/мм;
 - модуль скорости точки А, м/с;
- модуль скорости точки А, м/с;
 - произвольно выбранный отрезок,
изображающий на плане скоростей вектор скорости точки
- произвольно выбранный отрезок,
изображающий на плане скоростей вектор скорости точки  , мм.
, мм.
Примем 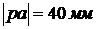 , и
подставив в выражение (3.3) получим:
, и
подставив в выражение (3.3) получим:

Для построения плана скоростей, найдем длину
отрезка pc,
изображающего на плане скорость точки С:
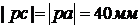
Разрешив графически векторные
уравнения, построим план скоростей.
Для построение векторов скоростей центров
тяжести шатунов 2 и 4 воспользуемся теоремой подобия.
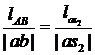 и
и  ,
,
следовательно:
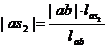 и
и  ,
,
где |ab| и |cd| - отрезки,
изображающие на плане скоростей векторы скоростей  и
и  соответственно,
мм.
соответственно,
мм.
lAC, lAB,  ,
,  - длины
звеньев АС, АВ, AS2, CS4
соответственно, м.
- длины
звеньев АС, АВ, AS2, CS4
соответственно, м.
Используя величины отрезков 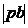 ,
,  ,
,  ,
,  ,
,  и
и  , определим
модули соответствующих скоростей:
, определим
модули соответствующих скоростей:
Модуль скорости точки 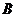 :
:

Модуль скорости  :
:

Модуль скорости точки 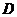 :
:

Модуль скорости  :
:

Модуль скорости точки S2:

Модуль скорости точки S4:

Угловая скорость кривошипа 1 по
условию задания постоянная, высчитывается по формуле 3.2. Ползуны 3 и 5
совершают прямолинейные возвратно-поступательные движения, следовательно, не
имеют угловых скоростей. Угловая скорость шатунов 2 и 4 находится по формулам:
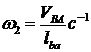 ,
,

Строим планы скоростей для всех положений
механизма. Вычисляем истинные величины линейных и угловых скоростей для всех
положений механизма и сводим их в таблицу 3.
Таблица 3 - Значения угловых и линейных
скоростей для двенадцати положений механизма
|
Номер
положения
|
VBA,
м/с
|
VB, м/с
|
VDC, м/с
|
VD, м/с
|
VS2, м/с
|
VS4, м/с
|
ω2,
с-1
|
ω4,
с-1
|
|
0,12
|
2,1
|
0
|
4,27
|
0
|
|
|
8,75
|
7,36
|
|
1
|
1,84
|
0,74
|
3,74
|
2,67
|
|
|
7,66
|
6,45
|
|
2
|
1,10
|
1,50
|
2,20
|
4,24
|
|
|
4,58
|
3,79
|
|
3
|
0
|
2,1
|
0
|
4,27
|
|
|
0
|
0
|
|
4
|
1,10
|
2,14
|
2,20
|
3,15
|
3,74
|
2,07
|
4,58
|
3,79
|
|
5
|
1,85
|
1,39
|
3,74
|
1,60
|
|
|
7,71
|
6,45
|
|
6
|
2,1
|
0
|
4,27
|
0
|
|
|
8,75
|
7,36
|
|
7
|
1,85
|
1,39
|
3,74
|
1,60
|
|
|
7,71
|
6,45
|
|
8
|
1,10
|
2,14
|
2,20
|
3,15
|
|
|
4,58
|
3,79
|
|
9
|
0
|
2,1
|
0
|
4,27
|
|
|
0
|
0
|
|
10
|
1,10
|
1,50
|
2,20
|
4,24
|
|
|
4,58
|
3,79
|
|
11
|
1,84
|
0,74
|
3,74
|
2,67
|
|
|
7,66
|
6,45
|
3.3 Построение планов ускорений относительно
12-ти положений ведущего звена
Для построения плана ускорений
составим векторные уравнения. Вектор ускорения точки  представляет
собой геометрическую сумму вектора ускорения точки
представляет
собой геометрическую сумму вектора ускорения точки  , вектора
нормального ускорения и вектора тангенциального ускорения относительного
вращательного движения точки
, вектора
нормального ускорения и вектора тангенциального ускорения относительного
вращательного движения точки  вокруг точки
вокруг точки  :
:
 (3.4)
(3.4)
В уравнении (3.4) первое слагаемое
равно нулю  так как
точка
так как
точка  является
неподвижной, а третье слагаемое равно нулю, так как угловая скорость звена ОА
постоянна
является
неподвижной, а третье слагаемое равно нулю, так как угловая скорость звена ОА
постоянна 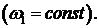 Тогда
уравнение (3.4) примет следующий вид:
Тогда
уравнение (3.4) примет следующий вид:
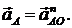
Модуль ускорения точки  :
:

Вектор ускорения точки 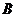 ,
принадлежащей шатуну 2, представляет собой геометрическую сумму вектора
ускорения точки
,
принадлежащей шатуну 2, представляет собой геометрическую сумму вектора
ускорения точки  , вектора
нормального ускорения и вектора тангенциального ускорения относительного
вращательного движения точки
, вектора
нормального ускорения и вектора тангенциального ускорения относительного
вращательного движения точки 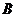 вокруг точки
вокруг точки  :
:

При этом модуль вектора  находим по
выражению:
находим по
выражению:

В то же время точка 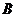 принадлежит
и ползуну 3. Ползун 3 совершает только прямолинейное возвратно-поступательное
движение вдоль направляющей (прямая
принадлежит
и ползуну 3. Ползун 3 совершает только прямолинейное возвратно-поступательное
движение вдоль направляющей (прямая  ), следовательно, линия действия
вектора ускорения точки
), следовательно, линия действия
вектора ускорения точки 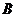 проходит
параллельно прямой
проходит
параллельно прямой  :
:

Вектор ускорения точки  представляет
собой геометрическую сумму вектора ускорения точки
представляет
собой геометрическую сумму вектора ускорения точки  , вектора
нормального ускорения и вектора тангенциального ускорения относительного вращательного
движения точки
, вектора
нормального ускорения и вектора тангенциального ускорения относительного вращательного
движения точки  вокруг
точки
вокруг
точки  :
:
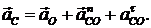 (3.5)
(3.5)
Ускорение точки О равно нулю, т.к.
это элемент стойки. Тангенциальное ускорение точки С относительно точки О также
равно нулю, т.к. кривошип 1 совершает вращательное движение с постоянной
угловой скоростью. Таким образом выражение (3.5) пример вид:

Модуль ускорения точки
C:

Вектор ускорения точки 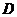 ,
принадлежащей шатуну 4, представляет собой геометрическую сумму вектора
ускорения точки
,
принадлежащей шатуну 4, представляет собой геометрическую сумму вектора
ускорения точки  , вектора
нормального ускорения и вектора тангенциального ускорения относительного
вращательного движения точки
, вектора
нормального ускорения и вектора тангенциального ускорения относительного
вращательного движения точки 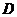 вокруг точки
вокруг точки  :
:

При этом модуль вектора  находим по
выражению:
находим по
выражению:

В то же время точка 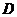 принадлежит
и ползуну 5. Ползун 5 совершает только прямолинейное возвратно-поступательное
движение вдоль направляющей (прямая
принадлежит
и ползуну 5. Ползун 5 совершает только прямолинейное возвратно-поступательное
движение вдоль направляющей (прямая 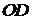 ), следовательно, линия действия
вектора ускорения точки
), следовательно, линия действия
вектора ускорения точки 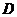 проходит
параллельно прямой
проходит
параллельно прямой 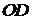 :
:
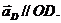
Масштабный коэффициент ускорений:
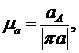 (3.6)
(3.6)
где µа - масштабный
коэффициент ускорений, м/(с2·мм);
 - модуль
ускорения точки
- модуль
ускорения точки  , м/с2;
, м/с2;
 - произвольно выбранный отрезок,
изображающий на плане ускорений вектор ускорения точки
- произвольно выбранный отрезок,
изображающий на плане ускорений вектор ускорения точки  , мм.
, мм.
Примем  , тогда
формула (3.6) примет вид:
, тогда
формула (3.6) примет вид:

Разрешив графически векторные
уравнения, построим план ускорений.
Длина отрезка, изображающего в
составе плана ускорений вектор 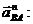

Длина отрезка, изображающего в
составе плана ускорений вектор 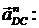

Длины отрезков, изображающих на
плане ускорений векторы ускорений центров тяжести шатунов 2 и 4, найдем,
воспользовавшись теоремой подобия:

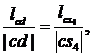
откуда
 и
и  ,
,
где  - отрезки с плана ускорений; lAB, lCD, lAS2, lCS4 - длины
звеньев АС, АВ, AS2 и CS4
соответственно, м.
- отрезки с плана ускорений; lAB, lCD, lAS2, lCS4 - длины
звеньев АС, АВ, AS2 и CS4
соответственно, м.
Измерив на плане ускорений величины
отрезков  и
и 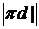 , определим
модули соответствующих ускорений.
, определим
модули соответствующих ускорений.
Модуль ускорения точки 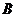 :
:

Модуль ускорения  :
:

Модуль ускорений  :
:
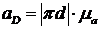
Модуль ускорения  :
:

Модуль ускорений 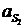 :
:
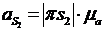
Модуль ускорений  :
:

Угловые ускорения шатунов 2 и 4:
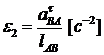 и
и 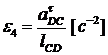
Угловые ускорения направлены в сторону действия
тангенциального ускорения рассматриваемого звена.
Угловая скорость кривошипа 1 является постоянной
величиной, следовательно, угловое ускорение этого звена равно нулю, т.е. e1
=0. Ползуны 3 и 5 совершают только поступательные движения, следовательно,
угловые ускорение этих звеньев равно нулю, т.е. e3=e5=0.
Строим планы ускорений для всех положений
механизма. Вычисляем истинные величины линейных и угловых ускорений для всех
положений механизма и сводим их в таблицу 4.
Таблица 4 - Значения угловых и линейных
ускорений для двенадцати положений механизма
|
aτBA,
м/с2
|
aB, м/с2
|
aτDC,
м/с2
|
aD, м/с2
|
ε2,
с-2
|
ε4,
с-2
|
aS2, м/с2
|
|
0,12
|
0
|
35,62
|
0
|
143,42
|
0
|
0
|
|
|
|
1
|
24,82
|
35,92
|
50,32
|
114,42
|
103,42
|
86,76
|
|
|
|
2
|
47,34
|
35,88
|
97,96
|
39,90
|
197,25
|
168,90
|
|
|
|
3
|
57,28
|
19,10
|
116,88
|
33,40
|
238,67
|
201,52
|
|
|
|
4
|
47,34
|
18,12
|
97,98
|
72,16
|
197,25
|
168,93
|
24,80
|
86,52
|
|
5
|
24,94
|
56,66
|
53,10
|
80,70
|
103,92
|
91,55
|
|
|
|
6
|
0
|
72,38
|
0
|
80,58
|
0
|
0
|
|
|
|
7
|
24,94
|
56,66
|
53,10
|
80,70
|
103,92
|
91,55
|
|
|
|
8
|
47,34
|
18,12
|
97,98
|
72,16
|
197,25
|
168,93
|
|
|
|
9
|
57,28
|
19,10
|
116,88
|
33,40
|
238,67
|
201,52
|
|
|
|
10
|
47,34
|
35,88
|
97,96
|
39,90
|
197,25
|
168,90
|
|
|
|
11
|
24,82
|
35,92
|
50,32
|
114,42
|
103,42
|
86,76
|
|
|
. Силовой анализ плоского рычажного механизма
плоский рычажный механизм скорость
Для проведения силового анализа воспользуемся
кинетостатическим методом, основанным на принципе Даламбера (в число заданных
сил при расчёте входят силы инерции), при этом определим реакции связей
кинематических пар и уравновешивающую силу (уравновешивающий момент).
Для проведения силового анализа построим в
заданном масштабном коэффициенте длин одно положение механизма, для которого
скорости и ускорения всех звеньев не равны нулю.
Возьмем четвертое положение
механизма и построим его в масштабном коэффициенте длин 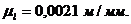
Рассчитаем силы, действующие на
звенья.
Сила тяжести  равна:
равна:
 , (4.1)
, (4.1)
где Gi - сила
тяжести i-го звена,
Н;
 - масса i-го звена,
кг;
- масса i-го звена,
кг;
 - ускорение свободного падения,
- ускорение свободного падения,  .
.
Масса звена  определяем
по формуле:
определяем
по формуле:
 , (4.2)
, (4.2)
где mi - масса i-го звена,
кг;
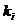 - удельная масса i-го звена,
кг/м;
- удельная масса i-го звена,
кг/м;
 - длина i-го звена,
м.
- длина i-го звена,
м.
Удельные массы равны:
для кривошипов  кг/м.
кг/м.
для шатунов 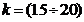 кг/м.
кг/м.
Масса ползуна рассчитывается по
формуле:
 , (4.3)
, (4.3)
где mползуна - масса
ползуна, кг;
mшатуна - масса
шатуна, к которому прикреплен ползун, кг.
По формулам (4.2) и (4.3) определим
массы звеньев:
 ,
,
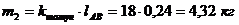 ,
,
 ,
,
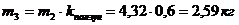 ,
,
 .
.
По формуле (4.1) определим силы
тяжести звеньев:
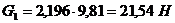 ,
,
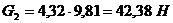 ,
,
 ,
,
 ,
,
 .
.
Откладываем вектора сил тяжести  ,
,  ,
,  ,
,  и
и 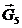 на
положении механизма соответственно от точек
на
положении механизма соответственно от точек  ,
,  ,
,  ,
,  и
и  .
.
Центр масс кривошипа лежит на оси
вращения кривошипа.
Определим силы инерции звеньев.
Вектор силы инерции  может быть
определен по формуле:
может быть
определен по формуле:
 (4.4)
(4.4)
где  - вектор
силы инерции i-го звена;
- вектор
силы инерции i-го звена;
 - масса i-го звена,
кг;
- масса i-го звена,
кг;
 - вектор полного ускорения центра
масс i-го звена.
- вектор полного ускорения центра
масс i-го звена.
Как видно из формулы (4.4) вектор
силы инерции направлен в противоположную сторону по отношению к вектору полного
ускорения центра масс звена.
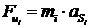 , (4.5)
, (4.5)
где Fиi - сила
инерции i-го звена,
Н;
mi - масса i-го звена,
кг;
аsi - полное
ускорение центра масс i-го звена, м/с2.
Момент пары сил инерции направлен
противоположно угловому ускорению  и может быть определён по формуле:
и может быть определён по формуле:
 (4.6)
(4.6)
где Миi - момент
пары сил инерции i-го звена, Н·м;
Isi - момент
инерции i-го звена
относительно оси, проходящей через центр масс si и
перпендикулярной к плоскости движения звена, кг·м2;
εi - угловое
ускорение i-го звена, с-2.
Момент инерции шатуна определяется
по формуле:
 (4.7)
(4.7)
Величины ускорений центров масс  ,
,  ,
,  и
и  возьмем из
таблицы 4. Т.к. точки S5, S3 и D, B
соответственно совпадают на схеме, то и их величины ускорений одинаковы.
возьмем из
таблицы 4. Т.к. точки S5, S3 и D, B
соответственно совпадают на схеме, то и их величины ускорений одинаковы.
Рассчитаем силы инерции по формуле
(4.5):





Проведем силы инерции на четвертом
положении механизма.
Рассчитаем моменты инерции шатунов
по формуле (4.7):
 ,
,
 .
.
Рассчитаем моменты пар сил инерции для второго и
четвертого звеньев по формуле (4.6):
 ,
,
 .
.
Покажем на чертеже моменты пар сил
инерции шатунов и укажем направление силы полезного сопротивления. Далее
разбиваем механизм на группы звеньев и проводим их силовой расчет.
.1 Силовой расчет структурной группы Ассура
звеньев 2-3
Рассмотрим структурную группу Ассура 2-3.
Запишем уравнение кинетостатического равновесия:
 (4.8)
(4.8)
Где  и
и  - силы реакций, приложенные соответственно
к звеньям 3 и 2 со стороны звеньев, образующих кинематические пары.
- силы реакций, приложенные соответственно
к звеньям 3 и 2 со стороны звеньев, образующих кинематические пары.
Запишем уравнение суммы моментов
относительно точки B:
 ,
,
где h2 -
наименьшее расстояние от линии действия силы тяжести G2 до точки В;
h1 - наименьшее
расстояние от линии действия силы Fu2 до точки В.

Таким образом, в уравнении (4.8)
осталось две неизвестных силы, их можно определить составлением векторного
силового многоугольника. Для его составления воспользуемся выражением (4.8).
Подберем масштабный коэффициент сил  :
:
 , (4.9)
, (4.9)
где µF -
масштабный коэффициент сил, Н/мм;
 - истинное значение известной
максимальной силы, входящей в уравнение, Н;
- истинное значение известной
максимальной силы, входящей в уравнение, Н;
 - длина вектора, изображающего
максимальную силу на плане сил, мм.
- длина вектора, изображающего
максимальную силу на плане сил, мм.
По формуле (4.9) определим
масштабный коэффициент сил:
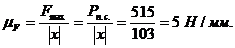 .
.
Для построения силового
многоугольника переведем величины всех сил в масштабный коэффициент:
 ,
,
 ,
,
 ,
,
 ,
,
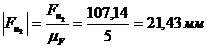 .
.
Из произвольной точки строим вектор , потом из
конца этого вектора вектор
, потом из
конца этого вектора вектор  и так далее по уравнению (4.8).
Завершаем многоугольник сил, проводя из начала вектора
и так далее по уравнению (4.8).
Завершаем многоугольник сил, проводя из начала вектора  прямую
параллельную AB, а из конца
вектора
прямую
параллельную AB, а из конца
вектора  прямую,
перпендикулярную OB. Точка пересечения позволяет
построить силы
прямую,
перпендикулярную OB. Точка пересечения позволяет
построить силы  и
и  на плане
сил и определить их истинное значение.
на плане
сил и определить их истинное значение.
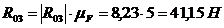 ,
,
 .
.
.2 Силовой расчет структурной группы
Ассура звеньев 4-5
Рассмотрим структурную группу Ассура
4-5. Запишем уравнение кинетостатического равновесия:
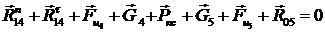 (4.10)
(4.10)
Где  и
и  - силы реакций, приложенные
соответственно к звеньям 5 и 4 со стороны звеньев, образующих кинематические
пары.
- силы реакций, приложенные
соответственно к звеньям 5 и 4 со стороны звеньев, образующих кинематические
пары.
Запишем уравнение суммы моментов
относительно точки D:
 ,
,
где h3 -
наименьшее расстояние от линии действия силы тяжести G4 до точки D;
h4 -
наименьшее расстояние от линии действия силы Fu4 до точки D.

Таким образом, в уравнении (4.10)
осталось две неизвестных силы, их можно определить составлением векторного
силового многоугольника. Для его составления воспользуемся выражением (4.10).
Для построения силового
многоугольника переведем величины всех сил в масштабный коэффициент :
:
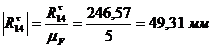 ,
,
 ,
,
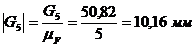 ,
,
 ,
,
 .
.
Из произвольной точки строим вектор , потом из
конца этого вектора вектор
, потом из
конца этого вектора вектор 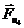 и так далее по уравнению (4.10). Завершаем
многоугольник сил, проводя из начала вектора
и так далее по уравнению (4.10). Завершаем
многоугольник сил, проводя из начала вектора  прямую параллельную CD, а из конца
вектора
прямую параллельную CD, а из конца
вектора  прямую,
перпендикулярную OD. Точка пересечения позволяет
построить силы
прямую,
перпендикулярную OD. Точка пересечения позволяет
построить силы 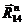 и
и  на плане
сил и определить их истинное значение.
на плане
сил и определить их истинное значение.
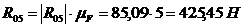 ,
,
 .
.
.3 Силовой расчет первичного механизма
Рассмотрим первичный механизм. Запишем уравнение
кинетостатического равновесия:
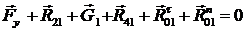 (4.12)
(4.12)
Для нахождения тангенциальной
составляющей силы R01 составим
уравнение суммы моментов относительно точки А:
 , (4.13)
, (4.13)
где h1 -
наименьшее расстояние от линии действия силы  до точки A;
до точки A;
h2 -
наименьшее расстояние от линии действия силы  до точки А.
до точки А.
Из уравнения (4.13) выразим
тангенциальную составляющую силы R01:
 .
.
Подберем масштабный коэффициент сил  :
:
 , (4.14)
, (4.14)
где µF -
масштабный коэффициент сил, Н/мм;
 - истинное значение известной
максимальной силы, входящей в уравнение, Н;
- истинное значение известной
максимальной силы, входящей в уравнение, Н;
 - длина вектора, изображающего
максимальную силу на плане сил, мм.
- длина вектора, изображающего
максимальную силу на плане сил, мм.
По формуле (4.14) определим
масштабный коэффициент сил:
 .
.
Для построения многоугольника сил
переведем все известные силы в масштабный коэффициент:
 ,
,
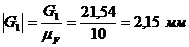 ,
,
 .
.
Согласно уравнению 4.12 построим
многоугольник сил. Для этого из произвольной точки строим вектор  , потом из
конца этого вектора проводим вектор
, потом из
конца этого вектора проводим вектор  , далее строим вектор
, далее строим вектор  и из его
конца проводим вектор
и из его
конца проводим вектор  . Для
завершения построения многоугольника сил из начальной точки построения проводим
прямую, параллельную вектору
. Для
завершения построения многоугольника сил из начальной точки построения проводим
прямую, параллельную вектору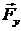 , а из конца вектора
, а из конца вектора  прямую,
параллельную вектору
прямую,
параллельную вектору  . Точка
пересечения проведенных прямых указывает на конечную точку многоугольника.
. Точка
пересечения проведенных прямых указывает на конечную точку многоугольника.
Найдем величины сил 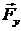 и
и 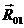 . Для этого
измерим длины соответствующих векторов на силовом многоугольнике и переведем
значения сил из масштабного коэффициента.
. Для этого
измерим длины соответствующих векторов на силовом многоугольнике и переведем
значения сил из масштабного коэффициента.
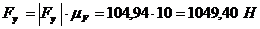 ,
,
 .
.
Рассчитаем величину
уравновешивающего момента:
 .
.
Сведем все полученные силы и моменты
в таблицу 5.
Таблица 5 - Значения сил и моменты
пар сил
|
Силы
тяжести звеньев, Н
|
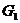 21,54 21,54
|
|
|
|
 42,38 42,38
|
|
|
|
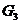 25,41 25,41
|
|
|
|
 84,76 84,76
|
|
|
|
 50,82 50,82
|
|
|
|
Силы
инерции звеньев, Н
|
 0 0
|
|
|
|
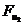 107,14 107,14
|
|
|
|
 46,93 46,93
|
|
|
|
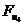 747,93 747,93
|
|
|
|
 373,79 373,79
|
|
|
|
Моменты
пар сил инерции звеньев, Н·м
|
 0 0
|
|
|
|
 3,95 3,95
|
|
|
|
 0 0
|
|
|
|
 40,54 40,54
|
|
|
|
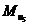 0 0
|
|
|
|
Реакции
связей, Н
|
 411,05 411,05
|
|
|
|
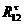 51,38 51,38
|
|
|
|
 414,25 414,25
|
|
|
|
 1257,35 1257,35
|
|
|
|
 246,57 246,57
|
|
|
|
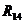 1257,35 1257,35
|
|
|
|
 1060,60 1060,60
|
|
|
|
 2185,66 2185,66
|
|
|
|
 2429,40 2429,40
|
|
|
|
Уравновешивающая
сила, Н
|
 1049,40 1049,40
|
|
|
|
Момент
уравновешивающий, Н·м
|
 83,95 83,95
|
|
5. Определение уравновешивающей силы с помощью
теоремы Жуковского
Для определения уравновешивающей силы,
воспользуемся теоремой В.И. Жуковского: если механизм под действием системы
силовых факторов, приложенных к характерным точкам механизма, находится в
равновесии, то в равновесии будет находиться повернутый на 90º
план
скоростей, рассматриваемый как жесткий рычаг вращающейся вокруг полюса плана и
нагруженный той же системой силовых факторов приложенных к одноименным точкам
планов.
Построим для четвертого положения механизма
повёрнутый на 90º по ходу
вращения кривошипа план скоростей, в масштабном коэффициенте.
 .
.
На повернутый план скоростей
переносим вектора сил, действующие на звенья, в соответствующие точки в том
направлении, в котором они действуют. При этом приложенные к звеньям 2 и 4
моменты пар сил инерции заменяем парами сил:
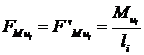 , (5.1)
, (5.1)
где 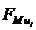 и
и  - силы,
образующие пару сил, Н;
- силы,
образующие пару сил, Н;
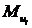 - моменты пар сил инерции i-го звена, Н·м;
- моменты пар сил инерции i-го звена, Н·м;
 - длина i-го звена,
м.
- длина i-го звена,
м.
Рассчитаем по формуле (5.1) пары
сил, действующие на звенья:
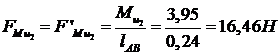 ,
,
 .
.
Силы  ,
,  приложены в крайних точках звена.
приложены в крайних точках звена.
Линия действия уравновешивающей силы
перпендикулярна звену OA.
По методу Жуковского, сумма моментов
всех сил 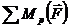 , включая
силы инерции и уравновешивающую силу, относительно полюса плана скоростей р
равна нулю:
, включая
силы инерции и уравновешивающую силу, относительно полюса плана скоростей р
равна нулю:
 ,
,
 , (5.2)
, (5.2)
 (5.3)
(5.3)
Измеряем плечи моментов на плане:
 ,
,
 ,
,
 ,
,
 ,
,
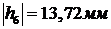 ,
,
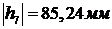 ,
,
 ,
,
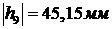 ,
,
 ,
,
 .
.
Подставляя все найденные значения в
формулу (5.3) и произведем вычисления, получим:
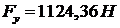 .
.
Высчитаем момент уравновешивающей
силы:
 .
.
Определим относительную погрешность,
допущенную при определении уравновешивающего момента двумя способами:
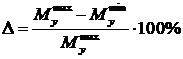 , (5.4)
, (5.4)
где ,
,  - максимальное и минимальное
значения уравновешивающего момента, полученные в результате двух расчетов, Н.
- максимальное и минимальное
значения уравновешивающего момента, полученные в результате двух расчетов, Н.
Подставляя полученные значения в
формулу (5.3), получим:

Данная погрешность получена в результате
применения графоаналитического метода расчёта и округления численных значений и
является допустимой.
Динамический анализ плоского рычажного механизма
.1 Определение значений фазовых углов рабочего и
холостого хода
Определим пределы рабочего хода механизма.
Рабочий ход в одну сторону и холостой в обратную соответствует углу поворота
или линейному перемещению ведомого звена от одного крайнего положения до
другого. Эти ходы равны. Однако с целью увеличения К.П.Д. механизма желательно,
чтобы ведомое звено при холостом ходе быстрее возвращалось в положение рабочего
хода. Это условие выполняется, если угол поворота ведущего звена,
соответствующий холостому ходу, будет меньше, чем соответствующий рабочему. Для
определения пределов рабочего хода проанализируем план положений механизма.
В состав механизма входят два ползуна,
являющихся ведомыми (выходными) звеньями. Рабочим ходом является фаза, в
которой ползуны движутся в сторону, противоположную направлению силы полезного
сопротивления.
.2 Определение Fу
и Fп
Построим 12 рычагов Жуковского для
определения уравновешивающей силы. Для этого используем 12 планов скоростей
соответствующих построенным кинематическим схемам. Перенесем на планы скоростей
все внешние силы, действующие на механизм, предварительно повернув их в
противоположную сторону вращения кривошипа на  . Поскольку сила полезного
сопротивления (
. Поскольку сила полезного
сопротивления ( ) действует
только при рабочем ходе, перенесем ее на те планы скоростей, которые
соответствуют рабочему ходу. Уравновешивающую силу (
) действует
только при рабочем ходе, перенесем ее на те планы скоростей, которые
соответствуют рабочему ходу. Уравновешивающую силу ( ) перенесем
в точку
) перенесем
в точку  всех планов
скоростей, силы тяжести - во все точки центров масс соответственно. Силы
инерции и моменты пар сил инерции не учитываем.
всех планов
скоростей, силы тяжести - во все точки центров масс соответственно. Силы
инерции и моменты пар сил инерции не учитываем.
Представим план скоростей в виде
жесткой системы, закрепленной (условно) в полюсе р. Силы, приложенные к ней,
создают вращающие моменты. Чтобы система находилась в равновесии, необходимо
уравновесить моменты вращения. Составим уравнение равновесия:
 (6.1)
(6.1)
.3 Построение диаграммы приведенных
моментов движущих сил
Для нахождения момента сил
необходимо найти приведенную силу  , которая по модулю равна
уравновешивающей силе, но направлена в противоположную сторону. Силу
уравновешивающую найдем из уравнения моментов составленного для каждого
положения механизма, относительно полюса (6.1).
, которая по модулю равна
уравновешивающей силе, но направлена в противоположную сторону. Силу
уравновешивающую найдем из уравнения моментов составленного для каждого
положения механизма, относительно полюса (6.1).
Составим уравнения моментов для
каждого положения механизма:
0) 
) 
) 
) 
) 
) 
) 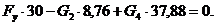
) 
) 
) 
) 
) 
Из последних равенств найдем
величины уравновешивающей силы ( ) для всех двенадцати положений
механизма:
) для всех двенадцати положений
механизма:
) 
) 
) 
) 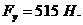
) 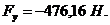
) 
) 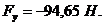
) 
) 
) 
) 
) 
Отрицательные значения
уравновешивающих сил говорят о том, что необходимо изменить направление силы в
противоположную сторону.
Определяем силу приведения ( ):
):
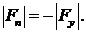
Для нулевого положения:

Для остальных положений расчет
ведется аналогично.
Момент приведенных сил для нулевого
положения найдем по формуле:

где  -
приведенная сила, Н;
-
приведенная сила, Н;
 - длина звена
- длина звена  , м.
, м.
Аналогично рассчитываем силу
приведения и момент приведенных сил ( ,
,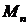 ) для остальных положений механизма,
и сводим их в одну таблицу 6.
) для остальных положений механизма,
и сводим их в одну таблицу 6.
Таблица 6 - Силы приведения и
моменты приведенных сил
|
Положения
механизма
|
Расчетная
величина
|
|
|
|
0,
12
|
94,65
|
-94,65
|
-7,57
|
|
1
|
264,13
|
-264,13
|
-21,13
|
|
2
|
411,20
|
-411,20
|
-32,90
|
|
3
|
515
|
-515
|
-41,20
|
|
4
|
476,16
|
-476,16
|
-38,09
|
|
5
|
258,29
|
-258,29
|
-20,66
|
|
6
|
94,65
|
-94,65
|
-7,57
|
|
7
|
310,80
|
-310,80
|
-24,86
|
|
8
|
703,83
|
-703,83
|
-56,31
|
|
9
|
1047,18
|
-1047,18
|
-83,77
|
|
10
|
1087,98
|
-1087,98
|
-87,04
|
|
11
|
736,56
|
-736,56
|
-58,92
|
Для построения диаграммы приведенных моментов
сил рассчитываем масштабные коэффициенты.
Масштабный коэффициент оси угла поворота:

где L -
произвольно выбранное расстояние от 0 до 12 положения механизма на диаграмме,
мм.
Масштабный коэффициент оси момента
приведенных сил:

где  -
максимальный момент приведенных сил (см. таблицу 5), Н·м;
-
максимальный момент приведенных сил (см. таблицу 5), Н·м;
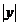 - расстояние, изображающее
максимальный момент приведенных сил на диаграмме, мм.
- расстояние, изображающее
максимальный момент приведенных сил на диаграмме, мм.
Переведем все приведенные моменты
через масштабный коэффициент в линейные значения:







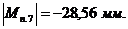

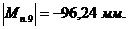

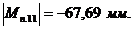
При построении диаграммы по оси
ординат ( ) отложим
произвольно выбранный отрезок
) отложим
произвольно выбранный отрезок 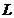 . По оси абсцисс (
. По оси абсцисс (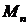 )
откладываем значения приведенных моментов
)
откладываем значения приведенных моментов  в соответствующих положениях. При
чем выше оси
в соответствующих положениях. При
чем выше оси  значение со
знаком «-», а ниже со знаком «+».
значение со
знаком «-», а ниже со знаком «+».
Соединив все точки плавной лекальной
кривой, получаем кривую изменения приведенного момента движущих сил.
Приведенный момент сил сопротивления
является величиной постоянной, и высчитывается по формуле:
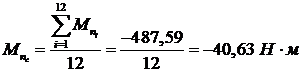
Для построения кривой изменения
приведенного момента сил сопротивления переведем полученную величину в
масштабный коэффициент:

По полученному значению построим
прямую приведенного момента сил сопротивления.
.4 Построение диаграммы работ
движущих сил и сил сопротивления
Для построения диаграммы работ
используем диаграмму приведенных моментов. Для этого замеряем величину момента
приведенных сил в точках, расположенных по середине между соседними положениями
механизма. Данную величину делим на коэффициент уменьшения ( ) и
откладываем на диаграмме работ. Для последующих положений величину отрезка
прибавляем к полученной ранее, также уменьшая в
) и
откладываем на диаграмме работ. Для последующих положений величину отрезка
прибавляем к полученной ранее, также уменьшая в  раз и откладывая на диаграмме.
Соединяя все отложенные точки плавной кривой, получаем диаграмму работ движущих
сил (
раз и откладывая на диаграмме.
Соединяя все отложенные точки плавной кривой, получаем диаграмму работ движущих
сил ( ). Соединяя
начальную и конечную точки прямой линией, получим диаграмму сил сопротивления (
). Соединяя
начальную и конечную точки прямой линией, получим диаграмму сил сопротивления ( ).
).
Рассчитываем масштабный коэффициент
работ:

где  - интервал
между соседними положениями по оси
- интервал
между соседними положениями по оси  ;
;
 - коэффициент уменьшения;
- коэффициент уменьшения;
 - масштабный коэффициент момента
приведенных сил;
- масштабный коэффициент момента
приведенных сил;
 - масштабный коэффициент угла
поворота.
- масштабный коэффициент угла
поворота.
.5 Построение диаграммы изменения
кинетической энергии
Масштабный коэффициент оси изменения
кинетической энергии:
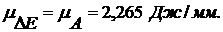
Для определения области нахождения
графика по формуле найдем значение:
 , (6.2)
, (6.2)
где  - изменения
кинетической энергии, Дж;
- изменения
кинетической энергии, Дж;
 - работа движущих сил, Дж;
- работа движущих сил, Дж;
 - работа сил сопротивления, Дж.
- работа сил сопротивления, Дж.
Для построения диаграммы изменения
кинетической энергии измерим расстояния между линиями работы движущих сил и сил
сопротивления и отложим эти значения выше или ниже оси угла поворота кривошипа
в зависимости от знака. Соединим отложенные точки плавной кривой.
.6 Построение диаграммы приведенных
моментов инерции
Приведенный момент инерции механизма
будет складываться из постоянной величины ( ) и переменной (
) и переменной ( ):
):
 (6.3)
(6.3)
Найдем постоянную величину ( ):
):
 , (6.4)
, (6.4)
где  - момент
инерции энергетической машины, кг·м2;
- момент
инерции энергетической машины, кг·м2;
 - передаточное отношение
преобразующего механизма;
- передаточное отношение
преобразующего механизма;
 - момент инерции кривошипа (рабочей
машины), кг·м2.
- момент инерции кривошипа (рабочей
машины), кг·м2.
Найдем момент инерции кривошипа ( ):
):

где m1 - масса
кривошипа, кг;
(lOA +lOC)- длина кривошипа,
м.
Для вычисления приведенного момента
инерции энергетической машины необходимо подобрать электродвигатель.
В качестве электродвигателя возьмем
двигатель серии 4А.
Рассчитаем частоту вращения и
мощность двигателя:


Примем передаточное отношение равным
4 ( ). Тогда:
). Тогда:


По полученным значениям подберем
стандартный электродвигатель с ближайшими наибольшими характеристиками.
Возьмем двигатель 4А90В4 (N=1,5 кВт, n=1415
об/мин). Приведенный момент инерции ротора этого двигателя равен:

Найдем приведенный момент инерции
энергетической машины, исключив влияние магнитного поля земли:

Подставляя полученные значения в
формулу (6.4), получим:

Найдем переменную величину ( ):
):

где 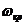 - угловая
скорость кривошипа, с-1;
- угловая
скорость кривошипа, с-1;
 - сумма энергий шатунов и ползунов.
- сумма энергий шатунов и ползунов.
 - для шатуна 2;
- для шатуна 2;
 - для ползуна 3;
- для ползуна 3;
 - для шатуна 4;
- для шатуна 4;
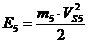 - для ползуна 5,
- для ползуна 5,
где 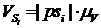 - скорость
центра масс i-го звена;
- скорость
центра масс i-го звена;
 - масса i-го звена;
- масса i-го звена;
 - угловая скорость i-го звена;
- угловая скорость i-го звена;
 - момент инерции шатуна i.
- момент инерции шатуна i.
Скорости центров масс:
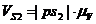 ,
,
 ,
,
 ,
,
 .
.
Угловые скорости кривошипа и
шатунов:
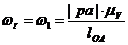 ,
, 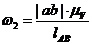 ,
,  .
.

Подставим значения скоростей центров
масс и угловых скоростей в выражение (6.5):
Преобразуем полученное выражение.
Для облегчения вычисления переменной части приведенного момента инерции для
каждого положения механизма необходимо каждое слагаемое из числителя дроби
представить в виде произведения квадрата длины отрезка на коэффициент ki:
 ,
,
Где  ;
;




 .
.
Измерим длины необходимых отрезков с
планов положений и рассчитаем приведенный момент инерции для каждого положения
механизма.
Полученные данные сведем в таблицу
7.
Таблица 7 - значения приведенных моментов
инерции
|
Положение
механизма
|
|ps2|,
мм
|
|ab|,
мм
|
|ps3|,
мм
|
|ps4|,
мм
|
|cd|,
мм
|
|ps5|,
мм
|
 ,
кг/м2 ,
кг/м2 , кг/м2 , кг/м2 ,
кг/м2 ,
кг/м2 , мм , мм
|
|
|
|
|
0
|
8,76
|
30
|
0
|
37,88
|
61
|
0
|
0,11159
|
0,02359
|
0,13518
|
31,19
|
|
1
|
14,10
|
26,35
|
10,61
|
46,81
|
53,81
|
38,13
|
0,21249
|
|
0,23608
|
54,47
|
|
2
|
23,20
|
15,67
|
21,46
|
58,91
|
31,48
|
60,62
|
0,37917
|
|
0,40276
|
92,92
|
|
3
|
30
|
0
|
30
|
61
|
0
|
61
|
0,40984
|
|
0,43343
|
100
|
|
4
|
29,51
|
15,67
|
30,50
|
53,37
|
31,48
|
45,04
|
0,29919
|
|
0,32278
|
74,47
|
|
5
|
19,92
|
26,42
|
19,82
|
42,88
|
53,38
|
22,88
|
0,16782
|
|
0,19141
|
44,16
|
|
6
|
8,76
|
30
|
0
|
37,88
|
61
|
0
|
0,11159
|
|
0,13518
|
31,19
|
|
7
|
19,92
|
26,42
|
19,82
|
42,88
|
53,38
|
22,88
|
0,16782
|
|
0,19141
|
44,16
|
|
8
|
29,51
|
15,67
|
30,50
|
53,37
|
31,48
|
45,04
|
0,29919
|
|
0,32278
|
74,47
|
|
9
|
30
|
0
|
30
|
61
|
0
|
61
|
0,40984
|
|
0,43343
|
100
|
|
10
|
23,20
|
15,67
|
21,46
|
58,91
|
31,48
|
60,62
|
0,37917
|
|
0,40276
|
92,92
|
|
11
|
14,10
|
26,35
|
10,61
|
46,81
|
53,81
|
38,13
|
0,21272
|
|
0,23608
|
54,47
|
|
12
|
8,76
|
30
|
0
|
37,88
|
61
|
0
|
0,11159
|
|
0,13518
|
31,19
|
Определим масштабный коэффициент приведенного
момента инерции по максимальному значению:

где  -
максимальный приведенный момент инерции, кг·м2;
-
максимальный приведенный момент инерции, кг·м2;
 - произвольно выбранный отрезок,
мм.
- произвольно выбранный отрезок,
мм.
Переведем все приведенные моменты
инерции ( ) в данный
масштабный коэффициент и построим диаграмму.
) в данный
масштабный коэффициент и построим диаграмму.
Для построения диаграммы по оси
абсцисс откладываем  , а по оси
ординат
, а по оси
ординат  .
.

Для построения диаграммы для каждого
положения откладываем соответствующие значения (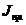 ) и соединяем полученные точки
плавной кривой.
) и соединяем полученные точки
плавной кривой.
.7 Построение диаграммы
энергия-масса
Построение диаграммы происходит
следующим образом: по оси  откладываем
ординаты
откладываем
ординаты  из
диаграммы изменения кинетической энергии, а по оси
из
диаграммы изменения кинетической энергии, а по оси 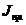 - ординаты
- ординаты 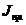 диаграммы
приведенных моментов инерции, соответствующие одному и тому же положению
механизма. Номера положений фиксируем на пересечении соответствующих координат
диаграммы. В итоге получим замкнутую кривую.
диаграммы
приведенных моментов инерции, соответствующие одному и тому же положению
механизма. Номера положений фиксируем на пересечении соответствующих координат
диаграммы. В итоге получим замкнутую кривую.
.8 Определение значения момента
инерции маховой массы
По справочной таблице выберем
коэффициент неравномерности хода ДВС:


Вычислим максимальный и минимальный
угол наклона касательной:

Проведем касательные к диаграмме
энергия-масса сверху и снизу под углами  и
и  до пересечения с осью
до пересечения с осью  .
.
Замерим отрезок  , между
точками пересечения касательных и осью изменения энергии, и определим
приведенный момент инерции маховой массы:
, между
точками пересечения касательных и осью изменения энергии, и определим
приведенный момент инерции маховой массы:
 .
.
. Простые зубчатые механизмы
.1 Структурный анализ простого
зубчатого механизма

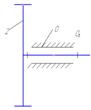
Рис.7.1 Схема простого зубчатого
механизма с внешним зацеплением.
Структурный анализ простых зубчатых
механизмов сводится к определению подвижности механизма.
Подвижность механизма определяем по
формуле Чебышева:
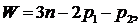 (5.1)
(5.1)
где W -
подвижность механизма;
n - число
подвижных звеньев;
p1 и p2 -
соответственно число пар пятого и четвертого класса.
Таблица 5.1 - звенья простого
зубчатого механизма
|
№
п.п
|
Номер
звена
|
Вид
совершаемого движения
|
Схема
|
Кинематическое
состояние
|
|
1
|
1
|
Вращательное
|

|
Подвижное
|
|
2
|
2
|
Вращательное
|

|
Подвижное
|
|
3
|
0
|
_____
|

|
неподвижное
|
В структуру механизма входят два подвижных звена
(зубчатые колеса) и стойка, представленная двумя шарнирно-неподвижными опорами.
Следовательно, n=2.
Таблица5.2 - кинематические пары
|
Номер
звена
|
Схема
|
Название
|
Класс/
подвижность
|
Вид
контакта/замыкание
|
|
1-2
|

|
4/2
|
Линия
(высшая)/ геометрическое
|
|
0-2
|
|
вращательная
|
5/1
|
По
поверхности (низшая)/
геометрическое
|
|
0-1
|

|
вращательная
|
5/1
|
По
поверхности (низшая)/
геометрическое
|
Кинематические пары 0-1 и 0-2 являются
вращательными парами пятого класса, следовательно, p1=2.
Кинематическая пара 1-2 является зубчатой парой
четвертого класса, следовательно, p2=1.
Подставим число подвижных звеньев и число пар
пятого и четвертого классов в формулу Чебышева:
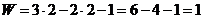 (5.2)
(5.2)
Полученный результат означает, что
для однозначного описания положения всех звеньев механизма в рассматриваемой
плоскости достаточно знать одну обобщенную координату.
.2 Синтез эвольвентного зацепления
простого зубчатого механизма
Данная задача сводится к выполнению синтеза
эвольвентных профилей зубчатых колес простой зубчатой передачи с внешним
зацеплением.
Дано: 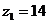 ;
;  ;
;  ;
;  ;
;  .
.
Найдем инволюту угла зацепления:
 (5.3)
(5.3)
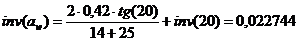 .
.
По таблице значений инвалют найдем
угол зацепления: 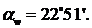
Найдем минимальную величину
коэффициента смещения для шестерни:
 (5.4)
(5.4)

Величина коэффициента смещения для
колеса определяется по блокирующему контуру.
Действительная величина коэффициента
смещения для колеса:
 (5.5)
(5.5)
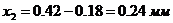
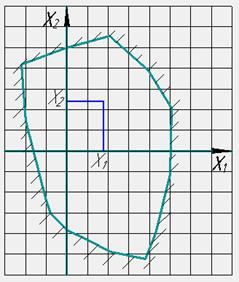
Рисунок 5.1 - блокирующий контур
Величину коэффициента смещения для
колеса найдем по блокирующему контуру (рисунок 5.1): полученная точка попадает
в границы контура, а это значит, что значения подобранны верно.
Далее будем находить диаметры
делительных окружностей:
Для шестерни:  ,
(5.6)
,
(5.6)
Для колеса:  .
(5.7)
.
(5.7)
Для шестерни:  ,
,
Для колеса: 
Диаметры начальных окружностей:
Для шестерни:  ,
(5.8)
,
(5.8)
Для колеса: 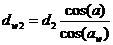 .
(5.9)
.
(5.9)
Для шестерни: 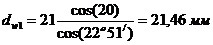 ,
,
Для колеса:  .
.
Шаг по делительной окружности:
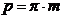 (5.10)
(5.10)

Шаг по основной окружности:
 (5.11)
(5.11)

Диаметры основных окружностей:
Для шестерни: 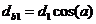 ,
(5.12)
,
(5.12)
Для колеса:  .
(5.13)
.
(5.13)
Для шестерни:  ,
,
Для колеса:  .
.
Диаметры окружностей впадин зубьев:
Для шестерни:  ,
(5.14)
,
(5.14)
Для колеса:  .
(5.15)
.
(5.15)
При 
Для шестерни:  ,
,
Для колеса: 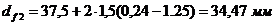 .
.
Диаметры окружностей вершин зубьев:
Для шестерни:  ,
(5.16)
,
(5.16)
Для колеса: 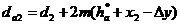 .
(5.17)
.
(5.17)
Где 
Коэффициент уравнительного смещения:
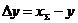 (5.18)
(5.18)
Коэффициент воспринимаемого
смещения:
 (5.19)
(5.19)
Уточненное межосевое расстояние:
 (5.20)
(5.20)
Делительное межосевое расстояние:
 (5.21)
(5.21)
Получаем:



И в итоге:
Для шестерни: 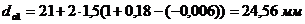 ,
,
Для колеса:  .
.
Толщина зуба по делительной
окружности:
Для шестерни: 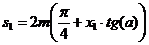 ,
(5.22)
,
(5.22)
Для колеса:  .
(5.23)
.
(5.23)
Для шестерни: 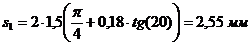 ,
,
Для колеса:  .
.
Толщина впадины по длительной
окружности:
Для шестерни:  ,
(5.24)
,
(5.24)
Для колеса:  .
(5.25)
.
(5.25)
Для шестерни:  ,
,
Для колеса:  .
.
Высота зубьев:
 , (5.26)
, (5.26)
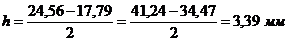 .
.
Углы профиля на окружности вершин:
Для шестерни:  ,
(5.27)
,
(5.27)
Для колеса:  .
(5.28)
.
(5.28)
Для шестерни:  ,
,
Для колеса:  .
.
Толщина зубьев по окружности вершин:
Для шестерни:  , (5.29)
, (5.29)
Для колеса:  .
(5.30)
.
(5.30)
Для шестерни:
 ,
,
Для колеса:
 .
.
Проверка: 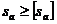 (5.31)
(5.31)
 , т.е.
, т.е. 
Оба значения толщины зубьев по
окружности больше значения минимальной толщины, проверка сходится.
Коэффициент торцевого перекрытия:
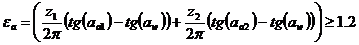 (5.32)
(5.32)
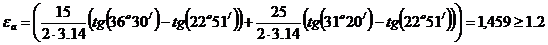
После проведенных выше расчетов
можно выполнять построение зубчатого зацепления:
Для построения зубчатого зацепления
определим масштабный коэффициент длин и переведем все геометрические параметры
зубчатых колес в данный масштабный коэффициент, при условии, что высота зуба
должна быть не менее на чертеже.
на чертеже.
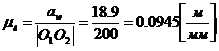

Данным способом переведем все
оставшиеся величины и получим:
 ;
;  ;
; 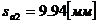 ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
 ;
;  ;
;
 ;
;  ;
;
 ;
; 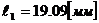 ;
;
 ;
; 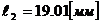 ;
;
 ;
;  ;
;
После этого отложим межосевое
расстояние ( ). Проведем
начальную, делительную, основную окружности, а также окружности вершин и впадин
зубьев для каждого зубчатого колеса.
). Проведем
начальную, делительную, основную окружности, а также окружности вершин и впадин
зубьев для каждого зубчатого колеса.
Начальные окружности (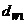 и
и  ) должны
сопрягаться в полюсе зацепления (
) должны
сопрягаться в полюсе зацепления ( ). Откладываем под углом (
). Откладываем под углом (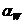 ) от линии
центров (
) от линии
центров ( ) для колеса
и для шестерни лучи, пересекающие основные окружности в точках
) для колеса
и для шестерни лучи, пересекающие основные окружности в точках  и
и  . Через
точки
. Через
точки  и
и  проводим
прямую - линию зацепления. Она проходит через полюс зацепления (
проводим
прямую - линию зацепления. Она проходит через полюс зацепления ( ). Отрезок
от точки сопряжения (
). Отрезок
от точки сопряжения ( ) до точки
пересечения (
) до точки
пересечения ( ), делим на
шесть равных частей аi. Проецируем
полученные точки на основную окружность, проводим через каждую из них
касательную к основной окружности, и на касательных откладываем величину
отрезка (
), делим на
шесть равных частей аi. Проецируем
полученные точки на основную окружность, проводим через каждую из них
касательную к основной окружности, и на касательных откладываем величину
отрезка ( ), каждый
раз уменьшая на величину аi. Полученные
точки соединяем плавной кривой и получаем нижнюю половину эвольвентного профиля
зуба. Аналогично построим вторую половину профиля зуба, только увеличивая
отрезок
), каждый
раз уменьшая на величину аi. Полученные
точки соединяем плавной кривой и получаем нижнюю половину эвольвентного профиля
зуба. Аналогично построим вторую половину профиля зуба, только увеличивая
отрезок  на величину
аi.
Откладываем толщину зуба по делительной окружности и ширину зуба по окружности
вершин. Симметрично отобразим вторую половину профиля зуба. По делительной
окружности откладывая ширину впадины и шаг, строим еще два - три зуба.
Аналогично строим профили зубьев шестерни.
на величину
аi.
Откладываем толщину зуба по делительной окружности и ширину зуба по окружности
вершин. Симметрично отобразим вторую половину профиля зуба. По делительной
окружности откладывая ширину впадины и шаг, строим еще два - три зуба.
Аналогично строим профили зубьев шестерни.
. Сложный зубчатый механизм
.1 Структурный анализ
Данный сложный зубчатый механизм образован
соединением трёх простых зубчатых передач и планетарного механизма.
Сложный зубчатый механизм является плоским,
следовательно, подвижность определяем по формуле Чебышева:
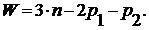 (8.1)
(8.1)
Анализируя схему, видим, что
механизм состоит из стойки 0, представленной четырьмя шарнирно неподвижными
опорами, и шестью подвижными звеньями (1; 2-3; 4-H; 6; 7-7` и
8).
Колесо 5 является неподвижным звеном
и относится к стойке. Таким образом, n=6.
Схема содержит шесть одноподвижных
кинематических пар: 0-1; 0-2; H-0; 4-H; 0-7; 0-8.
И пять высших двухподвижных кинематических пар: 1-2; 3-4; 4-5; 6-7; 7-8.
Следовательно, р1=6; р2=5.
Подставив найденные значения в формулу
(8.1), получим:
 .
.
Полученный результат означает, что
для однозначного описания положения всех звеньев механизма в рассматриваемой
плоскости достаточно знать одну обобщенную координату.
.2 Синтез сложного зубчатого
механизма
Поскольку данный сложный зубчатый
механизм состоит из четырёх ступеней (рядов) - планетарной и трёх простых, то
передаточное отношение 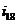 следует
разбить на произведение четырех отношений:
следует
разбить на произведение четырех отношений:
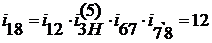 . (8.2)
. (8.2)
Проверим возможность реализации
заданного передаточного отношения:
 .
.
Разложим передаточное число по
ступеням (рядам):
 .
.
Передаточное отношение первого ряда:
 ,
,
тогда  .
.
Из условия отсутствия интерференции:
 , следовательно,
, следовательно,  .
.
Передаточное отношение второго ряда:
 . (8.3)
. (8.3)
Выразим из (8.3)  :
:
 .
.
Таким образом:
 .
.
Представим передаточные числа в виде
сомножителей:

Следовательно:

Рассмотрим три варианта числа зубьев
для каждого колеса:

Запишем условие соосности:
 ,
,
где di -
делительный диаметр колес:  .
.
 ,
,
Сократим на m/2 все
слагаемые в обеих частях уравнения, получим:
 . (8.4)
. (8.4)
Выражение (8.4) отображает условие
соосности однорядного планетарного механизма с внешним зацеплением.
Выразим условие соосности через
сомножители:
 ,
,
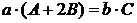 ,
,
где a=C;
b=(A+2B).
Выразим числа зубьев через
коэффициенты:
 .
.
Произведем расчет чисел зубьев для
трех вариантов и занесем все значения в таблицу 7.
Таблица 7 - числа зубьев колес
|
A
|
B
|
C
|
a
|
b
|
Z3
|
Z4
|
Z5
|
q
|
|
1
|
4
|
6
|
20
|
20
|
10
|
80
|
120
|
200
|
1
|
|
2
|
3
|
2
|
15
|
15
|
7
|
45
|
60
|
105
|
1
|
|
3
|
2
|
5
|
10
|
10
|
12
|
20
|
100
|
120
|
1
|
Так как в схеме данного планетарного механизма
присутствуют колеса с внутренним и внешним зацеплением, то необходимо
обеспечить отсутствие подреза зубьев колес с внешним зацеплением, а так же
отсутствие заклинивания зубьев колес во внутреннем зацеплении. Для выполнения
этого условия необходимо, чтобы число внешних зубьев колес было больше или
равно семнадцати, а так же чтобы число зубьев во внешнем и во внутреннем
зацеплении было больше или равно 20 и 85, соответственно. Из таблицы 7 видим,
что это условие выполняется, следовательно общий сомножитель q
во всех трёх вариантах будет равен 1.
Для обеспечения отсутствия контакта сателлитов
друг с другом необходимо проверить условие соседства:
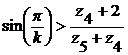 ,
,
где k - число
сателлитов;
z4 - число
зубьев сателлитов;
z5 и z4 - число
зубьев солнечного колеса и сателлита соответственно.
Рассмотрим условие соседства для
всех вариантов:
Вариант 1:
 ;
; 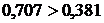 .
.
Следовательно, условие соседства для
первого варианта выполняется.
Вариант 2:
 ;
; 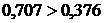 .
.
Следовательно, условие соседства для
второго варианта выполняется.
Вариант 3:
 ;
;  .
.
Следовательно, условие соседства для
третьего варианта выполняется.
Условие соседства выполняется для
всех вариантов, следовательно, при проверке условия сборки будут по-прежнему
проверяться все три варианта.
Для обеспечения собираемости
планетарного механизма необходимо проверить условие сборки:
 ,
,
где p -
количество полных оборотов, совершаемых солнечным колесом (целое число от 1 до
бесконечности);
B - целое
натуральное число.
Сборка возможна лишь при условии,
что при любом значении p значение B будет целым
числом.
Проверим условие сборки для всех
вариантов.
Вариант 1:
 .
.
Для первого варианта условие сборки
выполняется, поскольку при любом значении р значение В будет целым числом.
Вариант 2:
 .
.
Для второго варианта условие сборки
не выполняется, поскольку один из множителей - дробное число, при умножении
которого на любое нечетное число получится нецелое значение В.
Вариант 3:

Для третьего варианта условие сборки
выполняется, поскольку при любом значении р значение В будет целым числом.
В качестве окончательного принимаем
вариант 3, т.к. при данном варианте планетарный механизм имеет минимально
возможные габариты и массу:

Передаточное отношение третьего
ряда:
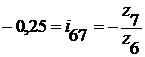 ,
,
тогда  .
.
Из условия отсутствия интерференции:
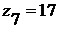 , следовательно,
, следовательно,  .
.
Передаточное отношение четвертого
ряда:
 ,
,
тогда  .
.
Из условия отсутствия интерференции:
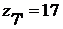 , следовательно,
, следовательно, 
Определим диаметры зубчатых колес
механизма.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Рассчитаем масштабный коэффициент
длин для данной схемы:
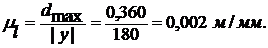
Переведем все диаметры в масштабный
коэффициент:
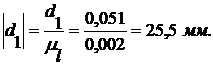
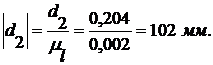






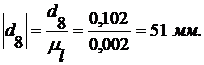
Построим кинематическую схему
механизма в найденном масштабном коэффициенте. Расстояние между колесами берем
произвольным, поскольку оно не влияет на передаточную функцию механизма.
8.3 Кинематический анализ
Построим план скоростей для данной
схемы сложного зубчатого механизма. По условию имеем число оборотов на первом
колесе  .
.
Определим угловую скорость на первом
колесе:

Найдем линейную скорость первого
колеса:
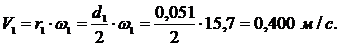
Найдем масштабный коэффициент
скоростей:
 ,
,
где |AA1| - отрезок,
изображающий скорость точки А на плане скоростей.
Построим план угловых скоростей
методом параллельного переноса годографов с плана скоростей на план угловых
скоростей от полюса и до пересечения с осью ω. Расстояния от нуля до
найденных точек и есть значения величин угловых скоростей. Составим пропорцию и
вычислим их значения.

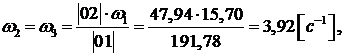

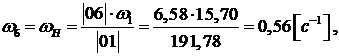


Определим передаточное число 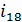 , используя
следующую формулу:
, используя
следующую формулу:

Вычислим погрешность:
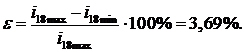
Полученная погрешность меньше
допустимых 5%, следовательно расчет сложного зубчатого механизма выполнен
верно.
9. Кулачковый механизм
.1 Структурный анализ
Так как все звенья данного механизма
лежат в одной плоскости, то его подвижность рассчитывается по формуле Чебышева:

Механизм состоит из стойки и трех
подвижных звеньев: кулачка 1, толкателя 2 и ролика 3. Ролик введен в схему
механизма для замены трения скольжения на трение качения, с целью уменьшения
интенсивности износа рабочих поверхностей контактирующих звеньев, а также с
целью увеличения КПД и ресурса работы механизма. Ролик образует с выходным
звеном вращательную кинематическую пару пятого класса. Подвижность этой
кинематической пары не изменяет подвижности кулачкового механизма, не влияет на
его передаточную функцию, так как является местной подвижностью.
Звенья 1 и 2 образуют со стойкой
низшие кинематические пары  ;
; 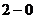 ; кинематическая пара
; кинематическая пара  является
дефектом структуры с местной подвижностью, равной 1, следовательно
является
дефектом структуры с местной подвижностью, равной 1, следовательно 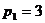 . Кинематическая
пара
. Кинематическая
пара  является
высшей, следовательно
является
высшей, следовательно  .
.
 .
.
При удалении дефекта структуры,
получим:
 ,
,
где  -
подвижность механизма в результате удаления дефектов;
-
подвижность механизма в результате удаления дефектов;
 - подвижность механизма;
- подвижность механизма;
 - местная подвижность.
- местная подвижность.
Следовательно, подвижность равна:
 .
.
.2 Функция аналога пути
Для построения диаграммы зависимости
перемещения от угла поворота кулачка вычислим перемещение:
 , (9.1)
, (9.1)
где  - перемещение,
м;
- перемещение,
м;
 - ход кулачкового механизма, м;
- ход кулачкового механизма, м;
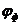 - фазовый угол соответствующей
фазы, рад;
- фазовый угол соответствующей
фазы, рад;
 - текущее значение фазового угла,
рад.
- текущее значение фазового угла,
рад.
Ход механизма с толкателем найдем из
равенства:
 ,
,
где  -
максимальное перемещение толкателя, мм.
-
максимальное перемещение толкателя, мм.
Определим масштабный коэффициент оси
аналога пути:

где h - ход
механизма (максимальное перемещение), м;
 - расстояние, изображающее
максимальное перемещение на диаграмме, мм.
- расстояние, изображающее
максимальное перемещение на диаграмме, мм.
Определим масштабный коэффициент
угла поворота:

где  -
произвольно выбранное расстояние, изображающее один период работы механизма на
диаграмме, мм.
-
произвольно выбранное расстояние, изображающее один период работы механизма на
диаграмме, мм.
Переведем все фазовые углы в
масштабный коэффициент.
Фаза удаления:

Фаза верхнего выстоя:

Фаза сближения:

Фаза нижнего выстоя:

Разобьем фазовые углы удаления и
сближения на шесть частей и посчитаем перемещения для каждого значения фазового
угла.
Для первого положения:

Переведем полученную величину
перемещения в масштабный коэффициент:

Таблица 8 - Значения перемещения
Для построения диаграммы отложим переведенные в
масштабный коэффициент величины перемещений, с учетом того, что в положениях,
соответствующих фазе сближения (7-13), отрезки откладываем в обратном порядке.
.3 Функция аналога скорости
Для построения диаграммы аналога скорости
воспользуемся формулой:
 . (9.2)
. (9.2)
Для первого положения:

Для остальных положений аналогично,
их результаты сводим в таблицу 9.1.
Таблица 9.1 - Значения скоростей
|
Фаза
удаления
|
   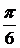   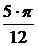 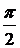 
|
|
|
|
|
|
|
|
|
|
 019,10857,32576,43357,32519,1080 019,10857,32576,43357,32519,1080
|
|
|
|
|
|
|
|
|
|
Фаза
сближения
|
   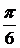   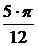 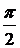 
|
|
|
|
|
|
|
|
|
|
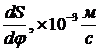 019,10857,32576,43357,32519,1080 019,10857,32576,43357,32519,1080
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассчитаем масштабный коэффициент:
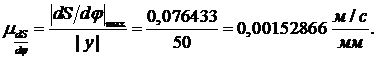
Для построения диаграммы переведем
все полученные значения в масштабный коэффициент. Отложим их на диаграмме, с
учетом того, что график на фазе сближения должен находиться ниже оси угла.
Таблица 9.2 - Значения скоростей,
переведенные в масштабный коэффициент
|
Фаза
удаления
|
   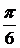   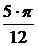 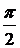 
|
|
|
|
|
|
|
|
|
|
 012,5037,5050,0037,5012,500 012,5037,5050,0037,5012,500
|
|
|
|
|
|
|
|
|
|
Фаза
сближения
|
   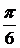   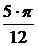 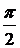 
|
|
|
|
|
|
|
|
|
|
 012,5037,5050,0037,5012,500 012,5037,5050,0037,5012,500
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.4 Функция аналога ускорения
Для построения диаграммы аналога воспользуемся
формулой:
 (9.3)
(9.3)
Для первого положения:

Для остальных положений вычисления
проводятся аналогично. Результаты сводим в таблицу 10.1.
Таблица 10.1 - Значения ускорений
Рассчитаем масштабный коэффициент:

Для построения диаграммы переведем
все полученные значения ускорений в масштабный коэффициент оси аналога
ускорения. Отложим рассчитанные отрезки на диаграмме. В положениях фазы
сближения график изображаем симметрично относительно оси угла.
Таблица 10.2 - Значения ускорений,
переведенные в масштабный коэффициент
.5 Определение радиуса исходного контура.
Построение диаграммы угла давления
Радиус определим из построенного треугольника, в
котором один из катетов будет искомым радиусом.
Отложим отрезок длиной равной длине толкателя
(60 мм) на оси перемещения S.
Отложим по отрезку, расстояния равные перемещениям. Возьмем значения в
миллиметрах с диаграммы скорости и отложим в соответствующих положениях (для
фазы удаления в положительную, для фазы сближения в отрицательную сторону
относительно оси S). Соединим
все найденные точки плавной кривой и получим диаграмму для определения радиуса
исходного контура кулачка.
Через третью и десятую точку
диаграммы проводим прямую и строим перпендикуляр к этой прямой. Проведем две
касательные к диаграмме, построенные под предельным углом давления  от
перпендикуляра в обе стороны. Таким образом мы получили область допустимых
решений.
от
перпендикуляра в обе стороны. Таким образом мы получили область допустимых
решений.
От оси перемещения S отложим в
обе стороны значения величины эксцентриситета, преобразованной с учетом
масштабного коэффициента. В результате получим две точки  и
и  в
пересечениях с касательными прямыми к исходному контуру, которые в пересечении
между собой дают точку
в
пересечениях с касательными прямыми к исходному контуру, которые в пересечении
между собой дают точку  . Соединив
образованные точки
. Соединив
образованные точки  ,
,  и
и  с началом
координат, получим радиус
с началом
координат, получим радиус  ,
,  и
и  , из которых
радиусом исходного контура
, из которых
радиусом исходного контура  является
является  , т.к.
эксцентриситет на кинематической схеме отложен вправо.
, т.к.
эксцентриситет на кинематической схеме отложен вправо.
К характерным точкам диаграммы для
определения радиуса исходного контура кулачка (1…14) проведем из точки  прямые. От
характерных точек отложим перпендикуляры и, замеряя углы, откладываем их на
диаграмме углов давления в масштабном коэффициенте угла давления:
прямые. От
характерных точек отложим перпендикуляры и, замеряя углы, откладываем их на
диаграмме углов давления в масштабном коэффициенте угла давления:

Таблица 11 - значения углов давления
|
№
|
0,
13, 14
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
 , град5,2113,2326,193022,699,553,13,12,9316,2723,8218,954,1 , град5,2113,2326,193022,699,553,13,12,9316,2723,8218,954,1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9.6 Синтез профиля кулачка
Определим масштабный коэффициент
длин 

На свободном месте выберем
произвольную точку О, являющуюся центром исходного контура кулачка. Из
выбранной точки О в масштабном коэффициенте длин проведем концентрические
окружности с радиусами R0 и е. К
окружности радиусом е проводим касательную до пересечения с окружностью R0, полученная
точка пересечения является началом отсчета оси пути S. От начала
отсчета на окружности радиусом R0 в
направлении вращения кривошипа откладываем фазовые углы, а на оси пути в
масштабном коэффициенте  -
перемещения толкателя. Дуги исходного контура, соответствующие фазовым углам
удаления и сближения, делим на равные части, количество которых равно числу
точек, входящих в состав фаз удаления и сближения. Полученные точки соединяем с
точкой О, являющейся центром вращения кулачка. Из каждой точки деления проводим
касательные к окружности радиусом е. Из точки О, являющейся центром окружности
радиусом R0, проводим
окружности радиусами, равными сумме R0 и
соответствующего перемещения толкателя до пересечения с касательными к
окружности радиусом е. Полученные точки соединяем плавной кривой, образуя
теоретический профиль кулачка, совпадающий на данном этапе с рабочим профилем.
-
перемещения толкателя. Дуги исходного контура, соответствующие фазовым углам
удаления и сближения, делим на равные части, количество которых равно числу
точек, входящих в состав фаз удаления и сближения. Полученные точки соединяем с
точкой О, являющейся центром вращения кулачка. Из каждой точки деления проводим
касательные к окружности радиусом е. Из точки О, являющейся центром окружности
радиусом R0, проводим
окружности радиусами, равными сумме R0 и
соответствующего перемещения толкателя до пересечения с касательными к
окружности радиусом е. Полученные точки соединяем плавной кривой, образуя
теоретический профиль кулачка, совпадающий на данном этапе с рабочим профилем.
Исходя из заданных условий
определяется радиус ролика грол. Из произвольно выбранных точек
теоретического профиля кулачка проводим радиусами  окружности,
имитирующие положения ролика в составе схемы кулачкового механизма. Проведя
огибающую кривую относительно всех положений ролика, получаем рабочий профиль
кулачка.
окружности,
имитирующие положения ролика в составе схемы кулачкового механизма. Проведя
огибающую кривую относительно всех положений ролика, получаем рабочий профиль
кулачка.
Радиус ролика найдем из выражения:

где  - начальный
радиус, мм.
- начальный
радиус, мм.
Радиус ролика должен быть целым
числом, укладывающимся в значения стандартного ряда натуральных чисел в
следующем диапазоне:
 .
.
Выберем стандартное целое значение
из полученного ряда. Возьмем:

Список используемой литературы
1. Теория
механизмов и машин / И.И. Артоболевский. - М.: Наука., 1988. - 640с.
2. Динамическое
исследование машинного агрегата / Д.М. Мехонцева. - Красноярск.: Издательство
Красноярского университета., 1986. - 240с.
.
Теория механизмов и машин. Версия 1.0 [Электронный ресурс] : электрон. учеб.
пособие / П. Н. Сильченко, М. А. Мерко, М. В. Меснянкин и др. - Красноярск :
ИПК СФУ, 2008. - Электрон. дан. (3 Мб).