Сложное напряженное состояние

Сложное напряженное состояние

Контрольная работа

Сложное напряженное состояние

Содержание

Введение

. Критерии пластичности

1.1 Гипотеза наибольших касательных напряжений

.2 Гипотеза энергии формоизменения

.3 Теория Мора

2. Примеры определения эквивалентных напряжений и коэффициентов запаса

. Тонкостенные оболочки

3.1 Тонкостенные оболочки, находящиеся под действием постоянного давления

.2 Тонкостенные оболочки, находящиеся под действием гидростатического давления

Список литературы

ВВЕДЕНИЕ

При расчете на прочность элементов конструкций необходимо знать допустимость того или иного состояния материала в отдельных их точках, называемых опасными.

Материал конструкции в зависимости от условий нагружения может находиться в различных механических состояниях. При небольших внешних силах возникают только упругие деформации, или, как говорят, материал находится в упругом состоянии. При больших силах обнаруживаются заметные остаточные деформации и материал находится в пластическом состоянии. При дальнейшем увеличении нагрузки происходит образование местных трещин и наступает состояние разрушения.

Механическое состояние материала в точке зависит в первую очередь от напряженного состояния в этой точке, хотя и не определяется им полностью. Задача заключается в том, чтобы установить меру напряженного состояния, по достижении которой происходит переход от упругого состояния к пластическому, и условий, при которых начинается разрушение, т. е. выработать критерий пластичности и критерий разрушения.

Более разработанными, определенными и сравнительно более простыми являются критерии пластичности.

При одноосном растяжении пластичного материала условием перехода из упругого состояния в пластическое является равенствоs=syt.

При таком подходе для каждого случая сложного напряженного состояния материала (с произвольным соотношением s1;s2 и s3) необходимо провести свои испытания для определения переходной точки. Такой подход требует огромного количества испытаний и технически сложен в проведении этих испытаний. Но, если увеличивать пропорционально все компоненты напряженного состояния, т. е. изменять его подобным образом, то состояние материала изменится: либо возникнут пластические деформации, либо начнется разрушение. (Число, показывающее, во сколько раз следует увеличить все компоненты напряженного состояния, чтобы изменилось механическое состояние материала, называется коэффициентом запаса при сложном напряженном состоянии.) Таким образом, как при простом, так и при сложном напряженных состояниях можно достигнуть состояния равноопасности. Если теперь уменьшить эти напряжения в одинаковое число раз, то равноопасность сохранится.

Если в двух напряженных состояниях коэффициенты запаса равны, то такие напряженные состояния называются равноопасными.

Для заданного материала сравнение напряженных состояний можно производить не по коэффициенту запаса, а по числовой характеристике какого-либо одного напряженного состояния, выбираемого в качестве эталона .За такой эталон (эквивалент) удобнее всего принять напряжение обычного растяжения.

Эквивалентное напряжение  - это такое напряжение, которое следует создать в растянутом образце, чтобы его напряженное состояние было равноопасно с заданным сложным напряженным состоянием.

1. КРИТЕРИИ ПЛАСТИЧНОСТИ

При определении критерия пластичности необходимо решить, какое из напряжений или какая их комбинация в сложном напряженном состоянии определяет переход материала к пластическому состоянию, которое далее будем называть предельным. Из существующих гипотез предельного состояния в настоящее время в технических расчетах используются три.

.1 Гипотеза наибольших касательных напряжений

Два напряженных состояния равноопасны, если наибольшие касательные напряжения в них равны.

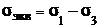
Экспериментальная проверка показала, что для пластичных материалов эта гипотеза дает удовлетворительные результаты.

.2 Гипотеза энергии формоизменения

Два напряженных состояния равноопасны, если их потенциальные энергии изменения формы равны.

Сложное напряженное состояние

Одноосное растяжение

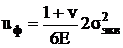
Применима для пластичных материалов.

.3 Теория Мора

Теория Мора основана на построении кругов Мора и не учитывает влияние 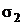. Как показывают экспериментальные данные, погрешность не превышает 15%. Однако, это единственная гипотеза, учитывающая, что предел текучести при растяжении  далеко не всегда равен пределу текучести при сжатии  и позволяющая оценивать прочность хрупких материалов.

sэкв=sks3, где

для пластичных и малопластичных материалов и

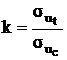для хрупких материалов.

2. ПРИМЕРЫ ОПРЕДЕЛЕНИЯ ЭКВИВАЛЕНТНЫХ НАПРЯЖЕНИЙ И КОЭФФИЦИЕНТОВ ЗАПАСА

Пример 1. Сопоставить напряженные состояния и найти наименьший коэффициент запаса.

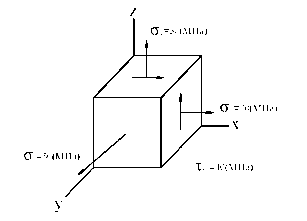
Рассмотрим первый случай напряженного состояния.

Главные напряжения определяем с помощью уравнения, записанного в инвариантной форме.

,

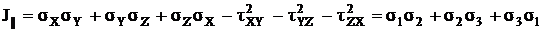
Для решения кубического уравнения используем подстановку:

 , тогда

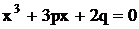
 и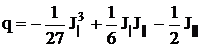

Все три корня кубического уравнения действительные числа, если дискриминант 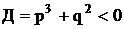. Для реальных напряженных состояний Д всегда меньше 0, т.к. главные напряжения могут быть только действительными величинами. В этом случае

;

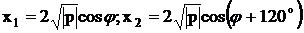|p| - абсолютное значение коэффициента p, а

Определяем инварианты напряженного состояния.

Находим коэффициенты p и q

Окончательно получаем:

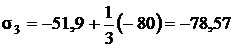
Так как , для определения эквивалентных напряжений используем теорию Мора:

 ;

Соответственно коэффициент запаса будет равен:

Рассмотрим второй случай напряженного состояния.

Площадка, пересекающая ось y, является главной, соответственно (МПа) - главное напряжение.

Определим два других главных напряжения:

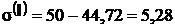
Получаем:  ;  ;

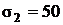
Так как пределы текучести при растяжении равны, можно использовать как гипотезу наибольших касательных напряжений,, так и гипотезу формоизменения.

По гипотезе наибольших касательных напряжений:

По гипотезе формоизменения:

Соответственно коэффициенты запаса равны

и

и имеет один порядок.

На основании выполненных расчетов можно сказать, что первое напряженное состояние более опасно.

Пример 2.

В поперечном сечении бруска возникают следующие внутренние силовые факторы: изгибающий момент в вертикальной плоскости ; изгибающий момент в горизонтальной плоскости ; крутящий момент . Сечение может быть выполнено в виде круга, прямоугольника ; квадрата или трубчатого профиля .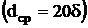

Найти наиболее рациональный вариант сечения, если F=500 н; l=20 см; 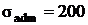 МПа.

Рассмотрим первый вариант сечения - круг диаметром d.

Опасная точка рассматриваемого сечения - точка 1 - лежит в плоскости действия суммарного момента. Изгиб происходит вокруг оси, перпендикулярной этой плоскости и проходящей через центр тяжести сечения.

; .

 ;  ;

Подставляя значения, получаем:

Касательные напряжения, возникающие от действия крутящего момента T, достигают в точке 1 максимального значения:

 ;

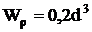
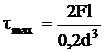
Выделим в окрестностях точки 1 элемент и проанализируем его напряженное состояние.

Одна из площадок рассматриваемого элемента свободна от действия касательных напряжений, следовательно, является главной. Нормальные напряжения на ней также отсутствует, что характерно для плоского напряженного состояния. По другой площадке действуют только касательные напряжения; на третьей площадке имеют место и нормальные, и касательные напряжения. Такое распределение напряжений характерно для плоского напряженного состояния.

Так как по условиям задачи механические характеристики материала не оговорены, можно воспользоваться гипотезой наибольших касательных напряжений.

 (мм)

Минимально необходимый диаметр бруса составляет 23 мм.

Рассмотрим второй вариант сечения - прямоугольное.

Из эпюр распределения напряжений видно, что наиболее опасными являются точки 1, 2 и 3.

Изгибающий момент  вызывает в точках 1 и 2 напряжения

 ,

Изгибающий момент  вызывает в точках 1 и 3 напряжения

 ,

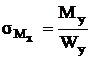Крутящий момент T вызывает максимальные касательные напряжения посередине широкой грани (точка 3)

,

где 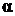 зависит от отношения 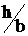. При 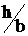=2 a=0,246

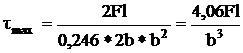
Напряжение посeредине узкой грани (точка 2) будет меньше t=htmax (hзависит от 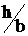 и равно 0,795 )

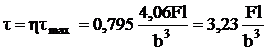
Выделим в окрестностях точек 1, 2 и 3 элементы и исследуем их напряженное состояние.

Точка1                          Точка2                         Точка3

Напряженное состояние в точке 1 является линейным.

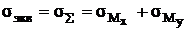
Напряженное состояние в точках 2 и 3 - плоское.

Точка 2.

Точка 3

Таким образом, наиболее опасной является точка 3.

Из условия  определяем размеры поперечного сечения.

 (мм)

 (мм)

Рассмотрим третий вариант сечения - квадрат.

Для квадрата

,

где a - сторона квадрата.

Характер распределения напряжений по сечению аналогичен предыдущему случаю, но т.к.

 , то

Касательные напряжения посередине всех четырех сторон одинаковы

(при 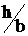=1 a=0,208

Точки 1, 2, и 3 расположены аналогично предыдущему случаю. Т.к. напряженные состояния в точках 2 и 3 полностью совпадают, ограничимся рассмотрением точек 1 и 2.

Точка 1

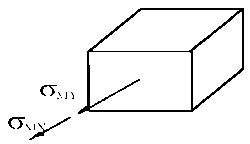
точка 2

Точка 2 находится в более опасном состоянии.

Рассмотрим четвертый вариант сечения - тонкостенную трубу.

Трубчатое сечение, как и круглое рассчитывается на изгиб от действия равнодействующего момента.

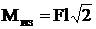
Касательные напряжения считаются равномерно распределенными по толщине стенки.

,

где ;

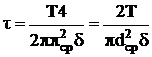, выполняя подстановку получаем:

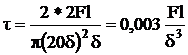
Нормальные напряжения

Рассмотрим напряженное состояние в точке 1.

Точка 1

Определяем толщину стенки

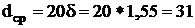 (мм)

Сопоставим полученные результаты. Наиболее рациональным будет брус наименьшего веса.

Вес  , где

 - плотность, A - площадь поперечного сечения, L - длина, g - ускорение свободного падения.

Будем все сравнивать с брусом круглого поперечного сечения.

Круглое сечение:

(Н)

Прямоугольное сечение:

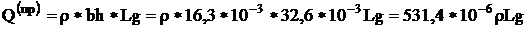 (Н)

Квадратное сечение:

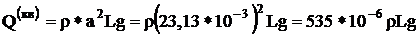 (Н)

Трубчатое сечение:

 (Н)

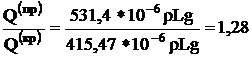
Таким образом, наиболее рациональным является трубчатое сечение.

3. ТОНКОСТЕННЫЕ ОБОЛОЧКИ

.1 Тонкостенные оболочки, находящиеся под действием постоянного давления

Особенностью расчета тонкостенных оболочек по безмоментной теории является основное допущение о том, что напряжение по толщине оболочки считается постоянным, а напряженное состояние - плоским. Расчет ведется по срединной поверхности. Исключением является случай, когда оболочка находится под действием внешнего и внутреннего давлений.

Пример 1.

Тонкостенная оболочка со сферическими днищами (D=80мм; δ=4мм.) находится под действием внутреннего давления Р=5Мпа; продольной нагрузки F=15,7кн и скручивающих моментов Т=2 кнм Оболочка изготовлена из стали 40ХН, имеющей предел текучести при растяжении , а предел текучести при сжатии . Определить коэффициент запаса. Расчет выполнить для участка достаточно удаленного от днищ. Задачу решаем, используя принцип независимости действия сил. Сложное нагружение оболочки можно разложить на три простых:

а) - оболочка находится только под действием внутреннего давления; б) - оболочка растягивается;

в) - оболочка скручивается.

а). Для определения напряжений возникающих от действия давления, используем уравнение Лапласа и уравнение равновесия.

Под действием давления Р оболочка растягивается в продольном и окружном направлениях. Соответственно в ней возникают напряжения: -меридиональное напряжение (возникает в продольном направлении) и 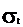-окружное напряжение (действует в окружном направлении).

Уравнение Лапласа 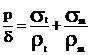содержит два неизвестных 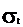 и  (-радиус в окружном направлении, - радиус в меридиональном направлении).

В нашем случае, для сечений достаточно удаленных от днищ  (стенки сосуда параллельны друг другу).

.

Для определения меридиональных напряжений составим уравнение равновесия

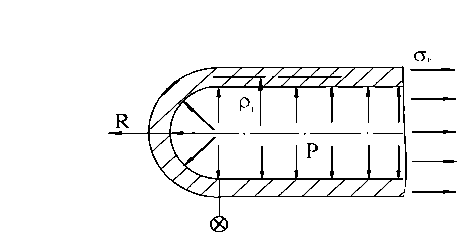
Согласно теореме о равнодействующей давления, проекция равнодействующей давления на какую-либо ось всегда равна произведению давления на площадь проекции поверхности, воспринимающей давление на плоскость, нормальную к этой оси:

.

Это усилие вызывает в поперечном сечении оболочки (  ) напряжения .

Б). Продольная сила F действует на оболочку аналогично равнодействующей R, вызывая напряжения в продольном направлении.

N -продольная растягивающая сила , равная F.

Напряженное состояние во всех точках поперечного сечения одинаково.). Скручивающий момент Т вызывает в поперечном сечении касательные напряжения τ

W_t-момент сопротивления при кручении тонкостенного круглого профиля уже был рассмотрен ранее (  ).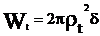

Напряженное состояние во всех точках поперечного сечения одинаково.

Рассмотрим суммарное воздействие этих сил.

Напряженное состояние стенки оболочки является плоским.

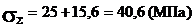
Так как материал имеет разные пределы текучести при растяжении и сжатии, используем теорию Мора:

sэкв=sks3

Главные напряжения s и s3 находим аналитически:

Коэффициент запаса равен:.

Для сосудов, находящихся под давлением, рекомендуемый коэффициент запаса составляет(5…15).

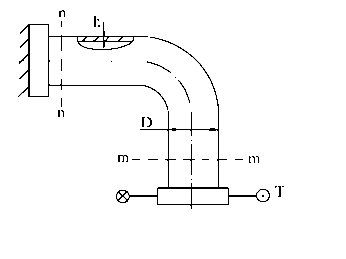
Пример 2.

Тонкостенная трубка находится под действием давления Р. На ее конус приложен крутящий момент T=РD³.

В какой точке сечений m-m и n-n напряженное состояние будет наиболее опасным, если .

Рассмотрим сечение m-m. Все точки этого сечения находятся в одинаковом напряженном состоянии, испытывая нормальные напряжения (меридиональные и окружные) от давления Р и касательные напряжения от действия крутящего момента T.

Определяем главные напряжения:

Рассмотрим сечение n-n.

Меридиональные и окружные напряжения в этом сечении такие же, как и в предыдущем случае.

Крутящий момент T для сечения n-n превращается в изгибающий момент.

В точке 1 должны возникнуть напряжения растяжения, а в точке 2 -сжатия.

Точка 1.

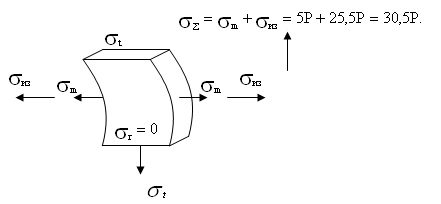
Напряженное состояние является плоским.

Точка 2.

Напряженное состояние является плоским :

Таким образом, наиболее опасным является сечение n-n.

Пример 3. Исследовать напряженное состояние тонкостенной трубки и определить коэффициент запаса n_т. Расчет выполнить для сечения, достаточно удаленное от концов трубки. Материал - сталь 50.

Для определения меридиональных напряжений составим условие равновесия (учитываем только усилия, проецирующиеся на продольную ось z).

Для определения окружных напряжений вырежем участок длиной L в средней части трубки.

В данном случае учитываем радиальные напряжения.

Точка на наружной           Точка на внутренней поверхности.

Во втором случае по модулю больше, чем в первом, поэтому во втором случае будет выше.

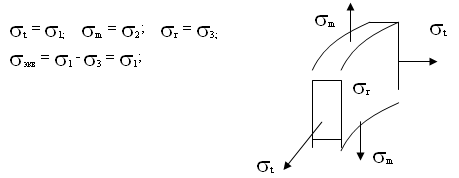
Пример 4. Конический резервуар с постоянным внутренним давлением и постоянной толщиной стенки.

«Меридианом» здесь является прямая, и поэтому р_m=∞. Располагая начало координат в вершине конуса, легко найдем второй главный радиус кривизны поверхности конуса.

Наибольшее значение напряжения st будет z=h т.е. у основания конуса.

Меридиональное напряжение найдется из уравнения

Радиальное напряжение принимаем равным 0.

.2 Тонкостенные оболочки, находящиеся под действием гидростатического давления

Основная теорема.

Если на кривую поверхность действует давление жидкости, то вертикальная составляющая полной силы давления равна весу жидкости в объеме, ограниченном рассматриваемой поверхностью, вертикальные образующие которой проходят через границы рассматриваемой поверхности.

Пример 1. Подобрать толщину стенки резервуара, наполненного жидкостью, удельный вес которой . Размеры резервуара Допускаемое напряжение .

Рассмотрим три участка. Первый участок (рис. а ,б) 0<Z1<(3/2)d: Давление 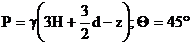, радиусы .

Второй участок (рис. в):

Третий участок (рис. г)

На всех участках радиус кривизны 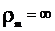, поэтому окружное напряжение  можно определить сразу из уравнения Лапласа по формуле

Первый участок

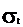Из условия  определяется координата Z^*, при которой напряжение  принимает экстремальное значение

 поэтому в интервале  окружное напряжение 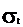 не может принимать экстремальное значение, и наибольшее напряжение будет возникать при

.

Для определения меридионального напряжения на первом участке коническая поверхность резервуара рассекается коническим нормальным сечением на расстоянии Z от вершины конуса. Вертикальная составляющая сил давления жидкости равна весу жидкости, заключенной в объеме АБВГД. Для части оболочки, изображенной на рисунке (а), уравнение равновесия записывается следующим образом:

,

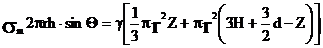Осевая составляющая сил давления жидкости могла быть определена иначе. Она складывается из веса жидкости в отсеченной части и силы давления выше расположенных слоев жидкости (рис.б).

.

Координата , определенная из условия , больше  и находится вне первого участка. Наибольшее напряжение  возникает в точках, определяемых координатой ,

.

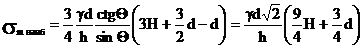Второй участок .

Окруженное напряжение 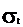, имеет вид

.

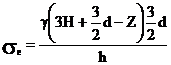при .

Меридиональное напряжение  определяется из условия равновесия отсеченной части оболочки. Вертикальная составляющая сил давления складывается из веса жидкости в отсеченной части и силы давления выше расположенных слоев жидкости:

,

.

Величина меридионального напряжения  не зависит от координаты Z.

Третий участок. Окружное напряжение .

Для определения меридионального напряжения  рассматривается равновесие отсеченной части резервуара. Вертикальная составляющая сил давления равна весу всей жидкости, помещенной в сосуде,

,

.

Согласно выражениям , полученным ранее строятся эпюры напряжений .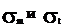

Наибольшие напряжения возникают в точках первого участка при . Так как напряжения  одного знака, то для точек срединной поверхности имеем:

.

Эквивалентное напряжение по гипотезе наибольших касательных напряжений .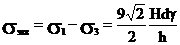

Толщина оболочки определяется из условия прочности

.

В этом случае

.

Пример 2. Расчет провесного днища и скрепляющего кольца.

На рисунке изображен открытый цилиндрический резервуар для хранения жидкости. Сферическое дно резервуара скрепляется с цилиндрическим корпусом с помощью специального элемента - кольца из размалкованного уголка (уголок, полки которого деформированы так, что внутренний угол между ними больше 90^○). Удельный вес жидкости -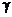. Общий вес жидкости -Q, прочие данные указаны на рисунке. В точке А в центре днища по симметрии

.

Давление жидкости здесь равно

.

.

пластичность напряжение формоизменение гидростатический

Здесь  - толщина стенок.

В точке В . Меридиональное напряжение  найдем из условия равновесия днища.

Окружное напряжение 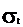 теперь можно найти из уравнения Лапласа, учитывая, что на уровне точки В давление жидкости равно .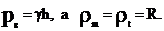

Отсюда

.

Угол  и основные размеры резервуара связаны очевидным уравнением .

Опасной точкой при постоянной толщине днища является точка А.

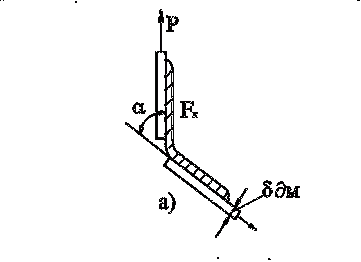
Соединительное кольцо (см. рис.) подвергается действию равномерно распределенного по вертикальной полке погонного усилия и по наклонной полке действию равномерного погонного усилия

.

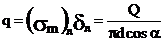Радиальная составляющая этого усилия 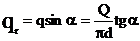 вызывает сжатие скрепляющего кольца по уравнению

.

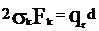
Отсюда получается формула проверки скрепляющего кольца на сжатие (наиболее опасное действие сил на кольцо)

Список литературы

1. Филин А.П. Прикладная механика твердого деформируемого тела.- М.: Машиностроение,2005.-832 с.

2. Требушко О.И. Основы теории упругости и пластичности.- .:Наука, 2004. -319 с.

3. Писаренко Г.С. и др. Справочник по сопротивлению материалов.- Киев.: Наук.думка, 2005.- 704 с. .

4. Тайтур Г.К. Курс сопротивления материалов.- Минск.: Высш. школа,2004.- 216 с. .

5. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 2006. -512 с.